Наудачу из отрезка 1 2 взяты два числа: Геометрическая вероятность

Геометрическая вероятность

Формула P(A)=m/n теряет смысл, если число всех равновозможных несовместных случаев неограниченo (образует бесконечное множество). Однако возможно иногда всей совокупности бесконечных равновозможных несовместных случаев дать количественную характеристику S в некоторых мерах длины, площади, объема, времени и так далее, а части этой совокупности, благоприятствующей наступлению рассматриваемого события A — характеристику S_б в тех же мерах. Тогда вероятность появления события A определяется соотношением:

Пример №1. Из промежутка [0; 2] наудачу выбраны два числа x и y. Найдите вероятность того, что эти числа удовлетворяют неравенствам x² ≤ 4y ≤ 4x.
Решение. Испытание состоит в случайном выборе из промежутка [0; 2] пары чисел x и y. Будем это интерпретировать как выбор наудачу точки M(x;y) из множества всех точек квадрата, сторона которого равна двум. Рассмотрим фигуру Ф, представляющую собой множество всех точек квадрата, координаты которых удовлетворяют системе неравенств x

2 ≤ 4y ≤ 4x. Интересующее событие происходит тогда и только тогда, когда выбранная точка M(x;y) принадлежит фигуре Ф.

По формуле (8) искомая вероятность равна отношению площади фигуры Ф к площади квадрата:

Пример №2. Двое договорились о встрече в определенном месте. Каждый из них приходит в условленное место независимо друг от друга в случайный момент времени из [0;T] и ожидает не более чем время . Какова вероятность встречи на таких условиях?

Решение. Обозначим через x время прихода первого в условленное место, а через y — время прихода туда второго лица. Из условия вытекает, что x и y независимо друг от друга пробегают промежуток времени [0;T]. Испытание состоит в фиксации времени прихода указанных лиц к месту встречи. Тогда пространство элементарных исходов данного испытания интерпретируется как совокупность всех точек M(x;y) квадрата Ω={(x;y) : 0 ≤ x ≤ T, 0 ≤ y ≤ T}. Интересующее нас событие A — “встреча произошла” наступает в том и только том случае, когда выбранная точка M(x;y) окажется внутри фигуры Ф, представляющей собой множество всех точек квадрата, координаты которых удовлетворяют неравенству |x – y| ≤ t.

По формуле (8) искомая вероятность
представляет собой отношение площади фигуры Ф к площади квадрата Ω:

Анализируя полученный в этой задаче результат, видим, что с возрастанием увеличивается вероятность встречи. Пусть, например, T = 1 час, t = 20 мин, тогда , то есть чаще чем в половине случаев встречи будут происходить, если многократно договариваться на указанных выше условиях.

Пример №3. На отрезке l наугад выбраны две точки.
P(0<k<l) — ? , вероятность того, что расстояние между ними меньше

k-l

Пример №4. В круг радиуса r случайным образом брошена точка так, что любое ее расположение в круге равновозможно. Найти вероятность того, что она окажется внутри находящегося в круге квадрата со стороной a.
Решение. Вероятность того, что точка окажется внутри лежащего в круге квадрата со стороной а будет равна отношению площади квадрат к площади круга.
Площадь квадрата: Sкв = a².
Площадь круга: S = πr²
Тогда вероятность составит: p = Sкв / S = a² / πr²

см. также Площадь треугольника

Пример №5. С промежутке [0, 4] выбирают наугад два действительных числа. Найдите вероятность того, что их сумма будет больше 4, а произведение — меньше 4.
Решение.
Всего чисел 5: 0,1,2,3,4. Вероятность их появления p=1/5 = 0.2

а) вероятность того, что их сумма будет больше 4
Всего количество таких исходов равно 8:
1+4, 2+3, 2+4, 3+4 и 4+1, 3+2, 4+2, 4+3
P = 0.2*0.2*8 = 0.32
б) произведение — меньше 4.
Всего количество таких исходов равно 13:
0*1, 0*2, 0*3, 0*4, 1*1, 1*2,1*3 и 1*0, 2*0, 3*0, 4*0, 2*1, 3*1
P = 0.2*0.2*13 = 0.52

Задачи для самостоятельного решения
4.3. После бури на участке между 40-м и 70-м километрами телефонной линии произошел обрыв провода. Какова вероятность того, что разрыв произошел между 45-м и 50-м километром линии? (Вероятность обрыва провода в любом месте считать одинаковой).
Ответ: 1/6.

4.4. В круг радиуса r наугад брошена точка. Найдите вероятность того, что эта точка окажется внутри вписанного в данный круг правильного треугольника.

Ответ:

4.5. Найдите вероятность того, что сумма двух случайно выбранных чисел из промежутка [-1; 1] больше нуля, а их произведение отрицательно.
Ответ: 0;25.

4.6. Во время боевой учебы н-ская эскадрилья бомбардировщиков получила задание атаковать нефтебазу “противника”. На территории нефтебазы, имеющей форму прямоугольника со сторонами 30 и 50 м, находятся четыре круглых нефтебака диаметром 10 м каждый. Найдите вероятность прямого поражения нефтебаков бомбой, попавшей на территорию нефтебазы, если попадание бомбы в любую точку этой базы равновероятно.
Ответ: π/15.

4.7. Два действительных числа x и y выбираются наудачу так, что сумма их квадратов меньше 100. Какова вероятность, что сумма квадратов этих чисел окажется больше 64?
Ответ: 0;36.

4.8. Двое друзей условились встретиться между 13 и 14 часами. Пришедший первым ждет второго в течение 20 минут, после чего уходит. Определите вероятность встречи друзей, если моменты их прихода в указанном промежутке времени равновозможны.

Ответ: 5/9.

4.9. Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов равновозможно в течение данных суток. Определите вероятность того, что одному из пароходов придется ожидать освобождения причала, если время стоянки первого парохода равно одному часу, а второго — двум часам.
Ответ: ≈ 0;121.

4.10. Наудачу взяты два положительных числа x и y, каждое из которых не превышает двух. Найдите вероятность того, что произведение x · y будет не больше единицы, а частное y/x не больше двух.
Ответ: ≈ 0;38.

4.11. В области G, ограниченной эллипсоидом , наудачу зафиксирована точка. Какова вероятность того, что координаты (x; y; z) этой точки будут удовлетворять неравенству x²+y²

+z²≤4?
Ответ: 1/3.

4.12. В прямоугольник с вершинами R(-2;0), L(-2;9), M (4;9), N (4;0) брошена точка. Найдите вероятность того, что ее координаты будут удовлетворять неравенствам 0 ≤ y ≤ 2x – x²+8.
Ответ: 2/3.

4.13. Область G ограничена окружностью x² + y² = 25, а область g — этой окружностью и параболой 16x — 3y² > 0. Найдите вероятность попадания в область g.
Ответ: ≈ 0;346.

4.14. Наудачу взяты два положительных числа x и y, каждое из которых не превышает единицы. Найдите вероятность того, что сумма x + y не превышает единицы, а произведение x · y не меньше 0,09.
Ответ: ≈ 0;198.

Задание 5

Решить задачу, используя геометрическое определение вероятности.

1. Наудачу выбираются два действительных числа x и y, причем 0  x  N, 0yN. Найти вероятность того, что y

   2  x.

2. Найти вероятность того, что корни уравнения , где коэффициенты p и q выбраны наудачу в квадрате , окажутся действительными.

3. Найти вероятность того, что корни уравнения , где коэффициенты p и q выбраны наудачу в квадрате , окажутся мнимыми.

4. Найти вероятность того, что корни уравнения , где коэффициенты p и q выбраны наудачу в квадрате , окажутся положительными.

5. Два действительных числа x и y выбираются наудачу так, что . Какова вероятность того, что дробь окажется положительной?

6. Два действительных числа x и y выбираются наудачу так, что . Какова вероятность того, что ?

7. Два действительных числа x и y выбираются наудачу так, что . Какова вероятность того, что x

   2 < y?

8. В квадрат с вершинами в точках (0, 0), (0, N + 2), (N + 2, 0), (N + 2, N + 2) наудачу брошена точка. Какова вероятность того, что ее координаты x и y будут удовлетворять неравенству y < 2x + 1?

9. В квадрат с вершинами в точках (0, 0), (0, N + 2), (N + 2, 0), (N + 2, N + 2) наудачу брошена точка. Какова вероятность того, что ее координаты x и y будут удовлетворять неравенству y > 2x + 1?

10. В треугольник с вершинами в точках (0, 0), (0, N + 2), (N + 2, 0) наудачу брошена точка. Какова вероятность того, что ее координаты x и y будут удовлетворять неравенству y < x + 2?

11. В треугольник с вершинами в точках (0, 0), (0, N + 2), (N + 2, 0) наудачу брошена точка. Какова вероятность того, что ее координаты x и y будут удовлетворять неравенству y < x + 1?

12. Наудачу выбираются два действительных числа x и y, причем 0  x  N, 0yN. Найти вероятность того, что y²  x.

13. В прямоугольник с вершинами в точках (0, 0), (0, N + 2), (2(N + 2), 0), (2(N + 2), N + 2) наудачу брошена точка. Какова вероятность того, что ее координаты x и y будут удовлетворять неравенству y < x + 2?

14. В прямоугольник с вершинами в точках (0, 0), (0, N + 2), (2(N + 2), 0), (2(N + 2), N + 2) наудачу брошена точка. Какова вероятность того, что ее координаты x и y будут удовлетворять неравенству y > x + 1?

15. Парабола y = ax² + bx + c касается нижней стороны квадрата с вершинами в точках (0, 0), (0, N + 1), (N + 1, N + 1), (N + 1, 0) и проходит через верхние его вершины. Какова вероятность того, что точка, наудачу брошенная в квадрат, попадет в область, заключенную между верхней стороной квадрата и параболой?

16. Парабола y = ax² + bx + c касается полукруга и проходит через границы его диаметра d = 2(N + 1). Какова вероятность того, что точка, наудачу брошенная в полукруг, попадет в область, ограниченную дугой полукруга и параболой?

17. Два действительных числа x и y выбираются наудачу так, что . Какова вероятность того, что дробь окажется отрицательной?

18. Два действительных числа x и y выбираются наудачу так, что . Какова вероятность того, что x² > y?

19. В фигуру, ограниченную линиями y = N + 1, y = 0, x = 0, y = x – N наудачу бросается точка. Какова вероятность того, что ее координаты x и y будут удовлетворять неравенству y < 3x + 1?

20. В фигуру, ограниченную линиями y = N + 1, y = 0, x = 0, y = x – N наудачу бросается точка. Какова вероятность того, что ее координаты x и y будут удовлетворять неравенству y > 3x + 1?

21. Парабола y = ax² + bx + c касается нижней стороны квадрата с вершинами в точках (0, 0), (0, N + 1), (N + 1, N + 1), (N + 1, 0) и проходит через верхние его вершины. Какова вероятность того, что точка, наудачу брошенная в квадрат, попадет в область, заключенную между параболой и прямыми y = 0, x = N + 1, x = 0?

22. Парабола y = ax² + bx + c касается полукруга и проходит через границы его диаметра d = 2(N + 1). Какова вероятность того, что точка, наудачу брошенная в полукруг, не попадет в область, ограниченную дугой полукруга и параболой?

23. Из отрезка [-N; N + 1] наудачу взяты два числа. Какова вероятность того, что их сумма больше N, а произведение меньше N?

24. Найти вероятность того, что корни уравнения , где коэффициенты p и q выбраны наудачу в квадрате , окажутся отрицательными.

25. На отрезок длиной N наудачу бросают две точки. Они разбивают отрезок на три меньших отрезка. Какова вероятность того, что из полученных отрезков можно построить треугольник?

26. Наудачу взяты два положительных числа x и y, каждое из которых не превышает N + 1. Найти вероятность того, что xy  1, а .

27. Наудачу взяты два положительных числа x и y, каждое из которых не превышает N. Найти вероятность того, что сумма их не превышает N, если сумма их квадратов больше 0,25.

28. Какова вероятность того, что сумма трех наудачу взятых отрезков, длина каждого из которых не превосходит N, будет больше N?

29. Какова вероятность, не целясь, попасть бесконечно малой пулей в прутья квадратной решетки, если толщина прутьев равна N + 1 мм, а расстояние между их осями равно N + 2 мм?

30. Даны две концентрические окружности радиусов r₁ = N + 2 см, r₂ = N + 4 см. На большей окружности наудачу ставятся две точки A и B. Какова вероятность того, что отрезок АВ не пересечет малую окружность?

31. Наудачу взяты два положительные числа x = 0,1(N + 1), y = 0,2N, каждое из которых не превышает двух. Найти вероятность того, что произведение xy будет больше единицы, а частное не больше двух.

32. Наудачу взяты два положительные числа x, y, каждое из которых не превышает единицы. Найти вероятность того, что сумма x + y не превышает единицы, а произведение xy не меньше 0,01N.

33. На отрезке ОА длины L = N + 12 числовой оси OX наудачу поставлены две точки M(x) и K(y). Найти вероятность того, что длина отрезка MK меньше расстояния от точки O до ближайшей к ней точки. Предполагается, что вероятность попадания точки на отрезке пропорциональна длине отрезка и не зависит от его расположения на числовой оси.

34. На отрезке ОА длины L = N + 10 числовой оси OX наудачу поставлены две точки D(x) и E(y), причем y  x. Найти вероятность того, что длина отрезка DE меньше, чем . Предполагается, что вероятность попадания точки на отрезке пропорциональна длине отрезка и не зависит от его расположения на числовой оси.

35. На отрезке ОА длины L = N + 15 числовой оси OX наудачу поставлены две точки L(x) и N(y). Найти вероятность того, что длина отрезка LN меньше, чем . Предполагается, что вероятность попадания точки на отрезке пропорциональна длине отрезка и не зависит от его расположения на числовой оси.

вероятность — $n$ случайных точек на отрезке, среднее расстояние между двумя последовательными точками

спросил 1 год, 5 месяцев назад

Изменено 1 год, 4 месяца назад

Просмотрено 304 раза

$\begingroup$

Раньше я задавал следующий вопрос из своего учебника по вероятностям: 91 |x-y|\,\text{d}x\,\text{d}y} = {1\over3}$. n dx = \frac{n}{n+1}, $$ и заключить с $$ 1 — \mathbb{E}[\max_i X_i] = \frac{1}{n+1}. $$

$\endgroup$

$\begingroup$

Среднее значение расстояний равно сумме расстояний всех отрезков между последовательными точками, деленной на количество взятых точек. Но поскольку вы рассматриваете расстояния последовательных точек, эти расстояния складываются в расстояние между крайними точками, поэтому это может упростить расчет, так как вам нужно только найти ожидаемое расстояние между первой и последней точками

$\endgroup$

$\begingroup$

Возьмем не конечную прямую, а окружность.

Вместо случайного выбора $n$ точек мы теперь выбираем случайным образом $n+1$ точек по окружности.

По симметрии длины дуг имеют одинаковое распределение, из чего сразу становится ясно, что среднее значение длины дуги между $2$ выбранными последовательно точками равно: $$\frac1{n+1}\times\text{ длина окружности} $$

Но (например) первая выбранная точка может быть впоследствии использована как место, где мы «разрезаем круг», чтобы «изогнуть» его в конечную прямую линию.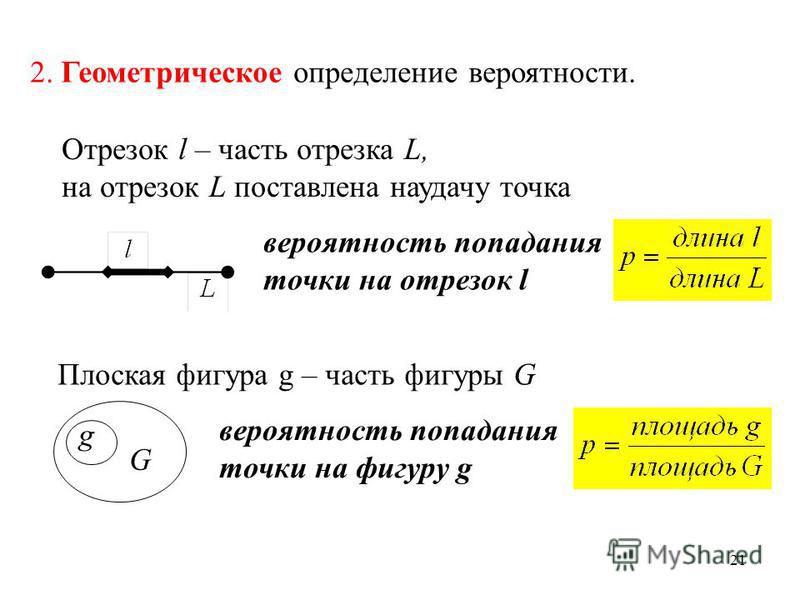

---

В этом смысле выбор $n$ случайных точек на конечной прямой сводится к выбору $n+1$ точек на окружности. Вторая ситуация здесь более красива, поскольку позволяет использовать симметрию.

$\endgroup$

вероятность — Средняя длина самого длинного сегмента

У меня есть другая идея для случая, когда палка разделена на $n$ кусков: пусть $X_{i}$ $1 \leq i \leq n$ будут отметками надрезов, которые являются независимыми случайными величинами, распределенными между $0$ и $1$ и установите $A=max{X_{i}}$. Теперь рассмотрим две части: одну длиной $A$, а другую длиной $1-A$. Затем кусок длины $A$ делится на $n-1$ кусков, а кусок длины $1-A$ остается целым. Если $1-A>A$, то кусок длины $1-A$ будет самым длинным (очевидно). Если $1-A