Название графиков в полярной системе координат: Примеры графиков функций в полярных координатах

5. Графики в полярных координатах

5.1. Полярные координаты

Положение точки в полярных координатах на плоскости (см. рис. 28) определяется:

1) ее расстоянием от некоторой данной точки , называемой полюсом;

2) углом , который образует отрезок с заданным направлением прямой , которая называется полярной осью).

Рис. 28. Точка в полярных координатах.

При этом называют радиусом-вектором и — полярным углом. Если принять полярную ось за , а полюс — за начало координат, то имеем, очевидно (см. рис. 29):

Рис. 29. Точка в полярных координатах.

Данному положению точки соответствует одно определенное положительное значение и бесчисленное множество значений , которые отличаются слагаемым, кратным . Если совпадает с , то и — неопределенно.

Всякая функциональная зависимость вида (явная) или (неявная) имеет в полярной системе координат свой график.

В дальнейшем мы будем рассматривать не только положительные, но и отрицательные значения , причем если некоторому значению соответствует отрицательное значение , то условимся откладывать это значение в направлении, прямо противоположном тому направлению, которое определяется значением .

5.2. Графики кривых в полярных координатах

Для того, чтобы построить график в полярных координатах по точкам нужно заполнить таблицу, в первой строке которой записать значения угла из интересующего промежутка, а во второй — соответствующие значения функции . Затем, отметить и соединить эти точки плавной линией.

Построим графики функций, которые часто бывают заданы в полярных координатах.

Спирали. Пусть , . Рассмотрим три вида спиралей:

• спираль Архимеда: ,

• гиперболическая спираль:

• логарифмическая спираль: .

Спираль Архимеда . График функции имеет вид, изображенный на рис. 30 а), причем пунктир соответствует части кривой при . Отрицательным значениям соответствуют и отрицательные значения , и их надо откладывать в направлении, противоположном тому направлению, которое определяется значением . При этом заполнять таблицу значений и нет необходимости в силу простой функциональной завиимости между и .

Рис. 30. Графики функций , и .

Гиперболическая спираль . Особенностью этого графика (см. рис. 30 б) является то, что расстояние между любой точкой этой кривой и полярной осью не превосходит (т.е. кривая имеет асимптоту, параллельную полярной оси и проведенную на расстоянии от нее).

Предполагая и заполним таблицу для и .

Таблица 4.

Замечаем, что будет увеличиваться при уменьшении . При этом, график не имеет общих точек с прямой, параллельной полярной оси и проходящей на расстоянии от неё. Далее, видим, что не обращается в нуль ни при каких конечных значениях , а только будет уменьшаться с увеличением . Кривая будет поэтому беспредельно приближаться к полюсу , закручиваясь около него, но никогда не пройдет через в противоположность спирали Архимеда.

Отметив и соединив плавной линией точки таблицы 2, а также учитывая поведение функции при увеличении и уменьшении угла получим график функции (см. рис. 30 б).

Логарифмическая спираль . При имеем . Если , то при увеличении увеличивается и . Если , то при уменьшении радиус-вектор приближается к нулю.

Логарифмическая спираль изображена на рис. 30 в.

Розы. Розами, или кривыми Гвидо Гранди, называютя кривые, полярное уравнение которых имеет вид или . Будем рассматривать случай, когда , — целое положительное число.

Заметим, что поскольку правая часть уравнения розы не может превышать , то вся кривая находится внутри круга радиуса .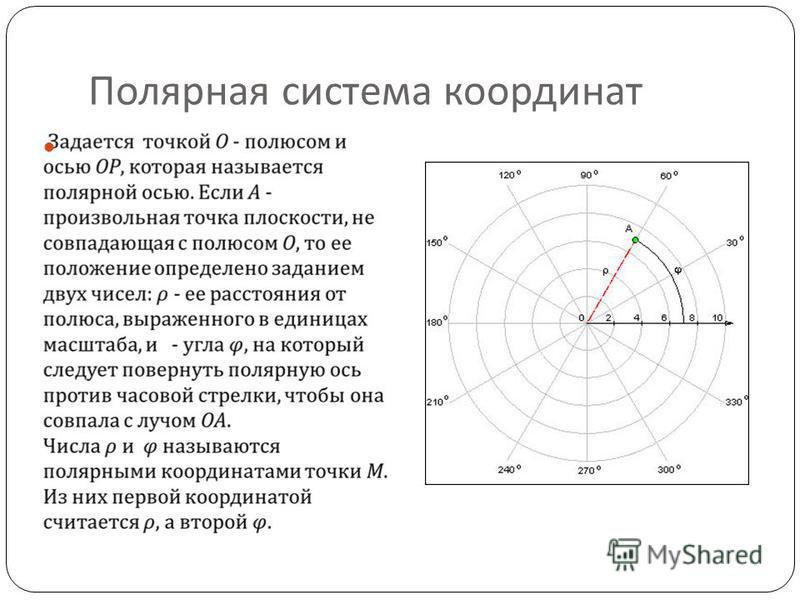 Так как и являются переодическими функциями, то роза состоит из лепетков, симметричных относительно наибольших радиусов, каждый из которых равен . При этом если нечетное число, то число лепестков равно , а если — чётное, то роза имеет лепестков.

Графики функций , , и изображены на рис. 31.

Рис. 31. Графики функций , , и .

Улитка Паскаля и кардиоида. Полярное уравнение улитки имеет вид . Если , то это уравнение дает только положительные значения (см. рис. 32 a)). Если , то будет принимать и отрицательные значения (см. рис. 32 б)). Наконец, при уравнение улитки будет и в этом случае улитка представляет собою

кардиоиду (см. рис. 32 в)).

В качестве примера приведем графики функций , и на рис. 32.

Рис. 32. Графики функций , и .

3 главных вида графиков в Plotly Express: практика Data Science

Автор Роман Котюбеев

Модуль Plotly Express содержит функции для создания разного вида графиков. Сегодня мы расскажем вам, как построить диаграмму рассеяния (scatter) и столбчатую диаграмму (bar chart) в обычном и фасеточном виде, а также рассмотрим аргументы функций Plotly Express, которые повысят интерактивность.

Особенности Plotly Express

Plotly Express (обычно импортиремый как px) является рекомендуемым способом визуализации данных и, в отличии от создания графических объектов напрямую (о чем мы говорили здесь), занимает несколько строчек кода.

В Plotly Express есть 30 функций для создания фигур. Для большинства Data Science проектов их достаточно. Причём API для этих функций очень простой, достаточно разобраться с их аргументами, которые для каждого типа фигуры могут отличаться.

Plotly Express содержит функции для построения:

• Базовые графики: scatter, line, area, bar, funnel, timeline
• Части целого: pie, sunburst, treemap, funnel_area
• 1D распределения: histogram, box, violin, strip
• 2D распределения: density_heatmap, density_contour
• С матричным входом: imshow
• 3D-графики: scatter_3d, line_3d
• Многомерные: scatter_matrix, parallel_coordinates, parallel_categories
• Тайловые карты: scatter_mapbox, line_mapbox, choropleth_mapbox, density_mapbox
• Контурные карты: scatter_geo, line_geo, choropleth
• Графики в полярной системе координат: scatter_polar, line_polar, bar_polar
• Тернарные диаграммы: scatter_ternary, line_ternary

Диаграмма рассеяния

Plotly Express может работать с данными Pandas, т.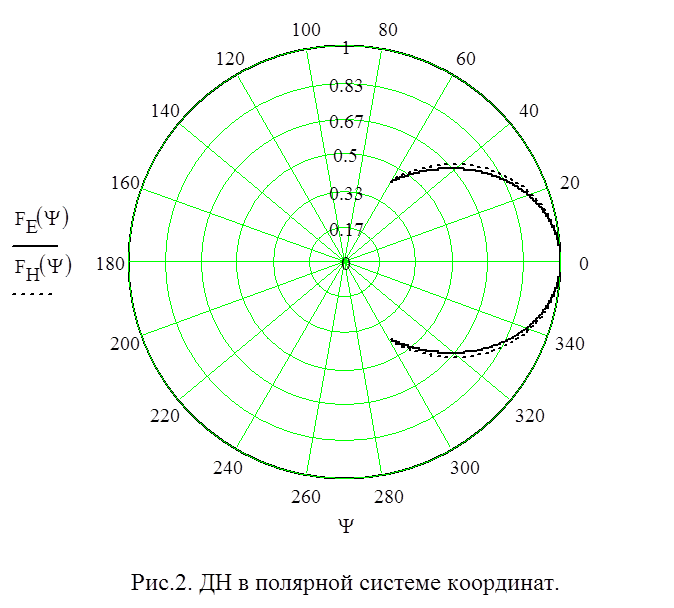 е. с данными в формате DataFrame. В Plotly есть также модуль data, который предоставляет разные наборы данных, т.н, там есть датасет с ирисом (растение). Мы можем посмотреть зависимость между шириной и длиной чашелистика для разных видов ириса. Следующий код на Python демонстрирует построение диаграммы рассеяния:

import plotly.express as px
df = px.data.iris()
fig = px.scatter(df, x="sepal_width", y="sepal_length", color="species")
fig.show()

Диаграмма рассеяния

Более того, мы можем указать размер точек в зависимости от атрибута. Вот так выглядит Python-код, где размер точек определяется длиной лепестка:

fig = px.scatter(df, x="sepal_width", y="sepal_length", 
                 color="species", size="petal_length",)

Диаграмма рассеяния с указанным размером точек

Уже по такой простому графику можно понять, что ирис вида virginica имеет большую длину лепестка и чашелистика, чем остальные.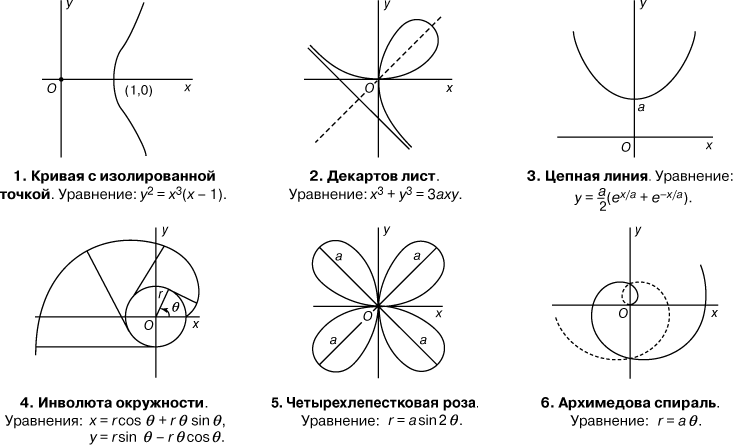

Столбчатая диаграмма

В Plotly есть датасет с демографическими показателями. Построим столбчатую диаграмму, которая будет показывать популяцию Канады в разные периоды. В функциях Plotly Express есть аргумент labels, в котором можно указать отображаемое на графике название атрибута. Это будет полезно в нашем случае, поскольку атрибут pop на графике будет малоинформативен. Вот так выглядит Python-код:

data = px.data.gapminder()

data_canada = data[data.country == 'Canada']
fig = px.bar(data_canada, x='year', y='pop')
fig.show()

Столбчатая диаграмма

Ещё одним полезным аргументом функций Plotly Express является hover_data, который необходим для отображения указанных значений атрибутов при наведении на один из столбцов. Также укажем цвет (color) для обозначения продолжительности жизни.

fig = px.bar(data_canada, x='year', y='pop',
             hover_data=['lifeExp', 'gdpPercap'], color='lifeExp',
             labels={'pop':'population of Canada'},)

Информативная столбчатая диаграмма

При наведении на один столбцов будет отображено дополнительно значение lifeExp (продолжительность жизни) и gdpPercap (ВВП на душу). А также по цвету можно определить, какая продолжительность жизни была в разные периоды.

Фасеточное отображение

Полезным инструментом является фасеточное построение, когда графики, разделенные по значению атрибута, отображаются в виде таблицы.

Для этого в аргументах функции Plotly Express указываются facet_row и/или facet_col. Они принимают название атрибута, по которому проводить разделение. Вдобавок к ним можно указать category_orders, который расположит графики в заданном порядке. Следующий код на Python это демонстрирует:

df = px.data.tips()
fig = px.bar(df, x="sex", y="total_bill", 
             color="smoker", barmode="group", 
             facet_row="time", facet_col="day",
             category_orders={"day": ["Thur", "Fri", "Sat", "Sun"], 
                              "time": ["Lunch", "Dinner"]})

Фасеточное отображение столбчатой диаграммы

Кроме того, мы указали barmode="group", который сгруппирует атрибут указанный в x, т.

е. «под капотом» выполнит метод groupby библиотеки Pandas.

 

 

Еще больше о визуализации данных в Plotly реальных примерах Data Science, вы узнаете на специализированном курсе «VIP: Визуализация данных на языке Python» в лицензированном учебном центре обучения и повышения квалификации IT-специалистов в Москве.

Смотреть расписание

Записаться на курс

Источники

1. https://plotly.com/python/

Как читать полярный график? — PlotDigitizer

Обновлено 1 год назад • 5 мин чтения

Полярные графики — это двумерная система координат, обычно используемая в навигации и изучении величин по направлениям. Как и в декартовой системе, полярная координата имеет две переменные (радиус и тета), однозначно определяющие точку.

Понимание полярных координат

Полярная система координат состоит из двух параметров: радиуса и тета. Радиус (r) — это расстояние между началом координат и точкой на полярном графике.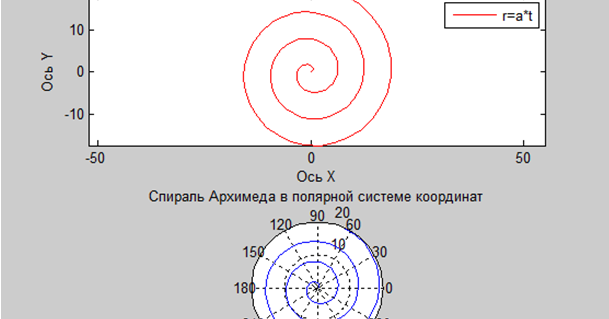 Это ненаправленный параметр; это означает, что у него нет направления. Тета (θ), или более известная как угол, определяет угловое положение точки относительно базовой линии. В отличие от радиуса, тета направлена.

В декартовой системе координат мы определяем положение точки с помощью x и y, которые являются перпендикулярными расстояниями от обеих осей, тогда как в полярных координатах точка определяется с помощью r и θ.

В зависимости от направления измерения угла мы классифицируем полярные диаграммы как против часовой стрелки и по часовой стрелке.

против часовой стрелки

Против часовой стрелки, как следует из названия, угол измеряется против часовой стрелки, противоположно движению стрелок часов.

Всякий раз, когда мы измеряем угол, мы используем опорную линию, от которой измеряется угол. На приведенном ниже рисунке опорной линией является правая ось X. Мы начинаем измерять угол от этой линии, и угол равен 0 ° для всех точек на правой оси x.

Угол 90° для верхней оси Y. Точно так же угол составляет 180° и 270° для левой оси x и нижней оси y.

Центр является исходной точкой с нулевыми радиусами. Под углом 360° мы достигаем той же опорной линии, завершая весь круг.

Полярный график против часовой стрелки

На предыдущей диаграмме углы указаны как в градусах, так и в радианах.

По часовой стрелке

На полярной диаграмме по часовой стрелке углы измеряются в направлении стрелок часов, как показано на следующем рисунке.

Полярный график по часовой стрелке

Направления

Как упоминалось ранее, угол имеет направление. Если угол отрицательный, то направление измерения угла противоположно направлению графика.

На приведенной ниже полярной диаграмме 150° и −210° достигают одинакового положения. Угол -210° означает, что угол измеряется в направлении, противоположном направлению графика, то есть против часовой стрелки.

Углы 150° и -210° обозначают одно и то же положение.

Примеры полярных графиков

Давайте возьмем несколько основных примеров, чтобы лучше понять полярные графы.

Очки

На следующем графике есть несколько случайных точек. Мы хотим определить координаты (радиус, угол) каждого из них.

Полярный график с точками от P1 до P6

Точка P1 расположена на 30° и имеет радиус 3. Итак, координаты 3, 30°.

Таким же образом можно вычислить полярные координаты для остальных.

Полярные координаты точек от P1 до P6

Точка	Радиус	Угол
Р1	3	30° (или π/6)
Р2	4	150° (или 5π/6)
Р3	3	180° (или π)
Р4	4	240° (или 4π/3)
Р5	5	270° (или 3π/6)
Р6	2	330° (или 11π/6)

Уравнения

На следующей диаграмме есть линия и круг.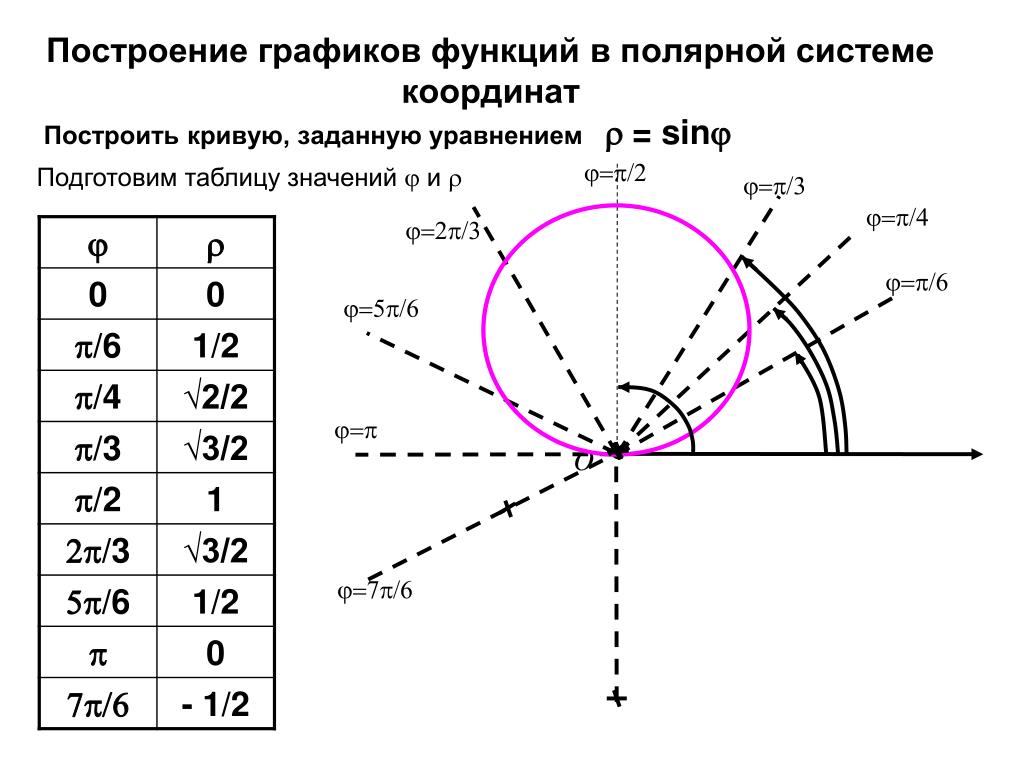 Мы хотим определить уравнения этих кривых.

Полярная диаграмма с кругом и линией.

Линия проходит в начало координат и наклонена под углом 60° (или π/3). Итак, уравнение θ = π/3. Поскольку в уравнении нет члена радиуса, он не зависит от радиуса.

Окружность радиусом 3 с центром в начале координат. Итак, уравнение r = 3, и оно не зависит от тета.

То же самое уравнение в декартовой системе координат будет иметь вид y = tan(π/3) × x для прямой и x2 + y2 = 32 для окружности.

Это гораздо более простые уравнения; в большинстве уравнений будут присутствовать как r, так и θ.

Как читать и извлекать данные из полярного графика с помощью PlotDigitizer?

Вы можете читать и извлекать данные из полярного графика с помощью PlotDigitizer. PlotDigitizer — это программное обеспечение для извлечения данных, которое может извлекать данные из нескольких типов графиков, включая полярные. У него есть бесплатное онлайн-приложение. Другие графики: XY, троичные, круговая/бубликовая, гистограмма, столбец.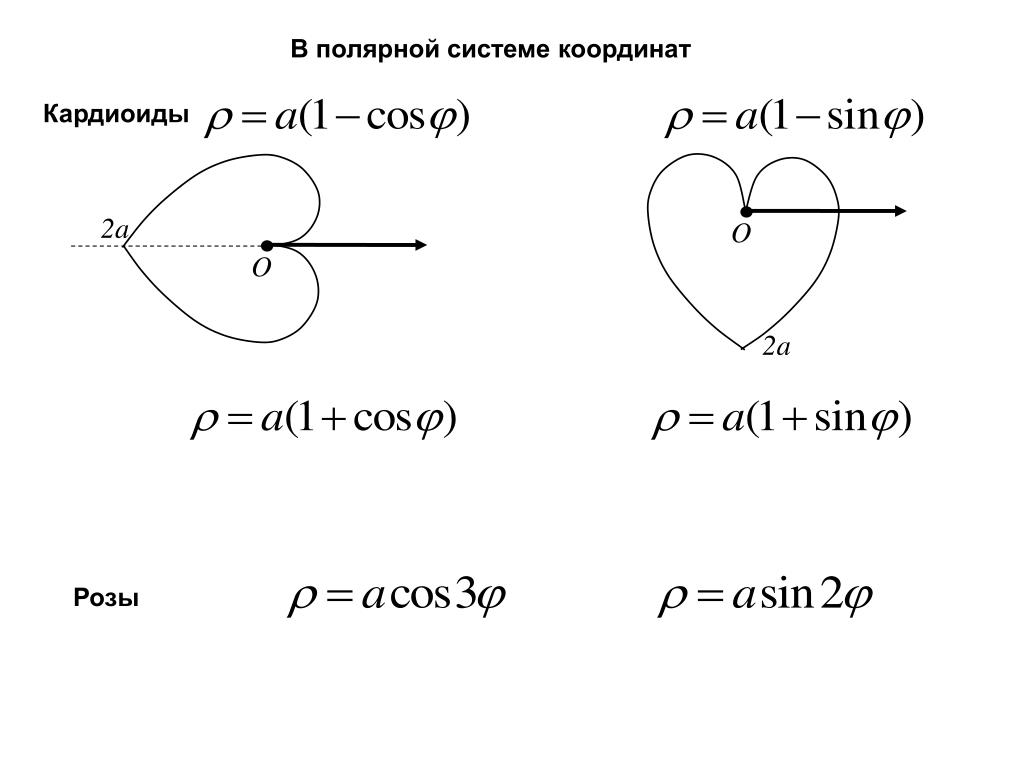

Вам необходимо выполнить несколько простых шагов. Мы возьмем следующий график в качестве примера нашего объяснения.

Полярный график

Шаг 1: Загрузка изображения полярного графика

Посетите https://plotdigitizer.com/app и загрузите или перетащите изображение.

Загрузите полярную диаграмму в PlotDigitizer

Шаг 2: Выбор типа диаграммы

По умолчанию используется тип графика XY, поэтому мы должны изменить его на полярный. Это может быть достигнуто с помощью меню выбора на панели окна.

Выбор типа графика в PlotDigitizer

Шаг 3: Калибровка графика

Теперь перетащите точку O в начало графика, поместите точку θ под любым известным углом. Здесь мы поместили θ на 30°. Переместите точку r на известный радиус.

Калибровка полярного графика

Введите значения θ и r на боковой панели. Здесь r = 15 и θ = 30°. Полярная диаграмма направлена ​​против часовой стрелки, поэтому направление сохраняется против часовой стрелки.

Ввод значений точки r и точки θ

Для повышения точности разметки можно использовать панель масштабирования (или лупу).

Шаг 4. Извлечение данных из графика

После калибровки графика мы видим координаты курсора под панелью масштабирования.

Вы можете начать рисовать красную кривую на рисунке, нажав на кривую. И соответствующие полярные координаты записываются на левой боковой панели.

Извлечение данных из графиков

Шаг 5. Экспорт извлеченных данных

Извлеченные данные можно экспортировать в файлы других форматов, например, CSV, MATLAB, JSON, MS Excel.

Полярные координаты

Сегодня широко используются многие системы и стили измерения. При построении графиков на плоской поверхности прямоугольная система координат и полярная система координат являются двумя наиболее популярными методами построения графиков отношений. Полярные координаты лучше всего использовать при рассмотрении периодических функций. Хотя обычно можно использовать любую систему, полярные координаты особенно полезны при определенных условиях.

Прямоугольная система координат является наиболее широко используемой системой координат. Второй по важности является полярная система координат . Он состоит из фиксированной точки 0 , называемой полюсом или началом координат . Из этой точки выходит луч, называемый полярной осью . Этот луч обычно располагается горизонтально и правее полюса. Любую точку P на плоскости можно определить, указав угол и расстояние. Угол θ измеряется от полярной оси до линии, проходящей через точку и полюс. Если угол измеряется против часовой стрелки, угол положительный. Если угол измеряется по часовой стрелке, угол отрицательный. Направленное расстояние, r , измеряется от полюса до точки P . Если точка P находится на конечной стороне угла θ, то значение r положительно. Если точка P находится на противоположной стороне полюса, то значение r отрицательно. полярных координат точки можно записать в виде упорядоченной пары ( r , θ).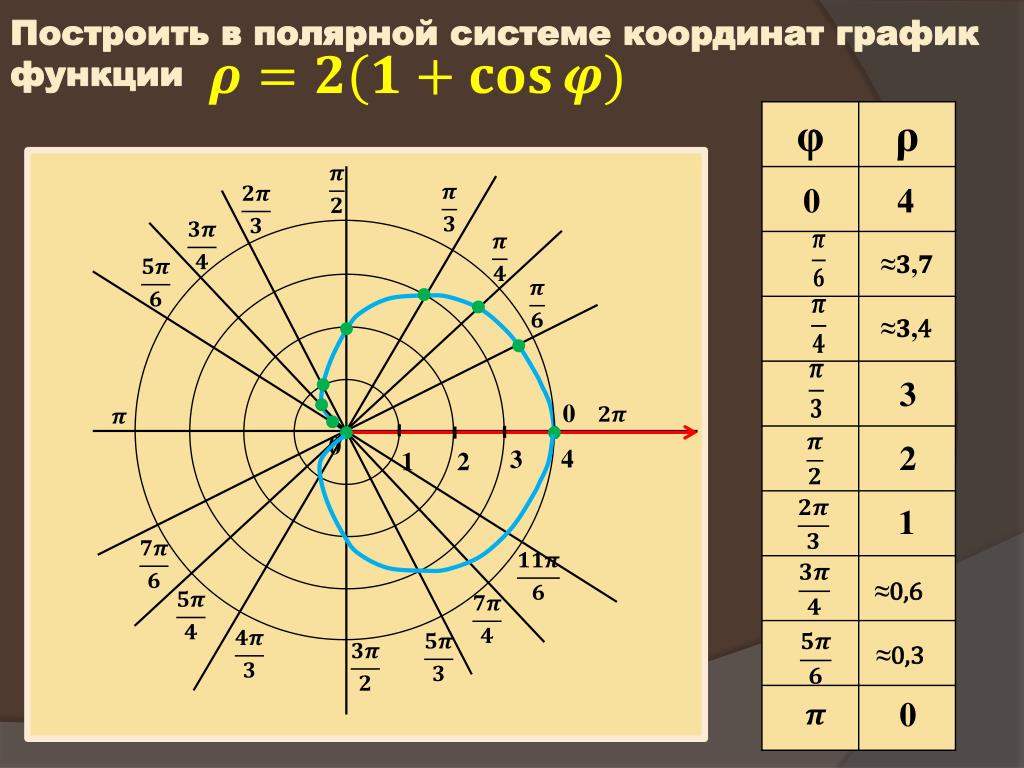 Местоположение точки можно назвать, используя множество различных пар полярных координат. На рисунке 1 показаны три разных набора полярных координат для точки 9.0161 P (4,50°).

Рисунок 1
              Полярные формы котерминальных углов.

Преобразование между полярными координатами и прямоугольными координатами показано ниже и на рис. 2.

Рисунок 2
              Преобразование полярных значений в прямоугольные.

Пример 1: Преобразование P (4,9) в полярные координаты.

Полярные координаты для P (4, 9) .

Пример 2: Преобразование P (5,20°) в прямоугольные координаты.

Прямоугольные координаты для P (5,20°) равны P (4.7, 1.7).

Пример 3 : Преобразуйте уравнение x ² + y ² + 5x = 0 в форму полярных координат.