Не рациональные числа: Иррациональные числа — урок. Алгебра, 10 класс.

Рациональные и иррациональные числа . Магия математики [Как найти x и зачем это нужно]

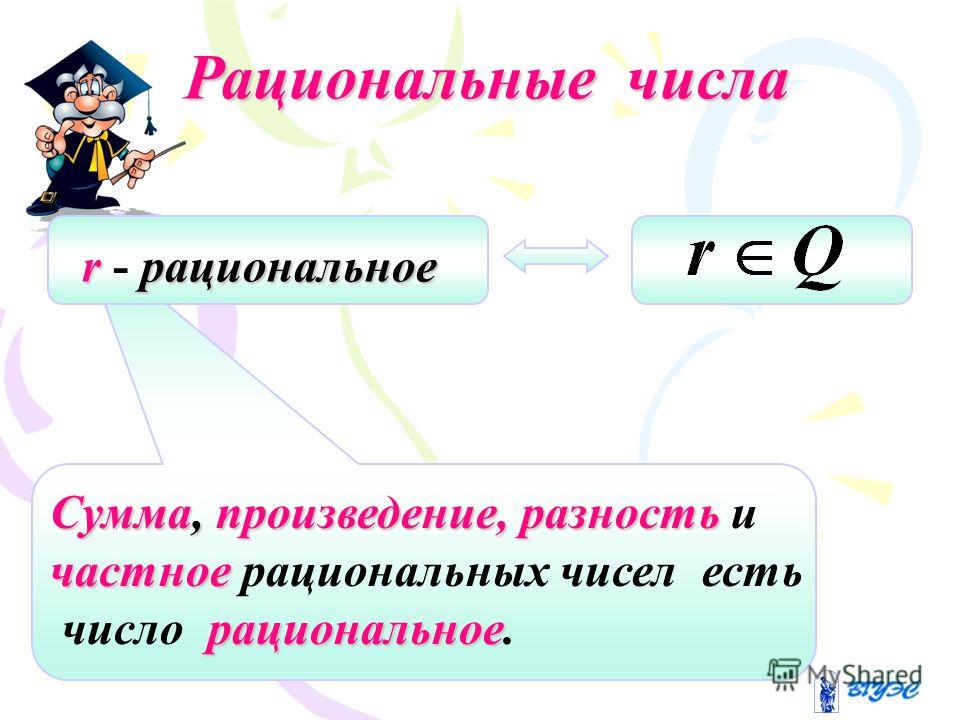
Возможно, теоремы, которые мы только что рассмотрели, ничем вас не удивили, а их доказательства показались вам весьма прямолинейными. Куда большее удовольствие получаешь, пытаясь подтвердить менее очевидные предположения. Пока что мы довольствовались целыми числами – не пора ли заняться дробями? Число, которое можно представить в дробном виде, называется рациональным. Если быть точным, то число r является рациональным, если r = a/b, где a и b – целые числа, а b ? 0. Например, 23/58, –22/7 или 42 (равное, по сути, 42/1) – числа рациональные. Если же число не является рациональным, его называют иррациональным. Яркий тому пример, о котором вы, наверняка, слышали – число ? = 3,14159…, но о нем чуть позже, в главе 8.

Для следующей нашей теоремы не лишним будет вспомнить, как вообще складывать дроби. И легче всего это делать, когда дроби имеют общий знаменатель, например:

В противном случае нам сперва придется привести дроби к общему знаменателю:

В целом же дроби a/b и c/d можно привести к общему знаменателю таким вот нехитрым способом:

И этого вполне достаточно, чтобы доказать несколько простых теорем, связанных с рациональными числами.

Теорема: Среднее арифметическое двух рациональных чисел также будет рациональным числом.

Доказательство: Возьмем два рациональных числа – x и y. Значит, в равенствах x = a/b и y = c/d значения a, b, c и d суть целые числа. Среднее арифметическое x и y, таким образом, можно представить как

Это дробь, числитель и знаменатель которой – целые числа. Следовательно, среднее арифметическое значение x и y является рациональным числом.

А теперь давайте подумаем, что же именно утверждается в этой теореме. А утверждается в ней то, что между двумя разными рациональными числами, насколько бы близки они друг другу ни были, всегда найдется еще одно рациональное число. Возникает искушение сделать из этого вывод, что все числа являются рациональными (как довольно долго думали древние греки). Нет, это не так. И смотрите, почему. Возьмем число ?

2, которое в десятичной записи выглядит как 1,4142… Если мы попробуем записать его как обычную дробь, получится что-нибудь вроде 10/7 или 1414/1000 (вариантов огромное множество), но все они будут приблизительными и никогда при возведении в квадрат не дадут 2. Но что, если мы просто плохо ищем? Да нет, не плохо, и следующая наша теорема как раз и показывает, что любые такие поиски бесполезны по определению. Доказательство будет строиться от противного, как это обычно и бывает, когда разговор заходит об иррациональных числах. А заодно мы увидим, как сократить дробь до ее несократимого значения – того предела, когда у числителя и знаменателя остается только один общий делитель – 1.

Теорема:?2 есть иррациональное число.

Доказательство: Предположим обратное: ?2 есть число рациональное. В таком случае существуют некие положительные целые числа a и b, для которых верно, что

?2 = a/b

где дробь a/b – несократимая. Возведя обе части уравнения в квадрат, получим

2 = a?/b?

или

a? = 2b?

что приводит нас к тому, что a? есть четное целое число.

А если a? – четное, значит, четным является и a (по аналогии с недавним нашим доказательством того, что, если нечетное a умножить на само себя, результат будет также нечетным). То есть a = 2k, где k – целое число. Добавим это в свое уравнение и получим

(2k)? = 2b?

То есть

4k? = 2b?

что приводит нас к

b? = 2k?

и констатации того факта, что b? является четным числом. Значит, четным должно быть и b. Но постойте! Ведь при четных значениях как a, так и b дробь a/b никак не может быть несократимой! Это противоречит нашим исходным условиям. И завело нас в эту ловушку предположение, что ?

2 является рациональным числом. Поэтому нам не остается ничего иного, кроме как признать: число ?2 – иррациональное.?

Лично я нахожу это доказательство восхитительным (и смайлик в конце строки тому подтверждение): прямая и хорошо освещенная тропа чистой, ничем не замутненной логики приводит нас к удивительному умозаключению. В главе 12 мы еще увидим, насколько велик на самом деле процент иррациональных чисел. Практически все действительные числа являются иррациональными, притом, что в повседневной жизни мы с ними почти не сталкиваемся.

Из доказанной нами только что теоремы следует одно любопытное заключение (его, пожалуй, даже можно назвать сопутствующей теоремой – такой, условия которой вытекают из только что доказанной). Основано оно на следующем правиле возведения в степень, согласно которому для любых положительных значений

a, b и c

(a^b)^c = a^bc

То есть утверждение, что (5?)? = 5⁶, будет вполне справедливым, потому что

(5?)? = (5 ? 5 ? 5) ? (5 ? 5 ? 5) = 5⁶

Сопутствующая теорема: Существуют иррациональные числа a и b, при которых число a^b будет рациональным.

Не пугайтесь, нам эта теорема вполне по плечу, хоть мы и знаем пока лишь одно иррациональное число – ?2. Приведенное ниже доказательство является, по сути, доказательством существования: мы же пытаемся просто узнать, есть ли вообще такие

a и b, а не определить их конкретные числовые выражения.

Доказательство: Раз уж мы знаем, что ?2 является иррациональным числом, возьмем число Будет ли оно рациональным? Если да, то теорема доказана (поскольку и a и b равны ?2). Если нет – что ж, по крайней мере мы узнаем еще одно иррациональное число примем и с помощью правила возведения в степень получим

то есть рациональное число. Следовательно, независимо от того, является рациональным или иррациональным числом, мы докажем, что a^b будет рациональным числом при иррациональных значениях a и b.?

Так обычно и выглядит любое доказательство существования чего бы то ни было: почти всегда остроумно и очень редко – исчерпывающе. (Кстати, уж коли зашла речь: число  – все-таки иррациональное число, но сейчас это для нас абсолютно не принципиально.)

Куда больше удовлетворения (равно как и куда больше существенной информации) получаешь, идя путем конструктивного доказательства. Одно из них, к примеру, – доказательство того, что любое рациональное число a/b либо вовсе не имеет цифр после запятой, либо эти цифры повторяются (иными словами, в затянувшемся делении b раз за разом становится делителем того числа, что уже делилось). Но будет ли верным обратное? Само собой, конечная десятичная дробь должна быть рациональным числом. Например, 0,12358 = 12 358/100 000. А если эта дробь – допустим, 0,123123123… – периодическая? Должна ли она быть рациональным числом? Ответ – да, и вот вам очень элегантный способ это доказать. А заодно и найти это самое число. Обозначим искомое буквой w (как в английском слове waltz, которое означает «проще простого»), то есть

w = 0,123123123…

Умножим обе части на 1000:

1000w =123,123123123…

вычтем первое уравнение из второго:

999w = 123

и получим

Возьмем еще одну периодическую десятичную дробь, но на этот раз такую, в которой цикл повторения начинается не с первой после запятой цифры, а чуть позже.

Какой обычной дроби будет соответствовать десятичная 0,83333…? Начнем с

х = 0,83333…

Затем сделаем так:

100x = 83,3333…

и так:

10x = 8,3333…

При вычитании 10x из 100x все, что стоит после запятой, отсекается, оставляя нас с

90x = (83,3333…) – (8,3333…) = 75

Значит,

Этот алгоритм позволяет нам с определенной долей уверенности утверждать, что число будет рациональным тогда и только тогда, когда его представление в виде десятичной дроби является либо конечным, либо периодическим. Иррациональной же будет та дробь, которая после запятой имеет бесконечное количество знаков, не образуюющих при этом цикл, например,

v = 0,123456789101112131415…

теория-чисел / Как прямо доказать, что √2 есть число иррациональное? / Математика

Само понятие иррационального числа так устроено, что оно определяется через отрицание свойства «быть рациональным», поэтому доказательство от противного является здесь наиболее естественным. Можно, однако предложить вот какое рассуждение.

Чем отличаются принципиально рациональные числа от иррациональных? Как те, так и другие, можно приблизить рациональными числами с любой заданной точностью, но для рациональных чисел имеется приближение с «нулевой» точностью (самим этим числом), а для иррациональных чисел это уже не так. Попытаемся на этом «сыграть».

Прежде всего, отметим такой простой факт. Пусть $%\alpha$%, $%\beta$% — два положительных числа, которые приближают друг друга с точностью $%\varepsilon$%, то есть $%|\alpha-\beta|=\varepsilon$%. Что произойдёт, если мы заменим числа на обратные? Как при этом изменится точность? Легко видеть, что $$\left|\frac1\alpha-\frac1\beta\right|=\frac{|\alpha-\beta|}{\alpha\beta}=\frac{\varepsilon}{\alpha\beta},$$ что будет строго меньше $%\varepsilon$% при $%\alpha\beta>1$%. Это утверждение можно рассматривать в качестве самостоятельной леммы.

Теперь положим $%x=\sqrt{2}$%, и пусть $%q\in{\mathbb Q}$% — рациональное приближение числа $%x$% с точностью $%\varepsilon$%. {-1}+1$%, то есть $%(q+2)/(q+1)$%, с «улучшенной» точностью. Это завершает доказательство, так как у рациональных чисел, как мы отмечали выше, существует «абсолютно точное» рациональное приближение с точностью $%\varepsilon=0$%, где точность в принципе повысить нельзя. А мы сумели это сделать, что говорит об иррациональности нашего числа.

Фактически, это рассуждение показывает, как строить конкретные рациональные приближения для $%\sqrt{2}$% со всё улушающейся точностью. Надо сначала взять приближение $%q=1$%, и далее применять одну и ту же формулу замены: $%q\mapsto(q+2)/(q+1)$%. В ходе этого процесса получается следующее: $$1,\frac32,\frac75,\frac{17}{12},\frac{41}{29},\frac{99}{70}$$ и так далее.

Существуют ли действительные числа, которые не являются ни рациональными, ни иррациональными?

Конечно, «традиционный» ответ — нет, не существует действительных чисел, которые не были бы ни рациональными, ни иррациональными. Однако, будучи противоположным человеком, позвольте мне предложить альтернативную интерпретацию, которая дает другой ответ.

Что делать, если вы используете интуитивистскую логику? — ПиРулез

В интуиционистской логике, где отвергается закон исключенного третьего (LEM) $P\vee\lnot P$, все становится несколько сложнее. Пусть $x\in \Bbb Q$ означает, что существуют два целых числа $p,q$, для которых $x=p/q$. Тогда традиционная интерпретация «$x$ иррациональна» — это $\lnot(x\in\Bbb Q)$, но вместо этого мы будем называть это «$x$ иррационально». Утверждение «$x$ не рационально», то есть $\lnot\lnot(x\in\Bbb Q)$, подразумевается $x\in\Bbb Q$, но не эквивалентно ему. 9{-\mu}$, где $x$ — приближаемое действительное число, $p/q$ — рациональное приближение, а $\mu$ — положительная действительная постоянная. Мы измеряем точность аппроксимации величиной $|x-p/q|$, но не позволяем знаменателю (а значит, и числителю, поскольку $p/q$ близко к $x$) быть слишком большими, требуя, чтобы аппроксимация быть в степени $q$. Чем больше $\mu$, тем меньше пар $(p,q)$ удовлетворяют уравнению, поэтому мы можем найти наименьшую верхнюю границу $\mu$ такую, что существует бесконечно много взаимно простых решений $(p,q)$ к уравнению, и это определяет меру иррациональности $\mu(x)$. Есть хорошая теорема из теории чисел, которая гласит, что мера иррациональности любого иррационального алгебраического числа равна $2$, а мера иррациональности трансцендентного числа равна $\ge2$, а мера иррациональности любого рационального числа равна $1$. 9{-2}$ имеет бесконечно много взаимно простых решений. Тогда $x\in\Bbb I\to x\notin\Bbb Q$, т.е. иррациональное число нерационально, а в классической логике $x\in\Bbb I\leftrightarrow x\notin\Bbb Q$, значит, это эквивалентно обычному определению иррационального. Это определение считается более конструктивным, потому что оно не утверждает отрицательное (что $x=p/q$ приводит к противоречию), а дает бесконечную последовательность хороших приближений, подтверждающих иррациональность числа.

Этот подход также подобен методу цепной дроби: иррациональные числа имеют бесконечное число представлений простой цепной дроби, а рациональные числа имеют конечное число, поэтому при представлении бесконечной цепной дроби вы автоматически знаете, что предел не может быть рациональным.

Плохая новость заключается в том, что, поскольку интуиционистская или конструктивная логика строго слабее классической логики, она не доказывает ничего, чего не может доказать классическая логика. Поскольку классическая логика доказывает, что каждое число рационально или иррационально, она не доказывает, что существует нерациональное нерациональное число (при условии непротиворечивости), поэтому интуиционистская логика также не может доказать существование нерационального нерационального числа. Он просто не может доказать, что это невозможно (это может быть правдой, в каком-то смысле «может быть»). С другой стороны, должна быть модель вещественных чисел с конструктивной логикой + $\lnot$LEM, такая, что существует нерациональное нерациональное число, и я приглашаю всех конструктивных аналитиков приводить такие примеры в комментариях.

Рациональные числа

Рациональное число — это число, которое можно записать в виде обыкновенной дроби двух целых чисел. Другими словами, это число, которое можно представить как одно целое число, деленное на другое целое число. Ниже приведены некоторые примеры.

Свойства рациональных чисел

Рациональные числа, как подмножество множества действительных чисел, обладают всеми свойствами действительных чисел. Ниже приведены некоторые специфические свойства рациональных чисел, некоторые из которых отличают их от иррациональных чисел.

Замыкание

Одним из свойств рациональных чисел, которое отличает их от их иррационального аналога, является свойство замыкания. Рациональные числа замкнуты относительно операций сложения, вычитания, умножения и деления. Это означает, что выполнение любой из этих операций с использованием двух рациональных чисел всегда приведет к другому рациональному числу:

2 + 2 = 4

2 — 2 = 0

2 × 2 = 4

2 ÷ 2 = 1

Все результаты являются рациональными числами, и результат этих операций всегда будет рациональным, учитывая, что начальные два значения являются рациональными числами. Это не относится к иррациональным числам, которые могут привести к рациональным или иррациональным числам в зависимости от исходных значений.

Аддитивные обратные

Все рациональные числа имеют аддитивные обратные. Учитывая рациональное число a/b, его аддитивный обратный равен:

Кроме того, если задано ненулевое рациональное число a/b, его обратное мультипликативное число равно:

Обратное мультипликативное число также известно как обратное.

Ниже приведены некоторые другие общие сведения о рациональных числах.

• Рациональные числа могут быть записаны в виде конечной десятичной дроби (десятичная дробь заканчивается) или повторяющейся десятичной дроби (десятичная дробь не заканчивается, но имеет повторяющиеся цифры).
• Неконечные десятичные дроби не являются рациональными числами, поскольку их нельзя представить в виде обыкновенной дроби.
• Знаменатель обыкновенной дроби, используемой для выражения рационального числа, не может быть равен 0.
• Все целые числа являются рациональными числами, так как знаменатель обыкновенной дроби может быть равен 1.

Примеры

1. Все примеры, использованные выше, могут быть преобразованы либо в конечные десятичные дроби, либо в повторяющиеся десятичные дроби:

2. Квадратный корень из 2 не является рациональным числом, потому что его десятичная дробь никогда не заканчивается, поэтому мы не можем выразить его в виде обыкновенной дроби:

Рациональные числа и другие наборы чисел

Существует множество различных наборов чисел, которые обычно используются в математике. Многие из них пересекаются, и может быть полезно знать различные различия между числовыми наборами и то, как они соотносятся друг с другом.

Множество рациональных чисел обычно обозначается как Q. Это подмножество множества действительных чисел (R), которое состоит из множеств рациональных и иррациональных чисел.

Множество рациональных чисел также включает два других часто используемых подмножества: множества целых чисел (Z) и натуральных чисел (N).