Регрессионный анализ в Excel – линейная, множественная, степенная и нелинейная регрессия, построить уравнение, расшифровка результата и примеры
Excel КомментироватьЗадать вопросНаписать пост
Регрессионный метод – это способ статистического исследования. Для проведения регрессионного анализа часто используют Excel – табличный процессор компании Microsoft, позволяющие быстро систематизировать и просчитывать данные. Программа имеет список определенных инструментов и техник, которые нужно активировать и изучить заранее для проведения подобных расчетов.
Что такое регрессионный анализ?
Исследование данного типа позволяет находить взаимосвязь или зависимость между независимой и постоянной переменной. Используется, например, для поиска различий между социальными группами (мужчинами и женщинами), температурными показателями. С точки зрения геометрии целью процесса является построение прямой или графика. Различают следующие типы регрессионного анализа:
Различают следующие типы регрессионного анализа:
- степенной;
- логарифмический;
- параболический;
- показательный;
- линейный;
- гиперболический;
- экспоненциальный.
Каждый из методов имеет собственное назначение и результаты. Дополнительные варианты – однофакторная и многофакторная технологии регрессионного анализа.
Как подключить пакет анализа?
Excel содержит технику регрессионного анализа внутри программы. Но чтобы начать использование, необходимо произвести активацию пакета функций. После этого требуемые инструменты начнут отображаться на общей панели доступа (в верхней части файла). Этапы действий:
- найти кнопку «Файл» — сверху, слева;
- откроется дополнительный список, внизу располагается подпункт «Параметры»;
- появится специальное окно, следует выбрать раздел «Надстройки» – девятая строка сверху;
- переключатель рядом с «Управлением» нужно перевести в положение «Надстройки Excel», потом клавиша «Перейти»;
- всплывет дополнительное окно с доступными возможностями;
- необходимо поставить галочку в квадратике рядом с пунктом «Пакет анализа» и «Ок»;
- после этого окна закроются, а на панели инструментов начнут отображаться новые символы.

Кнопка появится во вкладке «Данные», справа – «Анализ данных». Перезагрузка программы не требуется.
Линейная регрессия
Чтобы подробно объяснить схему работы, в Excel была создана таблица с указанием определенных данных. Цель – попытка обнаружить связь между температурой и числом посетителей торговой точки. Запустить процесс подсчета и регрессии необходимо с помощью кнопки «Анализ данных».
Откроется диалоговое окошко, из представленного списка выбирают пункт «Регрессия», клавиша «Ок». В полях «Входной интервал Y» и «Входной интервал X» – для первого указывают список ячеек переменного параметра (в примере – покупатели), для второго диапазон по температуре.
Внимание! Пункт «Параметры вывода» осуществляет сохранение результата разными способами – на новом листе, книге и т. д. Удобнее будет переставить значок и получить ответы на той же странице, что и начальная таблица.
д. Удобнее будет переставить значок и получить ответы на той же странице, что и начальная таблица.
Запуска процесса – кнопка «Ок». После необходимо правильно прочитать результат.
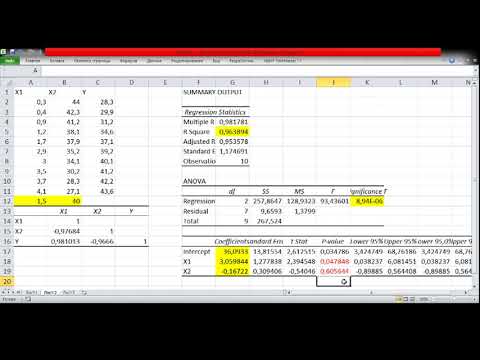
Расшифровка результата – анализ данных
Ответы по анализу помещаются в небольшую таблицу «Вывод итогов». Качество показывает R-квадрат – в данном примере 0,70, что является приемлемым. Y-пересечение указывает на уровень переменной, при остальных данных равных «0». Остальные характеристики указывают на взаимосвязь исходников.
Другие виды регрессии
В примере, который представлен выше, используется только две переменных. Такая ситуация является скорее редкостью. Для расчета нескольких или разных показателей используют иные методы регрессии.
Множественная
Техника применяется в случае, когда параметров Х больше одного. Чтобы корректно рассчитать характеристики можно использовать дополнительные инструменты: заданный тренд, коэффициент детерминации, проверка гипотез и иные. Выполнить расчеты может только подготовленный специалист.
Выполнить расчеты может только подготовленный специалист.
Степенная
Для этой модели формула расчета выглядит так: y = a*x˄b. Выбросы для данного метода вычисляются автоматически. Используется, если уровень достоверности техники выше остальных – графа R˄2.
Нелинейная
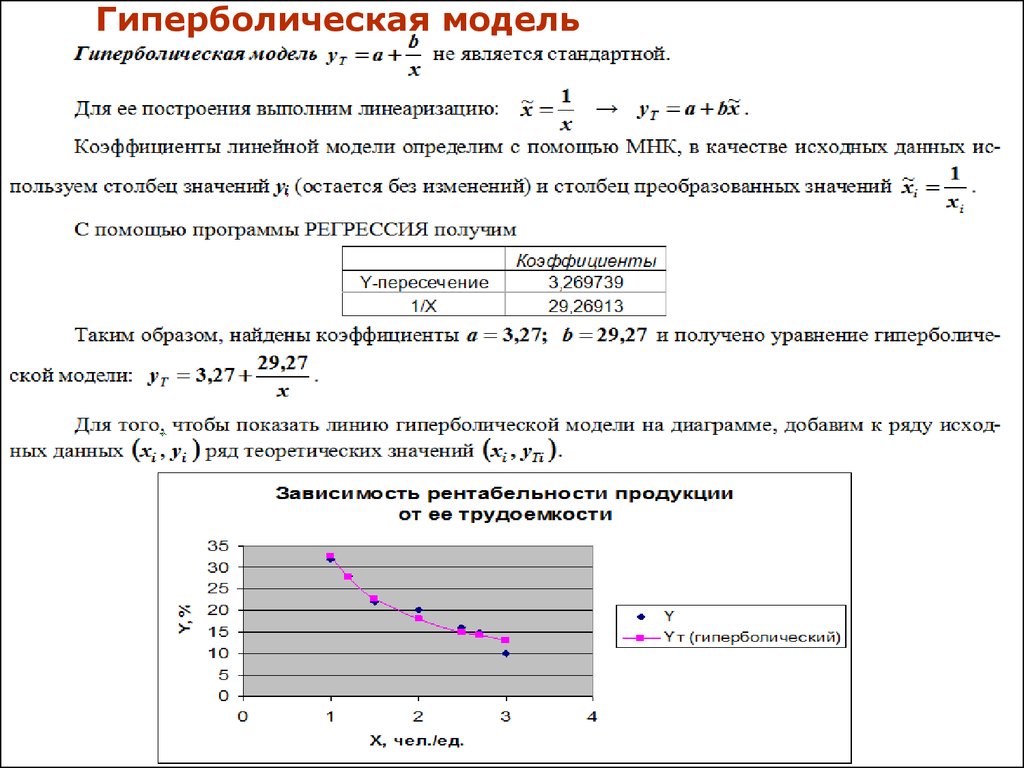
Для нелинейной методики важно рассчитать коэффициент корреляции. Характеристика указывает на наличие взаимосвязи различных показателей. Как правило, если параметр близок к единице, то взаимодействие есть, а анализ достаточно точный.
Дополнительным элементом является относительная ошибка. Характеристика должна находиться в пределах от 8% до 10% – значит, что расчеты точные и результаты можно использовать дальше.
Кроме основных типов регрессионного анализа в Excel используют различные сочетания техник. К примеру, для исследования данных в банковской сфере, колебаний демографических показателей и других. Чтобы корректно пользоваться результатами, важно детально изучить механизм работы подобного исследования. Чаще всего обращаются к специалистам соответствующего профиля.
К примеру, для исследования данных в банковской сфере, колебаний демографических показателей и других. Чтобы корректно пользоваться результатами, важно детально изучить механизм работы подобного исследования. Чаще всего обращаются к специалистам соответствующего профиля.
На главную
Reader Interactions
Регрессионный анализ в Excel
Примеры решенийКоэффициент СпирменаКоэффициент Фехнера Множественная регрессияНелинейная регрессия Уравнение регрессии Автокорреляция Расчет параметров трендаОшибка аппроксимации
- Шаг №1
- Шаг №2
- Видеоинструкция
Линейная
y=a+bx
Параболическая
y=a+bx+cx2
Экспоненциальная
y=a·exp(bx)
Степенная
y=a·x^b
Гиперболическая
y=b/x+a
Логарифмическая
y=b·ln(x)+a
Показательная
y=a·b^x
Формула для вычислений | Функция EXCEL или инструмент Анализа данных | Результат вычислений | ||||||||||
| Оценка параметров модели парной регрессии
| ЛИНЕЙН(изв_знач_у; изв_знач_х; константа; стат)
Смысл аргументов функции изв_знач_у – диапазон значений у; изв_знач_х – диапазон значений х; константа — устанавливается на 0, если заранее известно, что свободный член равен 0 и на 1 в противном случае; стат– устанавливается на 0, если не нужен вывод дополнительных сведений регрессионного анализа и на 1 в противном случае. 
| Возвращает следующую информацию
| ||||||||||
| Оценка параметров модели парной и множественной линейной регрессии. | Сервис / Анализ данных
Для вычисления параметров уравнения регрессии следует воспользоваться инструментом Регрессия | Возвращает подробную информацию о параметрах модели, качестве модели, расчетных значениях и остатках в виде четырех таблиц: Регрессионная статистика, Дисперсионный анализ, Коэффициенты, ВЫВОД ОСТАТКА. 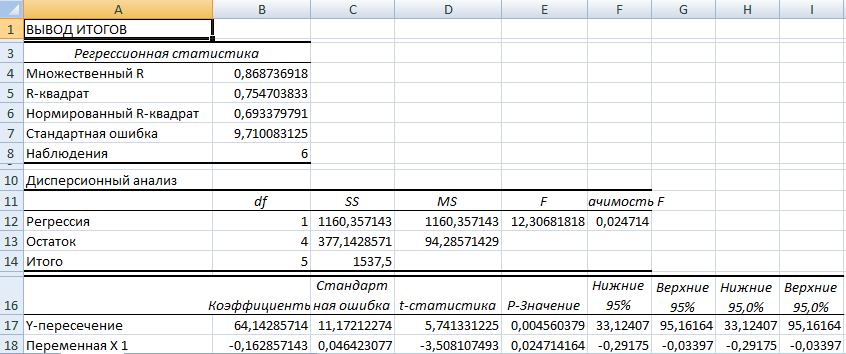
Так же может быть получен график подбора. | ||||||||||
| Оценка значимости параметров модели линейной регрессии с использованием t — критерия Стьюдента.
, Вычисленное по этой формуле значение сравнивается с критическим значением t-критерия, которое берется из таблицы значений t Стьюдента с учетом заданного уровня значимости и числа степеней свободы (n-k-1), где k количество факторов в модели. | СТЬЮДРАСПОБР(вероятность; степени_свободы)
Вероятность — вероятность, соответствующая двустороннему распределению Стьюдента. Степени_свободы — число степеней свободы, характеризующее распределение. | Возвращает t-значение распределения Стьюдента как функцию вероятности и числа степеней свободы. | ||||||||||
Проверка значимости модели регрессии с использованием F-критерий Фишера | FРАСПОБР(вероятность; степени_свободы1; степени_свободы2)
Вероятность — это вероятность, связанная с F-распределением. 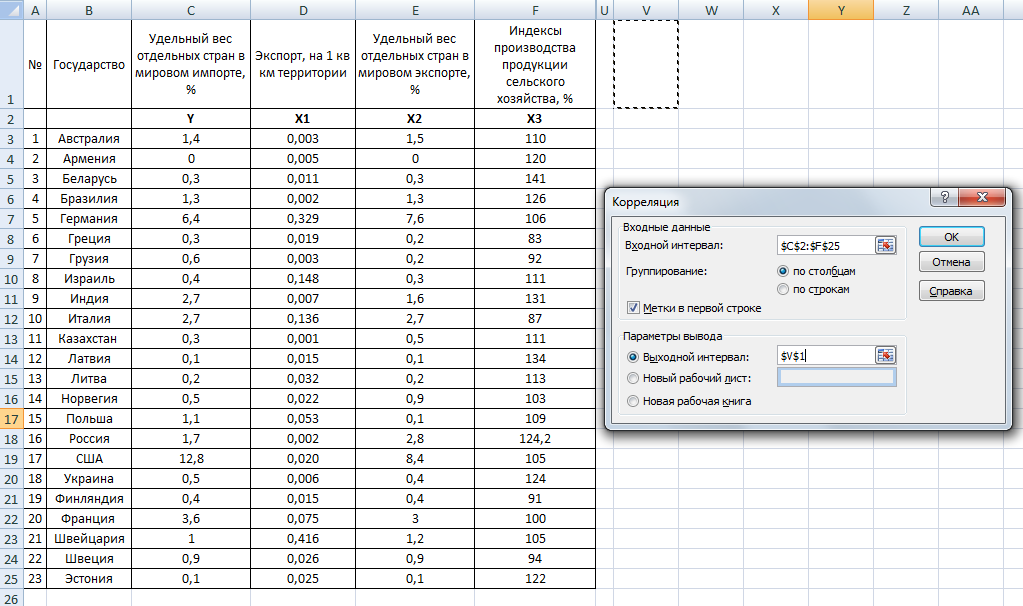
Степени_свободы 1 — это числитель степеней свободы-n1 = k. Степени_свободы 2 — это знаменатель степеней свободы-.n2 = (n — k — 1), где k – количество факторов, включенных в модель, | Возвращает обратное значение для F-распределения вероятностей.
FРАСПОБР можно использовать, чтобы определить критические значения F-распределения. Чтобы определить критическое значение F, нужно использовать уровень значимости α как аргумент вероятность для FРАСПОБР. |
см. также Корреляционный анализ в Excel.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Нелинейная регрессия в Excel | Пошаговое руководство
Нелинейная регрессия Excel является широко используемой моделью в области статистики.
Зависимые переменные моделируются как нелинейные функции переменных модели и одной или нескольких независимых переменных.
Мы должны помнить, что «линейная регрессия в Excel». Линейная регрессия — это статистический инструмент Excel, который используется в качестве модели прогнозирующего анализа для изучения взаимосвязи между двумя наборами данных. Используя этот анализ, мы можем оценить взаимосвязь между зависимыми и независимыми переменными. Читать далее соответствует прямым линейным линиям, в то время как нелинейная регрессия создает кривые из наборов данных».
Table of contents
- Excel Non-Linear Regression
- Examples of Non-Linear Regression in Excel
- Example #1
- Example #2
- Things to Remember
- Recommended Articles
- Examples of Non-Linear Regression in Excel
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку на авторство. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Нелинейная регрессия в Excel (wallstreetmojo.com)
Примеры нелинейной регрессии в Excel
Вы можете скачать этот шаблон Excel для нелинейной регрессии здесь — Шаблон Excel для нелинейной регрессии
Пример № 1
Давайте сначала посмотрим на линейную диаграмму и рассмотрим приведенные ниже данные. .
В приведенных выше данных у нас есть две переменные: «Продажи» и «Добавления».
Нам нужно понять, какая переменная является зависимой, а какая независимой.
В общем, все мы знаем, что «Добавления» играют жизненно важную роль в повышении вероятности получения дохода. Таким образом, «Продажи» зависят от «Добавлений», это означает, что «Продажи» — это зависимая переменная, а «Добавления» — независимая переменная.
Общее правило таково, что одна переменная влияет на другую. Итак, в этом случае наша независимая переменная «Добавления» влияет на нашу зависимую переменную «Продажи».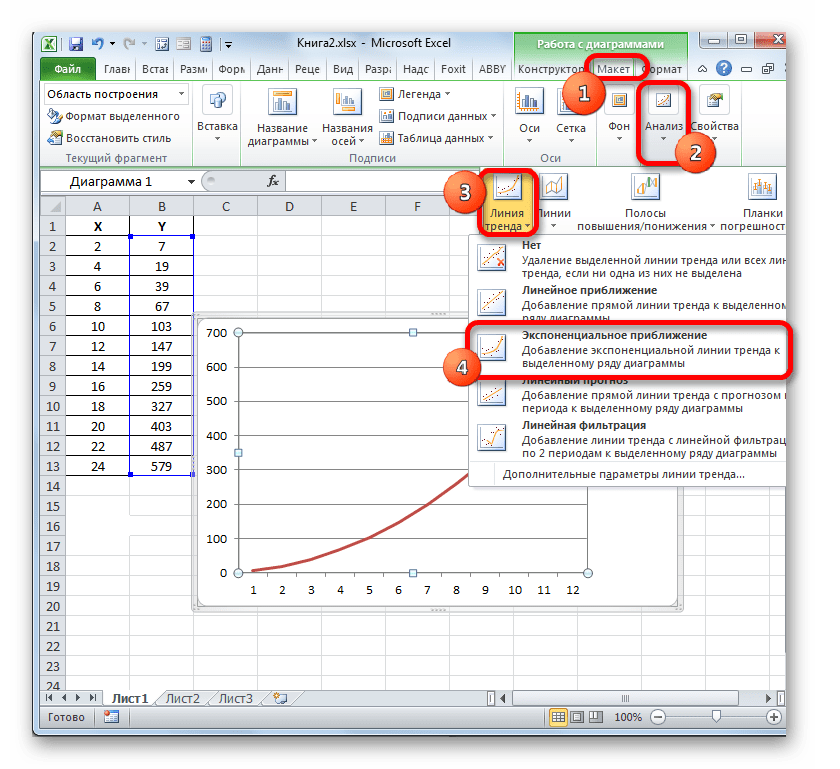
Для этих данных создадим «точечную» диаграмму, чтобы увидеть эти числа графически. Затем выполните следующие шаги, чтобы вставить диаграмму Excel. Вставьте диаграмму Excel. В Excel график или диаграмма позволяют нам визуализировать информацию, которую мы собрали из наших данных. Это позволяет нам визуализировать данные в простых для понимания графических формах. Для создания диаграмм или графиков в Excel необходимы следующие компоненты: 1 – числовые данные, 2 – заголовки данных и 3 – данные в правильном порядке.Подробнее
Выполните следующие действия, чтобы вставить диаграмму Excel.
- Во-первых, мы должны скопировать и вставить вышеуказанные данные в электронную таблицу.
- Затем выберите данные.
- Перейдите на вкладку «ВСТАВИТЬ» и вставьте точечную диаграмму.
- Теперь у нас будет такая диаграмма. Для этой диаграммы нам нужно вставить линейную линию, чтобы увидеть, насколько линейны эти точки данных.

- Выберите диаграмму, чтобы увидеть две новые вкладки на ленте: «Дизайн» и «Формат».
- На вкладке «Дизайн» перейдите к «Добавить элемент диаграммы».
- Щелкните раскрывающийся список «Добавить элемент диаграммы» >> «Линия тренда» >> «Линейный».
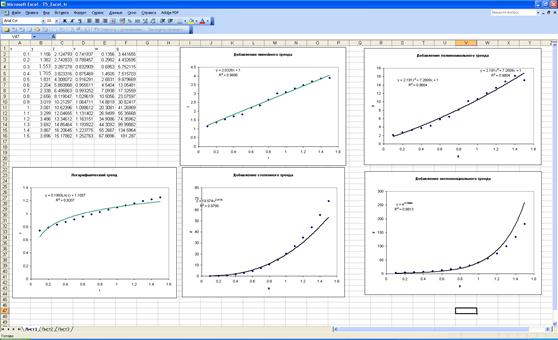
Он добавит на график линейную линию тренда, и она выглядит так.
На этой диаграмме мы видим четкую взаимосвязь между «Продажами» и «Добавлениями». По мере увеличения количества «добавлений» неизменно увеличиваются показатели «продаж», что подтверждается нашей линейной линией на диаграмме. Он просто вписывается в линейную линию.
Теперь посмотрите на пример данных того же объекта.
Если мы вставим диаграмму и линию тренда для этого набора данных, мы получим следующую диаграмму.
Если мы посмотрим на линейную линию и точку нашего набора данных, то увидим, что между двумя точками данных нет точной связи.
Эти наборы данных называются точками данных «нелинейной регрессии» Excel.
Пример #2
Мы увидим еще один пример этой точки данных нелинейной регрессии Excel. Рассмотрим приведенные ниже данные.
Выше приведены данные об осадках и закупленных сельскохозяйственных культурах.
- Теперь нам нужно увидеть взаимосвязь между осадками и купленным урожаем. Для этого мы должны создать точечную диаграмму.
- Вставьте линейную линию для диаграммы.
Мы видим, что для одного и того же набора осадков закупается разное количество урожая. Например, посмотрите на количество осадков в 20. В этом диапазоне осадков закупаемое количество урожая составляет 4598, 3562 и 1184.
Это также может быть связано с сезоном. Например, дождя может быть одинаковое количество, но фермеры закупили разное количество из-за разных временных рамок.
Что нужно помнить
- Линейность и нелинейность — две разные вещи.
- Чтобы понять эти вещи, требуется сильная статистическая база.

- Прежде чем изучать нелинейную регрессию, мы должны понять, что такое линейная регрессия.
Рекомендуемые статьи
Эта статья представляет собой руководство по нелинейной регрессии в Excel. Мы обсудим, как выполнять нелинейную регрессию в Excel, а также приведем примеры и загружаемый шаблон Excel. Вы можете узнать больше об Excel из следующих статей: –
- Интерполяция в Excel
- Как сделать линейную интерполяцию в Excel?
- Как выполнить регрессионный анализ в Excel?
- Что такое пакет инструментов анализа в Excel?
Нелинейная регрессия в учебнике Excel
XLSTAT присоединяется к семье Lumivero. Учить больше.
В этом руководстве объясняется, как настроить и интерпретировать нелинейную регрессию в Excel с помощью XLSTAT. Нелинейная регрессия используется для моделирования сложных явлений, которые не могут быть обработаны линейной моделью.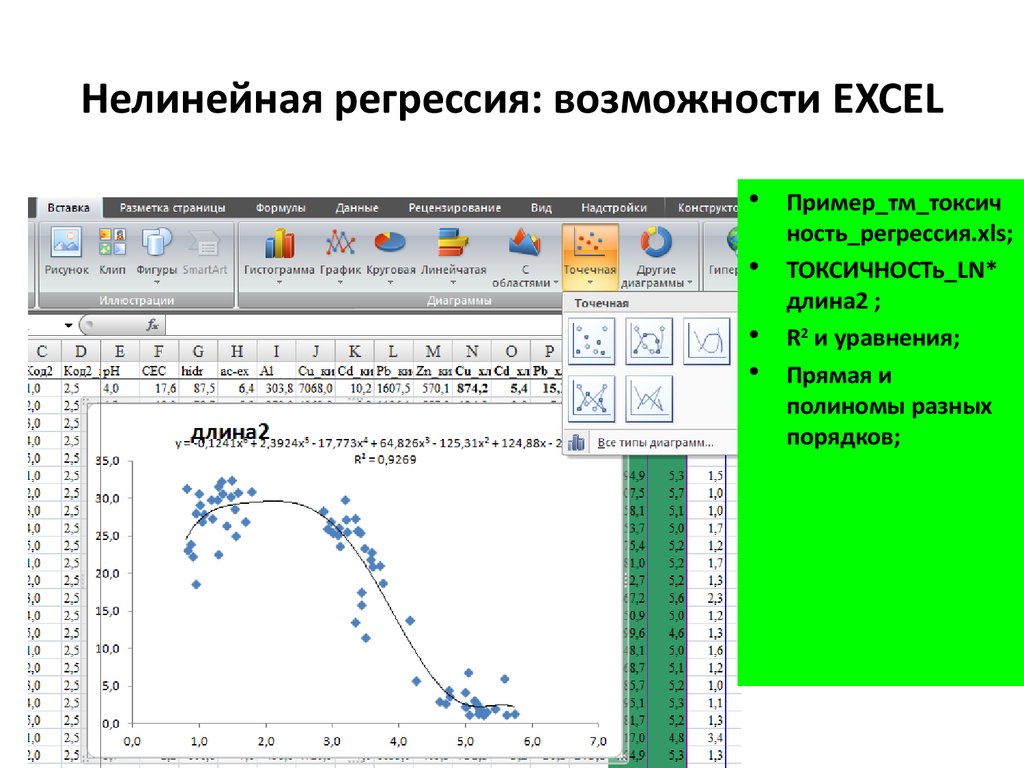
Цель этого руководства
Наша цель — изучить взаимосвязь между концентрацией субстрата фермента и его максимальной скоростью в двух разных группах. Для этого воспользуемся моделью Michaelis — Menten .
Настройка нелинейной регрессии
После открытия XLSTAT выберите команду XLSTAT / Данные моделирования / Нелинейная регрессия .
Появится диалоговое окно нелинейной регрессии. Выберите данные на листе Excel.
Зависимая переменная (или переменная для модели, или переменная отклика) в нашем случае — это «Скорость».
Количественная объясняющая переменная представляет собой концентрацию субстрата: «конц.». В этом уроке мы хотим объяснить изменчивость «Скорости» концентрацией субстрата: «конц».
Групповая переменная используется для разделения данных на две группы «a» и «b». Поскольку мы выбрали заголовки столбцов, мы оставили вариант 9.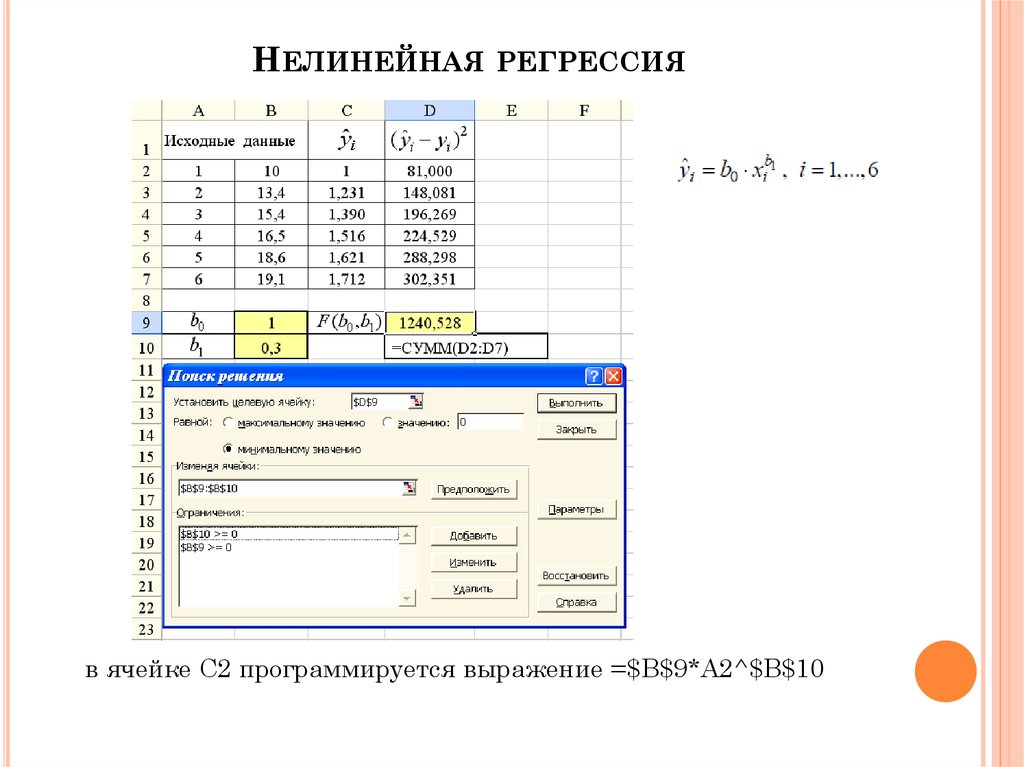 0057 Метки переменных активированы.
0057 Метки переменных активированы.
На вкладке Функции XLSTAT предлагает широкий выбор предопределенных функций, чьи производные учитываются напрямую. Здесь выберите Подгонка одной модели из раскрывающегося списка, а затем выберите функцию Михаэлиса-Ментен.
NB: XLSTAT также оставляет за пользователем возможность ввести функцию, определенную им самим. Затем у пользователя будет выбор: ввести свои собственные производные или позволить их оценить с помощью XLSTAT.
Вычисления начинаются после нажатия кнопки OK . Затем будут отображены результаты.
Интерпретация результатов нелинейной регрессии
Первая таблица результатов содержит простую статистику по выбранным данным. Во второй таблице (ниже) приведены коэффициенты соответствия модели, включая RMCE (среднеквадратичное значение ошибки), что дает представление о качестве модели. Модель, которая соответствует данным лучше, чем другая, будет иметь более низкий RMCE.
В нашем случае RMCE составляет 42,865 в первой группе и 86,893 во второй, что показывает, что изменчивость скорости лучше объясняется в первой группе.
В следующей таблице приведены подробные сведения о параметрах модели после настройки для каждой группы. Мы видим, что параметры pr1, соответствующие максимальной скорости группы «а» и группы «б», достаточно близки.
Уравнения модели отображаются и могут быть легко повторно использованы в Excel.
В следующей таблице (см. лист Excel) показан анализ остатков. Можно заметить, что модель хорошо подходит для первых двух наблюдений каждой группы.
Первый график (см. ниже) отображает данные и кривые подогнанных моделей и подтверждает, что максимальная скорость каждой группы близка. Другие графики позволяют анализировать остатки и особенно полезны, когда важен объем данных.
Как мы видели ранее, максимальная скорость двух групп очень близка.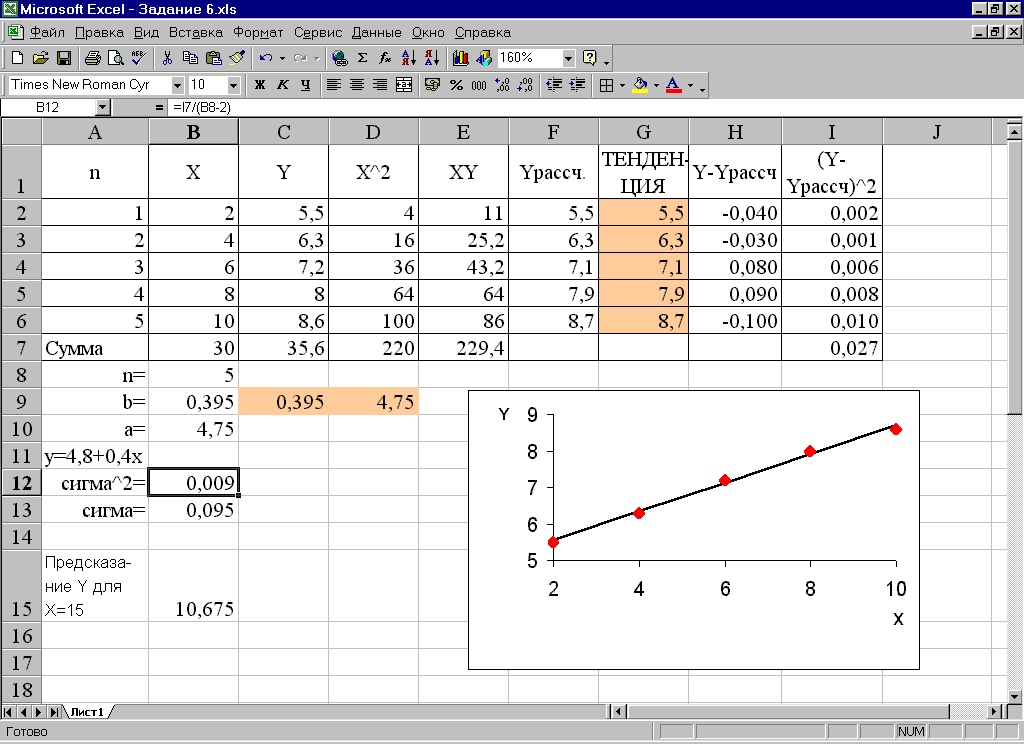

 Зависимые переменные моделируются как нелинейные функции переменных модели и одной или нескольких независимых переменных.
Зависимые переменные моделируются как нелинейные функции переменных модели и одной или нескольких независимых переменных.