Неопределенные интегралы с решением примеры: Примеры решений неопределенных интегралов

Примеры решения интегралов с ответам

Простое объяснение принципов решения интегралов и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения интегралов

Теорема

Неопределённым интегралом функции называется множество всех первообразных этой функции.

Первообразной функции называется такая функция, производная которой равна исходной функции, т.е., если – первообразная функции , то:

Операция интегрирования является операцией обратной операции дифференцирования.

Определённым интегралом функции на отрезке называется разность первообразных функции, вычисленных на концах этого отрезка.

Алгоритм

Определённый интеграл вычисляется при помощи формулы Ньютона-Лейбница:

   

Для нахождения интегралов функций, используются свойства интегралов, а также таблица интегралов.

Таблица основных интегралов, – постоянная величина

   

   

   

   

   

   

   

   

   

   

   

   

   

   

   

   

   

   

   

   

   

   

Примеры решений интегралов

Пример 1

Задача

Вычислить интеграл:

   

Решение

По таблице интегралов находим:

   

Ответ

   

Пример 2

Задача

Вычислить интеграл:

   

Решение

По таблице интегралов находим:

   

Ответ

   

Пример 3

Задача

Вычислить интеграл:

   

Решение

По таблице интегралов находим:

   

Ответ

   

Пример 4

Задача

Вычислить интеграл:

   

Решение

Вынося постоянный множитель 7 за знак интеграла, по таблице интегралов находим:

   

Ответ

   

Пример 5

Задача

Вычислить интеграл:

   

Решение

Интеграл суммы равен сумме интегралов, поэтому:

   

Ответ

   

Пример 6

Задача

Вычислить интеграл:

   

Решение

Интеграл суммы равен сумме интегралов, поэтому:

   

Ответ

   

Пример 7

Задача

Вычислить интеграл:

   

Решение

Преобразуя подынтегральную функцию к виду степенной, находим её интеграл по таблице интегралов:

   

Ответ

   

Пример 8

Задача

Вычислить интеграл:

   

Решение

Преобразуя подынтегральную функцию к виду степенной, находим её интеграл по таблице интегралов:

   

Ответ

   

Пример 9

Задача

Вычислить интеграл:

   

Решение

Интеграл суммы равен сумме интегралов, поэтому:

   

Далее найдём каждый интеграл суммы:

   

   

   

Ответ

   

Пример 10

Задача

Вычислить интеграл:

   

Решение

Интеграл суммы равен сумме интегралов, поэтому:

   

Далее, применяя таблицу интегралов, находим интегралы функций синус и косинус:

   

Ответ

   

Средняя оценка 3. 1 / 5. Количество оценок: 68

Поставьте вашу оценку

Сожалеем, что вы поставили низкую оценку!

Позвольте нам стать лучше!

Расскажите, как нам стать лучше?

57607

Закажите помощь с работой

Не отобразилась форма расчета стоимости? Переходи по ссылке

Не отобразилась форма расчета стоимости? Переходи по ссылке

Полезно

Неопределенный интеграл с примерами решения

Содержание:

1. Простейшие неопределенные интегралы
2. Примеры с решением:
3. Первообразная и неопределенный интеграл
4. Преобразования неопределенных интегралов

Неопределенным интегралом называется совокупность всех первообразных. Первообразной данной функции на некотором промежутке называется такая функция производная которой на всем промежутке равна данной функции Можно показать, что разные первообразные одной и той же функции отличаются на постоянную величину. Таким образом, если мы знаем одну из первообразных заданной функции то неопределенный интеграл

Эту формулу можно также записать в другом виде:

из которого следует, что интегрирование является операцией, обратной дифференцированию. Можно предположить (и это подтверждается на практике), что хорошо интегрировать будет тот, кто умеет хорошо дифференцировать.

Так же как техника дифференцирования опирается на знание таблицы производных, так и вычисление интегралов невозможно без знания таблицы основных интегралов.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Эта таблица фактически является переписанной наоборот (с небольшими изменениями) таблицей производных.

Относительно приводимой таблицы можно сделать следующие замечания. Полезно запомнить распространенный частный случай формулы 3 при

В восьмой формуле можно пользоваться любым из выражений, стоящих справа ( производные функции и равны). То же самое замечание относится и к девятой формуле (производные функций и также равны между собой).

Возможно вам будут полезны данные страницы:

Знакочередующиеся ряды

Сходимость знакочередующихся рядов

Найти неопределенный интеграл: примеры решения

Пределы: примеры решения

Последние четыре формулы относятся к так называемым гиперболическим функциям ( — гиперболический синус, — гиперболический косинус гиперболический тангенс, — гиперболический котангенс). Этим функциям в учебной литературе обычно уделяется незначительное внимание, хотя в приложениях они используются довольно часто. Следующий раздел будет посвящен гиперболическим функциям, что компенсирует имеющийся пробел в учебниках.

Наконец приведем известную задачу Л. Д. Ландау, которую он давал на экзамене по теоретическому минимуму для отбора физиков-теоретиков в свои группы. Она относится к самому первоначальному понятию и обозначению неопределенного интеграла.

Простейшие неопределенные интегралы

Непосредственное использование таблицы основано на свойстве линейности неопределенного интеграла:

Иа этого свойства следует, что если нам удалось представить подынтегральную функцию в виде линейной комбинации функций, интегралы от которых известны, то интеграл от этой функции равен линейной комбинации соответствующих табличных интегралов. Рассмотрим применение этого метода на примерах.

Примеры с решением:

На участке выполнено неравенство следовательно, и первообразная подынтегральной функции

На участке имеем и поэтому следовательно, первообразная подынтегральной функции Из условия непрерывности функции в точке находим соотношение между постоянными

т.е. Опуская индекс у константы получаем следующий ответ:

Первообразная и неопределенный интеграл

Определение. Первообразной от заданной функции называется функция такая, что ее дифференциал равен т. е.

Например, функция является первообразной от функции так как Площадь криволинейной трапеции (в соответствии с § 4 гл. IX) является первообразной от функции график которой ограничивает эту криволинейную трапецию, так как

Пример 1.

Покажем, что функция есть первообразная от функции В самом деле, производная равна следовательно, дифференциал равен Поэтому есть первообразная от

Определение первообразной можно дать в другой, эквивалентной форме: первообразной от функции называется функция имеющая своей производной

Обратим внимание на то, что первообразная от данной функции существует не одна. Например, как было указано, есть первообразная от но, взяв функцию где —любое постоянное число, получим, что т. е. также является первообразной от

Можно было бы доказать, что и обратное предложение верно, т. е. если функции и являются первообразными от функции то они отличаются друг от друга на постоянное слагаемое. Из сказанного следует, что операция нахождения первообразной, во-первых, является операцией, обратной дифференцированию, и, во-вторых, эта операция неоднозначная, т. е. в результате ее применения можно получить различные функции, отличающиеся на постоянные слагаемые.

Определение. Совокупность всех первообразных от заданной функции называется неопределенным интегралом от этой функции.

Неопределенный интеграл обозначается так и читается: неопределенный интеграл от функции Если — одна из первообразных функций то любая другая из первообразных от той же функции будет равна

где —любое число. Следовательно

Из определения первообразной и неопределенного интеграла следует, что

В самом деле,

Выпишем формулы, справедливость которых проверяется дифференцированием.

Проверим формулу 10. Возьмем дифференциал от левой части равенства, получим [в силу формулы (Б)]

Таким образом, мы убеждаемся в том, что левая часть есть первообразная от функции Теперь возьмем дифференциал от правой части равенства 10:

Убеждаемся в том, что правая часть равенства есть первообразная от функции часть может отличаться от правой только на постоянное слагаемое, но это постоянное у нас и написано в правой части формулы 10. Итак, формула 10 верна.

Преобразования неопределенных интегралов

Подобно тому, как в алгебре даются правила, позволяющие преобразовывать алгебраические выражения с целью их упрощения, так и для неопределенного интеграла существуют правила, позволяющие производить его преобразования.

Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от каждого члена в отдельности, т. е.

Постоянный множитель можно вынести за знак интеграла, т. е

(—постоянная величина).

Формула интегрирования по частям, а именно:

Докажем формулу

Возьмем дифференциал от правой части равенства

Применяя формулу 4 из таблицы § 2 гл. IX, получим

Член преобразуем по формуле 5 той же таблицы:

а член по формуле (Б) § 1 этой главы равен

Собирая все вместе, будем иметь

т. е. мы получили то, что получается при дифференцировании левой части равенства (III). Аналогично проверяются формулы (I) и (II).

Пример 2.

Применяя правило интегрирования I и формулы 1 и 5 из таблицы интегралов, получаем

Пример 3.

Применяя правило II и формулу 6 из таблицы интегралов, получаем

Пример 4.

В таблице интегралов, приведенных в § 1, такого интеграла нет. Вычислим его, интегрируя по частям; для этого перепишем данный интеграл следующим образом:

Положив применим правило интегрирования по частям:

Но так как то, применяя формулу 1 таблицы интегралов получим Окончательно получаем

Пример 4.

Рассмотрим Положим и Тогда так как Применяя интегрирование по частям, будем иметь

Неопределенные интегралы — исчисление 2

Все ресурсы исчисления 2

9 Диагностические тесты 308 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 5 6 7 8 9 … 25 26 Следующая →

Исчисление 2 Помощь » Интегралы » Нахождение интегралов » Неопределенные интегралы

Найдите неопределенный интеграл следующей функции:

 

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы интегрировать эту функцию, используйте подстановку u. Сделайте

  

, затем подставьте их в уравнение, чтобы получить

 .

Интеграл

 

затем снова подставьте u в уравнение

.

+C необходим, потому что интеграл не определен.

Сообщить об ошибке

Вычислить заданный неопределенный интеграл

.

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы интегрировать эту функцию, используйте подстановку u. Сделайте

  

, затем подставьте их в уравнение, чтобы получить

 .

Интеграл

 

затем снова подставьте u в уравнение

.

+C необходим, потому что интеграл не определен.

Сообщить об ошибке

Вычислить заданный неопределенный интеграл

 .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы интегрировать эту функцию, используйте подстановку u. Сделайте

  

, затем подставьте их в уравнение, чтобы получить

 .

Интеграл от

 

, поэтому мы имеем

.

+C необходим, потому что интеграл не определен.

Сообщить об ошибке

Вычислить следующий неопределенный интеграл.

Возможные ответы:

Правильный ответ:

Пояснение:

Для вычисления интеграла нам нужно использовать интегрирование по частям. Определение интегрирования по частям:

Здесь важно выбрать правильные члены u и dv из нашего исходного интеграла. В конечном итоге мы хотим, чтобы термины «ушли», когда мы возьмем его производную. Здесь мы замечаем, что из двух наших функций в нашем интеграле и производная x равна 1, что в конечном итоге очень просто интегрировать. Следовательно,  будет нашим термином, а  будет нашим термином dv. Обратите внимание, что термин dv — это не только dx, но и связанная с ним функция. Если бы это был наш термин, то это был бы наш термин dv.

                    

Теперь вычислите члены и  , необходимые для выполнения уравнения интегрирования по частям.

                

(вы можете установить константу интегрирования c=0)

 

Теперь, когда у нас есть нужные нам члены, мы можем подставить их в приведенную выше формулу интегрирования по частям.

 — 

Обратите внимание, что хотя нам все еще нужно интегрировать еще раз, этот новый интеграл состоит только из одной функции, которую легко интегрировать, в отличие от двух функций, которые у нас были раньше. Также обратите внимание, что член x из исходного интеграла «ушел», что упрощает вычисление результирующего интеграла.

Упрощение этого термина теперь становится

.

 

Сообщить об ошибке

Если 

Что такое 

 ?

Возможные ответы:

Правильный ответ:

Объяснение:

Хотя интеграл выглядит сложно, его можно значительно упростить. Помните об этой важной триггерной идентичности.

Используя это тождество, теперь интеграл можно упростить до

, который очень просто интегрировать.

Сообщить об ошибке

Решите следующее для .

Предположим, что постоянная интегрирования равна нулю.

Возможные ответы:

Правильный ответ:

Объяснение:

В этой задаче мы можем попытаться получить все термины с  с одной стороны и все термины с   с другой.

Теперь мы можем интегрировать обе стороны, используя определение  и степенное правило.

 и

Сообщить об ошибке

Решите следующее для .

Допустим константа интегрирования Объяснение:

Переместите все выражения с  в одну сторону, а все  – в другую.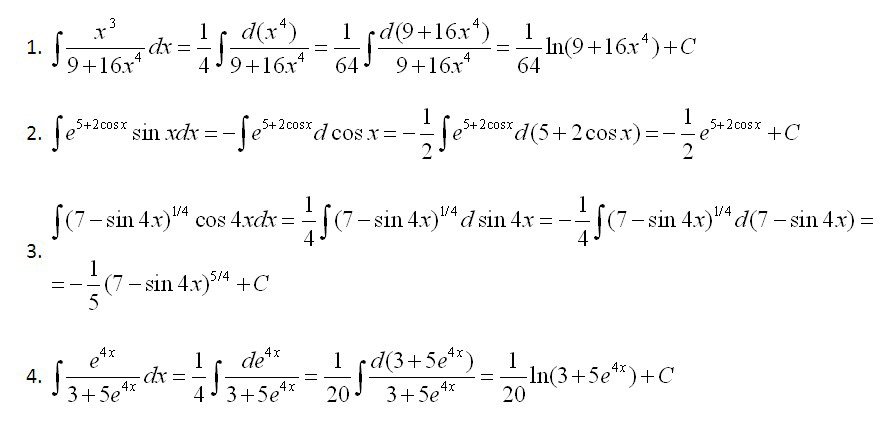

Теперь интегрируйте обе стороны, используя правило мощности и определение натурального логарифма.

Правило степени для состояний интегралов, 

 и определение натурального логарифма,

.

Применяя эти правила, мы можем решить проблему.

Сообщить об ошибке

Вычислите следующий интеграл.

Возможные ответы:

Правильный ответ:

Объяснение:

Нам нужно использовать следующее удостоверение:

 

Теперь наш интеграл становится равным

.

Обратите внимание, что внутри косинуса становится 4, потому что мы уже имели 2 в исходном выражении.

Можно разделить на два интеграла

.

Что становится

.

Сообщить об ошибке

Найдите неопределенный интеграл от .

Возможные ответы:

Ничего из вышеперечисленного

Правильный ответ:

Объяснение:

Мы можем найти неопределенный интеграл от   используя правило степени для интегралов, которое гласит, что

 для всех  и с произвольной константой интегрирования .

Применение этого правила к 

.

Сообщить об ошибке

Найдите неопределенный интеграл от .

Возможные ответы:

Ничего из вышеперечисленного

Правильный ответ:

Объяснение:

Мы можем найти неопределенный интеграл от  , используя правило степени для интегралов, которое гласит, что 

 для всех  и с произвольной константой интегрирования .

Применение этого правила к 

.

Сообщить об ошибке

← Предыдущая 1 2 3 4 5 6 7 8 9 … 25 26 Следующая →

Уведомление об авторских правах

Все ресурсы Calculus 2

9 Диагностические тесты 308 практических тестов Вопрос дня Карточки Learn by Concept

Неопределенный интеграл — определение, вычисление, формулы

Неопределенный интеграл — это интегрирование функции без каких-либо ограничений. Интегрирование является обратным процессом дифференцирования и называется первообразной функции. Неопределенный интеграл — важная часть исчисления, и приложение предельных точек к интегралу превращает его в определенный интеграл. Интегрирование определено для функции f(x) и помогает найти площадь, ограниченную кривой, относительно одной из осей координат.

Неопределенные интегралы далее решаются с помощью различных методов интегрирования по частям, интегрирования с заменой, интегрирования неполных дробей и интегрирования обратных тригонометрических функций. Давайте узнаем больше о неопределенных интегралах, важных формулах, примерах и разнице между неопределенными интегралами и определенными интегралами.

1.	Что такое неопределенный интеграл?
2.	Важные формулы неопределенных интегралов
3.	Разница между неопределенным интегралом и определенным интегралом
4.	Примеры на неопределенный интеграл
5.	Практические вопросы
6.	Часто задаваемые вопросы о Indefinite Integral

Что такое неопределенный интеграл?

Неопределенные интегралы — это интегралы, которые могут быть вычислены обратным процессом дифференцирования и называются первообразными функций. Для функции f(x), если производная представлена ​​f'(x), интегрирование равнодействующей f'(x) возвращает исходную функцию f(x). Этот процесс интегрирования можно определить как определенные интегралы. Давайте поймем это из приведенного ниже выражения.

• Если d/dx f(x) = f'(x), то ∫ f'(x) dx = f(x) + C

Здесь C — константа интегрирования, и вот пример того, почему нам нужно добавлять ее после значения каждого неопределенного интеграла.

Пример: Пусть f(x) = x ² и по степенному правилу f ‘(x) = 2x. Тогда интеграл от f ‘(x) равен x ² + C, поскольку дифференцирование не только x ² , но и таких функций, как x ² + 2, x ² — 1 и т. д., дает 2x. Неопределенный интеграл технически определяется, как показано ниже.

В приведенном выше определении:

• f(x) называется подынтегральной функцией
• dx означает, что переменная интегрирования равна x
• F(x) значение неопределенного интеграла

т. е. неопределенный интеграл функции f(x) равен F(x) + C, где производная от F(x) является исходной функцией f(x).

Вычисление неопределенного интеграла

Процесс вычисления неопределенного интеграла зависит от заданной функции. Вот шаги для вычисления неопределенных интегралов различных типов функций:

• Простые неопределенные интегралы можно решить с помощью формул прямого интегрирования, которые упомянуты в разделе ниже.
• Рациональные функции могут быть решены с помощью метода частных дробей. т. е. мы разделяем подынтегральное выражение на частичные дроби, а затем интегрируем каждую дробь отдельно.
• Некоторые неопределенные интегралы можно решить методом подстановки.
• Если подынтегральное выражение является произведением, то его можно решить с помощью интегрирования по частям.
• Чтобы вычислить определенный интеграл, сначала вычислите первообразную, используя один из вышеуказанных методов, а затем примените пределы, используя формулу ∫ _a ^b f(x)dx = F(b) — F(a).

Пример: Вычислить неопределенный интеграл ∫ 3x ² sin x ³ dx.

Решение:

Данный интеграл можно вычислить методом подстановки. Предположим, что x ³ = t, тогда 3x ² дх = дт. Тогда данный интеграл принимает вид ∫ sin t dt. По одному из правил интегрирования его значение равно — cos t + C. Подставляя t = x ³ обратно, значение данного неопределенного интеграла равно — cos x ³ + C.

Важные формулы неопределенных интегралов

Ниже перечислены некоторые важные формулы неопределенных интегралов. Чтобы узнать больше об этих формулах и правилах, нажмите здесь.

• ∫ x ⁿ dx = x ^{n + 1} / (n + 1) + C

• ∫ 1 дх = х + С

• ∫ е ^х dx = е ^х + С

• ∫1/x dx = ln |x| + С

• ∫ a ^x dx = a ^x / ln a + C

• ∫ cos x dx = sin x + C

• ∫ sin x dx = -cos x + C

• ∫ сек ² х dx = тангенс х + С

Свойства неопределенного интеграла

Нам может понадобиться применить следующие свойства при вычислении неопределенного интеграла.

• Свойство суммы : ∫ [f(x) + g(x)]dx = ∫ f(x)dx + ∫ g(x)dx
• Отличие: ∫ [f(x) — g(x)]dx = ∫ f(x)dx — ∫ g(x)dx
• Свойство постоянного кратного: ∫ k f(x)dx = k∫ f(x)dx
• ∫ f(x) dx = ∫ g(x) dx, если ∫ [f(x) — g(x)]dx = 0
• ∫ [k ₁ f ₁ (x) + k ₂ f ₂ (x) + …+k _n f _n (x)]dx = k ∫ f ₁ (x)dx + k ₂ ∫ f ₂ (x)dx + … + k _n ∫ f _n (x)dx

Разница между неопределенным интегралом и определенным интегралом

Неопределенный интеграл используется для нахождения интеграла функции, а результирующее выражение представляет площадь, ограниченную функцией относительно одной из осей. Определенный интеграл имеет определенное значение. Определенный интеграл представляется как ∫ ^b _a f(x)dx, где a — нижний предел, а b — верхний предел, для функции f(x), определенной относительно оси x. Определенные интегралы являются первообразной функции f(x) для получения функции F(x), а верхний и нижний пределы применяются для нахождения значения F(b) — F(a). Это следует из основной теоремы исчисления.

Кроме того, многочисленные формулы и теоремы, используемые для неопределенного интеграла, можно использовать и для определенных интегралов. Основное различие между неопределенными интегралами и определенными интегралами состоит в том, что неопределенные интегралы не имеют пределов, а у определенных интегралов есть верхний предел и нижний предел.

☛ Связанные темы:

• Формулы дифференцирования и интегрирования
• Дифференциальное уравнение

Часто задаваемые вопросы о неопределенном интеграле

В чем разница между неопределенными интегралами и определенными интегралами?

Определенный интеграл и неопределенный интеграл отличаются применением предельных точек. В неопределённых интегралах нижний предел и верхний предел применяются к точкам, а в неопределённых интегралах вычисляются для всего диапазона без каких-либо ограничений.

Каковы свойства неопределенных интегралов?

Свойства неопределенных интегралов аналогичны свойствам дифференцирования. Неопределенные интегралы обратны дифференцированию. Дифференцирование f(x) дает f'(x), которое при применении неопределенного интеграла возвращает функцию f(x).

Какие методы используются для вычисления неопределенных интегралов?

Мы используем следующие методы для вычисления/вычисления неопределенных интегралов:

• Использование формул интегрирования
• Использование метода u-замены
• Использование УФ-метода
• Путем разбиения на неполные дроби
• Путем применения тригонометрических формул

Каковы важные правила неопределенных интегралов?

Вот некоторые из важных правил неопределенных интегралов.

• ∫ x ⁿ dx = x ^{n + 1} / (n + 1) + C
• ∫ 1 дх = х + С
• ∫ е ^х dx = е ^х + С
• ∫ 1/x dx = ln |x| + С

Каковы приложения неопределенных интегралов?

Тема неопределенного интеграла имеет множество применений в исчислении.