Таблица основных неопределенных интегралов. Правила интегрирования. Интегралы от степенной, показательной, тригонометрических функций
Интегрирование степенной функции
Интегралы от показательной функции и гиперболических функций
Интегралы от тригонометрических функций
Интегралы, сводящиеся к обратным тригонометрическим функциям
Более сложные интегралы
Общие законы интегрирования
Несложный пример
Сводная таблица интегралов
Скачайте таблицу интегралов (часть I) по этой ссылке
Скачайте таблицу интегралов (часть II) по этой ссылке
Перечисленные интегралы — это базис, основа основ. Данные формулы, безусловно, следует запомнить. При вычислении более сложных интегралов вам придется постоянно ими пользоваться.
Обратите особое внимание на формулы (5), (7), (9), (12), (13), (17) и (19). Не забывайте при интегрировании добавлять к ответу произвольную постоянную С!
Интеграл от константы
∫Adx=Ax+C (1)
Интегрирование степенной функции
В действительности, можно было ограничиться только формулами (5) и (7), но остальные интегралы из этой группы встречаются настолько часто, что стоит уделить им немного внимания.
∫xdx=x22+C (2)
∫x2dx=x33+C (3)
∫1xdx=2x+C (4)
∫1xdx=ln|x|+C (5)
∫1x2dx=−1x+C (6)
∫xndx=xn+1n+1+C(n≠−1) (7)
Интегралы от показательной функции и от гиперболических функций
Разумеется, формулу (8) (пожалуй, самую удобную для запоминания) можно рассматривать как частный случай формулы (9). Формулы (10) и (11) для интегралов от гиперболического синуса и гиперболического косинуса легко выводятся из формулы (8), но лучше просто запомнить эти соотношения.
∫exdx=ex+C (8)
∫axdx=axlna+C(a>0,a≠1) (9)
∫shxdx=chx+C (10)
∫chxdx=shx+C (11)
Базовые интегралы от тригонометрических функций
Ошибка, которую часто делают студенты: путают знаки в формулах (12) и (13). Запомнив, что производная синуса равна косинусу, многие почему-то считают, что интеграл от функции sinx равен сosx. Это неверно! Интеграл от синуса равен «минус косинусу», а вот интеграл от cosx равен «просто синусу»:
∫sinxdx=−cosx+C (12)
∫cosxdx=sinx+C (13)
∫1cos2xdx=tgx+C (14)
∫1sin2xdx=−ctgx+C (15)
Сводная таблица интегралов
Скачайте таблицу интегралов (часть I) по этой ссылке
Скачайте таблицу интегралов (часть II) по этой ссылке
Интегралы, сводящиеся к обратным тригонометрическим функциям
Формула (16), приводящая к арктангенсу, естественно, является частным случаем формулы (17) при a=1. Аналогично, (18) — частный случай (19).
Аналогично, (18) — частный случай (19).
∫11+x2dx=arctgx+C=−arcctgx+C (16)
∫1×2+a2=1aarctgxa+C(a≠0) (17)
∫11−x2dx=arcsinx+C=−arccosx+C (18)
Репетитор по математическому анализу
Более сложные интегралы
Данные формулы тоже желательно запомнить. Они также используются достаточно часто, а их вывод довольно утомителен.
∫1×2+a2dx=ln|x+x2+a2|+C (20)
∫1×2−a2dx=ln|x+x2−a2|+C (21)
∫a2−x2dx=x2a2−x2+a22arcsinxa+C(a>0) (22)
∫x2+a2dx=x2x2+a2+a22ln|x+x2+a2|+C(a>0) (23)
∫x2−a2dx=x2x2−a2−a22ln|x+x2−a2|+C(a>0) (24)
1) Интеграл от суммы двух функций равен сумме соответствующих интегралов: ∫(f(x)+g(x))dx=∫f(x)dx+∫g(x)dx (25)
2) Интеграл от разности двух функций равен разности соответствующих интегралов: ∫(f(x)−g(x))dx=∫f(x)dx−∫g(x)dx (26)
3) Константу можно выносить за знак интеграла: ∫Cf(x)dx=C∫f(x)dx (27)
Легко заметить, что свойство (26) — это просто комбинация свойств (25) и (27).
4) Интеграл от сложной функции, если внутренняя функция является линейной: ∫f(Ax+B)dx=1AF(Ax+B)+C(A≠0) (28)
Здесь F(x) — первообразная для функции f(x). Обратите внимание: эта формула подходит только для случая, когда внутренняя функция имеет вид Ax + B.
Важно: не существует универсальной формулы для интеграла от произведения двух функций, а также для интеграла от дроби:
∫f(x)g(x)dx=?∫f(x)g(x)dx=? (30)
Это не означает, конечно, что дробь или произведение нельзя проинтегрировать. Просто каждый раз, увидев интеграл типа (30), вам придется изобретать способ «борьбы» с ним. В каких-то случаях вам поможет интегрирование по частям, где-то придется сделать замену переменной, а иногда помощь могут оказать даже «школьные» формулы алгебры или тригонометрии.
Простой пример на вычисление неопределенного интеграла
Пример 1. Найти интеграл: ∫(3×2+2sinx−7ex+12)dx
Воспользуемся формулами (25) и (26) (интеграл от суммы или разности функций равен сумме или разности соответствующих интегралов. Получаем:
∫3x2dx+∫2sinxdx−∫7exdx+∫12dx
Получаем:
∫3x2dx+∫2sinxdx−∫7exdx+∫12dx
Вспомним, что константу можно выносить за знак интеграла (формула (27)). Выражение преобразуется к виду
3∫x2dx+2∫sinxdx−7∫exdx+12∫1dx
А теперь просто воспользуемся таблицей основных интегралов. Нам потребуется применить формулы (3), (12), (8) и (1). Проинтегрируем степенную функцию, синус, экспоненту и константу 1. Не забудем добавить в конце произвольную постоянную С:
3×33−2cosx−7ex+12x+C
После элементарных преобразований получаем окончательный ответ:
x3−2cosx−7ex+12x+C
Проверьте себя дифференцированием: возьмите производную от полученной функции и убедитесь, что она равна исходному подинтегральному выражению.
Сводная таблица интегралов
| ∫Adx=Ax+C |
| ∫xdx=x22+C |
| ∫x2dx=x33+C |
| ∫1xdx=2x+C |
| ∫1xdx=ln|x|+C |
| ∫1x2dx=−1x+C |
| ∫xndx=xn+1n+1+C(n≠−1) |
| ∫exdx=ex+C |
| ∫axdx=axlna+C(a>0,a≠1) |
| ∫shxdx=chx+C |
| ∫chxdx=shx+C |
| ∫sinxdx=−cosx+C |
| ∫cosxdx=sinx+C |
| ∫1cos2xdx=tgx+C |
| ∫1sin2xdx=−ctgx+C |
| ∫11+x2dx=arctgx+C=−arcctgx+C |
| ∫1×2+a2=1aarctgxa+C(a≠0) |
| ∫11−x2dx=arcsinx+C=−arccosx+C |
| ∫1a2−x2dx=arcsinxa+C=−arccosxa+C(a>0) |
| ∫1×2+a2dx=ln|x+x2+a2|+C |
| ∫1×2−a2dx=ln|x+x2−a2|+C |
| ∫a2−x2dx=x2a2−x2+a22arcsinxa+C(a>0) |
| ∫x2+a2dx=x2x2+a2+a22ln|x+x2+a2|+C(a>0) |
| ∫x2−a2dx=x2x2−a2−a22ln|x+x2−a2|+C(a>0) |
Скачайте таблицу интегралов (часть I) по этой ссылке
Скачайте таблицу интегралов (часть II) по этой ссылке
Если Вы учитесь в ВУЗе, если у Вас возникли сложности с высшей математикой (математический анализ, линейная алгебра, теория вероятностей, статистика), если Вам нужны услуги квалифицированного преподавателя, зайдите на страничку репетитора по высшей математике. Будем решать Ваши проблемы вместе!
Будем решать Ваши проблемы вместе!
Возможно, вас заинтересуют также
Таблица производных элементарных функций
или другие разделы онлайн — справочника по математике.
Рекомендуемая литература для подготовки к экзамену по высшей математике.
Неопределенный интеграл. Понятия и определения. Интегрирование
Содержание.
1. Неопределенный интеграл. Основные определения.
2. Основные свойства неопределенного интеграла.
3. Таблица интегралов.
4. Непосредственное интегрирование.
5. Метод подстановки.
6. Метод интегрирования по частям.
Определение 1. Пусть функция f (x) определена на некотором интервале (a, b) и для всех x ∈ (a, b) существует такая функция F(x), что F’(x) = f (x). Тогда F(x) называется первообразной для f (x) на (a, b) .
Например, одной из первообразных функций для функции cos x будет sin x .
Первообразная не единственна, т. к. (cosx + 2)’ =(cosx)’ + 2’=sin x , (cosx — 3)’ = sin x , а поэтому cos x + 2, cos x — 3 также являются первообразными для sin x .
Теорема. Две различные первообразные одной и той же функции, определенной на
интервале (a, b) , отличаются друг от друга в этом промежутке на постоянное слагаемое, т.е. если F1 (x) и F2 (x) – некоторые первообразные, т. е. F1’ (x)= f (x) и F2’ (x) = f (x) то F1 (x) – F2 (x) = C .
Следствие. Прибавляя к какой-либо первообразной F(x) для данной функции f (x), определенной на промежутке (a, b) , всевозможные постоянные C , мы получим все первообразные для функции f (x) .
Определение 2. Общее выражение для всех первообразных данной непрерывной функции
При этом f (x) называется подынтегральной функцией, f (x)dx – подынтегральным выражением, x – переменной интегрирования.
Согласно определению неопределенного интеграла можно написать:
∫ f (x)dx = F(x)+ C , где F¢(x)= f (x), постоянная C может принимать любое значение и называется произвольной постоянной.
Основные свойства неопределенного интеграла
1. Неопределенный интеграл от дифференциала непрерывно дифференцируемой функции равен самой этой функции с точностью до постоянного слагаемого
2. Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции (1,2).
Замечание. В формулах (1) и (2) знаки и уничтожают друга. В этом смысле интегрирование и дифференцирование являются взаимно обратными математическими операциями.
Свойства линейности неопределенного интеграла.
т. е. любая формула интегрирования не изменяет свой вид, если вместо независимой переменной подставить любую дифференцируемую функцию . Поэтому таблицу интегралов от сложной функции запишем в виде:
Таблица интеграловНепосредственное интегрирование
Непосредственное интегрирование заключается в том, чтобы преобразовать подынтегральное выражение, если это возможно, так чтобы получился дифференциал f (x)dx, а затем в таблице
интегралов найти первообразную.
Пример 1.
Выражение cos xdx заменили на d (sin x) . Получили интеграл
который можно отыскать в таблице интегралов, где u(x) = sin x.
Пример 2.
Здесь мы умножили подынтегральную функцию и разделили на 2, затем внесли 2 под знак дифференциала. Заменим 2dx =d (2x +1) и получим табличный интеграл
Заменим 2dx =d (2x +1) и получим табличный интеграл
Проверим результат дифференцированием:
Пример 3.
В данном примере мы применили прием подведения под знак дифференциала cosx и постоянной 1. cos xdx = d(1+ sin x).
Пример 4.
Метод подстановки
Пример 6.
Здесь удобно применить тригонометрическую подстановку x = sint , с помощью которой мы избавимся от корня. Отсюда dx = costdt .
Метод интегрирования по частям.
Пусть u и v — непрерывно дифференцируемые функции от x . На основании формулы дифференциала произведения имеем d(uv)= udv + vdu.
Иногда формула интегрирования по частям применяется несколько раз. Рассмотрим пример такого интеграла.
Замечание. Иногда применение формулы интегрирования по частям приводит к исходному интегралу, который в таком случае называется циклическим или круговым.
Получили интеграл, в котором cosnx заменился на sin nx .
Проинтегрируем еще раз по частям, обозначим:
Это пример циклического интеграла.
Тема урока: Неопределенный интеграл. Таблица интегралов.
Дата проведения: 27.01.2022г.
Группа 1-3
Предмет: Математика
Преподаватель: Амирханова А. К.
Тема урока: Неопределенный интеграл. Таблица интегралов.
Идём дальше. Те студенты, которые хотя бы мало-мальски «шарят» в производных, — люди грамотные. И, возможно, уже приготовили мне убойный вопрос. 🙂
Скажем, чему равна производная для функции F(x) = x? Ну, единица, единица — слышу недовольные ответы… Всё верно. Единица. Но… Для функции
Также производная будет равна единице и для функции x+1234, и для функции x-10, и для любой другой функции вида x+C, где С — любая константа. Ибо производная любой константы равна нулю, а от прибавления/вычитания нуля никому ни холодно ни жарко.)
Ибо производная любой константы равна нулю, а от прибавления/вычитания нуля никому ни холодно ни жарко.)
Получается неоднозначность. Выходит, что для функции f(x) = 1 первообразной служит не только функция F(x) = x, но и функция F1(x) = x+1234 и функция F2(x) = x-10 и так далее!
Да. Именно так.) У всякой (непрерывной на промежутке) функции существует не какая-то одна первообразная, а бесконечно много — целое семейство! Не одна мама или папа, а целая родословная, ага.)
Но! Всех наших родственников-первообразных объединяет одно важное свойство. На то они и родственники.) Свойство настолько важное, что в процессе разбора приёмов интегрирования мы про него ещё не раз вспомним. И будем вспоминать ещё долго. )
)
Вот оно, это свойство:
Любые две первообразные F1(x) и F2(x) от одной и той же функции f(x) отличаются на константу:
F1(x) — F2(x) = С.
Кому интересно доказательство — штудируйте литературу или конспекты лекций.) Ладно, так уж и быть, докажу. Благо доказательство тут элементарное, в одно действие. Берём равенство
F1(x) — F2(x) = С
и дифференцируем обе его части. То есть, просто тупо ставим штрихи:
Вот и всё. Как говорится, ЧТД. 🙂
О чём говорит это свойство? А о том, что две различные первообразные от одной и той же функции f(x) не могут отличаться на какое-то выражение с иксом . Только строго на константу! Иными словами, если у нас есть график какой-то одной из первообразных (пусть это будет F(x)), то графики всех остальных наших первообразных строятся параллельным переносом графика F(x) вдоль оси игреков.
Только строго на константу! Иными словами, если у нас есть график какой-то одной из первообразных (пусть это будет F(x)), то графики всех остальных наших первообразных строятся параллельным переносом графика F(x) вдоль оси игреков.
Посмотрим, как это выглядит на примере функции f(x) = x. Все её первообразные, как нам уже известно, имеют общий вид F(x) = x2/2+C. На картинке это выглядит как бесконечное множество парабол, получаемых из «основной» параболы y = x2/2 сдвигом вдоль оси OY вверх или вниз в зависимости от значения константы С.
Помните школьное построение графика функции y=f(x)+a сдвигом графика y=f(x) на «а» единиц вдоль оси игреков?) Вот и тут то же самое.)
Причём, обратите внимание: наши параболы нигде не пересекаются! Оно и естественно. Ведь две различные функции y1(x) и y2(x) неизбежно будут соответствовать двум различным значениям константы — С1 и С2.
Поэтому уравнение y1(x) = y2(x) никогда не имеет решений:
С1 = С2
x ∊ ∅, так как С1 ≠ С2
А теперь мы плавненько подходим ко второму краеугольному понятию интегрального исчисления. Как мы только что установили, у всякой функции f(x) существует бесконечное множество первообразных F(x) + C, отличающихся друг от друга на константу. Это самое бесконечное множество тоже имеет своё специальное название.) Что ж, прошу любить и жаловать!
Что такое неопределённый интеграл?
Множество всех первообразных для функции f(x) называется неопределённым интегралом от функции f(x).
Вот и всё определение.)
«Неопределённый» — потому, что множество всех первообразных для одной и той же функции бесконечно. Слишком много различных вариантов.)
Слишком много различных вариантов.)
«Интеграл» — с подробной расшифровкой этого зверского слова мы познакомимся в следующем большом разделе, посвящённом определённым интегралам. А пока, в грубой форме, будем считать интегралом нечто общее, единое, целое. А интегрированием — объединение, обобщение, в данном случае переход от частного (производной) к общему (первообразным). Вот, как-то так.
Обозначается неопределённый интеграл вот так:
Читается так же, как и пишется: интеграл эф от икс дэ икс. Или интеграл от эф от икс дэ икс. Ну, вы поняли.)
Теперь разберёмся с обозначениями.
∫ — значок интеграла. Смысл тот же, что и штрих для производной.)
d — значок дифференциала. Не пугаемся! Зачем он там нужен — чуть ниже.
f(x) — подынтегральная функция (через «ы»).
f(x)dx — подынтегральное выражение. Или, грубо говоря, «начинка» интеграла.
Согласно смыслу неопределённого интеграла,
Здесь F(x) — та самая первообразная для функции f(x), которую мы так или иначе нашли сами. Как именно нашли — не суть. Например, мы установили, что F(x) = x2/2 для f(x)=x.
«С» — произвольная постоянная. Или, более научно, интегральная константа. Или константа интегрирования. Всё едино.)
А теперь вернёмся к нашим самым первым примерам на поиск первообразной. В терминах неопределённого интеграла можно теперь смело записать:
И так далее.) Идея понятна, думаю. Ни в коем случае не забываем приплюсовывать константу С!
Что такое интегральная константа и зачем она нужна?
Вопрос очень интересный. И очень (ОЧЕНЬ!) важный. Интегральная константа из всего бесконечного множества первообразных выделяет ту линию, которая проходит через заданную точку.
И очень (ОЧЕНЬ!) важный. Интегральная константа из всего бесконечного множества первообразных выделяет ту линию, которая проходит через заданную точку.
В чём суть. Из исходного бесконечного множества первообразных (т.е. неопределённого интеграла) надо выделить ту кривую, которая будет проходить через заданную точку. С какими-то конкретными координатами. Такое задание всегда и везде встречается при начальном знакомстве с интегралами. Как в школе, так и в ВУЗЕ.
Типичная задачка:
Среди множества всех первообразных функции f=x выделить ту, которая проходит через точку (2;2).
Начинаем думать головой… Множество всех первоообразных — это значит, сначала надо проинтегрировать нашу исходную функцию. То есть, икс (х). Этим мы занимались чуть выше и получили такой ответ:
А теперь разбираемся, что именно мы получили. Мы получили не одну функцию, а целое семейство функций. Каких именно? Вида y=x2/2+C. Зависящее от значения константы С. И вот это значение константы нам и предстоит теперь «отловить».) Ну что, займёмся ловлей?)
Каких именно? Вида y=x2/2+C. Зависящее от значения константы С. И вот это значение константы нам и предстоит теперь «отловить».) Ну что, займёмся ловлей?)
Удочка наша — семейство кривых (парабол) y=x2/2+C.
Константы — это рыбины. Много-много. Но на каждую найдётся свой крючок и приманка.)
А что же служит приманкой? Правильно! Наша точка (-2;2).
Вот и подставляем координаты нашей точки в общий вид первообразных! Получим:
y(2) = 2
Отсюда уже легко ищется C = 0.
Что сиё означает? Это значит, что из всего бесконечного множества парабол вида y=x2/2+C только парабола с константой С=0 нам подходит! А именно: y=x2/2. И только она. Только эта парабола будет проходить через нужную нам точку (-2; 2). А все остальные параболы из нашего семейства проходить через эту точку уже не будут. Через какие-то другие точки плоскости — да, а вот через точку (2; 2) — уже нет. Уловили?
И только она. Только эта парабола будет проходить через нужную нам точку (-2; 2). А все остальные параболы из нашего семейства проходить через эту точку уже не будут. Через какие-то другие точки плоскости — да, а вот через точку (2; 2) — уже нет. Уловили?
Для наглядности вот вам две картинки — всё семейство парабол (т.е. неопределённый интеграл) и какая-то конкретная парабола, соответствующая конкретному значению константы и проходящая через конкретную точку:
Видите, насколько важно учитывать константу С при интегрировании! Так что не пренебрегаем этой буковкой «С» и не забываем приписывать к окончательному ответу.
А теперь разберёмся, зачем же внутри интегралов везде тусуется символ dx. Забывают про него студенты частенько… А это, между прочим, тоже ошибка! И довольно грубая. Всё дело в том, что интегрирование — операция, обратная дифференцированию. А что именно является результатом дифференцирования? Производная? Верно, но не совсем. Дифференциал!
Всё дело в том, что интегрирование — операция, обратная дифференцированию. А что именно является результатом дифференцирования? Производная? Верно, но не совсем. Дифференциал!
В нашем случае, для функции f(x) дифференциал её первообразной F(x), будет:
Кому непонятна данная цепочка — срочно повторить определение и смысл дифференциала и то, как именно он раскрывается! Иначе в интегралах будете тормозить нещадно….
Напомню, в самой грубой обывательской форме, что дифференциал любой функции f(x) — это просто произведение f’(x)dx. И всё! Взять производную и помножить её на дифференциал аргумента (т.е. dx). То есть, любой дифференциал, по сути, сводится к вычислению обычной производной.
Поэтому, строго говоря, интеграл «берётся» не от функции f(x), как принято считать, а от дифференциала f(x)dx! Но, в упрощённом варианте, принято говорить, что «интеграл берётся от функции». Или: «Интегрируется функция f(x)«. Это одно и то же. И мы будем говорить точно так же. Но про значок dx при этом забывать не будем! 🙂
Или: «Интегрируется функция f(x)«. Это одно и то же. И мы будем говорить точно так же. Но про значок dx при этом забывать не будем! 🙂
И сейчас я подскажу, как его не забыть при записи. Представьте себе сначала, что вы вычисляете обычную производную по переменной икс. Как вы обычно её пишете?
Вот так: f’(x), y’(x), у’x. Или более солидно, через отношение дифференциалов: dy/dx. Все эти записи нам показывают, что производная берётся именно по иксу. А не по «игреку», «тэ» или какой-то там другой переменной.)
Так же и в интегралах. Запись ∫f(x)dx нам тоже как бы показывает, что интегрирование проводится именно по переменной икс. Конечно, это всё очень упрощённо и грубо, но зато понятно, я надеюсь. И шансы забыть приписать вездесущее dx резко снижаются.)
Итак, что такое же неопределённый интеграл — разобрались. Прекрасно.) Теперь хорошо бы научиться эти самые неопределённые интегралы вычислять. Или, попросту говоря, «брать». 🙂 И вот тут студентов поджидает две новости — хорошая и не очень. Пока начнём с хорошей.)
Или, попросту говоря, «брать». 🙂 И вот тут студентов поджидает две новости — хорошая и не очень. Пока начнём с хорошей.)
Новость хорошая. Для интегралов, так же как и для производных, существует своя табличка. И все интегралы, которые нам будут встречаться по пути, даже самые страшные и навороченные, мы по определённым правилам будем так или иначе сводить к этим самым табличным.)
Итак, вот она, таблица интегралов!
Вот такая вот красивая табличка интегралов от самых-самых популярных функций. Рекомендую обратить отдельное внимание на группу формул 1-2 (константа и степенная функция). Это — самые употребительные формулы в интегралах!
Третья группа формул (тригонометрия), как можно догадаться, получена простым обращением соответствующих формул для производных.
Например:
C четвёртой группой формул (показательная функция) — всё аналогично.
А вот четыре последние группы формул (5-8) для нас новые. Откуда же они взялись и за какие такие заслуги именно эти экзотические функции, вдруг, вошли в таблицу основных интегралов? Чем же эти группы функций так выделяются на фоне остальных функций?
Так уж сложилось исторически в процессе развития методов интегрирования. Когда мы будем тренироваться брать самые-самые разнообразные интегралы, то вы поймёте, что интегралы от перечисленных в таблице функций встречаются очень и очень часто. Настолько часто, что математики отнесли их к табличным.) Через них выражаются очень многие другие интегралы, от более сложных конструкций.
Ради интереса можно взять какую-нибудь из этих жутких формул и продифференцировать. 🙂 Например, самую зверскую 7-ю формулу.
Всё нормально. Не обманули математики. 🙂
Таблицу интегралов, как и таблицу производных, желательно знать наизусть. Во всяком случае, первые четыре группы формул. Это не так трудно, как кажется на первый взгляд. Заучивать наизусть последние четыре группы (с дробями и корнями) пока не стоит. Всё равно поначалу будете путаться, где логарифм писать, где арктангенс, где арксинус, где 1/а, где 1/2а … Выход тут один — решать побольше примеров. Тогда таблица сама собой постепенно и запомнится, а сомнения грызть перестанут.)
Во всяком случае, первые четыре группы формул. Это не так трудно, как кажется на первый взгляд. Заучивать наизусть последние четыре группы (с дробями и корнями) пока не стоит. Всё равно поначалу будете путаться, где логарифм писать, где арктангенс, где арксинус, где 1/а, где 1/2а … Выход тут один — решать побольше примеров. Тогда таблица сама собой постепенно и запомнится, а сомнения грызть перестанут.)
Особо любознательные лица, присмотревшись к таблице, могут спросить: а где же в таблице интегралы от других элементарных «школьных» функций — тангенса, логарифма, «арков»? Скажем, почему в таблице ЕСТЬ интеграл от синуса, но при этом НЕТУ, скажем, интеграла от тангенса tg x? Или нету интеграла от логарифма ln x? От арксинуса arcsin x? Чем они хуже? Но зато полно каких-то «левых» функций — с корнями, дробями, квадратами…
Ответ. Ничем не хуже.) Просто вышеназванные интегралы (от тангенса, логарифма, арксинуса и т.д.) не являются табличными. И встречаются на практике значительно реже, нежели те, что представлены в таблице. Поэтому знать наизусть, чему они равны, вовсе не обязательно. Достаточно лишь знать, как они вычисляются.)
И встречаются на практике значительно реже, нежели те, что представлены в таблице. Поэтому знать наизусть, чему они равны, вовсе не обязательно. Достаточно лишь знать, как они вычисляются.)
Что, кому-то всё-таки невтерпёж? Так уж и быть, специально для вас!
Ну как, будете заучивать? 🙂 Не будете? И не надо.) Но не волнуйтесь, все подобные интегралы мы обязательно найдём. В соответствующих уроках. 🙂
Что ж, теперь переходим к свойствам неопределённого интеграла. Да-да, ничего не поделать! Вводится новое понятие — тут же и какие-то его свойства рассматриваются.
Просмотр содержимого документа
«Тема урока: Неопределенный интеграл. Таблица интегралов.»
Дата проведения: 27.01.2022г.
Группа 1-3
Предмет: Математика
Преподаватель: Амирханова А. К.
К.
Тема урока: Неопределенный интеграл. Таблица интегралов.
Идём дальше. Те студенты, которые хотя бы мало-мальски «шарят» в производных, — люди грамотные. И, возможно, уже приготовили мне убойный вопрос. 🙂
Скажем, чему равна производная для функции F(x) = x? Ну, единица, единица — слышу недовольные ответы… Всё верно. Единица. Но… Для функции G(x) = x+1 производная тоже будет равна единице:
Также производная будет равна единице и для функции x+1234, и для функции x-10, и для любой другой функции вида x+C, где С — любая константа. Ибо производная любой константы равна нулю, а от прибавления/вычитания нуля никому ни холодно ни жарко.)
Получается неоднозначность. Выходит, что для функции f(x) = 1 первообразной служит не только функция F(x) = x, но и функция F1(x) = x+1234 и функция F2(x) = x-10 и так далее!
Да. Именно так.) У всякой (непрерывной на промежутке) функции существует не какая-то одна первообразная, а бесконечно много — целое семейство! Не одна мама или папа, а целая родословная, ага.)
Именно так.) У всякой (непрерывной на промежутке) функции существует не какая-то одна первообразная, а бесконечно много — целое семейство! Не одна мама или папа, а целая родословная, ага.)
Но! Всех наших родственников-первообразных объединяет одно важное свойство. На то они и родственники.) Свойство настолько важное, что в процессе разбора приёмов интегрирования мы про него ещё не раз вспомним. И будем вспоминать ещё долго.)
Вот оно, это свойство:
Любые две первообразные F1(x) и F2(x) от одной и той же функции f(x) отличаются на константу:
F1(x) — F2(x) = С.
Кому интересно доказательство — штудируйте литературу или конспекты лекций.) Ладно, так уж и быть, докажу. Благо доказательство тут элементарное, в одно действие. Берём равенство
F1(x) — F2(x) = С
и дифференцируем обе его части. То есть, просто тупо ставим штрихи:
То есть, просто тупо ставим штрихи:
Вот и всё. Как говорится, ЧТД. 🙂
О чём говорит это свойство? А о том, что две различные первообразные от одной и той же функции f(x) не могут отличаться на какое-то выражение с иксом . Только строго на константу! Иными словами, если у нас есть график какой-то одной из первообразных (пусть это будет F(x)), то графики всех остальных наших первообразных строятся параллельным переносом графика F(x) вдоль оси игреков.
Посмотрим, как это выглядит на примере функции f(x) = x. Все её первообразные, как нам уже известно, имеют общий вид F(x) = x2/2+C. На картинке это выглядит как бесконечное множество парабол, получаемых из «основной» параболы y = x2/2 сдвигом вдоль оси OY вверх или вниз в зависимости от значения константы С.
Помните школьное построение графика функции y=f(x)+a сдвигом графика y=f(x) на «а» единиц вдоль оси игреков?) Вот и тут то же самое.)
Причём, обратите внимание: наши параболы нигде не пересекаются! Оно и естественно. Ведь две различные функции y1(x) и y2(x) неизбежно будут соответствовать двум различным значениям константы — С1 и С2.
Поэтому уравнение y1(x) = y2(x) никогда не имеет решений:
С1 = С2
x ∊ ∅, так как С1 ≠ С2
А теперь мы плавненько подходим ко второму краеугольному понятию интегрального исчисления. Как мы только что установили, у всякой функции f(x) существует бесконечное множество первообразных F(x) + C, отличающихся друг от друга на константу. Это самое бесконечное множество тоже имеет своё специальное название.) Что ж, прошу любить и жаловать!
Это самое бесконечное множество тоже имеет своё специальное название.) Что ж, прошу любить и жаловать!
Что такое неопределённый интеграл?
Множество всех первообразных для функции f(x) называется неопределённым интегралом от функции f(x).
Вот и всё определение.)
«Неопределённый» — потому, что множество всех первообразных для одной и той же функции бесконечно. Слишком много различных вариантов.)
«Интеграл» — с подробной расшифровкой этого зверского слова мы познакомимся в следующем большом разделе, посвящённом определённым интегралам. А пока, в грубой форме, будем считать интегралом нечто общее, единое, целое. А интегрированием — объединение, обобщение, в данном случае переход от частного (производной) к общему (первообразным). Вот, как-то так.
Обозначается неопределённый интеграл вот так:
Читается так же, как и пишется: интеграл эф от икс дэ икс. Или интеграл от эф от икс дэ икс. Ну, вы поняли.)
Или интеграл от эф от икс дэ икс. Ну, вы поняли.)
Теперь разберёмся с обозначениями.
∫ — значок интеграла. Смысл тот же, что и штрих для производной.)
d — значок дифференциала. Не пугаемся! Зачем он там нужен — чуть ниже.
f(x) — подынтегральная функция (через «ы»).
f(x)dx — подынтегральное выражение. Или, грубо говоря, «начинка» интеграла.
Согласно смыслу неопределённого интеграла,
Здесь F(x) — та самая первообразная для функции f(x), которую мы так или иначе нашли сами. Как именно нашли — не суть. Например, мы установили, что F(x) = x2/2 для f(x)=x.
«С» — произвольная постоянная. Или, более научно, интегральная константа. Или константа интегрирования. Всё едино. )
)
А теперь вернёмся к нашим самым первым примерам на поиск первообразной. В терминах неопределённого интеграла можно теперь смело записать:
И так далее.) Идея понятна, думаю. Ни в коем случае не забываем приплюсовывать константу С!
Что такое интегральная константа и зачем она нужна?
Вопрос очень интересный. И очень (ОЧЕНЬ!) важный. Интегральная константа из всего бесконечного множества первообразных выделяет ту линию, которая проходит через заданную точку.
В чём суть. Из исходного бесконечного множества первообразных (т.е. неопределённого интеграла) надо выделить ту кривую, которая будет проходить через заданную точку. С какими-то конкретными координатами. Такое задание всегда и везде встречается при начальном знакомстве с интегралами. Как в школе, так и в ВУЗЕ.
Типичная задачка:
Среди множества всех первообразных функции f=x выделить ту, которая проходит через точку (2;2).
Начинаем думать головой… Множество всех первоообразных — это значит, сначала надо проинтегрировать нашу исходную функцию. То есть, икс (х). Этим мы занимались чуть выше и получили такой ответ:
А теперь разбираемся, что именно мы получили. Мы получили не одну функцию, а целое семейство функций. Каких именно? Вида y=x2/2+C. Зависящее от значения константы С. И вот это значение константы нам и предстоит теперь «отловить».) Ну что, займёмся ловлей?)
Удочка наша — семейство кривых (парабол) y=x2/2+C.
Константы — это рыбины. Много-много. Но на каждую найдётся свой крючок и приманка.)
А что же служит приманкой? Правильно! Наша точка (-2;2).
Вот и подставляем координаты нашей точки в общий вид первообразных! Получим:
y(2) = 2
Отсюда уже легко ищется C = 0.
Что сиё означает? Это значит, что из всего бесконечного множества парабол вида y=x2/2+C только парабола с константой С=0 нам подходит! А именно: y=x2/2. И только она. Только эта парабола будет проходить через нужную нам точку (-2; 2). А все остальные параболы из нашего семейства проходить через эту точку уже не будут. Через какие-то другие точки плоскости — да, а вот через точку (2; 2) — уже нет. Уловили?
Для наглядности вот вам две картинки — всё семейство парабол (т.е. неопределённый интеграл) и какая-то конкретная парабола, соответствующая конкретному значению константы и проходящая через конкретную точку:
Видите, насколько важно учитывать константу С при интегрировании! Так что не пренебрегаем этой буковкой «С» и не забываем приписывать к окончательному ответу.
А теперь разберёмся, зачем же внутри интегралов везде тусуется символ dx. Забывают про него студенты частенько… А это, между прочим, тоже ошибка! И довольно грубая. Всё дело в том, что интегрирование — операция, обратная дифференцированию. А что именно является результатом дифференцирования? Производная? Верно, но не совсем. Дифференциал!
В нашем случае, для функции f(x) дифференциал её первообразной F(x), будет:
Кому непонятна данная цепочка — срочно повторить определение и смысл дифференциала и то, как именно он раскрывается! Иначе в интегралах будете тормозить нещадно….
Напомню, в самой грубой обывательской форме, что дифференциал любой функции f(x) — это просто произведение f’(x)dx. И всё! Взять производную и помножить её на дифференциал аргумента (т.е. dx). То есть, любой дифференциал, по сути, сводится к вычислению обычной производной.
Поэтому, строго говоря, интеграл «берётся» не от функции f(x), как принято считать, а от дифференциала f(x)dx! Но, в упрощённом варианте, принято говорить, что «интеграл берётся от функции». Или: «Интегрируется функция f(x)«. Это одно и то же. И мы будем говорить точно так же. Но про значок dx при этом забывать не будем! 🙂
Или: «Интегрируется функция f(x)«. Это одно и то же. И мы будем говорить точно так же. Но про значок dx при этом забывать не будем! 🙂
И сейчас я подскажу, как его не забыть при записи. Представьте себе сначала, что вы вычисляете обычную производную по переменной икс. Как вы обычно её пишете?
Вот так: f’(x), y’(x), у’x. Или более солидно, через отношение дифференциалов: dy/dx. Все эти записи нам показывают, что производная берётся именно по иксу. А не по «игреку», «тэ» или какой-то там другой переменной.)
Так же и в интегралах. Запись ∫f(x)dx нам тоже как бы показывает, что интегрирование проводится именно по переменной икс. Конечно, это всё очень упрощённо и грубо, но зато понятно, я надеюсь. И шансы забыть приписать вездесущее dx резко снижаются.)
Итак, что такое же неопределённый интеграл — разобрались. Прекрасно.) Теперь хорошо бы научиться эти самые неопределённые интегралы вычислять. Или, попросту говоря, «брать». 🙂 И вот тут студентов поджидает две новости — хорошая и не очень. Пока начнём с хорошей.)
Или, попросту говоря, «брать». 🙂 И вот тут студентов поджидает две новости — хорошая и не очень. Пока начнём с хорошей.)
Новость хорошая. Для интегралов, так же как и для производных, существует своя табличка. И все интегралы, которые нам будут встречаться по пути, даже самые страшные и навороченные, мы по определённым правилам будем так или иначе сводить к этим самым табличным.)
Итак, вот она, таблица интегралов!
Вот такая вот красивая табличка интегралов от самых-самых популярных функций. Рекомендую обратить отдельное внимание на группу формул 1-2 (константа и степенная функция). Это — самые употребительные формулы в интегралах!
Третья группа формул (тригонометрия), как можно догадаться, получена простым обращением соответствующих формул для производных.
Например:
C четвёртой группой формул (показательная функция) — всё аналогично.
А вот четыре последние группы формул (5-8) для нас новые. Откуда же они взялись и за какие такие заслуги именно эти экзотические функции, вдруг, вошли в таблицу основных интегралов? Чем же эти группы функций так выделяются на фоне остальных функций?
Так уж сложилось исторически в процессе развития методов интегрирования. Когда мы будем тренироваться брать самые-самые разнообразные интегралы, то вы поймёте, что интегралы от перечисленных в таблице функций встречаются очень и очень часто. Настолько часто, что математики отнесли их к табличным.) Через них выражаются очень многие другие интегралы, от более сложных конструкций.
Ради интереса можно взять какую-нибудь из этих жутких формул и продифференцировать. 🙂 Например, самую зверскую 7-ю формулу.
Всё нормально. Не обманули математики. 🙂
Таблицу интегралов, как и таблицу производных, желательно знать наизусть. Во всяком случае, первые четыре группы формул. Это не так трудно, как кажется на первый взгляд. Заучивать наизусть последние четыре группы (с дробями и корнями) пока не стоит. Всё равно поначалу будете путаться, где логарифм писать, где арктангенс, где арксинус, где 1/а, где 1/2а … Выход тут один — решать побольше примеров. Тогда таблица сама собой постепенно и запомнится, а сомнения грызть перестанут.)
Это не так трудно, как кажется на первый взгляд. Заучивать наизусть последние четыре группы (с дробями и корнями) пока не стоит. Всё равно поначалу будете путаться, где логарифм писать, где арктангенс, где арксинус, где 1/а, где 1/2а … Выход тут один — решать побольше примеров. Тогда таблица сама собой постепенно и запомнится, а сомнения грызть перестанут.)
Особо любознательные лица, присмотревшись к таблице, могут спросить: а где же в таблице интегралы от других элементарных «школьных» функций — тангенса, логарифма, «арков»? Скажем, почему в таблице ЕСТЬ интеграл от синуса, но при этом НЕТУ, скажем, интеграла от тангенса tg x? Или нету интеграла от логарифма ln x? От арксинуса arcsin x? Чем они хуже? Но зато полно каких-то «левых» функций — с корнями, дробями, квадратами…
Ответ. Ничем не хуже.) Просто вышеназванные интегралы (от тангенса, логарифма, арксинуса и т.д.) не являются табличными. И встречаются на практике значительно реже, нежели те, что представлены в таблице. Поэтому знать наизусть, чему они равны, вовсе не обязательно. Достаточно лишь знать, как они вычисляются.)
Поэтому знать наизусть, чему они равны, вовсе не обязательно. Достаточно лишь знать, как они вычисляются.)
Что, кому-то всё-таки невтерпёж? Так уж и быть, специально для вас!
Ну как, будете заучивать? 🙂 Не будете? И не надо.) Но не волнуйтесь, все подобные интегралы мы обязательно найдём. В соответствующих уроках. 🙂
Что ж, теперь переходим к свойствам неопределённого интеграла. Да-да, ничего не поделать! Вводится новое понятие — тут же и какие-то его свойства рассматриваются.
1
Первый слайд презентации: Первообразная и неопределенный интеграл. Таблица интегралов. Подведение под знак дифференциала. Интегрирование по частям (1 и 2 типы). Определенный интеграл. Формула Ньютона – Лейбница.
 Замена переменной в определенном интеграле. Вычисление площади с помощью определенного интеграла
Замена переменной в определенном интеграле. Вычисление площади с помощью определенного интеграла
Занятие 3.
Изображение слайда
2
Слайд 2: Неопределенный интеграл, его свойства и вычисление Первообразная и неопределенный интеграл
Изображение слайда
3
Слайд 3
Изображение слайда
4
Слайд 4
Изображение слайда
5
Слайд 5
Изображение слайда
6
Слайд 6: Свойства интеграла
Производная неопределенного интеграла равна подынтегральной функции, а его дифференциал- подынтегральному выражению. Действительно:
Действительно:
Изображение слайда
7
Слайд 7: Свойства интеграла
3. Неопределенный интеграл от дифференциала непрерывно дифференцируемой функции равен самой этой функции с точностью до постоянной: так как является первообразной для
Изображение слайда
8
Слайд 8: Свойства интеграла
Изображение слайда
9
Слайд 9: Таблица неопределенных интегралов
Изображение слайда
10
Слайд 10: Таблица неопределенных интегралов
Изображение слайда
11
Слайд 11: Свойства дифференциалов
При интегрировании удобно пользоваться свойствами:
Изображение слайда
12
Слайд 12: Примеры
Изображение слайда
13
Слайд 13: Примеры
Изображение слайда
14
Слайд 14: Независимость от вида переменной
Изображение слайда
15
Слайд 15: Пример
Вычислим
Изображение слайда
16
Слайд 16: Методы интегрирования Интегрирование по частям
Изображение слайда
17
Слайд 17: Примеры
Изображение слайда
18
Слайд 18: Примеры
Изображение слайда
19
Слайд 19: Метод замены переменной
Изображение слайда
20
Слайд 20: Интегрирование функций, содержащих квадратный трехчлен
Изображение слайда
21
Слайд 21: Пример
Изображение слайда
22
Слайд 22: Пример
Найти
Изображение слайда
23
Слайд 23: Определенный интеграл, его основные свойства.
 Формула Ньютона- Лейбница. Приложения определенного интеграла
Формула Ньютона- Лейбница. Приложения определенного интеграла
К понятию определенного интеграла приводит задача нахождения площади криволинейной трапеции. Пусть на некотором интервале [ a, b ] задана непрерывная функция Задача: Построить ее график и найти F площадь фигуры, ограниченной этой кривой, двумя прямыми x = a и x = b, а снизу – отрезком оси абсцисс между точками x = a и x = b.
Изображение слайда
24
Слайд 24
Фигура aABb называется криволинейной трапецией
Изображение слайда
25
Слайд 25: Определение
Под определенным интегралом
от данной непрерывной функции f ( x ) на данном отрезке [ a ; b ] понимается соответствующее приращение ее первообразной, то есть
Числа a и b – пределы интегрирования, [ a ; b ] – промежуток интегрирования.
Изображение слайда
26
Слайд 26: Правило:
Определенный интеграл равен разности значений первообразной подынтегральной функции для верхнего и нижнего пределов интегрирования. Введя обозначения для разности Формула Ньютона – Лейбница.
Изображение слайда
27
Слайд 27: Основные свойства определенного интеграла
1) Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. где x и t – любые буквы. 2) Определенный интеграл с одинаковыми пределами интегрирования равен нулю
Изображение слайда
28
Слайд 28
3) При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный
( свойство аддитивности )
4) Если промежуток [ a ; b ] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутку [ a ; b ], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
Изображение слайда
29
Слайд 29
5) Постоянный множитель можно выносить за знак определенного интеграла. 6) Определенный интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
Изображение слайда
30
Слайд 30: 3. Замена переменной в определенном интеграле
где для, функции и непрерывны на Пример: = = x 1 5 t 0 4
Изображение слайда
31
Слайд 31: Несобственные интегралы
Определение. Пусть функция f ( x ) определена на бесконечном интервале [ a ; + ) и интегрируется на любом интервале [ a ; b ], где b < + . Если существует
,
то этот предел называется несобственным интегралом функции f(x) на интервале
[ a ; + ) и обозначается.
Пусть функция f ( x ) определена на бесконечном интервале [ a ; + ) и интегрируется на любом интервале [ a ; b ], где b < + . Если существует
,
то этот предел называется несобственным интегралом функции f(x) на интервале
[ a ; + ) и обозначается.
Изображение слайда
32
Слайд 32
Таким образом, по определению, Если этот предел — некоторое число, то интеграл называется сходящимся, если предела не существует, или он равен , то говорят, что интеграл расходится.
Изображение слайда
33
Слайд 33: Пример. Интеграл Пуассона:
если а = 1, то Интеграл сходится, и его значение.
Изображение слайда
34
Слайд 34: 5.
 Приложения определенного интеграла
Приложения определенного интеграла
1) Площадь плоских фигур. а) если б) если в )
Изображение слайда
35
Слайд 35
г) 2) Многие физические величины можно определить и задать через понятие интеграла. Например, работа для любой силы вычисляется как интеграл от величины силы по длине пути.
Изображение слайда
36
Слайд 36: ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
Если каждой паре ( x,y ) значений двух независимых переменных из области D ставится определенное значение z, то говорят, что z есть функция двух переменных ( x,y ).
Изображение слайда
37
Слайд 37: Частные приращения и частные производные
Изображение слайда
38
Слайд 38: Полное приращение функции 2-х переменных
Если обеим переменным дать приращение, то функция получит полное приращение
Изображение слайда
39
Слайд 39: Полное приращение и полный дифференциал
Изображение слайда
40
Слайд 40: Дифференциалы высшего порядка
Дифференциалом второго порядка функции z = f ( x,y ) называется
Вообще:
Если х и у независимые переменные, то.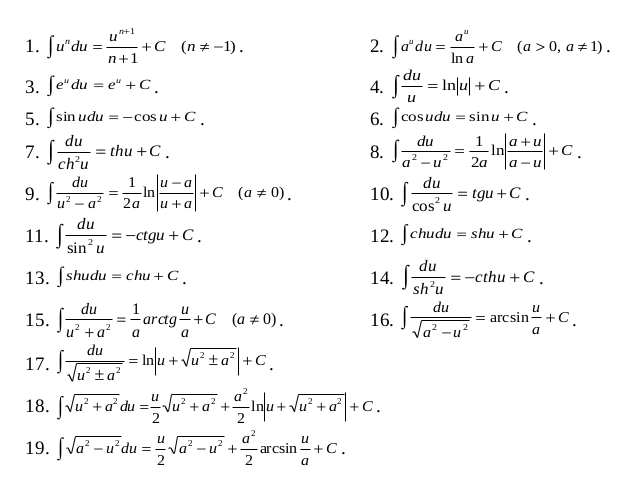
Изображение слайда
41
Слайд 41: Экстремумы функции двух переменных
Определение. Говорят, что в точке функция f ( x, y ) имеет максимум, если c уществует такая окрестность этой точки, что для всех точек P ( x, y ) этой окрестности, отличных от, выполнено неравенство Аналогично определяется минимум функции. Минимум и максимум функции называются ее экстремумами. .
Изображение слайда
42
Слайд 42: Экстремумы функции двух переменных
Теорема (необходимое условие экстремума ). В точке экстремума функции нескольких переменных каждая ее частная производная либо равна нулю, либо не существует.
Точки, в которых выполнены эти условия, называются критическими.
Изображение слайда
43
Слайд 43: Достаточные условия экстремума функции двух переменных
Теорема. Пусть функция z = f ( x,y ) определена и имеет непрерывные частные производные до 3-го порядка в некоторой окрестности точки , в которой. Если при этом в этой точке выполнено условие, то точка является точкой экстремума функции, причем точкой максимума, если , и точкой минимума, если. Если же в этой точке, то экстремума в точке нет. В том случае, если в точке, теорема ответа не дает.
Изображение слайда
44
Слайд 44: Пример
Исследовать на экстремум функцию
Изображение слайда
45
Слайд 45: Наибольшее и наименьшее значения функции
Определение. Наименьшее или наибольшее значение функции в данной области называется абсолютным экстремумом функции (абсолютным минимумом или абсолютным максимумом соответственно) в этой области.
Наименьшее или наибольшее значение функции в данной области называется абсолютным экстремумом функции (абсолютным минимумом или абсолютным максимумом соответственно) в этой области.
Изображение слайда
46
Слайд 46
Известно, что непрерывная в замкнутой ограниченной области функция достигает в ней своих наибольшего и наименьшего значений. Абсолютный экстремум достигается функцией либо в критических точках, либо на границе области.
Изображение слайда
47
Слайд 47
Пусть функция непрерывна в замкнутой ограниченной области G, дифференцируема внутри этой области. Чтобы найти наибольшее и наименьшее значения функции в этой области, нужно :
1)найти критические точки, принадлежащие этой области, и вычислить в них значения функции;
2)найти наибольшее и наименьшее значения функции на границе области;
3)из всех найденных значений выбрать наибольшее и наименьшее.
Изображение слайда
48
Слайд 48: Скалярное поле Основные определения
Пусть в области D пространства Охуz задана функция u = u ( х,у,z ). В этом случае говорят, что в области D задано скалярное поле, а саму функцию u = u ( х,у,z )называют функцией поля. Например, поле давлений, температур и т.д.
Изображение слайда
49
Слайд 49: Скалярное поле Основные определения
Множество точек М области D, для которых скалярное поле сохраняет постоянное значение, т. е. u ( М )=С, называется поверхностью уровня ( или изоповерхностью) скалярного поля.
Изображение слайда
50
Слайд 50
Если область D расположена на плоскости Оху, то поле u = u ( х,у ) является плоским. Поверхности уровня называют в этом случае линиями уровня.
Поверхности уровня называют в этом случае линиями уровня.
Изображение слайда
51
Слайд 51
Пусть
Изображение слайда
52
Слайд 52: Линии уровня
Пусть. Линии уровня этой поверхности имеют вид
Изображение слайда
53
Слайд 53
Пусть дан конус
Изображение слайда
54
Слайд 54: Линии уровня конуса
Изображение слайда
55
Слайд 55
Пусть задана дифференцируемая функция скалярного поля. Рассмотрим точку этого поля и луч
, выходящий из точки P в направлении единичного вектора
где –углы, образованные вектором
с осями координат.
Рассмотрим точку этого поля и луч
, выходящий из точки P в направлении единичного вектора
где –углы, образованные вектором
с осями координат.
Изображение слайда
56
Слайд 56: Определение
Пусть – какая-нибудь другая точка этого луча. Обозначим – расстояние между точками P и ; называют величиной перемещения. Приращением функции в направлении назовем разность x P γ y ℓ z x P 1 β α 0 Рис.
Изображение слайда
57
Слайд 57
Производной функции в точке P по направлению называется предел отношения приращения функции в направлении к величине перемещения при : .
Изображение слайда
58
Слайд 58: Вычисление производной по направлению
Формула вычисления производной по направлению:
Изображение слайда
59
Слайд 59: Градиент скалярного поля
Градиентом скалярного поля u = u ( x, y, z ), где u = u ( x, y, z )-дифференцируемая функция, называется вектор с координатами
. Таким образом,
или.
Таким образом,
или.
Изображение слайда
60
Слайд 60: Пример
Найти градиент функции u = в точке M (6,2,3). Решение. Вычислим градиент функции. Тогда grad u = + + А в точке М
Изображение слайда
61
Слайд 61: Направление градиента
Теорема. Производная функции по направлению равна проекции градиента этой функции на данное направление (в соответствующей точке).
Изображение слайда
62
Слайд 62: Направление градиента
Так как производная по направлению представляет собой скорость изменения функции в данном направлении, а проекция вектора на другой вектор имеет максимальное значение, если оба вектора совпадают по направлению, то
градиент функции в данной точке указывает направление наиболее быстрого возрастания функции.
Изображение слайда
63
Слайд 63: Величина градиента плоского скалярного поля
Величина градиента плоского скалярного поля,т.е. grad u = обозначается tg и определяет крутизну наибольшего ската или подъема поверхности u = f ( x, y ).
Изображение слайда
64
Слайд 64
Градиент скалярного поля в данной точке по величине и направлению равен максимальной скорости изменения поля в этой точке, т. е. , где.
Изображение слайда
65
Слайд 65: Обыкновенные дифференциальные уравнения
Обыкновенным дифференциальным уравнением называется уравнение, связывающее между собой значения независимой переменной x, неизвестной функции y = f(x) и её производных (или дифференциалов ):
Порядком уравнения называется максимальный порядок n входящей в него производной (или дифференциала). Пример: y (4) – y + x = 0 — уравнение четвёртого порядка.
Функция y ( x ) называется решением (или интегралом) дифференциального уравнения если при подстановке ее в уравнение обращает его в тождество.
Пример: y (4) – y + x = 0 — уравнение четвёртого порядка.
Функция y ( x ) называется решением (или интегралом) дифференциального уравнения если при подстановке ее в уравнение обращает его в тождество.
Изображение слайда
66
Слайд 66
ОДУ первого порядка Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида: где x — независимая переменная, y(x) — неизвестная функция Общее решение: Пример : общее решение:
Изображение слайда
67
Слайд 67
Разделяют несколько типов (видов) обыкновенных дифференциальных уравнений :
— Уравнения с разделяющимися переменными,
— Однородные уравнения,
— Линейные уравнения,
— Уравнение в полных дифференциалах,
-и т. д.
Остановимся подробнее на каждом из этих типов уравнений.
д.
Остановимся подробнее на каждом из этих типов уравнений.
Изображение слайда
68
Слайд 68
Уравнения с разделёнными переменными. Так называются уравнения вида удовлетворяющее начальному условию f ( x ) dx + g ( y ) dy = 0, Интегрируя, получим — общий интеграл (общее решение) этого уравнения. Пример : — общее решение
Изображение слайда
69
Слайд 69
Уравнения с разделяющимися переменными. Так называются уравнения вида Эти уравнения легко сводятся к уравнению с разделёнными переменными : Записываем уравнение в форме: затем делим на g(y) и умножаем на dx : . Это уравнение — с разделёнными переменными. Интегрируя, получим общий интеграл:
Изображение слайда
70
Слайд 70
Выразим у из последнего выражения как функцию х, получим общее решение: Пример :
Изображение слайда
71
Слайд 71
Уравнения с однородной правой частью. Так называются уравнения со специальным видом зависимости функции f ( x, y ) от своих аргументов:
Это уравнение сводится к уравнению с разделяющимися переменными относительно новой неизвестной функции u ( x ) заменой :
Подставляя в уравнение y = x · u, y ′ = u + x · u ′, получим
(это — уравнение с разделяющимися переменными),
— это общий интеграл уравнения относительно переменных x, u
Так называются уравнения со специальным видом зависимости функции f ( x, y ) от своих аргументов:
Это уравнение сводится к уравнению с разделяющимися переменными относительно новой неизвестной функции u ( x ) заменой :
Подставляя в уравнение y = x · u, y ′ = u + x · u ′, получим
(это — уравнение с разделяющимися переменными),
— это общий интеграл уравнения относительно переменных x, u
Изображение слайда
72
Слайд 72
Пример : — общее решение уравнения
Изображение слайда
73
Слайд 73
Окончательно, получим общее решение: Пример :
Изображение слайда
74
Слайд 74
Линейные уравнения. ДУ первого порядка называется линейным, если неизвестная функция y ( x ) и её производная входят в уравнение в первой степени:
здесь p ( x ), q ( x ) — непрерывные функции.
Пример :
ДУ первого порядка называется линейным, если неизвестная функция y ( x ) и её производная входят в уравнение в первой степени:
здесь p ( x ), q ( x ) — непрерывные функции.
Пример :
Изображение слайда
75
Слайд 75
Для решения уравнения представим y ( x ) в виде произведения двух новых неизвестных функций u(x) и v(x) : y(x) = u(x)v(x). Тогда и уравнение приводится к виду : или Это уравнение решаем в два этапа: сначала находим функцию v ( x ) как частное решение уравнения с разделяющимися переменными : затем находим u ( x ) из уравнения :
Изображение слайда
76
Слайд 76
Отметим, решая уравнение на v(x) мы не вводим в это решение произвольную постоянную C, нам достаточно найти одну функцию v(x), обнуляющую слагаемое со скобками. Запоминать эту формулу не надо, лучше усвоить порядок действий и воспроизводить его при решении каждой задачи.
Запоминать эту формулу не надо, лучше усвоить порядок действий и воспроизводить его при решении каждой задачи.
Изображение слайда
77
Слайд 77
Пример : Решение: и общее решение уравнения .
Изображение слайда
78
Слайд 78
Для нахождения частного решения, соответствующего начальным условиям (задача Коши), подставим в общее решение Решение задачи:
Изображение слайда
79
Слайд 79
Уравнение в полных дифференциалах. Так называется уравнение вида
( P ( x, y ), Q ( x, y ) — непрерывно дифференцируемы) в случае, если его левая часть является полным дифференциалом некоторой функции u ( x, y ), т. е. если существует такая функция u ( x, y ), что
Необходимым и достаточным условием существования такой функции является условие:
Если — уравнение в полных дифференциалах, то его правая часть равна 0, т.е. принимает вид du ( x, y ) = 0. На решении y ( x ) получим du ( x, y ( x )) = 0, следовательно, u ( x, y ( x )) = C, где C — произвольная постоянная. Соотношение u(x, y) = C и есть общее решение уравнения в полных дифференциалах.
P(x, y) dx + Q(x, y) dy = 0.
е. если существует такая функция u ( x, y ), что
Необходимым и достаточным условием существования такой функции является условие:
Если — уравнение в полных дифференциалах, то его правая часть равна 0, т.е. принимает вид du ( x, y ) = 0. На решении y ( x ) получим du ( x, y ( x )) = 0, следовательно, u ( x, y ( x )) = C, где C — произвольная постоянная. Соотношение u(x, y) = C и есть общее решение уравнения в полных дифференциалах.
P(x, y) dx + Q(x, y) dy = 0.
Изображение слайда
80
Слайд 80
Для нахождения функции u ( x, y ) решается система уравнений
Из первого уравнения этой системы находим :
с точностью до произвольной дифференцируемой по y функции (эта функция играет роль постоянной интегрирования; так как интегрирование ведётся по переменной x.
Дифференцируем эту функцию по y и приравниваем выражению, стоящему во втором уравнении системы ( т. е. ), получим дифференциальное уравнение из которого можно найти.
е. ), получим дифференциальное уравнение из которого можно найти.
Изображение слайда
81
Слайд 81
Пример : найти общее решение уравнения Убедимся, что это — уравнение в полных дифференциалах. .
Изображение слайда
82
Слайд 82
ОДУ высших порядков Обыкновенным дифференциальным уравнением называется уравнение, связывающее между собой значения независимой переменной x, неизвестной функции y = f(x) и её производных (или дифференциалов): Общим решением (общим интегралом) уравнения называется соотношение вида:
Изображение слайда
83
Слайд 83
Некоторые типы уравнений, допускающие понижение порядка. Уравнение вида
решается последовательным n -кратным интегрированием.
Переобозначив постояные, общее решение запишем в виде :
y = cos x + C 1 x 3 + C 2 x 2 + C 3 x + C 4.
Пример :
Уравнение вида
решается последовательным n -кратным интегрированием.
Переобозначив постояные, общее решение запишем в виде :
y = cos x + C 1 x 3 + C 2 x 2 + C 3 x + C 4.
Пример :
Изображение слайда
84
Слайд 84
Уравнение, не содержащее в явном виде неизвестную функцию и её младшие производные. Порядок уравнения вида F(x, y (k), y (k+1), y (k+2 ), …,y (n) ) = 0, не содержащего функции y(x) и (k – 1) младшую производную этой функции в явном виде, может быть понижен ровно на k единиц введением новой неизвестной функции z(x) = y (k) (x). Тогда уравнение примет вид т.е. будет уравнением (n – k) -го порядка. После нахождения z (x) последовательным интегрированием решается уравнение y (k) (x)= z(x).
Изображение слайда
85
Слайд 85
Пример: Понизить порядок уравнения: Младшая производная, входящая в явной форме в уравнения, — вторая, поэтому делаем замену искомой функции: Тогда : и уравнение примет вид
Изображение слайда
86
Слайд 86
Уравнение, не содержащее в явном виде независимую переменную x. Порядок уравнения
не содержащего явно x, может быть понижен на 1 с помощью приёма, который заключается в том, что вводится новая функциональная зависимость от y :
Пример: Понизить порядок уравнения:
Переменная x явно в уравнение не входит, поэтому полагаем,
тогда .
Просто сократить на p это уравнение нельзя, так как можно потерять семейство решений
поэтому рассматриваем два случая :
Порядок уравнения
не содержащего явно x, может быть понижен на 1 с помощью приёма, который заключается в том, что вводится новая функциональная зависимость от y :
Пример: Понизить порядок уравнения:
Переменная x явно в уравнение не входит, поэтому полагаем,
тогда .
Просто сократить на p это уравнение нельзя, так как можно потерять семейство решений
поэтому рассматриваем два случая :
Изображение слайда
87
Последний слайд презентации: Первообразная и неопределенный интеграл. Таблица интегралов. Подведение под: Спасибо за внимание !
Изображение слайда
Урок 5. Неопределённый интеграл | Уроки математики и физики для школьников и родителей
ВИДЕО УРОК
Нахождение производных и нахождение неопределённых интегралов
(дифференцирование и интегрирование) – это два взаимно обратных действия. Как,
например, сложение и вычитание или умножение и деление.
Как,
например, сложение и вычитание или умножение и деление.
В чём сложность изучения неопределённых интегралов ? Если в производных имеют место строго 5 правил дифференцирования, таблица производных и довольно чёткий алгоритм действий, то в интегралах всё иначе. Существуют десятки способов и приёмов интегрирования. И, если способ интегрирования изначально подобран неверно, то интеграл нельзя решить.
В первую очередь следует хорошо разобраться в простейших интегралах. Посмотрим на таблицу интегралов.
Свойства неопределённого интеграла.
Таблица интегралов. Метод интегрирования частями. Как и в производных, видно несколько правил интегрирования и таблицу интегралов от некоторых элементарных функций.
Любой табличный интеграл (и вообще любой неопределённый интеграл) имеет вид:
∫f(x)dx = F(x) + C,
где C = const
Обозначения и термины.
∫ – значок интеграла.
f(x) – подынтегральная функция.
dx – значок дифференциала.
f(x)dx – подынтегральное выражение.
F(x) – первообразная функция.
F(x) + С – множество первообразных функций.
Самое важное, что в любом неопределённом интеграле к ответу приплюсовывается константа С.
Решить неопределённый интеграл
– это значит превратить его в определённую функцию
F(x) + С,
пользуясь некоторыми правилами, приёмами и таблицей.
Например, табличный интеграл
превратился в функцию
–cos x + C
Как и
в случае с производными, для того, чтобы научиться находить интегралы, не
обязательно быть в курсе, что такое интеграл, первообразная функция с
теоретической точки зрения. Достаточно просто осуществлять превращения по
некоторым формальным правилам. Так, в случае
Достаточно просто осуществлять превращения по
некоторым формальным правилам. Так, в случае
совсем не обязательно понимать, почему интеграл
превращается именно в
–cos x + C.
Пока можно принять эту и другие формулы как данность. Все пользуются электричеством, но мало кто задумывается, как там по проводам бегают электроны.
Так как дифференцирование и интегрирование – противоположные операции, то для любой первообразной, которая найдена правильно, справедливо следующее:
(F(x) + С)‘ = F‘ (x) + 0 = f(x).
Другими словами, если продифференцировать правильный ответ, то обязательно должна получиться исходная подынтегральная функция.
ПРИМЕР:
Возьмём табличный интеграл:
Убедимся в справедливости
данной формулы. Для этого возьмём производную от правой части.
Для этого возьмём производную от правой части.
(–cos x + C)‘ = –(cos x)‘ + (C)‘ = –(– sin x) + 0 = sin x.
Получилась исходная подынтегральная функция.
Теперь стало понятнее, почему к функции F(x) всегда приписывается константа С. При дифференцировании константа всегда превращается в ноль.
Решить неопределённый интеграл – это значит найти множество всех первообразных, а не какую-то одну функцию.
ПРИМЕР:
При решении интеграла
∫ sin xdx = –cos x + C.
Получается бесконечно много решений, например
–cos x + 5,
–cos x – 4/7,
–cos x + sin 2,
–cos x + е3.
Поэтому записывают коротко:
∫ sin xdx = –cos x + C.
где С – const.
Таким образом, любой неопределённый интеграл можно легко проверить в отличии от производных.
ПРИМЕР:
Найти неопределённый интеграл. РЕШЕНИЕ: ПРИМЕР:
Найти неопределённый интеграл:
РЕШЕНИЕ: ПРИМЕР:
Найти неопределённый интеграл:
РЕШЕНИЕ:
Анализируя интеграл, видно, что имеется
произведение двух функций и возведения в степень целого выражения. Так как нет
хороших и удобных формул для интегрирования произведения и частного надо
попытаться преобразовать подынтегральную функцию в сумму. ПРИМЕР:
ПРИМЕР:
Найти неопределённый интеграл. РЕШЕНИЕ:
Используем формулу сокращённого умножения. ПРИМЕР:
Найти неопределённый интеграл:
РЕШЕНИЕ:
В данном примере подынтегральная функция
представляет собой дробь. Когда в подынтегральном выражении дробь, то сначала
необходимо попытаться избавиться от этой дроби или упростить её. Сначала делим
числитель на знаменатель. ПРИМЕР:
Найти неопределённый интеграл:
РЕШЕНИЕ:
Непосредственное интегрирование (интегрирование по таблице и с использованием простейших свойств).
Высшая математика »
Неопределённые интегралы » Непосредственное интегрирование.
В этой теме мы подробно поговорим о свойствах неопределённого интеграла и о нахождении самих интегралов с помощью упомянутых свойств. Также поработаем с таблицей неопределенных интегралов. Материал, изложенный здесь, есть продолжение темы «Неопределённый интеграл. Начало». Честно говоря, в контрольных работах редко встречаются интегралы, которые можно взять с использованием типичных таблиц и(или) простейших свойств. Эти свойства можно сравнить с азбукой, знание и разумение которой необходимы для понимания механизма решения интегралов в иных темах. Часто интегрирование с использованием таблиц интегралов и свойств неопределённого интеграла именуют непосредственным интегрированием.
Итак, начнём с таблицы неопределённых интегралов. В ней указаны восемнадцать формул, которых, в принципе, должно хватить для интегралов стандартного университетского курса. Однако эта таблица далеко не полна, ибо в справочниках указаны сотни или даже тысячи неопределенных инегралов. Можете заглянуть, например, в справочник под редакцией Бронштейна и Семендяева, где начиная с 91й страницы находятся 515 неопределенных интегралов. Начнём пока с малого, – а потом поговорим, почему указанные таблицы столь обширны.
Можете заглянуть, например, в справочник под редакцией Бронштейна и Семендяева, где начиная с 91й страницы находятся 515 неопределенных интегралов. Начнём пока с малого, – а потом поговорим, почему указанные таблицы столь обширны.
Само применение таблицы интегралов основано на свойстве, которое часто именуют инвариантностью неопределённого интеграла. В несколько упрощённой форме это свойство можно сформулировать так:
Пусть $\int f(x)dx=F(x)+C$ и $u=\varphi (x)$ – некоторая функция, имеющая непрерывную производную на соответствующем промежутке. Тогда $\int f(u)du=F(u)+C$.
Грубо говоря, это свойство означает следующее: в формулах таблицы интегралов вместо буквы, обозначающей переменную, может располагаться функция, – формула останется верной. Проиллюстрируем работу с таблицей интегралов на примерах.
Пример №1
Найти $\int \cos 2t \; d(2t)$.
Решение
Обратимся к таблице неопределённых интегралов. 2}+C$.
2}+C$.
Возможно, к этому моменту у читателя может возникнуть пару вопросов, посему постараюсь их предугадать и сразу дать ответы.
Вопрос №1
Минутку. Почему вы используете прямые скобки для обозначения подстановки? Наш преподаватель использует фигурные скобки $\{ \}$.
Ответ
И это совершенно нормально. Разные авторы используют разные обозначения, – кому что больше нравится. Главное, чтобы эти обозначения были понятными читателю.
Вопрос №2
В предыдущей теме вы говорили, что операция интегрирования есть обратная к операции нахождения производных, т.е. дифференцирования. Я открыл справочник Бронштейна, но таблица производных на странице 226 гораздо скромнее, чем таблица интегралов в том же справочнике: всего 32 формулы. А в таблице интегралов более пятисот формул!
Ответ
Да, этот вопрос действительно крайне важен. Более того, даже 500 формул – не столь значительное количество для интегральных таблиц. \frac{1}{3} dx$ потребуется применение нового метода – подстановок Чебышева.
\frac{1}{3} dx$ потребуется применение нового метода – подстановок Чебышева.
Ну и напоследок: для нахождения производной функции $y=\sin x\cdot\frac{1}{x}$ вновь применима формула $(u\cdot v)’=u’\cdot v+u\cdot v’$, в которую вместо $u$ и $v$ подставим соответственно $\sin x$ и $\frac{1}{x}$. А вот $\int \sin x\cdot\frac{1}{x} dx$ не берётся. Точнее, не выражается через конечное число элементарных функций.
Подведём итоги: там, где для нахождения производной понадобилась одна формула, для интеграла потребовались четыре (и это не предел), – причем в последнем случае интеграл находиться отказался вообще. Изменили функцию – понадобился новый метод интегрирования. Вот отсюда и имеем многостраничные таблицы в справочниках. Отсутствие общего метода (пригодного для решения «вручную») приводит к изобилию частных методик, которые применимы лишь для интегрирования своего, крайне ограниченного класса функций (в дальнейших темах мы займёмся этими методами подробно). Хотя не могу не отметить наличие алгоритма Риша (советую почитать описание в Википедии), но он пригоден лишь для программной обработки неопределённых интегралов.
Хотя не могу не отметить наличие алгоритма Риша (советую почитать описание в Википедии), но он пригоден лишь для программной обработки неопределённых интегралов.
Вопрос №3
Но если этих свойств так много, как же мне научиться брать интегралы? С производными было полегче!
Ответ
Для человека пока существует лишь один способ: решить как можно больше примеров на применение различных методик интегрирования, чтобы при появлении нового неопределённого интеграла можно было подобрать для него метод решения, основываясь на своём опыте. Понимаю, что ответ не слишком обнадёживает, но иного нет.
Свойство №1
Производная от неопределенного интеграла равна подынтегральной функции, т.е. $\left(\int f(x) dx\right)’=f(x)$.
Это свойство вполне естественно, ибо интеграл и производная – взаимно обратные операции. Примеры:
$$\left(\int \sin 3x dx\right)’=\sin{3x};\; \left(\int\left(3x^2+\frac{4}{\arccos x}\right) dx\right)’=3x^2+\frac{4}{\arccos x}. 2xdx=\tg x-x+C$.
2xdx=\tg x-x+C$.
Вернуться к списку тем
Задать вопрос на форуме
Записаться на занятия
Онлайн-занятия по высшей математике
{{2}}{\left({x}\right)}{d}{x}=-{\cot {{\left({x}\right)}}}+{C}$$$ }$$$
}$$$Интегрирование, неопределенный интеграл, основные формулы и правила
Интегрирование, неопределенный интеграл, основные формулы и правилаSolitaryRoad.com
Владелец сайта: Джеймс Миллер
[ Дом ] [ Вверх ] [ Информация ] [ Почта ]
ИНТЕГРАЦИЯ, НЕОПРЕДЕЛЕННАЯ ИНТЕГРАЦИЯ, ФУНДАМЕНТАЛЬНАЯ ФОРМУЛЫ И ПРАВИЛА
По умолчанию Неопределенный интеграл. Неопределенный интеграл функции f(x) — это функция F(x)
производная которой есть f(x). Неопределенный интеграл функции — это первообраз функции.
термины «неопределенный интеграл», «интеграл», «примитив» и «противопроизводная» означают одно и то же.
Они используются взаимозаменяемо. Из четырех терминов наиболее часто используется термин интегральный,
сокращение от неопределенного интеграла. Если F(x) является интегралом от f(x), то F(x) + C также является интегралом от
f(x), где C — любая константа.
По умолчанию Интегрировать (функцию). Чтобы интегрировать функцию, нужно пройти через процесс нахождение интеграла или первообразной функции.
Обозначение, используемое для обозначения интегралов. Обозначение, используемое для обозначения интеграла (или примитив) функции f(x) равно
Это обозначение может показаться немного нелогичным, громоздким и запутанным читателю в первый раз, и он может задаться вопросом, почему такое сложное обозначение используется для обозначения примитива F(x) функция f(x). Конечно, простое обозначение, такое как Λ f(x), можно использовать для обозначения примитива f(x). Зачем использовать такие заумные, запутанные, громоздкие обозначения? Ну, есть причины обозначение.
Это обозначение логически следует, если предположить, что мы можем использовать обычные алгебраические правила в
манипулирование дифференциалами в форме уравнения. Обозначение следует как логическое следствие
правила. Например, рассмотрим следующее.
По определению интеграла или примитива мы имеем следующую связь между функция f(x) и ее примитив F(x):
Затем, используя алгебраические правила манипуляции,
Взятие интеграла от обеих сторон,
или
Таким образом, используя правила алгебраической обработки, мы начали с
.и пришел к выводу, что примитив F(x) задается как
Таким образом, это обозначение позволяет нам использовать алгебраические манипуляции при решении задач интегрирования.
Кроме того, большинство задач интегрирования имеют форму определенных интегралов вида
, и мы работаем алгебраически из этой формы. Источник обозначения, несомненно, интеграл. Это определенный интеграл без ограничений. Действительно, если вы посмотрите на верхнюю границу b определенный интеграл 1) в качестве переменной замените его на x, тогда он станет функцией площади
, а функция площади A(x) действительно представляет примитив f(x).
Основные формулы интегрирования. Ниже приведены основные формулы и правила интегрирования, наиболее важные из которых необходимо запомнить. Многие следуют непосредственно из стандартных формул дифференцирования. a и m являются константами.
По умолчанию Вычислите (интеграл). Провести указанное интегрирование, и если это определенный интеграл, подставить пределы интегрирования.
Процесс интеграции. Определение производной носило формальный характер. процесс, с помощью которого можно найти производную данной функции. Учитывая любой аналитически определенной функции (алгебраической, тригонометрической и т. д.) мы можем найти производную от нее через довольно простой процесс. Иная ситуация с интеграцией. Нет прямого, прямой процесс интегрирования функции. Процесс выглядит следующим образом: нам предоставляется интеграл, такой как
для оценки. Для этого спросим себя: «Какой примитив имеет дифференциал f(x)dx?» Мы используем наши
знание заученных формул и правил плюс различные приемы, которым мы научились плюс
возможно, таблицы интеграции, чтобы попытаться найти примитив, если он существует. Установленной процедуры нет.
Часто требуются творческий подход и изобретательность. Обычно мы можем много манипулировать и
экспериментировать. Если мы найдем примитив F(x), то интеграл будет равен
Установленной процедуры нет.
Часто требуются творческий подход и изобретательность. Обычно мы можем много манипулировать и
экспериментировать. Если мы найдем примитив F(x), то интеграл будет равен
, где C — любая константа.
Если нам представят определенный интеграл, такой как
для оценки, тогда решение будет иметь вид
Однако нет никакой гарантии, что существует решение, выражаемое в терминах элементарных функции. Например, ни одна из функций
имеют примитивы, которые могут быть выражены в терминах элементарных функций. Нет, например, конечная комбинация элементарных функций (например, алгебраических, тригонометрических, экспоненциальных и т. д.), производная .
Еще от SolitaryRoad.com:
Путь Истины и Жизни
Божье послание миру
Иисус Христос и Его Учение
Мудрые слова
Путь просветления, мудрости и понимания
Путь истинного христианства
Америка, коррумпированная, развратная, бессовестная страна
О честности и ее отсутствии
Критерием христианства человека является то, что он есть
Кто попадет в рай?
Высшее лицо
О вере и делах
Девяносто пять процентов проблем, с которыми большинство людей пришли от личной глупости
Либерализм, социализм и современное государство всеобщего благосостояния
Желание причинить вред, мотив поведения
Учение это:
О современном интеллектуализме
О гомосексуализме
О самодостаточной загородной жизни, приусадебном хозяйстве
Принципы жизни
Тематические пословицы, поучения,
Цитаты. Общие поговорки. Альманах бедного Ричарда.
Общие поговорки. Альманах бедного Ричарда.
Америка сбилась с пути
Действительно большие грехи
Теория формирования характера
Моральное извращение
Ты то, что ты ешь
Люди как радиотюнеры — они выбирают и слушать одну длину волны и игнорировать остальные
Причина черт характера — по Аристотелю
Эти вещи идут вместе
Телевидение
Мы то, что мы едим — живем по дисциплине диеты
Избегание проблем и неприятностей в жизни
Роль привычки в формировании характера.
Истинный христианин
Что такое истинное христианство?
Личные качества истинного христианина
Что определяет характер человека?
Любовь к Богу и любовь к добродетели тесно связаны
Прогулка по одинокой дороге
Интеллектуальное неравенство между людьми и властью в хороших привычках
Инструменты сатаны. Тактика и Уловки, используемые Дьяволом.
О реакции на обиды
Настоящая христианская вера
Естественный путь – неестественный путь
Мудрость, Разум и Добродетель тесно связаны
Знание одно, мудрость другое
Мои взгляды на христианство в Америке
Самое главное в жизни это понимание
Оценка людей
Мы все примеры — хорошо это или плохо
Телевидение — духовный яд
Перводвигатель, который решает, «Кто мы есть»
Откуда берутся наши взгляды, взгляды и ценности?
Грех — дело серьезное. Наказание за это настоящее. Ад реален.
Наказание за это настоящее. Ад реален.
Самостоятельная дисциплина и регламентация
Достижение счастья в жизни — вопрос правильных стратегий
Самодисциплина
Самообладание, сдержанность, самодисциплина — основа стольких вещей в жизни.
Мы наши привычки
Что формирует нравственный характер?
[ Дом ] [ Вверх ] [ Информация ] [ Почта ]
Счет, математика и статистика — Набор академических навыков
Бессрочная интеграция
Главное меню ContentsToggle 1 Определение и обозначения 2 Свойства 3 Таблица интегралов 4 Рабочий пример 5 Видео примеры 6 Рабочие тетради 7 Проверка себя 8 Внешние ресурсы
Определение и обозначения
Неопределенная интеграция может рассматриваться как противоположность или инверсия дифференцирования. По этой причине неопределенный интеграл также называют первообразной .
Неопределенный интеграл функции $f(x)$ по $x$ обозначается:
\[\int f(x) \mathrm{d} x. \]
\]
Функция, входящая в интеграл , $f(x)$, известен как подынтегральная функция .
Для функции $f(x)=F'(x)$, где штрих означает производную по $x$, неопределенный интеграл от $f(x)$ равен
\[\int f(x) \mathrm{d} x = F(x) + C,\]
$C$ — это произвольная константа, известная как константа интегрирования , которая возникает из правила констант: для постоянной функции $g(x)=C$, где $C$ — любое число, производная от $g(x)$ равна $g'(x)=0.$ Следовательно, производная любой функции $F( x)+C$ равно $F'(x) = f(x)$. Значение $C$ может быть определено граничными условиями на функцию $F(x)$.
Примечание: Традиционно строчные буквы используются для обозначения производных, а прописные буквы используются для обозначения соответствующей первообразной производной. 95}{2x-3}\;\mathrm{d}x\end{align}$, интеграл вида $\begin{align}\int f'(x)g(f(x))\;\ mathrm{d}x\end{align}$.
Рабочие тетради
Эти рабочие тетради, выпущенные HELM, являются хорошими вспомогательными средствами, содержащими ключевые моменты для повторения и множество рабочих примеров.
- Основные понятия интеграции
- Интегрирование тригонометрических функций
Проверь себя
Проверь себя: тест Numbas на бесконечное интегрирование
Внешние ресурсы
- Интеграция как рабочая тетрадь, обратная дифференциации, в математическом центре .
- Интеграция с использованием таблицы антипроизводных рабочей тетради в математическом центре .
- Таблица интегралов по математике по центру
- Рабочая тетрадь по правилам интегрирования линейности в математическом центре .
- Листовка «Факты и формулы», содержащая таблицу производных и правила интегрирования на математика центр.
- Неопределенный интеграл как антипроизводное видео в Академии Хана.
Неопределенная интегральная формула — объяснение, свойства, примеры решений и часто задаваемые вопросы
В исчислении интегрирование — это обратная сторона дифференцирования. Интегрирование — это процесс, с помощью которого мы можем найти функцию с заданной производной. Неопределенные формулы интегрирования можно применять к различным функциям. Интеграция может быть как неопределенного, так и определенного типа. В алгебраическом методе интегрирование — это способ понять концепцию неопределенного интеграла и найти интеграл для некоторой математической функции в любой точке.
Интегрирование — это процесс, с помощью которого мы можем найти функцию с заданной производной. Неопределенные формулы интегрирования можно применять к различным функциям. Интеграция может быть как неопределенного, так и определенного типа. В алгебраическом методе интегрирование — это способ понять концепцию неопределенного интеграла и найти интеграл для некоторой математической функции в любой точке.
Интеграл, который следует за процессом, помогает определить функцию по ее производным. Кроме того, понятие неопределенного интеграла также полезно при решении многих задач как в математике, так и в естественных науках. Неопределенные интегралы не ограничены, но свободны от обоих концов. Это означает, что независимая переменная не будет нести какой-либо заданный интервал. Для определенного интегрирования оба конца вполне конкретны и определены, тогда как для неопределенного интеграла границ нет.
(изображение будет загружено в ближайшее время)
Таким образом, мы можем найти уравнение вместо набора граничных значений для получения интеграла из-за дифференцирования без границ, нам не нужно использовать значения для получения определенный ответ.
Для данного f(x), F’(x) будем рассматривать как его производную. Очевидно, что наиболее общей первообразной функции f(x) будет неопределенный интеграл. Итак, интеграл функции f(x) по переменной x будет равен:
\[\int f(x) dx\]
Кроме того, мы знаем, что операция, обратная дифференцированию, является интегрированием, это означает, что если,
\[\frac{d}{dx} f( x) = g(x)\]
Таким образом,
g(x) dx = f(x) + C
Здесь C представляет постоянную интегрирования, что является обязательным. Для вычислений определенные интегралы всегда представляют некоторую ограниченную область. Это не то же самое с неопределенным интегралом.
Некоторые свойства неопределенного интеграла можно вынести мультипликативные константы.
\[\int -f(x)dx = c\int f(x) dx\]
Из-за отрицательной функции неопределенный интеграл также отрицателен.
\[\int f(x) \pm g(x) dx = \int f(x) dx \pm \int g(x) dx\] 9{\ frac {3} {2}}} {\ frac {3} {2}} + 2 \ sqrt {x} + C = \ frac {2 \ sqrt {3}} {3} + 2 \ sqrt {x } + C \]
Найдите неопределенный интеграл
\ [\ int \ frac {x + 1} {\ sqrt {x}} dx \]
9000
40204 9104 9102
\[\int \frac{x + 1}{\sqrt{x}} dx = \int \begin{pmatrix} \frac{x}{\sqrt{x}} + \frac{1}{\sqrt{ x}} \end{pmatrix} = \int \begin{pmatrix} \sqrt{x} + \frac{1}{\sqrt{x}} \end{pmatrix} = \int \sqrt{x} dx + \ интервал \frac{1}{\sqrt{x}} \] 93}}{3} + 2\sqrt{x} + C\]
Пункты для запоминания
Интегрирование или интегрирование f(x) также является процессом нахождения неопределенного интеграла функции.

Подходящие формулы используются для получения первообразной функции.
Семейство функций представлено неопределенным интегралом, а производные функции равны f.
Неопределенный интеграл очень похож на определенный интеграл, но оба они не совпадают, поскольку неопределенный интеграл дает функцию, а определенный интеграл дает действительное число.
Только неопределенные интегралы содержат действительное число C в процессе интегрирования.
Неопределенный интеграл не имеет границ, тогда как определенный интеграл содержит верхний и нижний пределы, то есть начальное и конечное значение.
Интеграл от 0 равен C или любой константе, поскольку производная любой константы равна нулю и, следовательно, ∫0 dx = C.

Неопределенный интеграл — это функция, которая объясняет площадь под кривой функции из неопределенной точки в другую произвольную точку.
Существует пять методов интегрирования, а именно: метод подстановки, интегрирование по неполным дробям, интегрирование по частям, подстановка Эйлера и метод редукции.
Интегральное исчисление особенно используется для
Для вычисления f из f’.
Если функция f дифференцируема на рассматриваемом интервале, то f’ определена.
В дифференциальном исчислении уже известно вычисление производных функции, но это можно отменить с помощью интегрального исчисления.

Используется для расчета площади под кривой.
Математические слова: неопределенный интеграл
Математические слова: неопределенный интегралиндекс: нажмите на букву индекс: предметные области Неопределенный интеграл
Семейство функций, которые имеют заданную функцию как общую производную.
 Неопределенный интеграл от f ( x ) записывается как
Неопределенный интеграл от f ( x ) записывается как
∫ f ( x ) dx .См. также
Методы интегрирования, интегральные правила, интегральная таблица
эта страница обновлена 19 июля 17
Математические слова: термины и формулы от алгебры I до исчисления
написано, проиллюстрировано и создано веб-мастером Брюсом Симмонсом
Авторские права © Брюс Симмонс, 2000 г.
Все права защищены[PDF] Две формулы для численного неопределенного интегрирования
- DOI:10.
 1090/S0025-5718-1993-1149292-9 9Идентификатор корпуса 1630: 121935784
1090/S0025-5718-1993-1149292-9 9Идентификатор корпуса 1630: 121935784
- С. Хабер
- Опубликовано в 1993 г.
- Математика
- Математика вычислений
- Кенитиро Танака, М.
 Сугихара, К. Мурота
Сугихара, К. Мурота Математика
Матем. вычисл.
- 2005
- М. Мухаммед, M. Mori
Математика
- 2003
Математика, информатика
Надежн. вычисл.
- 2013
- Aeyoung Park Jang, S. Haber
Математика, информатика
Math. вычисл.
- 2001
- Томоаки Окаяма, Такаясу Мацуо, М. Сугихара
Математика, информатика
Numerische Mathematik
- 2013
- Ф.
 Стенгер, Б. Киз, М. О’Рейли, К. Паркер
Стенгер, Б. Киз, М. О’Рейли, К. Паркер Математика
- 1992
- M. A. Araghi, G. K. Gelian
Mathematics
- 2012
- 2012 9000 3.
- F. Stenger, S. Gustafson, B. Keyes, M. O’Reilly, K. Parker
Математика
Численные алгоритмы
- 2004 3 Единый пакет программ для начальной обработки ЭВМ задачи для систем обыкновенных дифференциальных уравнений, реализующие численный метод, эффективный для общего класса дифференциальных уравнений.
- Э. Джон, Нкем Огбонна
Математика
- 2016
- Р.
 Б. Кирфотт
Б. Кирфотт Математика
92$. Определен оптимальный выбор параметров и показано, что норма функционала ошибки равна…- Ф. Стенгер
Математика
- К. Сикорский, Ф. Стенгер
Математика, информатика
TOMS
- 1984
- И. Стегун, Р. Цукер
Информатика
- 1970
- J. McNamee, F. Stenger, E. Whitney
Математика
- 1971
- М. Абрамовиц, И. Стегун, Дэвид М. Миллер
Математика
- 4
- 4
Справочник по математическим функциям, предназначенный для обеспечения научных исследований всесторонним и самодостаточным обзором математических функций, возникающих в физических и…
Алгоритм 614: подпрограмма FORTRAN для численного интегрирования в H(sub)p
- K. Sikorski, F. Stenger, J. Schwing
Информатика
TOMS
- 1984 4 Контракт армии США на исследования DAAG-29-77-G-0139, Департамент компьютерных наук, Колумбийский университет, Нью-Йорк, штат Нью-Йорк 10027, и Университет Олд-Доминион, Норфолк, Вирджиния, 23508.

- 4
@article{Haber1993TwoFF,
title={Две формулы для неопределенного числового интегрирования},
автор={Сеймур Хабер},
журнал={Математика вычислений},
год = {1993},
объем={60},
страницы = {279-296}
} Мы выводим две формулы для аппроксимации неопределенного интеграла на конечном интервале. Ошибка аппроксимации равномерно равна 0(c-cv’), где m — количество вычислений подынтегральной функции. Подынтегральная функция должна быть аналитической внутри интервала интегрирования, но может быть сингулярной на концах. Некоторые примерные расчеты показывают, что фактическая скорость сходимости соответствует полученной границе ошибки.
Просмотр через Publisher
ams.orgЧисленное бесконечное интегрирование методом двойного экспоненциального sinc
Численный метод аппроксимации неопределенного интеграла методом двойного экспоненциального синка с N вычислениями подынтегральных функций для достаточно широкого класса подынтегральных выражений, в том числе имеющих концевые особенности.
двойные экспоненциальные формулы для численной неопределенной интеграции
Оценка ошибки. Оценка по ошибкам. Оценка не индиковых контейнеров для неэпентации для невыполнного кротификата.
Для проверенного автоматического интегрирования недавно были даны более явные вычислимые границы погрешности на конечном интервале, а в остальных случаях даны полубесконечные и бесконечные интервалы.
Численное неопределенное интегрирование функций с особенностями
На основании теоремы Ганелиуса выведена неопределенная квадратурная формула для H p функций при p > 1 на интервале (-1,1), которая предполагает, что формула имеет наилучшую возможную значение этой константы.
Оценки ошибок с явными константами для аппроксимации Sinc, квадратур Sinc и неопределенного интегрирования Sinc
Эта статья раскрывает все константы в той же форме, что и вычисление в той же форме, что и вычисление теоремы: приближаемая функция аналитична в подходящей области.
SINC БЕСКОНЕЧНАЯ ИНТЕГРАЦИЯ И ПРОБЛЕМЫ НАЧАЛЬНЫХ ЗНАЧЕНИЙ
Неопределенный интеграл Sinc обсуждался несколькими авторами: Kear-fott (1983), Haber (1991) и Stenger (1981). Следующая презентация суммирует некоторые результаты в…
Сравнение производительности четырех методов Sinc для численного неопределенного интегрирования
Цели/задачи: Сравнить производительность четырех методов Sinc для численной аппроксимации неопределенных интегралов с алгебраическим или логарифмическим окончанием. -точечные особенности. Методология:…
Численное решение дифференциальных уравнений интеграции, основанных на двойной экспоненциальной трансформации в методе COLLOCATE
9000 3
 решать интегро-дифференциальные уравнения методом коллокаций Синка. Численные примеры иллюстрируют правильность и применимость…
решать интегро-дифференциальные уравнения методом коллокаций Синка. Численные примеры иллюстрируют правильность и применимость…ODE-IVP-PACK через неопределенное интегрирование Sinc и метод Ньютона
ДВОЙНОЙ ЭКСПОНЕНЦИАЛЬНЫЙ МЕТОД SINC ДЛЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ ВОЛЬТЕРРА-ФРЕДГОЛЬМА ВТОРОГО РОДА
Синк метод коллокации для численного решения интегральных уравнений Вольтерра-Фредгольма второго рода разработан путем включения переменного экспоненциального преобразования интегральных уравнений второго рода в…
ПОКАЗАНЫ 1-9 ИЗ 9 ССЫЛОК
Синк-приближение для неопределенного интеграла
Численные методы, основанные на кардинале Уиттекера, или функциях Sinc
3 1941
В статье обобщены известные на сегодняшний день результаты использования синусоидальных функций, составленных из других функций, в качестве основы для аппроксимаций в численном анализе. В данной статье описаны методы…
Оптимальные квадратуры в H(sub)p-пространствах
∫ ω −1 ([−1,1]) f(z)dz, или кажущийся классом Харди Hp(D),1 Часть I настоящей статьи посвящена функциям ошибки, вероятности и связанным с ними функциям. . математический инструмент. Кардинальная функция выводится с использованием теоремы Пэли-Винера. В… Автоматические методы вычислений для специальных функций

Кардинальная функция Whittaker в ретроспективе*
Справочник по математическим функциям с формулами, графиками и математическими таблицами (Национальное бюро стандартов прикладной математики, серия № 55)

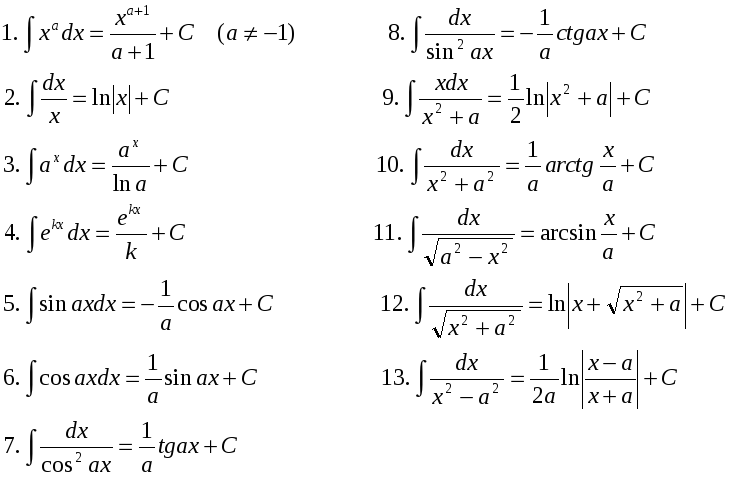


 Неопределенный интеграл от f ( x ) записывается как
Неопределенный интеграл от f ( x ) записывается как  1090/S0025-5718-1993-1149292-9
1090/S0025-5718-1993-1149292-9