Электронный учебник по математическому анализу
3.3 Непрерывные функции
3.2 Функции непрерывной переменной
3.3.1 Определения
Обсуждаются функции вещественной переменной, заданные на некотором интервале вещественной оси $(a,b) \subset \mathbb{R}$.
Определение. Функция $f(x)$ называется непрерывной в точке $x_0 \in (a,b)$, если
1. Имеется конечный предел \[ A=\lim _{x \rightarrow x_0}f(x) . \]
2. Этот предел совпадает со значением функции $f(x)$ в точке $x_0$, $A=f(x_0)$.
Определение. Функция $f(x)$ называется непрерывной в точке $x_0 \in (a,b)$ слева, если
1. Имеется конечный предел \[ A=\lim _{x \rightarrow x_0-0}f(x) . \]
2. Этот предел совпадает со значением функции $f(x)$ в точке $x_0$, $A=f(x_0)$.
Определение. Функция $f(x)$ называется непрерывной в точке $x_0 \in (a,b)$ справа, если
1. Имеется конечный предел
\[
A=\lim _{x \rightarrow x_0+0}f(x) . \]
\]
2. Этот предел совпадает со значением функции $f(x)$ в точке $x_0$, $A=f(x_0)$.
Теорема. Функция $f(x)$ непрерывна в точке $x_0 \in (a,b)$ тогда и только тогда, когда она одновременно непрерывна слева и справа в этой точке.
Определение. Функция $f(x)$ называется непрерывной на интервале $(a,b)$, если она непрерывна в любой точке этого интервала.
Определение. Функция $f(x)$ называется непрерывной на интервале $\left[a,b\right]$, если она непрерывна в любой точке интервала $(a,b)$, в точке $a$ непрерывна справа, а в точке $b$ непрерывна слева.
3.3.2 Основные свойства
С помощью арифметики пределов нетрудно доказать соответствующие свойства непрерывных функций.
Если функции $f(x)$, $g(x)$ непрерывны в точке $x_0$, то
1. Функция $f(x)+g(x)$ непрерывна в точке $x_0$,
2. Функция $f(x)\cdot g(x)$ непрерывна в точке $x_0$,
3. Если при этом $g(x_0)\neq 0$, то функция $\frac{f(x)}{g(x)}$ непрерывна в точке $x_0$.
Теорема.
Теорема. Если $f(x)$ непрерывна в точке $x_0$, функция $g(y)$ непрерывна в точке $y_0=f(x_0)$, то сложная функция $h(h)=g(f(x))$ непрерывна в точке $x_0$.
Теорема. Пусть $f(x)$ непрерывна на интервале $\left [a,b\right ]$. Тогда существуют конечные числа $m$ и $M$ со следующими свойствами.
1. Для всех $x \in \left [a,b\right ]$ выполняются неравенства: $ m \leq f(x) \leq M $.
2. Существуют точки $ x_1,x_2 \in \left [a,b\right ] $ такие, что $ f(x_1)=m $, $ f(x_2)=M $.
3. Для любого числа $ C $, удовлетворяющего неравенству $ m
Число $m$ называется глобальным минимумом функции $f(x)$ на интервале $\left [a,b\right ]$ (наименьшим значением), Число $m$ называется глобальным максимумом функции $f(x)$ на интервале $\left [a,b\right ]$ (наибольшим значением). Теорема, в частности, утверждает, что на интервале $\left [a,b\right ]$ существует решение уравнения $f(x)=C$ для любого $C$, $m \leq C \leq M$.
3.3.3 Разрывы функции
Нарушение того или иного условия, фиксирующего непрерывность функции в точке $x_0$, приводит к появлению особенности в локальном поведении функции в данной точке.
Определение. Если существует конечный предел $A=\lim _{x \to x_0} f(x)$, причем $A \neq f(x_0)$, точка $x=x_0$ называется устранимой особой точкой функции $f(x)$.
Устранимую особую точку можно «исправить», определив $f(x)=A$, так что точка $x_0$ становится точкой непрерывности «исправленной» $f(x)$.
Определение. Если существуют конечные левые и правые пределы $f(x)$ в точке $x_0$, но они не совпадают, точка $x_0$ называется точкой \textbf{разрыва первого рода} функции $f(x)$.
Пример.
Типичным примером функции с разрывом первого рода является функция-ступенька $\theta (x)$, которая определяется следующим образом: $\theta (x) =0, x
Определение. Если существуют левый и правый пределы функции $f(x)$ в точке $x=x_0$, причем хотя бы один из них бесконечен, точка $x=x_0$ называется точкой \textbf{разрыва второго рода} функции $f(x)$.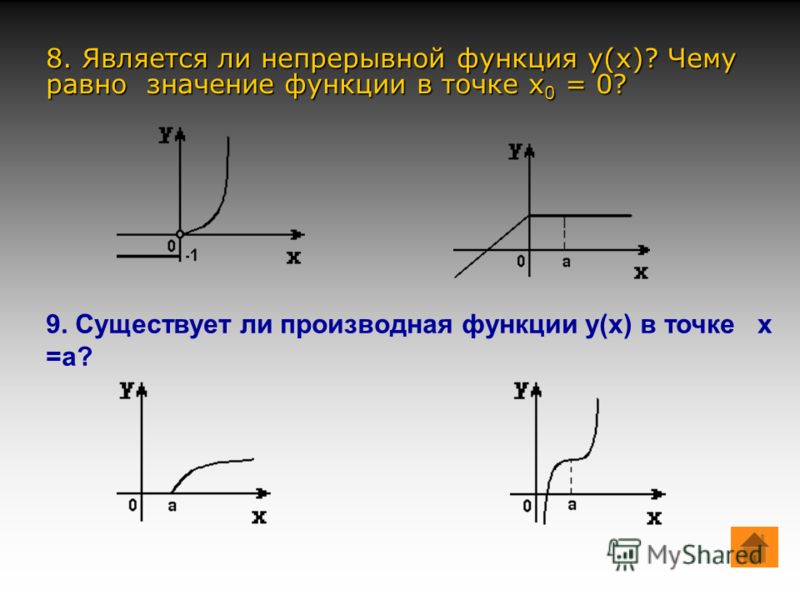 2-4}.$$
2-4}.$$
3. $$ y=\sin \left(\frac{\pi }{x+3}\right).$$
4. $$ y=arctg \left( \frac{1}{x}\right ). $$
3.2 Функции непрерывной переменной
10.3. Свойства непрерывных на отрезке функций
Свойства непрерывных на отрезке функций
Приведем без доказательства ряд теорем, относящихся к функциям, непрерывным на отрезке. Каждая из этих теорем имеет важное самостоятельное значение в математическом анализе. Несмотря на кажущуюся простоту и очевидность смысла данных теорем, доказать их оказалось делом нелегким. Это удалось осуществить сравнительно недавно – в XIX веке – выдающимся математикам: Вейерштрассу, Больцано, Коши. Современные ученые по достоинству оценили эти результаты и распространили их на наиболее сложные математические объекты исследования.
ТЕОРЕМА 1. Если функция непрерывна на отрезке , то она достигает на нем своего наибольшего и наименьшего значений.
Рис. |
Геометрический смысл данной теоремы иллюстрируется на рис. 10.4.
Наибольшее значение функции достигается сразу в двух точках области определения функции: на конце отрезка в точке и в его внутренней точке C, которая является ее максимумом. Наименьшее значение достигается не в точке минимума, а на конце B этого отрезка. Этот пример показывает, что минимум и максимум функции не всегда являются ее наименьшим и наибольшим значениями.
Условия непрерывности функции и замкнутости промежутка, на котором она рассматривается, чрезвычайно важны. Невыполнение хотя бы одного из этих условий может нарушить справедливость теоремы. Например, функция на отрезке [-3,1] не является непрерывной, она имеет при бесконечный разрыв, поэтому указать для нее наибольшее и наименьшее значения невозможно. Более того, если непрерывную на отрезке функцию переопределить всего лишь в одной (!) точке, то есть допустить устранимый разрыв, то сформулированная теорема может оказаться неверной.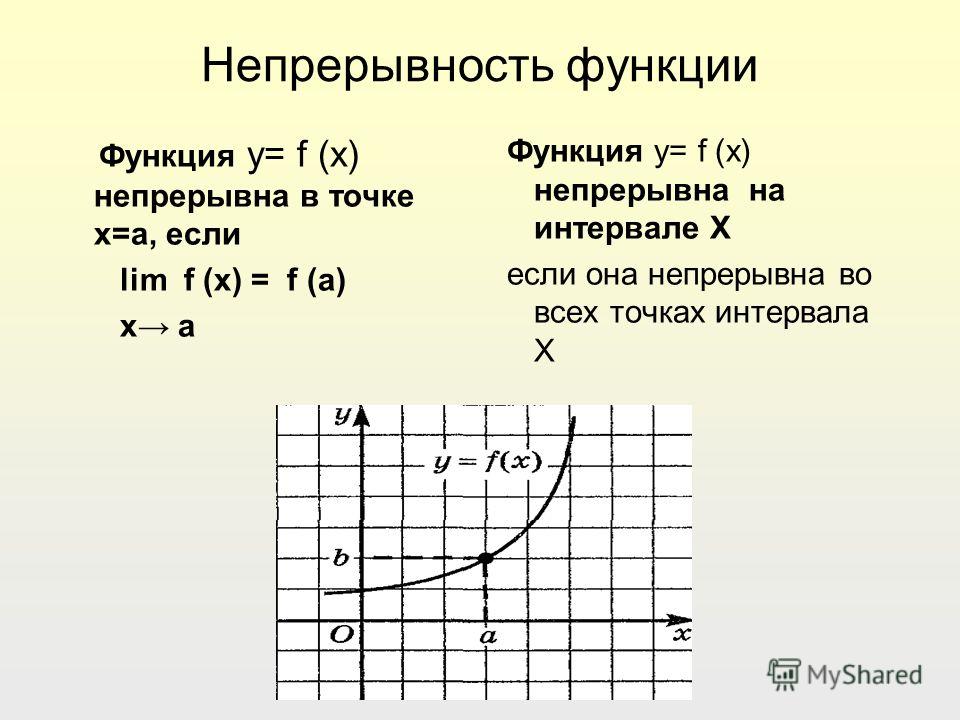 Например, функция на достигает наименьшее значение, равное нулю, при и . Наибольшее значение, равное единице, достигается при . Однако стоит только переопределить эту функцию, положив, что
Например, функция на достигает наименьшее значение, равное нулю, при и . Наибольшее значение, равное единице, достигается при . Однако стоит только переопределить эту функцию, положив, что
(рис. 10.5), как возможность достижения наибольшего значения новой функцией окажется неосуществима: как бы близко мы ни подошли к значению , функция будет принимать значения, сколь угодно близкие к единице, но не равные ей. Следует отметить, что если принять , то утверждения теоремы 1 будут выполнены; то есть теорема 1 дает лишь достаточное условие достижения наибольшего и наименьшего значений функции.
Рис. 10.5. Существование глобального экстремума при нарушении одного из условий теоремы 1. |
Аналогично, если только допустить, что функция непрерывна не на отрезке , а, предположим, на полуинтервале, например, , то утверждение теоремы 1 может оказаться верным, а может и не быть таковым. Например, функция на Достигает наименьшего значения – нуля, в точке , а наибольшего – единицы, когда . Однако этой же функцией на наименьшее значение, равное нулю, при достигается, а наибольшее значение достигнуто быть не может.
Например, функция на Достигает наименьшего значения – нуля, в точке , а наибольшего – единицы, когда . Однако этой же функцией на наименьшее значение, равное нулю, при достигается, а наибольшее значение достигнуто быть не может.
ТЕОРЕМА 2. Если функция непрерывна на отрезке и принимает на его концах значения разных знаков, то в интервале найдется хотя бы одна такая точка c , в которой функция обратится в нуль:
.
Сохранится ли утверждение теоремы, если функция имеет в некоторой точке отрезка устранимый разрыв? |
Геометрический смысл теоремы иллюстрируется рисунком 10.6. Функция, график которой здесь приведен, обращается в нуль даже в трех точках.
Данная теорема имеет важное значение для обоснования методов отыскания приближенных решений уравнения:
Рис. |
.
Согласно ей, достаточно найти для непрерывной функции отрезки, на концах которых она имеет разные знаки, чтобы утверждать о существовании на них хотя бы одного действительного корня. Эта теорема могла бы иметь еще большее значение, если бы она указывала способ отыскания таких корней. В настоящее время математика богата самыми разнообразными методами приближенного решения уравнения . Все они основываются на теореме 2.
Она важна также для обоснования метода интервалов при решении неравенств
,
Где – непрерывная функция.
Пусть … – Корни уравнения
.
Они разбивают область определения функции на отрезки так, что на их концах функция обращается в нуль. Внутри этих отрезков функция сохраняет знак, так как в противном случае существовали бы внутренние точки промежутков, в которых функция обратилась бы в нуль, что невозможно: ведь все корни уравнения мы уже выделили. Если функция имеет разрывы, то при решении неравенства их надо присоединить к корням уравнения. Взяв произвольную точку на каждом из полученных интервалов, мы определим на нем знак функции.
Если функция имеет разрывы, то при решении неравенства их надо присоединить к корням уравнения. Взяв произвольную точку на каждом из полученных интервалов, мы определим на нем знак функции.
Рассмотрим пример:
.
Свяжем с данным неравенством функцию
.
Отметим на числовой оси нули, точки разрыва функции, а также интервалы знакопостоянства (рис. 10.7).
Рис. 10.7. Интервалы знакопостоянства данной функции. |
Отсюда видно, что решением неравенства будет
.
ТЕОРЕМА 3. Если функция непрерывна на отрезке и M – ее наименьшее значение, а М – наибольшее, то для любого числа , лежавшего между m и М, найдется такое значение аргумента , что (рис. 10.8).
Рис. 10.8. Функция, удовлетворяющая условиям Теоремы 3. |
Смысл данной теоремы состоит в том, что непрерывная на отрезке функция принимает все значения, заключенные между ее наименьшим и наибольшим значениями, а потому ее называют теоремой о промежуточных значениях непрерывных функций.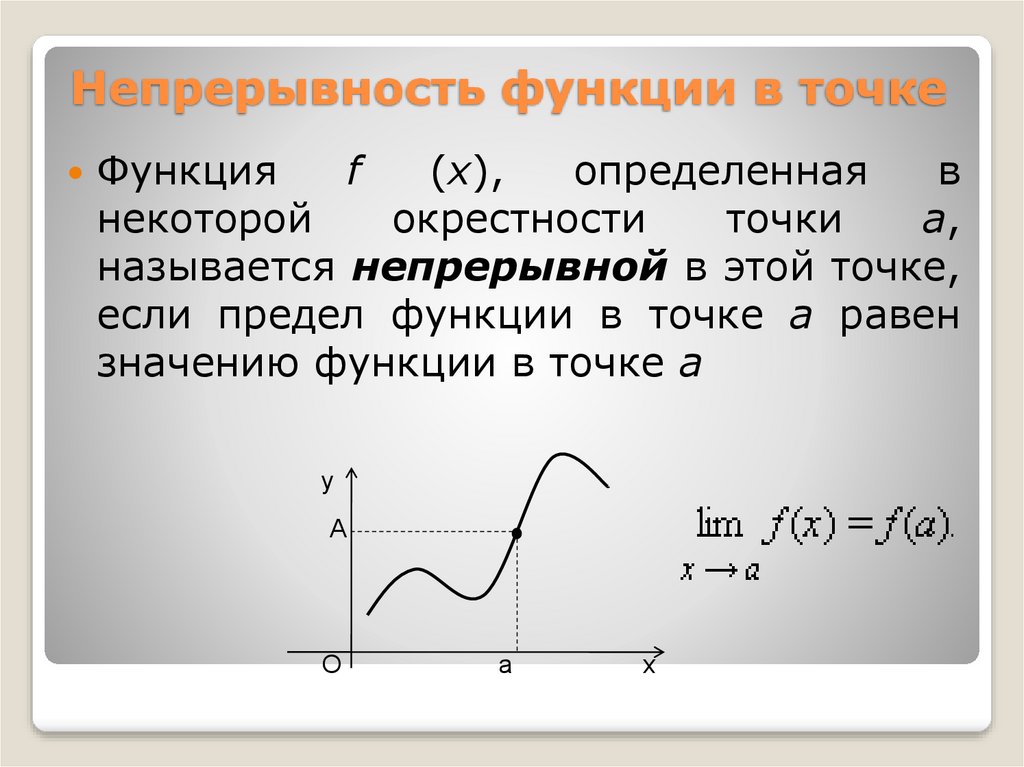
| < Предыдущая | Следующая > |
|---|
7. Непрерывные и прерывистые функции
М. Борна
Этот раздел связан с предыдущим разделом, посвященным домену и диапазону функции. Есть некоторые функции, которые не определены для определенных значений x .
Непрерывные функции
Рассмотрим график f ( x ) = x 3 — 6 x 2 — x + 30:
1234567-1-2-3-43060-30-60-92 — x + 30`, непрерывный граф.Мы видим, что на кривой нет «пробелов». Любое значение x даст нам соответствующее значение y . Мы могли бы продолжить график в отрицательном и положительном направлениях, и нам никогда не пришлось бы отрывать карандаш от бумаги.
Такие функции называются непрерывными функциями .
Функции с разрывами
Теперь рассмотрим функцию `f(x) = 1/(x-1)`
Заметим, что кривая не является непрерывной при `x =
1`.
График `y=1/(x-1)`, прерывистый граф.
Мы видим, что мелочи в x вблизи `x = 1` дает очень большое изменение значения функция.
Чтобы функция была непрерывной в точке, функция должна существовать в точке, и любое небольшое изменение в 92-x)`, разрывная функция.
Мы видим, что небольшие изменения в x около 0 (и около 1) производят большие изменения значения функции.
Мы говорим, что функция является прерывистой , когда x = 0 и x = 1.
Для этой функции существует 3 асимптот (линий, к которым кривая приближается, но не касается). Это ось «x», ось «y» и вертикальная линия «x=1» (обозначена пунктирной линией на графике выше). 92-x)` в представлении графика по умолчанию в Scientific Блокнот:
Он показывает нам все вертикальные значения, которые он может (от
чрезвычайно малое отрицательное число в очень большое положительное число)
— но мы не можем видеть никаких деталей (конечно, ни одной из кривых).
Нам нужно ограничить значения и , чтобы мы могли видеть истинные форму кривой, вот так (я изменил вид вертикальная ось от -12 до 10):
Непрерывность и дифференциация
Позже вы познакомитесь с концепцией дифференциации. Мы узнаем, что функция дифференцируема только тогда, когда она непрерывна.
Непрерывные функции, три сильные теоремы |
Какими должны быть функции стоимости машинного обучения
В этом посте мы рассмотрим некоторые теоремы, необходимые для применения непрерывных функций.
В прошлом посте наши теоремы включали непрерывность в какой-то точке, в следующих они требуют непрерывности на всем интервале, если непрерывность не выполняется в одной точке, выводы этих теорем могут быть неверны.
Теорема 1
IF F — непрерывность [A, B] и F (A) <0 
Проще говоря, это означает, что график непрерывной функции, начинающийся ниже горизонтальной оси и заканчивающийся над ней, должен пересечь эту ось в какой-то точке.
Пример теоремы 1, сгенерированный самостоятельно.Теорема 2
Если f непрерывна на [a,b] , то f ограничена сверху на [a,b] , то есть, есть около N , так что F (x) ≤n для всех x в x в x в x в x . .
Проще говоря, это означает, что график f линий ниже некоторой линии, параллельной горизонтальной оси.
Пример теоремы 2, сгенерированный самостоятельно.Теорема 3
Если f непрерывно на [A, B] , затем приходит около номера Y в [A, B] Такой, что F (Y)> F (x) для всех x в [a,b] .
Проще говоря, это означает, что непрерывная функция на замкнутом интервале принимает максимальное значение на этом интервале.
Пример теоремы 3, сгенерированный самостоятельно.Четвертая и пятая теоремы являются обобщениями теоремы 1, где вы можете переместить 0 строк в любое c между концом и началом функции:
Теоремы 4 и 5
непрерывно на [A, B] и F (A)
IF F — непрерывно на [A, B] и F (A)> C> F (B) , то есть около 6. x в [a,b] такое, что f (x)= c .
Теоремы 4 и 5 вместе показывают, что f принимает любое значение от f(a) до f(b) .
Теорема 6
IF F — непрерывно на [A, B] , затем F . , то есть существует некоторое число N такое, что f(x) > N для всех x в [a,b] .
Теоремы 2 и 6 вместе показывают, что непрерывная функция f на [a,b] ограничена на [a,b] .
Теорема 7
IF F — непрерывность [A, B] , затем около Y в Y в Y . Таким образом, F (Y) ≤ F (x) для всех x в [A, B] .
Таким образом, F (Y) ≤ F (x) для всех x в [A, B] .
Это означает, что непрерывная функция на замкнутом интервале принимает свое минимальное значение на этом интервале.
Теоремы 8 и 9
Каждое положительное число имеет квадратный корень. Другими словами, если a > 0 , то существует некоторое число 9(n-1)+…+a0 = c и предположим, что n четно. Тогда существует число m такое, что уравнение имеет решение для c ≥m и не имеет решения для c < m 6 .
Ограниченное множество
Множество действительных чисел ограничено выше , если есть число x таким образом, что x ≥ a для каждого a в A .
Такое число называется верхней границей.
Это может определить функцию, ограниченную сверху и снизу, используя x ≤ a.
Некоторые примеры неограниченных множеств: R (действительные числа), N (натуральные числа), ограниченное множество A = {x:1 ≤ x < 4} .
Наименьшая верхняя граница
Число x — Наименьшая верхняя граница из A IF x — верхняя граница A и Y — верхняя ограниченная ограничение 9963 99669 3 . , затем x≤y .
Как и в случае с ограничениями выше, мы можем определить наибольшую нижнюю границу, просто инвертируя определение:
Число x является наибольшей нижней границей из A IF x — нижняя граница A и Y — нижняя граница A , затем 5666.

Отсюда мы можем показать, что существуют две верхние границы x и y , x≤y и y≤x, , поэтому x3 6 y 9000.
Мы будем использовать супремум из A для выражения наименьшей верхней границы и сокращения до sup A . Мы будем называть наибольшую нижнюю границу infimum of A , сокращенно inf A .
Наличие только одной наименьшей верхней границы
Если A не ограничено сверху, то A вообще не имеет верхней границы, поэтому нельзя ожидать, что A будет иметь наименьшую верхнюю границу.
Свойство наименьшей верхней границы : Если A является набором действительных чисел, A ≠ ∅ и A ограничено сверху, то A имеет наименьшую верхнюю границу.

 10.4. Достижение непрерывной функцией своих
10.4. Достижение непрерывной функцией своих  10.6. Функция, удовлетворяющая условиям
10.6. Функция, удовлетворяющая условиям  Такое число называется верхней границей.
Такое число называется верхней границей.
