Примеры решения задач
5.1. Случайная величина X задана функцией распределения
Найти вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (0, 1/3).
Решение: Вероятность того, что Х примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале: Р (а < Х < b) = F (b)—F (а). Положив a=0, b= 1/3, получим
Р (0 < Х < 1/3)=F(1/3)—F(0)=[(3/4)x+3/4]x=1/3 – F[(3/4)x+3/4]x=0=l/4.
5.2. Случайная величина Х задана на всей оси Ох функцией распределения F (х) . Найти возможное значение

Решение: События и X>x1 – противоположные, поэтому . Следовательно,
Т. к. P(X=x)=0, то
По определению функция распределения,
Следовательно,
или
Отсюда , или .
5.3. Непрерывная случайная величина Х задана плотностью распределения в интервале ; вне этого интервала f(x)=0. Найти вероятность того, что Х примет значение, принадлежащее интервалу .
Решение: Воспользуемся формулой (5.6) P(a Х b) = . По условию , . Следовательно, искомая вероятность
.
5.4. Задана плотность распределения непрерывной случайной величины Х
Найти
функцию распределения F(x).
Решение: Используем формулу (5.7)
Если х 0, то f(x)=0, следовательно,
.
Если , то
Если х> , то
Итак, искомая функция распределения
5.5. Случайная величина Х задана плотностью распределения f(x)=2x в интервале (0,1); вне этого интервала
Решение: Используем формулы (5.8б), (5.12)
,
Подставив а=0, b=1, f(x)=2x, получим
и
Т.к. , то .
Глава 6.
 Распределения непрерывных случайных величин
Распределения непрерывных случайных величин6.1. Равномерное распределение.
В качестве примера рассмотрим случайную величину Х, равномерно распределённую на промежутке [a; b]. В этом случае f(х) постоянна внутри этого промежутка:
a
b
f(x)
(6.1)
Г
Рис. 6.1
рафик функции f(х) представлен на рисунке 6.1.
Для равномерного распределения функция F(x) имеет вид:
(6.2)
График функции F(x) представлен на рисунке 6.2.
Математическое ожидание равномерно распределенной непрерывной случайной величины равно . В силу симметричности равномерного распределения медиана равна , моды нет.
Дисперсия равномерного распределения равно . Стандартное отклонение .
Асимметрия
равномерного распределения равна нулю ,
эксцесс равен .
Вероятность попадания равномерно распределенной случайной величины в интервал определяется по формуле:
(6.3)
6.2. Показательное (экспоненциальное) распределение.
Показательным (экспоненциальным) распределением называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью вероятностей:
, (6.4)
г
де — постоянная и называется параметром показательного распределения. График плотности распределения представлен на рисунке 6.3.
Функция распределения случайной величины, распределенной по показательному закону, равна:
(6.5)
График функции распределения приведен на рисунке 6.4.
Математическое
ожидание случайной величины, распределенной
по показательному закону, равно M(X)= .
Медиана – .
Дисперсия – D(X)= .
Среднее квадратическое отклонение
совпадает с математическим ожиданием
и равно (X)= . Коэффициент асимметрии равен A(X)=2, эксцесс
– Е(Х)=6.
Коэффициент асимметрии равен A(X)=2, эксцесс
– Е(Х)=6.
Вероятность попадания случайной величины, распределенной по показательному закону, в интервал определяется по формуле:
(6.6)
Непрерывные случайные величины (3.3)
§ 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
3.3. Непрерывные случайные величины.
Кроме дискретных случайных величин, возможные значения которых образуют конечную или бесконечную последовательность
чисел, не заполняющих сплошь никакого интервала, часто встречаются случайные величины, возможные значения которых образуют некоторый интервал.
Примером такой случайной величины может служить отклонение от номинала некоторого размера детали при правильно налаженном технологическом
процессе. Такого рода, случайные величины не могут быть заданы с помощью закона распределения вероятностей р(х). Однако их можно
задать с помощью функции распределения вероятностей F(х).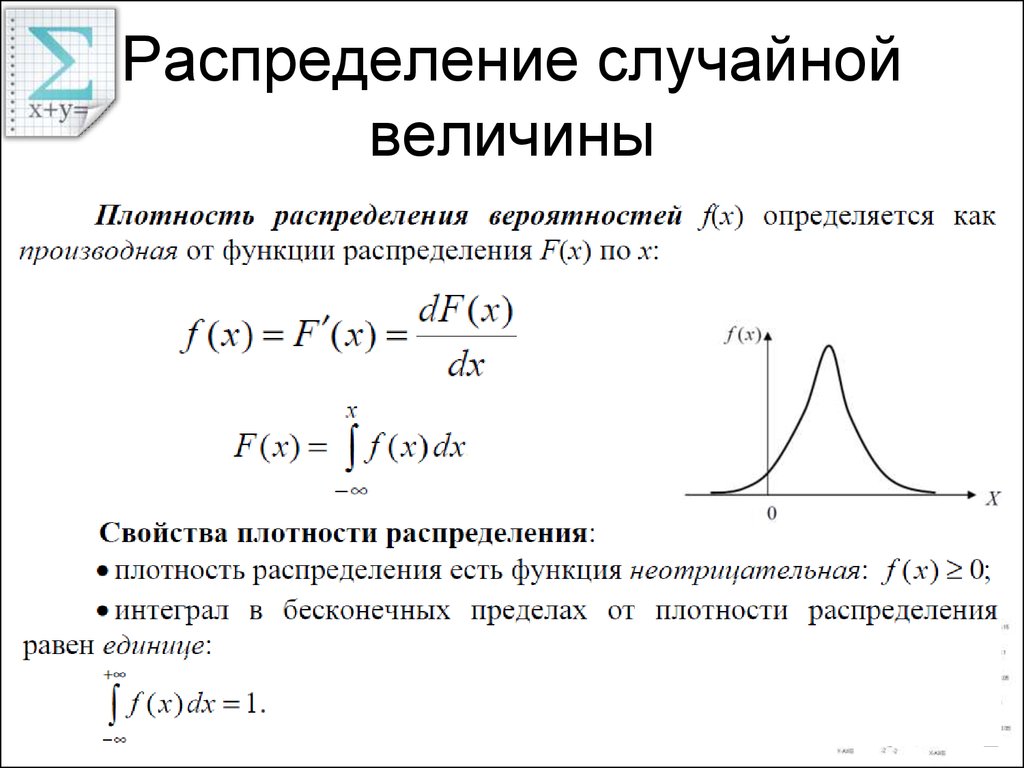 Эта функция определяется точно так же, как и в случае дискретной случайной
величины:
Эта функция определяется точно так же, как и в случае дискретной случайной
величины:
Таким образом, и здесь функция F(х) определена на всей числовой оси, и ее значение в точке х равно
вероятности того, что случайная величина примет значение, меньшее чем
Формула (19) и свойства 1° и 2° справедливы для функции распределения любой случайной величины. Доказательство проводится аналогично случаю дискретной величины.
Случайная величина называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция* , удовлетворяющая для любых значений x равенству
| (22) |
Функция называется плотностью распределения вероятностей, или кратко, плотностью распределения. Если x1<x2, то на основании формул (20) и (22) имеем
| (23) |
Исходя из геометрического смысла интеграла как площади, можно сказать, что вероятность выполнения неравенств
равна площади криволинейной трапеции с основанием [x1,x2], ограниченной сверху кривой (рис. 6).
6).
Так как , а на основании формулы (22)
, то
| (24) |
Пользуясь формулой (22), найдем как производную интеграла по переменной верхней границе, считая плотность распределения непрерывной**:
| (25) |
Заметим, что для непрерывной случайной величины функция распределения F(х) непрерывна в любой точке х, где функция непрерывна. Это следует из того, что F(х) в этих точках дифференцируема.
На основании формулы (23), полагая x1=x, , имеем
В силу непрерывности функции
Следовательно
Таким образом, вероятность того, что непрерывная случайная величина может принять любое отдельное значение х, равна нулю.
Отсюда следует, что события, заключающиеся в выполнении каждого из неравенств
Имеют одинаковую вероятность, т.е.
В самом деле, например,
так как
Замечание. Как мы знаем, если событие невозможно, то вероятность его наступления равна нулю. При
классическом определении вероятности, когда число исходов испытания конечно, имеет место и обратное предложение: если вероятность
события равна нулю, то событие невозможно, так как в этом случае ему не благоприятствует ни один из исходов испытания. В случае
непрерывной случайной величины число возможных ее значений бесконечно. Вероятность того, что эта величина примет какое-либо конкретное
значение x1 как мы видели, равна нулю. Однако отсюда не следует, что это событие невозможно, так как в результате
испытания случайная величина может, в частности, принять значение x1. Поэтому в случае непрерывной случайной величины
имеет смысл говорить о вероятности попадания случайной величины в интервал, а не о вероятности того, что она примет какое-то конкретное значение.
Поэтому в случае непрерывной случайной величины
имеет смысл говорить о вероятности попадания случайной величины в интервал, а не о вероятности того, что она примет какое-то конкретное значение.
Так, например, при изготовлении валика нас не интересует вероятность того, что его диаметр будет равен номиналу. Для нас важна вероятность того, что диаметр валика не выходит из поля допуска.
Пример. Плотность распределения непрерывной случайной величины задана следующим образом:
График функции представлен па рис. 7. Определить вероятность того, что случайная величина примет значение, удовлетворяющее неравенствам .Найти функцию распределения заданной случайной величины. (Решение)
Следующие два пункта посвящены часто встречающимся на практике распределениям непрерывных случайных величин — равномерному и нормальному распределениям.
* Функция называется кусочно-непрерывной на всей числовой оси, если она на любом сегменте или непрерывна, или имеет конечное число точек разрыва I рода.
** Правило дифференцирования интеграла с переменной верхней границей, выведенное в случае конечной нижней границы, остается справедливым и для интегралов с бесконечной нижней границей. В самом деле,
Так как интеграл
есть величина постоянная.
{\infty} P(X \geq x) dx$.Задача
Пусть $X \sim Uniform(-\frac{\pi}{2},\pi)$ и $Y=\sin(X)$. Найдите $f_Y(y)$.
- Решение
Здесь $Y=g(X)$, где $g$ — дифференцируемая функция. Хотя $g$ не монотонна, она может разбить на конечное число областей, в которых оно монотонно. Таким образом, мы можем использовать Уравнение 4.6. Отметим, что поскольку $R_X=[-\frac{\pi}{2},\pi]$, $R_Y=[-1,1]$. Глядя на график $g(x)=\sin(x)$ над $[-\frac{\pi}{2},\pi]$, мы замечаем, что для $y \in (0,1)$ есть два решения для $y=g(x)$, а для $y \in (-1,0)$ есть только одно решение.
 В частности, если $y \in (0,1)$, у нас есть два решения: $x_1=\arcsin(y)$ и $x_2=\pi-\arcsin(y)$.
Если $y \in (-1,0)$, у нас есть одно решение, $x_1=\arcsin(y)$. Таким образом, для $y \in(-1,0)$ имеем
92}} & \quad -1
В частности, если $y \in (0,1)$, у нас есть два решения: $x_1=\arcsin(y)$ и $x_2=\pi-\arcsin(y)$.
Если $y \in (-1,0)$, у нас есть одно решение, $x_1=\arcsin(y)$. Таким образом, для $y \in(-1,0)$ имеем
92}} & \quad -1
← предыдущая
следующая →
Печатная версия книги доступна на Amazon здесь.
Непрерывная случайная величина — определение, формулы, решенные примеры задач
Случайная величина X, которая может принимать любое значение (целое и дробное) в интервале, называется непрерывной случайной величиной.
Непрерывный случайная величина
Определение 6.5
Случайная величина X который может принимать любое значение (как целое, так и дробное) в интервале называется непрерывной случайной величиной.
Примеры непрерывных случайная величина
· Количество воды в бутылке на 10 унций.
·
Скорость автомобиля.
· Потребление электроэнергии в киловатт-часах.
· Рост людей в популяции.
· Вес учеников в классе.
· Время, за которое водитель грузовика едет из Ченнаи в Мадурай и др.
Вероятность функция плотности
Определение 6.6
Вероятность того, что случайная величина X принимает значение в интервале [ т 1 , т 2 ] (открытый или закрытый) задается интегралом от функции, называемой функция плотности вероятности ф х ( х ) :
P ( t 1 ≤ X ≤ t 2 )= t2 ∫ t 1 f X ( х ) дх .
Другие имена, которые
используется вместо функции плотности вероятности, включает функцию плотности,
непрерывная функция вероятности, интегрирующая функция плотности.
Плотность вероятности функции f X ( x ) или просто f ( x ) должны удовлетворять следующим условиям.
(и) f ( x ) ≥ 0 ∀ x и
(II) ∞∫ -Ch
Пример 6.8
Непрерывный случайный Переменная x имеет следующий P.D.F
F ( x ) = AX , 0 ≤ x ≤ 1
Определяет концепту а также найти Р [ X ≤ 1/2]Решение:
Случайное 2.29 90 переменная X имеет pdf
f ( x ) = 5 x 4 ,0 ≤ x ≤ 1
Найти a 1 и a 2 такие, что (i) P [ х ≤ a 1 ] = P [ X > a 1 ] (ii) P [ X > a 2 ] = 0. 05
05
Solution
Непрерывный функция распределения
Определение 6.7
Если X это непрерывная случайная величина с функцией плотности вероятности f X ( x ), затем функция F x ( x ) определяется
F x ( x ) ( x ) = ( x ) = ( x ) x x x ( x ) x x x x ( x ). ] = x ∫ -∞ f ( t ) dt , −∞ < x < ∞ называется функцией распределения (d.f) или иногда кумулятивной функция распределения (c.d.f) непрерывной случайной величины X
Свойства кумулятивной функции распределения
Функция F X ( x ) или просто F ( x ) обладает следующими свойствами
(i) 0 ≤ F ( x ) ≤ 1, F (⋅) — монотон,
неубывающая функция; то есть F ( a )≤ F ( b ) для а < б .
(iv) F (⋅) непрерывный справа; то есть
(v)
(vi)
dF ( x ) есть известный как дифференциал вероятностей X .
(vii)
= P ( X ≤ b ) − P ( X ≤ 9Пример 6.10
Предположим, жизнь в часов радиолампы имеет следующий п.д.ф
Найти дистрибутив функция.
Решение:
Пример 6.11
Количество хлеба (в сотен фунтов) х, которые некая пекарня способна продать за день быть числовым случайным явлением с функцией вероятности задается функцией плотности вероятности f ( x ) равно
(a) Найдите значение A.
(b) Чему равно Вероятность того, что количество фунтов хлеба, которое будет продано завтра, равно
(i) Более 10 фунтов,
(ii) Менее 10 фунтов и
(iii) От 5 до 15 фунты?
Решение:
(a) Мы знаем, что
(b) (i) Вероятность того, что
количество фунтов хлеба, которое будет продано завтра, больше 10 фунтов.

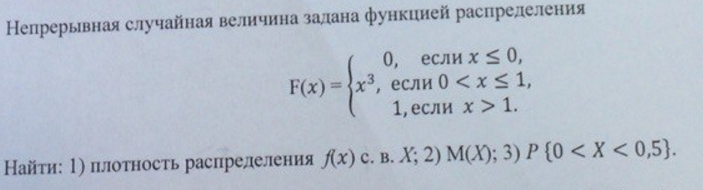 В частности, если $y \in (0,1)$, у нас есть два решения: $x_1=\arcsin(y)$ и $x_2=\pi-\arcsin(y)$.
Если $y \in (-1,0)$, у нас есть одно решение, $x_1=\arcsin(y)$. Таким образом, для $y \in(-1,0)$ имеем
92}} & \quad -1
В частности, если $y \in (0,1)$, у нас есть два решения: $x_1=\arcsin(y)$ и $x_2=\pi-\arcsin(y)$.
Если $y \in (-1,0)$, у нас есть одно решение, $x_1=\arcsin(y)$. Таким образом, для $y \in(-1,0)$ имеем
92}} & \quad -1