Тест по математике «Неравенства» (2 класс)
Неравенства 2 класс
МатематикаКласс
2
Учебник
Математика. 2 класс. В 2 ч. Моро М.И. и др. 6-е изд. — М.: 2015. —
Ч.1 — 96с., Ч.2 — 112с.
Вопрос №1
Поставь знак вместо звёздочки
12+5 * 12+3
<
>
Вопрос №2
Какое неравенство верно?
20 + 10 > 10 + 10
30 — 20 > 10 + 30
1
2
Вопрос №3
Какое число нужно поставить вместо *, чтобы неравенство было верным?
15 + 10 > 30 — *
5
Вопрос №4
Поставь знак вместо *
35 — 5 * 25 — 5
<
>
Вопрос №5
25 < *5
1
3
Вопрос №6
Поставь число вместо * так, чтобы неравенство было верным
* — 40 > 30
60
80
Вопрос №7
Какое неравенство верно?
60 – 30 > 100 – 50
70 – 40 < 80 – 20
1
2
Вопрос №8
Поставь знак вместо *
85 — 40 * 55
<
>
Вопрос №9
Поставь число вместо * так, чтобы получилось верное неравенство
48 > 4*
7
9
Вопрос №10
Выбери верное равенство
99 – 9 > 80
78 + 2 < 70
1
2
Вопрос №11
Поставь знак вместо *
37 – 30 * 47 – 7
<
>
infourok.ru
Неравенства 2 класс.doc — урок математики по теме «Неравенства» …
3) Математический диктант. ( 3 учащийся у доски каждый за свой ряд)
А) запиши наибольшее число четвёртого десятка
Б) запиши число большее 28 на 2
В) запиши число меньшее 30 на 1
Г) первое слагаемое 8, второе на 5 больше. Найди сумму
Д) уменьшаемое 38, вычитаемое 13. Найди разность.
Е) на сколько 87 больше числа 7
Ж) увеличь 9 на 6
З) сторона квадрата 6 см. Найди периметр
И) запиши число, в котором десятков на 3 больше, чем единиц.
Взаимопроверка по ключу( на доске). Оценка в тетради на полях.
По результату выполнения ряд получает балл.
4) Задачи на смекалку. ( 2 задачи ряду 1 балл ряду за правильный ответ)
1.Заяц вытащил 25 морковок и съел все, кроме 3. Сколько морковок осталось?
Устно.
2. У животного 2 левые ноги, 2 правые, 2 спереди и 2 сзади. Сколько ног у животного?
3. Когда гусь стоит на одной ноге , то весит 3 кг. Сколько будет весить гусь, если
встанет на две ноги?
4. У бабушки Даши был внучок Паша, котик Пушок, собака Дружок. Сколько внучат у
бабушки Даши?
5. Сколько орехов в пустом стакане?
6. Сколько ложек соли нужно положить в стакан с чаем, чтобы чай был сладким?
Физкультминутка для глаз.
4. Подготовка к восприятию учебного материала. Сообщение темы и
целей.
Повторение понятий «равенство», «неравенство».
5) На карточках (в парах) запись:
10 + 70 = 80
80 – 20 = 60 9 + 4 > 14 – 6
Х + 14 = 100 40 < 40 + 8
39 + 30 + 9 2 м > 20 см
15 + 5 = 28 – 8 1 м = 10 дм
– Рассмотрите внимательно записи.
– Как называется запись, в которой есть знак «равно» (=)? (Равенство.)
– Как называется запись, в которой есть знаки: «больше» (>), «меньше»
(<)? (Неравенство.)
Как называется выделенное равенство? ( равенство с неизвестной – уравнение)
Найдите лишнюю запись…( это 39 + 30 + 9 ). Измените эту запись так, чтобы она
стала НЕРАВЕНСТВОМ. ( 30 + 30> 9)
– Вы догадались, чему будет посвящен урок? (Мы будем составлять неравенства,
сравнивать числа и величины; различать равенства и неравенства)
Тема нашего урока: «Неравенства».
znanio.ru
Учебно-методический материал по математике (2 класс) по теме: 2 класс. Неравенства.
По теме: методические разработки, презентации и конспекты
Разработка урока литературного чтения во 2 классе Автор Пушкарных Людмила Ивановна, учитель начальных классов МОУ «СОШ № 17» г. Палласовки Волгоградской области 2 «А» класс 2010/2011 учебный год УРОК ЛИТЕРАТУРНОГО ЧТЕНИЯ (2 КЛАСС, СИСТЕМА Л.В. ЗАНКОВРазработка урока литературного чтения во 2 классеАвтор Пушкарных Людмила Ивановна,учитель начальных классовМОУ «СОШ № 17»г. Палласовки Волгоградской области2 «А» класс 2010/2011 учебный год…
конспект урока по математике в 1 классе «Неравенства»урок математики в 1 классе по программе «Начальная школа 21 века»…
Tschűs, 2. Klasse! Праздник на немецком языке для учеников 2 класса « Прощай, 2 класс!»Цель занятия: формирование коммуникативной компетенции учащихся. Основные практические задачи:- повторить лексический и грамматический материал за 2 класс….
Конспект урока математики во 2 классе «Числовые неравенства»Конспект в виде технологической карты с подробным описанием формируемых УУД…
Урок математики. «Неравенства. Решение задач». 2 класс, «Гармония»Урок математики…
Проект урока математики во 2 классе «Вычитание суммы из числа» (авт. Петерсон Л. Г. Математика 2 класс , часть 2, урок 15)Проект урока математики во 2 классе «Вычитание суммы из числа» Цель: познакомить с новым правилом вычитания;развивать внимание, речь, мыслительные и коммуникативные способности при работе в паре…
Однопредметный разнотемный урок литературного чтения во 2 и 4 классе (для малокомплектной школы). 2 класс: Обобщение по разделу «О братьях наших меньших». 4 класс: В.Ф. Одоевский «Городок в табакерке». Составление плана сказки. (2-ой урок)В архиве конспект урока и презентация для занятия в малокомплектной школе….
nsportal.ru
План-конспект урока по математике (2 класс) по теме: урок математики тема: «Закрепление изученного: равенства и неравенства»
Урок 61
Тема: ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО: РАВЕНСТВА
И НЕРАВЕНСТВА
Педагогические задачи: повторить понятия «равенство», «неравенство»; развивать вычислительные навыки, мышление.
Планируемые образовательные результаты:
Личностные: овладевают начальными навыками адаптации в обществе; принимают и осваивают социальную роль обучающегося; стремятся развивать внимание, память, логическое мышление, навыки сотрудничества со сверстниками и со взрослыми; проявляют самостоятельность, личную ответственность.
Предметные: знают: различные приемы сложения и вычитания двузначного числа с однозначным и двузначного числа с двузначным; что такое равенство и неравенство; что значит «сравнить числа или числовые выражения»; устную и письменную нумерацию чисел в пределах 100; как проверить результат действия сложения, разные способы проверки результата действия вычитания; умеют: проверять результат действия сложения вычитанием, результат действия вычитания сложением и вычитанием, выражения изученных видов; сравнивать числовые выражения.
Метапредметные (критерии сформированности/оценки компонентов УУД): регулятивные: формулируют учебную задачу урока; составляют план и последовательность действий, прогнозируют результат собственной деятельности, контролируют и оценивают свою деятельность и деятельность партнеров по образовательному процессу, при необходимости вносят корректировки; способны к саморегуляции; познавательные: формулируют познавательную цель; осознанно и произвольно строят речевое высказывание в устной форме; создают алгоритм деятельности; строят логическую цепочку рассуждений, анализируют, сравнивают, устанавливают причинно-следственные связи; контролируют и оценивают процесс и результаты деятельности; коммуникативные: знают правила ведения диалога и применяют их на практике; достаточно полно и точно выражают свои мысли, аргументируют свою точку зрения, при этом уважают всех участников образовательного процесса; эффективно сотрудничают как со сверстниками, так и со взрослыми.
методы и формы обучения: частично-поисковый; индивидуальная, фронтальная, групповая.
Образовательные ресурсы: http://www.liveinternet.ru/users/byxtelka/post104646979 – Цитатник
Основные понятия и термины: сравнить, сложить, вычесть, слагаемое, сумма, значение суммы, уменьшаемое, вычитаемое, разность, значение разности, проверка, геометрические фигуры, треугольник, квадрат, круг, прямоугольник.
организационная структура (сценарий) урока
I. Каллиграфическая минутка.
2 12 20 2 12 20… 3 13 30 3 13 30…
II. Устный счет.
1. «Цепочка».
2. Какое число пропущено?
62 + = 70 – 6 = 9
+ 8 = 30 33 – =28
3. Вставьте знаки арифметических действий (+ или –) так, чтобы равенства были верными.
72 * 8 * 35 = 45 62 * 20 * 7 = 49
54 * 9 * 20 = 25 36 * 30 * 8 = 58
III. Подготовка к восприятию учебного материала. Сообщение темы и целей. Повторение понятий «равенство», «неравенство».
На доске запись:
15 + 5 = 28 – 8 9 + 4 > 14 – 6
39 + 30 + 9 40 < 40 + 8
1 м = 10 дм 2 м > 20 см
– Рассмотрите внимательно запись на доске. Что вы заметили?
– Чем похожи записи каждого столбика?
– Как называется запись, в которой есть знак «равно» (=)? (Равенство.)
– Как называется запись, в которой есть знаки: «больше» (>), «меньше» (<)? (Неравенство.)
– Вы догадались, чему будет посвящен урок? (Мы будем составлять равенства и неравенства, сравнивать и решать выражения.) Верно. Тема нашего урока: «Равенства и неравенства».
– Составьте верные равенства и неравенства, используя выражения:
6 + 8, 17 – 10, 24 – 10, 37 – 30.
IV. Сравнение выражений.
На данном этапе урока ученикам может быть предложено задание 6 (с. 90), которое они выполняют с устным объяснением, а затем в качестве самостоятельной работы – задание по карточкам:
К-1. 63 + 17 * 17 + 63 25 + 20 * 25 + 2
59 – 34 * 59 – 36 45 – 17 * 55 – 17
К-2. 80 – 31 * 80 – 21 18 + 4 * 18 + 40
72 + 8 * 8 + 72 67 – 24 * 47 – 24
К-3. 82 + 8 * 8 + 82 15 + 7 * 7 + 15
91 – 40 * 91 – 42 74 – 38 * 84 – 38
Дети утром рано встали, За грибами в лес пошли. Приседали, приседали, Белый гриб в траве нашли. | (Ходьба на месте.) (Приседания.) |
На пеньке растут опята, Наклонитесь к ним, ребята, Наклоняйся, раз-два-три, И в лукошко набери! Вон на дереве орех. Кто подпрыгнет выше всех? Если хочешь дотянуться, Надо сильно потянуться. Три часа в лесу бродили, Все тропинки исходили. Утомил всех долгий путь – Дети сели отдохнуть. | (Наклоны.) (Прыжки.) (Потягивания – руки вверх.) (Ходьба на месте.) (Дети садятся за парты.) |
V. Решение выражений.
– Выполните с подробным устным объяснением задание 2 (с. 90). Найдите значения данных выражений, а затем проверьте их.
После этого выполняется задание 8 (с. 90) следующим образом: учащиеся рассматривают выражения 1-го столбика и приходят к выводу: для решения выражений необходимо воспользоваться приемом группировки слагаемых; данный столбик выполняется с комментированием.
Запись в тетради:
40 + 7 + 3 + 18 = 40 + (7 + 3) + 18 = 40 + 10 + 18 = 50 + 18 = 68
50 + 26 + 8 + 2 = 50 + 26 + (8 + 2) = 50 + 10 + 26 = 60 + 26 = 86
30 + 9 + 6 + 1= 30 + (9 + 1) + 6 = 30 + 10 + 6 = 40 + 6 = 46
Далее учитель предлагает ученикам рассмотреть выражения 2-го столбика.
– Чем интересны выражения этого столбика?
– Как, по вашему мнению, будут изменяться значения данных выражений? Решите выражения.
Групповая работа.
Учащимся могут быть предложены задания 1, 3 (с. 90). Выполняя задание 1, ученики находят ошибки и исправляют их. В задании 3 ставят скобки таким образом, чтобы записи были верными.
VI. Задание на смекалку.
Учащиеся выполняют задание 9 (с. 90), в котором заполняют таблицу с геометрическими фигурами. (Вторая строка – в зеленом квадрате красный круг, в синем треугольнике красный круг, в желтом прямоугольнике красный круг, в белом круге красный круг; третья строка – в зеленом квадрате черный треугольник, в синем треугольнике черный треугольник, в желтом прямоугольнике черный треугольник, в белом круге черный треугольник.)
VII. Самостоятельная работа обучающихся.
В заключение урока ученикам может быть предложена самостоятельная работа: проверочные задания (с. 38, 39 тетради для проверочных работ).
VIII. Рефлексия учебной деятельности.
– Какие понятия, правила повторяли сегодня на уроке?
– Как вы сегодня работали? Что бы хотели выполнить еще?
nsportal.ru
Равенства и неравенства / Сравнение чисел / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Сравнение чисел
- Равенства и неравенства
Сначала повтори тему «Больше. Меньше» и вспомни, что такое больше, меньше, поровну, столько же.
Рассмотри рисунок.
Сколько синих кругов? 5.
Сколько красных кругов? 5.
Каких кругов больше? Каких меньше?
Синих кругов столько же, сколько красных. Их поровну.
Красных кругов столько же, сколько синих. Их поровну.
Составим запись к рисунку:
5 = 5.
Прочитаем запись: пять равно пяти.
Это равенство.
Запись, в которой есть знак РАВНО, называется РАВЕНСТВОМ.
Рассмотри рисунок.
Сколько синих кругов? 5.
Сколько красных кругов? 6.
Каких кругов больше? Красных.
Каких кругов меньше?
Синих.Синих кругов меньше, чем красных.
Красных кругов больше, чем синих.
Составим запись к рисунку:
6 > 5
Прочитаем запись: шесть больше пяти.
Это неравенство.
5 < 6
Прочитаем запись: пять меньше шести.
Это неравенство.
Запись, в которой есть знак БОЛЬШЕ или МЕНЬШЕ, называется НЕРАВЕНСТВОМ.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Уменьшить на… Увеличить на…
Сравнение чисел
Правило встречается в следующих упражнениях:
1 класс
Страница 48, Моро, Волкова, Степанова, Учебник, 1 часть
Страница 63, Моро, Волкова, Степанова, Учебник, 1 часть
Страница 115, Моро, Волкова, Степанова, Учебник, 1 часть
Страница 29, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 40, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 47, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 39, Моро, Волкова, Степанова, Учебник, 2 часть
Страница 57, Моро, Волкова, Степанова, Учебник, 2 часть
Страница 8, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 28, Моро, Волкова, Рабочая тетрадь, 2 часть
2 класс
Страница 57, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Задание 75, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 14. Вариант 1. Тест 2, Моро, Волкова, Проверочные работы
Страница 15. Вариант 2. Тест 2, Моро, Волкова, Проверочные работы
Страница 23. Вариант 2. № 4-5, Моро, Волкова, Проверочные работы
Страница 40. Вариант 1. Тест 2, Моро, Волкова, Проверочные работы
Страница 62. Вариант 1. № 3, Моро, Волкова, Проверочные работы
Страница 63. Вариант 2. № 3, Моро, Волкова, Проверочные работы
Страница 15, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 69, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
3 класс
Страница 80, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 86, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 105, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 17, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 56, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 47, Моро, Волкова, Рабочая тетрадь, 2 часть
Страница 4. Вариант 1. № 1, Моро, Волкова, Проверочные работы
Страница 10. Вариант 1. № 1, Моро, Волкова, Проверочные работы
Страница 21. Вариант 2. Тест 1, Моро, Волкова, Проверочные работы
4 класс
Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 3, Моро, Волкова, Рабочая тетрадь, 1 часть
© 2019 — budu5.com, Буду отличником!
budu5.com
Выражение. Равенство. Неравенство. Уравнение. Видеоурок. Математика 4 Класс
Определение числового выражения.Числовое выражение – это числа, соединенные знаками арифметических действий.
Выберите из приведенных записей выражения:
Ответ: данная строка не является числовым выражением. Все остальные записи – это числовые выражения.
Выполнив действия, указанные в числовом выражении, можно найти значение выражения.
Буквенные выражения – это выражения, когда вместо одного или нескольких чисел записаны латинские буквы. Например:
Подставив вместо буквы ее значение и выполнив арифметическое действие, которое указано в выражении, можно найти значение выражения.
Дано буквенное выражение: . Найдите значение выражения при следующих значениях:
1. ;
2. ;
3. .
Решение
Подставим вместо его значение . Получаем разность чисел и следующее значение выражения: .
Подставим вместо его значение . Получаем разность чисел и следующее значение выражения: .
Подставим вместо его значение . Получаем разность чисел и следующее значение выражения: .
Ответ:.
Числа или выражения, соединенные знаком «равно», образуют равенства. Например:
Если числа или выражения соединены знаком «больше» или «меньше», то они образуют неравенства. Например:
Равенства и неравенства могут быть верными и неверными.
Необходимо разделить следующие равенства и неравенства на две группы: верные и неверные.
Решение
Значение произведения равно , значит, равенство верное.
Значение частного чисел равно , значение частного чисел равно . То есть равенство неверное.
Значение произведения равно , а меньше, чем . Значит, неравенство верное.
Значение частного чисел равно , а значение произведения равно . Значит, неравенство неверное.
Ответ:1. Верное; 2. Неверное; 3. Верное; 4. Неверное.
Равенство, содержащее неизвестное число, называется уравнением. Неизвестное число обозначено латинской буквой. Например:
Решить уравнение – это значит найти такое значение буквы, чтобы равенство стало верным (или доказать, что таких значений не существует). В уравнении решением является , так как сумма чисел , то есть получилось верное равенство. Число называют корнем уравнения.
Чтобы найти корень уравнения, надо знать, как связаны компоненты действия между собой.
Необходимо решить уравнение .
Решение
Упростим правую часть уравнения – найдем ее значение.
Получили уравнение:
Воспользуемся знаниями, как связаны компоненты при вычитании. Чтобы найти уменьшаемое, надо к значению разности прибавить вычитаемое.
Выполним проверку:
Левая и правая часть уравнения совпадают. Значит, является корнем уравнения.
Ответ: 564.
Необходимо решить уравнение .
Решение
Чтобы найти вычитаемое, надо из уменьшаемого вычесть значение разности.
Получаем:
Выполним проверку. Для этого подставим полученное число вместо неизвестного в исходное уравнение:
;
.
Левая и правая часть уравнения совпадают. Значит, является корнем уравнения.
Ответ: 252.
Необходимо самостоятельно составить уравнение с
Решение
Проверим возможные варианты составления уравнения.
1.
В данном уравнении используется действие «сложение» и нужно найти слагаемое.
2.
В этом уравнении необходимо н
interneturok.ru
Равенство и неравенство. Видеоурок. Математика 1 Класс
Тема: Знакомство с основными понятиями в математике
Урок: Равенство и неравенство
На данном уроке мы познакомимся с математическими понятиями: «равенство» и «неравенство».
Попробуйте ответить на вопрос:
У стены стоят кадушки,
В каждой ровно по лягушке.
Если б было пять кадушек,
Сколько б было в них лягушек? (рис. 1)
Рис. 1
В стихотворении говорится, что кадушек было 5, в каждой кадушке по 1 лягушке, никто не остался без пары, значит число лягушек равно числу кадушек.
Обозначим кадушки буквой К, а лягушек – буквой Л.
Запишем равенство: К = Л. (рис. 2)
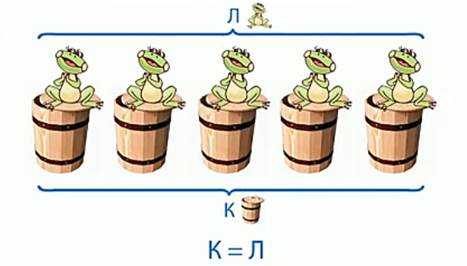
Рис. 2
Сравните по количеству две группы фигур. Фигур много, они разного размера, расположены без порядка. (рис. 3)
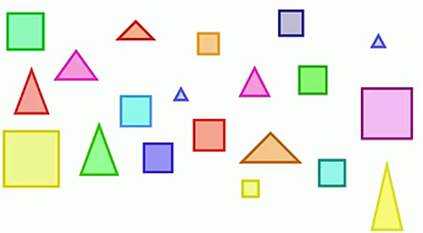
Рис. 3
Составим из этих фигур пары. Каждый квадрат соединим с треугольником. (рис. 4)
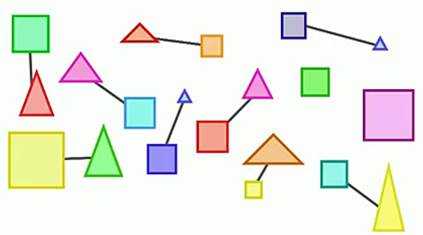
Рис. 4
Два квадрата остались без пары. Значит, количество квадратов не равно количеству треугольников. Обозначим квадраты буквой К, а треугольники – буквой Т.
Запишем неравенство: К ≠ Т. (рис. 5)
Рис. 5
Вывод: сравнивать количество элементов в двух группах можно, составляя пары. Если всем элементам хватает пары, то соответствующие числа равны, в этом случае ставим между цифрами или буквами знак равно. Эта запись называется равенством. (рис. 6)
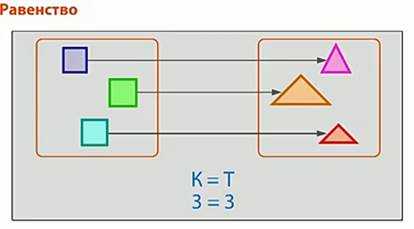
Рис. 6
Если не хватает пары, то есть остаются лишние предметы, то эти числа неравны. Ставим между числами или буквами знак неравно. Эта запись называется неравенством. (рис. 7)
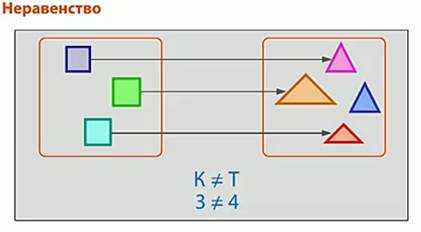
Рис. 7
Оставшиеся без пары элементы показывают, какое из двух чисел больше и на сколько. (рис. 8)
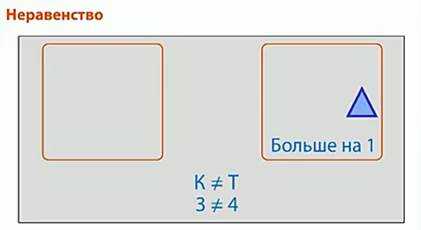
Рис. 8
Способ сравнения групп фигур с помощью составления пар не всегда удобен и занимает много времени. Можно сравнивать числа с помощью числового луча. (рис. 9)
Рис. 9
Сравните данные числа с помощью числового луча и поставьте знак сравнения.
Пример 1
2 ⃞ 5
Нужно сравнить числа 2 и 5. Посмотрим на числовой луч. Число 2 находится ближе к 0, чем число 5, или говорят, число 2 на числовом луче левее, чем число 5. Значит, 2 не равно 5. Это неравенство.
2 ≠ 5
Знак «≠» (не равно) лишь фиксирует неравенство чисел, но не указывает, какое из них больше, а какое – меньше.
Из двух чисел на числовом луче меньшее расположено левее, а большее – правее. (рис. 10)
Рис. 10
Можно данное неравенство записать по-другому, используя знак меньше « < » или знак больше « > » :
2 < 5
Пример 2
7 ⃞ 4
На числовом луче число 7 находится правее, чем число 4, следовательно:
7 ≠ 4 и 7 > 4
Пример 3
9 ⃞ 9
Числа 9 и 9 равны, поэтому ставим знак =, это равенство:
9 = 9
Сравните количество точек и число и поставьте соответствующий знак. (рис. 11)
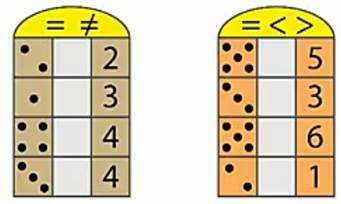
Рис. 11
На первом рисунке нам необходимо поставить знак = или ≠ .
Сравниваем две точки и число 2, ставим между ними знак =. Это равенство.
Сравниваем одну точку и число 3, на числовом луче число 1 находится левее, чем число 3, ставим знак ≠.
Сравниваем четыре точки и 4. Между ними ставим знак =. Это равенство.
Сравниваем три точки и число 4. Три точки – это число 3. На числовом луче оно левее, ставим знак ≠. Это неравенство. (рис. 12)
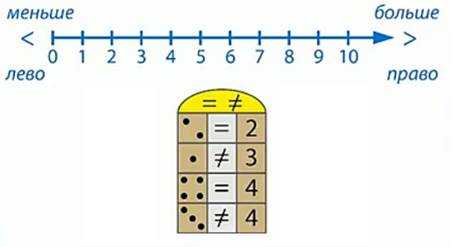
Рис. 12
На втором рисунке между точками и числами надо поставить знаки = , <, >.
Сравним пять точек и число 5. Между ними ставим знак =. Это равенство.
Сравним три точки и число 3. Здесь тоже можно поставить знак =.
Сравним пять точек и число 6. На числовом луче число 5 левее, чем число 6. Ставим знак <. Это неравенство.
Сравним две точки и единицу, число 2 правее на числовом луче, чем число 1. Ставим знак >. Это неравенство. (рис. 13)
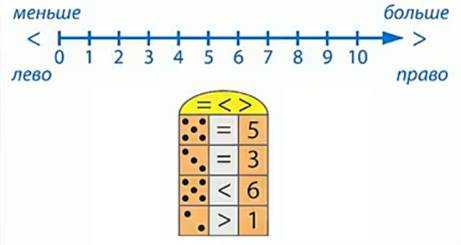
Рис. 13
Вставьте в окошко число, чтобы полученное равенство и неравенство стали верными.
1. ⃞ < 7
Это неравенство. Посмотрим на числовой луч. Раз мы ищем число меньше, чем число 7, значит оно должно быть левее числа 7 на числовом луче. (рис. 14)
Рис. 14
В окошко можно вставить несколько чисел. Сюда подходят числа 0, 1, 2, 3, 4, 5, 6. Любое из них можно подставить в окошко и получить несколько верных неравенства. Например, 5 < 7 или 2 < 7
2. 5 > ⃞
На числовом луче найдём числа, которые будут меньше 5. (рис. 15)
Рис. 15
Это числа 4, 3, 2, 1, 0. Следовательно, любое из этих чисел можно подставить в окошко, мы получим несколько верных неравенств. Например, 5 >4, 5 >3
3. 8 = ⃞
В можно подставить только одно число 8.
8 = 8.
На данном уроке мы познакомились с математическими понятиями: «равенство» и «неравенство», научились правильно расставлять знаки сравнения, потренировались сравнивать группы фигур с помощью составления пар и сравнивать числа с помощью числового луча, что поможет в дальнейшем изучении математики.
Список литературы
- Александрова Л.А., Мордкович А.Г. Математика 1 класс. – М: Мнемозина, 2012.
- Башмаков М.И., Нефедова М.Г. Математика. 1 класс. – М: Астрель, 2012.
- Беденко М.В. Математика. 1 класс. – М7: Русское слово, 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Igraem.pro (Источник).
- Slideshare.net (Источник).
- Iqsha.ru (Источник).
Домашнее задание
1. Какие знаки сравнения вы знаете, в каких случаях они используются? Запишите знаки сравнения чисел.
2. Сравните количество предметов на рисунке и поставьте знак «<», «>» или «=».
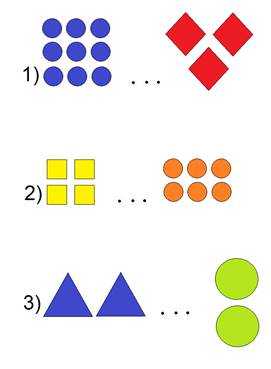
3. Сравни числа, поставив знак «<», «>» или «=».
|
5 … 8 |
9 … 2 |
5 … 5 |
|
10 … 1 |
7 … 8 |
3 … 5 |
interneturok.ru
