Неравенства с модулем
Продолжаем изучать модуль числа. Сегодня мы научимся решать неравенства с модулем.
Чтобы решать неравенства с модулем, нужно прежде всего уметь решать простейшие линейные неравенства, а также знать что такое модуль и как его раскрывать.
Независимо от того, решаем мы уравнение или неравенство, нужно уметь раскрывать модуль.
Рассмотрим к примеру простейшее неравенство с модулем:
|x| > 2
Чтобы решить данное неравенство раскроем его модуль.
Если подмодульное выражение больше или равно нулю, то исходное неравенство примет вид:
x > 2
Решением этого неравенства является множество всех чисел, бóльших 2. Отметим их на координатной прямой:
А если подмодульное выражение меньше нуля, то исходное неравенство примет вид:
−x > 2
Умнóжим обе части этого неравенства на −1. Тогда полýчим неравенство x < −2. Решением этого неравенства является множество всех чисел, мéньших −2.
Забавно, но получившиеся промежутки x < −2 и x > 2 являются ответом к нашей задаче. Если в исходное неравенство |x| > 2 подставить какое-нибудь значение x, удовлетворяющее данному неравенству, то это значение будет принадлежать промежутку (−∞ ; −2) или промежутку (2 ; +∞).
То есть решением исходного неравенства является совокупность из x < −2 и x > 2
Совокупностью неравенств мы будем называть несколько неравенств, объединённых квадратной скобкой, и которые имеют множество решений, удовлетворяющих хотя бы одному из неравенств, входящих в данную совокупность.
Чтобы записать окончательный ответ, промежутки x < −2 и x > 2 следует объединить. В математике знаком объединения служит ∪. Тогда:
x ∈ (−∞ ; −2) ∪ (2 ; +∞)
Знак объединения ∪ читается как «или». Тогда запись x ∈ (−∞ ; −2) ∪ (2 ; +∞) можно прочитать так:
Тогда запись x ∈ (−∞ ; −2) ∪ (2 ; +∞) можно прочитать так:
Значение переменной x принадлежит промежутку (−∞ ; −2) или промежутку (2 ; +∞)
Действительно, если подставить какое-нибудь значение x, являющееся решением исходного неравенства, то это значение будет принадлежать промежутку (−∞ ; −2) или промежутку (2 ; +∞).
Например, число 3, является решением исходного неравенства |x| > 2
|3| > 2 ⇔ 3 > 2
Значение 3 принадлежит промежутку (2 ; +∞). Также оно удовлетворяет хотя бы одному из неравенств совокупности , а именно неравенству x>2.
Значение −4 тоже является решением исходного неравенства |x| > 2. Это значение принадлежит промежутку (−∞ ; −2)
|−4| > 2 ⇔ 4 > 2
Также значение −4 удовлетворяет хотя бы одному из неравенств совокупности , а именно неравенству x < −2.
Согласно определению, модуль числа x есть расстояние от начала координат до точки x. В неравенстве |x| > 2 это расстояние больше чем 2.
В неравенстве |x| > 2 это расстояние больше чем 2.
Действительно, от начала координат (точка 0) любое расстояние бóльшее двух, будет решением неравенства |x| > 2
Ответ: x ∈ (−∞ ; −2) ∪ (2 ; +∞)
Обратите внимание, что границы −2 и 2 не включены в соответствующие промежутки. Это потому, что при подстановке этих чисел в исходное неравенство, получается неверное неравенство.
Теперь немного поменяем наш пример. В неравенстве|x| > 2 поменяем знак > на знак <
|x| < 2
Решим это неравенство.
Как и раньше для начала раскрываем модуль. Если подмодульное выражение больше или равно нулю, то получим неравенство x < 2. Решениями этого неравенства являются все числа, мéньшие двух. Отметим их:
А если подмодульное выражение меньше нуля, то получим неравенство −x < 2. Умнóжим обе части этого неравенства на −1. Тогда получим неравенство x > −2.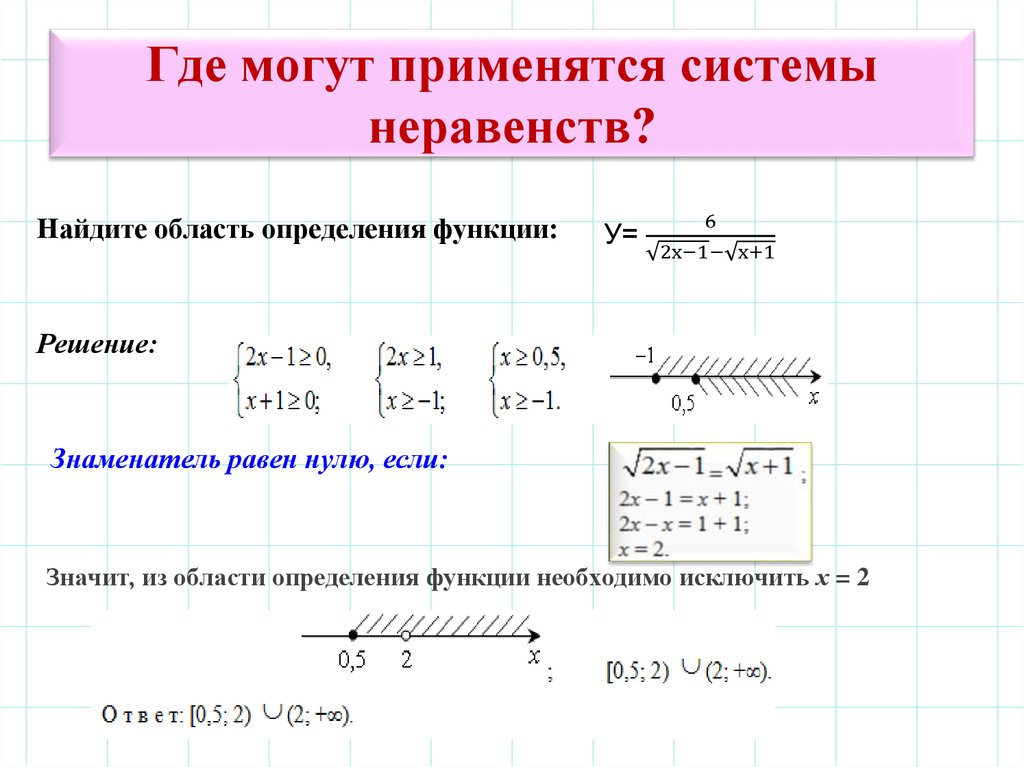 Решениями этого неравенства являются все числа, бóльшие −2. Отметим эти решения на том же рисунке, где мы отметили решения для неравенства x < 2.
Решениями этого неравенства являются все числа, бóльшие −2. Отметим эти решения на том же рисунке, где мы отметили решения для неравенства x < 2.
Для наглядности, решения неравенства x > −2 отметим красным цветом:
Если выражение |x| это расстояние от начала координат до точки x, то неравенство |x| < 2 говорит, что это расстояние меньше чем 2. На рисунке видно, что от начала координат расстояния, мéньшие двух, лежат в промежутках от −2 до 0 и от 0 до 2
А эти расстояния одновременно будут принадлежать промежуткам x < 2 и x > −2
Обратите внимание, что в этот раз промежутки обрамлены знáком системы, а не знáком совокупности как в прошлом примере. Это означает, что значения x одновременно удовлетворяют обоим неравенствам (промежуткам x < 2 и x > −2)
То есть решением неравенства |x| < 2 является пересечение промежутков x < 2 и x > −2. Напомним, что пересечением двух промежутков является промежуток, состоящий из чисел, которые принадлежат как первому промежутку так и второму:
Напомним, что пересечением двух промежутков является промежуток, состоящий из чисел, которые принадлежат как первому промежутку так и второму:
x ∈ (−2 ; 0) ∩ (0 ; 2)
Знак пересечения ∩ читается как «и». Тогда запись x ∈ (−∞ ; 2) ∩ (−2 ; +∞) можно прочитать так:
Значение переменной x одновременно принадлежит промежутку (−∞ ; 2) и промежутку (−2 ; +∞)
Действительно, если подставить какое-нибудь значение x, являющееся решением неравенства |x| < 2, то это значение будет принадлежать одновременно промежутку (−∞ ; 2) и (−2 ; +∞).
Например, число 1 является решением исходного неравенства |x| < 2
|1| < 2 ⇔ 1 < 2
Значение 1 одновременно принадлежит промежутку (−∞ ; 2) и промежутку (−2 ; +∞)
Также, значение 1 удовлетворяет обоим неравенствам системы
А если к примеру подставить значение, не являющееся решением неравенства |x| < 2, то это значение не будет одновременно принадлежать промежуткам (−∞ ; 2) и (−2 ; +∞). Например, значение 7
Например, значение 7
|7| < 2 ⇔ 7 < 2
Несмотря на то, что значение 7 принадлежит одному из промежутков, а именно промежутку (−2 ; +∞), данное значение не является решением исходного неравенства, поскольку оно не удовлетворяет ему. Также, данное значение не принадлежит одновременно обоим промежуткам: (−∞ ; 2) и (−2 ; +∞).
Для неравенства |x| < 2 ответ можно записать покороче:
x ∈ (−2 ; 2)
Из рассмотренных примеров видно, что решением неравенства с модулем может быть либо объединение промежутков либо их пересечение.
В первом примере мы решили неравенство |x| > 2, то есть неравенство вида |x| > a. Это неравенство при котором модуль больше какого-нибудь числа или буквенного выражения. Решением такого неравенства является объединение решений неравенств, получающихся после раскрытия модуля исходного неравенства. Неравенства, получающиеся после раскрытия модуля, следует записывать в виде совокупности:
Совокупность свóдится потому, что итоговые решения будут удовлетворять хотя бы одному из неравенств, полученных после раскрытия модуля исходного неравенства.
Во втором примере мы решили неравенство |x| < 2, то есть неравенство вида |x| < a. От предыдущего неравенства оно отличается только знáком. Но это неравенство при котором модуль меньше какого-нибудь числа или буквенного выражения. Решением такого неравенства является пересечение решений неравенств, получающихся после раскрытия модуля исходного неравенства. Неравенства, получающиеся после раскрытия модуля, следует записывать в виде системы:
Система записывается потому, что итоговые решения будут удовлетворять обоим неравенствам, полученным после раскрытия модуля исходного неравенства.
Эти же правила сохраняются и для неравенств, содержащих знаки ≥ и ≤
Например, решим неравенство |x| ≥ 1. Модуль больше или равен
Решением служит объединение промежутков x ≤ −1 и x ≥ 1
x ∈ (−∞ ; −1] ∪ [1 ; +∞)
Обратите внимание, что границы −1 и 1 включены в соответствующие промежутки. Это потому что при подстановке этих чисел в исходное неравенство, получается верное неравенство.
Это потому что при подстановке этих чисел в исходное неравенство, получается верное неравенство.
Решим теперь к примеру неравенство |x| ≤ 1. Модуль меньше или равен числу. Поэтому решением будет пересечение решений неравенств, которые получатся после раскрытия модуля. После раскрытия модуля и выполнения необходимых тождественных преобразований, получим систему неравенства: x ≤ 1 и x ≥ −1
Решением служит пересечение промежутков x ≤ 1 и x ≥ −1
x ∈ (−∞ ; 1] ∩ [−1 ; +∞)
или покороче:
x ∈ [−1 ; 1]
Обратите внимание, что границы −1 и 1 включены в соответствующие промежутки. Это потому что при подстановке этих чисел в исходное неравенство, получается верное неравенство.
Аналогично решаются неравенства, в левой части которого модуль, а справа не просто число, а буквенное выражение.
Пример 4. Решить неравенство |7x − 6| < x + 12
Решение
Для начала раскроем модуль. Вспоминаем, что если неравенство содержит знак < или ≤, то неравенства получившиеся после раскрытия модуля, следует записать в виде системы. Это будет означать, что итоговые решения будут удовлетворять обоим неравенствам.
Итак, после раскрытия модуля получим следующую систему:
В данном случае система содержит не совсем элементарные неравенства как в прошлых примерах. Данные неравенства следует упростить, используя известные тождественные преобразования.
Раскроем скобки во втором неравенстве. Тогда получим следующую систему:
В обоих неравенствах выражения, содержащие неизвестные, перенесём в левую часть, а числовые выражения — в правую. Затем приведём подобные слагаемые. Тогда получим систему:
В первом неравенстве разделим обе части на 6. Во втором неравенстве разделим обе части на −8. Тогда получим окончательную систему:
Тогда получим окончательную систему:
Изобразим решения на координатной прямой:
Решением является пересечение промежутков (−∞ ; 3) и , то есть промежуток
Ответ:
Пример 5. Решить неравенство |1 − 2x| ≥ 4 − 5x
Решение
Для начала раскроем модуль. Вспоминаем, что если неравенство содержит знак > или ≥, то неравенства получившиеся после раскрытия модуля, следует записать в виде совокупности:
После раскрытия модуля получим следующую совокупность:
Выполним необходимые тождественные преобразования в обоих неравенствах. В результате получим:
Изобразим решения на координатной прямой:
Решением является объединение промежутков и [1 ; +∞), то есть промежуток
Ответ: .
Задание 1. Решить неравенство:
Решение:
Ответ: x ∈ (−36 ; 36).
Показать решение
Задание 2. Решить неравенство:
Решить неравенство:
Решение:
Ответ: x ∈ (−∞ ; −2) ∪ (2 ; +∞).
Показать решение
Задание 3. Решить неравенство:
Решение:
Ответ:
Показать решение
Задание 4. Решить неравенство:
Решение:
Ответ: x ∈ [−5 ; 2]
Показать решение
Задание 5. Решить неравенство:
Решение:
Ответ: x ∈ (−∞ ; 0)
Показать решение
Задание 6. Решить неравенство:
Решение:
Ответ:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
25.
 Неравенства с модулем
Неравенства с модулемI тип: Неравенство содержит некоторое выражение под модулем и число вне модуля:
где (3.27)
Решение зависит от знака числа А.
1. Если то неравенство (3.27) не имеет решений.
2. Если то неравенство (3.27) равносильно системе неравенств
где (3.28)
1. Если то неравенство (3.28) не имеет решений.
2. Если то неравенство (3.28) равносильно уравнению
3. Если , то неравенство (3.28) равносильно системе неравенств
где (3.29)
1. Если то решением неравенства (3.29) является множество всех значений Х из ОДЗ выражения
2. Если то решением неравенства (3.29) является множество всех значений Х из ОДЗ выражения таких, что
3. Если то неравенство (3.29) равносильно совокупности
где (3.30)
1. Если то решением неравенства (3.30) является множество всех значений Х из ОДЗ выражения
2. Если то неравенство (3. 30) равносильно совокупности
30) равносильно совокупности
II тип: Неравенство, которое содержит выражение с переменной под знаком модуля и вне его:
(3.31)
Где – некоторые выражения с переменной Х.
Для решения неравенств типа (3.31) можно использовать следующие способы.
1-й способ: используя определение модуля, получаем равносильную совокупность систем:
2-й способ: Решаем аналогично решению неравенства (3.29) при дополнительном ограничении на знак выражения
1. Если
(3.32)
То решением является множество всех значений Х из ОДЗ выражения которые удовлетворяют условию (3.32).
2. Если
То решением является множество всех значений Х, которые удовлетворяют системе
3. Если решение определяется системой
Ответом в решении неравенства (3.31) является объединение всех решений, полученных на этапах 1–3.
3-й способ: метод интервалов.
Для решения необходимо:
1) найти значения Х, для которых
2) найденные значения Х нанести на числовую ось;
3) определить знак выражения на всех полученных промежутках;
4) нарисовать кривую знаков;
5) раскрыть модуль, пользуясь рисунком, и получить соответствующее неравенство, которое следует решить вместе с условием принадлежности переменной Х определенному промежутку;
6) в ответе неравенства указать совокупность полученных решений.
III тип: Неравенство содержит несколько модулей и решается двумя способами:
1-й способ: Можно использовать определение модуля и решать совокупность систем неравенств. Этот способ, как правило, не является рациональным.
2-й способ: использовать метод интервалов. Необходимо нарисовать столько числовых осей и кривых знаков, сколько модулей содержится в неравенстве. Для каждого промежутка следует решать полученное после раскрытия модулей неравенство при условии, что переменная Х принадлежит конкретному промежутку. В ответе указывают объединение всех полученных решений.
IV тип: Неравенство вида
где (3.33)
Решается двумя способами:
1-й способ: метод интервалов.
2-й способ: согласно теореме равносильности (см. свойства равносильности неравенств (3.22) и (3.23)) неравенство (3.33) можно возводить в квадрат:
Решение неравенства (3.33) сводится к решению неравенства
Аналогично решают неравенства IV типа (3. 33), если они заданы со знаками
33), если они заданы со знаками
V тип: Неравенства, решаемые заменой переменной.
В таком случае выражение с модулем обозначают новой переменной. Неравенство с новой переменной решают до конца (т. е. до возможного получения промежутков решения для новой переменной). Затем возвращаются к старой переменной и решают полученные неравенства с модулем как неравенства I типа.
Пример 1. Решить неравенства:
1) 2)
3) 4)
5) 6)
Решение. 1) Решаем как неравенство I типа:
Получаем ответ:
2) Решаем как неравенство I типа:
Второе неравенство совокупности не имеет решения (соответствующая парабола лежит над осью Ох). Первое неравенство сводится к виду
Его решение: это и есть ответ.
3) Решаем как неравенство II типа. Оно имеет решение, если Поэтому получаем равносильную систему:
Получаем ответ:
4) Заданное неравенство может быть записано в виде
Заменим переменную Решаем неравенство
Его решение
Возвращаемся к переменной Х и решаем совокупность
Получаем
Т. е. приходим к ответу
е. приходим к ответу
5) Для решения неравенства используем метод интервалов. Запишем неравенство в виде
Построим числовые прямые и определим знаки выражений, стоящих под модулем (рис. 3.10).
ОДЗ:
Рис. 3.10
А) рассмотрим неравенство на 1-м промежутке. Получаем систему
(3.34)
Решаем неравенство
Получаем
Система (3.34) сводится к системе
На данном промежутке решений нет.
Б)
Если , то С учетом рассматриваемого промежутка имеем:
Получаем
В)
Решением является промежуток:
Объединим полученные решения и приходим к ответу:
6)
ОДЗ:
Введем новую переменную:
тогда и приходим к неравенству вида
Решаем его
Используем метод интервалов (рис. 3.11).
Рис. 3.11
3.11
Запишем полученное решение в виде совокупности:
Вернемся к переменной Х:
(3.35)
– выполняется при любых
С учетом ОДЗ второе неравенство системы (3.35) равносильно системе
Получаем ответ:
| < Предыдущая | Следующая > |
|---|
Решение неравенств с модулями (21 слайд)
Слайд 1
Неравенства с модулями
11 класс презентация—— Абрамова Светлана Ивановна
Слайд 2
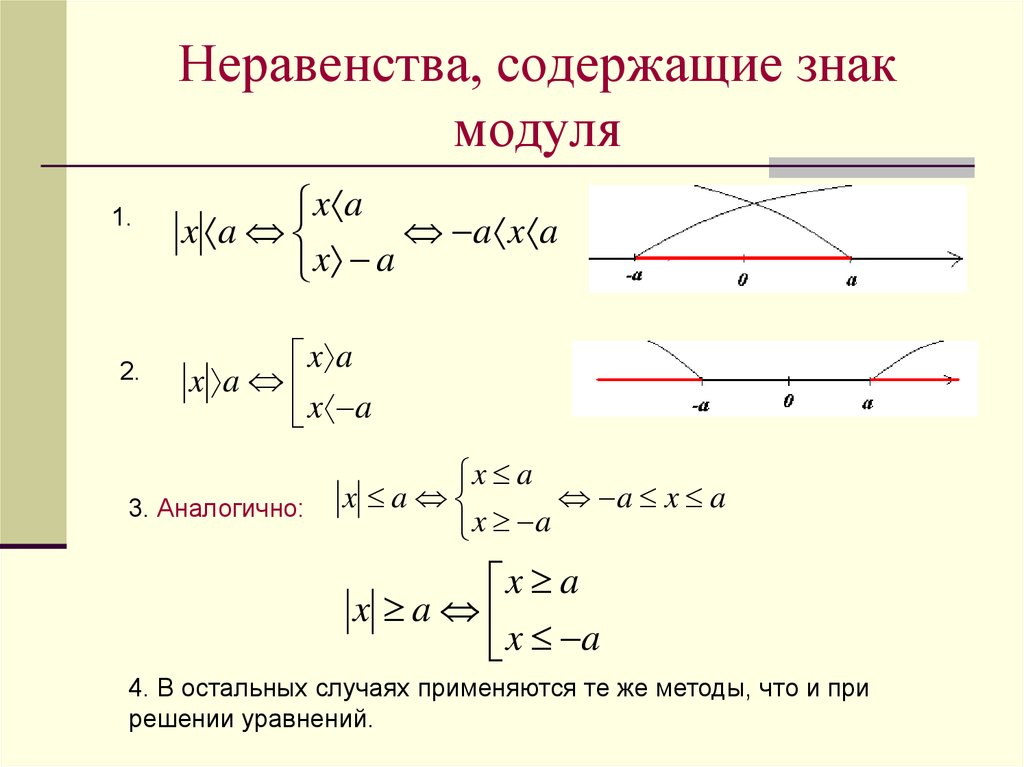
Неравенства вида |f(x)| 0 равносильны двойному неравенству –a Неравенства вида |f(x)| > a при a ≤ 0 имеют решением всю область определения функции f(x). При a > 0 исходное неравенство равносильно двум неравенствам : f(x) > a и f(x)
Слайд 3
Решить неравенство : |3 — 8×2| > -3
Решение.
Поскольку модуль всегда заведомо больше отрицательного числа, решением этого неравенства является область определения функции, стоящей под знаком модуля, т. е. любое рациональное число.
е. любое рациональное число.
Ответ : x ∈ (-∞;∞)
Слайд 4
Решить неравенство: |x2 — 2x| ≤ 0
Решением этого неравенства будут корни уравнения x2-2x=0 ,т.е. x1=0 и x2=2.
Ответ : x ϵ {0} ᴜ {2}
Решить неравенство : |7×2 + 8| ≤ -3
Неравенство решений не имеет, так как модуль всегда положителен.
Ответ : x ϵ ∅
Решение.
Решение.
Слайд 5
Решить неравенство : |x2 — 7x| ≥ 12
Решение.
Корни уравнения: x1=3 и x2=4 ; решением этого неравенства будет интервал: x ∈[3;4]
Равносильные неравенства x2 — 7x ≥ 12 и x2 — 7x ≤ -12 сводятся к квадратным x2 — 7x -12 ≥ 0 и x2 — 7x + 12 ≤ 0.
Решаем первое неравенство.
Корни уравнения :x1= 7− 97 2 и x2= 7+ 97 2 ; решением этого неравенства будут два полубесконечных интервала : (-∞; 7− 97 2 ] и [ 7+ 97 2 ;∞)
Решаем второе неравенство.
Следовательно, решением исходного неравенства будут три интервала решений квадратных неравенств.
Ответ : x ∈(−∞; ????− ???????? ???? ] ᴜ ????;???? ᴜ [ ????+ ???????? ???? ;∞)
Слайд 6
Решить неравенство : | 3????+1 ????−3 | ≤ 3
Решение.
Данное неравенство равносильно двойному : -3 ≤ 3????+1 ????−3 ≤ 3.
3????+1 ????−3 ≤ 3
3????+1 ????−3 ≥ -3
3????+1 ????−3 + 3 ≥ 0
3????+1+3???? −9 ????−3 ≥ 0
6???? −8 ????−3 ≥0
(6x – 8)(x – 3) ≥ 0
x ≠ 3
x ϵ ( -∞ ; 4 3 ] ᴜ ( 3 ; ∞)
3????+1 ????−3 — 3 ≤ 0
3????+1−3????+9 ????−3 ≤ 0
10 ???? −3 ≤ 0
x – 3 x ϵ ( — ∞ ; 3 )
Ответ : x ϵ ( — ∞ ; 4 3 )
Слайд 7
Неравенства вида |f(x)|≤ g(x) сводятся к равносильной системе:
f(x) ≤ g(x) f(x) ≥ -g(x) ,
а неравенства вида |f(x)|≥ g(x) – к аналогичной равносильной системе:
f(x) ≥ g(x) f(x) ≤ -g(x) .
Слайд 8
Решить неравенство : |x2 — 8x + 15|Решение .
Равносильная система неравенств
x2 — 8x + 15 3 — x
сводится к решению двух равносильных неравенств :
x2 — 9x + 18 0
x1 = 3 x2 = 6
x1 = 3 x2 = 4
x ϵ ( 3 ; 6 ) x ϵ ( -∞ ; 3) ᴜ ( 4 ; ∞ )
Ответ : x ϵ ( 4 ; 6 )
3
3
4
6
Слайд 9
Решить неравенство : |x2 – 2x — 3| > 3x — 3
Решение .
Равносильная система неравенств
x2 – 2x – 3 > 3x – 3 x2 – 2x – 3 как и в предыдущем примере, сводится к системе квадратных неравенств :
x2 –5x > 0 x2 + x – 6 x1 = 0 x2 = 5
x1 = -3 x2 = 2
x ϵ ( -∞ ; 0 ) ᴜ ( 5 ; ∞ ) x ϵ ( -3 ; 2 )
-3
2
0
5
Ответ : x ϵ ( -3 ; 0 )
Слайд 10
Неравенства вида F(|f(x)|) v 0 заменой y=|f(x)| сводятся к равносильной системе :
F(y) v 0 y ≥ 0
Слайд 11
Решить неравенство : |x — 4|3 + |x — 4|> 2
Решение .
Заменой y=|x — 4| исходное неравенство сводится к равносильной системе :
y 3 + y > 2 y ≥ 0
y3 + y – 2 y3 – y2
y2 + y y2 – y
2у – 2 2у – 2
y — 1 y2 + y + 2
0
—
—
—
Первое неравенство y 3 + y — 2 > 0 – рациональное. Решать его нужно методом интервалов для рациональных и дробно-рациональных неравенств, предварительно разложив левую часть на множители. Корень у=1 кубического трехчлена угадывается сразу. Поэтому, деля y 3 + y — 2 на у – 1 или применяя метод неопределенных коэффициентов с использованием теоремы Безу, разложим выражение на два сомножителя – линейный и квадратный.
Слайд 12
Таким образом,
y 3 + y – 2 = (у – 1)(y2 + y + 2)
Итак, равносильная система приняла вид :
(у – 1)(y2 + y + 2)>0 y≥0 ,
откуда у>1
Переходя к переменной х, получаем простейшее неравенство |х — 4| > 1, которое разбивается на два равносильных : х – 4 > 1, или х > 5, и х – 4 Ответ : x ϵ ( -∞ ; 3) ᴜ ( 5 ; ∞ )
Слайд 13
Неравенства вида F(ϕ(x) ;|f(x)|) v 0 сводятся к двум равносильным системам :
f(x)≥0 F(ϕ(x) ; f(x)) v 0
f(x)
Слайд 14
Решить неравенство : x2 + 2|x + 3| — 10 ≤ 0
Решение .
Равносильные системы :
x + 3 ≥ 0 x2 + 2(x + 3) – 10 ≤ 0
x + 3 x ≥ -3 x2 + 2x – 4 ≤ 0
x x ≥ -3 x1= -1 + 5 x2= -1 — 5
x x ϵ [-3 ; -1 + 5 ]
x ϵ [1 — 17 ; -1 + 5 ]
Ответ : x ϵ [ 1 — ???????? ; -1 + ???? ]
и
Слайд 15
Неравенства вида |f(x)|>|g(x)|, как и соответствующие уравнения, сводятся к равносильному [ f(x) ]2 > [ g(x) ]2 .
Слайд 16
Решить неравенство : |2x — 5| — |4x + 7|≥ 0
Решение .
Приводим исходное неравенство к виду
|2x — 5| ≥ |4x + 7|
и возводим в квадрат :
(2x – 5)2 ≥ (4x + 7)2
Раскрывая скобки и приводя подобные члены, получаем квадратное неравенство :
3×2 + 19x + 6 ≤ 0
3×2 + 19x + 6 = 0
x1= — 6 x2= — 1 3
Решением неравенства является интервал [ -6 ; — 1 3 ] , он же – решением исходного неравенства с модулями.
Ответ : x ϵ [ -6 ; — 1 3 ]
Слайд 17
Неравенства вида |f1(x)|±|f2(x)|±…±|fn(x)| v a решаются тем же самым методом интервалов, что и уравнения с модулем. Разница лишь в том, что в данном случае в каждом интервале решается не уравнение, а неравенство и из решений неравенства выбираются те, которые принадлежат данному интервалу. В остальном метод интервалов остается тем же, что и при решении уравнений с модулем.
Не следует путать этот метод с методом интервалов, применяемым для решения рациональных и дробно-рациональных неравенств.
Внимание!
Слайд 18
Решить неравенство : |x|- 2|x + 1|+ 3|x + 2|≥ 4
Решение .
Найдем сначала все xi , разбивающие числовую ось на интервалы и получающиеся как решения уравнений fj (xi )=0 : х=0; х + 1=0 ; х + 2=0. Таким образом, границами интервалов являются числа x1=0, x2=-1 и x3=-2. Отметим эти значения на числовой оси для каждого из полученных интервалов определим знаки выражений, стоящих под знаком модуля :
I
II
III
IV
-2
-1
0
x x 0
x 0 x + 2 > 0
x>0 x + 1 > 0 x + 2 > 0
Раскроем модули на интервале I (x≤-2) :
-x + 2( + 1) – 3(x + 2) ≥ 4
После преобразования получаем
-2х – 4 ≥ 4 ,
откуда х ≤ -4
Слайд 19
Этот интервал входит в интервал I и является решением исходного неравенства.
II интервал ( -2≤ х ≤-1 ) :
-х+ 2(х + 1) + 3(х + 2) ≥ 4
4х + 8 ≥ 4 ,
откуда х≥-1
Решением в этом интервале является точка х=-1
III интервал ( -1≤ х ≤0 ) :
-х – 2(х + 1) + 3(х + 2) ≥ 4
4 ≥ 4
В результате мы получили истинное неравенство ( заметим, что, если бы неравенство было строгим, оно становилось бы ложным). Следовательно, весь интервал III является решением исходного неравенства.
Следовательно, весь интервал III является решением исходного неравенства.
IV интервал ( х≥0 )
х – 2(х + 1) + 3( + 2) ≥ 4
2х + 4 ≥ 4 ,
откуда х≥0
Таким образом, весь интервал IV является решением исходного неравенства. Заметим, что решения, полученные в интервалах II, III и IV, «сливаются» по граничным точкам x1=-1 и x2=0 в единый интервал [-1 ; ∞). ????+ ???????? ???? ;∞)
Ответ : ( -∞ ; -4 ] ᴜ [ -1 ; ∞ )
Слайд 20
! Презентация составлена учителем математики Абрамовой С.И. К элективному курсу 11 класс по теме
« Решение Неравенств модулями»
24.12.18г
Слайд 21
Неравенства с модулем
Продолжаем изучать модуль числа. Сегодня мы научимся решать неравенства с модулем.
Чтобы решать неравенства с модулем, нужно сначала уметь решать простейшие линейные неравенства, а также знать, что такое модуль и как его решать.
Независимо от того, решаем ли мы уравнение или неравенство, нам нужно уметь решать модуль.
Рассмотрим, например, простейшее неравенство с модулем:
| х | > 2
Чтобы решить это неравенство, разверните модуль.
Если подмодульное выражение больше или равно нулю, то исходное неравенство примет вид:
x > 2
Решением этого неравенства является множество всех чисел больше 2. Отметьте их на координатная линия:
А если подмодульное выражение меньше нуля, то исходное неравенство примет вид:
− x > 2
Умножьте обе части этого неравенства на -1. Тогда получаем неравенство x < -2. Решением этого неравенства является множество всех чисел, меньших -2. Отметьте эти решения на том же рисунке, где мы отметили решения неравенства x > 2.
Как ни странно, полученные интервалы x < -2 и x > 2 являются ответом на нашу задачу. Если в исходное неравенство подставить |x| > 2 любое значение x, удовлетворяющее этому неравенству, то это значение будет принадлежать интервалу (-∞ ; -2) или интервал (2 ; +∞).
То есть решением исходного неравенства является множество x < -2 и x > 2
Будем называть множеством неравенств , объединенных квадратной скобкой и имеющих множество решений, удовлетворяющих хотя бы одному неравенств в множестве.
Чтобы написать окончательный ответ, нужно сложить интервалы x < -2 и x > 2. В математике знаком союза является ∪. Тогда:
x ∈ (−∞ ; −2) ∪ (2 ; +∞)
Знак объединения ∪ читается как «или». Тогда обозначение x ∈ (-∞ ; -2) ∪ (2 ; +∞) можно прочитать следующим образом:
Значение переменной x принадлежит интервалу (-∞ ; -2) или интервалу ( 2 ; +∞)
Действительно, если подставить любое значение x, являющееся решением исходного неравенства, то это значение будет принадлежать интервалу (-∞ ; -2) или интервалу (2 ; +∞) .
Например, число 3 является решением исходного неравенства |x| > 2
|3| > 2 ⇔ 3 > 2
Значение 3 принадлежит интервалу (2 ; +∞). Он также удовлетворяет хотя бы одному из неравенств множества
Он также удовлетворяет хотя бы одному из неравенств множества
, а именно неравенству x>2.
Значение -4 также является решением исходного неравенства |x| > 2. Это значение принадлежит интервалу (-∞ ; -2)
|−4| > 2 ⇔ 4 > 2
Также значение -4 удовлетворяет хотя бы одному из неравенств множества
, а именно неравенству x < -2.
Согласно определению, модуль числа x равен расстоянию от начала координат до точки x. В неравенстве |x| > 2 это расстояние больше 2.
Действительно, любое расстояние от начала координат (точка 0) больше двух будет решением неравенства |x| > 2
Ответ: x ∈ (−∞ ; −2) ∪ (2 ; +∞)
Заметим, что границы -2 и 2 не входят в соответствующие интервалы. Это потому, что когда вы подставляете эти числа в исходное неравенство, вы получаете неправильное неравенство.
Теперь немного изменим наш пример.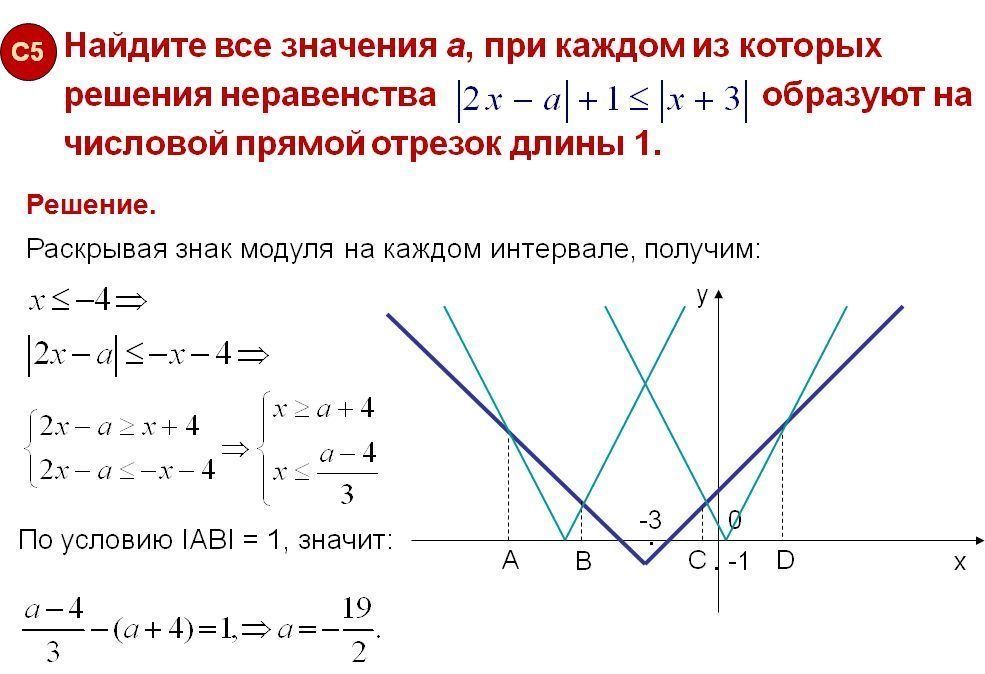 В неравенстве |x| > 2, меняем знак > на знак <
В неравенстве |x| > 2, меняем знак > на знак <
| х | < 2
Решим это неравенство.
Как и раньше, сначала решаем модуль. Если подмодульное выражение больше или равно нулю, получаем неравенство x < 2. Решениями этого неравенства являются все числа меньше двух. Заметим их:
И если подмодульное выражение меньше нуля, то получим неравенство -x < 2. Умножим обе части этого неравенства на -1. Тогда получаем неравенство x > -2. Решениями этого неравенства являются все числа больше -2. Отметьте эти решения на том же рисунке, где мы отметили решения неравенства x < 2,9.0003
Для наглядности решения неравенства x > -2 отмечены красным цветом:
Если выражение |x| — расстояние от начала координат до точки x, то выполняется неравенство |x| < 2 говорит, что это расстояние меньше 2. На рисунке видно, что от начала координат расстояния меньше 2 лежат между -2 до 0 и от 0 до 2.
И эти расстояния будут одновременно принадлежать интервалам x < 2 и x > -2
Обратите внимание, что на этот раз интервалы обрамлены знаком системы, а не знаком совокупности, как в последнем примере. Это означает, что значения x одновременно удовлетворяют обоим неравенствам (интервалы x < 2 и x > -2)
Это означает, что значения x одновременно удовлетворяют обоим неравенствам (интервалы x < 2 и x > -2)
То есть решение неравенства |x| < 2 есть пересечение интервалов x < 2 и x > -2. Напомним, что пересечением двух интервалов называется интервал, состоящий из чисел, принадлежащих как первому интервалу, так и второму:
x ∈ (−2 ; 0) ∩ (0 ; 2)
Знак пересечения ∩ читается как «а также». Тогда обозначение x ∈ (-∞ ; 2) ∩ (-2 ; +∞) можно прочитать следующим образом:
Значение переменной x одновременно принадлежит интервалу (-∞ ; 2) и интервалу (- 2 ; +∞)
Действительно, если мы подставим любое значение x, которое является решением неравенства |x| < 2, то это значение будет принадлежать как (-∞ ; 2), так и (-2 ; +∞) интервалам.
Например, число 1 является решением исходного неравенства |x| < 2
|1| < 2 ⇔ 1 < 2
Значение 1 одновременно принадлежит интервалу (-∞ ; 2) и интервалу (-2 ; +∞)
Также значение 1 удовлетворяет обоим неравенствам системы
А если подставить значение, не являющееся решением неравенства |x| < 2, то это значение не будет одновременно принадлежать интервалам (-∞ ; 2) и (-2 ; +∞). Например, значение 7
Например, значение 7
|7| < 2 ⇔ 7 < 2
Несмотря на то, что значение 7 принадлежит одному из интервалов, а именно интервалу (-2 ; +∞), это значение не является решением исходного неравенства, поскольку не удовлетворить его. Также это значение не принадлежит обоим интервалам: (-∞ ; 2) и (-2 ; +∞).
Для неравенства |x| < 2 ответ можно записать короче:
x ∈ (−2 ; 2)
Из этих примеров видно, что решением неравенства с модулем может быть либо объединение интервалов, либо их пересечение .
В первом примере мы решили неравенство |x| > 2, т. е. неравенство вида |x| > а. Это неравенство , в котором модуль больше некоторого числового или буквенного выражения . Решением такого неравенства является объединение решений неравенств, полученных после выставления модуля исходного неравенства. Неравенства, полученные после выставления модуля, следует записать в виде совокупности:
Набор сокращен, так как окончательные решения будут удовлетворять хотя бы одному из неравенств, полученных после выставления модуля исходного неравенства.
Во втором примере мы решили неравенство |x| < 2, т. е. неравенство вида |x| < а. Оно отличается от предыдущего неравенства только знаком. Но это неравенство , где модуль меньше некоторого числа или буквенного выражения . Решением такого неравенства является пересечение решений неравенств, полученных после выставления модуля исходного неравенства. Неравенства, полученные после выставления модуля, следует записать в виде системы:
Система написана потому, что окончательные решения будут удовлетворять обоим неравенствам, полученным после выставления модуля исходного неравенства.
Те же правила справедливы для неравенств, содержащих знаки ≥ и ≤
Например, решить неравенство |x| ≥ 1. Модуль больше или равен числу . Поэтому решением будет объединение решений неравенств, которые будут получены после выставления модуля. После выставления модуля и выполнения необходимых тождественных преобразований получаем набор неравенств x ≥ 1 и x ≤ -1
Решение представляет собой объединение интервалов x ≤ -1 и x ≥ 1
x ∈ (−∞ ; −1] ∪ [1 ; +∞) и 1 — , включающих в соответствующие интервалы. Это потому, что когда вы подставляете эти числа в исходное неравенство, вы получаете правильное неравенство.
Это потому, что когда вы подставляете эти числа в исходное неравенство, вы получаете правильное неравенство.
Теперь решите, например, неравенство |x| ≤ 1. Модуль на меньше или равен числу . Следовательно, решение будет пересечение решений неравенств, которые будут получены после выставления модуля. После выставления модуля и выполнения необходимых тождественных преобразований получаем систему неравенств: x ≤ 1 и x ≥ -1
Решением является пересечение интервалов x ≤ 1 и x ≥ -1
x ∈ (−∞ ; 1] ∩ [−1 ; +∞)
или короче:
x ∈ [−1 ; 1]
Обратите внимание, что границы -1 и 1 равны включал в соответствующие интервалы. Это потому, что когда вы подставляете эти числа в исходное неравенство, вы получаете правильное неравенство.
Точно так же можно решать неравенства с модулем слева и буквенным выражением справа.
Пример 4. Решить неравенство |7x — 6| < x + 12
Решение
Сначала расширим модуль. Напомним, что если неравенство содержит знак < или ≤, то неравенства, полученные после выставления модуля, следует записать в виде системы. Это означает, что окончательные решения будут удовлетворять обоим неравенствам.
Напомним, что если неравенство содержит знак < или ≤, то неравенства, полученные после выставления модуля, следует записать в виде системы. Это означает, что окончательные решения будут удовлетворять обоим неравенствам.
Итак, после расширения модуля получаем следующую систему:
В этом случае система содержит не совсем элементарные неравенства, как в предыдущих примерах. Эти неравенства следует упростить, используя известные тождественные преобразования.
Раскройте скобки во втором неравенстве. Тогда получим следующую систему:
В обоих неравенствах перенесите выражения, содержащие неизвестные, в левую часть, а числовые выражения — в правую. Затем мы добавляем подобные термины. Тогда получаем систему:
В первом неравенстве обе части разделите на 6. Во втором неравенстве обе части разделите на -8. Тогда получим окончательную систему:
Представим решения на координатной прямой:
Решение есть пересечение интервалов (-∞ ; 3) и
, то есть интервал
0 Ответ: Пример 5. Решить неравенство |1 — 2x| ≥ 4 — 5x
Решить неравенство |1 — 2x| ≥ 4 — 5x
Решение
Сначала расширим модуль. Напомним, что если неравенство содержит знак > или ≥, то неравенства, полученные после расширения модуля, следует записать в виде набора:
После расширения модуля получим следующий набор:
Выполним необходимые тождественные преобразования в оба неравенства. В результате получаем:
Представим решения на координатной прямой:
Решение представляет собой объединение интервалов
и [1 ; +∞), то есть интервал
Ответ :
.
Задача 1. Решите неравенство:
Решение:
Ответ : x ∈ (−36 ; 36).
Показать решение
Задача 2. Решить неравенство:
Решение:
Ответ : x ∈ (−∞ ; −2) ∪ (2 ; +∞).
Показать раствор
Задача 3. Решить неравенство:
Решить неравенство:
Решение:
Ответ :
Покажите решение
Задача 4. Решение неравенства:
Решение:
Ответ : x ∈ [5; 2]
Показать решение
Задача 5. Решить неравенство:
Решение:
Ответ : x ∈ (−∞; 0)
Показать решение
Задача 6. Решение. Неравенство:
Решение:
Ответ :
Показать решение
абсолютное значение — Двойной модуль в неравенстве
$\begingroup$
Может кто-нибудь объяснить мне (или дать ссылку на сайт, который делает), как решить эту проблему? $$ ||х+1| -1| \geq 3 $$ Я понятия не имею, как вычислить этот знак двойного абсолютного значения.
- неравенство
- абсолютное значение
$\endgroup$
1
$\begingroup$
Работайте снаружи внутрь. Для начала у вас есть неравенство $|u-1|\ge 3$, где $u=|x+1|$. Это эквивалентно $$u-1\le -3\quad\mathbf{or}\quad u-1\ge 3\;.$$ Решая их, мы находим, что $$u\le-2\quad\mathbf {или}\quad u\ge 4\;,$$, что в терминах исходной переменной $x$ равно
Для начала у вас есть неравенство $|u-1|\ge 3$, где $u=|x+1|$. Это эквивалентно $$u-1\le -3\quad\mathbf{or}\quad u-1\ge 3\;.$$ Решая их, мы находим, что $$u\le-2\quad\mathbf {или}\quad u\ge 4\;,$$, что в терминах исходной переменной $x$ равно
$$|x+1|\le -2\quad\mathbf{or}\quad|x+ 1|\ge 4\;.\tag{1}$$
Абсолютное значение не может быть отрицательным, поэтому $(1)$ сводится к $|x+1|\ge 4$. Как и в самом первом шаге, это эквивалентно
$$x+1\le-4\quad\mathbf{or}\quad x+1\ge 4\;,$$, решение которого равно
$$x\le-5\quad\mathbf{or} \quad x\ge 3\;.$$
$\endgroup$
4
$\begingroup$
Так как у вас уже есть раствор снаружи, я дам вам изнанку.
Сначала возьмем случай $x+1\geq 0$. Таким образом, $||x+1|-1|=|x+1-1|=|x|$.
$|x|\geq3$ имеет решение $x\leq-3$ или $x\geq3$. Зная, что $x\geq-1$, первое невозможно.
 2=(a-b)(a+b)\ \
&\Longleftrightarrow (x-3)(x+5)\geq 0\\
&\Longleftrightarrow x\in(-\infty,-5]\cup[3,+\infty)
\end{выравнивание}
$$
2=(a-b)(a+b)\ \
&\Longleftrightarrow (x-3)(x+5)\geq 0\\
&\Longleftrightarrow x\in(-\infty,-5]\cup[3,+\infty)
\end{выравнивание}
$$$\endgroup$
$\begingroup$
Если бы я был перед классом, который столкнулся с этой проблемой, я бы изобразил ее на графике, проанализировав ее изнутри. Во-первых, $|x+1|$ имеет V-образный граф с вершиной в $(-1,0)$. Тогда $|x+1|-1$ также имеет V-образный граф с вершиной в $(-1,-1)$. Обратите внимание, что этот график пересекает ось $x$ в точке $(-2,0)$ и начале координат. Когда вы берете абсолютное значение функции $|x+1|-1$, часть графика, расположенная ниже оси $x$, отражается выше. Результат теперь W -образный график с левым углом в $(-2,0)$, средним углом в $(-1,1)$ и прямым углом в начале координат. Слева от $(-2,0)$ график поднимается (по мере удаления от начала координат) с наклоном $-1$, т.е. имеет уравнение $y=-x-2$, а справа от начала координат, график поднимается с наклоном $1$, т.
 е. просто $y=x$. Чтобы значение этой функции было не меньше $3$, нужно справа $x\ge3$, а слева $x\le-5$.
е. просто $y=x$. Чтобы значение этой функции было не меньше $3$, нужно справа $x\ge3$, а слева $x\le-5$.$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
неравенств в повседневном мире | SSPC1006
Обзор модуля Цели и задачи Учебный план Обучение и преподавание Оценка
Обзор модуля
Модуль предлагает строго интерсекционный подход к проблеме неравенства, еженедельно предлагая несколько структур, с помощью которых можно рассматривать опыт и значения неравенства. К концу модуля учащиеся познакомятся с 8 ключевыми темами для понимания неравенства и смогут говорить о том, как они со-конструируют друг друга и способствуют структурированию общества, а также о влиянии и для Реакция социальной политики на эти проблемы. Изучая ряд культурных и социальных текстов, модуль будет прочно закреплен в современном моменте, предлагая «живую социологию» (Back, 2012), побуждая студентов смотреть вокруг себя на свой социальный мир и глобальное положение, давая им возможность понять и критикуйте их повседневные интернациональные миры.
 Модуль основан на теоретических введениях в ключевые социальные теории, предложенных в первом семестре, и обеспечивает основу для студентов, чтобы перейти ко второму и третьему году обучения, знакомя с ключевыми областями обучения, подробно изученными в других модулях
Модуль основан на теоретических введениях в ключевые социальные теории, предложенных в первом семестре, и обеспечивает основу для студентов, чтобы перейти ко второму и третьему году обучения, знакомя с ключевыми областями обучения, подробно изученными в других модуляхЦели и задачи
Результаты обучения
Результаты обучения
Успешно завершив этот модуль, вы сможете:
- Работа в команде: работа в группах для обсуждения, дебатов и предоставления критических оценок определенных тем и аргументов
- Предоставьте аналитический отчет о том, как проявляется социальное неравенство, обращаясь к вопросам идентичности, различиям, виктимизации, отклонениям и причинению вреда
- Создать четко сформулированный и хорошо структурированный пост в блоге или подкаст, в котором точно описываются дебаты и теоретические подходы к неравенству
- Дать аналитический отчет о социальном неравенстве (классовом, гендерном, сексуальном, возрастном, расовом и этническом, инвалидности, глобальном), роли власти в его формировании и последствиях для общества
- Определите и опишите ключевые теории и подходы к пониманию и изучению неравенства
- Понять и изучить процессы интернационализации, чтобы предложить критические глобальные взгляды на неравенство, социальные изменения и власть.

Учебный план
1. Введение в тему неравенства
2. Инвалидность
3. Раса
4. Пол
5. Сексуальная принадлежность
6. Класс
7. Возраст
8. Глобальные неравенства
9. Здоровье
10. Выводы
Обучение и преподавание
Методы преподавания и обучения
Этот модуль проводится по программе из 10 лекций и 9 семинаров. Используется сочетание синхронных и асинхронных методов со смешанным подходом к обучению, включающим лекции, семинары и чтение рабочих листов. Семинары будут синхронными, и студентам будет предложено обсудить современный пример из новостных или развлекательных СМИ, который имеет какое-то отношение к теме недели. Эта структура предлагает гибкость в том, как учащиеся хотят участвовать, обеспечивая при этом достаточное время для обсуждения тем и изучения тем.
 Дальнейшее время контакта предлагается через учебные пособия по оценке
Дальнейшее время контакта предлагается через учебные пособия по оценкеУчебное время Тип часов Учебник 2 Лекция 10 Независимое исследование 129 Семинар 9 Общее время обучения 150 Оценка
Стратегия оценки
Каждую неделю будет выдаваться задание/рабочий лист по чтению, который учащиеся используют для управления своим чтением. Завершение этого позволяет попрактиковаться в письме на эти темы и обеспечивает структурированный подход к подготовке и пересмотру семинара.
 Студенты должны представить минимум 6 из 9рабочие листы, чтобы получить максимум 12% итоговой оценки
Студенты должны представить минимум 6 из 9рабочие листы, чтобы получить максимум 12% итоговой оценкиОкончательной оценкой будет публикация в блоге или подкаст, в котором учащиеся работают в парах, чтобы критически обсудить заданное неравенство со ссылкой на современный пример и соответствующие теории и подходы. Учащиеся будут оценивать собственные усилия и усилия и вклад своих партнеров в итоговую оценку, и это будет учитываться в их оценках.
Суммарный
Так мы официально оценим то, что вы узнали в этом модуле.
Поломка Метод Процентный вклад Подкаст 88% Лист с краткими ответами 12% Направление
Вот как мы будем оценивать вас, если вы не соответствуете критериям для прохождения этого модуля.


 2=(a-b)(a+b)\ \
&\Longleftrightarrow (x-3)(x+5)\geq 0\\
&\Longleftrightarrow x\in(-\infty,-5]\cup[3,+\infty)
\end{выравнивание}
$$
2=(a-b)(a+b)\ \
&\Longleftrightarrow (x-3)(x+5)\geq 0\\
&\Longleftrightarrow x\in(-\infty,-5]\cup[3,+\infty)
\end{выравнивание}
$$ е. просто $y=x$. Чтобы значение этой функции было не меньше $3$, нужно справа $x\ge3$, а слева $x\le-5$.
е. просто $y=x$. Чтобы значение этой функции было не меньше $3$, нужно справа $x\ge3$, а слева $x\le-5$.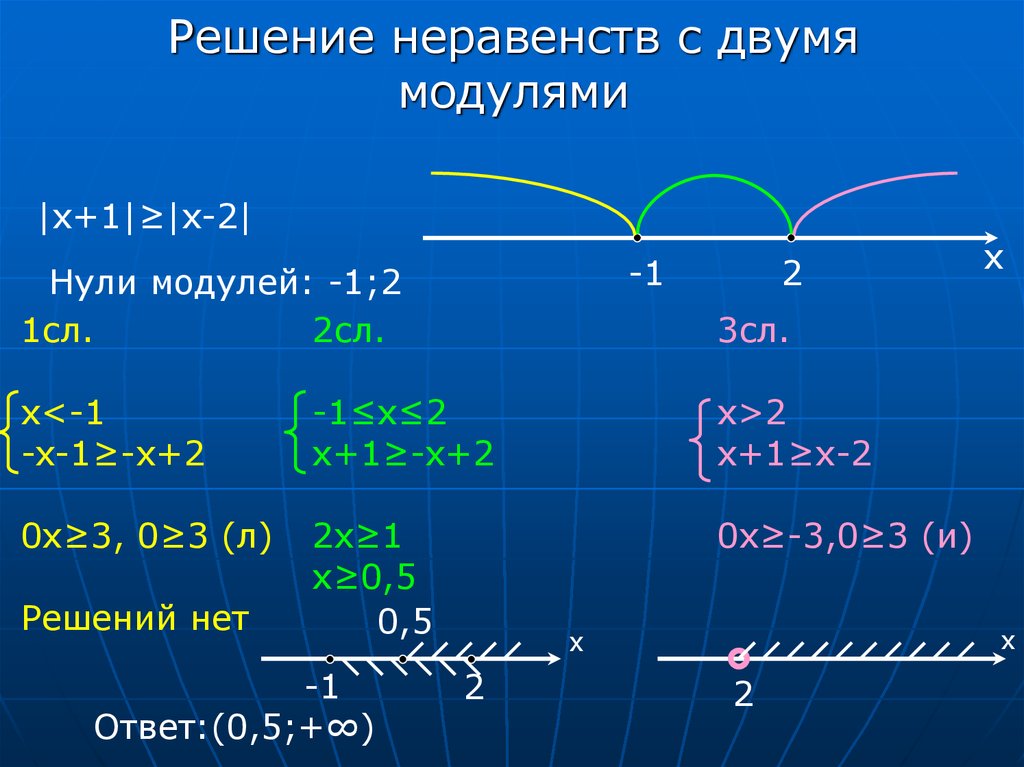
 Модуль основан на теоретических введениях в ключевые социальные теории, предложенных в первом семестре, и обеспечивает основу для студентов, чтобы перейти ко второму и третьему году обучения, знакомя с ключевыми областями обучения, подробно изученными в других модулях
Модуль основан на теоретических введениях в ключевые социальные теории, предложенных в первом семестре, и обеспечивает основу для студентов, чтобы перейти ко второму и третьему году обучения, знакомя с ключевыми областями обучения, подробно изученными в других модулях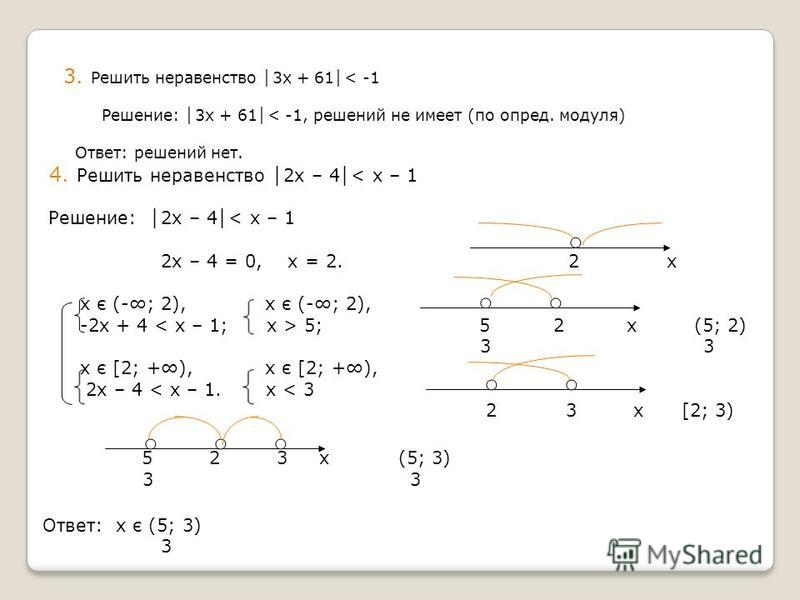
 Дальнейшее время контакта предлагается через учебные пособия по оценке
Дальнейшее время контакта предлагается через учебные пособия по оценке Студенты должны представить минимум 6 из 9рабочие листы, чтобы получить максимум 12% итоговой оценки
Студенты должны представить минимум 6 из 9рабочие листы, чтобы получить максимум 12% итоговой оценки