Таблица операторов — Служба поддержки Майкрософт
Access для Microsoft 365 Access 2021 Access 2019 Access 2016 Access 2013 Access 2010 Access 2007 Еще…Меньше
Оператором называется знак или символ, указывающий на тип вычислений, которые выполняются в выражении. Существуют математические, логические операторы, а также операторы сравнения и ссылок. Access поддерживает различные операторы, включая арифметические операторы, такие как +, —, умножение (*) и деление (/), а также операторы для сравнения значений, текстовые операторы для сцепления текста и логические операторы для определения значений «Истина» и «Ложь». Эта статья содержит сведения об использовании таких операторов.
Примечание: В Access 2010 и более поздних версий построитель выражений включает функцию IntelliSense, которая указывает требуемые аргументы.
В этой статье
-
Арифметические операторы
-
Операторы сравнения
-
Логические операторы
-
Операторы объединения
-
Специальные операторы
Арифметические операторы
|
Арифметические операторы используется для вычисления значения на основе нескольких чисел или изменения знака числа из положительного в отрицательный и наоборот.
|
К началу страницы
Операторы сравнения
Операторы сравнения позволяют сравнивать значения. Они возвращают результат «Истина», «Ложь» или Null.
|
Оператор |
Назначение |
Пример |
|
< |
Возвращает значение «Истина», если первое значение меньше второго. |
значение1 < значение2 |
|
<= |
Возвращает значение «Истина», если первое значение не больше второго. |
значение1 <= значение2 |
|
> |
Возвращает значение «Истина», если первое значение больше второго. |
значение1 > значение2 |
|
>= |
Возвращает значение «Истина», если первое значение не меньше второго. |
значение1 >= значение2 |
|
= |
Возвращает значение «Истина», если первое значение равно второму. |
значение1 = значение2 |
|
<> |
Возвращает значение «Истина», если первое значение не равно второму. |
значение1 <> значение2 |
Примечание: Если первое или второе значение в любом из случаев равно Null, результатом также является Null.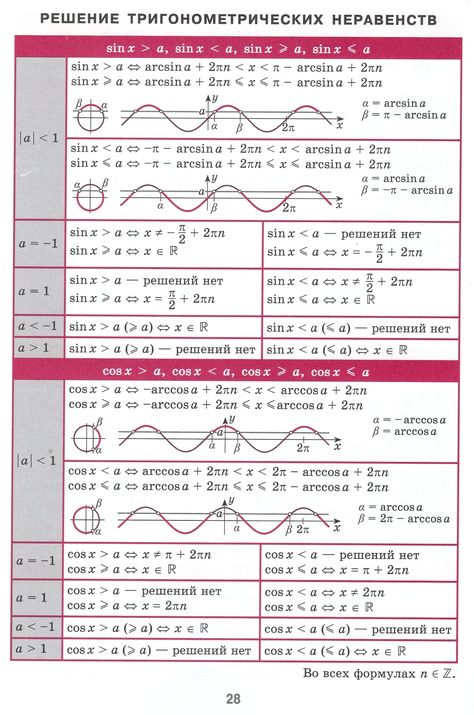 Так как Null представляет собой неизвестное значение, результат сравнения со значением Null также неизвестен.
Так как Null представляет собой неизвестное значение, результат сравнения со значением Null также неизвестен.
К началу страницы
Логические операторы
|
Используйте логические операторы для объединения двух логических значений и возврата результата «Истина», «Ложь» или Null. Логические операторы также называются булевыми.
|
К началу страницы
Операторы объединения
|
Операторы объединения позволяют объединить два текстовых значения в одно.
|
К началу страницы
Специальные операторы
|
Специальные операторы возвращают результат «Истина» или «Ложь», как описано в таблице ниже.
|
Неравенства. 9 класс — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Урок алгебры в 9 классе по теме: «Неравенства».
2. Повторение основных понятий.
1.2.
Линейное неравенство –
неравенство вида ах+в>0
(ах+в<0), где а и в – любые числа,
а≠0.
Квадратное неравенство –
неравенство вида ах2+вх+с>0
(ах2+вх +с<0), где а≠0.
3. Равносильные преобразования неравенств.
Правило 1. Любой член неравенства можноперенести из одной части неравенства в
другую с противоположным знаком, не
меняя при этом знак неравенства.
Правило 2. Обе части неравенства можно
умножить или разделить на одно и то же
положительное число, не меняя при
этом знак неравенства.
4. Основные правила решения неравенств.
Правило 3. Обе части неравенства можноумножить или разделить на одно и то же
отрицательное число, изменив при этом
знак неравенства на противоположный.
5. Алгоритм решения квадратного неравенства ах2+вх+с>0
Алгоритм решения квадратногонеравенства ах2+вх+с>0
1.
2.
3.
4.
Определить, куда (вверх или вниз)
направлены ветви параболы, служащей
графиком функции у=ах2+вх+с.

Найти точки пересечения параболы с ось Х,
решив уравнение ах2+вх+с=0.
Отметить найденные корни на оси Х и
сделать эскиз графика.
С помощью полученной геометрической
модели определить, на каких промежутках
оси Х ординаты графика положительны
(отрицательны) и включить эти промежутки
в ответ.
6. Таблица 1
хх1
х2
х
х
х
х1
х2
х
х
х
х
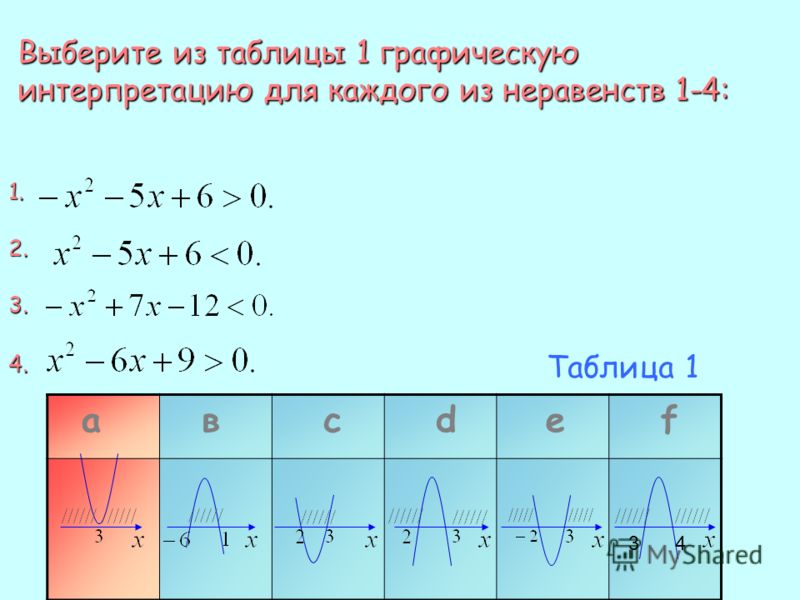
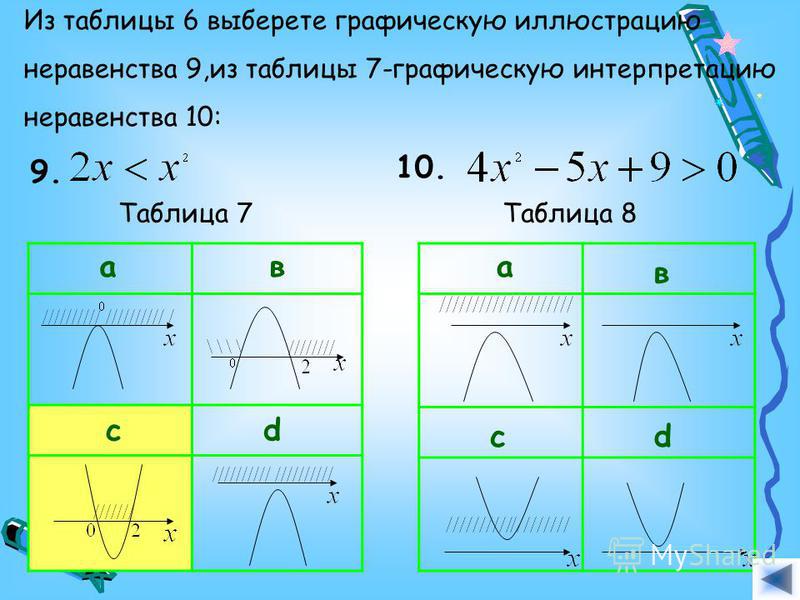
7. Выберите из таблицы 1 графическую интерпретацию для каждого из неравенств 1-4:
1. -х² — 5х + 6> 02. х² — 5х + 6< 0
3. –x² + 7x – 12< 0
4. x² — 6x + 0 > 0
-6
2
1
3
3
2
3
3
2
3
Ответ: 1- B, 2- C, 3 – F, 4 – A.
4
8. Решение квадратных неравенств методом интервалов.
1.2.
3.
4.
Разложить квадратный трехчлен на
множители, воспользовавшись формулой
ах2+вх+с=а(х-х1)(х-х2).
Отметить на числовой прямой корни
квадратного трехчлена.
Определить на каких промежутках трехчлен
имеет положительный или отрицательный
знак.

Учитывая знак неравенства, включить
нужные промежутки в ответ.
9. Решение дробно-рациональных неравенств методом интервалов
f ( x)0
g ( x)
1. Привести данное неравенство к виду
2. Разложить числитель и знаменатель дроби на
множители;
3. Нанести на числовую ось числа, при которых
каждый множитель равен нулю и разделить числовую
ось на промежутки;
4.Изобразить выбитыми те точки, которые не являются
решением неравенства;
5. Выяснить знаки промежутков;
6. Выбрать ответ.
10. Решение неравенств
1. Решить линейное неравенство:3х – 5 ≥ 7х — 15
3х – 7х ≥ -15 + 5
-4х ≥ -10
х ≤ 2,5
Ответ: (-∞; 2,5].
Перенесите слагаемые, не забыв
поменять знаки слагаемых
Приведите подобные слагаемые
в левой и в правой частях неравенства.
Разделите обе части на -4, не забыв
поменять знак неравенства.
11. Решение неравенств
2. Решить квадратное неравенство:а) х2>16
х2-16>0
(х-4)(х+4)>0
+
+
-4
4
х
Ответ:(-∞;-4)U(4;+∞)
б) х2+5>0
Ответ: верно при
любом значении Х.

в) х2+ 5<0
Ответ: не имеет
решений.
12. Решение неравенств
3. Решить квадратное неравенство:1 способ: х2+6х+8<0
У=х2+6х+8-парабола
а=1> 0 → ветви вверх
Точки пересечения с осью ох :
х2+6х+8=0
х1=-4; х2=-2
Как найти х1,2?
1)
x1, 2
b D
2a
2) используя т. Виета
х1+х2=-в
х1х2=с
Ответ: (-4;- 2)
13. Решение неравенств
Решить квадратное неравенство:2 способ (метод интервалов): х2+6х+8<0
Рассмотрим функцию у = х2+6х+8
Нули функции
х2+6х+8=0
х1=-4; х2=-2
(x+4)(x+2)<0
+
+
-4 -2
x
Ответ: -4<x<-2
14. Решите неравенства(самостоятельно)
I вариантII вариант
1) 4x 2 – 12x + 9 < 0
1) –10x 2 + 9x > 0
2) 2x 2 – 7x + 6 > 0
2) –5х 2 + 11x – 6 > 0
Проверь себя
I вариант
II вариант
1) Решений нет
1) ( 0; 0,9)
2) (–∞; 1.5) U ( 2; +∞ )
2) (1; 1,2)
15.11.12
English Русский Правила
3.
 8: Полиномиальные и рациональные неравенства
8: Полиномиальные и рациональные неравенства- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 44357
Развитие навыков
- Решение полиномиальных неравенств.
- Решите рациональные неравенства.
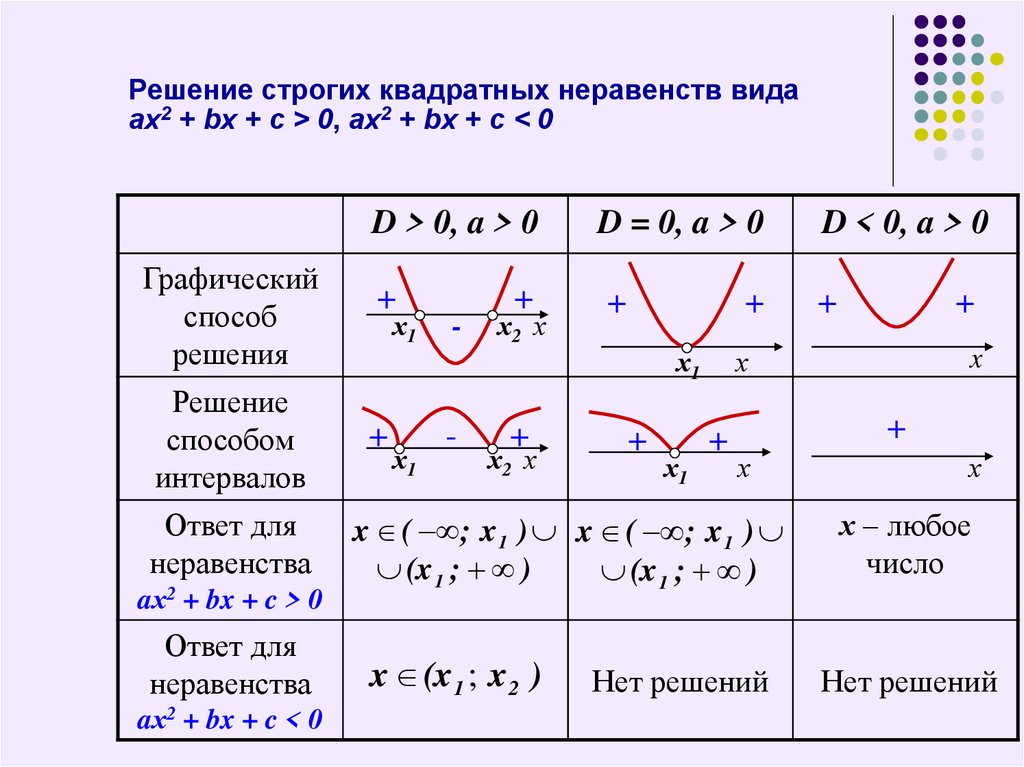
Решение полиномиальных неравенств
Полином Неравенство – это математическое утверждение, которое связывает полиномиальное выражение как меньшее или большее другого. Мы можем использовать таблицы знаков для решения полиномиальных неравенств с одной переменной.
Графики помогают визуализировать решения полиномиальных неравенств. Изучите приведенный ниже график, чтобы увидеть взаимосвязь между графиком полинома и соответствующей ему диаграммой знаков.
На этом графике \(x\)-пересечения, -3, 0 и 4, являются критическими точками , которые являются единственными местами, где график может измениться от того, чтобы быть выше \(x \)-оси (где мы говорим, что \(f(x) > 0) \) ), ниже оси \(x\) (где мы говорим, что \(f(x) < 0) \). В пределах каждого интервала между двумя соседними критическими точками график либо всегда выше оси \(х\), либо всегда ниже оси \(х\). Таким образом, нахождение критических точек полиномиального неравенства играет фундаментальную роль в решении полиномиального неравенства.
Как решить полиномиальное неравенство.
- Шаг 1 : Перепишите неравенство так, чтобы в правой части неравенства был ноль. Выражение в левой части обозначим как \(f(x)\).
- Шаг 2 : Найдите критических числа . Критические числа для полиномиальных функций — это действительные числовые решения \ (f (x) = 0 \).
 Нарисуйте числовую линию, отметив критические числа. Нарисуйте незакрашенный кружок возле каждого критического числа, если в неравенстве используются знаки «<» или «>»; нарисуйте закрашенный кружок у каждого критического числа, если в неравенстве используется « \ ( \ le \)» или «\ ( \ ge \)».
Нарисуйте числовую линию, отметив критические числа. Нарисуйте незакрашенный кружок возле каждого критического числа, если в неравенстве используются знаки «<» или «>»; нарисуйте закрашенный кружок у каждого критического числа, если в неравенстве используется « \ ( \ le \)» или «\ ( \ ge \)». - Шаг 3 : Создайте таблицу знаков . Критические числа разбивают числовую прямую на области. Выберите тестовое значение для каждого региона, в том числе одно слева от всех критических значений и одно справа от всех критических значений. Для каждого тестового значения \(v\) определите, является ли \(f(v)\) положительным или отрицательным, и запишите результат на диаграмме знаков для каждого региона.
- Шаг 4 : Используйте диаграмму знаков, чтобы найти множество всех значений \(x\), для которых выполняется неравенство. Запишите ответ в интервальной записи. 9{2} (x − 4) \) дано в факторизованной форме, корни очевидны. Здесь корни: \(0, −3\) и \(4\).
 Из-за строгого неравенства постройте их, используя открытые точки на числовой прямой. Рисунок 3.7.1 Критические числа
Из-за строгого неравенства постройте их, используя открытые точки на числовой прямой. Рисунок 3.7.1 Критические числаШаг 3 . В этом случае критические числа разбивают числовую прямую на четыре области. Протестируйте значения в каждой области, чтобы определить, является ли \(f\) положительным или отрицательным. Здесь мы выбираем тестовые значения \(−5, −1, 2\) и \(6\). Помните, что нас интересует только знак \((+\) или \(-)\) результата. 9{2}(+)&=+\color{Cerulean} { Positive } \end{aligned}\)
После проверки значений мы можем заполнить диаграмму знаков.
Рисунок 3.7.2 Таблица знаковШаг 4 . Вопрос просит нас найти значения, где \(f (x) < 0\), или где функция отрицательна. Из таблицы знаков видно, что функция отрицательна для \(x\)-значений между \(0\) и \(4\).
Рисунок 3.7.3 Набор решений на числовой прямойМы можем выразить этот набор решений двумя способами:
\(\begin{aligned}\{x | 0<&x<4\} &\color{Cerulean} { Set\ : обозначение } \\ (0,&4) &\color{Cerulean} { Интервал\: обозначение }\end{выравнивание}\)
В этом разделе мы продолжим представлять наборы решений с использованием интервальной записи.
 Ответ : \((0,4)\)
Ответ : \((0,4)\)Графики могут помочь нам визуализировать решения полиномиальных неравенств. Ниже приведен график функции в приведенном выше примере. Сравните график с соответствующей таблицей знаков. Обратите внимание, что диаграмма со знаками положительна, когда график находится выше оси \(x\), и отрицательна, когда график находится ниже оси \(x\). График пересекает или касается оси \(х\) в критических точках. 9{2}(+)(+)=+\end{aligned}\)
С помощью этой информации мы можем завершить таблицу знаков.
Рисунок 3.7.6 Таблица знаковШаг 4 : Используйте таблицу знаков, чтобы ответить на вопрос. Здесь решение состоит из всех значений, для которых \(f (x) > 0\). Заштрихуйте значения, дающие положительные результаты, а затем выразите этот набор в виде интервалов.
Рисунок 3.7.7 Набор решений на числовой прямойОтвет : \(\left(-\infty,-\frac{3}{2}\right) \cup(3, \infty)\) 9{2}-4\right) &=0 \\(x+1)(x+2)(x-2) &=0 \end{aligned}\)
Критические числа равны \(−2, − 1\) и \(2\).
Рисунок 3.7.8 Критические числа Из-за инклюзивного неравенства \((≤)\) мы нанесем их на график с помощью закрытых точек.
Из-за инклюзивного неравенства \((≤)\) мы нанесем их на график с помощью закрытых точек.Шаг 3 . Используйте тестовые значения \(-3\), \(-\frac{3}{2}\), \(0\) и \(3\) для создания диаграммы знаков.
\(\begin{aligned} f(\color{OliveGreen}{-3}\color{black}{)}&=(\color{OliveGreen}{-3}\color{black}{+}1) (\color{OliveGreen}{-3}\color{black}{+}2)(\color{OliveGreen}{-3}\color{black}{-}2) &=(-)(-)(- )=- \\ f(\color{OliveGreen}{-\frac{3}{2}}\color{black}{)}&=(\color{OliveGreen}{-\frac{3}{2}} \color{black}{+}1)(\color{OliveGreen}{-\frac{3}{2}}\color{black}{+}2)(\color{OliveGreen}{-\frac{3} {2}}\color{black}{-}2) &=(-)(+)(-)=+\\ f(\color{OliveGreen}{0}\color{black}{)}&=( \color{OliveGreen}{0}\color{black}{+}1)(\color{OliveGreen}{0}\color{black}{+}2)(\color{OliveGreen}{0}\color{black }{-}2)&=(+)(+)(-)=- \\ f(\color{OliveGreen}{3}\color{black}{)}&=(\color{OliveGreen}{3} \color{black}{+}1)(\color{OliveGreen}{3}\color{black}{+}2)(\color{OliveGreen}{3}\color{black}{-}2)&= (+)(+)(+)=+\конец{выровнено}\) 9{2}>0\).

- Ответить
\((1,3)\)
Решение рациональных неравенств. Поскольку рациональные функции имеют ограничения на область определения, мы должны соблюдать осторожность при решении рациональных неравенств. Кроме нулей, в множество критических чисел включим ограничения на область определения функции.
Графики помогают визуализировать решения рациональных неравенств. Изучите приведенный ниже график, чтобы увидеть взаимосвязь между графиком рациональной функции и соответствующей ему диаграммой знаков . Она очень похожа на диаграмму знаков для многочленов, за исключением того, что в список критических точек включены вертикальные асимптоты.
Обе точки пересечения по оси x, -2 и 4, и вертикальная асимптота \(x=1\) составляют критических точки . Вертикальная асимптота возникает при \(x=1\), потому что это значение, которое делает знаменатель равным нулю и, таким образом, делает рациональное выражение неопределенным.
 Опять же, эти критические точки являются единственными местами, где график может измениться от положения выше оси \(x\) (где \(f(x) > 0)\) ) до уровня ниже \(x\)- ось (где \(f(x) < 0) \). В пределах каждого интервала между двумя соседними критическими точками график либо всегда выше оси \(х\), либо всегда ниже оси \(х\). Таким образом, нахождение критических точек рационального неравенства играет фундаментальную роль в его решении.
Опять же, эти критические точки являются единственными местами, где график может измениться от положения выше оси \(x\) (где \(f(x) > 0)\) ) до уровня ниже \(x\)- ось (где \(f(x) < 0) \). В пределах каждого интервала между двумя соседними критическими точками график либо всегда выше оси \(х\), либо всегда ниже оси \(х\). Таким образом, нахождение критических точек рационального неравенства играет фундаментальную роль в его решении.Как решить рациональное неравенство.
- Шаг 1 : Перепишите неравенство так, чтобы в правой части неравенства был ноль. Запишите выражение слева в виде одной алгебраической дроби. Обозначьте эту дробь как \(f(x)\).
- Шаг 2 : Найдите критические числа. Для рациональных неравенств эти критические числа поступают из двух источников.
- Решите \(f((x)=0\). Найдите значения, при которых числитель \(f(x)\) равен нулю. Эти критические точки являются пересечениями \(x\). Если в неравенстве используется » <" или ">«, нарисуйте незакрашенный кружок у каждого из этих критических чисел; если в неравенстве используется » \( \le \)» или «\( \ge \)», нарисуйте закрашенный кружок у каждого из этих критических чисел.
 цифры
цифры - Решите \(f((x)=undefined\). Найдите значения, при которых знаменатель \(f(x)\) равен нулю. Эти критические точки находятся там, где находятся вертикальные асимптоты. Эти значения не являются частью области определения \(f(x)\). Следовательно, эти критические значения никогда не входят в набор решений. Всегда рисуйте незакрашенный кружок возле каждого из этих критических чисел.
- Решите \(f((x)=0\). Найдите значения, при которых числитель \(f(x)\) равен нулю. Эти критические точки являются пересечениями \(x\). Если в неравенстве используется » <" или ">«, нарисуйте незакрашенный кружок у каждого из этих критических чисел; если в неравенстве используется » \( \le \)» или «\( \ge \)», нарисуйте закрашенный кружок у каждого из этих критических чисел.
- Шаг 3 : Создайте диаграмму знаков. Критические числа разбивают числовую прямую на области. Выберите тестовое значение для каждого региона, в том числе одно слева от всех критических значений и одно справа от всех критических значений. Для каждого тестового значения \(v\) определите, является ли \(f(v)\) положительным или отрицательным, и запишите результат на диаграмме знаков для каждого региона.
- Шаг 4 : Используйте диаграмму знаков, чтобы найти множество всех значений \(x\), для которых выполняется неравенство.
 Запишите ответ в интервальной записи.
Запишите ответ в интервальной записи.
Пример \(\PageIndex{4}\)
Решить: \(\dfrac{(x-4)(x+2)}{(x-1)} \geq 0\)
Решение
Шаг 2 . Нули рациональной функции возникают, когда числитель равен нулю, а значения, дающие ноль в знаменателе, являются ограничениями. В данном случае
\(\ begin{array}{c | c}{\text {Корни (числитель)}} & {\text{Ограничение(знаменатель)}} \\ {x-4=0 \text {или} x+2 =0} & {x-1=0} \\ { x=4 \quad\quad\quad x=-2}& {x=1}\end{массив}\)
Следовательно, критические числа равны \( −2, 1\) и \(4\). Из-за инклюзивного неравенства \((≥)\) используйте закрытую точку для корней \({−2, 4}\) и всегда используйте открытую точку для ограничений \({1}\). Ограничения никогда не включаются в набор решений.
Рисунок 3.7.11 Критические числаШаг 3 . Используйте тестовые значения \(x = −4, 0, 2, 6\).
\(\begin{aligned} f(\color{OliveGreen}{-4}\color{black}{)} &=\frac{(\color{OliveGreen}{-4}\color{black}{- }4)(\color{OliveGreen}{-4}\color{black}{+}2)}{(\color{OliveGreen}{-4}\color{black}{-}1)}&=\frac {(-)(-)}{(-)}=-\\ f(\color{OliveGreen}{0}\color{black}{)} &=\frac{(\color{OliveGreen}{0}\ color{black}{-}4)(\color{OliveGreen}{0}\color{black}{+}2)}{(\color{OliveGreen}{0}\color{black}{-}1)} &=\frac{(-)(+)}{(-)}=+\\ f(\color{OliveGreen}{2}\color{black}{)} &=\frac{(\color{OliveGreen} {2}\color{black}{-}4)(\color{OliveGreen}{2}\color{black}{+}2)}{(\color{OliveGreen}{2}\color{black}{- }1)}&=\frac{(-)(+)}{(+)}=-\\ f(\color{OliveGreen}{6}\color{black}{)} &=\frac{(\ color{OliveGreen}{6}\color{black}{-}4)(\color{OliveGreen}{6}\color{black}{+}2)}{(\color{OliveGreen}{6}\color{ черный}{-}1)}&=\frac{(+)(+)}{(+)}=+\end{выровнено}\)
Затем заполните таблицу знаков.
Рисунок 3.7.12 Таблица знаков
Шаг 4 . Вопрос просит нас найти значения, для которых \(f (x) ≥ 0\), другими словами, положительно или равно нулю. Заштрихуйте соответствующие области и представьте набор решений в интервальной записи.
Рисунок 3.7.13 Набор решений на числовой прямойОтвет: \([-2,1) \cup[4, \infty)\)
Еще раз график этой функции ниже дает визуализацию того, какой знак значит график. Как и в случае с полиномиальным неравенством, знак диаграммы положителен, когда график находится выше оси \(х\), и отрицателен, когда график находится ниже оси \(х\). График (потенциально) изменяется от положения выше оси \(x\) до уровня ниже оси \(x\) при критических значениях. В отличие от многочлена, где критические значения находятся только там, где график пересекает или касается оси \(x\), для рациональных функций критические значения также существуют на вертикальных асимптотах графика.
Рисунок 3.7.14 Рациональная функция с диаграммой знаков и набором решений
Обратите внимание, что ограничение \(x = 1\) соответствует вертикальной асимптоте, ограничивающей области, в которых функция изменяется с положительной на отрицательную.
 Хотя это ограничение не включено в набор решений, оно является критическим числом. Перед созданием диаграммы знаков мы должны убедиться, что неравенство имеет ноль с одной стороны. Общие шаги решения рационального неравенства показаны в следующем примере.
Хотя это ограничение не включено в набор решений, оно является критическим числом. Перед созданием диаграммы знаков мы должны убедиться, что неравенство имеет ноль с одной стороны. Общие шаги решения рационального неравенства показаны в следующем примере.Пример \(\PageIndex{5}\)
Решить \(\dfrac{7}{x+3}<2\).
Решение
Шаг 1 : Начните с получения нуля в правой части.
\(\begin{aligned}\frac{7}{x+3}&<2 \\ \frac{7}{x+3}-2&<0\end{align}\)
Шаг 2 : Определите критические числа. Критические числа — это нули и ограничения. Начните с упрощения до одной алгебраической дроби.
\(\begin{align}\frac{7}{x+3}-\frac{2}{1}&<0 \\ \frac{7-2(x+3)}{x+3} &<0 \\ \frac{7-2 x-6}{x+3}&<0 \\ \frac{-2 x+1}{x+3}&<0\end{выровнено}\)
Затем найдите критические числа. Приравняйте числитель и знаменатель к нулю и решите.
\(\begin{array}{c|c} {\text{Корень}}&{\text{Ограничение}}\\ {-2x+1=0}\\{-2x=-1}&{ x+3=0}\\{x=\frac{1}{2}}&\quad\quad\:\:{x=-3} \end{array}\)
В этом случае строгое неравенство указывает, что мы должны использовать открытую точку для корня.
 Любое ограничение всегда использует открытую точку.
Любое ограничение всегда использует открытую точку.
Рисунок 3.7.15 Критические числаШаг 3 : Создайте диаграмму знаков. Выберите тестовые значения \(−4, 0\) и \(1\).
\(\begin{aligned} f(\color{OliveGreen}{-4}\color{black}{)} &=\frac{-2(\color{OliveGreen}{-4}\color{black} {)}+1}{\color{OliveGreen}{-4}\color{black}{+}3}&=\frac{+}{-}=-\\ f(\color{OliveGreen}{0} \color{black}{)} &=\frac{-2(\color{OliveGreen}{0}\color{black}{)}+1}{\color{OliveGreen}{0}\color{black}{ +}3}&=\frac{+}{+}=+\\ f(\color{OliveGreen}{1}\color{black}{)} &=\frac{-2(\color{OliveGreen}{ 1}\color{black}{)}+1}{\color{OliveGreen}{1}\color{black}{+}3}&=\frac{-}{+}=-\end{aligned}\ )
И у нас есть
Рисунок 3.7.16 Таблица знаковШаг 4 : Используйте таблицу знаков, чтобы ответить на вопрос. В этом примере мы ищем значения, для которых функция отрицательна, \(f (x) < 0\). Заштрихуйте соответствующие значения, а затем представьте свой ответ, используя обозначение интервала.
 {2}-4} \leq \dfrac{1}{2-x}\). 9{2}-4}-\dfrac{1}{2-x} \leq 0} \\ {\dfrac{1}{(x+2)(x-2)}-\dfrac{1}{-( x-2)} \leq 0} \\ {\ frac {1} {(x + 2) (x-2)} + \ frac {1 \ color {Cerulean} {(x + 2)}} {\ color {черный}{(x-2)}\color{Cerulean}{(x+2)}}\color{black}{\leq} 0} \\ {\dfrac{1+x+2}{(x+ 2)(x-2)} \leq 0} \\ \boxed{{f(x) = \dfrac{x+3}{(x+2)(x-2)}} \leq 0}\end{ array}\)
{2}-4} \leq \dfrac{1}{2-x}\). 9{2}-4}-\dfrac{1}{2-x} \leq 0} \\ {\dfrac{1}{(x+2)(x-2)}-\dfrac{1}{-( x-2)} \leq 0} \\ {\ frac {1} {(x + 2) (x-2)} + \ frac {1 \ color {Cerulean} {(x + 2)}} {\ color {черный}{(x-2)}\color{Cerulean}{(x+2)}}\color{black}{\leq} 0} \\ {\dfrac{1+x+2}{(x+ 2)(x-2)} \leq 0} \\ \boxed{{f(x) = \dfrac{x+3}{(x+2)(x-2)}} \leq 0}\end{ array}\)Критические числа равны \(−3, −2\) и \(2\). Обратите внимание, что \(±2\) являются ограничениями, и поэтому мы будем использовать открытые точки при их построении на числовой прямой. Из-за инклюзивного неравенства мы будем использовать закрытую точку в корне \(−3\).
Рисунок 3.7.18 Критические числаШаг 3 . Выберите тестовые значения \(-4, -2\frac{1}{2} = -\frac{5}{2}, 0\) и \(3\).
\(\begin{align}f(\color{OliveGreen}{-4}\color{black}{)}&= \frac{\color{OliveGreen}{-4}\color{black}{+} 3}{(\color{OliveGreen}{-4}\color{black}{+}2)(\color{OliveGreen}{-4}\color{black}{-}2)}&=\frac{( -)}{(-)(-)}=- \\ f(\color{OliveGreen}{-\frac{5}{2}}\color{black}{)} &= \frac{\color{OliveGreen }{-\frac{5}{2}}\color{black}{+}3}{(\color{OliveGreen}{-\frac{5}{2}}\color{black}{+}2) (\color{OliveGreen}{-\frac{5}{2}}\color{black}{-}2)}&=\frac{(+)}{(-)(-)}=+\\ f (\ color{OliveGreen}{0}\color{black}{)}&=\frac{\color{OliveGreen}{0}\color{black}{+}3}{(\color{OliveGreen}{0} \color{black}{+}2)(\color{OliveGreen}{0}\color{black}{-}2)}&=\frac{(+)}{(+)(-)}=- \ \ f(\color{OliveGreen}{3}\color{black}{)}&=\frac{\color{OliveGreen}{3}\color{black}{+}3}{(\color{OliveGreen}{ 3}\color{black}{+}2)(\color{OliveGreen}{3}\color{black}{-}2)} &=\frac{(+)}{(+)(+)}= +\конец{выровнено}\) 9{2}+7 x-4} \geq \dfrac{x}{x+4}\).

- Ответить
\((-4,0] \cup\left(\frac{1}{2}, \infty\right)\)
Ключевые выводы
- Когда полиномиальное неравенство имеет стандартную форму с нулем на одной стороне, корни полинома являются критическими числами. Создайте диаграмму знаков, которая моделирует функцию, а затем используйте ее, чтобы ответить на вопрос.
- Когда рациональное неравенство записывается в виде одной алгебраической дроби с нулем на одной стороне, критическими числами являются как корни, так и ограничения. Значения, дающие нуль в числителе, являются корнями, а значения, дающими нуль в знаменателе, являются ограничениями. Всегда используйте открытые точки для ограничений, независимо от заданного неравенства, потому что ограничения не являются частью предметной области. Создайте диаграмму знаков, которая моделирует функцию, а затем используйте ее, чтобы ответить на вопрос.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Теги

Глобальное экономическое неравенство – наш мир в данных
Примечание: это только предварительная подборка соответствующих материалов
Данные и исследования, представленные здесь, являются предварительными подборками или относящимися к делу материалами. Мы продолжим нашу работу по этой теме в будущем (чтобы осветить ее так же подробно, как, например, в нашей статье о приросте населения мира).
Если у вас есть опыт в этой области и вы хотели бы внести свой вклад, подайте заявку здесь, чтобы присоединиться к нам в качестве исследователя.
В этой статье представлены данные о глобальном экономическом неравенстве. Он рассматривает экономическую историю и то, как глобальное неравенство изменилось и, по прогнозам, продолжит меняться в будущем.
В соответствующей статье «Наш мир в данных» представлены эмпирические данные о том, как неравенство доходов менялось с течением времени и как уровни неравенства в разных странах могут значительно различаться.
 В нем также представлены некоторые исследования факторов, определяющих неравенство доходов.
В нем также представлены некоторые исследования факторов, определяющих неравенство доходов.Глобальное неравенство возможностей
Сегодня условия жизни в разных местах нашего мира сильно различаются. Во многом это следствие изменений последних двух столетий: где-то условия жизни менялись резко, где-то медленнее.
Наши индивидуальные истории разыгрываются среди этих крупных глобальных изменений и неравенства, и именно эти обстоятельства во многом определяют, насколько здоровым, богатым и образованным будет каждый из нас в своей жизни. 1 Да, наша собственная тяжелая работа и жизненный выбор имеют значение. Но, как мы увидим из данных, они имеют гораздо меньшее значение, чем одна большая вещь, над которой мы не властны: где и когда мы родились. Этот единственный, совершенно случайный фактор во многом определяет условия, в которых мы живем.
Сегодняшнее глобальное неравенство является следствием двух столетий неравного прогресса. В некоторых местах произошли кардинальные улучшения, а в других нет.
 Сегодня мы должны уравнять шансы и дать всем — независимо от того, где они родились — шанс на хорошую жизнь. Это не только правильно, но, как мы увидим ниже, и реалистично. Наша надежда на то, чтобы дать следующим поколениям шанс жить хорошей жизнью, заключается в широком развитии, которое делает возможным для всех то, что сегодня доступно лишь немногим.
Сегодня мы должны уравнять шансы и дать всем — независимо от того, где они родились — шанс на хорошую жизнь. Это не только правильно, но, как мы увидим ниже, и реалистично. Наша надежда на то, чтобы дать следующим поколениям шанс жить хорошей жизнью, заключается в широком развитии, которое делает возможным для всех то, что сегодня доступно лишь немногим.Многим кажется несправедливым по своей сути то, что некоторые люди могут наслаждаться здоровой, богатой и счастливой жизнью, в то время как другие продолжают жить в нездоровье, бедности и печали. Для них имеет значение неравенство в результатах жизни людей. Для других несправедливо неравенство возможностей — возможность добиться хороших результатов. Но смысл этого текста в том, чтобы сказать, что эти два аспекта неравенства неразделимы. Тони Аткинсон сказал это очень четко: «Неравенство результатов среди сегодняшнего поколения является источником несправедливого преимущества, получаемого следующим поколением. Если нас беспокоит равенство возможностей завтра, нам нужно беспокоиться о неравенстве результатов сегодня».
 2
2 Степень глобального неравенства – это не то, кем вы являетесь, а то, где вы находитесь
Сегодняшнее глобальное неравенство возможностей означает, что для ваших условий жизни важнее всего удача или неудача вашего места жительства рождения.
Неравенство между странами, на котором я акцентирую внимание в этом тексте, — не единственный аспект, который необходимо учитывать. Неравенство внутри стран и обществ — региональные различия, расовые различия, гендерные различия и неравенство по другим измерениям — также могут быть значительными, и все они находятся вне контроля любого человека и в равной степени несправедливы.
Эта визуализация показывает неравенство в условиях жизни между самыми бедными и самыми благополучными странами мира сегодня по ряду аспектов:
- Здоровье: У ребенка, родившегося в одной из стран с самым плохим здоровьем, вероятность умереть в 60 раз выше, чем у ребенка, родившегося в стране с самым лучшим здоровьем.
 В некоторых африканских странах более одного из десяти родившихся сегодня детей не доживут до пяти лет. В самых здоровых странах мира — в Европе и Восточной Азии — только 1 из 250 детей умирает, не дожив до 5 лет.
В некоторых африканских странах более одного из десяти родившихся сегодня детей не доживут до пяти лет. В самых здоровых странах мира — в Европе и Восточной Азии — только 1 из 250 детей умирает, не дожив до 5 лет.- Вот карта мира, показывающая уровень детской смертности по всему миру.
- Образование: В странах, где люди имеют лучший доступ к образованию – в Европе и Северной Америке – дети школьного возраста сегодня могут рассчитывать на 15-20 лет формального образования. В Австралии, которая является исключением, ожидаемая продолжительность школьной жизни составляет 22,9 года. Дети, поступающие в школу одновременно в странах с самым плохим доступом к образованию, могут ожидать только 5 лет. Кроме того, как мы объясняли ранее, дети, как правило, гораздо меньше учатся в школах в более бедных странах.
- Вот мировая карта ожидаемых лет обучения.
- Доход: Если вы посмотрите на средние доходы и сравните самую богатую страну — Катар с ВВП на душу населения почти 117 000 долларов США — с самой бедной страной в мире — Центральноафриканской Республикой с 661 долларом США — то вы обнаружите 177- кратная разница.
 Это учитывает разницу в ценах между странами и, следовательно, выражается в международных долларах (вот пояснение). Катар и другие страны, очень богатые природными ресурсами, можно считать здесь исключениями, предполагая, что более уместно сравнивать очень богатые страны, не полагаясь в основном на экспорт природных ресурсов. В США ВВП на душу населения составляет 54 225 долларов США, а в Швейцарии — 57 410 долларов США. Это означает, что швейцарцы могут потратить за 1 месяц столько, сколько люди в Центральноафриканской Республике могут потратить за 7 лет.
Это учитывает разницу в ценах между странами и, следовательно, выражается в международных долларах (вот пояснение). Катар и другие страны, очень богатые природными ресурсами, можно считать здесь исключениями, предполагая, что более уместно сравнивать очень богатые страны, не полагаясь в основном на экспорт природных ресурсов. В США ВВП на душу населения составляет 54 225 долларов США, а в Швейцарии — 57 410 долларов США. Это означает, что швейцарцы могут потратить за 1 месяц столько, сколько люди в Центральноафриканской Республике могут потратить за 7 лет.- Вот мировая карта различий ВВП на душу населения.
Неравенство между разными местами в мире намного больше, чем разница, которую вы можете сделать самостоятельно. Когда вы родились в бедной стране, где умирает каждый десятый ребенок, вы не сможете снизить вероятность смерти вашего ребенка до среднего уровня стран с лучшим здоровьем детей. Там, где средний ребенок может рассчитывать только на 5-летнее образование, ребенку будет намного труднее получить уровень образования даже 9-летнего.
 0463 в среднем ребенка попадают в самые обеспеченные места.
0463 в среднем ребенка попадают в самые обеспеченные места.Разница в доходах еще более заметна. В стране, где ВВП на душу населения составляет менее 1000 долларов, а большинство живет в условиях крайней нищеты, средние доходы богатой страны недостижимы. Место, где вы живете, не просто важнее всех остальных ваших характеристик, оно важнее всего остального вместе взятого .
Вы не можете стать здоровыми и богатыми в одиночку – прогресса добиваются общества, а не отдельные люди
То, что сегодня верно для неравенства в странах по всему миру, верно и для изменений с течением времени. Что дает людям шанс на хорошую жизнь, так это когда все общество и экономика вокруг них меняются к лучшему. Вот что такое развитие и экономический рост: преобразование места таким образом, чтобы то, что раньше было доступно лишь немногим самым удачливым, стало доступным для большинства.
Когда все больны,
все больныСиняя линия на этой визуализации показывает преобразование Финляндии, страны, население которой сегодня является одним из самых здоровых и богатых в мировой истории.

Точка данных в верхнем левом углу описывает жизнь в Финляндии в 1800 году (время, когда страна еще не была автономной или независимой). Из всех детей, родившихся в этом году, 42% умерли в первые пять лет своей жизни. А средний доход в Финляндии был крайне низким: ВВП на душу населения составлял всего 827 долларов в год (с поправкой на рост цен, чтобы покупательная способность оставалась сопоставимой с сегодняшней). Точно так же для большинства было недоступно даже базовое образование.
Общество, в котором умерла почти половина всех детей, не было чем-то необычным: до недавнего времени оно было таким же высоким в истории человечества. Фиолетовая пунктирная линия на диаграмме показывает, что в 1800 году во всем мире такая же высокая доля детей умерла, не дожив до своего пятого дня рождения. В то время не было глобального неравенства; жизнь везде была коротка, и где бы ребенок ни родился, шансы, что он скоро умрет, были высоки.
И точно так же, как не было неравенства в показателях смертности и здоровья между разными точками мира, неравенство внутри стран также было небольшим.
 Здоровье всего общества было плохим. У нас есть данные о смертности английской аристократии с 1550 года. Аристократы умирали так же рано, как и все остальные. 3 Средняя продолжительность их жизни тоже была ниже 40 лет. До более широкого социального развития даже самый привилегированный статус в обществе не давал бы вам шанса на здоровую жизнь. Вы просто не можете быть здоровым в нездоровом месте.
Здоровье всего общества было плохим. У нас есть данные о смертности английской аристократии с 1550 года. Аристократы умирали так же рано, как и все остальные. 3 Средняя продолжительность их жизни тоже была ниже 40 лет. До более широкого социального развития даже самый привилегированный статус в обществе не давал бы вам шанса на здоровую жизнь. Вы просто не можете быть здоровым в нездоровом месте.Развитие и глобальное неравенство
После двух столетий медленных, но неуклонных преобразований Финляндия сегодня является одним из самых здоровых и богатых мест в мире. Это не было гладким прогрессом — во время голода в Финляндии в 1860-х годах уровень смертности увеличился более чем наполовину, — но постепенно здоровье детей улучшилось, и сегодня уровень детской смертности составляет 0,23%. За два столетия шансы финского ребенка дожить до первых пяти лет жизни увеличились с 58% до 9%.9,77%.
То же самое относится и к доходам. Еще в 1800 году глобальное неравенство между странами было намного ниже, чем сегодня.
 Даже в тех странах, которые сегодня являются самыми богатыми в мире, большинство людей до недавнего времени жили в условиях крайней нищеты. Финляндия не стала исключением.
Даже в тех странах, которые сегодня являются самыми богатыми в мире, большинство людей до недавнего времени жили в условиях крайней нищеты. Финляндия не стала исключением.Красные кружки на том же графике показывают детскую смертность и доходы в мире сегодня. Это те же данные, которые мы обсуждали выше при обсуждении степени глобального неравенства сегодня, но теперь вы видите данные по всем странам мира, а не только по самым бедным и самым обеспеченным.
Примерно до 1800 года сегодняшние самые благополучные места были такими же бедными, как и самые неблагополучные, а детская смертность была еще выше. Все они находились в верхнем левом углу диаграммы. Глобальное неравенство, которое мы наблюдаем сегодня, было вызвано большими различиями в улучшении здоровья и экономического роста между странами за последние два столетия. Ангус Дитон назвал это «Большим побегом». Он написал об этом книгу с таким названием, в которой рассказывает, как некоторые части мира избежали ужаснейшей бедности и болезней, а другие отстали.

Не глядя на данные, невозможно понять, насколько резко могут измениться процветание и здоровье общества. Здоровье и процветание в прошлом были настолько плохими, что никто в Финляндии не мог представить себе жизнь, которая сегодня является реальностью для среднего жителя Финляндии.
Развитие вызвало неравенство между местами и между поколениями
Даже страны, где здоровье и доступ к образованию сегодня хуже, добились прогресса в этих измерениях. В первой диаграмме этого текста я добавил оценки глобального среднего значения для каждого измерения два столетия назад под каждой шкалой. С точки зрения здоровья, даже сегодня самые неблагополучные места обстоят лучше, чем самые благополучные места в прошлом. Вот данные по ожидаемой продолжительности жизни, а вот по детской смертности.
И точно так же, как распределение доходов в сегодняшних бедных и богатых странах почти не пересекается, почти нет совпадений и между распределением доходов в богатой стране сегодня и в той же стране в прошлом.

Тот факт, что эти преобразования так резко улучшили условия жизни целых обществ, означает, что не только , где вы родились, имеет значение для условий вашей жизни, но и время, когда ты родился. Дети с хорошими шансами на выживание рождаются не только в нужном месте, но и в нужное время. В мире улучшения здоровья и экономического роста у всех нас, родившихся в недавнем прошлом, было гораздо больше шансов на хорошее здоровье и процветание, чем у всех, кто жил до нас.
Заключение
Как сказал Аткинсон, «если нас беспокоит равенство возможностей завтра, нам нужно беспокоиться о неравенстве результатов сегодня».
Глобальное неравенство возможностей в современном мире является следствием глобального неравенства в отношении здоровья, благосостояния, образования и многих других аспектов, имеющих значение для нашей жизни.
Условия вашей жизни гораздо больше определяются тем, что находится вне вашего контроля — местом и временем, в котором вы родились, — чем вашими собственными усилиями, самоотверженностью и выбором, который вы сделали в жизни.

Тот факт, что случайность места рождения ребенка определяет его или ее шансы на выживание, получение образования или жизнь без бедности, не может быть принята. Мы должны положить конец этой несправедливости, чтобы дети с лучшими условиями жизни рождались в странах Африки к югу от Сахары с такой же вероятностью, как и в Европе или Северной Америке.
Мы знаем, что это возможно. Это то, что проясняет историческая перспектива. Сегодня Финляндия находится в правом нижнем углу диаграммы выше: одно из самых здоровых и богатых мест на планете. Два столетия назад Финляндия была в самом верхнем левом углу: такое же бедное место, как сегодняшние беднейшие страны, и с уровнем детской смертности намного ниже, чем в любом другом месте в мире сегодня.
Неравенство, которое мы наблюдаем сегодня в мире, является следствием неравного прогресса. У нашего поколения есть возможность — и я считаю, что это ответственность — позволить каждой части мира развиваться и превращаться в место, где здоровье, доступ к образованию и процветание являются реальностью.

Нет никаких оснований полагать, что то, что было возможно для Финляндии – и всех других стран в правом нижнем углу, которые сегодня намного здоровее и богаче, чем два века назад, – не должно быть возможным для остального мира. Действительно, как показывает массовое снижение детской смертности в мире в период с 1800 по 2017 год — с 43% в среднем по миру до 3,9%, как показано горизонтальными пунктирными линиями, — большая часть мира движется по этому пути.
Как прогресс прошлого, так и огромное неравенство в мире сегодня показывают, что возможно в будущем. Цитата Уильяма Гибсона «будущее уже здесь, оно просто неравномерно распределено» была верна для всего курса улучшения условий жизни и была хорошим руководством для того, что возможно для будущего повсюду.
Мы в «Нашем мире данных» уделяем особое внимание «данным и исследованиям для достижения прогресса в решении крупнейших глобальных проблем» (это наша миссия), и глобальное неравенство — одна из них. Как только мы узнаем, что возможно, мы, конечно же, не сможем принять сегодняшнюю жестокую реальность, согласно которой именно место, где рождается ребенок, определяет его шансы на богатую и здоровую жизнь.

История глобального экономического неравенства
В этом разделе
- Глобальная дивергенция, за которой следует конвергенция
- Глобальное неравенство в доходах увеличивалось в течение 2 столетий и сейчас снижается
- Последние данные о глобальном неравенстве и взгляд в будущее
- Неравенство внутри стран и неравенство между странами
Глобальное расхождение с последующим сближением
На диаграмме показаны оценки распределения годового дохода среди всех граждан мира за последние два столетия.
Чтобы сделать доходы сопоставимыми в разных странах и во времени, ежедневные доходы измеряются в международных долларах — гипотетической валюте, на которую можно было бы купить сопоставимое количество товаров и услуг, которое можно было бы купить на доллар США в Соединенных Штатах в 2011 году (для получения более подробной информации). объяснение см. здесь).
Распределение доходов показано в 3 момента времени:
- В 1800 году лишь немногие страны достигли экономического роста.
 Диаграмма показывает, что большая часть мира жила в бедности с доходом, подобным беднейшим странам сегодня. Наша статья о глобальной крайней бедности показывает, что в начале XIX века подавляющее большинство — более 80% — людей в мире жили в материальных условиях, которые сегодня мы назвали бы крайней нищетой.
Диаграмма показывает, что большая часть мира жила в бедности с доходом, подобным беднейшим странам сегодня. Наша статья о глобальной крайней бедности показывает, что в начале XIX века подавляющее большинство — более 80% — людей в мире жили в материальных условиях, которые сегодня мы назвали бы крайней нищетой. - В 1975 году, 175 лет спустя, мир изменился — он стал очень неравным. Распределение доходов в мире было «бимодальным» в форме двугорбого верблюда: один горб ниже международной черты бедности, а второй горб при значительно более высоких доходах. Мир разделился на бедный, развивающийся мир и развитый мир, который был более чем в 10 раз богаче.
- За следующие 4 десятилетия мировое распределение доходов снова резко изменилось. Произошло сближение доходов: во многих более бедных странах, особенно в Юго-Восточной Азии, доходы росли быстрее, чем в богатых странах. Хотя огромная разница в доходах сохраняется, мир больше не делится четко на две группы «развитых» и «развивающихся» стран.
 Мы перешли от двугорбого мира к одногорбому. И в то же время распределение также сместилось вправо — доходы многих беднейших граждан мира выросли, а крайняя бедность сократилась быстрее, чем когда-либо прежде в истории человечества.
Мы перешли от двугорбого мира к одногорбому. И в то же время распределение также сместилось вправо — доходы многих беднейших граждан мира выросли, а крайняя бедность сократилась быстрее, чем когда-либо прежде в истории человечества.
Здесь мы визуализировали аналогичный набор данных из ОЭСР. 4
Глобальное неравенство в 1800, 1975 и 2015 гг. экономисты Бранко Миланович и Кристоф Лакнер.
6Чтобы увидеть изменение во времени, выберите годы над распределением.
Предыдущая визуализация, показывающая изменение с 1820 по 2000 год, основана на оценках средних доходов в стране с поправкой на инфляцию (ВВП на душу населения) и показателе неравенства доходов только внутри страны. Он дает нам приблизительное представление о том, как изменилось распределение доходов, но не очень подробно и не очень точно. В отличие от этого работа Бранко Милановича и Кристофа Лакнера основана на гораздо более подробных данных обследования домохозяйств.
 Эти данные измеряют доход домохозяйства в каждом дециле распределения доходов, и два автора использовали эту информацию для получения глобального распределения доходов. Недостатком этого подхода является то, что мы можем вернуться только к тому времени, когда проводились обследования домохозяйств.
Эти данные измеряют доход домохозяйства в каждом дециле распределения доходов, и два автора использовали эту информацию для получения глобального распределения доходов. Недостатком этого подхода является то, что мы можем вернуться только к тому времени, когда проводились обследования домохозяйств.Визуализация показывает конец долгой эпохи в истории человечества, когда глобальное неравенство росло. Начиная с индустриализации в Северо-Западной Европе доходы в этой части мира начали расти, в то время как материальное благополучие в остальном мире оставалось низким. В то время как некоторые страны следовали европейской индустриализации — сначала Северная Америка, Океания и некоторые части Южной Америки, а затем Япония и Восточная Азия — другие страны Азии и Африки оставались бедными. Как следствие этого, глобальное неравенство увеличивалось в течение длительного периода времени. Это изменилось только в период, показанный на этой визуализации: в связи с быстрым ростом, особенно в большей части Азии, глобальное распределение доходов стало менее неравномерным.
 Доходы более бедной половины населения мира росли быстрее, чем доходы более богатой половины населения мира.
Доходы более бедной половины населения мира росли быстрее, чем доходы более богатой половины населения мира.Если вы хотите использовать эту визуализацию для презентации или в целях обучения и т. д., вы можете скачать zip-папку с файлом изображения для каждого года и анимированным .gif здесь.
Глобальное распределение доходов с 1988 по 2011 год
7Последние данные о глобальном неравенстве и взгляд в будущее
Эта визуализация показывает, как глобальное распределение доходов изменилось за десятилетие до 2013 года. Томаш и Хеллебрандт Паоло Мауро, авторы статьи 8 , откуда взяты эти данные, подтверждают вывод о снижении глобального неравенства: коэффициент Джини глобального неравенства снизился с 68,7 до 64,9.
Визуализация выше показывает распределение дохода по логарифмической оси x. На этой диаграмме, напротив, доходы отложены по линейной оси x и тем самым подчеркнуто, насколько все еще очень велико глобальное неравенство: основная часть населения мира живет с очень низкими доходами, а распределение доходов простирается очень далеко в сторону более высоких доходов справа.
 ручная сторона графика; а доходы свыше 14 000 международных долларов обрезаны, поскольку они сделали бы эту диаграмму с линейной осью X нечитаемой.
ручная сторона графика; а доходы свыше 14 000 международных долларов обрезаны, поскольку они сделали бы эту диаграмму с линейной осью X нечитаемой.Вторым поразительным и очень позитивным глобальным изменением, показанным на этой диаграмме, является рост глобального медианного дохода. В 2003 году половина населения мира жила менее чем на 1090 международных долларов в год, а другая половина жила на более чем 1090 международных долларов. Этот уровень глобального медианного дохода почти удвоился за последнее десятилетие и составил 2010 международных долларов в 2013 году.
на вставке в правом верхнем углу авторы прогнозируют дальнейшее снижение глобального неравенства и достижение коэффициента Джини 61,3. В то же время доходы беднейшей половины мира будут продолжать сильно расти, так что глобальный медианный доход может снова удвоиться и достичь 4000 международных долларов в 2035 году9.0024
Если вам нужна визуализация только наблюдаемого глобального распределения доходов в 2003 и 2013 годах, вы найдете ее здесь.

Глобальное распределение доходов в 2003, 2013 гг. и прогноз на 2035 г.
9Изменение глобального неравенства с 2003 по 2013 г.
показан на диаграмме выше.На диаграмме показан годовой располагаемый доход всех граждан мира как в 2003, так и в 2013 году. На оси X вы видите положение человека в глобальном распределении доходов, а на логарифмической оси Y вы видите годовой располагаемый доход. на той должности.
Увеличение благосостояния и уменьшение бедности существенно. Порог дохода беднейших 10% увеличился с 260 международных долларов до 480 международных долларов, а средний доход почти удвоился с 1100 международных долларов до 2010. Средний глобальный доход в 2013 году составляет 5 375 международных долларов. 11
Глобальное распределение доходов в 2003 и 2013 годах
12Глобальное неравенство доходов очень велико и будет оставаться очень высоким в течение длительного времени
Визуализация представляет те же данные таким же образом, за исключением того, что ось Y теперь не логарифмическая, а линейная.
 Эта перспектива еще более четко показывает все еще очень высокий уровень глобального неравенства.
Эта перспектива еще более четко показывает все еще очень высокий уровень глобального неравенства.Предыдущая и следующая визуализации показывают, насколько все еще очень велико глобальное неравенство в доходах: пороговое значение для 10 % самых богатых людей мира в 2013 году составляло 14 500 инт-$; пороговое значение для 10% самых бедных составляло 480 инт-$. Соотношение 30,2.
Хотя глобальное неравенство по-прежнему очень велико, сейчас мы живем в период снижения неравенства: в 2003 году это соотношение составляло 37,6. Коэффициент Джини также снизился с 68,7 до 64,9..
Взяв исторический опыт за ориентир того, что возможно в будущем, мы должны сделать вывод, что глобальное неравенство будет оставаться высоким еще долгое время. Чтобы понять это, мы можем спросить, сколько времени потребуется людям с доходами на уровне 10% самых бедных, чтобы достичь текущих доходов на уровне 10% самых богатых (что составляет 14 500 международных долларов). Этот уровень дохода примерно равен уровню ВВП на душу населения, выше которого численность бедного населения приближается к 0 % для большинства стран (см.
 здесь).
здесь).Сколько времени потребуется, чтобы доходы выросли с 480 до 14 500 доларов?
The global income distribution in 2003 and 2013
132% growth 172.1 years 4% growth 86.9 years 6% growth 58.5 years 8% рост 44,3 года 10% рост 35,8 лет Даже при очень оптимистичном сценарии беднякам потребуется несколько десятилетий, чтобы достичь уровня доходов 10% самых богатых людей мира.
2% — это примерно темпы роста, которые самые богатые страны на сегодняшний день испытали за последние десятилетия (см. здесь). Мы видели, что более бедные страны могут добиться более быстрого роста, но мы не видели, чтобы темпы роста превышали 6 % в течение периода времени, необходимого для достижения уровня глобальных 10 % в столь короткое время.
 Если прошлое является хорошим ориентиром для будущего, то, скорее всего, мир еще долгое время будет крайне неравным.
Если прошлое является хорошим ориентиром для будущего, то, скорее всего, мир еще долгое время будет крайне неравным.Неравенство внутри стран и неравенство между странами
Глобальное неравенство обусловлено изменениями как неравенства внутри стран, так и неравенства между странами. Эта визуализация показывает, как оба эти изменения определяют изменение глобального неравенства.
– Неравенство внутри стран имело U-образную форму на протяжении 20-го века.
– Неравенство между странами увеличивалось на протяжении 2 веков и достигло пика в 19 веке.80-е годы по приведенным здесь данным Бургиньона и Моррисона. С тех пор неравенство между странами уменьшилось.
Как показано на этой визуализации, неравенство доходов между разными странами намного выше, чем неравенство внутри стран. Следствием этого является то, что тенденция глобального неравенства во многом определяется тем, что происходит с неравенством между странами.
Качество данных и определение
Изменение относительного и абсолютного неравенства
Глобальное неравенство чрезвычайно велико, и на многих предыдущих диаграммах доходы отложены на логарифмической оси.




 Степень
Степень





 Нарисуйте числовую линию, отметив критические числа. Нарисуйте незакрашенный кружок возле каждого критического числа, если в неравенстве используются знаки «<» или «>»; нарисуйте закрашенный кружок у каждого критического числа, если в неравенстве используется « \ ( \ le \)» или «\ ( \ ge \)».
Нарисуйте числовую линию, отметив критические числа. Нарисуйте незакрашенный кружок возле каждого критического числа, если в неравенстве используются знаки «<» или «>»; нарисуйте закрашенный кружок у каждого критического числа, если в неравенстве используется « \ ( \ le \)» или «\ ( \ ge \)». Из-за строгого неравенства постройте их, используя открытые точки на числовой прямой. Рисунок 3.7.1 Критические числа
Из-за строгого неравенства постройте их, используя открытые точки на числовой прямой. Рисунок 3.7.1 Критические числа Ответ : \((0,4)\)
Ответ : \((0,4)\) Из-за инклюзивного неравенства \((≤)\) мы нанесем их на график с помощью закрытых точек.
Из-за инклюзивного неравенства \((≤)\) мы нанесем их на график с помощью закрытых точек.
 Опять же, эти критические точки являются единственными местами, где график может измениться от положения выше оси \(x\) (где \(f(x) > 0)\) ) до уровня ниже \(x\)- ось (где \(f(x) < 0) \). В пределах каждого интервала между двумя соседними критическими точками график либо всегда выше оси \(х\), либо всегда ниже оси \(х\). Таким образом, нахождение критических точек рационального неравенства играет фундаментальную роль в его решении.
Опять же, эти критические точки являются единственными местами, где график может измениться от положения выше оси \(x\) (где \(f(x) > 0)\) ) до уровня ниже \(x\)- ось (где \(f(x) < 0) \). В пределах каждого интервала между двумя соседними критическими точками график либо всегда выше оси \(х\), либо всегда ниже оси \(х\). Таким образом, нахождение критических точек рационального неравенства играет фундаментальную роль в его решении. цифры
цифры Запишите ответ в интервальной записи.
Запишите ответ в интервальной записи.
 Хотя это ограничение не включено в набор решений, оно является критическим числом. Перед созданием диаграммы знаков мы должны убедиться, что неравенство имеет ноль с одной стороны. Общие шаги решения рационального неравенства показаны в следующем примере.
Хотя это ограничение не включено в набор решений, оно является критическим числом. Перед созданием диаграммы знаков мы должны убедиться, что неравенство имеет ноль с одной стороны. Общие шаги решения рационального неравенства показаны в следующем примере. Любое ограничение всегда использует открытую точку.
Любое ограничение всегда использует открытую точку. {2}-4} \leq \dfrac{1}{2-x}\). 9{2}-4}-\dfrac{1}{2-x} \leq 0} \\ {\dfrac{1}{(x+2)(x-2)}-\dfrac{1}{-( x-2)} \leq 0} \\ {\ frac {1} {(x + 2) (x-2)} + \ frac {1 \ color {Cerulean} {(x + 2)}} {\ color {черный}{(x-2)}\color{Cerulean}{(x+2)}}\color{black}{\leq} 0} \\ {\dfrac{1+x+2}{(x+ 2)(x-2)} \leq 0} \\ \boxed{{f(x) = \dfrac{x+3}{(x+2)(x-2)}} \leq 0}\end{ array}\)
{2}-4} \leq \dfrac{1}{2-x}\). 9{2}-4}-\dfrac{1}{2-x} \leq 0} \\ {\dfrac{1}{(x+2)(x-2)}-\dfrac{1}{-( x-2)} \leq 0} \\ {\ frac {1} {(x + 2) (x-2)} + \ frac {1 \ color {Cerulean} {(x + 2)}} {\ color {черный}{(x-2)}\color{Cerulean}{(x+2)}}\color{black}{\leq} 0} \\ {\dfrac{1+x+2}{(x+ 2)(x-2)} \leq 0} \\ \boxed{{f(x) = \dfrac{x+3}{(x+2)(x-2)}} \leq 0}\end{ array}\)
 В нем также представлены некоторые исследования факторов, определяющих неравенство доходов.
В нем также представлены некоторые исследования факторов, определяющих неравенство доходов. Сегодня мы должны уравнять шансы и дать всем — независимо от того, где они родились — шанс на хорошую жизнь. Это не только правильно, но, как мы увидим ниже, и реалистично. Наша надежда на то, чтобы дать следующим поколениям шанс жить хорошей жизнью, заключается в широком развитии, которое делает возможным для всех то, что сегодня доступно лишь немногим.
Сегодня мы должны уравнять шансы и дать всем — независимо от того, где они родились — шанс на хорошую жизнь. Это не только правильно, но, как мы увидим ниже, и реалистично. Наша надежда на то, чтобы дать следующим поколениям шанс жить хорошей жизнью, заключается в широком развитии, которое делает возможным для всех то, что сегодня доступно лишь немногим. 2
2  В некоторых африканских странах более одного из десяти родившихся сегодня детей не доживут до пяти лет. В самых здоровых странах мира — в Европе и Восточной Азии — только 1 из 250 детей умирает, не дожив до 5 лет.
В некоторых африканских странах более одного из десяти родившихся сегодня детей не доживут до пяти лет. В самых здоровых странах мира — в Европе и Восточной Азии — только 1 из 250 детей умирает, не дожив до 5 лет. Это учитывает разницу в ценах между странами и, следовательно, выражается в международных долларах (вот пояснение). Катар и другие страны, очень богатые природными ресурсами, можно считать здесь исключениями, предполагая, что более уместно сравнивать очень богатые страны, не полагаясь в основном на экспорт природных ресурсов. В США ВВП на душу населения составляет 54 225 долларов США, а в Швейцарии — 57 410 долларов США. Это означает, что швейцарцы могут потратить за 1 месяц столько, сколько люди в Центральноафриканской Республике могут потратить за 7 лет.
Это учитывает разницу в ценах между странами и, следовательно, выражается в международных долларах (вот пояснение). Катар и другие страны, очень богатые природными ресурсами, можно считать здесь исключениями, предполагая, что более уместно сравнивать очень богатые страны, не полагаясь в основном на экспорт природных ресурсов. В США ВВП на душу населения составляет 54 225 долларов США, а в Швейцарии — 57 410 долларов США. Это означает, что швейцарцы могут потратить за 1 месяц столько, сколько люди в Центральноафриканской Республике могут потратить за 7 лет. 0463 в среднем ребенка попадают в самые обеспеченные места.
0463 в среднем ребенка попадают в самые обеспеченные места.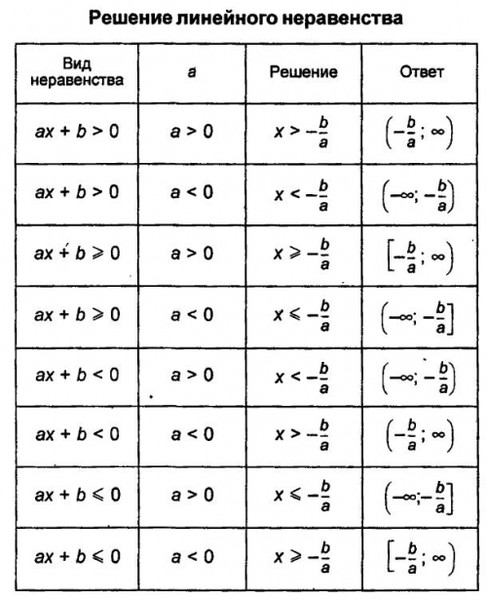
 Здоровье всего общества было плохим. У нас есть данные о смертности английской аристократии с 1550 года. Аристократы умирали так же рано, как и все остальные. 3 Средняя продолжительность их жизни тоже была ниже 40 лет. До более широкого социального развития даже самый привилегированный статус в обществе не давал бы вам шанса на здоровую жизнь. Вы просто не можете быть здоровым в нездоровом месте.
Здоровье всего общества было плохим. У нас есть данные о смертности английской аристократии с 1550 года. Аристократы умирали так же рано, как и все остальные. 3 Средняя продолжительность их жизни тоже была ниже 40 лет. До более широкого социального развития даже самый привилегированный статус в обществе не давал бы вам шанса на здоровую жизнь. Вы просто не можете быть здоровым в нездоровом месте. Даже в тех странах, которые сегодня являются самыми богатыми в мире, большинство людей до недавнего времени жили в условиях крайней нищеты. Финляндия не стала исключением.
Даже в тех странах, которые сегодня являются самыми богатыми в мире, большинство людей до недавнего времени жили в условиях крайней нищеты. Финляндия не стала исключением.
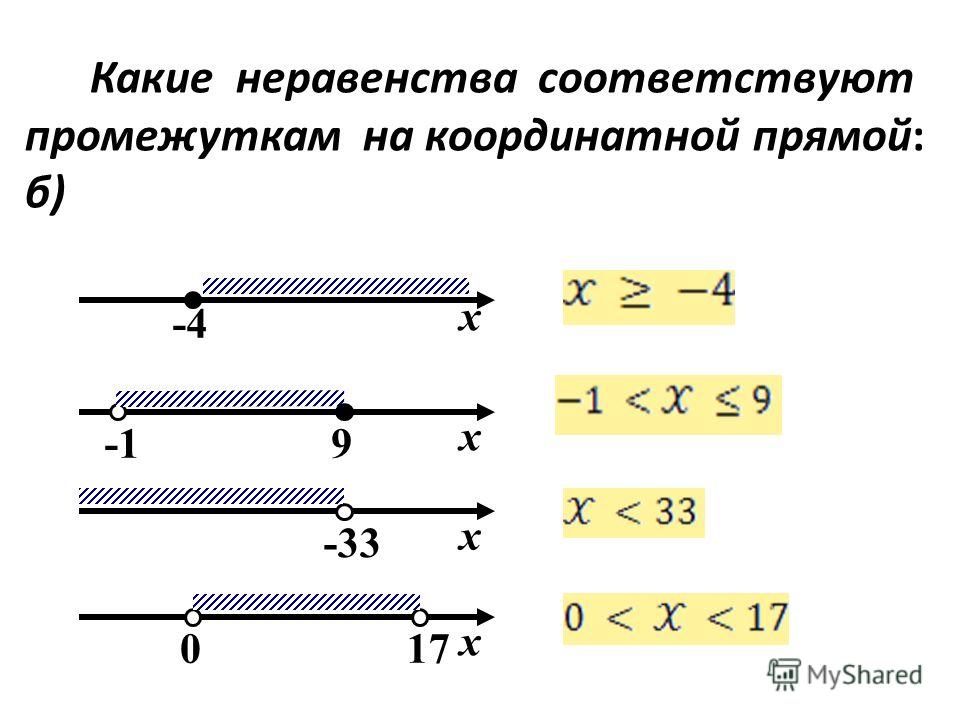


 Диаграмма показывает, что большая часть мира жила в бедности с доходом, подобным беднейшим странам сегодня. Наша статья о глобальной крайней бедности показывает, что в начале XIX века подавляющее большинство — более 80% — людей в мире жили в материальных условиях, которые сегодня мы назвали бы крайней нищетой.
Диаграмма показывает, что большая часть мира жила в бедности с доходом, подобным беднейшим странам сегодня. Наша статья о глобальной крайней бедности показывает, что в начале XIX века подавляющее большинство — более 80% — людей в мире жили в материальных условиях, которые сегодня мы назвали бы крайней нищетой. Мы перешли от двугорбого мира к одногорбому. И в то же время распределение также сместилось вправо — доходы многих беднейших граждан мира выросли, а крайняя бедность сократилась быстрее, чем когда-либо прежде в истории человечества.
Мы перешли от двугорбого мира к одногорбому. И в то же время распределение также сместилось вправо — доходы многих беднейших граждан мира выросли, а крайняя бедность сократилась быстрее, чем когда-либо прежде в истории человечества. Эти данные измеряют доход домохозяйства в каждом дециле распределения доходов, и два автора использовали эту информацию для получения глобального распределения доходов. Недостатком этого подхода является то, что мы можем вернуться только к тому времени, когда проводились обследования домохозяйств.
Эти данные измеряют доход домохозяйства в каждом дециле распределения доходов, и два автора использовали эту информацию для получения глобального распределения доходов. Недостатком этого подхода является то, что мы можем вернуться только к тому времени, когда проводились обследования домохозяйств. Доходы более бедной половины населения мира росли быстрее, чем доходы более богатой половины населения мира.
Доходы более бедной половины населения мира росли быстрее, чем доходы более богатой половины населения мира. ручная сторона графика; а доходы свыше 14 000 международных долларов обрезаны, поскольку они сделали бы эту диаграмму с линейной осью X нечитаемой.
ручная сторона графика; а доходы свыше 14 000 международных долларов обрезаны, поскольку они сделали бы эту диаграмму с линейной осью X нечитаемой.
 Эта перспектива еще более четко показывает все еще очень высокий уровень глобального неравенства.
Эта перспектива еще более четко показывает все еще очень высокий уровень глобального неравенства. здесь).
здесь). Если прошлое является хорошим ориентиром для будущего, то, скорее всего, мир еще долгое время будет крайне неравным.
Если прошлое является хорошим ориентиром для будущего, то, скорее всего, мир еще долгое время будет крайне неравным.