Неравенство бернулли доказательство: Неравенства и лемма Бернулли (с доказательствами)

Доклад Методы, основанные на применении численных неравенств

    Скачать с Depositfiles 

 2011 год ИГГ, ДонНТУ;

Руководитель: Рубцова Ольга Алексадровна,

Старший преподаватель,

Кафедра высшей математики им. В.В.Пака, ДонНТУ

МЕТОДЫ, ОСНОВАННЫЕ НА ПРИМЕНЕНИИ ЧИСЛЕННЫХ НЕРАВЕНСТВ

Нестандартными методами в математике являются также методы, в основу которых положено использование известных численных неравенств (Коши, Бернулли и Коши-Буняковского), изучению которых в общеобразовательной школе не уделяется или почти не уделяется никакого внимания. Однако многие математические задачи (особенно задачи повышенной сложности) эффективно решаются именно такими методами. В этой связи незнание последних может существенно ограничить круг успешно решаемых задач.

Первоначально приведем формулировки неравенства Коши, неравенства Бернулли и неравенства Коши-Буняковского, а затем проиллюстрируем их применение на примерах, взятых из программы вступительных экзаменов.

Неравенство Коши

Пусть , ,…, , тогда  (1)

где . Причем неравенство превращается в равенство тогда и, только тогда, когда . В частности, если в (1) положить , то

 (2)

Это неравенство чаще всего встречается при решении школьных задач по математике. Если в (2) положить  и , где , то

 (3)

Здесь неравенство равносильно равенству лишь при .

Следует отметить, что имеется аналог неравенства (3) для отрицательных значений , а именно, если , то

 (4)

Данное неравенство превращается в равенство при .

Неравенство Бернулли

Наиболее распространенным является классическое неравенство Бернулли, которое формулируется в следующей форме: если , то для любого натурального  имеет место

 (5)

Причем равенство в (5) достигается при  или .

Наряду с (5) существует обобщенное неравенство Бернулли, которое содержит в себе два неравенства:

 если  или , то

 (6)

если , то

 (7)

где .

Следует отметить, что равенства в (6) и (7) имеют место только при . Верно также и обратное утверждение.

Неравенство Коши-Буняковского

Для произвольных  и  имеет место

 (8)

где .

Причем равенство в (8) достигается в том и, только в том случае, когда числа . и  пропорциональны, т.е. существует константа  такая, что для всех  выполняется равенство .

На основе использования неравенства Коши-Буняковского (8) можно доказать неравенство

 (9)

которое справедливо для произвольных ,  и натурального числа .

Задачи и решения

Пример 1. Доказать неравенство

где .

Доказательство. Преобразуем левую часть неравенства с использованием неравенства (7), т.е.

Так как по условию , то равенства в неравенстве Бернулли не будет, поэтому доказано строгое неравенство.

Пример 2. Доказать, если , то

Доказательство. Для получения нижней оценки левой части требуемого неравенства первоначально воспользуемся неравенством Бернулли (6), а затем неравенством Коши (2), тогда

Пример 3.  Решить уравнение

Решение. Используя неравенство Коши (2), можно записать

т.е. имеет место неравенство

Из зданного уравнения следует, что приведенные выше неравенства Коши обращаются в равенства. А это возможно лишь в том случае, когда  и .

Следовательно, имеем  и .

Ответ: , ; , ; , ; , .

Пример 4. Решить уравнение

Решение. Применим к левой части уравнения неравенство Бернулли (7), а к правой части — неравенство (6), тогда

и

Отсюда следует, что неравенства Бернулли, примененные к обеим частям уравнения, обращаются в равенство, а это возможно лишь в том случае, когда .

Ответ: .

Литература:

1. А.И.Назаров «Задачи-ловушки», Мн., «Аверсэв»,2006

2.С.А. Барвенов «Математика для старшеклассников», «Аверсэв»,2004

3. С.А. Барвенов «Методы решения алгеброическиж уравнений», «Аверсэв»,2006

4. http://www.refsru.com/referat-655-4. {n}\leqslant 1+nx}

при этом равенство достигается в двух случаях:




[




∀
x
≠
−
1
,
n
=

,
n
=
1




∀
n
≠

,
x
=









{\displaystyle \left[{\begin{matrix}\forall x\neq -1,n=0,n=1\\\forall n\neq 0,x=0\end{matrix}}\right.}

Замечания

• Неравенство также справедливо для
  
  
  
  x
  ⩾
  −
  2
  
  
  {\displaystyle x\geqslant -2}
  

  (при

  
  
  
  n
  ∈
  
  
  N
  
  
  
  
  
  
  
  {\displaystyle n\in \mathbb {N} _{0}}
  

  ), если исключить случай, когда получается ноль в степени ноль. Доказательство для случая

  
  
  
  x
  ∈
  
  [
  
  −
  2
  ,
  −
  1
  
  )
  
  
  
  {\displaystyle x\in \left[-2,-1\right)}
  

  можно провести тем же методом математической индукции. n)$ для всех целых неотрицательных чисел $n$. 9к(1+ч)$. Как они получили левую сторону?

• $1 + kh + h ≤ (1 + h)(k + kh)$. Как они оказались на правой стороне?

• дискретная математика
• неравенство
• индукция

$\endgroup$

$\begingroup$

Примечание:

Индуктивное доказательство дано как ответ Дэвида У.Фарлоу.

---

Объяснение некоторых шагов и недостатков вашего индуктивного рассуждения: 92k\geq 0$

---

Теперь, почему мы делаем $(1)$ и $(2)$ и как мы получаем левое или правое положение в различных неравенствах?

Это сделано потому, что для доказательства $a \leq b$, если мы получим $a \leq c$ и $c \leq b$, то получим требуемое неравенство. Соответственно, мы можем выбрать требуемое значение $c$, которое не только делает эту задачу возможной, но и легкой. n>1+nx.$ $ 92>0$}\\[1em] &= 1+(k+1)x.\tag{множитель} \end{выравнивание} Таким образом, $S(k+1)$ также верно, что завершает индуктивный шаг. $\blacksquare$

---

Теперь все это имеет смысл? Примечания на полях к доказательству должны очень помочь (действительно, они

должны ответить на оба ваших вопроса о различных моментах в других доказательствах). Несмотря на это, всегда пробуйте как можно больше подходов и только затем (после многочисленных бесплодных попыток) прибегайте к внешнему решению.

$\endgroup$

6

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

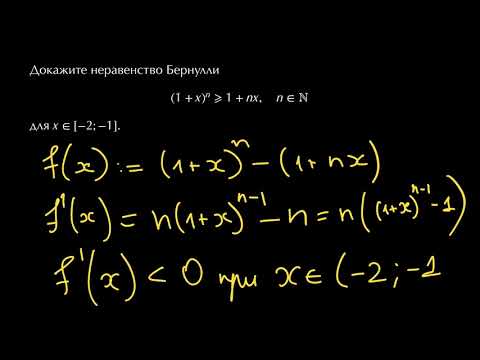. 9р$$ Не могли бы вы подсказать первый?

• анализ
• неравенство

$\endgroup$

4

$\begingroup$

Для вашего неравенства $(1)$ есть способ: пусть $p = \dfrac{m}n \in (0, 1)$, где $m, n \in \mathbb N$. Таким образом, $m < n$, и мы можем записать $(1)$ как $ $ \ sqrt [n] {\ color {red} {1 \ cdot1 \ cdot1 \ cdots1} \ cdot \ color {blue} {(1 + x) (1 + x) (1 + x) \ cdots (1+) x)}} \leqslant \frac{\color{red}{(1+1+1+\cdots+1)}+\color{blue}{(1+x)+(1+x)+\cdots ( 1+x)}}{n}$$ что является AM-GM, поскольку все члены неотрицательны. Обратите внимание, что количество синих терминов с каждой стороны равно $m$, а количество красных терминов равно $n-m$. 9{n+1}\left(1+\frac xn\right) \tag 1\\\\ &\ge \left(1+\frac{-x}{n+x}\right)\left(1+\frac xn\right)\tag 2\\\\ &=1 \end{align}$$

где при переходе от $(1)$ к $(2)$ мы использовали неравенство Бернулли.

No related posts.