Несобственный интеграл решить: Решение несобственного интеграла online

5.20. Несобственные интегралы с бесконечными пределами интегрирования

Пусть Y = F(X) – заданная и непрерывная для всех X ≥ α функция. Тогда для любого B ≥ A существует . Поставим вопрос о пределе этого интеграла при B → ¥.

Определение.

(6.1)

Называется Несобственным интегралом От функции F(X) с бесконечным верхним пределом. Если этот предел существует и конечен, то несобственный интеграл называется Сходящимся. А если же он не существует или равен
± ¥, то этот несобственный интеграл называется Расходящимся.

Если F(X) ≥ 0 для всех X ≥ A, то У несобственного интеграла (6.

1) имеется очевидный геометрический смысл, вытекающий из геометрического смысла (4.3) обычного определенного интеграла. Действительно, согласно рис. 5.14

(6.2)

А тогда

 

 

(6.3)

Здесь S¥ — площадь бесконечно протяженной в направлении оси Ох криволинейной трапеции (рис. 5.15). Несмотря на свою бесконечную протяженность, она может оказаться и конечной. Но это может произойти, согласно рис. 5.15, лишь в случае, когда Y =F(X) → 0 при X →¥. Да и то, если функция Y =F(X) → 0 при X → ¥ достаточно быстро.

Пример 1. Найти площадь S¥, изображенную на рис. 5.16.

Решение:

,
так как lnB → ¥ при B → ¥.

Итак, S¥ = ¥. И это несмотря на то, что функция при X

→ ¥. Несобственный интеграл , а значит, он расходится.

Пример 2. Найти площадь S¥ , изображенную на рис. 5.17.

Решение:

Здесь S¥ = 1. То есть бесконечно протяженная площадь оказалась конечной. Это произошло потому, что подинтегральная функция при X → ¥ достаточно быстро (по крайней мере, гораздо быстрее, чем подинтегральная функция в предыдущем примере). Несобственный интеграл (число), а значит, он сходится.

Пример 3. Выяснить, сходится или расходится несобственный интеграл .

Решение. Вычислим это интеграл:

– не существует. Это очевидно, если вспомнить поведение графика функции Y= = SinX (синусоиды) при X → ¥. Таким образом, не существует, а значит, он расходится. Впрочем, это и не могло быть иначе, ибо подинтегральная функция cos

X не стремится к нулю при Х → ¥.

Заметим, что при вычислении несобственных интегралов типа , как и при вычислении обычных определенных интегралов , можно сразу применять формулу Ньютона-Лейбница:

Здесь

(6. 4)

Действительно:

Если значение F(¥) существует и конечно, то согласно формуле (6.4) Ньютона-Лейбница сходится и несобственный интеграл .

Примечание. Совершенно аналогично интегралам с бесконечным верхним пределом можно рассматривать несобственные интегралы с бесконечным нижним пределом и даже с обоими бесконечными пределами интегрирования. То есть интегралы вида

(6.5)

Для их вычисления тоже можно применять формулу Ньютона-Лейбница.

Пример 4.

Итак, (число), то есть этот интеграл сходится. Его величина π равна площади S¥ бесконечно протяженной в обе стороны фигуры, изображенной на рис. 5.18.

Заметим, что сам факт сходимости-расходимости несобственных интегралов с бесконечными пределами интегрирования не обязательно устанавливать с помощью прямого вычисления этих интегралов. Это вопрос часто можно решить и гораздо проще, сравнив данный несобственный интеграл с каким-либо другим, для которого сходимость-расходимость уже установлена.

 

 

 

 

Пусть, например, для всех имеет место неравенство F(X)£ G(X), Где Y = F(X) И Y = G(X) – Две непрерывные и неотрицательные функции (рис. 5.19). Тогда очевидно, что

(6.6)

Из неравенства (6.6) и рис. 5.19 очевидным образом следует так называемый Признак сравнения несобственных интегралов:

1) Если (число) — сходится, то и (число) — сходится, причем B<A. 2) Если — расходится, то и — расходится. 3) Если — расходится, то — об этом интеграле ничего сказать нельзя. 4) Если (число) — сходится, то — об этом интеграле ничего сказать нельзя.

(6.7)

В качестве функции G(X), с которой на промежутке Сравнивают данную функцию F(X), часто используют функцию , а в качестве интеграла сравнения – интеграл , учитывая при этом, что при A > 0 и любых α функция — положительная и непрерывная функция, и что

(6.8)

Пример 5.

Исследовать на сходимость-расходимость

Решение. Очевидно, что для всех X Î [2; ¥). Поэтому

.

Но согласно (6.8) интеграл сходится. Поэтому, по признаку сравнения, сходится и (он представляет собой некоторой конкретное число). Более того, предыдущее неравенство дает и оценку этого числа: так как, согласно (6.8), , то

.

Пример 6. Исследовать на сходимость-расходимость .

Решение. Очевидно, что

для всех X Î [3; ¥).

Следовательно,

.

Но последний интеграл равен ¥. Следовательно, равен ¥ и . То есть он расходится.

Примечание. Справедлив и более сильный (обобщенный) признак сравнения, который применим для любых непрерывных и неотрицательных на
[A

; ¥) функций. А именно, если

,

(6. 9)

То есть если F(X) эквивалентна G(X) (F(X) ~ G(X)) при Х ® ¥, то несобственные интегралы

Сходятся или расходятся одновременно.

Пример 2. Исследовать на сходимость-расходимость .

Решение. Исследовав функцию , легко показать, что она определена, а следовательно и непрерывна для всех Х Î [10; ¥). При этом

Но, согласно (6.8), сходится. Поэтому и сходится.

Теперь перейдем к более сложному случаю несобственных интегралов с бесконечными пределами интегрирования, когда подинтегральная функция знакопеременна на своей области интегрирования (рис. 5.20). Тогда

(6. 10)

Где А>0 – сумма площадей, находящихся над осью Ох, а В>0 – сумма площадей, находящихся под осью Ох.

Рассмотрим еще один несобственный интеграл, только уже от |F(X)|:

(6.11)

А) Допустим, что сходится. Тогда

А + В – Конечное положительное число. А значит, и его положительные слагаемые А и В – Конечные положительные числа. Но тогда и их разность А – В – Конечное число (его знак может быть любым). А значит, согласно (6.10), несобственный интеграл сходится.

Б) Допустим, что расходится (равен +¥). Тогда сумма А +В = +¥, а значит, или А, или В, или оба они одновременно равны +¥. Но их разность А – В может оказаться как бесконечной, так и конечной. То есть может как сходиться, так и расходиться.

Если сходится, и при этом сходится, то говорят, что Сходится абсолютно. Величину абсолютно сходящегося несобственного интеграла можно и оценить:

(6.12)

Действительно, неравенство (6.12) равносильно очевидному неравенству

(6.13)

А если сходится, но при этом расходится, то говорят, что Сходится условно.

Пример 8. Показать, что сходится, причем абсолютно.

Решение. Рассматривая и используя признак сравнения (6. 7), получаем:

Таким образом, сходится. Но тогда и сходится, причем абсолютно. Более того, мы можем произвести, используя неравенство (6.12), оценку этого интеграла:

То есть абсолютная величина интеграла заключена в пределах
[0; 1].

Пример 9. Доказать, что сходится, но условно.

Решение. Применим к этому интегралу формулу (5.5) интегрирования по частям:

Интеграл , как и рассмотренный в примере 8 интеграл , сходится. А значит, сходится и . Но сходится он условно, ибо (расходится).

Действительно, так как для всех Х, то для всех Х. А значит

Но

Последний интеграл , как и аналогичные интегралы и , сходится (это можно подтвердить интегрированием по частям). То есть — число. А значит, (расходится). Но тогда и бóльший интеграл (расходится). То есть сходится, но условно.

< Предыдущая		Следующая >

5.

3. Несобственные интегралы. Примеры решений

К изучению несобственных интегралов лучше приступать в последнюю очередь в ходе изучения интегрального исчисления функции одной переменной. Читатель данного урока должен быть хорошо подкован в неопределенных интегралах, определенных интегралах, уметь находить площадь плоской фигуры с помощью определенного интеграла. Кроме того, потребуются знания простейших пределов и графиков элементарных функций. По логике изложения материала эта статья является продолжением урока Определенный интеграл. Как вычислить площадь фигуры. Тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки.

Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, к тому же у несобственного интеграла есть очень хороший геометрический смысл.

Что значит вычислить несобственный интеграл?

Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа).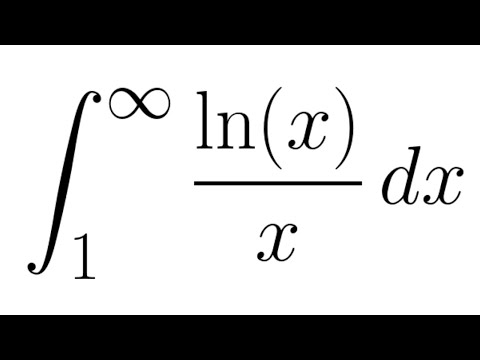

Несобственные интегралы бывают двух видов: первого и второго рода.

Иногда такой несобственный интеграл еще называют несобственным интегралом первого рода. В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так:

.

В чем его отличие от определенного интеграла? В верхнем пределе.

Он бесконечный:

.

Встречаются интегралы и с бесконечным нижним пределом

или с двумя бесконечными пределами:

.

Мы рассмотрим самый популярный случай . Техника работы с другими разновидностями – аналогична.

Всегда ли существует несобственный интеграл ?

Нет, не всегда.

Подынтегральная функция должна быть непрерывной на интервале . Строго говоря, последнее утверждение неверно: если есть разрывы функции, то в ряде случаев можно разбить интервал на несколько частей и вычислить несколько несобственных интегралов.

Изобразим на чертеже график подынтегральной функции . Типовой график и криволинейная трапеция для данного случая выглядит так:

Здесь всё хорошо, подынтегральная функция непрерывна на интервале , а, значит, несобственный интеграл существует. Обратите внимание, что криволинейная трапеция у нас – бесконечная (не ограниченная справа) фигура.

Несобственный интеграл численно равен площади заштрихованной фигуры, при этом возможны два случая:

1) Первая мысль, которая приходит в голову: «Раз фигура бесконечная, то и », иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что, что несобственный интеграл расходится.

2) Но! Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например:

.

Может ли так быть? Да. В этом случае несобственный интеграл сходится.

В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции .

А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл

«расходится», либо равен отрицательному числу.

Несобственный интеграл может быть отрицательным.

Важно! Когда Вам для решения предложен ПРОИЗВОЛЬНЫЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно. Ваша задача найти ЧИСЛО, либо доказать, что несобственный интеграл расходится. Геометрический смысл несобственного интеграла рассказан только для того, чтобы легче было понять материал.

Поскольку несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница:

.

На самом деле формула применима и к несобственным интегралам, только ее нужно немного модифицировать. В чем отличие? В бесконечном верхнем пределе интегрирования:  . Наверное, многие догадались, что здесь необходимо применение теории пределов, и формула запишется так:

.

В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию (неопределенный интеграл) и уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела. У кого с ними плохо, изучите урок Пределы функций. Примеры решений, ибо лучше поздно, чем в армии. Рассмотрим два классических примера:

Пример 1

Вычислить несобственный интеграл или установить его расходимость.

Для наглядности построим чертеж, хотя, еще раз подчеркиваю, на практике строить чертежи в данном задании не нужно.

Подынтегральная функция непрерывна на интервале , значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.

Применение нашей формулы

и решение задачи выглядит так:

То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.

В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применятся эта формула под знаком предела. Вместо привычной буквы   «динамической» переменной выступает буква «бэ». Это не должно смущать или ставить в тупик, потому-что любая буква ничем не хуже стандартного «икса».

Если Вам непонятно почему при , то это очень плохо, либо Вы не понимаете простейшие пределы (и вообще не понимаете, что такое предел), либо не знаете, как выглядит график логарифмической функции. Во втором случае посетите урок Графики и свойства элементарных функций.

При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!

Чистовое оформление задания должно выглядеть примерно так:

Подынтегральная функция непрерывна на «полубесконечном» интервале

Несобственный интеграл расходится.

При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией на границах интервала.

Этим мы идентифицируем тип несобственного интеграла.

Если Вам встретится интеграл вроде

,

то с вероятностью, близкой к 100%, можно сказать, что это опечатка. Здесь подынтегральная функция не является непрерывной на интервале интегрирования , она терпит разрыв в точке . Теоретически и практически допустимо вычислить два несобственных интеграла на интервалах и , а потом их сложить, но со здравой точки зрения такая вещь выглядит довольно абсурдно. Опечатка.

Иногда вследствие опечатки несобственного интеграла может вообще не существовать. Например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть интервала интегрирования вообще не войдёт в область определения подынтегральной функции.

Всегда смотрим и записываем, является ли подынтегральная функция непрерывной на интервале интегрирования.

Пример 2

Вычислить несобственный интеграл или установить его расходимость: .

Выполним чертеж:

Во-первых, замечаем следующее: подынтегральная функция

непрерывна на интервале . Хорошо. Решаем с помощью формулы

:

(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.

(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.

(3) Указываем, что , если (это нужно понимать) и упрощаем ответ.

Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.

Чистовое оформление примера должно выглядеть примерно так:

“ Подынтегральная функция непрерывна на полубесконечном интервале “

Пример 3

Вычислить несобственный интеграл или установить его расходимость.

Подынтегральная функция непрерывна на .

Интеграл не так прост, особенно для чайника. Что делать, если интеграл кажется не самым простым или не сразу понятно как его решать? В этом случае целесообразно применить алгоритм, о котором я уже рассказал в статье Определенный интеграл. Примеры решений.

Сначала попытаемся найти первообразную функцию F(X) (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.

На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс:

.

Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.

Проведем замену , тогда:

.

Неопределенный интеграл найден, константу C в данном случае добавлять не имеет смысла.

На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:

.

Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.

Теперь находим несобственный интеграл:

(1) Записываем решение в соответствии с формулой

.

Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.

(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница.

Почему при ? Смотрите график арктангенса.

(3) Получаем окончательный ответ. Тот факт, что arctg(0) = 0, полезно знать наизусть.

Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:

Подынтегральная функция непрерывна на интервале .

.

А сейчас два примера для самостоятельного решения.

Пример 4

Вычислить несобственный интеграл или установить его расходимость.

ВНИМАНИЕ! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей.

Пример 5

Вычислить несобственный интеграл или установить его расходимость.

Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала. У кого какая математическая подготовка. Полные решения и ответы в конце урока.

Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения определённых и несобственных интегралов. Там же разобран случай, когда оба предела интегрирования бесконечны.

Как решать неправильные интегралы — Криста Кинг Математика

Что такое неправильные интегралы?

Несобственные интегралы аналогичны определенным интегралам, за исключением того, что нижний и/или верхний пределы интегрирования бесконечны.

Помните, что определенный интеграл — это интеграл, который мы вычисляем на определенном интервале. Несобственный интеграл — это просто определенный интеграл, где один конец интервала равен ???\pm\infty???.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать больше.

Формулы, которые мы используем для работы с несобственными интегралами, таковы:

Если предел в случае ???1??? или ???2??? существует (если он порождает действительный числовой ответ), мы говорим, что он сходится. Если предел в случае ???1??? или ???2??? не существует, говорят, что он расходится. Это означает, что ответ не является реальным числом (ответ может быть ???\pm\infty???).

В случае ???3???, уравнение будет расходиться, если расходится один из интегралов в правой части. Это означает, что для случая ???3??? чтобы сходиться, оба интеграла в правой части должны иметь действительные числа.

Что делает интеграл неправильным?

Пройти курс

Хотите узнать больше об исчислении 2? У меня есть пошаговый курс для этого. 🙂 9б_0???

Вычисляя интервал ???[0,b]???, получаем

???\lim_{b\to\infty}\left[\arctan{(b)}-\arctan{(0 )}\правильно]???

???\arctan{(\infty)}???

???\frac{\pi}{2}???

В этом случае, поскольку мы получаем ответ в виде вещественного числа, мы знаем, что наш интеграл сходится.

Когда бесконечность является частью интервала или когда один конец интервала приближается к бесконечности, мы говорим, что уравнение имеет бесконечный разрыв. Другими словами, уравнение имеет асимптоту на интервале или на одном конце интервала.

Для несобственных интегралов, бесконечно разрывных где-то в интервале, мы используем следующие формулы.

Если лимит в случае ???4??? или ???5??? существует (если он дает вещественный ответ), мы говорим, что он сходится. Если предел в случае ???4??? или ???5??? не существует, говорят, что он расходится. Это означает, что ответ не является реальным числом (ответ может быть ???\pm\infty???).

В случае ???6??? уравнение будет расходиться, если расходится любой из интегралов в правой части. Это означает, что для случая ???6??? чтобы сходиться, оба интеграла в правой части должны иметь действительные числа. 92}\право)???

???\infty???

В этом случае, поскольку мы получаем бесконечный ответ, мы знаем, что наш интеграл расходится.

Получите доступ к полному курсу Calculus 2

Начать

Изучите математикуКриста Кинг 20 января 2021 г. математика, выучите онлайн, онлайн-курс, онлайн-математика, исчисление 2, исчисление 2, исчисление 2, исчисление ii, исчисление с одной переменной, вычисление с одной переменной, неправильные интегралы, несобственные, интегралы с бесконечностью, бесконечные интегралы, интегралы с разрывами, интегралы, интегрирование

0 лайков

2.6: Несобственные интегралы — Mathematics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

10270

Эта страница является черновиком и находится в активной разработке.

Область между графиком \(f(x)=\frac{1}{x}\) и осью x на интервале \([1,+∞)\) конечна или бесконечна? Если эта же самая область вращается вокруг оси абсцисс, будет ли ее объем конечным или бесконечным? Удивительно, но площадь описываемой области бесконечна, но объем тела, полученного при вращении этой области вокруг оси x, конечен. t_af(x)dx, \label{improper1}\] при условии, что этот предел существует. 9{+∞}_af(x)dx\) для любого значения a.).

В нашем первом примере мы возвращаемся к вопросу, поставленному в начале этого раздела: является ли площадь между графиком \(f(x)=\frac{1}{x}\) и \(x\ )-ось на интервале \([1,+∞)\) конечна или бесконечна?

Пример \(\PageIndex{1}\): поиск площади

Определить, находится ли площадь между графиком \(f(x)=\frac{1}{x}\) и осью X на интервале \([1,+∞)\) конечна или бесконечна.

Раствор

9t_1 \tag{Найти первообразную} \\[5pt] &=\lim_{t→+∞}(\ln |t|−\ln 1) \tag{Вычислить первообразную} \\[5pt] &=+∞ . \tag{Вычислите предел.} \end{align}\]

Поскольку несобственный интеграл расходится к \(+∞,\), площадь области бесконечна.

Пример \(\PageIndex{2}\): нахождение объема и ось \(x\) на интервале \([1,+∞)\) относительно оси \(x\). 9t_1\) Найдите первообразную.

\(=π\lim_{t→+∞}(−\frac{1}{t}+1)\) Вычислить первообразную.

\(=π\)

Несобственный интеграл сходится к \(π\). Следовательно, объем тела вращения равен \(π\).

В заключение, хотя площадь области между осью x и графиком \(f(x)=1/x\) на интервале \([1,+∞)\) бесконечна, объем твердого тела, образованного вращением этой области вокруг оси x, является конечным. Образовавшееся твердое тело известно как Рог Габриэля.

Примечание: Рог Габриэля (также называемый трубой Торричелли) представляет собой геометрическую фигуру, которая имеет бесконечную площадь поверхности, но конечный объем. Название относится к традиции, идентифицирующей архангела Гавриила как ангела, который трубит в рог, чтобы объявить Судный день, связывая божественное или бесконечное с конечным. Свойства этой фигуры впервые были изучены итальянским физиком и математиком Эванджелистой Торричелли в 17 веке.

Пример \(\PageIndex{3}\): ДТП в городе

Предположим, что на оживленном перекрестке дорожно-транспортное происшествие происходит в среднем одно каждые три месяца. После жалоб жителей внесены изменения в светофор на перекрестке. Прошло уже восемь месяцев с тех пор, как были внесены изменения, и никаких аварий не было. Были ли изменения эффективными или 8-месячный перерыв без происшествий — результат случайности?

Рисунок \(\PageIndex{4}\): (кредит: модификация работы Дэвида Маккелви, Flickr)

Теория вероятностей говорит нам, что если среднее время между событиями равно \(k\), то 92_0\frac{1}{x}dx\) в предельной форме с использованием уравнения.

Ответить

\(+∞\), расходится с

Теорема сравнения

Не всегда легко или даже возможно вычислить несобственный интеграл напрямую; однако, сравнивая его с другим тщательно подобранным интегралом, можно определить его сходимость или расходимость. Чтобы убедиться в этом, рассмотрим две непрерывные функции \(f(x)\) и \(g(x)\), удовлетворяющие \(0≤f(x)≤g(x)\) при \(x≥a\) ( Фигура). В этом случае мы можем рассматривать интегралы этих функций по интервалам вида \([a,t]\) как площади, так что мы имеем соотношение 9{+∞}_e\frac{\ln x}{x}dx\) расходится.

Преобразования Лапласа

В последних нескольких главах мы рассмотрели несколько способов использования интеграции для решения реальных задач. В следующем проекте мы собираемся изучить более продвинутое применение интеграции: интегральные преобразования. В частности, мы опишем преобразование Лапласа и некоторые его свойства. Преобразование Лапласа используется в технике и физике для упрощения вычислений, необходимых для решения некоторых задач. Он принимает функции, выраженные через время и 9{−st}dt\). Кстати, обратите внимание, что мы определили \(g(t), du=f(t)dt.\))

Как и следовало ожидать, вы должны увидеть, что

\(L{g(t)} =\frac{1}{s}⋅L{f(t)}.\)

Интегрирование во временной области упрощается до деления на s в частотной области.

Ключевые понятия

• Интегралы функций по бесконечным интервалам определяются в терминах пределов.
• Интегралы функций по интервалу, для которого функция имеет разрыв в конечной точке, могут быть определены в терминах пределов.

  No related posts.