Нод 36 и 24: НОД и НОК чисел 36 и 24

Наибольший общий делитель 24 и 36

Калькулятор «Наибольший общий делитель»

Какой наибольший общий делитель у чисел 24 и 36?

Ответ: НОД чисел 24 и 36 это 12

(двенадцать)

Нахождение наибольшего общего делителя для чисел 24 и 36 используя перечисление всех делителей

Первый способ нахождения НОД для чисел 24 и 36 — это перечисление всех делителей для обоих чисел и выбор из них наибольшего общего:

Все делители числа 24: 1, 2, 3, 4, 6, 8, 12, 24

Все делители числа 36: 1, 2, 3, 4, 6, 9, 12, 18, 36

Следовательно, наибольший общий делитель для чисел 24 и 36 это 12

Нахождение наибольшего общего делителя для чисел 24 и 36 используя разложение чисел на простые множители

Второй способ нахождения наибольшего общего делителя для числе 24 и 36 — это перечисление всех простых множителей для чисел и перемножение общих.

Простые множители числа 24: 2, 2, 2, 3

Простые множители числа 36: 2, 2, 3, 3

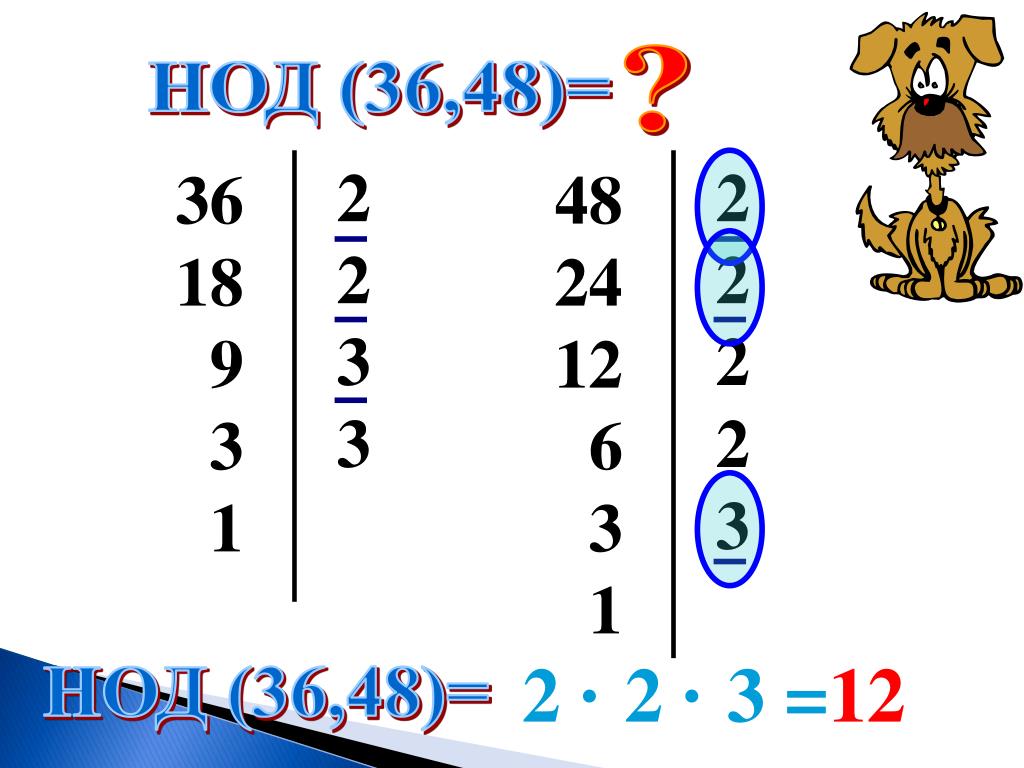
Как мы видим, у чисел есть общие простые множители: 2, 2, 3

Для нахождения НОД необходимо их перемножить: 2 × 2 × 3 = 12

Поделитесь текущим расчетом

Печать

https://calculat.io/ru/number/greatest-common-factor-of/24—36

<a href=»https://calculat.io/ru/number/greatest-common-factor-of/24—36″>Наибольший общий делитель 24 и 36 — Calculatio</a>

О калькуляторе «Наибольший общий делитель»

Данный калькулятор поможет найти наибольший общий делитель двух чисел. Например, он может помочь узнать какой наибольший общий делитель у чисел 24 и 36? Выберите первое число (например ’24’) и второе число (например ’36’). После чего нажмите кнопку ‘Посчитать’.

Наибольший общий делитель (НОД) для двух чисел - это наибольшее положительное целое число, которое делит каждое из целых чисел с нулевым остатком. 

Калькулятор «Наибольший общий делитель»

Таблица наибольших общих делителей

Число 1	Число 2	НОД
9	36	9
10	36	2
11	36	1
12	36	12
13	36	1
14	36	2
15	36	3
16	36	4
17	36	1
18	36	18
19	36	1
20	36	4
21	36	3
22	36	2
23	36	1
24	36	12
25	36	1
26	36	2
27	36	9
28	36	4
29	36	1
30	36	6
31	36	1
32	36	4
33	36	3
34	36	2
35	36	1
36	36	36
37	36	1
38	36	2

Mathway | Популярные задачи

1	Множитель	x^2-4
2	Множитель	4x^2+20x+16
3	График	y=-x^2
4	Вычислить	2+2
5	Множитель	x^2-25
6	Множитель	x^2+5x+6
7	Множитель	x^2-9
8	Множитель	x^3-8
9	Вычислить	квадратный корень из 12
10	Вычислить	квадратный корень из 20
11	Вычислить	квадратный корень из 50
12	Множитель	x^2-16
13	Вычислить	квадратный корень из 75
14	Множитель	x^2-1
15	Множитель	x^3+8
16	Вычислить	-2^2
17	Вычислить	квадратный корень из (-3)^4
18	Вычислить	квадратный корень из 45
19	Вычислить	квадратный корень из 32
20	Вычислить	квадратный корень из 18
21	Множитель	x^4-16
22	Вычислить	квадратный корень из 48
23	Вычислить	квадратный корень из 72
24	Вычислить	квадратный корень из (-2)^4
25	Множитель	x^3-27
26	Вычислить	-3^2
27	Множитель	x^4-1
28	Множитель	x^2+x-6
29	Множитель	x^3+27
30	Множитель	x^2-5x+6
31	Вычислить	квадратный корень из 24
32	Множитель	x^2-36
33	Множитель	x^2-4x+4
34	Вычислить	-4^2
35	Множитель	x^2-x-6
36	Множитель	x^4-81
37	Множитель	x^3-64
38	Вычислить	4^3
39	Множитель	x^3-1
40	График	y=x^2
41	Вычислить	2^3
42	Вычислить	(-12+ квадратный корень из -18)/60
43	Множитель	x^2-6x+9
44	Множитель	x^2-64
45	График	y=2x
46	Множитель	x^3+64
47	Вычислить	(-8+ квадратный корень из -12)/40
48	Множитель	x^2-8x+16
49	Вычислить	3^4
50	Вычислить	-5^2
51	Множитель	x^2-49
52	Вычислить	(-20+ квадратный корень из -75)/40
53	Множитель	x^2+6x+9
54	Множитель	4x^2-25
55	Вычислить	квадратный корень из 28
56	Множитель	x^2-81
57	Вычислить	2^5
58	Вычислить	-8^2
59	Вычислить	2^4
60	Множитель	4x^2-9
61	Вычислить	(-20+ квадратный корень из -50)/60
62	Вычислить	(-8+ квадратный корень из -20)/24
63	Множитель	x^2+4x+4
64	Множитель	x^2-10x+25
65	Вычислить	квадратный корень из -16
66	Множитель	x^2-2x+1
67	Вычислить	-7^2
68	График	f(x)=2^x
69	Вычислить	2^-2
70	Вычислить	квадратный корень из 27
71	Вычислить	квадратный корень из 80
72	Множитель	x^3+125
73	Вычислить	-9^2
74	Множитель	2x^2-5x-3
75	Вычислить	квадратный корень из 40
76	Множитель	x^2+2x+1
77	Множитель	x^2+8x+16
78	График	y=3x
79	Множитель	x^2+10x+25
80	Вычислить	3^3
81	Вычислить	5^-2
82	График	f(x)=x^2
83	Вычислить	квадратный корень из 54
84	Вычислить	(-12+ квадратный корень из -45)/24
85	Множитель	x^2+x-2
86	Вычислить	(-3)^3
87	Множитель	x^2-12x+36
88	Множитель	x^2+4
89	Вычислить	квадратный корень из (-8)^2
90	Множитель	x^2+7x+12
91	Вычислить	квадратный корень из -25
92	Множитель	x^2-x-20
93	Вычислить	5^3
94	Множитель	x^2+8x+15
95	Множитель	x^2+7x+10
96	Множитель	2x^2+5x-3
97	Вычислить квадратный корень	квадратный корень из 116
98	Множитель	x^2-x-12
99	Множитель	x^2-x-2
100	Вычислить	2^2

36 вопросов, которые ведут к любви

Стиль|36 вопросов, которые ведут к любви

https://www. nytimes.com/2015/01/09/style/no-37-big-wedding-or-small .html. другие), в котором исследуется, можно ли ускорить близость между двумя незнакомцами, если они зададут друг другу определенную серию личных вопросов. 36 вопросов в исследовании разбиты на три группы, каждая из которых должна быть более тщательной, чем предыдущая.

Идея состоит в том, что взаимная уязвимость способствует сближению. Цитируя авторов исследования, «один из ключевых паттернов, связанных с развитием близких отношений между сверстниками, — это устойчивое, обостряющееся, взаимное личное самораскрытие». Позволить себе быть уязвимым с другим человеком может быть чрезвычайно сложно, поэтому это упражнение усиливает проблему.

Последняя задача, которую пытаются выполнить мисс Катрон и ее подруга — смотреть друг другу в глаза в течение четырех минут, — документирована хуже, предполагаемая продолжительность варьируется от двух до четырех минут. Но г-жа Катрон была недвусмысленна в своей рекомендации. «Двух минут достаточно, чтобы испугаться, — сказала она мне. «Четверка действительно куда-то идет».

Набор I

1. Учитывая выбор любого человека в мире, кого бы вы выбрали в качестве гостя на ужин?

2. Хотели бы вы быть знаменитым? В каком смысле?

3. Прежде чем сделать телефонный звонок, вы когда-нибудь репетируете то, что собираетесь сказать? Почему?

4. Что для вас является «идеальным» днем?

5. Когда вы в последний раз пели про себя? Кому-то другому?

6. Если бы вы могли дожить до 90 лет и в течение последних 60 лет своей жизни сохранять либо разум, либо тело 30-летнего человека, что бы вы выбрали?

7. Есть ли у вас тайное предчувствие о том, как вы умрете?

8. Назовите три вещи, которые, по-видимому, у вас и вашего партнера схожи.

9. За что в своей жизни вы испытываете наибольшую благодарность?

10. Если бы вы могли что-то изменить в своем воспитании, что бы это было?

11. Найдите четыре минуты и расскажите своему партнеру историю своей жизни как можно подробнее.

12. Если бы вы могли проснуться завтра с каким-то одним качеством или способностью, что бы это было?

Набор II

13. Если бы хрустальный шар мог рассказать вам правду о себе, своей жизни, будущем или о чем-либо еще, что бы вы хотели узнать?

14. Есть ли что-то, чем вы давно мечтали заняться? Почему ты этого не сделал?

15. Какое самое большое достижение в вашей жизни?

16. Что вы больше всего цените в дружбе?

17. Какое у тебя самое дорогое воспоминание?

18. Какое у тебя самое ужасное воспоминание?

19. Если бы вы знали, что через год внезапно умрете, изменили бы вы что-нибудь в том, как живете сейчас? Почему?

20. Что для вас значит дружба?

21. Какую роль в вашей жизни играют любовь и привязанность?

22. Попеременно делитесь чем-то, что вы считаете положительной характеристикой своего партнера. Разделите в общей сложности пять предметов.

23. Насколько дружна и теплая ваша семья? Считаете ли вы, что ваше детство было более счастливым, чем у большинства других людей?

24. Как вы относитесь к своим отношениям с матерью?

Набор III

25. Сделайте по три верных утверждения «мы». Например, «Мы оба в этой комнате чувствуем…»

26. Завершите это предложение: «Я бы хотел, чтобы у меня был кто-то, с кем я мог бы разделить…»

27. Если бы вы собирались стать близким друг с вашим партнером, пожалуйста, поделитесь тем, что ему или ей было бы важно знать.

28. Расскажите своему партнеру, что вам в нем нравится; Будьте очень честны на этот раз, говоря вещи, которые вы, возможно, не сказали бы кому-то, кого вы только что встретили.

29. Расскажите своему партнеру о неловком моменте в вашей жизни.

30. Когда вы в последний раз плакали в присутствии другого человека? Самостоятельно?

31. Расскажите своему партнеру о том, что вам в нем уже нравится.

32. Что, во всяком случае, слишком серьезно, чтобы над ним шутили?

33. Если бы вы умерли сегодня вечером, не имея возможности ни с кем пообщаться, о чем бы вы больше всего сожалели, если бы никому не сказали? Почему ты им еще не сказал?

34. Ваш дом, в котором есть все, что у вас есть, загорается. После спасения ваших близких и домашних животных у вас есть время безопасно совершить последний рывок, чтобы спасти любой предмет. Что бы это могло быть? Почему?

35. Из всех членов вашей семьи, чью смерть вы бы сочли наиболее тревожной? Почему?

36. Поделитесь личной проблемой и попросите вашего партнера посоветовать, как он или она может с ней справиться. Кроме того, попросите вашего партнера рассказать вам о том, как вы относитесь к выбранной вами проблеме.

Факторы 36 | Простая факторизация числа 36, Факторное дерево числа 36

Факторы числа 36 — это те числа, которые полностью делят 36, не оставляя остатка. Есть 9множители 36, среди которых 36 — самый большой множитель, а 2 и 3 — его простые множители. Разложение на простые множители числа 36 может быть выполнено путем умножения всех его простых множителей так, чтобы произведение было равно 36. Давайте узнаем, как записать все множители 36 , на простые множители 36 и дерево факторов. 36 в этой статье.

1.	Какие множители числа 36?
2.	Прост-факторизация числа 36
3.	Факторное дерево из 36
4.	Фактор Пары по 36
5.	Часто задаваемые вопросы о факторах 36

Какие множители числа 36?

Делители числа 36 могут быть перечислены как 1, 2, 3, 4, 6, 9, 12, 18 и 36. Согласно определению делителей, делители числа 36 — это те числа, которые делят 36 без остатка . Другими словами, мы можем сказать, что если умножить два числа и произведение равно 36, то числа являются делителями 36. Это означает, что 36 полностью делится на все эти числа. Помимо этого, 36 также имеет отрицательные факторы, которые могут быть перечислены как -1, -2, -3, -4, -6, -9., -12, -18 и -36. Для отрицательных множителей нам нужно умножить отрицательный множитель на отрицательный множитель, например, (-12) × (-3) = 36.

Как найти множители 36?

Факторизация числа означает запись числа как произведения его множителей. Наиболее часто используемый метод нахождения множителей числа — метод умножения. Найдем множители числа 36 с помощью умножения.

Все множители числа 36 с помощью умножения

Найдем все множители числа 36 , используя метод умножения, используя следующие шаги.

• Шаг 1: Чтобы найти множители 36 с помощью умножения, нам нужно проверить, какие пары чисел умножаются, чтобы получить 36, поэтому нам нужно разделить 36 на натуральные числа, начиная с 1, и продолжать до 9. Нам нужно записать те числа, которые полностью делят 36.
• Шаг 2: Числа, которые полностью делят 36, называются его делителями. Мы записываем это конкретное число вместе с его парой и составляем список, как показано на рисунке выше. Как мы проверяем и перечисляем все числа до 9, вместе с ним мы автоматически получаем другой парный множитель. Например, начиная с 1, мы пишем 1 × 36 = 36, а 2 × 18 = 36 и так далее. Здесь (1, 36) образует первую пару, (2, 18) образует вторую пару, и список продолжается, как показано. Итак, когда мы записываем 1 как множитель 36, мы получаем другой множитель как 36; и поскольку мы пишем 2 как множитель 36, мы получаем 18 как другой множитель. Таким образом, мы получаем все факторы.
• Шаг 3 : После того, как список отмечен, мы получаем все делители числа 36, начиная с 1 вверх, вниз, а затем снова поднимаемся вверх до 36. Это дает нам полный список всех делителей числа 36 в виде показано на рисунке, приведенном выше.

Следовательно, делители числа 36 могут быть перечислены как 1, 2, 3, 4, 6, 9, 12, 18 и 36. Теперь давайте узнаем о простой факторизации числа 36.

Простые делители числа 36

простых делителей числа 36 — это те делители числа 36, которые являются простыми числами. Простые делители числа 36 отличаются от делителей числа 36. Как мы видели в предыдущем разделе, делители числа 36 могут быть перечислены как 1, 2, 3, 4, 6, 9, 12, 18 и 36. Однако все это не простые числа. Итак, давайте найдем простые делители числа 36, используя простую факторизацию в следующем разделе.

Прост-факторизация числа 36

Факторизация простых чисел — это способ представления числа в виде произведения его простых множителей. Простые делители числа — это те делители, которые являются простыми числами. Первичную факторизацию числа 36 можно выполнить, выполнив следующие шаги. Обратите внимание на приведенный ниже рисунок, чтобы понять разложение числа 36 на простые множители.

• Шаг 1: Первым шагом является деление числа 36 на его наименьший простой делитель. Мы знаем, что простой делитель — это простое число, являющееся делителем данного числа. Итак, с помощью правил делимости находим наименьший делитель заданного числа. Здесь мы получаем 2. Следовательно, 2 — наименьший простой делитель числа 36. Итак, 36 ÷ 2 = 18
• Шаг 2: Нам нужно многократно делить частное на 2, пока мы не получим число, которое больше не делится на 2. Итак, мы снова делим 18 на 2, что равно 18 ÷ 2 = 9
• Шаг 3: Разделите 18 еще раз на 2, чтобы получить 18 ÷ 2 = 9
• Шаг 4: Теперь 9 не делится полностью на 2, поэтому мы переходим к следующему простому множителю 36, который равен 3. То есть 9 ÷ 3 = 3
• Шаг 5: Разделите частное на 3 еще раз, что равно 3 ÷ 3 = 1
• Шаг 6: Нам не нужно продолжать, так как мы получили 1 как наше частное.
• Шаг 7: Следовательно, разложение числа 36 на простые множители выражается как 2 × 2 × 3 × 3 = 2 ² × 3 ² ; где 2 и 3 — простые числа и простые множители числа 36.

Таким образом, простые делители числа 36 равны 2 и 3, а простая факторизация числа 36 = 2 × 2 × 3 × 3

Факторное дерево из 36

Мы также можем найти простые множители числа 36 с помощью дерева множителей.

Факторное дерево 36 можно построить, разлагая 36 на множители, пока мы не достигнем его простых множителей. Эти факторы разделены и записаны в виде ветвей дерева. Окончательные множители обведены кружком и считаются простыми множителями числа 36. Давайте найдем простые множители числа 36, используя следующие шаги и дерево факторов, приведенное ниже.

• Шаг 1: Разделите 36 на два множителя. Возьмем 2 и 18.
• Шаг 2: Изучите эти множители, чтобы определить, являются ли они простыми или нет.
• Шаг 3: Поскольку 2 — простое число, мы обводим его кружком как один из простых множителей числа 36. Мы переходим к 18, составному числу, и далее разбиваем его на другие множители. Другими словами, мы повторяем процесс факторизации 18 и разбиения его на ветви, пока не достигнем простого числа.
• Шаг 4: Здесь мы получаем 2 и 9. Итак, мы обводим 2, потому что это простое число, и разделяем 9на 3 и 3. На этом этапе у нас остались простые числа 2 и 3. Мы обводим их кружком, так как знаем, что их нельзя разложить на множители. Это конец дерева факторов.
• Шаг 5: Следовательно, простые множители числа 36 = 2 × 2 × 3 × 3

Примечание: Следует отметить, что могут быть разные деревья множителей числа 36. Например, мы можем начать с разделения 36 на 4 и 9. Затем 4 можно разделить на 2 и 2, а 9 можно разделить на 3 и 3. Наконец, мы можем наблюдать те же самые простые множители, то есть 36 = 2 × 2 × 3 × 3

Фактор Пары по 36

Множители числа 36 можно записывать парами. Это означает, что произведение парных множителей 36 всегда равно 36.

множителей 36 в парах можно записать, как показано в таблице ниже:

Факторы	Коэффициенты положительной пары
1 × 36 = 36	1, 36
2 × 18 = 36	2, 18
3 × 12 = 36	3, 12
4 × 9 = 36	4, 9
6 × 6 = 36	6, 6

Возможны и отрицательные парные множители, потому что произведение двух отрицательных чисел также дает положительное число. Давайте посмотрим на отрицательные парные множители числа 36.

Факторы	Коэффициенты отрицательной пары
-1 × -36 = 36	-1, -36
-2 × -18 = 36	-2, -18
-3 × -12 = 36	-3, -12
-4 × -9 = 36	-4, -9
-6 × -6 = 36	-6, -6

Следующие пункты объясняют некоторые особенности парных множителей числа 36.

• Парные множители числа 36 — это целые числа в парах, которые перемножаются для получения исходного числа, т. е. 36.
• Парные множители могут быть как положительными, так и отрицательными, но они не могут быть дробями или десятичными числами.
• Положительные парные множители числа 36 следующие: (1, 36), (2, 18), (3, 12), (4, 9) и (6, 6). Отрицательные парные множители числа 36: (-1, -36), (-2, -18), (-3, -12), (-4, -9) и (-6, -6)

Важные примечания

• Только составные числа могут иметь более двух делителей.
  Поскольку 36 — составное число, оно имеет более двух делителей.
• Каждый делитель заданного числа либо меньше, либо равен заданному числу.
• Количество множителей заданного числа конечно. 36 имеет 9 делителей.
• Делители 36 — это те числа, которые делят 36 полностью, не оставляя остатка.
• 36 имеет всего 9 факторов: 1, 2, 3, 4, 6, 9, 12, 18 и 36.
• Существует трюк, позволяющий вычислить общее количество делителей числа. Например, 36 = 2 × 2 × 3 × 3 = 2 ² × 3 ² . Мы получаем простые факторизации 36 как 2 ² × 3 ² . Просто добавьте один (1) к показателям степени 2 и 2 по отдельности и умножьте их суммы. (2 + 1) × (2 + 1) = 3 × 3 = 9. Это означает, что 36 имеет всего 9 делителей.

Что нужно помнить

Вспомним список делителей, отрицательных и простых делителей числа 36.

• Делители числа 36: 1, 2, 3, 4, 6, 9, 12, 24 , и 36.
• Отрицательные коэффициенты 36: -1, -2, -3, -4, -6, -9, -12, -18 и -36.
• Простые множители числа 36: 2, 3
• Факторизация числа 36: 2 × 2 × 3 × 3 = 2 ² × 3 ²

☛ Связанные статьи

• Множители 33: Множители 33 равны 1, 3, 11 и 33.
• Факторы 34: множители 34 равны 1, 2, 17 и 34.
• Факторы 38: множители 38 равны 1, 2, 19 и 38.
• Коэффициенты 30: множители 30 равны 1, 2, 3, 5, 6, 10, 15 и 30.
• Множители числа 360: Множители числа 360 равны 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180 и 360.
• Множители 35: Множители 35 равны 1, 5, 7 и 35.
• Факторы 37: множители 37 равны 1 и 37.

 

Примеры множителей 36

1. Пример 1: Укажите истинное или ложное значение делителей числа 36.

   a.) 3 и 6 — делители числа 36.

   b.) 2 и 3 — простые делители числа 36.

   Решение :

   а.) Верно, 3 и 6 являются делителями 36.

   b.) Верно, 2 и 3 являются простыми делителями числа 36.

2. Пример 2: Запишите все положительные множители числа 36.

   Решение:

   Все положительные множители числа 36 равны 1, 2, 3, 4, 6, 9, 12, 18 и 36.

3. Пример 3:

   Перечислите положительные и отрицательные парные множители числа 36.

   Решение:

   Положительные парные множители числа 36 следующие: (1, 36), (2, 18), (3 , 12), (4, 9) и (6, 6). Отрицательные парные множители числа 36: (-1, -36), (-2, -18), (-3, -12), (-4, -9) и (-6, -6)

перейти к слайдуперейти к слайдуперейти к слайду

Разбейте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по коэффициентам 36

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о факторах 36

Каковы все множители числа 36?

множителей 36 равны 1, 2, 3, 4, 6, 9, 12, 18, 36, а его отрицательные множители равны -1, -2, -3, -4, -6, -9, — 12, -18, -36.

Каковы простые делители числа 36?

Есть два простых делителя числа 36: 2 и 3. Простые делители числа — это те делители, которые являются простыми числами. В этом случае, если мы разложим число 36 на простые множители, мы получим 2 × 2 × 3 × 3 = 2 ² × 3 ² , где 2 и 3 — простые числа и простые делители числа 36.

Каковы общие делители чисел 36 и 42?

Множители 36 могут быть перечислены как 1, 2, 3, 4, 6, 9, 12, 18, 36, а множители 42 могут быть перечислены как 1, 2, 3, 6, 7, 14, 21, 42. Среди них мы можем перечислить общие делители чисел 36 и 42 как 1, 2, 3 и 6. Теперь мы можем найти наибольший общий делитель (НОД) чисел 36 и 42, который равен 6.

Какие Общие делители 36 и 40?

Множители 36 могут быть перечислены как 1, 2, 3, 4, 6, 9, 12, 18, 36, а множители 40 могут быть перечислены как 1, 2, 4, 5, 8, 10, 20, 40. , Среди них мы можем перечислить общие делители 36 и 40 как 1, 2 и 4. С помощью этого мы можем найти наибольший общий делитель (GCF) 36 и 40, который равен 4.

Что такое наибольший общий делитель 36 и 20?

Множители 36 и 20 равны 1, 2, 3, 4, 6, 9, 12, 18, 36 и 1, 2, 4, 5, 10, 20 соответственно. Общие делители чисел 36 и 20: (1, 2, 4). Следовательно, GCF 36 и 20 равен 4,9.0003

Чему равна сумма всех делителей числа 36?

Сумма всех множителей 36 может быть рассчитана путем сложения 1, 2, 3, 4, 6, 9, 12, 18, 36, что равно 1 + 2 + 3 + 4 + 6 + 9 + 12 + 18 + 36 = 91.

Сколько Факторов у 36?

36 имеет в общей сложности 9 делителей, которые могут быть перечислены как 1, 2, 3, 4, 6, 9, 12, 18, 36.