Наибольший общий делитель равен наименьшему общему кратному » задачи
НОД и НОК »
Найдите наибольший общий делитель чисел:
1)220,165,77
2)63,42,168
3)230,92,138
4)42,650,260
Решение: 1, 220/11= 22 наибольший общий делитель 11
165/11= 15
77/11=7
2, 63/7=9
42/7=6
168/7=24 наибольший общий делитель 7
3. 230/2=115
92/2=46
138/2=69 наибольший общий делитель 2
4. 42/2=21
650/2=325
260/2=130 наибольший общий делитель 2найдите наибольший общий делитель чисел наиболее удобным способом 163, 310 и 997
Решение: 1 это наибольший общий делитель эти числа взаимно простыепросто у них нет общих множителей
раскладываем
163/163 310/2 997/997
155/5 1/
31/31
1/
тут нет одинаков множителей значит наибольш общ дел 1
Найдите наибольший общий делитель чисел наиболее удобным способом:
163, 310, 997
Решение: 163 — простое число (делится только само на себя и на 1 естественно), делители числа 310 — 1,2,5,10,31,62,55,310, а число 997, также как и 163 — простое число.
Их наибольший общий делитель — 1, он же и вообще единственный общий делитель у данного множества чисел.163:163 по другому нельзя 310:155 997:997 по другому никак
Найдите наибольший общий делитель чисел a) 212 и 318 б) 15 и 16 в) 135,315 и 450.
Докажите что числа 25 и 26 взаимно простые.
Найдите наибольший общий делитель чисел 1456 и 1560.
Решение: Наибольший общий делитель — НОД.
а) НОД(212,318) = 106
Раскладываем на множители каждое число и находим общие множители.
212 = 2*2*53 и 318 = 2*3*53 и общие — 2*53 = 106
. Проверка 106*2 = 212 и 106*3 = 318.
б) НОД(15,16) = 1 — общих делителей нет.
в) НОД(135,315,450) = 45
135 = 3*3*3*5 и 315 = 3*3*5*7 и 450 = 2*3*3*5*5. Общие — 3*3*5=45.
Проверка 45*3 =135 и 45*7=315 и 45*10=450.
НОД(1456,1560) = 104Найдите наибольший общий делитель чисел способом разложения на простые множители: 1)48 и 84 2)70 и 98 4)52 и 78 3)16 и 45 5)44 и 65
Решение: Для НОД нужно выписать все множители, которые входят в разложения данных чисел. 2
265=5*13
НОД=1
Найдите наибольший общий делитель чисел способ разложения на простые множители:
1)48 и 84 4)52 и 78
2)70 и 98 5)44 и 65
3)16 и 45 6)72 и 96
Решение: 1) 48=2*2*2*2*3; 84=2*2*3*7; НОД(48;84)=2*2*3=12; 2) 70=2*5*7; 98=2*7*7; НОД(70;98)=2*7=14; 3) 16=2*2*2*2; 45=3*3*5; НОД(16;45)=1; 16 и 45 это взаимно простые числа, у них общий дели ель только 1; 4) 52=2*2*13; 78=2*3*13; НОД(52;78)=2*13=26; 5) 44=2*2*11; 65=5*13; НОД(44;65)=1; 44 и 65 взаимно простые числа; 6) 72=2*2*2*3*3; 96=2*2*2*2*2*3; НОД(72;96)=2*2*2*3=24;1)48 и 84
48=2*2*2*2*3
84=2*2*3*7
НОД(48;84)=2*2*3=12
2)70 и 98
70=2*5*7
98=2*7*7
НОД(70;98)=2*7=14
3)16 и 45
16=2*2*2*2
45=5*3*3
НОД(16;45)=1
4)52 и 78
52=2*2*13
78=2*3*13
НОД(52;78)=2*13=26
5)44 и 65
44=2*2*11
65=5*13
НОД(44;65)=1
6)72 и 96
72=2*2*2*3*3
96=2*2*2*2*2*3
НОД(72;96)=2*2*2*3=24Найдите наибольший общий делитель чисел 48 и 84,70 и 98, 16 и 45,52 и 78,44 и 65,72 и 96.

Решение: И последние два
НОД (44;65)=1
44|2
22|2
.11|11
.1|
65|5
.13|13
.1|
НОД (72;96)=2*3*2*2=24
72|2
36|3
.12|2
.6|2
.3|3
.1|
96|3
32|2
.16|2
.8|2
.4|2
.1|Найдите наибольший общий делитель чисел 15 и 60; 45 и 56 ; 16 и 24?
Решение: 1) НОД(15 и 60)=15
2) НОД(45 и 56)=1, они являются взаимно простыми
3) НОД(16 и 24)=81. Наибольший Общий Делитель чисел 15 и 60, это 15 т. к. 15:15=1, а 60:15=4.
___________________________
2. Наибольший Общий Делитель 45 и 56, это 1 т. к. больше нет чисел на что, одновременно можно поделить и 45 и 56.(45:1=45;56:1=56.)
_______________________________
3. Наибольший Общий Делитель чисел 16 и 24, это 8, т. к. 16:8=2, а 24:8=3.
_________________________
Ответ:1)15; 2)1; 3)8.
____________________________Найдите наибольший общий делитель чисел способом разложения на простые множители:48и84;
70и98;
16и45;
52и78;
Решение: 48 = 2 * 2 * 2 * 2 * 3
84 = 2 * 2 * 3 * 7
НОД (48 и 84) = 2 * 2 * 3 = 12 — наибольший общий делитель
48 :12 = 4 84 : 12 = 7
70 = 2 * 5 * 7
98 = 2 * 7 * 7
НОД (70 и 98) = 2 * 7 = 14 — наибольший общий делитель
70 : 14 = 5 98 : 14 = 7
16 = 2 * 2 * 2 * 2
45 = 3 * 3 * 5
НОД (16 и 45) = 1 — наибольший общий делитель
Числа 16 и 45 взаимно простые, так как у них нет общих делителей, кроме единицы
52 = 2 * 2 * 13
78 = 2 * 3 * 13
НОД (52 и 78) = 2 * 13 = 26 — наибольший общий делитель
52 : 26 = 2 78 : 26 = 3Найдите наибольший общий делитель чисел наиболее удобным способом 42 и 60 45 и 81 28 и-33 75 и-90 26 65 и 130 48 240 и 260 72 432 и 792 163 310 и 997
Решение: 42 = 2*3*7
60 = 2*3*2*5
НОД (42; 60) = 2 * 3 = 6
45 = 3*3*5
81 = 3*3*9
НОД (45; 81) = 3 * 3 = 9
28 = 2*2*7
33 = 3*11
НОД(28; 33) = 1
75 = 5*3*5
90 = 5*3*6
НОД(75; 90) = 5 * 3 = 15
26 = 2*13
65 = 5*13
130 = 2*5*13
НОД(26; 65; 130) = 13
48 = 2*2*2*2*3
240 = 2*2*2*2*3*5
260 = 2*2*5*13
НОД(48; 240; 260) = 2*2 = 4
72 = 2*2*2*3*3
432 = 2*2*2*2*3*3*3
792 = 2*2*2*3*3*11
НОД(72; 432; 792) = 2*2*2*3*3 = 72
345 6 7 > >>
Математика 6 Мерзляк.
 Упражнения 138-162
Упражнения 138-162Упражнения по математике для УМК Мерзляк с ответами на некоторые задачи. §5. Наибольший общий делитель (2019, 2020, 2021 годы). Математика 6 Мерзляк. Упражнения 138-162.
ОГЛАВЛЕНИЕ (2021 год) ТЕОРИЯ: § 5.
Математика 6 Мерзляк (2021 год)
§ 5. Упражнения 138-162
№ 138. Найдите наибольший общий делитель чисел: 1) 12 и 18; 2) 24 и 30; 3) 6 и 36; 4) 48 и 64; 5) 35 и 18; 6) 14, 21 и 28.
Нажмите на этот спойлер, чтобы увидеть РЕШЕНИЕ
№ 139. Найдите наибольший общий делитель чисел: 1) 16 и 24; 2) 15 и 60; 3)10 и 15; 4) 45 и 56; 5) 21 и 49; 6) 12, 18 и 24.
Правильный ответ: 1) НОД (16; 24) = 23 = 8; 2) НОД (15; 60) = 3 • 5 = 15; 3) НОД (10; 15) = 5; 4) НОД (45; 56) = 1; 5) НОД (21; 49) = 7; 6) НОД (12, 18, 24) = 2 • 3 = 6.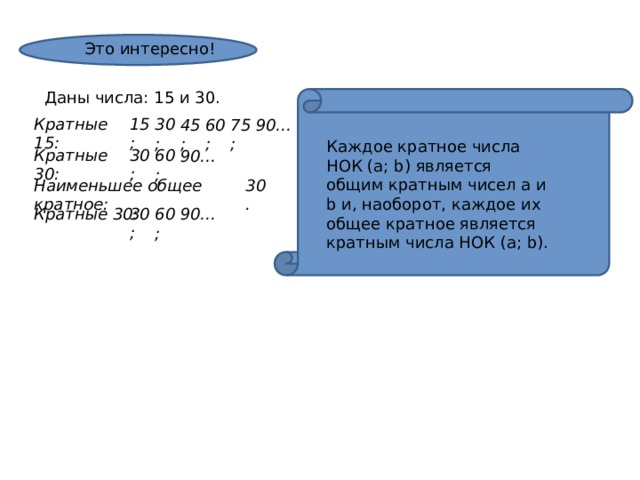
Нажмите на этот спойлер, чтобы увидеть РЕШЕНИЕ
№ 140. Найдите наибольший общий делитель чисел а и b: 1) а = 2 • 2 • 3 • 5 • 7 • 19 и b = 2 • 3 • 3 • 7 • 11 • 13; 2) а = 2 3 • 32 • 73 • 112 • 19 и b = 22 • 35 • 112 • 193.
Правильный ответ: 1) Если а = 2 • 2 • 3 • 5 • 7 • 19; b = 2 • 3 • 3 • 7 • 11 • 13, то НОД (а; b) = 2 • 3 • 7 = 42.
2) Если а = 23 • 32 • 73 • 112 • 19; b = 22 • 35 • 112 • 193, то НОД (а; b) = 22 • 32 • 112 • 19.
№ 141. Найдите наибольший общий делитель чисел: 1) 72 и 120; 2) 792 и 1188; 3) 924 и 396; 4) 116 и 111.
Правильный ответ: 1) НОД (72; 120) = 23 • 3 = 8 • 3 = 24; 2) НОД (792; 1188) = 22 • 32 • 11 = 4 • 9 • 11 = 396; 3) НОД (924; 396) = 22 • 3 • 11 = 4 • 33 = 132; 4) НОД (116; 111) = 1.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 142. Найдите наибольший общий делитель чисел: 1) 42 и 105; 2) 588 и 252; 3) 680 и 612.
Правильный ответ: 1) НОД (42; 105) = 3 • 7 = 21; 2) НОД (588; 252) = 22 • 3 • 7 = 4 • 21 = 84; 3) НОД (680; 612) = 22 • 17 = 68.
Нажмите на этот спойлер, чтобы увидеть РЕШЕНИЕ
№ 143. Среди данных нар чисел выберите пары взаимно простых чисел: 1) 14 и 21; 2) 54 и 65; 3) 42 и 55; 4) 14 и 70; 5) 28 и 39; 6) 63 и 42. Для пар чисел, не являющихся взаимно простыми, укажите наибольший общий делитель.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 144. Составьте все пары взаимно простых чисел из чисел 12, 14, 33, 25.
Правильный ответ: Взаимно простые числа: 12 и 25; 14 и 33; 14 и 25; 33 и 25.
Нажмите на этот спойлер, чтобы увидеть РЕШЕНИЕ
№ 145. Составьте все пары взаимно простых чисел из чисел 15, 16, 21, 77.
Правильный ответ: Взаимно простые числа: 15 и 16; 15 и 77; 16 и 21; 16 и 77.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 146. Запишите все правильные дроби со знаменателем 15, у которых числитель и знаменатель – взаимно простые числа.
Правильный ответ: 1/15; 2/15; 4/15; 7/15; 8/15; 11/15; 13/15; 14/15.
№ 147. Запишите все неправильные дроби с числителем 16, у которых числитель и знаменатель – взаимно простые числа.
Правильный ответ: 16/1; 16/3; 16/5; 16/7; 16/9; 16/11; 16/13; 16/15.
№ 148. Докажите, что: 1) числа 364 и 495 – взаимно простые; 2) числа 380 и 399 не являются взаимно простыми.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 149. Докажите, что: 1) числа 945 и 572 – взаимно простые; 2) числа 1095 и 738 не являются взаимно простыми.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 150. Используя цифры 2, 3, 4, запишите все возможные двузначные числа (цифры в каждом двузначном числе должны быть различными). Из полученных чисел выпишите пары взаимно простых чисел.
Используя цифры 2, 3, 4, запишите все возможные двузначные числа (цифры в каждом двузначном числе должны быть различными). Из полученных чисел выпишите пары взаимно простых чисел.
Правильный ответ: Все двузначные числа: 23, 24, 32, 34, 42, 43.
Взаимно простые: 23 и 24; 23 и 32; 23 и 34; 23 и 42; 23 и 43; 24 и 43; 32 и 43; 34 и 43; 42 и 43.
№ 151. Напишите три пары составных чисел такие, что в парах числа являются взаимно простыми.
Правильный ответ: 8 и 15; 9 и 20; 15 и 22.
№ 152. Между учениками 6 класса поделили поровну 155 тетрадей и 62 ручки. Сколько в этом классе учеников?
Правильный ответ: 31 ученик
Нажмите на этот спойлер, чтобы увидеть РЕШЕНИЕ
№ 153. На автомобили погрузили 96 контейнеров с картофелем и 64 контейнера с капустой. Сколько было автомобилей, если известно, что их не меньше 20 и на всех автомобилях было одинаковое количество контейнеров с картофелем и одинаковое количество контейнеров с капустой?
Правильный ответ: 32 автомобиля.
Нажмите на этот спойлер, чтобы увидеть РЕШЕНИЕ
№ 154. Между школьными библиотеками разделили 92 толковых и 138 орфографических словарей русского языка. Сколько было школ, если известно, что их не менее 25 и все школы получили одинаковые комплекты, состоящие из словарей двух видов?
Правильный ответ: 46 школ.
Нажмите на этот спойлер, чтобы увидеть РЕШЕНИЕ
№ 155. Для новогодних подарков приобрели 96 шоколадок, 72 апельсина и 84 банана. Какое наибольшее количество одинаковых подарков можно из них составить, если необходимо использовать все продукты? Сколько в отдельности шоколадок, апельсинов и бананов будет в каждом подарке?
Нажмите на этот спойлер, чтобы увидеть РЕШЕНИЕ
№ 156. Из 156 жёлтых, 234 белых и 390 красных роз составляли букеты. Какое наибольшее количество одинаковых букетов можно составить, если необходимо использовать все цветы?
Правильный ответ: 78 букетов.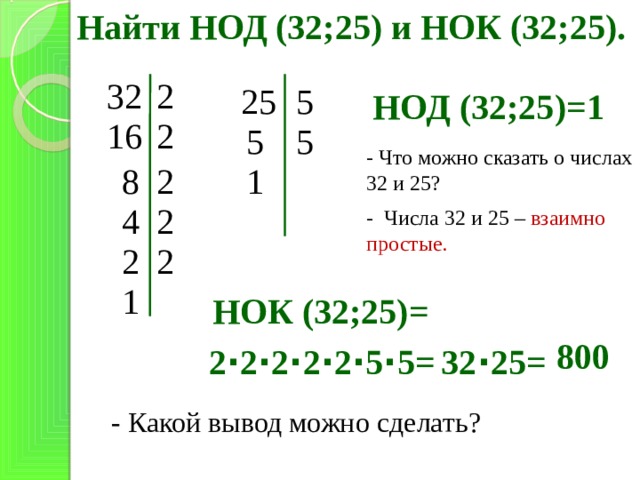
Нажмите на этот спойлер, чтобы увидеть РЕШЕНИЕ
№ 157. Используя цифры 2, 5 и 9 (цифры не могут повторяться), запишите трёхзначное число, которое: 1) кратно 2; 2) кратно 5. Можно ли с помощью этих цифр записать число, кратное 3?
Правильный ответ
Число, кратное 3, записать нельзя, так как 2 + 5 + 9 = 16; а 16 не делится на 3.
№ 158. Какую цифру можно поставить вместо звёздочки в записи 1*8, чтобы полученное число делилось нацело на 18?
Правильный ответ: 108; 198.
№ 159. Запишите число 19 в виде суммы трёх простых чисел.
Правильный ответ: 19 = 3 + 5 + 11.
№ 160. Если к некоторому двузначному числу справа дописать нуль, то данное число увеличится на 432. Найдите это число.
Правильный ответ: 48.
Решение. Пусть число х – было; тогда число 10х – стало. По условию задачи известно, что полученное число на 432 больше данного. Составим уравнение: 10х – х = 432 ⇒ 9х = 432 ⇒ х = 48 – данное число.
Пусть число х – было; тогда число 10х – стало. По условию задачи известно, что полученное число на 432 больше данного. Составим уравнение: 10х – х = 432 ⇒ 9х = 432 ⇒ х = 48 – данное число.
№ 161. Найдите числа, которых недостаёт в цепочке вычислений:
1) 38 → •а → 1,9 → +b → 2,24 → :c → 56;
2) а → +2,5 → 4 → •х → 1,6 → :y → 32.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 162. Барон Мюнхгаузен рассказывал, что он разрезал арбуз на четыре части, а после того, как его съели, осталось пять корок. Может ли такое быть, если корки не ломать?
Правильный ответ: Такое может быть.
Нужно вырезать сквозной кусок в центре, в форме цилиндра, у которого будет 2 корки – сверху и снизу. Затем оставшуюся часть арбуза разрезать на 3 части – 3 корки. Итого получаем 4 части и 5 корок.
ОГЛАВЛЕНИЕ (2021 год) ДАЛЕЕ: Упражнения 163-186
Вы смотрели: Упражнения по математике для УМК Мерзляк с ответами на некоторые задачи.
|
Нахождение нод онлайн. Общий делитель и кратное
Продолжим разговор о наименьшем общем кратном, который мы начали в разделе « НОК – наименьшее общее кратное, определение, примеры». В этой теме мы рассмотрим способы нахождения НОК для трех чисел и более, разберем вопрос о том, как найти НОК отрицательного числа.
Yandex.RTB R-A-339285-1
Вычисление наименьшего общего кратного (НОК) через НОД
Мы уже установили связь наименьшего общего кратного с наибольшим общим делителем. Теперь научимся определять НОК через НОД. Сначала разберемся, как делать это для положительных чисел.
Определение 1
Найти наименьшее общее кратное через наибольший общий делитель можно по формуле НОК (a , b) = a · b: НОД (a , b) .
Пример 1
Необходимо найти НОК чисел 126 и 70 .
Решение
Примем a = 126 , b = 70 . Подставим значения в формулу вычисления наименьшего общего кратного через наибольший общий делитель НОК (a , b) = a · b: НОД (a , b) .
Найдет НОД чисел 70 и 126 . Для этого нам понадобится алгоритм Евклида: 126 = 70 · 1 + 56 , 70 = 56 · 1 + 14 , 56 = 14 · 4 , следовательно, НОД (126 , 70) = 14 .
Вычислим НОК: НОК (126 , 70) = 126 · 70: НОД (126 , 70) = 126 · 70: 14 = 630 .
Ответ: НОК (126 , 70) = 630 .
Пример 2
Найдите нок чисел 68 и 34 .
Решение
НОД в данном случае нейти несложно, так как 68 делится на 34 . Вычислим наименьшее общее кратное по формуле: НОК (68 , 34) = 68 · 34: НОД (68 , 34) = 68 · 34: 34 = 68 .
Ответ: НОК (68 , 34) = 68 .
В этом примере мы использовали правило нахождения наименьшего общего кратного для целых положительных чисел a и b: если первое число делится на второе, что НОК этих чисел будет равно первому числу.
Нахождение НОК с помощью разложения чисел на простые множители
Теперь давайте рассмотрим способ нахождения НОК, который основан на разложении чисел на простые множители.
Определение 2
Для нахождения наименьшего общего кратного нам понадобится выполнить ряд несложных действий:
- составляем произведение всех простых множителей чисел, для которых нам нужно найти НОК;
- исключаем их полученных произведений все простые множители;
- полученное после исключения общих простых множителей произведение будет равно НОК данных чисел.

Этот способ нахождения наименьшего общего кратного основан на равенстве НОК (a , b) = a · b: НОД (a , b) . Если посмотреть на формулу, то станет понятно: произведение чисел a и b равно произведению всех множителей, которые участвуют в разложении этих двух чисел. При этом НОД двух чисел равен произведению всех простых множителей, которые одновременно присутствуют в разложениях на множители данных двух чисел.
Пример 3
У нас есть два числе 75 и 210 . Мы можем разложить их на множители следующим образом: 75 = 3 · 5 · 5 и 210 = 2 · 3 · 5 · 7 . Если составить произведение всех множителей двух исходных чисел, то получится: 2 · 3 · 3 · 5 · 5 · 5 · 7 .
Если исключить общие для обоих чисел множители 3 и 5 , мы получим произведение следующего вида: 2 · 3 · 5 · 5 · 7 = 1050 . Это произведение и будет нашим НОК для чисел 75 и 210 .
Пример 4
Найдите НОК чисел 441 и 700 , разложив оба числа на простые множители.
Решение
Найдем все простые множители чисел, данных в условии:
441 147 49 7 1 3 3 7 7
700 350 175 35 7 1 2 2 5 5 7
Получаем две цепочки чисел: 441 = 3 · 3 · 7 · 7 и 700 = 2 · 2 · 5 · 5 · 7 .
Произведение всех множителей, которые участвовали в разложении данных чисел, будет иметь вид: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 · 7 . Найдем общие множители. Это число 7 . Исключим его из общего произведения: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 . Получается, что НОК (441 , 700) = 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 = 44 100 .
Ответ: НОК (441 , 700) = 44 100 .
Дадим еще одну формулировку метода нахождения НОК путем разложения чисел на простые множители.
Определение 3
Раньше мы исключали из всего количества множителей общие для обоих чисел. Теперь мы сделаем иначе:
- разложим оба числа на простые множители:
- добавим к произведению простых множителей первого числа недостающие множители второго числа;
- получим произведение, которое и будет искомым НОК двух чисел.

Пример 5
Вернемся к числам 75 и 210 , для которых мы уже искали НОК в одном из прошлых примеров. Разложим их на простые множители: 75 = 3 · 5 · 5 и 210 = 2 · 3 · 5 · 7 . К произведению множителей 3 , 5 и 5 числа 75 добавим недостающие множители 2 и 7 числа 210 . Получаем: 2 · 3 · 5 · 5 · 7 . Это и есть НОК чисел 75 и 210 .
Пример 6
Необходимо вычислить НОК чисел 84 и 648 .
Решение
Разложим числа из условия на простые множители: 84 = 2 · 2 · 3 · 7 и 648 = 2 · 2 · 2 · 3 · 3 · 3 · 3 . Добавим к произведению множителей 2 , 2 , 3 и 7 числа 84 недостающие множители 2 , 3 , 3 и
3 числа 648 . Получаем произведение 2 · 2 · 2 · 3 · 3 · 3 · 3 · 7 = 4536 . Это и есть наименьшее общее кратное чисел 84 и 648 .
Ответ: НОК (84 , 648) = 4 536 .
Нахождение НОК трех и большего количества чисел
Независимо от того, с каким количеством чисел мы имеем дело, алгоритм наших действий всегда будет одинаковым: мы будем последовательно находить НОК двух чисел. На этот случай есть теорема.
На этот случай есть теорема.
Теорема 1
Предположим, что у нас есть целые числа a 1 , a 2 , … , a k . НОК m k этих чисел находится при последовательном вычислении m 2 = НОК (a 1 , a 2) , m 3 = НОК (m 2 , a 3) , … , m k = НОК (m k − 1 , a k) .
Теперь рассмотрим, как можно применять теорему для решения конкретных задач.
Пример 7
Необходимо вычислить наименьшее общее кратное четырех чисел 140 , 9 , 54 и 250 .
Решение
Введем обозначения: a 1 = 140 , a 2 = 9 , a 3 = 54 , a 4 = 250 .
Начнем с того, что вычислим m 2 = НОК (a 1 , a 2) = НОК (140 , 9) . Применим алгоритм Евклида для вычисления НОД чисел 140 и 9: 140 = 9 · 15 + 5 , 9 = 5 · 1 + 4 , 5 = 4 · 1 + 1 , 4 = 1 · 4 . Получаем: НОД (140 , 9) = 1 , НОК (140 , 9) = 140 · 9: НОД (140 , 9) = 140 · 9: 1 = 1 260 . Следовательно, m 2 = 1 260 .
Теперь вычислим по тому е алгоритму m 3 = НОК (m 2 , a 3) = НОК (1 260 , 54) . В ходе вычислений получаем m 3 = 3 780 .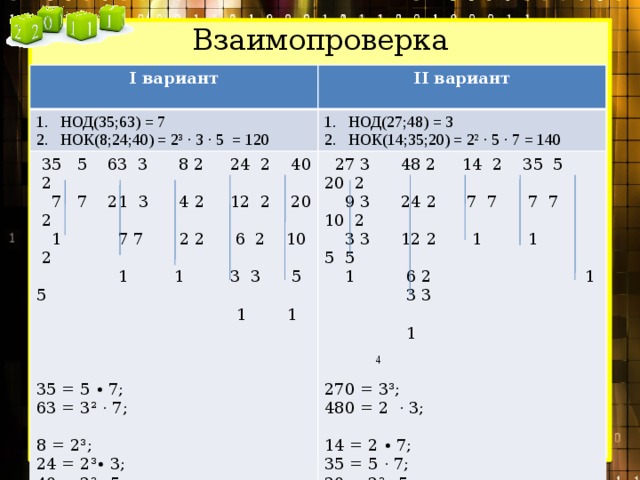
Нам осталось вычислить m 4 = НОК (m 3 , a 4) = НОК (3 780 , 250) . Действуем по тому же алгоритму. Получаем m 4 = 94 500 .
НОК четырех чисел из условия примера равно 94500 .
Ответ: НОК (140 , 9 , 54 , 250) = 94 500 .
Как видите, вычисления получаются несложными, но достаточно трудоемкими. Чтобы сэкономить время, можно пойти другим путем.
Определение 4
Предлагаем вам следующий алгоритм действий:
- раскладываем все числа на простые множители;
- к произведению множителей первого числа добавляем недостающие множители из произведения второго числа;
- к полученному на предыдущем этапе произведению добавляем недостающие множители третьего числа и т.д.;
- полученное произведение будет наименьшим общим кратным всех чисел из условия.
Пример 8
Необходимо найти НОК пяти чисел 84 , 6 , 48 , 7 , 143 .
Решение
Разложим все пять чисел на простые множители: 84 = 2 · 2 · 3 · 7 , 6 = 2 · 3 , 48 = 2 · 2 · 2 · 2 · 3 , 7 , 143 = 11 · 13 . Простые числа, которым является число 7 , на простые множители не раскладываются. Такие числа совпадают со своим разложением на простые множители.
Простые числа, которым является число 7 , на простые множители не раскладываются. Такие числа совпадают со своим разложением на простые множители.
Теперь возьмем произведение простых множителей 2 , 2 , 3 и 7 числа 84 и добавим к ним недостающие множители второго числа. Мы разложили число 6 на 2 и 3 . Эти множители уже есть в произведении первого числа. Следовательно, их опускаем.
Продолжаем добавлять недостающие множители. Переходим к числу 48 , из произведения простых множителей которого берем 2 и 2 . Затем добавляем простой множитель 7 от четвертого числа и множители 11 и 13 пятого. Получаем: 2 · 2 · 2 · 2 · 3 · 7 · 11 · 13 = 48 048 . Это и есть наименьшее общее кратное пяти исходных чисел.
Ответ: НОК (84 , 6 , 48 , 7 , 143) = 48 048 .
Нахождение наименьшего общего кратного отрицательных чисел
Для того, чтобы найти наименьшее общее кратное отрицательных чисел, эти числа необходимо сначала заменить на числа с противоположным знаком, а затем провести вычисления по приведенным выше алгоритмам.
Пример 9
НОК (54 , − 34) = НОК (54 , 34) , а НОК (− 622 , − 46 , − 54 , − 888) = НОК (622 , 46 , 54 , 888) .
Такие действия допустимы в связи с тем, что если принять, что a и − a – противоположные числа,
то множество кратных числа a совпадает со множеством кратных числа − a .
Пример 10
Необходимо вычислить НОК отрицательных чисел − 145 и − 45 .
Решение
Произведем замену чисел − 145 и − 45 на противоположные им числа 145 и 45 . Теперь по алгоритму вычислим НОК (145 , 45) = 145 · 45: НОД (145 , 45) = 145 · 45: 5 = 1 305 , предварительно определив НОД по алгоритму Евклида.
Получим, что НОК чисел − 145 и − 45 равно 1 305 .
Ответ: НОК (− 145 , − 45) = 1 305 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Определение. Наибольшее натуральное число, на которое делятся без остатка числа а и b, называют наибольшим общим делителем (НОД) этих чисел.
Найдём наибольший общий делитель чисел 24 и 35.
Делителями 24 будут числа 1, 2, 3, 4, 6, 8, 12, 24, а делителями 35 будут числа 1, 5, 7, 35.
Видим, что числа 24 и 35 имеют только один общий делитель — число 1. Такие числа называют взаимно простыми .
Определение. Натуральные числа называют взаимно простыми , если их наибольший общий делитель (НОД) равен 1.
Наибольший общий делитель (НОД) можно найти, не выписывая всех делителей данных чисел.
Разложим на множители числа 48 и 36, получим:
48 = 2 * 2 * 2 * 2 * 3, 36 = 2 * 2 * 3 * 3.
Из множителей, входящих в разложение первого из этих чисел, вычеркнем те, которые не входят в разложение второго числа
(т. е. две двойки).
Остаются множители 2 * 2 * 3. Их произведение равно 12. Это число и является наибольшим общим делителем чисел 48 и 36.
Так же находят наибольший общий делитель трёх и более чисел.
Чтобы найти наибольший общий делитель
2) из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел;
3) найти произ ведение оставшихся множителей.
Если все данные числа делятся на одно из них, то это число и является наибольшим общим делителем данных чисел.
Например, наибольшим общим делителем чисел 15, 45, 75 и 180 будет число 15, так как на него делятся все остальные числа: 45, 75 и 180.
Наименьшее общее кратное (НОК)
Определение. Наименьшим общим кратным (НОК) натуральных чисел а и Ь называют наименьшее натуральное число,
которое кратно и a, и b.
Наименьшее общее кратное (НОК) чисел 75 и 60 можно найти и не выписывая подряд кратные этих чисел. Для этого разложим 75 и 60 на
простые множители: 75 = 3 * 5 * 5, а 60 = 2 * 2 * 3 * 5.
Выпишем множители, входящие в разложение первого из этих чисел, и добавим к ним недостающие множители 2 и 2 из разложения
второго числа (т.е. объединяем множители).
Получаем пять множителей 2 * 2 * 3 * 5 * 5, произведение которых равно 300. Это число является наименьшим общим кратным чисел 75 и 60.
Так же находят наименьшее общее кратное для трёх и более чисел.
Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) выписать множители, входящие в разложение одного из чисел;
3) добавить к ним недостающие множители из разложений остальных чисел;
4) найти произведение получившихся множителей.
Заметим, что если одно из данных чисел делится на все остальные числа, то это число и является наименьшим общим кратным данных
чисел.
Например, наименьшим общим кратным чисел 12, 15, 20 и 60 будет число 60, так как оно делится на все данные числа.
Пифагор (VI в. до н. э.) и его ученики изучали вопрос о делимости чисел. Число, равное сумме всех его делителей (без самого числа),
они называли совершенным числом. Например, числа 6 (6 = 1 + 2 + 3), 28 (28 = 1 + 2 + 4 + 7 + 14) совершенные. Следующие совершенные
числа — 496, 8128, 33 550 336. Пифагорейцы знали только первые три совершенных числа. Четвёртое — 8128 — стало известно в I в. н. э.
Пятое — 33 550 336 — было найдено в XV в. К 1983 г. было известно уже 27 совершенных чисел. Но до сих пор учёные не знают, есть ли
нечётные совершенные числа, есть ли самое большое совершенное число.
К 1983 г. было известно уже 27 совершенных чисел. Но до сих пор учёные не знают, есть ли
нечётные совершенные числа, есть ли самое большое совершенное число.
Интерес древних математиков к простым числам связан с тем, что любое число либо простое, либо может быть представлено в виде
произведения простых чисел, т. е. простые числа — это как бы кирпичики, из которых строятся остальные натуральные числа.
Вы, наверное, обратили внимание, что простые числа в ряду натуральных чисел встречаются неравномерно — в одних частях ряда их больше,
в других — меньше. Но чем дальше мы продвигаемся по числовому ряду, тем реже встречаются простые числа. Возникает вопрос: существует
ли последнее (самое большое) простое число? Древнегреческий математик Евклид (III в. до н. э.) в своей книге «начала», бывшей на
протяжении двух тысяч лет основным учебником математики, доказал, что простых чисел бесконечно много, т. е. за каждым простым числом
есть ещё большее простое число.
Для отыскания простых чисел другой греческий математик того же времени Эратосфен придумал такой способ. Он записывал все числа
от 1 до какого-то числа, а потом вычёркивал единицу, которая не является ни простым, ни составным числом, затем вычёркивал через
одно все числа, идущие после 2 (числа, кратные 2, т. е. 4, 6, 8 и т. д.). Первым оставшимся числом после 2 было 3. Далее
вычёркивались через два все числа, идущие после 3 (числа, кратные 3, т. е. 6, 9, 12 и т. д.). в конце концов оставались
невычеркнутыми только простые числа.
Он записывал все числа
от 1 до какого-то числа, а потом вычёркивал единицу, которая не является ни простым, ни составным числом, затем вычёркивал через
одно все числа, идущие после 2 (числа, кратные 2, т. е. 4, 6, 8 и т. д.). Первым оставшимся числом после 2 было 3. Далее
вычёркивались через два все числа, идущие после 3 (числа, кратные 3, т. е. 6, 9, 12 и т. д.). в конце концов оставались
невычеркнутыми только простые числа.
Математические выражения и задачи требуют множества дополнительных знаний. НОК — это одно из основных, особенно часто применяемое в Тема изучается в средней школе, при этом не является особо сложным в понимании материалом, человеку знакомому со степенями и таблицей умножения не составит труда выделить необходимые числа и обнаружить результат.
Определение
Общее кратное — число, способное нацело разделиться на два числа одновременно (а и b). Чаще всего, это число получают методом перемножения исходных чисел a и b. Число обязано делиться сразу на оба числа, без отклонений.
НОК — это принятое для обозначения краткое название, собранной из первых букв.
Способы получения числа
Для нахождения НОК не всегда подходит способ перемножения чисел, он гораздо лучше подходит для простых однозначных или двухзначных чисел. принято разделять на множители, чем больше число, тем больше множителей будет.
Пример № 1
Для простейшего примера в школах обычно берутся простые, однозначные или двухзначные числа. Например, необходимо решить следующее задание, найти наименьшее общее кратное от чисел 7 и 3, решение достаточно простое, просто их перемножить. В итоге имеется число 21, меньшего числа просто нет.
Пример № 2
Второй вариант задания гораздо сложнее. Даны числа 300 и 1260, нахождение НОК — обязательно. Для решения задания предполагаются следующие действия:
Разложение первого и второго чисел на простейшие множители. 300 = 2 2 * 3 * 5 2 ; 1260 = 2 2 * 3 2 *5 *7. Первый этап завершен.
Второй этап предполагает работу с уже полученными данными. Каждое из полученных чисел обязано участвовать в вычислении итогового результата. Для каждого множителя из состава исходных чисел берется самое большое число вхождений. НОК — это общее число, поэтому множители из чисел должны в нем повторятся все до единого, даже те, которые присутствуют в одном экземпляре. Оба изначальных числа имеют в своем составе числа 2, 3 и 5, в разных степенях, 7 есть только в одном случае.
Каждое из полученных чисел обязано участвовать в вычислении итогового результата. Для каждого множителя из состава исходных чисел берется самое большое число вхождений. НОК — это общее число, поэтому множители из чисел должны в нем повторятся все до единого, даже те, которые присутствуют в одном экземпляре. Оба изначальных числа имеют в своем составе числа 2, 3 и 5, в разных степенях, 7 есть только в одном случае.
Для вычисления итогового результата необходимо взять каждое число в наибольшей их представленных степеней, в уравнение. Остается только перемножить и получить ответ, при правильном заполнении задача укладывается в два действия без пояснений:
1) 300 = 2 2 * 3 * 5 2 ; 1260 = 2 2 * 3 2 *5 *7.
2) НОК = 6300.
Вот и вся задача, если попробовать вычислить нужное число посредством перемножения, то ответ однозначно не будет верным, так как 300 * 1260 = 378 000.
Проверка:
6300 / 300 = 21 — верно;
6300 / 1260 = 5 — верно.
Правильность полученного результата определяется посредством проверки — деления НОК на оба исходных числа, если число целое в обоих случаях, то ответ верен.
Что значит НОК в математике
Как известно, в математике нет ни одной бесполезной функции, эта — не исключение. Самым распространенным предназначением этого числа является приведение дробей к общему знаменателю. Что изучают обычно в 5-6 классах средней школы. Также дополнительно является общим делителем для всех кратных чисел, если такие условия стоят в задаче. Подобное выражение может найти кратное не только к двум числам, но и к гораздо большему количестве — трем, пяти и так далее. Чем больше чисел — тем больше действий в задаче, но сложность от этого не увеличивается.
Например, даны числа 250, 600 и 1500, необходимо найти их общее НОК:
1) 250 = 25 * 10 = 5 2 *5 * 2 = 5 3 * 2 — на этом примере детально описано разложение на множители, без сокращения.
2) 600 = 60 * 10 = 3 * 2 3 *5 2 ;
3) 1500 = 15 * 100 = 33 * 5 3 *2 2 ;
Для того чтобы составить выражение, требуется упомянуть все множители, в этом случае даны 2, 5, 3, — для всех этих чисел требуется определить максимальную степень.
Внимание: все множители необходимо доводить до полного упрощения, по возможности, раскладывая до уровня однозначных.
Проверка:
1) 3000 / 250 = 12 — верно;
2) 3000 / 600 = 5 — верно;
3) 3000 / 1500 = 2 — верно.
Данный метод не требует каких-либо ухищрений или способностей уровня гения, все просто и понятно.
Еще один способ
В математике многое связано, многое можно решить двумя и более способами, то же самое касается поиска наименьшего общего кратного, НОК. Следующий способ можно использовать в случае с простыми двузначными и однозначными числами. Составляется таблица, в которую вносятся по вертикали множимое, по горизонтали множитель, а в пересекающихся клетках столбца указывается произведение. Можно отразить таблицу посредством строчки, берется число и в ряд записываются результаты умножения этого числа на целые числа, от 1 до бесконечности, иногда хватает и 3-5 пунктов, второе и последующие числа подвергаются тому же вычислительному процессу. Все происходит вплоть до того, как найдется общее кратное.
Все происходит вплоть до того, как найдется общее кратное.
Даны числа 30, 35, 42 необходимо найти НОК, связывающий все числа:
1) Кратные 30: 60, 90, 120, 150, 180, 210, 250 и т. д.
2) Кратные 35: 70, 105, 140, 175, 210, 245 и т. д.
3) Кратные 42: 84, 126, 168, 210, 252 и т. д.
Заметно, что все числа достаточно разные, единственное общее среди них число 210, вот оно и будет НОК. Среди связанных с этим вычислением процессов есть также наибольший общий делитель, вычисляющийся по похожим принципам и часто встречающийся в соседствующих задачах. Различие невелико, но достаточно значимо, НОК предполагает вычисление числа, которое делится на все данные исходные значения, а НОД предполагает под собой вычисление наибольшего значение на которое делятся исходные числа.
Но многие натуральные числа делятся нацело ещё и на другие натуральные числа.
Например :
Число 12 делится на 1, на 2, на 3, на 4, на 6, на 12;
Число 36 делится на 1, на 2, на 3, на 4, на 6, на 12, на 18, на 36.
Числа, на которые число делится нацело (для 12 это 1, 2, 3, 4, 6 и 12) называются делителями числа . Делитель натурального числа a — это такое натуральное число, которое делит данное число a без остатка. Натуральное число, которое имеет более двух делителей, называется составным .
Обратите внимание, что числа 12 и 36 имеют общие делители. Это числа: 1, 2, 3, 4, 6, 12. Наибольший из делителей этих чисел — 12. Общий делитель двух данных чисел a и b — это число, на которое делятся без остатка оба данных числа a и b .
Общим кратным нескольких чисел называется число, которое делится на каждое из этих чисел. Например , числа 9, 18 и 45 имеют общее кратное 180. Но 90 и 360 — тоже их общие кратные. Среди всех jбщих кратных всегда есть наименьшее, в данном случае это 90. Это число называется наименьшим общим кратным (НОК) .
НОК всегда натуральное число, которое должно быть больше самого большого из чисел, для которых оно определяется.
Наименьшее общее кратное (НОК). Свойства.
Коммутативность:
Ассоциативность:
В частности, если и — взаимно-простые числа , то:
Наименьшее общее кратное двух целых чисел m и n является делителем всех других общих кратных m и n . Более того, множество общих кратных m, n совпадает с множеством кратных для НОК(m, n ).
Асимптотики для могут быть выражены через некоторые теоретико-числовые функции.
Так, функция Чебышёва . А также:
Это следует из определения и свойств функции Ландау g(n) .
Что следует из закона распределения простых чисел.
Нахождение наименьшего общего кратного (НОК).
НОК(a, b ) можно вычислить несколькими способами:
1. Если известен наибольший общий делитель , можно использовать его связь с НОК:
2. Пусть известно каноническое разложение обоих чисел на простые множители:
где p 1 ,…,p k — различные простые числа, а d 1 ,. ..,d k и e 1 ,…,e k — неотрицательные целые числа (они могут быть нулями, если соответствующее простое отсутствует в разложении).
..,d k и e 1 ,…,e k — неотрицательные целые числа (они могут быть нулями, если соответствующее простое отсутствует в разложении).
Тогда НОК (a ,b ) вычисляется по формуле:
Другими словами, разложение НОК содержит все простые множители , входящие хотя бы в одно из разложений чисел a, b , причём из двух показателей степени этого множителя берётся наибольший.
Пример :
Вычисление наименьшего общего кратного нескольких чисел может быть сведено к нескольким последовательным вычислениям НОК от двух чисел:
Правило. Чтобы найти НОК ряда чисел, нужно:
— разложить числа на простые множители;
— перенести во множители искомого произведения самое большое разложение (произведение множителей самого большого числа из заданных), а потом добавить множители из разложения других чисел, которые не встречаются в первом числе или стоят в нем меньшее число раз;
— полученное произведение простых множителей будет НОК заданных чисел.
Любые два и более натуральных чисел имеют свое НОК. Если числа не кратны друг другу или не имеют одинаковых множителей в разложении, то их НОК равно произведению этих чисел.
Простые множители числа 28 (2, 2, 7) дополнили множителем 3 (числа 21), полученное произведение (84) будет наименьшим числом, которое делится на 21 и 28 .
Простые множители наибольшего числа 30 дополнили множителем 5 числа 25, полученное произведение 150 больше самого большого числа 30 и делится на все заданные числа без остатка. Это наименьшее произведение из возможных (150, 250, 300…), которому кратны все заданные числа.
Числа 2,3,11,37 — простые, поэтому их НОК равно произведению заданных чисел.
Правило . Чтобы вычислить НОК простых чисел, нужно все эти числа перемножить между собой.
Еще один вариант:
Чтобы найти наименьшее общее кратное (НОК) нескольких чисел нужно:
1) представить каждое число как произведение его простых множителей, например:
504 = 2 · 2 · 2 · 3 · 3 · 7 ,
2) записать степени всех простых множителей:
504 = 2 · 2 · 2 · 3 · 3 · 7 = 2 3 · 3 2 · 7 1 ,
3) выписать все простые делители (множители) каждого из этих чисел;
4) выбрать наибольшую степень каждого из них, встретившуюся во всех разложениях этих чисел;
5) перемножить эти степени.
Пример . Найти НОК чисел: 168, 180 и 3024.
Решение . 168 = 2 · 2 · 2 · 3 · 7 = 2 3 · 3 1 · 7 1 ,
180 = 2 · 2 · 3 · 3 · 5 = 2 2 · 3 2 · 5 1 ,
3024 = 2 · 2 · 2 · 2 · 3 · 3 · 3 · 7 = 2 4 · 3 3 · 7 1 .
Выписываем наибольшие степени всех простых делителей и перемножаем их:
НОК = 2 4 · 3 3 · 5 1 · 7 1 = 15120.
Наибольший общий делитель и наименьшее общее кратное — ключевые арифметические понятия, которые позволяют без усилий оперировать обыкновенными дробями. НОК и чаще всего используются для поиска общего знаменателя нескольких дробей.
Основные понятия
Делитель целого числа X — это другое целое число Y, на которое X разделяется без остатка. К примеру, делитель 4 — это 2, а 36 — 4, 6, 9. Кратное целого X — это такое число Y, которое делится на X без остатка. К примеру, 3 кратно 15, а 6 — 12.
Для любой пары чисел мы можем найти их общие делители и кратные. К примеру, для 6 и 9 общим кратным является 18, а общим делителем — 3. Очевидно, что делителей и кратных у пар может быть несколько, поэтому при расчетах используется наибольший делитель НОД и наименьшее кратное НОК.
Очевидно, что делителей и кратных у пар может быть несколько, поэтому при расчетах используется наибольший делитель НОД и наименьшее кратное НОК.
Наименьший делитель не имеет смысла, так как для любого числа это всегда единица. Наибольшее кратное также бессмысленно, так как последовательность кратных устремляется в бесконечность.
Нахождение НОД
Для поиска наибольшего общего делителя существует множество методов, самые известные из которых:
- последовательный перебор делителей, выбор общих для пары и поиск наибольшего из них;
- разложение чисел на неделимые множители;
- алгоритм Евклида;
- бинарный алгоритм.
Сегодня в учебных заведениях наиболее популярными являются методы разложения на простые множители и алгоритм Евклида. Последний в свою очередь используется при решении диофантовых уравнений: поиск НОД требуется для проверки уравнения на возможность разрешения в целых числах.
Нахождение НОК
Наименьшее общее кратное точно также определяется последовательным перебором или разложением на неделимые множители. Кроме того, легко найти НОК, если уже определен наибольший делитель. Для чисел X и Y НОК и НОД связаны следующим соотношением:
Кроме того, легко найти НОК, если уже определен наибольший делитель. Для чисел X и Y НОК и НОД связаны следующим соотношением:
НОК (X,Y) = X × Y / НОД(X,Y).
Например, если НОД(15,18) = 3, то НОК(15,18) = 15 × 18 / 3 = 90. Наиболее очевидный пример использования НОК — поиск общего знаменателя, который и является наименьшим общим кратным для заданных дробей.
Взаимно простые числа
Если у пары чисел нет общих делителей, то такая пара называется взаимно простой. НОД для таких пар всегда равен единице, а исходя из связи делителей и кратных, НОК для взаимно простых равен их произведению. К примеру, числа 25 и 28 взаимно просты, ведь у них нет общих делителей, а НОК(25, 28) = 700, что соответствует их произведению. Два любых неделимых числа всегда будут взаимно простыми.
Калькулятор общего делителя и кратного
При помощи нашего калькулятора вы можете вычислить НОД и НОК для произвольного количества чисел на выбор. Задания на вычисление общих делителей и кратных встречаются в арифметике 5, 6 класса, однако НОД и НОК — ключевые понятия математики и используются в теории чисел, планиметрии и коммуникативной алгебре.
Примеры из реальной жизни
Общий знаменатель дробей
Наименьшее общее кратное используется при поиске общего знаменателя нескольких дробей. Пусть в арифметической задаче требуется суммировать 5 дробей:
1/8 + 1/9 + 1/12 + 1/15 + 1/18.
Для сложения дробей выражение необходимо привести к общему знаменателю, что сводится к задаче нахождения НОК. Для этого выберите в калькуляторе 5 чисел и введите значения знаменателей в соответствующие ячейки. Программа вычислит НОК (8, 9, 12, 15, 18) = 360. Теперь необходимо вычислить дополнительные множители для каждой дроби, которые определяются как соотношение НОК к знаменателю. Таким образом, дополнительные множители будут выглядеть как:
- 360/8 = 45
- 360/9 = 40
- 360/12 = 30
- 360/15 = 24
- 360/18 = 20.
После этого умножаем все дроби на соответствующий дополнительный множитель и получаем:
45/360 + 40/360 + 30/360 + 24/360 + 20/360.
Такие дроби мы можем легко суммировать и получить результат в виде 159/360. Сокращаем дробь на 3 и видим окончательный ответ — 53/120.
Сокращаем дробь на 3 и видим окончательный ответ — 53/120.
Решение линейных диофантовых уравнений
Линейные диофантовы уравнения — это выражения вида ax + by = d. Если отношение d / НОД(a, b) есть целое число, то уравнение разрешимо в целых числах. Давайте проверим пару уравнений на возможность целочисленного решения. Сначала проверим уравнение 150x + 8y = 37. При помощи калькулятора находим НОД (150,8) = 2. Делим 37/2 = 18,5. Число не целое, следовательно, уравнение не имеет целочисленных корней.
Проверим уравнение 1320x + 1760y = 10120. Используем калькулятор для нахождения НОД(1320, 1760) = 440. Разделим 10120/440 = 23. В результате получаем целое число, следовательно, диофантово уравнение разрешимо в целых коэффициентах.
Заключение
НОД и НОК играют большую роль в теории чисел, а сами понятия широко используются в самых разных областях математики. Используйте наш калькулятор для расчета наибольших делителей и наименьших кратных любого количества чисел.
После обновления ONTAP перестал работать агрегат LACP a0a на двух узлах кластера
- Последнее обновление
- Сохранить как PDF
- Просмотры:
- 217
- Видимость:
- Общедоступный
- голосов:
- 0
- Категория:
- FAS-Systems
- Специальность:
- HW
- Последнее обновление:
Применяется к
- Порты Qlogic CNA 8324 Обновление
- ONTAP до 9.7Px
- Расширитель коммутационной сети Cisco Nexus 2232PP 10 GE
- Расширитель коммутационной сети Cisco Nexus C2348UPQ 10 GE
Проблема
- Порты отсутствуют в
sysconfig -a
слот 0: 10-гигабитный Ethernet-контроллер IX1-SFP+ e0a MAC-адрес: 00:a0:98:55:75:6e (авто-10g_sr-fd-up) Поставщик SFP: AVAGO Номер детали SFP: AFBR-703SMZ-NA3 Серийный номер SFP: AD1404A08XT MAC-адрес e0b: 00:a0:98:55:75:6f (авто-10g_sr-fd-up) Поставщик SFP: AVAGO Номер детали SFP: AFBR-703SMZ-NA3 Серийный номер SFP: AD1404A08XN Тип устройства: 82599 Версия прошивки: 4.2-2 слот 0: контроллер Gigabit Ethernet 82580 e0f MAC-адрес: 00:a0:98:55:75:77 (auto-unknown-fd-down) MAC-адрес e0e: 00:a0:98:55:75:76 (авто-1000t-fd-up) Тип устройства: 1516 Версия прошивки: 3.1d 0x8000021A
- Порты видны в режиме обслуживания, но канал не работает
слот 0: 10-гигабитный Ethernet-контроллер IX1-SFP+
MAC-адрес e0a: 00:a0:98:56:45:54 (auto-unknown-fd-down)
MAC-адрес e0b: 00:a0:98:56:45:55 (auto-unknown-fd-down)
Тип устройства: 82599
Версия прошивки: 4.2-2
слот 0: Контроллер Ethernet 1G/10G CNA EP 8324
(двухпортовый, QLogic CNA 8324(8362) ред. 2)
e0d MAC-адрес: 00:a0:98:56:45:57 (авто-неизвестно-вниз)
e0c MAC-адрес: 00:a0:98:56:45:56 (авто-неизвестно-вниз)
Тип устройства: EP8324N
Версия прошивки: 5.4.66.0
слот 0: контроллер Gigabit Ethernet 82580
e0f MAC-адрес: 00:a0:98:56:45:5d (авто-неизвестно-fd-вниз)
MAC-адрес e0e: 00:a0:98:56:45:5c (авто-1000t-fd-up)
Тип устройства: 1516
Версия прошивки: 3. 1d 0x8000021A
1d 0x8000021A
- Порты были видны в предыдущей версии ONTAP
слот 0: 10-гигабитный Ethernet-контроллер IX1-SFP+ e0a MAC-адрес: 00:a0:98:55:75:6e (авто-10g_sr-fd-up) Поставщик SFP: AVAGO Номер детали SFP: AFBR-703SMZ-NA3 Серийный номер SFP: AD1404A08XT e0b MAC-адрес: 00:a0:98:55:75:6f (авто-10g_sr-fd-up) Поставщик SFP: AVAGO Номер детали SFP: AFBR-703SMZ-NA3 Серийный номер SFP: AD1404A08XN Тип устройства: 82599 Версия прошивки: 4.2-2 слот 0: Контроллер Ethernet 1G/10G CNA EP 8324 (двухпортовый, QLogic CNA 8324(8362) ред. 2) e0d MAC-адрес: 02:a0:98:55:75:79 (auto-10g_twinax-fd-up) MAC-адрес e0c: 02:a0:98:55:75:79 (авто-10g_twinax-fd-up) Тип устройства: EP8324N Версия прошивки: 5.4.66.0 слот 0: контроллер Gigabit Ethernet 82580 e0f MAC-адрес: 00:a0:98:55:75:77 (auto-unknown-fd-down) MAC-адрес e0e: 00:a0:98:55:75:76 (авто-1000t-fd-up) Тип устройства: 1516 Версия прошивки: 3.1d 0x8000021A
- Порты подключены к Cisco Nexus FEX (удлинитель ткани)
Войдите, чтобы просмотреть все содержимое этой статьи базы знаний.
Впервые в NetApp?
Узнайте больше о нашей отмеченной наградами поддержке
NetApp не дает никаких заверений или гарантий в отношении точности, надежности или пригодности к использованию какой-либо информации или рекомендаций, представленных в данной публикации, или в отношении любых результатов, которые могут быть получены при использовании информации или соблюдении каких-либо рекомендаций, представленных в данной публикации. Информация в этом документе распространяется КАК ЕСТЬ, и использование этой информации или реализация любых рекомендаций или методов, изложенных в данном документе, является обязанностью заказчика и зависит от способности заказчика оценить и интегрировать их в операционную среду заказчика. Этот документ и содержащаяся в нем информация могут использоваться исключительно в связи с продуктами NetApp, обсуждаемыми в этом документе.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Артикул
- Уверенность
- Утверждено
- Флаг
- Ложь
- Управление
- Опыт
- KCS включен
- Да
- Видимость
- Общедоступный
- Категории товаров
- Системы ФАС
- Специальность
- ГВ
- Теги
- 2008
2
- 2008
Двоичное дерево поиска | Пример | Строительство
Двоичное дерево-
Прежде чем читать эту статью, убедитесь, что вы прочитали предыдущую статью о Двоичных деревьях .
Мы обсудили-
- Двоичное дерево — это специальная древовидная структура данных.
- В бинарном дереве каждый узел может иметь не более двух дочерних элементов.
- В бинарном дереве узлы могут располагаться в произвольном порядке.
В этой статье мы обсудим бинарные деревья поиска.
Двоичное дерево поиска-
| Двоичное дерево поиска — это особый вид двоичного дерева, в котором узлы расположены в определенном порядке. |
В бинарном дереве поиска (BST) каждый узел содержит-
- Только меньшие значения в его левом поддереве
- Только большие значения в его правом поддереве
Example-
Number of Binary Search Trees-
Example-
Number of distinct binary search trees possible with 3 Отличительные ключи
= 2 × 3 C 3 /3+1
= 6 C 3 /4
= 5
IF Three Consult A A — B и C, затем B и C, затем B и C и C, затем B и C и C и C -Keyys, затем B и C и C и C -Keyys A, затем B и C и C и C -Keyys A — B и C, а затем — это. 5 различных бинарных деревьев поиска:
5 различных бинарных деревьев поиска:
Binary Search Tree Construction-
Let us understand the construction of a binary search tree using the following example-
Example-
Construct a Binary Search Дерево (BST) для следующей последовательности чисел:
50, 70, 60, 20, 90, 10, 40, 100
Когда элементы даны в последовательности,
- Всегда считать первый элемент корневым узлом.
- Рассмотрите данные элементы и вставьте их в BST один за другим.
The binary search tree will be constructed as explained below-
Insert 50-
Insert 70-
- As 70 > 50, so insert 70 справа от 50.
Insert 60-
- As 60 > 50, so insert 60 to the right of 50.

- As 60 < 70, so insert 60 to the left of 70.
Insert 20-
- As 20 < 50, so insert 20 to the left of 50.
Insert 90-
- As 90 > 50, поэтому вставьте 90 справа от 50.
- AS 90> 70, SO Вставьте 90 справа от 70.
- AS 10, так что 100329
- AS 10, SO ASTERT 100091
- AS 10, SO ASTER. Слева от 50.
- AS 10 <20, так же вставьте 10 слева от 20.
- AS 40 <50, так носите слева от 50.
- Поскольку 40 > 20, вставьте 40 справа от 20.
- AS 100> 50, так что вставьте 100 справа от 50.

- AS 100> 70, So Insert 100 до 70.1010 10101010101010101010101010101010101010101010101010101010101010101010101010101010101010101
- Поскольку 100 > 90, вставьте 100 справа от 90.
Это требуемое двоичное дерево поиска.
Чтобы лучше понять двоичные деревья поиска,
Посмотрите эту видео-лекцию
Практические задачи на основе бинарных поисковых деревьев- Проблема-01:ABIN
50, 15, 62, 5, 20, 58, 91, 3, 8, 37, 60, 24
Количество узлов в левом и правом поддеревьях корня соответственно _____.
- (4, 7)
- (7, 4)
- (8, 3)
- (3, 8)
Решение-, Используя рассмотренное выше бинарное дерево поиска, построим шаги, описанные выше.
Результирующее бинарное дерево поиска будет:
Таким образом, вариант (Б) верен.

Задача-02:Сколько различных двоичных деревьев поиска можно построить из 4 различных ключей?
- 5
- 14
- 24
- 35
Solution-Number of distinct binary search trees possible with 4 distinct keys
= 2n C n / n+ 1
= 2×4 C 4 / 4+1
= 8 C 4 / 5
= 14
, таким образом, правильный вариант
, 900.
Задача-03:Числа 1, 2, …, n вставлены в двоичное дерево поиска в некотором порядке. В полученном дереве правое поддерево корня содержит p узлов. Первое число, которое будет вставлено в дерево, должно быть —
- p
- p+1
- N-P
- N-P+1
LET N = 4 и P = 3.

Тогда даны варианты уменьшить до
- 9003 3
- 1
- 2
, даны варианты.
Наше двоичное дерево поиска будет таким, как показано на рисунке:
Таким образом, первое вставленное число = 90,091.
Задача-04:Нам дан набор из n различных элементов и непомеченное двоичное дерево с n узлами. Сколькими способами можно заполнить дерево данным набором так, чтобы оно стало бинарным деревом поиска?
- 0
- 1
- н!
- C(2n, n) / n+1
Решение-Вариант (Б) правильный.
Чтобы посмотреть видео решения и попрактиковаться в других задачах,
Посмотрите эту видео-лекцию
Скачать Рукописные примечания здесьСледующая статья- 9691
Следующая статья- 691
Следующая статья- 6691
Следующая статья- 66691
Следующая статья- 666696 Binar
.
 Структуры данных .
Структуры данных .Смотрите видеолекции, посетив наш канал YouTube LearnVidFun .
Резюме
Сравнение N- и О-связанных гликопептидов клеток лимфатических узлов мышей C57 BL/6 lpr/lpr и C57 BL/6
Сравнительное исследование
. 1992;14(1):45-56.
дои: 10.3109/08
- AS 10, SO ASTERT 100091
- 93056.
С Ди Виргилио 1 , Э. Монтесино-Родригес, М. Рампельберг, Г. Шнек, Р. Хуге, Ф. Лоор
принадлежность
- 1 Laboratoire de Chimie Générale I, CP160, Unité de Recherche des Glycoprotéines, Свободный университет Брюсселя, Бельгия.
- PMID: 1299347
- DOI:
10.
 3109/08
3109/08 - 93056
Сравнительное исследование
S Di Virgilio et al. Аутоиммунитет. 1992.
. 1992;14(1):45-56.
дои: 10.3109/08
- 93056.
Авторы
С Ди Виргилио 1 , Э. Монтесино-Родригес, М. Рампельберг, Г. Шнек, Р. Хуге, Ф. Лоор
принадлежность
- 1 Laboratoire de Chimie Générale I, CP160, Unité de Recherche des Glycoprotéines, Свободный университет Брюсселя, Бельгия.
- PMID: 1299347
- DOI:
10.
 3109/08
3109/08 - 93056
Абстрактный
Мы проверили гипотезу о том, что некоторые фенотипические характеристики лимфоцитов мышей с лимфопролиферативным заболеванием (ЛПР) можно объяснить аномальным гликозилированием мембранных белков. Клетки лимфатических узлов от нормальных мышей C57 BL/6 и от мышей C57 BL/lpr метили тритиевыми сахарами. Мембранные белки высвобождались трипсином, затем проназой. После полного расщепления проназой гликопептиды сначала разделяли на Bio Gel P-6, а затем на Con A-Sepharose. Фракции, не связывающиеся с Con A (отрицательные по Con A), также разделяли на агглютинин-сефарозе Lens culinaris. Были замечены заметные различия между нормальными клетками и клетками lpr. Во-первых, на клетках lpr было больше меченых глюкозамином пептидов с очень высокой молекулярной массой (быстро элюирующихся на Bio Gel P-6), чем на нормальных лимфоцитах. Во-вторых, доля меченных маннозой пептидов, связывающихся с Con A, была меньше в клетках lpr.
 В-третьих, среди Con A-негативных пептидов доля связывания с агглютинином Lens culinaris была выше в клетках lpr. Таким образом, клетки lpr, по-видимому, несут больше альфа-1-6 фукозилированных цепей и углеводов большего размера. Эти изменения также были подтверждены гель-электрофорезом лектин-селектированных йодированных антигенов клеточной поверхности и, по-видимому, ограничены очень ограниченным числом пептидов. Таким образом, могут иметь место первичные изменения гликозилирования в клетках lpr. Альтернативно, характер гликозилирования клеток lpr может быть характерен для субпопуляции Т-лимфоцитов, размножающейся при этом заболевании, или для определенной стадии активации. Большая доля Con A-негативных, Lens culinaris-позитивных пептидов является довольно необычной особенностью мышиных клеток и требует дальнейшего изучения.
В-третьих, среди Con A-негативных пептидов доля связывания с агглютинином Lens culinaris была выше в клетках lpr. Таким образом, клетки lpr, по-видимому, несут больше альфа-1-6 фукозилированных цепей и углеводов большего размера. Эти изменения также были подтверждены гель-электрофорезом лектин-селектированных йодированных антигенов клеточной поверхности и, по-видимому, ограничены очень ограниченным числом пептидов. Таким образом, могут иметь место первичные изменения гликозилирования в клетках lpr. Альтернативно, характер гликозилирования клеток lpr может быть характерен для субпопуляции Т-лимфоцитов, размножающейся при этом заболевании, или для определенной стадии активации. Большая доля Con A-негативных, Lens culinaris-позитивных пептидов является довольно необычной особенностью мышиных клеток и требует дальнейшего изучения.Похожие статьи
Влияние монензина на остановку передачи крови и гликозилирование клеток лимфомы BL/VL3.

Ди Вирхилио С., Рампельберг М., Граймерс Р., Шнек Г., Хуге Р. Ди Вирджилио С. и др. Клеточная биохимия Функц. 1992 март; 10(1):41-52. doi: 10.1002/cbf.2
108. Клеточная биохимия Функц. 1992. PMID: 1349514Сравнение N-связанных гликопептидов молекул DQw1 и DR1.
Итурбе С., Нарасимхан С., Меррик Дж. М., Фальк Дж. А., Летарте М. Итурбе С. и др. Дж Иммунол. 1986 15 июня; 136 (12): 4588-95. Дж Иммунол. 1986 год. PMID: 3486905
Фенотипические, функциональные и молекулярно-генетические сравнения аномальных лимфоидных клеток мышей C3H-lpr/lpr и C3H-gld/gld.
Дэвидсон В.Ф., Дюмон Ф.Дж., Бедигиан Х.Г., Фаулкс Б.Дж., Морс Х.К. 3-й. Дэвидсон В.Ф. и соавт. Дж Иммунол. 1986 1 июня; 136 (11): 4075-84.
 Дж Иммунол. 1986 год.
PMID: 3009614
Дж Иммунол. 1986 год.
PMID: 3009614N-связанные олигосахариды рецептора трансферрина мыши из клеточной линии плазмоцитомы. Сравнение с общими клеточными N-гликанами.
Глисон Пенсильвания, Диас В. Глисон П.А. и соавт. Биохим Биофиз Акта. 1990 12 октября; 1036(1):47-54. doi: 10.1016/0304-4165(90)
-ф. Биохим Биофиз Акта. 1990. PMID: 2223825
Клональный анализ гликозилирования иммуноглобулина G, секретируемого мышиными гибридомами.
Ротман Р.Дж., Уоррен Л., Флигентхарт Дж.Ф., Хард К.Дж. Ротман Р.Дж. и соавт. Биохимия. 1989 г., 7 февраля; 28 (3): 1377-84. doi: 10.1021/bi00429a065. Биохимия. 1989. PMID: 2713370
Посмотреть все похожие статьи
Типы публикаций
термины MeSH
вещества
Вирус папилломы человека и рак шейки матки
1.
 Адам Э., З. Беркова, З. Дакснерова, Дж. Айсногл, У. К. Ривз и Р. Х. Кауфман. 2000. Обнаружение вируса папилломы: демографические и поведенческие характеристики, влияющие на выявление заболевания шейки матки. Являюсь. Дж. Обст. Гинекол. 182 : 257-264. [PubMed] [Google Scholar]
Адам Э., З. Беркова, З. Дакснерова, Дж. Айсногл, У. К. Ривз и Р. Х. Кауфман. 2000. Обнаружение вируса папилломы: демографические и поведенческие характеристики, влияющие на выявление заболевания шейки матки. Являюсь. Дж. Обст. Гинекол. 182 : 257-264. [PubMed] [Google Scholar]2. Аллен М., М. Калантари, Н. Илитало, Б. Петтерссон, Б. Хагмар, Л. Шайбенплаг, Б. Йоханссон, У. Петтерсон и У. Гилленстен. 1996. Гаплотип HLA DQ-DR и предрасположенность к раку шейки матки: признаки повышенного риска развития рака шейки матки у лиц, инфицированных ВПЧ 18. Тканевые антигены 48 : 32-37. [PubMed] [Google Scholar]
3. Андерссон С., Э. Риландер, Б. Ларссон, А. Стрэнд, К. Сильфверсвард и Э. Виландер. 2001. Роль вируса папилломы человека в канцерогенезе аденокарциномы шейки матки. Евро. Дж. Рак 37 : 246-250. [PubMed] [Google Scholar]
4. Андрей Г., Р. Снок, Дж.
 Пиетт, П. Делвенн и Э. ДеКлерк. 1998. Антипролиферативное действие ациклических нуклеозидфосфонатов на клеточные линии, несущие вирус папилломы человека (ВПЧ), по сравнению с ВПЧ-отрицательными клеточными линиями. Онкол. Рез. 10 : 523-531. [PubMed] [Google Scholar]
Пиетт, П. Делвенн и Э. ДеКлерк. 1998. Антипролиферативное действие ациклических нуклеозидфосфонатов на клеточные линии, несущие вирус папилломы человека (ВПЧ), по сравнению с ВПЧ-отрицательными клеточными линиями. Онкол. Рез. 10 : 523-531. [PubMed] [Google Scholar]5. Apple R. J., TM Becker, CM Wheeler и HA Erlich. 1995. Сравнение ассоциации человеческого лейкоцитарного антигена DR-DQ с дисплазией шейки матки и инвазивной карциномой шейки матки. Дж. Натл. Рак инст. 87 : 427-436. [PubMed] [Google Scholar]
6. Апт, Д., Р. М. Уоттс, Г. Суске и У. Бернард. 1996. Высокие отношения Sp1/Sp3 в эпителиальных клетках во время эпителиальной дифференцировки и клеточной транскрипции коррелируют с активацией промотора HPV-16. Вирусология 224 : 281-291. [PubMed] [Google Scholar]
7. Остин Р. М. и И. Рамзи. 1998. Улучшенное обнаружение аномалий эпителиальных клеток с помощью жидких гинекологических цитологических препаратов.
 Акта Цитол. 42 : 178-184. [PubMed] [Google Scholar]
Акта Цитол. 42 : 178-184. [PubMed] [Google Scholar]8. Бейкер, Т. С., У. В. Ньюкомб, Н. Х. Олсон, Л. М. Каусерт, К. Олсон и Дж. К. Браун. 1991. Структуры вирусов папилломы крупного рогатого скота и человека. Анализ методом криоэлектронной микроскопии и реконструкция трехмерного изображения. Биофиз. Дж. 60 : 1445-1456. [Бесплатная статья PMC] [PubMed] [Google Scholar]
9. Боденон, С., Д. Кремсдорф, О. Круассан, С. Яблонска, С. Уэйн-Хобсон и Г. Орт. 1986. Новый тип вируса папилломы человека, ассоциированный с генитальными неоплазиями. Природа 321 : 246-249. [PubMed] [Google Scholar]
10. Beaudenon, S., D. Kremsdorf, S. Obalek, S. Jablonska, G. Pehau-Amaudet, O. Croissant и G. Orth. 1987. Множественность генитальных папилломавирусов человека: характеристика двух новых типов с различными биологическими свойствами. Вирусология 161 : 373-384.
 [PubMed] [Google Scholar]
[PubMed] [Google Scholar]11. Беделл, М. А., Дж. Б. Хадсон, Т. Р. Голуб, М. Э. Турик, М. Хоскен, Г. Д. Уилбэнкс и Л. А. Лайминс. 1991. Амплификация геномов вируса папилломы человека in vitro зависит от дифференцировки эпителия. Дж. Вирол. 65 : 2254-2260. [Бесплатная статья PMC] [PubMed] [Google Scholar]
12. Bonnez, W., and RC Reichman. 2000. Папилломавирусы, с. 1630-1640 гг. В Г. Л. Манделл, Дж. Э. Беннетт и Р. Долин (ред.), Принципы и практика инфекционных заболеваний Манделла, Дугласа и Беннета, 5-е изд. Черчилль Ливингстон, Филадельфия, Пенсильвания,
13. Бонткес, Х. Дж., М. Ван Дуин, Т. Д. де Груйл, М. Ф. Дагган-Кин, Дж. М. Уолбумерс, М. Дж. Стукарт, Р. Х. Верехейен, Т. Дж. Хелмерхорст, С. Дж. Мейер, Р. Дж. Шепер, Ф. Р. Стивенс, П. А. Дайер, П. Синнотт и П. Л. Стерн. 1998. Инфекция ВПЧ 16 и прогрессирование цервикальной интраэпителиальной неоплазии: анализ полиморфизма HLA и вариантов последовательностей Е6 ВПЧ 16.
 Междунар. Дж. Рак 78 : 166-171. [PubMed] [Google Scholar]
Междунар. Дж. Рак 78 : 166-171. [PubMed] [Google Scholar]14. Bontkes, HJ, TD deGruijl, JM Walboomers, JT Schiller, J. Dillner, TJ Helmerhorst, RH Vereheijen, RJ Scheper и CJ Meijer. 1999. Иммунный ответ против вирусоподобных частиц папилломавируса человека (ВПЧ) типа 16 в когортном исследовании женщин с цервикальной интраэпителиальной неоплазией. II. Системные, но не локальные ответы IgA коррелируют с клиренсом ВПЧ-16. Дж. Генерал Вирол. 80 : 409-417. [PubMed] [Google Scholar]
15. Бош, Ф., М. М. Манос, Н. Муньос, М. Шерман, А. М. Янсен, Дж. Пето, М. Х. Шиффман, В. Морено, Р. Курман, К. В. Шах и Международное биологическое исследование рака шейки матки (IBSCC). Исследовательская группа. 1995. Распространенность вируса папилломы человека при раке шейки матки: мировая перспектива. Дж. Натл. Рак инст. 87 : 796-802. [PubMed] [Google Scholar]
16. Бриссон, Дж., К.
 Морен, М. Фортье, М. Рой, К. Бушар, Дж. Леклерк, А. Кристен, К. Гимон, Ф. Пено и А. , Майзельс. 1994. Факторы риска цервикальной интраэпителиальной неоплазии: различия между поражениями низкой и высокой степени. Являюсь. Дж. Эпидемиол. 40 : 700-710. [PubMed] [Академия Google]
Морен, М. Фортье, М. Рой, К. Бушар, Дж. Леклерк, А. Кристен, К. Гимон, Ф. Пено и А. , Майзельс. 1994. Факторы риска цервикальной интраэпителиальной неоплазии: различия между поражениями низкой и высокой степени. Являюсь. Дж. Эпидемиол. 40 : 700-710. [PubMed] [Академия Google]17. Broder, S. 1992. Система Bethesda для отчетности о цервикальном/влагалищном цитологическом диагнозе — отчет семинара Bethesda 1991 года. JAMA 267 : 1892. [Google Scholar]
18. Burk, R.D., P. Kelly, J. Feldman, J. Bromberg, S.H. Vermund, J.A. Deltovitz, and S.H. Landesman. 1996. Снижение частоты цервиковагинальной папилломавирусной инфекции человека с возрастом не зависит от других факторов риска. Секс. Трансм. Дис. 23 : 333-341. [PubMed] [Академия Google]
19. Калор, Э. Э., С. М. М. Перейра и М. Дж. Кавальер. 2001. Прогрессирование поражения шейки матки у ВИЧ-серопозитивных женщин: цитологическое исследование.
 Диагн. Цитопатол. 24 : 117-119. [PubMed] [Google Scholar]
Диагн. Цитопатол. 24 : 117-119. [PubMed] [Google Scholar]20. Кейтс, В., и комиссия Американской ассоциации социального здравоохранения. 1999. Оценки заболеваемости и распространенности заболеваний, передающихся половым путем, в Соединенных Штатах. Секс. Трансм. Дис. 26 : S2-S7. [PubMed] [Академия Google]
21. Чан, П. К., М. Ю. Чан, В. В. Ли, Д. П. Чан, Дж. Л. Ченг и А. Ф. Ченг. 2001. Ассоциация бета-герпесвирусов человека с развитием рака шейки матки: свидетели или кофакторы? Дж. Клин. Патол. 54 : 48-53. [Бесплатная статья PMC] [PubMed] [Google Scholar]
22. Chang, YE, and L.A. Laimins. 2000. Микроматричный анализ идентифицирует гены, индуцируемые интерфероном, и Stat-1 в качестве основных мишеней транскрипции вируса папилломы человека типа 31. J. Virol. 74 : 4174-4182. [Бесплатная статья PMC] [PubMed] [Google Scholar]
23.
 Чен, М., Н. Попеску, К. Вудворт, З. Бернеман, М. Корбеллино, П. Луссо, Д. В. Аблаши и Дж. А. ДиПаоло. 1994. Вирус герпеса человека 6 инфицирует эпителиальные клетки шейки матки и трансактивирует экспрессию генов вируса папилломы человека. Дж. Вирол. 68 : 1173-1178. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Чен, М., Н. Попеску, К. Вудворт, З. Бернеман, М. Корбеллино, П. Луссо, Д. В. Аблаши и Дж. А. ДиПаоло. 1994. Вирус герпеса человека 6 инфицирует эпителиальные клетки шейки матки и трансактивирует экспрессию генов вируса папилломы человека. Дж. Вирол. 68 : 1173-1178. [Бесплатная статья PMC] [PubMed] [Google Scholar]24. Chua, K.L., and A. Hjerpe. 1996. Персистенция вируса папилломы человека (ВПЧ), предшествующая раку шейки матки. Рак 77 : 121-127. [PubMed] [Google Scholar]
25. Поправки об улучшении клинических лабораторий 1988 г. 1988 г. П.Л. 100-578. Конгресс. Рек. 134 : 3828-3863. [Google Scholar]
26. Кокер А. Л., Рассел Р. Б., Бонд С. М., Пиризи Л., Лю Ю., Мане М., Кокорина Н., Герасимова Т., Гермонат П. Л. 2001. Аденоассоциированный вирус связан с более низким риском неоплазии шейки матки высокой степени. Эксп. Мол. Патол. 70 : 83-89.
 [ПубМед]
[ПубМед]27. Conrad-Stöppler, M.C., K. Ching, H. Stöppler, K. Clancy, R. Schlegle и J. Icenogle. 1996. Природные варианты белка Е6 вируса папилломы человека типа 16 различаются по своей способности изменять дифференцировку кератиноцитов и индуцировать деградацию р53. Дж. Вирол. 70 : 6987-6993. [Бесплатная статья PMC] [PubMed] [Google Scholar]
28. Куби, Х. А., А. Л. Сигар, Г. Дж. Битти, С. Монаган и А. Р. В. Уильямс. 2000. Продольное исследование выявления ВПЧ и патологии шейки матки у ВИЧ-инфицированных женщин. Секс. Трансм. Заразить. 76 : 257-261. [Бесплатная статья PMC] [PubMed] [Google Scholar]
29. Davey, D.D., S. Naryskin., ML Nielsen, and TS Kline. 1994. Атипичные плоскоклеточные клетки неопределенного значения: межлабораторное сравнение и контроль качества. Диагн. Цитопатол. 11 : 390-396. [PubMed] [Google Scholar]
30. ДеВиллес Р.
 Л. и К.С. Стивенс. 1980. Бовеноидный папулез гениталий. Случай, прогрессирующий до болезни Боуэна. Варенье. акад. Дерматол. 3 : 149-152. [PubMed] [Google Scholar]
Л. и К.С. Стивенс. 1980. Бовеноидный папулез гениталий. Случай, прогрессирующий до болезни Боуэна. Варенье. акад. Дерматол. 3 : 149-152. [PubMed] [Google Scholar]31. Ссылка удалена.
32. Донг, X.-P., Ф. Штубенраух, Э. Бейер-Финклер и Х. Пфистер. 1994. Распространенность делеций сайтов связывания YY1 в эписомальной ДНК ВПЧ 16 при раке шейки матки. Междунар. Дж. Рак 58 : 803-808. [PubMed] [Google Scholar]
33. Evander, M., IH Frazer, E. Payne, YM Qui, K. Hengst, and N.A. McMillan. 1997. Идентификация интегрина альфа6 в качестве потенциального рецептора папилломавирусов. Дж. Вирол. 71 : 2449-2456. [Статья бесплатно PMC] [PubMed] [Google Scholar]
34. Favre, M. 1975. Структурные полипептиды вирусов папилломы кролика, крупного рогатого скота и человека. Дж. Вирол. 15 : 1239-1247. [Бесплатная статья PMC] [PubMed] [Google Scholar]
35.
 Флорес, Э. Р. и П. Ф. Ламберт. 1997. Доказательства переключения режима репликации ДНК вируса папилломы человека типа 16 во время жизненного цикла вируса. Дж. Вирол. 71 : 7167-7179. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Флорес, Э. Р. и П. Ф. Ламберт. 1997. Доказательства переключения режима репликации ДНК вируса папилломы человека типа 16 во время жизненного цикла вируса. Дж. Вирол. 71 : 7167-7179. [Бесплатная статья PMC] [PubMed] [Google Scholar]36. Флорес, Э. Р., Б. Л. Аллен-Хоффман, Д. Ли, К. А. Сэттлер и П. Ф. Ламберт. 1999. Установление жизненного цикла вируса папилломы человека типа 16 (ВПЧ-16) в иммортализованной линии клеток кератиноцитов крайней плоти человека. Вирусология 262 : 344-354. [PubMed] [Google Scholar]
37. Franco, EL 1995. Новый взгляд на причины рака: вирус папилломы человека и неоплазия шейки матки. Дж. Натл. Рак инст. 87 : 779-780. [PubMed] [Академия Google]
38. Fuchs, P.G., F. Girardi, and H. Pfister. 1988. ДНК вируса папилломы человека в нормальном, метапластическом, предопухолевом и неопластическом эпителиях шейки матки.
 Междунар. Дж. Рак 41 : 41-45. [PubMed] [Google Scholar]
Междунар. Дж. Рак 41 : 41-45. [PubMed] [Google Scholar]39. Джанноудис А. и К. С. Херрингтон. 2001. Варианты вируса папилломы человека и плоскоклеточная неоплазия шейки матки. Дж. Патол. 193 : 295-302. [PubMed] [Google Scholar]
40. Gilbert, DM, and S.N. Cohen. 1987. Плазмиды бычьего папилломавируса случайным образом реплицируются в мышиных фибробластах на протяжении S фазы клеточного цикла. Сотовый 50 : 59-68. [PubMed] [Google Scholar]
41. Гироглу Т., Л. Флорин, Ф. Шефер, Р. Э. Стрик и М. Сапп. 2001. Для инфицирования вирусом папилломы человека требуется гепарансульфат клеточной поверхности. Дж. Вирол. 75 : 1565-1570. [Бесплатная статья PMC] [PubMed] [Google Scholar]
42. Gissmann, L., L. Wolnik, H. Ikenberg, U. Koldovsky, H.G. Schnurch и H. zur Hausen. 1983. Последовательности ДНК вирусов папилломы человека типов 6 и 11 в папилломах половых органов и гортани, а также при некоторых видах рака шейки матки.
 проц. Натл. акад. науч. США 80 : 560-563. [Бесплатная статья PMC] [PubMed] [Google Scholar]
проц. Натл. акад. науч. США 80 : 560-563. [Бесплатная статья PMC] [PubMed] [Google Scholar]43. Гонсалес, Д. И., К. М. Зан, М. Г. Рецлофф, В. Ф. Мур, Э. Р. Кост и Р. Р. Снайдер. 2001. Рецидив дисплазии после петлевой электроэксцизии с отдаленным наблюдением. Являюсь. Дж. Обст. Гинекол. 184 : 315-321. [PubMed] [Академия Google]
44. Халберт, К.Л., Г.В. Демерс и Д.А. Галлоуэй. 1991. Гена Е7 вируса папилломы человека типа 16 достаточно для иммортализации эпителиальных клеток человека. Дж. Вирол. 65 : 473-478. [Бесплатная статья PMC] [PubMed] [Google Scholar]
45. Harro, C.D., Y.-Y. С. Панг, Р. Б. С. Роден, А. Хильдесхайм, З. Ван, М. Дж. Рейнольдс, Т. К. Маст, Р. Робинсон, Б. Р. Мерфи, Р. А. Каррон, Дж. Диллнер, Дж. Т. Шиллер и Д. Р. Лоуи. 2001. Испытание безопасности и иммуногенности вакцины на основе вирусоподобных частиц вируса папилломы человека 16 L1 на взрослых добровольцах.
 Дж. Натл. Рак инст. 93 : 284-292. [PubMed] [Google Scholar]
Дж. Натл. Рак инст. 93 : 284-292. [PubMed] [Google Scholar]46. Хильдесхайм, А., М. Шиффман, К. Бромли, С. Вакхолдер, Р. Эрреро, А. К. Родриус, М. К. Братти, М. Э. Шерман, У. Скарпидис, Q.-Q . Лин, М. Тераи, Р. Л. Бромли, К. Буэтоу, Р. Дж. Эппл и Р. Д. Берк. 2001. Варианты вируса папилломы человека 16 типа и риск рака шейки матки. Дж. Натл. Рак инст. 93 : 315-318. [PubMed] [Google Scholar]
47. Ho, G.Y., R. Bierman, L. Beardsley, CJ Chang, and RD Burk. 1998. Естественное течение цервиковагинальной папилломавирусной инфекции у молодых женщин. Н. англ. Дж. Мед. 338 : 413-428. [PubMed] [Google Scholar]
48. Holowaty, P., A.B. Miller, T. Rohan, and T.To. 1999. Естественная дисплазия шейки матки. Дж. Натл. Рак инст. 91 : 252-258. [PubMed] [Google Scholar]
49. Howell, LP, RL Davis, TI Belk, R. Agdigos, and J. Lowe. 1998.
 Система подготовки AutoCyte для гинекологического цитологического исследования. Акта Цитол. 42 : 171-177. [PubMed] [Google Scholar]
Система подготовки AutoCyte для гинекологического цитологического исследования. Акта Цитол. 42 : 171-177. [PubMed] [Google Scholar]50. Hummel, M., JB Hudson, and L.A. Laimins. 1992. Индуцированная дифференцировкой и конститутивная транскрипция вируса папилломы человека типа 31b в клеточных линиях, содержащих вирусные эписомы. Дж. Вирол. 66 : 6070-6080. [Бесплатная статья PMC] [PubMed] [Google Scholar]
51. Хатчинсон, М. Л., Л. М. Изенштейн, А. Гудман, А. А. Херли, К. Л. Дуглас, К. К. Муи, Ф. В. Паттен и Д. Дж. Захнисер. 1994. Однородная выборка обеспечивает повышенную точность диагностики при использовании процессора ThinPrep. Являюсь. Дж. Клин. Патол. 101 : 215-219. [PubMed] [Google Scholar]
52. Джейкобс, М. В., П. Дж. Снейдерс, А. Дж. ван ден Брюле, Т. Дж. Хелмерхорст, К. Дж. Мейер и Дж. М. Уолбумерс. 1997. Общий метод иммуноферментного ПЦР-опосредованного праймера P5+/GP6(+) для быстрого выявления 14 генотипов вируса папилломы человека высокого риска и 6 генотипов вируса папилломы человека низкого риска в соскобах шейки матки.
 Дж. Клин. микробиол. 35 : 791-795. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Дж. Клин. микробиол. 35 : 791-795. [Бесплатная статья PMC] [PubMed] [Google Scholar]53. Чон С., Б. Л. Аллен-Хоффман и П. Ф. Ламберт. 1995. Интеграция вируса папилломы человека типа 16 в геном человека коррелирует с избирательным преимуществом клеток в росте. Дж. Вирол. 69 : 2989-2997. [Бесплатная статья PMC] [PubMed] [Google Scholar]
54. Jin, X.W., J. Cash и A.W. Kennedy. 1999. Типирование вируса папилломы человека и снижение риска рака шейки матки. Кливленд Клин. Дж. Мед. 66 : 533-539. [PubMed] [Google Scholar]
55. Джойс, Дж. Г., Дж.-С. Тунг, К. Т. Пшисецкий, Дж. К. Кук, Э. Д. Леман, Дж. А. Сэндс, К. У. Янсен и П. М. Келлер. 1999. Главный капсидный белок L1 рекомбинантных вирусоподобных частиц вируса папилломы человека 11 типа взаимодействует с гепарином и гликозаминогликанами клеточной поверхности на кератиноцитах человека. Дж. Биол. хим. 274 : 5810-5822.
 [PubMed] [Google Scholar]
[PubMed] [Google Scholar]56. Ким К.Ю., Л. Блатт и М.В. Тейлор. 2000. Влияние интерферона на экспрессию онкогенов вируса папилломы человека. Дж. Генерал Вирол. 81 : 695-700. [PubMed] [Google Scholar]
57. Ким, Дж. Дж., Т. С. Райт и С. Дж. Голди. 2002. Экономическая эффективность альтернативных стратегий сортировки атипичных плоскоклеточных клеток неопределенного значения. JAMA 287 : 2382-2390. [PubMed] [Google Scholar]
58. Кивиат Н. Б. и Л. А. Коутский. 1993. Конкретные типы вирусов папилломы человека как возбудители большинства цервикальных интраэпителиальных неоплазий: последствия для современных взглядов и лечения. Дж. Натл. Рак инст. 85 : 934-935. [PubMed] [Google Scholar]
59. Клетер Б., Л. Дж. ван Доорн, Л. Шраувен, А. Молийн, С. Састровийото, Дж. ТерШеггет, Дж. Линдеман, Б. Тер Хармсель, М. Бургер, и В. Квинт. 1999.
 Разработка и клиническая оценка высокочувствительного ПЦР-обратногибридизационного линейного зонда для обнаружения и идентификации аногенитального вируса папилломы человека. Дж. Клин. микробиол. 37 : 2508-2517. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Разработка и клиническая оценка высокочувствительного ПЦР-обратногибридизационного линейного зонда для обнаружения и идентификации аногенитального вируса папилломы человека. Дж. Клин. микробиол. 37 : 2508-2517. [Бесплатная статья PMC] [PubMed] [Google Scholar]60. Koopmanschap, MA, G.A. van Oortmarssen, HMA van Agt, M. van Ballegooijen, JD Habbema и KT Lubbe. 1990. Скрининг рака шейки матки: посещаемость и экономическая эффективность. Инт Дж. Рак 45 : 410-415. [PubMed] [Google Scholar]
61. Курман Р. Дж., Д. Э. Хенсон, А. Л. Хербст, К. Л. Ноеллер и М. Х. Шиффман. 1994. Временные рекомендации по ведению аномальной цитологии шейки матки. Национальный семинар по раку 1992 года. JAMA 271 : 1866-1869. [PubMed] [Google Scholar]
62. Ли, Дж. С. Дж., П. Вильгельм, Л. Куан, Д. Г. Эллисон, X. Лей, С. О и С. Ф. Паттен. 1997. Производительность системы AutoPap позволяет выявить низкую распространенность и аномалии мелких клеток.
 Акта Цитол. 41 : 56-64. [PubMed] [Google Scholar]
Акта Цитол. 41 : 56-64. [PubMed] [Google Scholar]63. Ли, К. Р., Р. Ашфак, Г. Г. Бердсонг, М. Э. Коркилл, К. М. Макинтош и С. Л. Инхорн. 1997. Сравнение обычных мазков Папаниколау и жидкостной тонкослойной системы для скрининга рака шейки матки. Обст. Гинекол. 90 : 278-284. [PubMed] [Google Scholar]
64. Ящерица Г., М.-Дж. Демар-Пуле, П. Руаньо и П. Гамбер. 2001. Обнаружение гибридизации in situ единичной копии вируса папилломы человека на изолированных клетках с использованием системы каталитической амплификации сигнала: GenPoint™. Диагн. Цитопатол. 24 : 112-116. [PubMed] [Google Scholar]
65. Lonquet, M., S. Beaudenon, and G. Orth. 1996. Два новых типа вируса генитальной папилломы (ВПЧ): HPV68 и HPV70, связанные с потенциально онкогенным HPV39. Дж. Клин. микробиол. 34 : 738-744. [Бесплатная статья PMC] [PubMed] [Google Scholar]
66.
 Лоринц А. Т., В. Д. Ланкастер и Г. Ф. Темпл. 1986. Клонирование и характеристика ДНК нового вируса папилломы человека от женщины с дисплазией шейки матки. Дж. Вирол. 58 : 225-229. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Лоринц А. Т., В. Д. Ланкастер и Г. Ф. Темпл. 1986. Клонирование и характеристика ДНК нового вируса папилломы человека от женщины с дисплазией шейки матки. Дж. Вирол. 58 : 225-229. [Бесплатная статья PMC] [PubMed] [Google Scholar]67. Лоринц, А. Т., А. П. Куинн, В. Д. Ланкастер и Г. Ф. Темпл. 1987. Новый тип папилломавируса ассоциирован с раком шейки матки. Вирусология 159 : 187-190. [PubMed] [Google Scholar]
68. Лоринц А. Т., Г. Ф. Темпл, Р. Дж. Курман, А. Б. Дженсон и В. Д. Ланкастер. 1987. Онкогенная ассоциация определенных типов вируса папилломы человека с неоплазией шейки матки. JNCI 79 : 671-677. [PubMed] [Google Scholar]
69. Лоринц А. Т., А. П. Куинн, М. Д. Голдсборо, П. Макаллистер и Г. Ф. Темпл. 1989. Вирус папилломы человека типа 56: новый вирус, обнаруженный при раке шейки матки. Дж. Генерал Вирол. 70 : 3099-3104.
 [PubMed] [Google Scholar]
[PubMed] [Google Scholar]70. Лоринц А. Т., А. П. Куинн, М. Д. Голдсборо, Б. Дж. Шмидт и Г. Ф. Темпл. 1989. Клонирование и частичное секвенирование ДНК двух новых типов вируса папилломы человека, ассоциированных с кондиломами и низкодифференцированной неоплазией шейки матки. Дж. Вирол. 63 : 2829-2834. [Бесплатная статья PMC] [PubMed] [Google Scholar]
71. Лоринц, А. Т. и Р. Рейд. 1989. Ассоциация вируса папилломы человека с гинекологическим раком. Курс. мнение Онкол. 1 : 123-132. [PubMed] [Google Scholar]
72. Лоринц А. Т., Р. Рейд, А. Б. Дженсон, М. Д. Гринберг, В. Ланкастер и Р. Дж. Курман. 1992. Папилломавирусная инфекция шейки матки: относительный риск ассоциации 15 распространенных аногенитальных типов. Обст. Гинекол. 79 : 328-337. [PubMed] [Google Scholar]
73. Magnusson, P.K.E., P. Lichtenstein, and UB Gyllenstein. 2000.
 Наследуемость опухолей шейки матки. Междунар. Дж. Рак 88 : 698-701. [PubMed] [Google Scholar]
Наследуемость опухолей шейки матки. Междунар. Дж. Рак 88 : 698-701. [PubMed] [Google Scholar]74. Mandelblatt, JS, WF Lawrence, S.M. Womack, D. Jacobson, B. Yi, Y.-T. Хван, К. Голд, Дж. Бартер и К. Шах. 2002. Преимущества и затраты на использование тестирования на ВПЧ для скрининга рака шейки матки. JAMA 287 : 2372-2381. [PubMed] [Академия Google]
75. Манос, М. М., В. К. Кинни, Л. Б. Херли, М. Э. Шерман, Дж. Ши-Нгаи, Р. Дж. Шерман, Дж. Э. Рэмси, Б. Дж. Феттерман, Дж. С. Хартингер, К. М. Макинтош, Г. Ф. Павлик и Р. А. Хиатт. 1999. Выявление женщин с неоплазией шейки матки: Использование ДНК-тестирования вируса папилломы человека для получения сомнительных результатов по Папаниколау. JAMA 281 : 1605-1610. [PubMed] [Google Scholar]
76. Мацукура Т. и М. Сугасе. 1990. Молекулярное клонирование нового вируса папилломы человека (тип 58) из инвазивной карциномы шейки матки.
 Вирусология 177 : 833-836. [PubMed] [Google Scholar]
Вирусология 177 : 833-836. [PubMed] [Google Scholar]77. Meyers, C., M.G. Frattini, JB Hudson, and L.A. Laimins. 1992. Биосинтез вируса папилломы человека из непрерывной клеточной линии при эпителиальной дифференцировке. Наука 257 : 971-973. [PubMed] [Google Scholar]
78. Москицки А. Б., Дж. Палефски, Г. Смит, С. Сибошски и Г. Школьник. 1993. Вариабельность тестирования ДНК вируса папилломы человека в лонгитюдной когорте молодых женщин. Обст. Гинекол. 82 : 578-585. [PubMed] [Google Scholar]
79. Муньос Н., Ф. X. Бош, К. В. Шах и А. Мехеус. 1992. Эпидемиология рака шейки матки и вируса папилломы человека. Научная публикация 119. Международное агентство по изучению рака, Лион, Франция.
80. Нагашфар, З. С., Н. Б. Розеншейн, А. Т. Лоринц, Дж. Бушема и К. В. Шах. 1987. Характеристика вируса папилломы человека типа 45, нового родственного вирусу половых путей типа 18.
 Дж. Генерал Вирол. 68 : 3073-3079. [PubMed] [Google Scholar]
Дж. Генерал Вирол. 68 : 3073-3079. [PubMed] [Google Scholar]81. Nobbenhuis, MA, CJ Meijer, AJ van den Brule, L. Rozendaal, FJ Voorhoost, EK Risse, RH Verheijen и TJ Helmerhorst. 2001. Добавление тестирования на ВПЧ высокого риска улучшает текущие рекомендации по последующему наблюдению после лечения цервикальной интраэпителиальной неоплазии. бр. Дж. Рак 84 : 796-801. [Бесплатная статья PMC] [PubMed] [Google Scholar]
82. Nuovo, GJ, CP Crum, EM de Villiers, RU Levine, and SJ Silverstein. 1988. Выделение нового вируса папилломы человека (тип 51) из кондиломы шейки матки. Дж. Вирол. 62 : 1452-1455. [Бесплатная статья PMC] [PubMed] [Google Scholar]
83. Обалек С., С. Яблонска и Г. Орт. 1985. ВПЧ-ассоциированная интраэпителиальная неоплазия наружных половых органов. клин. Дерматол. 3 : 104-113. [PubMed] [Google Scholar]
84. Окамото А.
 , С. Д. Вудворт, К. Йен, Дж. Чанг, С. Исониси, Т. Никайдо, Т. Киёкава, Х. Сео, Ю. Китахара, К. Очиаи и Т. Танака. 1999. Комбинированная терапия подофиллином и видарабином для лечения цервикальной интраэпителиальной неоплазии, положительной по отношению к вирусу папилломы человека. Онкол. Респ. 6 : 269-276. [PubMed] [Google Scholar]
, С. Д. Вудворт, К. Йен, Дж. Чанг, С. Исониси, Т. Никайдо, Т. Киёкава, Х. Сео, Ю. Китахара, К. Очиаи и Т. Танака. 1999. Комбинированная терапия подофиллином и видарабином для лечения цервикальной интраэпителиальной неоплазии, положительной по отношению к вирусу папилломы человека. Онкол. Респ. 6 : 269-276. [PubMed] [Google Scholar]85. Ostor, AG 1993. Естественное течение цервикальной интраэпителиальной неоплазии: критический обзор. Междунар. Дж. Гинекол. Патол. 12 : 186-192. [PubMed] [Google Scholar]
86. Папаниколау, Г. Н. 1949. Обзор актуальности и возможностей эксфолиативной цитологии в диагностике рака. Анна. Стажер Мед. 31 : 661-674. [PubMed] [Google Scholar]
87. Philips, D.H., and M. NiShé. 1993. Аддукты ДНК, связанные с курением, в биоптатах шейки матки человека. МАИР научн. Опубл. 124 : 327-330. [PubMed] [Google Scholar]
88.
 Quint, WGV, G. Scholte, LJ Van Doorn, B. Kleeter, PHM Smits и J. Lindeman. 2001. Сравнительный анализ папилломавирусной инфекции в соскобах и биоптатах шейки матки методом общей SPF 10 ПЦР и генотипирования ВПЧ. Дж. Патол. 194 : 51-58. [PubMed] [Google Scholar]
Quint, WGV, G. Scholte, LJ Van Doorn, B. Kleeter, PHM Smits и J. Lindeman. 2001. Сравнительный анализ папилломавирусной инфекции в соскобах и биоптатах шейки матки методом общей SPF 10 ПЦР и генотипирования ВПЧ. Дж. Патол. 194 : 51-58. [PubMed] [Google Scholar]89. Razzaque, A., O. Williams, J. Wang, and JS Rhim. 1993. Неопластическая трансформация иммортализованных эпидермальных кератиноцитов человека двумя клонами ДНК HHV-6. Вирусология 195 : 113-120. [PubMed] [Google Scholar]
90. Рейд Р., М. Гринберг, А. Б. Дженсон, М. Хусейн, Дж. Уиллетт, Ю. Дауд, Г. Темпл, К. Р. Стэнхоуп, А. И. Шерман, Г. Д. Фиббс и А. Т. Лоринц. 1987. Папилломавирусные инфекции, передающиеся половым путем. 1. Анатомическое распределение и степень патогенности неопластических поражений, связанных с различными типами вирусов. Являюсь. Дж. Обст. Гинекол. 156 : 212-222. [PubMed] [Google Scholar]
91.
 Ро, Дж., А. Рой-Бурман, Х. Ким, Э. М. де Вильерс, Т. Мацукура и Дж. Чоу. 1994. Нуклеотидная последовательность и филогенетическая классификация вируса папилломы человека типа 59. Вирусология 203 : 158-161. [PubMed] [Google Scholar]
Ро, Дж., А. Рой-Бурман, Х. Ким, Э. М. де Вильерс, Т. Мацукура и Дж. Чоу. 1994. Нуклеотидная последовательность и филогенетическая классификация вируса папилломы человека типа 59. Вирусология 203 : 158-161. [PubMed] [Google Scholar]92. Richart, RM 1973. Цервикальная интраэпителиальная неоплазия. Патол. Анну. 3 : 301-328. [PubMed] [Google Scholar]
93. Рис, Л. А. Г., М. П. Эйснер, К. Л., Косари, Б. Ф. Хэнки, Б. А. Миллер, Л. Глегг и Б. К. Эдвардс. 2001. Обзор статистики рака SEER за 1973-1998 гг. Национальный институт рака, Бетесда, Мэриленд,
94. Роден, Р. Б., Д. Р. Лоуи и Дж. Т. Шиллер. 1997. Папилломавирус устойчив к высыханию. Дж. Заразить. Дис. 176 : 1076-1079. [PubMed] [Google Scholar]
95. Романо Н., Ф. М. Романо, Э. Вивиано, Ф. Витале, М. Р. Виаальфрате, А. М. Перна и Ф. Бонура. 1996. Редкая ассоциация ДНК вируса герпеса человека 6 с ДНК вируса папилломы человека в мазках из шейки матки женщин с нормальными и аномальными цитологиями.
 Дж. Клин. микробиол. 34 : 1589-1591. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Дж. Клин. микробиол. 34 : 1589-1591. [Бесплатная статья PMC] [PubMed] [Google Scholar]96. Ronnett, B.M., MM Manos, JE Ransley, BJ Fetterman, WK Kinney, LB Hurley, JS Ngai, RJ Kurman и ME Sherman. 1999. Атипичные железистые клетки неопределенного значения (AGUS): цитопатологические особенности, гистопатологические результаты и обнаружение ДНК вируса папилломы человека. Гум. Патол. 30 : 816-825. [PubMed] [Google Scholar]
97. Райан, М. Р., Дж. Ф. Штастны, Р. Реммерс, М. А. Педиго, Л. А. Кэхилл и У. Дж. Фрейбл. 1996. PapNet-направленный повторный скрининг цервиковагинальных мазков: исследование 101 случая атипичных плоскоклеточных клеток неопределенного значения. Являюсь. Дж. Клин. Патол. 105 : 711-718. [PubMed] [Google Scholar]
98. Сапп, М., К. Вольперс, М. Мюллер и Р. Э. Стрек. 1995. Организация основных и минорных капсидных белков в вирусоподобных частицах вируса папилломы человека типа 33.
 Дж. Генерал Вирол. 76 : 2407-2412. [PubMed] [Google Scholar]
Дж. Генерал Вирол. 76 : 2407-2412. [PubMed] [Google Scholar]99. Савайя Г. Ф., К. Керликовске, Г. Гилденгорин и А. Э. Вашингтон. 2000. Частота аномалий мазка Папаниколау в течение 3 лет после нормального мазка Папаниколау — США, 1991–1998 гг. Морб. Смертный. еженедельно. Реп. 49 : 1001-1003. [PubMed] [Google Scholar]
100. Шиффман М., Р. Эрреро, А. Хильдесхайм, М. Э. Шерман, М. Братти, С. Вакхолдер, М. Альфаро, М. Хатчинсон, Дж. Моралес, М. Д. Гринберг и А. Т. Лоринц. 2000. Анализ ДНК ВПЧ при скрининге рака шейки матки. Результаты от женщин из провинции высокого риска Коста-Рики. ДЖАМА 283 : 87-93. [PubMed] [Google Scholar]
101. Sheets, EE, NM Constantine, S. Sinisco, B. Dean и ES Cibas. 1995. Биопсия под кольпоскопическим контролем дает основу для сравнения точности мазков ThinPrep и Папаниколау. Дж. Гинекол. Технол. 1 : 27-34. [Google Scholar]
102.
 Shen, C.Y., M.S. Ho, S.F. Chang, M.S. Yen, H.T. Ng, E.S. Huang, and C.W. Wu. 1993. Высокая частота сопутствующих половых инфекций цитомегаловирусом человека и вирусом папилломы человека у больных раком шейки матки. Дж. Заразить. Дис. 168 : 449-452. [PubMed] [Google Scholar]
Shen, C.Y., M.S. Ho, S.F. Chang, M.S. Yen, H.T. Ng, E.S. Huang, and C.W. Wu. 1993. Высокая частота сопутствующих половых инфекций цитомегаловирусом человека и вирусом папилломы человека у больных раком шейки матки. Дж. Заразить. Дис. 168 : 449-452. [PubMed] [Google Scholar]103. Шерман, М. Э., Л. Дж. Манго, Д. Келли, Г. Полл, В. Лудин, К. Коупленд, Д. Соломон и М. Х. Шиффман. 1994. PapNet-анализ предположительно отрицательных мазков, предшествующий диагностике плоскоклеточного внутриэпителиального поражения высокой степени или карциномы. Мод. Патол. 7 : 578-581. [PubMed] [Google Scholar]
104. Шерман, М. Э., М. Х. Шиффман, А. Т. Лоринц, М. М. Манос, Д. Р. Скотт, Р. Дж. Курман, Н. Б. Кивиат, М. Столер, А. Г. Гласс и Б. Б. Раш. 1994. На пути к объективному обеспечению качества в цитопатологии шейки матки: корреляция цитопатологических диагнозов с обнаружением типов вируса папилломы человека высокого риска.
 Являюсь. Дж. Клин. Патол. 102 : 182-187. [PubMed] [Google Scholar]
Являюсь. Дж. Клин. Патол. 102 : 182-187. [PubMed] [Google Scholar]105. Шимода К., А. Т. Лоринц, Ф. Темпл и В. Д. Ланкастер. 1988. Вирус папилломы человека типа 52: новый вирус, связанный с неоплазией шейки матки. Дж. Генерал Вирол. 69 : 2925-2928. [PubMed] [Google Scholar]
106. Snoeck, R., J.C. Noel, C. Muller, E. De Clercq и M. Bossens. 2000. Цидофовир, новый подход к лечению внутриэпителиальной неоплазии шейки матки III степени (CIN III). Дж. Мед. Вирол. 60 : 205-209. [PubMed] [Google Scholar]
107. Соломон Д., М. Шиффман и Р. Тароне. 2001. Сравнение трех стратегий лечения пациентов с атипичными плоскоклеточными клетками неопределенного значения. Исходные результаты рандомизированного исследования. Дж. Натл. Рак инст. 93 : 293-299. [PubMed] [Google Scholar]
108. Соломон Д., Д. Дэйви, Р. Курман, А. Мориарти, Д.
 О’Коннор, М. Прей, С. Рааб, М. Шерман, Д. Уилбур , Т. Райт и Н. Янг. 2002. Система Bethesda 2001 года. Терминология для представления результатов цитологии шейки матки. JAMA 287 : 2114-2119. [PubMed] [Google Scholar]
О’Коннор, М. Прей, С. Рааб, М. Шерман, Д. Уилбур , Т. Райт и Н. Янг. 2002. Система Bethesda 2001 года. Терминология для представления результатов цитологии шейки матки. JAMA 287 : 2114-2119. [PubMed] [Google Scholar]109. Spitzer, M. 1998. Дополнительные средства для скрининга шейки матки: последние достижения. Являюсь. Дж. Обст. Гинекол. 179 : 544-556. [PubMed] [Академия Google]
110. Su, P. F., S. Y. Chiang, C. W. Wu и F. Y. Wu. 2000. Основной белок Rep78 аденоассоциированного вируса нарушает связывание ТАТА-связывающего белка с промотором p97 вируса папилломы человека типа 16. J. Virol. 74 : 2459-2465. [Бесплатная статья PMC] [PubMed] [Google Scholar]
111. Свон, округ Колумбия, Р. А. Такер, Г. Тортолеро-Луна, М. Ф. Митчелл, Л. Видерофф, Э. Р. Унгер, Р. А. Нисенбаум, У. К. Ривз и Дж. П. Айсногл. 1999. Число копий ДНК папилломы человека (ВПЧ) зависит от степени заболевания шейки матки и типа ВПЧ.
 Дж. Клин. микробиол. 37 : 1030-1034. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Дж. Клин. микробиол. 37 : 1030-1034. [Бесплатная статья PMC] [PubMed] [Google Scholar]112. Syrjänen, KJ 1996. Естественная история генитальных папилломавирусных инфекций человека, с. 189-206. В К. Лейси (ред.), Обзоры папилломавируса. Издательство Лидского университета, Лидс, Соединенное Королевство.
113. Сирьянен С. М. и К. Дж. Сирьянен. 1999. Новые представления о роли вируса папилломы человека в регуляции клеточного цикла. Анна. Мед. 31 : 175-187. [PubMed] [Академия Google]
114. Тевари, К. С., Дж. А. Тейлор, С. Ю. Ляо, П. Дж. ДиСайя, Р. А. Бургер, Б. Дж. Монк, К. С. Хьюз и Л. П. Вильярреал. 2000. Разработка и оценка общей теории канцерогенеза шейки матки с использованием модели ксенотрансплантата человека и мыши с тяжелым комбинированным иммунодефицитом. Гинекол. Онкол. 77 : 137-148. [PubMed] [Google Scholar]
115. Группа сортировки атипичных плоскоклеточных клеток неопределенного значения/низкосортных плоскоклеточных интраэпителиальных поражений (ALTS).
 2000. Тестирование на вирус папилломы человека для сортировки женщин с цитологическими признаками низкодифференцированных плоскоклеточных интраэпителиальных поражений: исходные данные рандомизированного исследования. Дж. Натл. Рак инст. 92 : 397-402. [PubMed] [Google Scholar]
2000. Тестирование на вирус папилломы человека для сортировки женщин с цитологическими признаками низкодифференцированных плоскоклеточных интраэпителиальных поражений: исходные данные рандомизированного исследования. Дж. Натл. Рак инст. 92 : 397-402. [PubMed] [Google Scholar]116. Томас М., Д. Пим и Л. Бэнкс. 1999. Роль взаимодействия Е6-р53 в молекулярном патогенезе ВПЧ. Онкоген 18 : 7690-7000. [PubMed] [Google Scholar]
117. Торриси А., А. Дель Мистро, Г. Л. Оннис, Ф. Мерлин, Р. Берторель и Д. Минуччи. 2000. Кольпоскопия, цитология и тестирование на ВПЧ у ВИЧ-положительных и ВИЧ-отрицательных женщин. Евро. Дж. Гинекол. Онкол. 21 : 168-172. [PubMed] [Google Scholar]
118. VanRanst, M., R. Tachezy, and R.D. Burk. 1996. Вирусы папилломы человека: бесконечная история, с. 1-20. В К. Лейси (ред.), Обзоры папилломавируса. Издательство Лидского университета, Лидс, Соединенное Королевство.

119. Василаскос П., Дж. Сорель и Р. Рондес. 1999 г. Применение препарата AutoCyte PREP на жидкой основе непосредственно во флаконе для цервикально-вагинальных образцов в трех европейских лабораториях. Акта Цитол. 43 : 65-68. [PubMed] [Google Scholar]
120. Вересс Г., К. Шарка, X.-П. Донг, Л. Гергели и Х. Пфистер. 1999. Функциональное значение вариации последовательности в гене Е2 и длинной контрольной области вируса папилломы человека типа 16. J. Gen. Virol. 80 : 1053-1043. [PubMed] [Google Scholar]
121. Villa, LL 1997. Вирусы папилломы человека и рак шейки матки. Доп. Рак рез. 71 : 321-341. [PubMed] [Академия Google]
122. Волперс, К. и Р. Э. Стрик. 1991. Организация генома и последовательность нуклеотидов вируса папилломы человека типа 39. Вирусология 181 : 419-423. [PubMed] [Google Scholar]
123.
 Walboomers, JMM, and CJLM Meijer. 1997. Существуют ли ВПЧ-отрицательные карциномы шейки матки? Дж. Патол. 181 : 253-254. [PubMed] [Google Scholar]
Walboomers, JMM, and CJLM Meijer. 1997. Существуют ли ВПЧ-отрицательные карциномы шейки матки? Дж. Патол. 181 : 253-254. [PubMed] [Google Scholar]124. Walboomers, JMM, MV Jacobs, MM Manos, FX Bosch, JA Kummer, KV Shah, PJF Snijders, J. Peto, CJLM Meijer и N. Munoz. 1999. Вирус папилломы человека является необходимой причиной инвазивного рака шейки матки во всем мире. Дж. Патол. 189 : 12-19. [PubMed] [Google Scholar]
125. Райт Т.С. и Р.Т. Курман. 1994. Критический обзор системы морфологической классификации преинвазивных поражений шейки матки: научная основа для смены парадигмы. Папилломавирусная респ. 5 : 175-182. [Google Scholar]
126. Райт Т.С., Л. Денни, Л. Кун, А. Поллак и А. Лоринц. 2000. Тестирование ДНК ВПЧ самостоятельно взятых вагинальных образцов в сравнении с цитологическим скринингом для выявления рака шейки матки. JAMA 283 : 81-86.
 [PubMed] [Google Scholar]
[PubMed] [Google Scholar]127. Райт, Т. К., Дж. Т. Кокс, Л. С. Массад, Л. Б. Твиггс и Э. Дж. Уилкинсон. 2002. Согласованные рекомендации 2001 года по ведению женщин с цитологическими аномалиями шейки матки. JAMA 287 : 2120-2129. [PubMed] [Google Scholar]
128. Ян X., Г. Джин, Ю. Накао, М. Рахимтула, М. М. Патер и А. Патер. 1996. Злокачественная трансформация иммортализованных клеток эндоцервикса человека ВПЧ-16 конденсатом сигаретного дыма и характеристика многостадийного канцерогенеза. Int J. Cancer 65 : 338-344. [PubMed] [Google Scholar]
129. Йошиноути М., А. Хонго, К. Накамура, Дж. Кодама, С. Ито, Х. Сакаи и Т. Кудо. 1999. Анализ с помощью мультиплексной ПЦР физического состояния ДНК вируса папилломы человека типа 16 при раке шейки матки. Дж. Клин. микробиол. 37 : 3514-3517. [Бесплатная статья PMC] [PubMed] [Google Scholar]
130. Зербини М.
 , С. Вентуроли, М. Крикка, Г. Галлинелла, П. Де Симоне, С. Коста, Д. Сантини и М. Мусиани. 2001. Распределение и вирусная нагрузка типоспецифических ВПЧ в различных поражениях шейки матки по данным ПЦР-ИФА. Дж. Клин. Патол. 54 : 377-380. [Бесплатная статья PMC] [PubMed] [Google Scholar]
, С. Вентуроли, М. Крикка, Г. Галлинелла, П. Де Симоне, С. Коста, Д. Сантини и М. Мусиани. 2001. Распределение и вирусная нагрузка типоспецифических ВПЧ в различных поражениях шейки матки по данным ПЦР-ИФА. Дж. Клин. Патол. 54 : 377-380. [Бесплатная статья PMC] [PubMed] [Google Scholar]131. zur Hausen, H. 1982. Рак половых органов человека: синергизм между двумя вирусными инфекциями и/или синергизм между вирусной инфекцией и исходными событиями? Ланцет II : 1370-1372. [PubMed] [Google Scholar]
132. zur Hausen, H. 1996. Папилломавирусные инфекции — основная причина рака человека. Биохим. Биофиз. Acta 1288 : 55-78. [PubMed] [Google Scholar]
133. zur Hausen, H. 1999. Папилломавирусы при раке человека. проц. доц. Являюсь. Врачи 111 : 581-587. [PubMed] [Google Scholar]
узлов | Творческая вики | Фэндом
Содержание
- 1 Основная информация
- 2 Где найти
- 2.
 1 Уголь
1 Уголь - 2.2 Обсидиан
- 2,3 Железо
- 2,4 Алмаз
- 2,5 Люмит
- 2.
- 3 Извлечение руды из узлов
- 4 Переплавка руды в слитки
- 4.1 Топливо уровня 1
- 4.2 Топливо уровня 2
- 4.3 Топливо уровня 3
- 4.4 Топливо уровня 10
- 5 Крафт из руды
- 6 Общая информация
Основная информация[]
Узлы представляют собой естественные кубические блоки, содержащие руду. В Creativerse существует 5 типов руд: уголь, обсидиановая руда, железная руда, алмазная руда и люмитовая руда. Все 5 руд можно извлечь из соответствующих узлов с помощью размещение одноразовых экстракторов непосредственно на узлах.
Узлы руды невозможно разрушить, за исключением извлечения всей руды. После того, как экстрактор завершит свою работу и игроки заберут всю добытую руду, сам блок руды полностью исчезнет, и его нельзя будет «повторно использовать», а также он не возродится.

Во всех игровых мирах Creativerse узлы руды в основном можно найти под землей и в скалах. Лишь несколько узлов редко можно увидеть на поверхности (угольные узлы и обсидиановые узлы), больше узлов может быть видно на потолках, полу и стенах пещер, особенно на уровне порчи — самом глубоком слое каждого игрового мира Creativerse.
Узлы являются предварительно сгенерированными частями шаблона Worlds of Creativerse и не появляются сами по себе после создания мира. Однако угольные узлы и алмазные узлы могут быть «созданы» игроками в бесконечном количестве.
Кроме того, узлы не являются единственным источником руды, за исключением люмитовой руды. Три типа руды (уголь, обсидиановая руда и железная руда) могут быть собраны из случайно появляющихся сундуков с сокровищами и могут быть получены из определенных существ, таких как Кипы, Серебро. Keepas, Golden Keepas, Hot Feet или Warmworms.
Четыре типа руды можно собирать в бесконечном количестве, только люмитовая руда доступна в ограниченном количестве, но в каждом игровом мире Creativerse (в основном на уровне коррупции) по-прежнему есть тысячи люмитовых узлов.

Угольные Узлы и Обсидиановые Узлы обычно сгруппированы вместе в патчи из 2-5 блоков Узлов, в то время как Железные Узлы чаще можно найти в патчах из 2-4 блоков, участки Алмазных Узлов чаще всего состоят только из 3 Блоков Узлов и Люмита Узлы чаще всего бывают только парами из 2 блоков узлов, в то время как патчи из 4 или даже 5 узлов Lumite встречаются довольно редко. Однако в гораздо более старых игровых мирах это может быть немного по-другому.
Где найти[]
Все руды можно добывать из многих тысяч узлов, встроенных во все подземные слои в каждом игровом мире Creativerse.
Обратите внимание, что хотя иногда можно обнаружить узлов , явно встроенных в стены, потолки и полы пещер, в то время как угольные узлы и обсидиановые узлы даже редко видны на склонах гор, большинство узлов полностью встроены в скалы и могут быть только достигнуто путем копания через соответствующие подземные слои.
Для рытья шахт потребуются определенные элементы питания.

- Вам понадобится каменная ячейка для добычи камня, чтобы добывать камни слоя ископаемых, такие как коренная порода и известняк.
- Вам понадобится обсидиановая шахтная ячейка, чтобы добывать камни сталактитового слоя, такие как алевролит и сталактит.
- Вам понадобится железная шахтная ячейка, чтобы добывать камни слоя лавы, такие как вулканическая порода и затвердевшая лава.
- Вам понадобится алмазная ячейка для добычи алмазов, чтобы добывать камни слоя порчи, такие как испорченный камень и испорченная грязь.
- Ношение еще более мощных элементов питания ускорит копание, а если вы используете сильные элементы питания для «вытягивания» (добычи) мягких камней, элементы питания даже не потеряют прочности.
Взрывчатка и экскаваторы тротилового типа (не путать с экстракторами, которые необходимы для извлечения руды из их узлов) могут сильно помочь при копании подземных слоев, поскольку они оставят все рудные узлы нетронутыми.
 Однако они предоставят вам только половину своего «урожая», который включает в себя довольно редкие породы, такие как магнетит и турмалин.
Однако они предоставят вам только половину своего «урожая», который включает в себя довольно редкие породы, такие как магнетит и турмалин.Как упоминалось выше, игровые миры Creativerse не генерируются процедурно, вместо этого каждый вновь «созданный» игровой мир является копией одного из 4 шаблонных миров, в которых уже есть все доступные узлы руды в фиксированных позициях.
Уголь []Уголь можно добывать из узлов угля по всему слою ископаемых, который охватывает весь игровой мир, иногда также на слое сталактитов, а часто дополнительно на поверхности в горных биомах.
Обсидиан []Обсидиановая руда может быть извлечена из обсидиановых узлов, которые можно найти по всему слою ископаемых под землей, реже достигая слоя сталактита, но иногда также на поверхности в горных биомах.
Железо []Железная руда может быть извлечена в основном из железных узлов, найденных по всему сталактитовому слою (а также в верхних частях слоя лавы и нижних уровнях слоя ископаемых, в основном в более старых шаблонных мирах).
Алмаз []
Алмазная руда может быть извлечена из алмазных узлов по всему слою лавы (а также в больших количествах в слое порчи и на нижних уровнях сталактитового слоя только в более старых шаблонных мирах).
Люмит []Люмитовая руда может быть извлечена из узлов люмита, которые можно найти по всему подземному слою порчи (плюс на нижних уровнях слоя лавы в основном в старых шаблонных мирах).
Узлы люмита встречаются реже, чем все остальные рудные узлы, но хорошо видны на потолке, земле (иногда покрытой оскверненной водой) и стенах «холмов» в гигантской болотной пещере, которая является слоем порчи.
Извлечение руды из узлов[]
Чтобы извлечь руду из узлов, вы не можете использовать свою перчатку ArcTek, работающую от силовых ячеек, вместо этого вам придется использовать одноразовые экстракторы — базовые экстракторы, расширенные экстракторы или суперэкстракторы могут применяться к любому типу узлов. Взрывчатка и экскаваторы тротилового типа никак не влияют на рудные узлы.

Суперэкстракторы могут быть изготовлены только из рецепта крафта, который Существо (Существо на уровне порчи глубоко под землей) предоставляет либо в своей сумке с добычей, когда вы его убиваете, либо в качестве питомца после того, как вы его приручили и накормили. .
Всем экстракторам потребуется некоторое время, чтобы извлечь всю руду; однако чем лучше экстрактор, тем быстрее он работает и тем больше руды будет получено. Не отказывайтесь от создания продвинутых экстракторов в ближайшее время; они действительно окупаются.
Базовый экстрактор:
Узел Количество руд Необходимое время Угольный узел 6 х Уголь 1 минута Обсидиановый узел 6 x Обсидиановая руда 5 минут Железный узел 5 x Железная руда 5 минут Алмазный узел 3 х Алмазная руда 10 минут Люмитовый узел 2 узла Lumite 10 минут Расширенный экстрактор:
Узел Количество руд Необходимое время Угольный узел 12 х Уголь 30 секунд Обсидиановый узел 12 х Обсидиановая руда 2:30 минут Железный узел 10 x Железная руда 2:30 минут Алмазный узел 6 х Алмазная руда 5 минут Люмитовый узел 4 узла Lumite 5 минут Супер Экстрактор:
Узел Количество руд Необходимое время Угольный узел 21 х Уголь 18 секунд Обсидиановый узел 21 х Обсидиановая руда 1:30 минут Железный узел 18 x Железная руда 1:30 минут Алмазный узел 10 х Алмазная руда 3 минуты Люмитовый узел 7 люмитных узлов 3 минуты Сначала поместите стопку экстракторов (и/или расширенных экстракторов или суперэкстракторов) в любой слот панели быстрого доступа.
 Затем выберите этот быстрый слот (желательно, набрав его номер) и щелкните правой кнопкой мыши, указывая курсором на узел руды, чтобы поместить экстрактор, чтобы он мог извлечь руду из узла.
Затем выберите этот быстрый слот (желательно, набрав его номер) и щелкните правой кнопкой мыши, указывая курсором на узел руды, чтобы поместить экстрактор, чтобы он мог извлечь руду из узла.Все типы экстракторов являются одноразовыми; они будут израсходованы, когда закончат свою работу, и их нельзя будет удалить из узла, пока они не закончат извлекать всю руду.
Разрешение Экстракторов по умолчанию «только я» (в отличие от большинства других активируемых объектов и контейнеров для хранения), и его можно изменить вручную, щелкнув символ замка, чтобы позволить другим игрокам также брать руду. Экстракторы начнут процесс извлечения сразу после размещения на узле, их нельзя активировать позже.
Рекомендуется как можно быстрее создавать продвинутые экстракторы, так как поиск большего количества узлов занимает гораздо больше времени, чем добыча вдвое большего количества руды из одного узла и быстрее. Вы можете легко использовать излишки руды, которые вы добываете таким образом, для создания более продвинутых экстракторов.

После размещения экстрактора вы можете проверить, сколько времени займет извлечение, взглянув на него с помощью курсора и либо щелкнув правой кнопкой мыши, либо набрав «f» в качестве клавиши по умолчанию.
Из нижнего слота Экстрактора можно взять любое количество руды, которое уже было переработано на тот момент. Вы не можете удалить сам экстрактор, пока он не завершит свою работу.
Когда Экстрактор закончит работу, он перестанет «петь» и «свернется» с громким щелчком. Вы можете взять всю (оставшуюся) руду сразу, снова набрав «f» (как клавиша по умолчанию). Это затем удалит узел и также израсходует экстрактор. Иногда экстракторы, в которых все еще есть руда, будут повторять щелкающий звук, когда игроки подходят ближе, как напоминание о необходимости собрать оставшуюся руду.
Нет другого способа уничтожить или удалить узлы руды, кроме как разместить экстракторы и забрать их после того, как они извлекли всю руду из узлов. Даже самые сильные виды ТНТ и Экскаваторов оставят их нетронутыми.

Однако угольные узлы могут быть преобразованы в алмазные узлы.
Переплавка руды в слитки[]
Хотя уголь можно использовать непосредственно для изготовления, а также в качестве топлива для кузниц, все остальные 4 типа руд необходимо переплавить в слитки, прежде чем их можно будет использовать для изготовления, например, путем их резки. в плиты и/или стержни в процессоре.
Для работы кузниц требуется топливо, которое нужно поместить в кузницу вместе с рудой.
Переплавка руды в слитки в кузнице не требует разблокировки каких-либо рецептов крафта.
Для этого вам нужно иметь в инвентаре руду и любой вид топлива (см. ниже). Затем вам нужно будет активировать кузницу, которая была помещена в игровой мир, щелкнув правой кнопкой мыши кузницу или набрав «f» (клавиша по умолчанию), указывая курсором на кузницу.
При активации кузницы экран инвентаря заменяется списком всего, что вы носите в инвентаре, разделенного на: материалы, которые можно выковать, материалы, которые можно использовать в качестве топлива, и остальное.

Щелкните правой кнопкой мыши руду в верхней части списка инвентаря, чтобы переместить ее в кузницу, а затем щелкните правой кнопкой мыши любой доступный тип топлива в списке инвентаря, чтобы переместить его в слот для топлива кузницы.
Тип топлива, который вы выберете, определит, сколько времени потребуется, чтобы руда была переплавлена в слитки в кузнице.
Топливо уровня 1 []Примеры топлива уровня 1: 2 деревянных блока большинства типов, 4 блока листьев большинства типов, 8 деревянных стержней, множество растений, таких как высокая трава, и несколько деревянных предметов или блоков, часто 2 -8 единиц / штук за раз
- Топливо Tier 1 позволяет переплавить одну обсидиановую руду в обсидиановый слиток за 20 секунд.
- Топливо Tier 1 позволяет переплавить одну железную руду в железный слиток за 20 секунд.
- Топливо уровня 1 позволяет переплавить 1 алмазную руду в 1 алмаз (слиток) за 1 минуту.
- Топливо Tier 1 позволяет переплавить 1 люмитовую руду в 1 люмит (слиток) за 1 минуту.

Примеры топлива уровня 2: 1 уголь, 4 блока затвердевшей лавы или 1 блок серы
- Топливо уровня 2 переплавит одну обсидиановую руду в обсидиановый слиток за 10 секунд.
- Топливо уровня 2 позволяет переплавить одну железную руду в железный слиток за 10 секунд.
- Топливо уровня 2 переплавит 1 алмазную руду в 1 алмаз (слиток) за 30 секунд.
- Топливо Tier 2 позволяет переплавить 1 люмитовую руду в 1 люмит (слиток) за 30 секунд.
Примеры топлива уровня 3: 2 блока порченого дерева любого типа, 4 блока порченых листьев любого типа
- Топливо уровня 3 переплавит одну обсидиановую руду в обсидиановый слиток за 6 секунд.
- Топливо уровня 3 переплавит одну железную руду в железный слиток за 6 секунд.
- Топливо уровня 3 переплавит 1 алмазную руду в 1 алмаз (слиток) за 20 секунд.
- Топливо уровня 3 переплавит 1 люмитовую руду в 1 люмит (слиток) за 20 секунд.

Примеры топлива уровня 10: 1x Дегтярный хлеб, 1x Дегтярный суп, 1x Дегтярный бутерброд
- Топливо Tier 10 переплавит одну обсидиановую руду в обсидиановый слиток за 2 секунды.
- Топливо Tier 10 переплавит одну железную руду в железный слиток за 2 секунды.
- Топливо Tier 10 переплавит 1 алмазную руду в 1 алмаз (слиток) за 6 секунд.
- Топливо Tier 10 переплавит 1 люмитовую руду в 1 люмит (слиток) за 6 секунд.
Изготовление с помощью руды[]
Только уголь можно использовать непосредственно для изготовления (например, каменных шахтных ячеек или угольных факелов), а также в качестве обычного топлива для кузниц.
Все остальные 4 типа руд должны быть сначала переплавлены в слитки, прежде чем их можно будет использовать для изготовления.
В кузнице железные слитки можно дополнительно закалить в слитки закаленного железа, которые потребуются для изготовления алмазной брони и легендарного золотого меча.

В процессоре,
- 1 часть угля можно переработать в 1 единицу пороха
- 1 обсидиановый слиток можно переработать либо в 2 обсидиановых плиты, либо в 8 обсидиановых стержней каждый
- 1 обсидиановую плиту можно переработать в 4 обсидиановых стержня
- 8 железных стержней каждый
- 1 железная плита может быть переработана в 4 железных стержня
- 1 алмазный брусок может быть переработан либо в 2 алмазных плиты, либо в 8 алмазных стержней каждый
- 1 алмазная плита может быть переработана в 4 Алмазные стержни
- 1 люмитовый брусок может быть переработан либо в 2 люмитовых плиты, либо в 8 люмитовых стержней каждый, а
- 1 люмитовая плита может быть переработана в 4 люмитовых стержня
Плиты можно размещать непосредственно в игровых мирах для строительства или их можно использовать для крафта, например, для создания продвинутых экстракторов, телепортов или суперэкстракторов.

Переплавка руды в слитки в кузницах и создание плит, стержней, откосов и т. д. в процессорах не требует рецептов крафта; но создание оборудования, объектов и предметов, таких как силовые элементы, доспехи, оружие, инструменты, инструменты для крафта, машины, взрывчатые вещества, мебель, строительные блоки и многое другое, делается в меню крафта (чтобы открыть, набрав «Q» в качестве клавиши по умолчанию ) и потребуется разблокировать рецепты крафта, прежде чем их можно будет использовать.
Общая информация[]
Руды любого вида нельзя размещать в игровом мире, нельзя помещать в какой-либо быстрый слот и нельзя отображать на/в контейнерах-витринах, таких как салфетки, полки из каменной стены, алтари скрытого храма, деревянные плантаторы, Цветочные горшки, галактические гравитационные камеры, замороженные контейнеры, засыпанные снегом контейнеры и тому подобное.
Обратите внимание, что поиск люмитового снаряжения и создание люмитового снаряжения, такого как люмитовые мечи и люмитовые доспехи, не означает, что вы достигли «конца» игры!
Creativerse — это игра-песочница, в которой есть гораздо больше функций и различных возможных целей, которые вы можете определить для своего собственного игрового процесса по своему усмотрению.
 Обычно игроки стремятся создавать чертежи, чтобы делиться ими с другими игроками, или приключения с индивидуально определяемыми целями и всевозможными препятствиями или даже квестами.
Обычно игроки стремятся создавать чертежи, чтобы делиться ими с другими игроками, или приключения с индивидуально определяемыми целями и всевозможными препятствиями или даже квестами.Связывание центральной сети измеряет близость и степень
Теория
Общие определения
Для простоты в этой статье мы будем предполагать, что анализируем простой граф \({{{{{{{\mathcal{G}} }}}}}}\) всего с одним компонентом. Обозначим степень каждой вершины v как k v . Путь в сети длины ℓ — это последовательность ( ℓ + 1) различных узлов, такая что каждая последовательная пара узлов в пути соединена ребром. Мы определим расстояние между двумя узлами u и v в сети как длину кратчайшего пути между двумя узлами, обозначенного здесь как d u v .
Близость с v 2,16,17,18,19 вершины v определяется как величина, обратная среднему расстоянию от v до каждой другой вершины графа, поэтому
$ $\frac{1}{{c}_{v}}=\frac{1}{(N-1)}\mathop{\sum}\limits_{u\in {{{{{{{\mathcal{ V}}}}}}}}\setminus v}{d}_{uv}$$
(1)
где \({{{{{{{\mathcal{V}}}}}}} }\) — набор узлов, а \(N=| {{{{{{{\mathcal{V}}}}}}}}|\) — количество узлов.
 Ясно, что чем ближе вершина v относится к другим вершинам сети, чем больше близость. Таким образом, близость имитирует свойства точек геометрической формы, где точки, ближайшие к геометрическому центру, будут иметь наибольшую близость.
Ясно, что чем ближе вершина v относится к другим вершинам сети, чем больше близость. Таким образом, близость имитирует свойства точек геометрической формы, где точки, ближайшие к геометрическому центру, будут иметь наибольшую близость.Деревья 16,17,18,19 — это связанные сети без петель, поэтому количество ребер всегда на единицу меньше количества узлов. Здесь мы используем остовное дерево 36 , которое является связным подграфом исходного графа \({{{{{{{\mathcal{G}}}}}}}}}\), содержащим все исходные вершины \({{ {{{{{\mathcal{V}}}}}}}}\), но подмножество ( N − 1) ребер, которых как раз достаточно для того, чтобы каждый узел оставался связанным со всеми остальными. Мы также будем работать с корневыми деревьями \({{{{{{{\mathcal{T}}}}}}}}(r)\), в которых мы выделили один специальный узел, корень r дерева.
Оценка близости
Мы исходим из того, что некоторые статистические свойства реальных сетей могут быть зафиксированы остовными деревьями 36 .
 Здесь нас интересует близость, которая использует длины кратчайших путей между узлами, поэтому наиболее полезными деревьями для этой работы являются деревья кратчайших путей, \({{{{{{{\mathcal{T}}}}}}}} }(r)\), который содержит один кратчайший путь из корневого узла r каждому оставшемуся узлу в сети. Поскольку наши сети не взвешиваются, деревья кратчайших путей всегда существуют и легко определяются как часть алгоритма поиска в ширину. Дополнительные сведения см. в дополнительном примечании 2 к алгоритму дерева кратчайших путей. Каждый узел может выступать в качестве корневого узла, поэтому существует по крайней мере одно дерево кратчайших путей, \({{{{{{{\mathcal{T}}}}}}}}(r)\), для каждого узла 92 107 р . Эти деревья не уникальны, так как между парой узлов может быть много кратчайших путей.
Здесь нас интересует близость, которая использует длины кратчайших путей между узлами, поэтому наиболее полезными деревьями для этой работы являются деревья кратчайших путей, \({{{{{{{\mathcal{T}}}}}}}} }(r)\), который содержит один кратчайший путь из корневого узла r каждому оставшемуся узлу в сети. Поскольку наши сети не взвешиваются, деревья кратчайших путей всегда существуют и легко определяются как часть алгоритма поиска в ширину. Дополнительные сведения см. в дополнительном примечании 2 к алгоритму дерева кратчайших путей. Каждый узел может выступать в качестве корневого узла, поэтому существует по крайней мере одно дерево кратчайших путей, \({{{{{{{\mathcal{T}}}}}}}}(r)\), для каждого узла 92 107 р . Эти деревья не уникальны, так как между парой узлов может быть много кратчайших путей.Наша картина для этих деревьев кратчайших путей показана на рис. 1. Начнем с наблюдения, что вблизи корневого узла структура этих деревьев кратчайших путей будет меняться и, в частности, число ближайших соседей k r корневой вершины r будут различаться.
Рис. 1: Иллюстрация аппроксимации дерева кратчайших путей. Однако по мере удаления от корневого узла число узлов n r ( ℓ ) на некотором расстоянии ℓ от корневого узла r растет в геометрической прогрессии с каждым шагом в большинстве сетей. Это является источником эффекта маленького мира, наблюдаемого во многих сетях, где расстояние между узлами обычно намного меньше, чем в сетях аналогичного размера, которые ограничены евклидовой геометрией, такой как регулярная квадратная сетка улиц или случайная геометрическая сетка. график. Независимо от локального контекста корневого узла деревья кратчайших путей быстро получают доступ к аналогичному набору узлов в основной массе сети при условии, что в сети нет крупномасштабной неоднородности. Таким образом, мы предполагаем, что структура и статистические свойства этих деревьев вдали от корневого узла одинаковы для всех возможных корневых узлов. Вклад в плотность каждого узла в массиве тем больше, чем они дальше от корня и более многочисленны. Таким образом, мы ожидаем, что наибольший вклад в близость всегда исходит от одних и тех же объемных областей, где мы можем ожидать статистического сходства.
Однако по мере удаления от корневого узла число узлов n r ( ℓ ) на некотором расстоянии ℓ от корневого узла r растет в геометрической прогрессии с каждым шагом в большинстве сетей. Это является источником эффекта маленького мира, наблюдаемого во многих сетях, где расстояние между узлами обычно намного меньше, чем в сетях аналогичного размера, которые ограничены евклидовой геометрией, такой как регулярная квадратная сетка улиц или случайная геометрическая сетка. график. Независимо от локального контекста корневого узла деревья кратчайших путей быстро получают доступ к аналогичному набору узлов в основной массе сети при условии, что в сети нет крупномасштабной неоднородности. Таким образом, мы предполагаем, что структура и статистические свойства этих деревьев вдали от корневого узла одинаковы для всех возможных корневых узлов. Вклад в плотность каждого узла в массиве тем больше, чем они дальше от корня и более многочисленны. Таким образом, мы ожидаем, что наибольший вклад в близость всегда исходит от одних и тех же объемных областей, где мы можем ожидать статистического сходства.
Каждый узел r , здесь красная звезда, считается корневым узлом дерева кратчайших путей \({{{{{{{\mathcal{T}}}}}}}}(r) \). У него k r ближайших соседей, как показано пятью сплошными черными линиями. Каждый из соседних узлов, здесь синие кружки, рассматривается как корень ветви дерева кратчайшего пути. Эти ветви рассматриваются как статистически идентичные с номером ветвления \((1+\bar{z})\), как указано здесь, за счет использования одной и той же заштрихованной формы с корнем в каждом соседнем узле. Серые пунктирные линии обозначают некоторые из множества ребер в графе \({{{{{{{\mathcal{G}}}}}}}}\), которые не включены в дерево кратчайших путей.
Полноразмерное изображение
Таким образом, наиболее важное различие при сравнении различных корневых узлов заключается в локальной структуре каждого корневого узла. В частности, большое влияние будет иметь начальное значение экспоненциального роста числа узлов на расстоянии 92 107 ℓ 92 108 от корня.
 Это будет зависеть от локальной структуры, и самый простой эффект исходит от количества непосредственных соседей, которые имеет корневой узел, то есть степени корневого узла k 9{\ell}\), где \(\bar{z}\) — некоторая мера скорости экспоненциального роста дерева кратчайших путей. Обратите внимание, что наше предположение о статистическом сходстве предполагает, что коэффициент ветвления этих деревьев в среднем одинаков, поэтому мы используем один параметр \(\bar{z}\) для представления экспоненциального роста от любого корневого узла r .
Это будет зависеть от локальной структуры, и самый простой эффект исходит от количества непосредственных соседей, которые имеет корневой узел, то есть степени корневого узла k 9{\ell}\), где \(\bar{z}\) — некоторая мера скорости экспоненциального роста дерева кратчайших путей. Обратите внимание, что наше предположение о статистическом сходстве предполагает, что коэффициент ветвления этих деревьев в среднем одинаков, поэтому мы используем один параметр \(\bar{z}\) для представления экспоненциального роста от любого корневого узла r .Наша грубая аппроксимация явно ошибается, когда мы смотрим на большие расстояния от корня, так как рано или поздно в любой реальной сети закончатся вершины, поэтому 9{{L}_{r}}-1)}{(\bar{z}-1)}\,.$$
(2)
Мы можем инвертировать это выражение, чтобы выразить это отсечение L r in terms of parameters N and k r , giving us L r = L ( N , k r ) where for большой N
$$L(N,k)\приблизительно \frac{\ln \left(N(\bar{z}-1)/k\right)}{\ln (\bar{z}) }\,.
 $$
$$(3)
Отдельные расстояния являются целыми числами, но это ясно из формы в уравнении. (3) что нам нужно, чтобы L было действительным числом; в некотором смысле L — это среднее значение фактических расстояний от корня до листьев (узлов с первой степенью) дерева. Это также говорит нам о том, что шкала расстояний, связанная с узлом, зависит от логарифма степени этого узла. Поскольку обратная близость представляет собой сумму расстояний, эта шкала расстояний L определяет результат, и это объясняет, почему \(\ln (k)\) появляется в нашем выражении для обратной близости. Кроме того, \(\ln (N)\) зависимость этого масштаба расстояния 9{\ell -1}\) for ℓ < L ( N , k r ) and zero for larger ℓ which depends on local parameters k r , степень каждого корневого узла и два глобальных параметра, общее количество узлов N и некоторая мера скорости роста деревьев кратчайших путей \(\bar{z}\).
 Теперь мы можем переписать уравнение близости c r . (1) вершины 9{2}}\right)$$
Теперь мы можем переписать уравнение близости c r . (1) вершины 9{2}}\right)$$(4)
Используя уравнения. (2) и (3) мы можем исключить L r , чтобы найти, что
$$\frac{1}{{c}_{r}}=-\frac{1}{\ln ( \bar{z})}\ln ({k}_{r})+\beta \,.$$
(5)
Наш расчет показывает, что параметр β также не зависит от корневой вершины r , но это функция глобальных сетевых параметров N и \(\bar{z}\), так что \(\beta =\beta (\bar{z},N)\), где
$$\beta (\bar{z},N)=\left(\frac{1}{(\bar{z}-1)}+\frac{\ln (\bar{z}-1) }{\ln (\bar{z})}\right)+\frac{1}{\ln (\bar{z})}\ln (N)\,.$$
(6)
Наш предсказание состоит в том, что обратная величина близости c r любого узла r должна показывать линейную зависимость от логарифма степени k r этого узла с обратным наклоном журнала параметра роста \(\bar{z}\).
В нашем анализе мы не будем предполагать, что параметр β задается уравнением.
 (6). Добавляя один дополнительный подобранный параметр, мы немного теряем предсказательную силу, поскольку для характеристики сети требуется много параметров. Это оставляет нам предположение, основанное на количестве узлов N и степени каждого узла k r , которые обычно известны. Тогда, в принципе, у нас есть два неизвестных значения глобальных параметров, которые мы находим из линейной подгонки к нашим данным для 9{{{{{{{{\rm{(подходит)}}}}}}}}}\) и β (подходит) .
(6). Добавляя один дополнительный подобранный параметр, мы немного теряем предсказательную силу, поскольку для характеристики сети требуется много параметров. Это оставляет нам предположение, основанное на количестве узлов N и степени каждого узла k r , которые обычно известны. Тогда, в принципе, у нас есть два неизвестных значения глобальных параметров, которые мы находим из линейной подгонки к нашим данным для 9{{{{{{{{\rm{(подходит)}}}}}}}}}\) и β (подходит) .Численные результаты для теоретических моделей
Мы рассмотрели взаимосвязь между близостью и степенью, используя простые сети, полученные из трех различных теоретических моделей 17,18,19 : модель Эрдёша-Рейни (ER) модель с чистым предпочтительным подключением 38 и сетью модели конфигурации 39 , начиная с сети, созданной с той же моделью Барабаши-Альберта. В первой и третьей модели ребра полностью рандомизированы, поэтому корреляции между вершинами нет.
Таблица 1 Результаты для искусственных сетей. Обе последние модели имеют распределение степеней с толстыми хвостами. Наши сети, построенные из искусственных моделей, были созданы стандартными методами в пакете networkx 9.{{{{{{{{\rm{(fit)}}}}}}}}}\) и β (fit) , и показатели качества соответствия в таблице 1 показывают, что это хорошее соответствие, визуально подтверждается графиками на рис. 2а. Обратите внимание, что на рис. Штадлер 6 .
Обе последние модели имеют распределение степеней с толстыми хвостами. Наши сети, построенные из искусственных моделей, были созданы стандартными методами в пакете networkx 9.{{{{{{{{\rm{(fit)}}}}}}}}}\) и β (fit) , и показатели качества соответствия в таблице 1 показывают, что это хорошее соответствие, визуально подтверждается графиками на рис. 2а. Обратите внимание, что на рис. Штадлер 6 .Полноразмерный стол
Рис. 2: Плотность и степень для искусственных сетей.В ( a ) на каждом графике показаны результаты для сетей, сформированных из одной искусственной модели: модели Эрдёша-Рейни (ER), модели Барабаси-Альберта (BA) и модели конфигурации сети, начиная с модели Барабаси-Альберта. модель (Конфиг-БА). Пунктирные линии показывают наилучшую линейную подгонку 1/ c к \(\ln (k)\) с использованием уравнения (5).
 Одни и те же данные из всех девяти искусственных сетей показаны на точечной диаграмме ( b ) с данными \(1/\hat{c}\) по сравнению с предсказанным значением c , полученным из уравнения наилучшего соответствия. (5) и заштрихованная область соответствует 5% отклонению от теоретического предсказания. Панель c показывает дробную ошибку, подогнанное значение близости, деленное на значение данных. Результаты представлены для трех сетей разного размера: N = 1000 (красные точки), N = 2000 (синие точки) и N = 4000 (желтые точки), где N — количество узлов. Все сети имеют среднюю степень 10,0 и для каждого случая было взято 100 реализаций. Значения близости для каждого значения степени объединены в бины, среднее значение показано в виде точки данных с планками погрешностей в виде стандартной ошибки среднего. Результаты показывают, что нелинейная корреляция близости и степени, предсказанная в уравнении. (5) работает большую часть времени с отклонением в 2%.
Одни и те же данные из всех девяти искусственных сетей показаны на точечной диаграмме ( b ) с данными \(1/\hat{c}\) по сравнению с предсказанным значением c , полученным из уравнения наилучшего соответствия. (5) и заштрихованная область соответствует 5% отклонению от теоретического предсказания. Панель c показывает дробную ошибку, подогнанное значение близости, деленное на значение данных. Результаты представлены для трех сетей разного размера: N = 1000 (красные точки), N = 2000 (синие точки) и N = 4000 (желтые точки), где N — количество узлов. Все сети имеют среднюю степень 10,0 и для каждого случая было взято 100 реализаций. Значения близости для каждого значения степени объединены в бины, среднее значение показано в виде точки данных с планками погрешностей в виде стандартной ошибки среднего. Результаты показывают, что нелинейная корреляция близости и степени, предсказанная в уравнении. (5) работает большую часть времени с отклонением в 2%. Есть некоторые намеки на небольшие, но систематические значения более высокой степени, но данные здесь немногочисленны и менее надежны.
Есть некоторые намеки на небольшие, но систематические значения более высокой степени, но данные здесь немногочисленны и менее надежны.Полноразмерное изображение
Грубо говоря, мы обнаружили, что средние обратные значения близости для любой степени обычно находятся в пределах 2% от прогноза, сделанного на основе наилучшего соответствия, как мы можем видеть в разделе «Результаты», показанном на рис. 2b. Небольшие отклонения, наблюдаемые на рис. 2с, особенно для модели Config-BA, относятся к более высоким значениям степени, когда данные скудны, а неопределенности велики. Это означает, что из рис. 2с нельзя сделать однозначных выводов о наличии поправок более высокого порядка к нашей форме (уравнение). (5). 9{{{{{{{{\rm{(fit)}}}}}}}}}\), подгонка коэффициента роста дерева кратчайшего пути с размером сети. Что представляет больший интерес, так это различия в значениях между этими тремя типами искусственных сетей. Все эти сети имели среднюю степень около 10,0, а бесконечное дерево с постоянной степенью 10 (решетка Бете) имело бы коэффициент роста \(\bar{z}=9\), на единицу меньше средней степени.
 {{{{ {{{{\rm{(fit)}}}}}}}}}\) в реальных сетях Эрдеша-Рейни все еще немного выше, чем эта оценка. Для сетей Барабаши-Альберта и их рандомизированных версий 〈 k 〉 nn составляет примерно от двадцати двух до двадцати пяти для сетей в таблице 1. Это значение намного ближе, но все еще не полностью совпадает. Это говорит о том, что наши деревья кратчайших путей представляют собой узлы выборки разными способами, начиная с диффузии, но все же с уклоном в сторону узлов более высокой степени.
{{{{ {{{{\rm{(fit)}}}}}}}}}\) в реальных сетях Эрдеша-Рейни все еще немного выше, чем эта оценка. Для сетей Барабаши-Альберта и их рандомизированных версий 〈 k 〉 nn составляет примерно от двадцати двух до двадцати пяти для сетей в таблице 1. Это значение намного ближе, но все еще не полностью совпадает. Это говорит о том, что наши деревья кратчайших путей представляют собой узлы выборки разными способами, начиная с диффузии, но все же с уклоном в сторону узлов более высокой степени.Поскольку остовные деревья имеют намного меньше ребер, чем исходные графы, возможно, несколько удивительно, что мы обнаруживаем, что коэффициенты роста сопоставимы с любыми мерами средней степени в исходной сети. Таким образом, высокие значения \(\bar{z}\) говорят нам о том, что деревья кратчайших путей выбирают узлы своих сетей с большим уклоном в сторону узлов высокой степени в частях дерева, близких к корневому узлу. и именно поэтому нам нужна такая высокая скорость роста \({\bar{z}}^{{{{{{{{{\rm{(fit)}}}}}}}}}\), когда мы данные для близости.
 Таким образом, когда мы обрезаем ребра для создания дерева, у нас все еще будут высокие степени в дереве рядом с корневым узлом. Следствием этого является то, что во внешних частях деревьев кратчайших путей преобладают листья (узлы первой степени) и другие узлы низкой степени, и они также соответствуют узлам низкой степени в исходной сети.
Таким образом, когда мы обрезаем ребра для создания дерева, у нас все еще будут высокие степени в дереве рядом с корневым узлом. Следствием этого является то, что во внешних частях деревьев кратчайших путей преобладают листья (узлы первой степени) и другие узлы низкой степени, и они также соответствуют узлам низкой степени в исходной сети.Также ясно, что корреляции узлов играют важную роль, поскольку они присутствуют в модели Барабаси-Альберта, но отсутствуют в рандомизированной версии. Большая разница в значениях \(\bar{z}\) для этих двух случаев показывает, что такие корреляции узлов важны, и все же нелинейная зависимость в уравнении. (6) все еще хорошо выполняется в этих искусственных сетях, с этими корреляциями или без них.
Параметр β в уравнении. (5) сложнее интерпретировать, но в таблице 1 показано сравнение двух значений 9{{{{{{{{\rm{(fit)}}}}}}}}},N)\), постоянно хуже, чем значения β (fit) , полученные из двухпараметрической аппроксимации .
 Это подчеркивает, что детали нашей теоретической формы, такие как точная формула для β , здесь уравнение. (6), можно улучшить. Однако наш простой расчет зафиксировал важные особенности проблемы, так что форма уравнения. (5) работает в этих теоретических моделях при условии, что мы рассматриваем как \(\bar{z}\), так и β в уравнении. (5) как свободные параметры, подлежащие определению.
Это подчеркивает, что детали нашей теоретической формы, такие как точная формула для β , здесь уравнение. (6), можно улучшить. Однако наш простой расчет зафиксировал важные особенности проблемы, так что форма уравнения. (5) работает в этих теоретических моделях при условии, что мы рассматриваем как \(\bar{z}\), так и β в уравнении. (5) как свободные параметры, подлежащие определению.Численные результаты для реальных данных
Для сетей, представляющих данные реального мира, мы использовали данные, находящиеся в открытом доступе и легко доступные 41,42,43,44 . Мы стремились к широкому спектру сетей как с точки зрения размера, так и с точки зрения типа взаимодействия, закодированного в этих реальных сетях.
Первый набор из восемнадцати наборов данных мы называем сетями Konect-SNAP. Они были получены из реальных данных и были выбраны, чтобы отразить пять широких категорий сетей: социальные сети (социальные-…), коммуникационные сети (общие-.
Таблица 2 Результаты для крупнейших компонентов сетей Konect-SNAP. ..), сети цитирования (цитирование-…), сети соавторов (соавторские сети). …) и сети гиперссылок (гиперссылка-…). Более подробное описание этих сетей Konect-SNAP дано в дополнительном примечании 3 к наборам данных. 9{2}\) показатель находится в диапазоне от 1,05 до 1,61 для десяти, более чем половины, наших примеров, а еще четыре сети имеют значения от 2,09 до 2,86. Учитывая широкий диапазон как размера, так и характера этих сетей, а также простоту нашего теоретического вывода, такой уровень согласия, возможно, не ожидался. Мы также даем меру корреляции Пирсона между близостью и степенью, ρ ( c , k ), и она обычно высока, как было отмечено ранее 23,24,25,26,27,28,29,30,31,32 . Успех нашего нелинейного отношения между близостью и степенью не является несовместимым с высокими значениями ρ ( c , k ).
..), сети цитирования (цитирование-…), сети соавторов (соавторские сети). …) и сети гиперссылок (гиперссылка-…). Более подробное описание этих сетей Konect-SNAP дано в дополнительном примечании 3 к наборам данных. 9{2}\) показатель находится в диапазоне от 1,05 до 1,61 для десяти, более чем половины, наших примеров, а еще четыре сети имеют значения от 2,09 до 2,86. Учитывая широкий диапазон как размера, так и характера этих сетей, а также простоту нашего теоретического вывода, такой уровень согласия, возможно, не ожидался. Мы также даем меру корреляции Пирсона между близостью и степенью, ρ ( c , k ), и она обычно высока, как было отмечено ранее 23,24,25,26,27,28,29,30,31,32 . Успех нашего нелинейного отношения между близостью и степенью не является несовместимым с высокими значениями ρ ( c , k ).Полноразмерная таблица
Данные для каждой сети показаны более подробно на рис.
Рис. 3: Близость и степень для сетей Konect-SNAP. 3. Опять же, мы можем видеть, что в рамках планок погрешностей средняя близость в каждой степени обычно следует форме, которую мы предсказываем с точностью до 5%, когда наилучшие используются подходящие параметры. Кроме того, неопределенности, оцененные для этих точек данных, предполагают, что подавляющее большинство средних значений близости статистически согласуются с прогнозируемым значением для этой степени, что уже отражено в уменьшенных значениях хи-квадрат в таблице 2.
3. Опять же, мы можем видеть, что в рамках планок погрешностей средняя близость в каждой степени обычно следует форме, которую мы предсказываем с точностью до 5%, когда наилучшие используются подходящие параметры. Кроме того, неопределенности, оцененные для этих точек данных, предполагают, что подавляющее большинство средних значений близости статистически согласуются с прогнозируемым значением для этой степени, что уже отражено в уменьшенных значениях хи-квадрат в таблице 2.Результаты для крупнейших компонентов восемнадцати сетей Konect-SNAP, полученные на основе реальных данных, см. Таблицу 2 для статистики каждого набора данных. Желтая заштрихованная область соответствует отклонению 5%, а серая область соответствует отклонению 10%. Графики в столбце ( a ) показывают обратное значение прогнозируемого результата \(1/\hat{c}\) из наилучшего соответствия обратному среднему измеренному значению 1/ c = 1/〈 c 〉 k усредненные по узлам с одинаковой степенью k .
 Обе оси по существу \(\ln (k)\). Столбец ( b ) показывает отношение значения наилучшего соответствия \(\hat{c}\) к измеренному значению c как функцию степени k , перемасштабированной на наибольшую степень в каждой сети \({k}_ {\Максимум }\). Если прогноз полностью соответствует данным, точки будут лежать на пунктирных линиях. Столбики погрешностей представляют собой стандартную ошибку среднего значения обратной близости. Для большинства точек мы можем увидеть наше уравнение прогноза. (5) фиксирует связь между близостью и степенью, обычно с погрешностью в пределах 5%.
Обе оси по существу \(\ln (k)\). Столбец ( b ) показывает отношение значения наилучшего соответствия \(\hat{c}\) к измеренному значению c как функцию степени k , перемасштабированной на наибольшую степень в каждой сети \({k}_ {\Максимум }\). Если прогноз полностью соответствует данным, точки будут лежать на пунктирных линиях. Столбики погрешностей представляют собой стандартную ошибку среднего значения обратной близости. Для большинства точек мы можем увидеть наше уравнение прогноза. (5) фиксирует связь между близостью и степенью, обычно с погрешностью в пределах 5%.Изображение в натуральную величину
Наконец, мы рассмотрели нашу взаимосвязь между степенью и близостью в 112 сетях, взятых из архива Netzschleuder, состоящего из 276 наборов сетевых данных 44 . Нашим единственным критерием выбора было то, что мы могли автоматически загружать сеть и ее можно было успешно проанализировать с помощью нашего стандартного кода без дополнительной работы.
Таблица 3. Вероятность успеха для разреженных сетей Netzschleuder. Это исключило несколько примеров в этом архиве, например, с несколькими сетями (например, amazon_copurchases) или некоторые, которые были слишком большими для нашего кода (например, academia_edu). Дополнительное примечание 3 содержит дополнительную информацию об этих сетях Netzschleuder. В результате в нашей выборке есть много объектов, для которых мы не ожидаем большого успеха: некоторые из них очень маленькие, некоторые очень плотные, а в некоторые добавлены дополнительные известные структуры, например, двудольная сеть. В то же время есть много вещей, для которых мы ожидаем успеха, обычно это что-то разреженное и большое. Мы представили каждый из них в виде простого графа и проанализировали самый большой компонент связности, который имел до 40 000 узлов и среднюю степень <300. 9{2}\) расчет не выполнен из-за отсутствия оценки ошибки в каждой точке, что происходит, когда у нас есть один узел на k значений. Справа (слева) от штриховой (пунктирной) линии сети имеют плотность 〈 k 〉/( N − 1) <0,01 (>0,1).
Это исключило несколько примеров в этом архиве, например, с несколькими сетями (например, amazon_copurchases) или некоторые, которые были слишком большими для нашего кода (например, academia_edu). Дополнительное примечание 3 содержит дополнительную информацию об этих сетях Netzschleuder. В результате в нашей выборке есть много объектов, для которых мы не ожидаем большого успеха: некоторые из них очень маленькие, некоторые очень плотные, а в некоторые добавлены дополнительные известные структуры, например, двудольная сеть. В то же время есть много вещей, для которых мы ожидаем успеха, обычно это что-то разреженное и большое. Мы представили каждый из них в виде простого графа и проанализировали самый большой компонент связности, который имел до 40 000 узлов и среднюю степень <300. 9{2}\) расчет не выполнен из-за отсутствия оценки ошибки в каждой точке, что происходит, когда у нас есть один узел на k значений. Справа (слева) от штриховой (пунктирной) линии сети имеют плотность 〈 k 〉/( N − 1) <0,01 (>0,1). {2} \ < \ 3.0\).
{2} \ < \ 3.0\).Полноразмерная таблица
Использование близости
Наши численные результаты подтверждают нашу аналитическую работу, что обратная близость линейно зависит от логарифма степени Уравнение. (5) для большинства сетей. Это корреляция, в среднем верная, но не точная для каждого узла. Давно известно, что узлы с более высокими степенями, как правило, имеют меньшую близость, что приводит к значительным показателям корреляции 9.0267 19,23,24,25,26,27,28,29,30,31,32,33 , но это часто обсуждается с точки зрения коэффициента корреляции Пирсона, который наиболее чувствителен к линейным корреляциям. Нелинейная связь между степенью и близостью не обсуждалась в предыдущих исследованиях, и наша взаимосвязь ставит это интуитивное понимание отношения степень-близость на прочную основу.
Наша работа показывает, что в большинстве сетей в первом приближении близость отдельных узлов захватывает в среднем немного больше информации, чем содержится в степени.
 Нет смысла тратить время на расчет близости, если вам нужна только грубая мера центральности, вы можете просто использовать степень. Однако измерения близости могут дать полезную информацию о сети при правильном использовании. 9{{{{{{{{\rm{(fit)}}}}}}}}}\) характеризует экспоненциальный рост, характерный для большинства сложных сетей и лежащий в основе многих хорошо известных явлений, как мы отметим позже в этом обсуждении.
Нет смысла тратить время на расчет близости, если вам нужна только грубая мера центральности, вы можете просто использовать степень. Однако измерения близости могут дать полезную информацию о сети при правильном использовании. 9{{{{{{{{\rm{(fit)}}}}}}}}}\) характеризует экспоненциальный рост, характерный для большинства сложных сетей и лежащий в основе многих хорошо известных явлений, как мы отметим позже в этом обсуждении.Есть несколько способов определить \(\bar{z}\) и β из нашего уравнения уравнения. (5). Мы обнаружили, что наиболее эффективным подходом является более простой метод, в котором мы определили \(\bar{z}\) и β из линейной подгонки наших данных к уравнению. (5). Существуют альтернативы, но они проливают свет на различные возможные приближения, а не имеют практического применения, см. разделы по определению \(\bar{z}\) и β в дополнительном примечании 1 и результаты полиномиальных подгонок более высокого порядка в дополнительном примечании 4.
 {({{{{{{{\rm{fit}}}}}}}})}\) для каждого узла. Наконец, мы используем эту подгонку, чтобы найти узлы, которые заметно более (или менее) центральны, чем ожидалось. Один из способов сделать это — посмотреть на нормализованную близость 9{({{{{{{{\rm{norm}}}}}}}}}}\) выделит выбросы, которые будут представлять наибольший интерес. См. Дополнительное примечание 4, чтобы увидеть некоторые примеры колебаний значений близости вокруг нашего прогнозируемого значения.
{({{{{{{{\rm{fit}}}}}}}})}\) для каждого узла. Наконец, мы используем эту подгонку, чтобы найти узлы, которые заметно более (или менее) центральны, чем ожидалось. Один из способов сделать это — посмотреть на нормализованную близость 9{({{{{{{{\rm{norm}}}}}}}}}}\) выделит выбросы, которые будут представлять наибольший интерес. См. Дополнительное примечание 4, чтобы увидеть некоторые примеры колебаний значений близости вокруг нашего прогнозируемого значения.Можно также сравнить близость со степенью, запустив модель конфигурации, которая поддерживает постоянную степень узла, и измерив близость каждого узла в такой сети с нулевой моделью. Однако наш метод, требующий простой линейной подгонки к уже полученным данным, будет намного быстрее, чем запуск модели конфигурации.
Общее представление о сетях
Успех нашей гипотезы также предполагает, что большинство сетей удовлетворяют двум ключевым предположениям, заложенным в нашем выводе.
Сначала мы предположили, что количество узлов на расстоянии 92 107 ℓ 92 108 от любого узла растет экспоненциально.
 Такой экспоненциальный рост распространен в сетях, поскольку это механизм, лежащий в основе концепций «шести степеней разделения» и эффекта «маленького мира» 45 , о которых часто сообщается в сетях. Формально это связано с масштабами длин в моделях сетей с N вершин, которые растут как \(O(\ln (N))\). Этому противопоставляется сеть, управляемая геометрией 92 107 d 92 108 -мерного евклидова пространства (например, случайные геометрические графы), где количество узлов на расстоянии 92 107 ℓ 92 108 от узла растет по степенному закону 92 107 ℓ 92 108 90 267 d −1 и масштабы длин в таких сетях растут как O ( N 1/ d ). Мы рассмотрим шкалы длины более подробно в подразделе Масштабы длины сети ниже.
Такой экспоненциальный рост распространен в сетях, поскольку это механизм, лежащий в основе концепций «шести степеней разделения» и эффекта «маленького мира» 45 , о которых часто сообщается в сетях. Формально это связано с масштабами длин в моделях сетей с N вершин, которые растут как \(O(\ln (N))\). Этому противопоставляется сеть, управляемая геометрией 92 107 d 92 108 -мерного евклидова пространства (например, случайные геометрические графы), где количество узлов на расстоянии 92 107 ℓ 92 108 от узла растет по степенному закону 92 107 ℓ 92 108 90 267 d −1 и масштабы длин в таких сетях растут как O ( N 1/ d ). Мы рассмотрим шкалы длины более подробно в подразделе Масштабы длины сети ниже.Такое неевклидово поведение большинства сетей указывает на одну ситуацию, когда близость является полезной мерой центральности, независимой от степени и не коррелирующей со степенью, поэтому ситуация, когда наше соотношение Ур.
 (5) не получится. Это для графов, встроенных в евклидово пространство. Это несколько иронично, поскольку этот тип планарной сети, такой как сеть, представляющая соединения между перекрестками улиц в городе, является прототипом, используемым для обоснования идеи о том, что близость меры сети связана с нашей интуицией относительно концепции центральности. в сети. Действительно, Бавелас 2 использовали только примеры плоских графов для построения близости, поэтому связь между близостью и степенью в большинстве сетей никогда не была проблемой в исходной мотивации измерения близости.
(5) не получится. Это для графов, встроенных в евклидово пространство. Это несколько иронично, поскольку этот тип планарной сети, такой как сеть, представляющая соединения между перекрестками улиц в городе, является прототипом, используемым для обоснования идеи о том, что близость меры сети связана с нашей интуицией относительно концепции центральности. в сети. Действительно, Бавелас 2 использовали только примеры плоских графов для построения близости, поэтому связь между близостью и степенью в большинстве сетей никогда не была проблемой в исходной мотивации измерения близости.Второе предположение, которое поддерживает наша работа, заключается в том, что ветви деревьев кратчайших путей статистически подобны, как показано на рис. 1. Успех нашего анализа показывает, что это предположение хорошо работает, когда мы рассматриваем измерения, которые зависят от объема сети. Таким образом, это простое приближение может помочь проанализировать другие измерения сети, и мы рассмотрим некоторые из них в подразделе «Масштабы длины сети» ниже.

Близость и сети реального мира
Учитывая простые предположения и приближения, использованные при выводе нашего уравнения отношения. (5), возможно, удивительно обнаружить, что это отношение степени близости хорошо работает для столь многих сетей, основанных на реальных данных. Как часто наши отношения бывают успешными? Кроме того, можем ли мы понять, когда наши отношения степени близости могут быть успешными, а когда, скорее всего, потерпят неудачу?
Для первого набора из восемнадцати сетей Konect-SNAP, показанных на рис. 3 и в таблице 2, у нас было одиннадцать (61%) с приведенным хи-квадрат <2,0 и все, кроме двух (89%) имеют уменьшенный хи-квадрат с <3,0. Вероятность успеха для 112 сетей Netzschleuder, измеряемая уменьшенным хи-квадратом, ниже. Из девяноста девяти сетей Netzschleuder, где у нас было уменьшенное измерение хи-квадрат, пятьдесят (51%) имели уменьшенный хи-квадрат <2,0, а шестьдесят три (64%) имели уменьшенный хи-квадрат ниже 3,0. Более низкий уровень успеха для сетей Netzschleuder можно понять, поскольку мы беспристрастно отбираем разнообразный набор наборов сетевых данных, и во многих случаях у нас есть информация о сетях, которая предполагает, что мы, возможно, никогда не ожидали успеха.
 {2}\ < \ 3,0\), см. Таблицу 3.
{2}\ < \ 3,0\), см. Таблицу 3.В более общем плане, неудача в наших отношениях — это мощный инструмент, чтобы показать, где в сети есть дополнительная структура. Наш теоретический анализ предполагает общую сеть, в которой каждый узел видит один и тот же экспоненциальный рост числа узлов на расстоянии 92 107 ℓ 92 108, как обсуждалось в подразделе «Общая информация о сети». Если эта родовая структура отсутствует, у нас нет оснований ожидать, что наши отношения будут работать хорошо.
Чтобы увидеть эту структурную проблему, рассмотрим некоторые заметные исключения из нашего критерия низкой плотности. Глядя на рис. 4, сети с низкой плотностью с 9{2}=2,4\). Это по-прежнему хорошо подходит, но это также «двусторонняя сеть языков и стран», поэтому, опять же, лучший результат может быть достигнут, если мы адаптируем наш подход для двухрежимных сетей.
В некоторых случаях метаданные, которые у нас есть для сети, могут уже говорить нам о крупномасштабной структуре, такой как двудольная сеть, которая сделает недействительным наше соотношение (уравнение).
 (5). В простых случаях можно скорректировать наш вывод, чтобы найти более подходящее отношение, соответствующее известной структуре. Например, для двудольных сетей мы могли бы представить наши деревья кратчайших путей, используя два параметра скорости роста, \({\bar{z}}_{a}\) и \({\bar{z}}_{b}\ ), для нечетных и четных расстояний от корневого узла.
(5). В простых случаях можно скорректировать наш вывод, чтобы найти более подходящее отношение, соответствующее известной структуре. Например, для двудольных сетей мы могли бы представить наши деревья кратчайших путей, используя два параметра скорости роста, \({\bar{z}}_{a}\) и \({\bar{z}}_{b}\ ), для нечетных и четных расстояний от корневого узла.В других случаях сбой может указывать на наличие структуры, которая еще не известна. Например, сеть может иметь сильные неоднородности, такие как узлы высокой степени, сгруппированные вместе в плотном ядре. Это сделало бы недействительным наше предположение о том, что все ветви деревьев кратчайших путей выглядят статистически одинаково. Мы можем видеть этот тип проблемы в обсуждениях средней длины пути в моделях случайных графов 46,47 . Там было отмечено, что типичная \(\ln (N)\) зависимость масштабов длин в сложных сетях не наблюдается, когда эти модели имеют распределение степеней вида p ( k ) ~ k − γ с 2 < γ < 3.
 46 , звездообразная структура с одним плотным ядром, соединенным со многими ногами. Этот тип сети опровергает наши предположения, и мы не ожидаем увидеть отношения степени близости.
46 , звездообразная структура с одним плотным ядром, соединенным со многими ногами. Этот тип сети опровергает наши предположения, и мы не ожидаем увидеть отношения степени близости.Масштабы длины сети
Мы можем сравнить наш аналитический подход с другими теоретическими работами по шкалам длины в сетях. Подавляющее большинство аналитических результатов по расстоянию в сетях относится к четко определенным простым теоретическим моделям, как правило, графу Эрдёша-Рейни 17,46,48,49 , модель Барабаши-Альберта 50,51 или безмасштабные случайные графы 52 (наша модель BA-Configuration). В литературе внимание, как правило, сосредоточено на характерных масштабах длины для графа, таких как средняя длина пути 〈 92 107 ℓ 92 108 〉 или диаметр, а не на масштабах длины, связанных с каждой вершиной, таких как близость, которую мы рассматриваем.
Отличительной особенностью нашего подхода является то, что мы фокусируемся на общих сетевых свойствах, которые, по-видимому, сохраняются во многих сетях.
 Таким образом, наш подход можно использовать в гораздо более широком диапазоне сетей и, в частности, работать с реальными сетями, а не только с одной простой моделью. Обратной стороной является то, что у нас нет математической строгости тех, кто работает с простыми моделями. Итак, давайте рассмотрим, как наш подход может быть связан с другими расчетами масштаба длины в литературе.
Таким образом, наш подход можно использовать в гораздо более широком диапазоне сетей и, в частности, работать с реальными сетями, а не только с одной простой моделью. Обратной стороной является то, что у нас нет математической строгости тех, кто работает с простыми моделями. Итак, давайте рассмотрим, как наш подход может быть связан с другими расчетами масштаба длины в литературе.Мы уже отмечали, что концепции «шести степеней разделения» и эффекта «маленького мира» 45 связаны с сетевыми моделями, где масштаб длины растет как \(O(\ln (N)) \), намного медленнее, чем для O ( N 1/ d ) поведение, ожидаемое для сетей, вложенных в d -мерное евклидово пространство. Один из распространенных способов изучить это более точно — рассмотреть среднее расстояние между узлами 〈 92 107 ℓ 92 108 〉, где каждая пара узлов вносит равный вклад в среднее значение. Вот что мы получим, если возьмем половину среднего обратного уравнения близости.
 {-1} \). Из наших результатов близости мы видим, что N зависимость в 〈 ℓ 〉 происходит от члена \(\ln (N)\) в выражении для β уравнения. (6), см. раздел о средней длине кратчайшего пути в дополнительном примечании 1 для получения более подробной информации. Таким образом, наш результат согласуется с поведением, найденным более строго для средней длины пути в моделях случайных графов 46,47 . Успех нашего метода с точки зрения этого среднего результата длины пути показывает, что поведение маленького мира может быть связано с простыми сетевыми функциями, встроенными в наш метод, которые обсуждались в подразделе «Общая информация о сети».
{-1} \). Из наших результатов близости мы видим, что N зависимость в 〈 ℓ 〉 происходит от члена \(\ln (N)\) в выражении для β уравнения. (6), см. раздел о средней длине кратчайшего пути в дополнительном примечании 1 для получения более подробной информации. Таким образом, наш результат согласуется с поведением, найденным более строго для средней длины пути в моделях случайных графов 46,47 . Успех нашего метода с точки зрения этого среднего результата длины пути показывает, что поведение маленького мира может быть связано с простыми сетевыми функциями, встроенными в наш метод, которые обсуждались в подразделе «Общая информация о сети».Наше теоретическое отсечение L ( N , k ) уравнения. (3) дает другую шкалу длины для каждого узла, и снова это имеет такое же поведение маленького мира \(\ln (N)\). Можно предположить, что эта шкала длины отсечки L ( N , k ) может быть связана со шкалой длины эксцентриситета.
 {{{{ {{{{\rm{(fit)}}}}}}}})\), чтобы соответствовать нашему теоретическому порогу Л ( Н , к ). Как видно на рис. 1 Wuchty & Stadler 6 и подтверждено в нашем собственном анализе, эксцентриситет действительно линейно зависит от \(\ln (k)\), но градиент, похоже, не соответствует предсказанию нашего теоретического порога L ( N , к ). Грубо говоря, наша отсечка L ( N , k ) представляет собой типичное среднее крупномасштабное, а не экстремальное значение распределения, поэтому нам никогда не следует ожидать тесной связи с эксцентриситетом. Для получения дополнительной информации см. раздел об эксцентриситете и L ( N , k ) в дополнительном примечании 1.
{{{{ {{{{\rm{(fit)}}}}}}}})\), чтобы соответствовать нашему теоретическому порогу Л ( Н , к ). Как видно на рис. 1 Wuchty & Stadler 6 и подтверждено в нашем собственном анализе, эксцентриситет действительно линейно зависит от \(\ln (k)\), но градиент, похоже, не соответствует предсказанию нашего теоретического порога L ( N , к ). Грубо говоря, наша отсечка L ( N , k ) представляет собой типичное среднее крупномасштабное, а не экстремальное значение распределения, поэтому нам никогда не следует ожидать тесной связи с эксцентриситетом. Для получения дополнительной информации см. раздел об эксцентриситете и L ( N , k ) в дополнительном примечании 1.Поскольку наибольший эксцентриситет является диаметром графика, мы можем видеть \(O(\ln (N))\) поведение нашего L ( N , k ) соответствует этому поведению, наблюдаемому аналитически для диаметра в простых моделях.
 Однако, как и в случае с эксцентриситетом и L ( N , k ), мы не ожидаем, что сможем получить точное представление о диаметре в нашем подходе.
Однако, как и в случае с эксцентриситетом и L ( N , k ), мы не ожидаем, что сможем получить точное представление о диаметре в нашем подходе.Мы также видим сильное сходство между нашим подходом и подходом, использованным в нескольких статьях 48,52 , где сеть сводится к набору колец узлов, каждое кольцо содержит все узлы на одинаковом расстоянии ℓ от корня узел. Например, среднее время первого прохождения случайных блуждающих по сети до заданной вершины v — это обратная величина близости, где теперь близость определяется в терминах новой функции расстояния d u против в уравнении. (1), где d u v — среднее время первого перехода случайного блуждающего из вершины u в вершину v (известна также как марковская центральность 63 или случайное блуждание по близости). Было обнаружено, что среднее время первого прохождения пропорционально степени 48 , и применение наших простых приближений к «кольцевому» методу Барончелли и Лорето 48 быстро обнаруживает эту особенность, см.
 раздел о кольцевых расчетах времени первого прохождения. в дополнительном примечании 1 для получения более подробной информации.
раздел о кольцевых расчетах времени первого прохождения. в дополнительном примечании 1 для получения более подробной информации.В целом, наш подход может дать представление о поведении многих масштабов длины сети, иногда только очень грубо, иногда с большей точностью. Он никогда не сможет сравниться с точностью аналитических расчетов, выполненных для простейших моделей, но наш подход можно использовать в гораздо более широком диапазоне сетей.
Улучшения
Мы уже отметили одно простое улучшение при работе с двудольными сетями. То есть использовать два параметра скорости роста, \({\bar{z}}_{a}\) и \({\bar{z}}_{b}\) для нечетных и четных расстояний от корневого узла в дерево кратчайших путей двудольных сетей.
Другие расширения предлагаются после более детального изучения наших численных результатов. Для нашего меньшего набора из 18 сетей Konect-SNAP, помимо двух плохо подходящих случаев, наше соотношение Уравнение. (5) очень успешен для большинства отдельных узлов с запасом в 5%, успеха, которого нельзя ожидать, учитывая простой аналитический вывод.
 Тем не менее, мы можем видеть некоторые четкие, хотя и небольшие тенденции отклонений на рис. 3. Мы предполагаем, что эти тенденции подчеркивают ограничения нашего аналитического подхода, но наши теоретические методы можно улучшить.
Тем не менее, мы можем видеть некоторые четкие, хотя и небольшие тенденции отклонений на рис. 3. Мы предполагаем, что эти тенденции подчеркивают ограничения нашего аналитического подхода, но наши теоретические методы можно улучшить.At the simplest level, we could replace the sharp cutoff used for n ℓ ( r ) where n ℓ ( r ) = 0 for ℓ > Л . Примеры таких распределений для некоторых простых моделей есть в Baronchelli & Loreto 48 . Лучшее отсечение вполне может привести к лучшим предсказаниям для β , что позволит подобрать функцию с одним независимым параметром, а не с двумя, которые мы использовали, сохранив 9{(2)})+\beta\), так как степень k r теперь вносит вклад в близость лишь небольшим числом терминов. Таким образом, в этом подходе с использованием второй степени нам нужно измерить другой набор параметров N , вторую степень каждого узла.
 Нахождение второй степени численно медленнее, чем степени, но обе они масштабируются одинаково с увеличением размера сети. Успех нашего более простого метода здесь указывает на идею о том, что вторая степень и степень часто могут коррелировать, поэтому вполне вероятно, что использование второй степени может улучшить результаты только в нескольких случаях.
Нахождение второй степени численно медленнее, чем степени, но обе они масштабируются одинаково с увеличением размера сети. Успех нашего более простого метода здесь указывает на идею о том, что вторая степень и степень часто могут коррелировать, поэтому вполне вероятно, что использование второй степени может улучшить результаты только в нескольких случаях.Потребуются более серьезные изменения в расчетах, если необходимо включить другие эффекты, которые здесь не учитываются, такие как структура сообщества или степень ассортативности.
Расстояние и логарифм степени
Ранее было обнаружено, что логарифм степени \(\ln (k)\) играет важную роль в сетевом анализе. Большая часть статей о сетях будет показывать распределение степеней, где горизонтальная ось является зависимой переменной \(\ln (k)\), а не просто степенью k . Более конкретный пример исходит от Zhou et al. 55 , где отношение степеней узлов на двух концах каждого ребра (наибольшее значение в числителе) используется для присвоения «расстояния» η ( u , v ) каждому ребру ( u , v ).



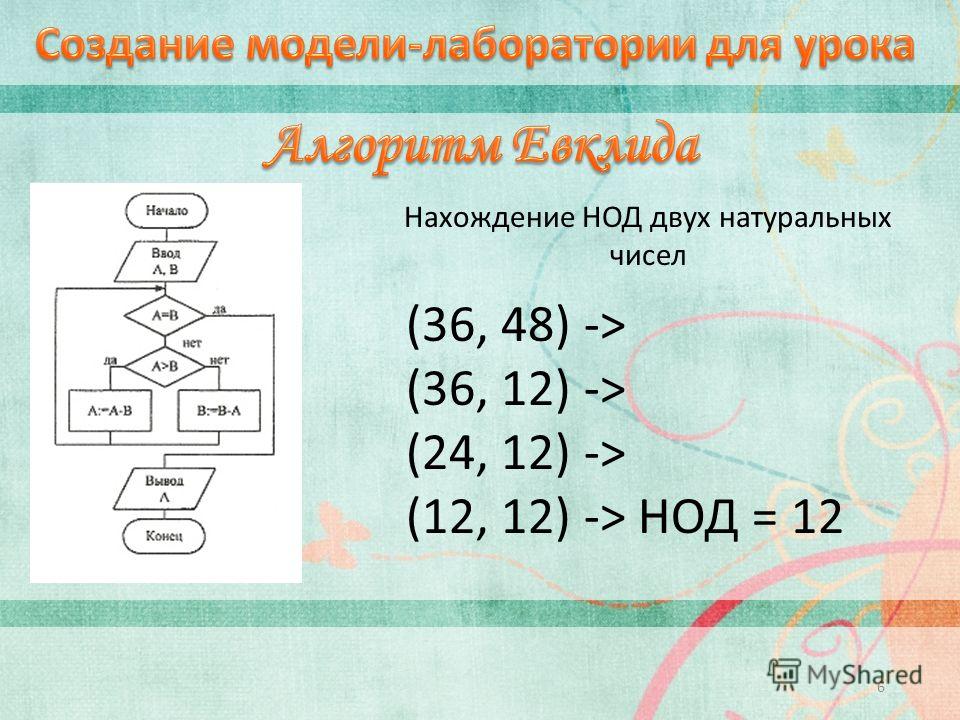 2
2


 Сколько учащихся в классе, если известно, что их больше 25?
Сколько учащихся в классе, если известно, что их больше 25?



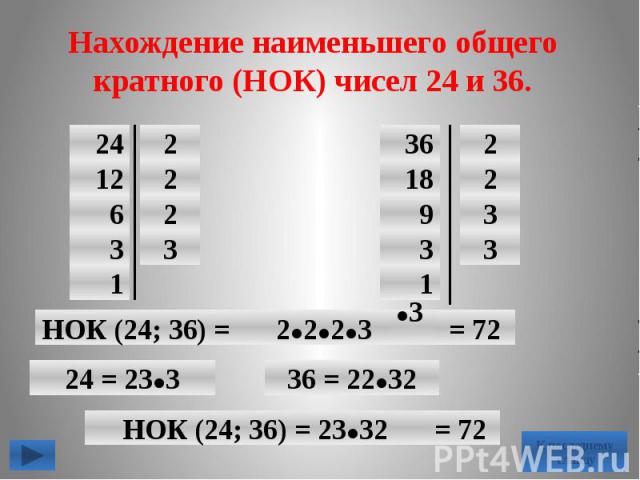 2-2
слот 0: контроллер Gigabit Ethernet 82580
e0f MAC-адрес: 00:a0:98:55:75:77 (auto-unknown-fd-down)
MAC-адрес e0e: 00:a0:98:55:75:76 (авто-1000t-fd-up)
Тип устройства: 1516
Версия прошивки: 3.1d 0x8000021A
2-2
слот 0: контроллер Gigabit Ethernet 82580
e0f MAC-адрес: 00:a0:98:55:75:77 (auto-unknown-fd-down)
MAC-адрес e0e: 00:a0:98:55:75:76 (авто-1000t-fd-up)
Тип устройства: 1516
Версия прошивки: 3.1d 0x8000021A
 1d 0x8000021A
1d 0x8000021A
