Ньютон (единица измерения) | это… Что такое Ньютон (единица измерения)?
У этого термина существуют и другие значения, см. Ньютон.
Ньютон (обозначение: Н) — единица измерения силы в Международной системе единиц (СИ). Принятое международное название — newton (обозначение: N).
Ньютон — производная единица. Исходя из второго закона Ньютона она определяется как сила, изменяющая за 1 с скорость тела массой 1 кг на 1 м/с в направлении действия силы. Таким образом, 1 Н = 1 кг·м/с2.
Единица названа в честь английского физика Исаака Ньютона, открывшего законы движения и связавшего понятия силы, массы и ускорения. В своих работах, однако, Исаак Ньютон не вводил единиц измерения силы и рассматривал её как абстрактное явление.[1] Измерять силу в ньютонах стали спустя более чем два века после смерти великого учёного, когда была принята система СИ.
Содержание
|
Связь с другими единицами
С другими единицами измерения силы ньютон связывают следующие выражения:
- 1 Н = 105дин.
- 1 Н ≈ 0,10197162 кгс.
- 1 Н = 10−3стен.
- 1 Н ≈ 8,262619·10−45Fp.
- 1 Н ≈ 0,224808943 lbf.
- 1 Н ≈ 7,233013851 pdl.
Кратные и дольные единицы
Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 101 Н | деканьютон | даН | daN | 10−1 Н | дециньютон | дН | dN |
| 102 Н | гектоньютон | гН | hN | 10−2 Н | сантиньютон | сН | cN |
| 103 Н | килоньютон | кН | kN | 10−3 Н | миллиньютон | мН | mN |
| 106 Н | меганьютон | МН | MN | 10−6 Н | микроньютон | мкН | µN |
| 109 Н | гиганьютон | ГН | GN | 10−9 Н | наноньютон | нН | nN |
| 1012 Н | тераньютон | ТН | TN | 10−12 Н | пиконьютон | пН | pN |
| 1015 Н | петаньютон | ПН | PN | 10−15 Н | фемтоньютон | фН | fN |
| 1018 Н | эксаньютон | ЭН | EN | 10−18 Н | аттоньютон | аН | aN |
| 1021 Н | зеттаньютон | ЗН | ZN | 10−21 Н | зептоньютон | зН | zN |
| 1024 Н | йоттаньютон | ИН | YN | 10−24 Н | йоктоньютон | иН | yN |
| применять не рекомендуется | |||||||
Примеры
| Описание | Значение |
|---|---|
| Сила, действующая на электрон со стороны ядра атома водорода | 3,6967·10−10 Н |
| Сила, которая давила бы на солнечный парус спутника Космос 1 в случае его успешного запуска | 3,5343·10−3 Н |
Вес тела массой 102 г (т. е. сила гравитации, действующая на это тело на поверхности Земли) | 1 Н |
| Сила притяжения, действующая на человека массой 70 кг | 686 Н |
| Суммарная сила давления воздуха на тело человека [2] (при нормальных условиях) | 202 650 Н |
Примечания
- ↑ Механика Ньютона. Марио Льоцци
- ↑ Площадь тела человека приближённо принята за 2 м²
Так было ли яблоко? Тайны великого девственника Исаака Ньютона | История | Cвободное время
В научном календаре 4 января отмечено как День Ньютона. Именно в этот день 380 лет назад в небольшой британской деревушке Вулсторп родился хилый мальчик. Он появился на свет намного раньше срока и, по мнению его близких, был обречён. Тем не менее младенец выжил, был крещён и назван Исааком в память об отце, который как раз до рождения сына не дожил.
О знаменитом учёном, основоположнике классической механики Исааке Ньютоне сложено много легенд.
«АиФ» вспоминает самые интересные факты его биографии.
Сам сочинил байку о себе
О том, что отдыхавшему в саду Ньютону упало на голову яблоко и это позволило ему открыть закон всемирного тяготения, мы знаем со школьной скамьи. Это самый распространённый миф о нём, и это не более чем байка. Над физической теорией тяжести в те годы задумывались многие исследователи, и её суть не может свестись к одномоментному озарению. Самому Ньютону на то, чтобы сформулировать её, понадобилось около двух десятков лет.
Наблюдение за падающим яблоком, возможно, и навело его на определённые мысли, но расплачиваться за это шишкой на голове учёному не пришлось. Как он уже на склоне лет рассказывал своему биографу Уильяму Стьюкли, однажды, пребывая в созерцательном настроении, он сидел в саду и увидел сорвавшийся с ветки плод. «Почему яблоки всегда падают перпендикулярно земле?» — подумал Ньютон.
Впрочем, некоторые современники и последователи учёного полагали, что история с яблоком была полностью им придумана.
Пытался трактовать Библию
Знаменитый физик был верующим и даже набожным человеком. Факт своего рождения под Рождество он воспринимал как знак свыше. Кроме того, он верил, что Бог избрал его для толкования Библии и обличения тех, кто исказил тексты Нового Завета. Ньютон бы убеждён, что в IV веке Святое Писание было фальсифицировано, а пророчества из Откровения Иоанна Богослова якобы это и предсказывали.
Ещё его интересовали видения пророка Даниила. Он трактовал их как иносказательное изложение политической и церковной истории. Исследователь был уверен, что знает точную дату апокалипсиса. Изучая Книгу пророка Даниила и Откровение Иоанна Богослова, он пришёл к выводу, что мир погибнет не ранее 2060 года. В этом году, согласно предсказаниям Исаака Ньютона, по небу должен пролететь ангел, который возвестит второе пришествие 
Искал философский камень
О том, что Ньютон был алхимиком и посвятил этим исследованиям около 30 лет, при его жизни не было известно. Свои работы на эту тему он никогда не публиковал, с современниками-алхимиками не общался.
Лишь в 1936 году, когда на аукционе были проданы рукописи учёного (их приобрёл экономист Джон Мейнард Кейнс), общественность узнала, что в последние годы своей жизни Исаак Ньютон занимался поисками философского камня – мистической субстанции, способной превращать любой металл в золото и помогать в создании эликсира жизни.
Похоже, великий физик был убеждён, что философский камень реально существует. Он изучал каждую статью об алхимии, какую только мог найти, и экспериментировал с различными веществами в своей лаборатории. Ключевым элементом в создании эликсира, дарующего вечную жизнь, учёный, по всей видимости, считал ртуть.
Ради алхимических экспериментов он забрасывал занятия математикой и физикой. Но, как считают историки, изучавшие биографию Ньютона, он искал философский камень вовсе не для того, чтобы обогатиться.
Его больше привлекала нравственная сторона алхимии: среди оставленных им бумаг находят множество молитв о даровании философского камня, обещаний не употреблять его для собственного обогащения и охранять полученный секрет от грешников.
Объяснил радугу
Исаак Ньютон был первым, кто доказал, что белый цвет раскладывается на смесь цветов спектра. Как-то он купил на ярмарке обычную стеклянную призму, с которой впоследствии провёл множество экспериментов. Их итогом стал трактат «Оптика», изданный в 1704 году. В нём физик изложил фундаментальные законы, касающиеся преломления света через призмы и линзы, и разъяснил причины возникновения такого всем хорошо известного явления, как радуга.
Ньютон продемонстрировал, что обычный свет искривляется (преломляется) под разными углами, когда проходит через стеклянную призму, и распадается на красочную гамму, состоящую из красного, оранжевого, жёлтого, зелёного, голубого, синего и фиолетового.
Эту смесь он впервые назвал спектром.
Чуть не сошёл с ума
В расцвете жизненных сил, приблизившись к возрасту 50 лет, Ньютон серьёзно заболел. Это было похоже на психическое расстройство: учёный безвылазно сидел дома, ударился в мистику, изредка заходившие друзья находили его невыносимым, а близкие опасались за его рассудок.
Было время, он почти не спал и не притрагивался к еде, а как-то провёл без сна пять ночей. У него стали возникать параноидальные мысли, что его хотят схватить, а то и вовсе убить. Также он опасался, что друзья хотят втянуть его в отношения с женщинами. Тут стоит сказать, что Исаак Ньютон никогда не был женат и, похоже, до конца своих дней оставался девственником. Он говорил, что целомудрие помогает ему творить.
Через пару лет душевное здоровье учёного полностью восстановилось. Историки склоняются к мысли, что причиной временного помешательства ума стало отравление ртутью в ходе алхимических опытов.
Исследование его волос в ХХ веке показало очень высокую концентрацию этого элемента.
На могиле Исаака Ньютона красуется надпись, перечисляющая его научные заслуги, а завершается эпитафия словами, к которым нечего прибавить: «Да возрадуются смертные, что среди них жило такое украшение рода человеческого».
Расширяющаяся Вселенная глазами Ньютона
Расширяющаяся Вселенная глазами Ньютона Авторское право © Майкл Ричмонд. Эта работа находится под лицензией Creative Commons License.Это обсуждение близко следует версии, напечатанной в Введение в современную астрофизику Брэдли В. Кэрролл и Дейл А. Остли, в главе 27. книга Шнайдера охватывает те же идеи в разделе 4.2.
Сегодня мы рассмотрим два вопроса:
- как универсальное расширение должно меняться со временем?
- как мы можем измерить такие изменения?
Мы будем следовать упрощенной версии космологии,
тот, в котором космологическая постоянная предполагается
быть нулем.
Мне легче понять сложные идеи
если я начну с простого случая и добавлю сложности позже…
Ньютоновская механика применительно к Вселенной
Представьте, что Вселенная однородна и однородна, заполнены веществом, имеющим одинаковую плотность повсюду. Запишем плотность материала как р(т) , поэтому в настоящее время это имеет значение р(т 0 ) , Рассмотрим сферическую оболочку из материала радиуса
Что произойдет с оболочкой с течением времени?
Ответ не слишком сложно понять. Можно провести близкую аналогию с движением пушечное ядро, выпущенное вертикально вверх из поверхности Земли. Есть два варианта с практической точки зрения, или три, если один математик.
- мяч падает на землю
- мяч не падает на землю
- (мяч не падает на землю более энергично)
То же верно и для этой оболочки из материала.
Давайте продемонстрируем.
Поскольку Вселенная однородна, гравитационные силы из всего материала ВНЕ оболочки гасят друг друга. Это означает, что динамика оболочки зависит только на всю заключенную в нем массу. Предположим, что специфические движения материи настолько малы, по сравнению с крупномасштабным движением оболочки в целом, что внутренняя масса не меняется при расширении оболочки.
Сам снаряд имеет какую-то массу м . Мы можем записать полную энергию оболочки в виде суммы его кинетическая и гравитационная потенциальные энергии. По причинам, которые станут ясны позже, Я напишу эту общую энергию одним особым способом.
Теперь, как упоминалось
в предыдущей лекции
астрономы разбивают расстояние до объекта на часть
который не меняется при расширении,
называется «сопутствующей координатой» и
обозначается как ω с тильдой над ним,
и часть, которая делает,
называется «масштабным коэффициентом» и записывается как a(t) .
Если мы заменим
где
и сделать небольшое упрощение, мы заканчиваем с
Давайте остановимся на мгновение и посмотрим на результат. В левой части показаны два члена, которые в сумме дают образуют полную механическую энергию (на единицу массы) нашей оболочки материи, а значит, и правая часть должна быть пропорциональна этому энергия. Каковы возможности?
- к > 0
- В этом случае полная энергия отрицательна, что означает, что гравитационная потенциальная энергия больше по величине, чем кинетическая энергия. Это соответствует пушечному ядру, выпущенному вверх с начальная скорость меньше, чем скорость убегания. Оболочка какое-то время будет расширяться, но со временем остановиться, а затем вернуться к себе.
- к = 0
- В этом случае полная энергия равна нулю,
что означает, что гравитационная потенциальная энергия
по модулю равна кинетической энергии. Это соответствует пушечному ядру, выпущенному вверх с
начальная скорость, точно равная
скорость убегания.
Оболочка будет расширяться, всегда замедляясь
но никогда не достигает скорости, равной нулю.
- к < 0
- В этом случае полная энергия положительна, что означает, что гравитационная потенциальная энергия по величине меньше кинетической энергии. Это соответствует пушечному ядру, выпущенному вверх с начальной скоростью больше скорости убегания. Оболочка будет расширяться навсегда.
Это соответствует пушечному ядру, выпущенному вверх с
начальная скорость, точно равная
скорость убегания.
Оболочка будет расширяться, всегда замедляясь
но никогда не достигает скорости, равной нулю.Что такое критическая плотность?
Конечно, было бы неплохо выяснить судьбу наша вселенная. Давайте посмотрим, есть ли способ преобразовать это выражение в тот, который содержит наблюдаемые величины.
Вы можете вспомнить из
предыдущая лекция
что параметр Хаббла H(t) связан
к масштабному коэффициенту a(t) и скорости его изменения.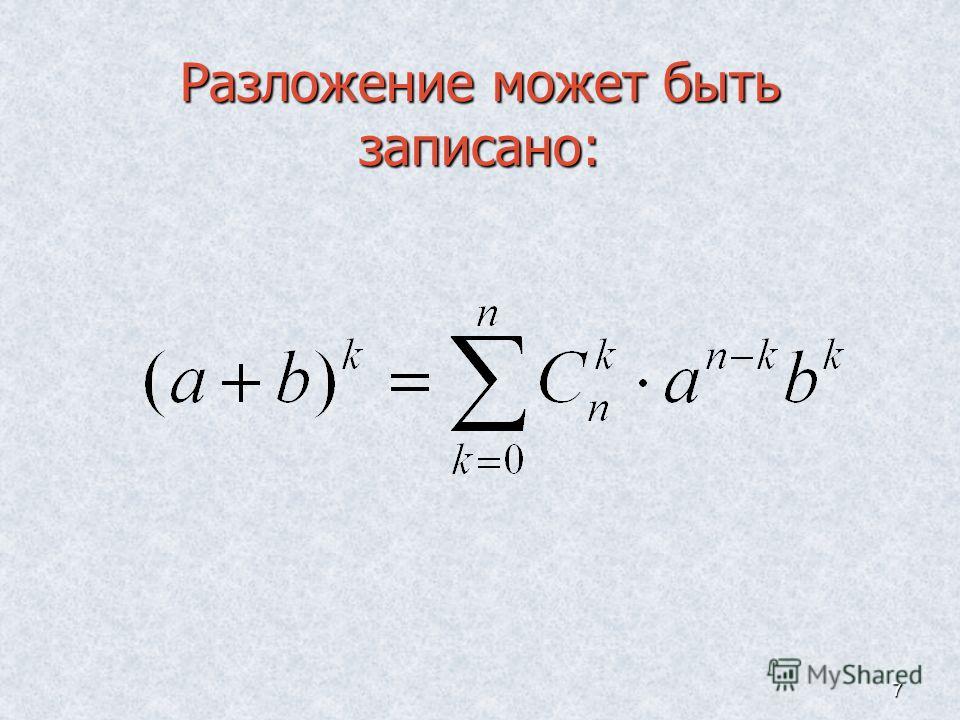
Если мы подставим это выражение в наше предыдущее «энергетическое уравнение», мы заканчиваем с
Теперь это уравнение справедливо для любого выбора времени. Обратите внимание, что правая часть вообще не меняется — все действие находится в терминах слева. Если мы сможем измерить некоторые значения, которые появляются на в левой части при ЛЮБОМ выборе времени мы можем вычислить значение правой части раз и навсегда. Тот, в свою очередь, расскажет нам о судьбе Вселенной.
Итак, какое время выбрать? Как насчет …. ПРЯМО СЕЙЧАС! Я буду использовать сокращение для t = теперь , поместив нулевой индекс количества; который превращает H(t) в H 0 , которые могут показаться вам знакомыми.
В: Каково значение H 0 ?
В: Каково значение 0 ?
В: Можете ли вы вычислить стоимость
критическая плотность Вселенной при
текущее время?
Критическая плотность является важной величиной, но если
указывает его в граммах на кубический сантиметр или кг на кубический метр
или атомов на кубический метр,
кажется, что он всегда включает большой отрицательный показатель.
Для удобства космологи часто обсуждают этот вопрос.
плотность относительным образом:
Нижний индекс «М» относится ко всей материи, как обычная барионная, так и экзотическая темная материя.
Каково значение Ω M ? Есть много способов его измерить..
Рисунок взят из
Шиндлер, ССРв 100, 299 (2002)
…. но вывод довольно ясен: это не близко к критическому значению. Это означает, что если Вселенная настолько проста, как мы предположили, он будет расширяться навсегда.
Вычисление эволюции масштабного фактора
Итак, у нас есть хорошее качественное представление для будущего нашей (слишком упрощенной) Вселенной; Можем ли мы сделать его более количественным? Мы знаем, как быстро Вселенная расширяется здесь и сейчас, и у нас есть некоторые меры плотности материи; это означает, что мы должны быть в состоянии вычислить будущая скорость расширения и размер Вселенной, верно?
Верно.
Вернемся к более ранней версии
«энергетическое уравнение» для оболочки материи
в единой вселенной.
Плотность вещества меняется со временем, а масштабный фактор меняется со временем… но общее количество материи внутри оболочки НЕ меняется со временем.
Мы можем использовать это соотношение, чтобы создать дифференциальное уравнение для масштабного коэффициента как функции времени.
Вот оно: дифференциальное уравнение для масштабного фактора и его первой производной. Теперь мы знаем значение коэффициента масштабирования, и значение скорости изменения сейчас, так что по идее мы должны быть в состоянии вычислить значение коэффициента масштабирования для любого произвольное время в будущем или прошлом. Конечно, мы можем не знать точно, какое значение константы в правой части есть, но мы можем выяснить результат для каждой из возможностей.
- к > 0
- В этом случае оболочка материи в конце концов
перестать расширяться и свернуть на себя. Записать решение в аналитической форме не так сложно
если мы выберем параметрический подход.
- к = 0
- В этом случае оболочка материи никогда не остановится
расширяется, но будет асимптотически приближаться к нулевой скорости.
- к < 0
- При этом оболочка материи вечно расширяется
и не приближается к нулевой скорости.
Опять же, параметрическое решение написать несложно:
Записать решение в аналитической форме не так сложно
если мы выберем параметрический подход. Ниже приведен график, показывающий изменение коэффициента масштабирования.
как функция времени для трех вариантов Ом М .
По горизонтальной оси отложено время, но не единицы измерения.
секунды или годы или гигагоды;
вместо этого они указаны в единицах «времени Хаббла».
Одно «хаббловское время» — это просто обратная величина
текущее значение параметра Хаббла.
Для грубых целей, один звонок скажем
что одно время Хаббла составляет около 10 млрд лет,
для нынешней вселенной, в которой мы живем.
Несмотря на то, что каждая вселенная имеет очень разные масштабные коэффициенты в далеком будущем, их не так просто отличить либо в ближайшем будущем, или, что более важно, в недалеком прошлом.
Добавление красного смещения к миксу
Итак, у нас есть способ описать масштабный коэффициент как функцию времени. Это хорошо, но это не совсем помочь астрономам-наблюдателям. Когда мы получаем изображения и спектры удаленных объектов, мы не получаем метку времени, говорящую нам, когда излучался свет. Тем не менее, мы ДЕЙСТВИТЕЛЬНО получаем одну часть информации, которая говорит нам что-то эквивалентное времени: красное смещение з .
Красное смещение обычно выражается в терминах испускаемого и наблюдаемые длины волн света, но с тем же успехом его можно записать в терминах масштабные коэффициенты во время излучения и наблюдения.
Вопрос: Напишите уравнение, выражающее красное смещение.
z с точки зрения , шкала
фактор в момент испускания света.
Вопрос: Напишите уравнение, выражающее
масштабный коэффициент и в то время
когда свет излучался как функция
красного смещения з .
Вопрос: Напишите уравнение, выражающее
масштабный коэффициент и в то время
когда свет излучался как функция
красного смещения з .
Поскольку у нас есть процедуры для вычисления масштаба фактор как функция времени, мы можем использовать эти отношения между красное смещение и масштабный коэффициент составлять таблицы или графики красное смещение как функция времени.
Параметр замедления q
Параметр Хаббла связан со скоростью в масштабный коэффициент которого меняется со временем; можно подумать об этом как о чем-то вроде «скорость» масштабного фактора. Иногда полезно обсудить вторая производная масштабного коэффициента — что-то вроде его «ускорения».
Космологи приняли параметр замедления q в качестве меры этого свойства масштаб. Формально он определяется как
но для простой вселенной, которую мы рассматриваем сегодня, который содержит только материю (и не космологический постоянный),
Если рассматривать значение этого параметр в текущее время, к 0 , мы видим (снова) космологический параметр, который можно разделить на три важные области:
- q 0 > 0,5
- Вселенная быстро замедляется,
так что он перестает расширяться и разрушается сам по себе.
- q 0 = 0,5
- Замедление вызывает расширение Вселенной асимптотически приближаться к нулевой скорости, но это никогда не прекращается.
- q 0 < 0,5
- Вселенная замедляется настолько медленно, что он никогда не перестает расширяться.
Правильное расстояние
Наконец-то мы готовы ответить на второй вопрос. изложенное в начале сегодняшней лекции:
- как мы можем измерить такие изменения расширения во времени?
Нам нужно найти способ получить наблюдаемые величины… такие как величины и красные смещения — в обсуждение масштабных факторов. Для этого начнем с метрики Робертсона-Уокера:
«Что это за количество ds », — спросите вы? Ну, в простом случае, когда пространство плоское ( k = 0 ) и статический ( a(t) = 1 ), это выражение для ds превращается в Пространственно-временной интервал.
- События и пространственно-временной интервал
- Пространство-время и импульс-энергия
Это интервал между двумя событиями, который будет
такой же, как измеряется любым инерциальным наблюдателем.
Смущенный? Попробуйте прочитать немного из вводной
курс специальной теории относительности.Так как мы будем наблюдать световые лучи, испускаемые предметами давно и далеко, давайте рассмотрим движение светового луча. Пространственно-временной интервал ds между испускание и поглощение светового луча будет ноль, так
Мы можем проинтегрировать обе части этого уравнения чтобы найти правильное расстояние ω между эмиссией (t = 0 и ω = ω e ) и поглощения (t = t obs и ω = 0 ) светового луча.
Выполнение этого интеграла даст нам
правильное расстояние как функция ВРЕМЕНИ;
но было бы гораздо полезнее иметь
выражение для правильного расстояния как функция
КРАСНОГО СДВИГА.
К счастью, мы знаем, как связано красное смещение и .
к масштабному коэффициенту a , и как масштаб
фактор a связан со временем,
так что можно сделать интеграл по
также красное смещение.
Давайте просто перейдем к результату:
Это сложное уравнение, но его можно свести к довольно простому результат. Если посмотреть на очень маленькое красное смещение, обнаруживается, что расстояния для разных космологических моделей все примерно одинаковые, И все они линейны с красным смещением.
Но при больших красных смещениях расстояния расходятся с между собой и из простой линейной зависимости.
Q: Для случая, когда k = 0 ,
вывести более простое выражение
для правильного расстояния как функции
красного смещения.
Расстояние светимости
Вы помните определение расстояния по светимости?
Если мы знаем светимость L источника,
и измерьте поток f , тогда мы сможем вычислить
расстояние по закону обратных квадратов.
Поскольку теперь у нас есть способ вычислить правильное расстояние до объект как функция красного смещения, может показаться ненужным вычислять светимость расстояние: разве это не то же самое, что и правильное расстояние? Если это так, то мы могли бы просто написать:
- замедление времени
- Когда мы смотрим на свет, излучаемый удаленным объектом,
мы измеряем события в ссылке на этот объект
кадр происходит с другой скоростью, чем наблюдатели
в системе отсчета этого объекта.
Если наблюдатели в какой-нибудь галактике вспыхивают один раз в
секунда ( Δt источник = 1 с ), и мы наблюдаем эту галактику с красным смещением z = 1 , будем измерять продолжительность между вспышками
что больше — одна вспышка каждые две секунды: Δt обс = 2 с . Интервалы между
события связаны между собой Δt наб = Δt источник * (1+z) .
Это приводит к тому, что фотоны реже достигают нашего детектора. в (1+z) раз.
- красное смещение длины волны фотона
- Когда мы смотрим на свет, излучаемый удаленным объектом,
мы воспринимаем его как более длинную волну
чем наблюдатели в системе отсчета объекта.
Другими словами, свет кажется смещенным в красную сторону.
Например, если наблюдатели в какой-нибудь галактике прольют свет
с длиной волны λ источник = 400 Ангстрем ,
и мы наблюдаем эту галактику с красным смещением
из г = 1 , будем измерять длину волны
что больше: λ obs = 800 Ангстрем . Длины волн
связаны λ наб = λ источник * (1+z) .
Поскольку длина волны каждого фотона больше, энергия, которую он несет, меньше: E наб = E источник / (1+z) .
Интервалы между
события связаны между собой Δt наб = Δt источник * (1+z) .
В зависимости от типа детектора, который мы используем для измерения света издалека. объекта, мы найдем поток, отличный от наивного ожидания на другую сумму.
Если мы используем детектор, который считает фотоны, такие как ПЗС, тогда мы будем страдать от фактора замедления времени; но если мы должным образом учтем сдвиг в полоса пропускания между кадрами источника и наблюдателя, на нас не повлияет уменьшение энергии каждого фотон. Мы можем определить расстояние светимости на основе фотонов вот так:
С другой стороны, если мы используем детектор, который преобразует входящий поток энергии в выходной сигнал, как болометр, то на нас влияет как замедление времени и уменьшение энергии каждого фотона. В этом случае — который описан в большинстве учебников — мы можем определить расстояние светимости на основе энергии вот так:
Как только мы получим правильное выражение для светимости расстояния,
мы можем использовать его для вычисления модуля расстояния
объект с любым конкретным красным смещением.
Это означает, что мы, наконец, можем начать сравнивать
модели Вселенной с различными космологическими
параметров к фактически наблюдаемым величинам.
Рисунок взят из
Рисс и др., ApJ 659, 98 (2007)
Для дополнительной информации
- Шиндлер, ССРв 100, 299 (2002) обобщает результаты многих исследований плотности материи во Вселенной.
- Обсуждение экспертов в 1978 г. о том, как можно измерить плотность материи во Вселенной.
- Фельтен и Исаакман, RvMP 58, 689 (1986) предоставить алгоритмы для вычисления эволюции масштабный коэффициент Вселенной, включая ненулевую лямбду.
- Рисс и др., ApJ 607, 665 (2004) прекрасно сочетает теорию и наблюдение.
- Кэрролл, Пресс и Тернер, ARA&A 30, 499 (1992).
выводит многие уравнения, определяющие расстояние светимости
и правильное расстояние и т. д., и делают это
для общего случая, включающего космологическую постоянную.
д., и делают это
для общего случая, включающего космологическую постоянную.Авторское право © Майкл Ричмонд. Эта работа находится под лицензией Creative Commons License.
| |||||||||||||||||||||||
Ключевое слово SearchAdvanced Поиск Поисковые книги для: Советы по поиску
| |||||||||||||||||||||||
