Интерактивный учебник языка Python
1. Множества
Множество в языке Питон — это структура данных, эквивалентная множествам в математике. Множество может состоять из различных элементов, порядок элементов в множестве неопределен. В множество можно добавлять и удалять элементы, можно перебирать элементы множества, можно выполнять операции над множествами (объединение, пересечение, разность). Можно проверять принадлежность элемента множеству.
В отличие от массивов, где элементы хранятся в виде последовательного списка, в множествах порядок хранения элементов неопределен (более того, элементы множества хранятся не подряд, как в списке, а при помощи хитрых алгоритмов). Это позволяет выполнять операции типа “проверить принадлежность элемента множеству” быстрее, чем просто перебирая все элементы множества.
Элементами множества может быть любой неизменяемый тип данных:
числа, строки, кортежи. Изменяемые типы данных не могут быть
элементами множества, в частности, нельзя сделать элементом
множества список (но можно сделать кортеж) или другое множество.
Задание множеств
Множество задается перечислением всех его элементов в фигурных скобках.
Исключением явлеется пустое множество, которое можно создать при помощи
функции set(). Если функции set передать в качестве
параметра список, строку или кортеж, то она вернёт множество, составленное из элементов
списка, строки, кортежа. Например:
A = {1, 2, 3}
A = set('qwerty')
print(A)выведет {'e', 'q', 'r', 't', 'w', 'y'}.
Каждый элемент может входить в множество только один раз, порядок задания элементов неважен. Например, программа:
A = {1, 2, 3}
B = {3, 2, 3, 1}
print(A == B)выведет True, так как A и B — равные
множества.
Каждый элемент может входить в множество только один раз. set('Hello') вернет множество из четырех элементов: {'H', 'e', 'l', 'o'}.
Работа с элементами множеств
Узнать число элементов в множестве можно при помощи функции len.
Перебрать все элементы множества (в неопределенном порядке!) можно при помощи цикла for:
primes = {2, 3, 5, 7, 11}
for num in primes:
print(num)Проверить, принадлежит ли элемент множеству можно при помощи операции in, возвращающей значение типа bool.
Аналогично есть противоположная операция not in.
Для добавления элемента в множество есть метод add:
A = {1, 2, 3}
print(1 in A, 4 not in A)
A.add(4)Для удаления элемента x из множества есть два метода: discard и remove. Их поведение различается
только в случае, когда удаляемый элемент отсутствует в множестве.
В этом случае метод remove генерирует исключение KeyError.
Наконец, метод pop удаляет из множества один случайный
элемент и возвращает его значение. Если же множество пусто, то генерируется
исключение
Если же множество пусто, то генерируется
исключение KeyError.
Из множества можно сделать список при помощи функции list.
Операции с множествами
С множествами в питоне можно выполнять обычные для математики операции над множествами.
A | B A.union(B) | Возвращает множество, являющееся объединением множеств | |
A |= B A.update(B) | Добавляет в множество | |
A & B A.intersection(B) | Возвращает множество, являющееся пересечением множеств | |
A &= B A.intersection_update(B) | Оставляет в множестве | Записывает в |
A <= B A.issubset(B) | Возвращает | |
A >= B A.issuperset(B) | Возвращает | |
A < B | Эквивалентно | |
A > B | Эквивалентно |
Ссылки на задачи доступны в меню слева. Эталонные решения теперь доступны на странице самой задачи.
как обозначается, определение, формула, примеры
Содержание:
-
Что такое объединение и пересечение множеств А и Б
- Понятие и свойства объединения множеств
- Понятие и свойства пересечения множеств
- Правила нахождения пересечений и объединений, формулы
- Исследование множеств с помощью координатной прямой
-
Как определить пересечение и объединение при помощи изображений числовых множеств
- Изображение пересечения
- Изображение объединения
-
Основные законы операций объединения и пересечения множеств
- Закон коммутативности
- Закон ассоциативности
- Закон дистрибутивности
Содержание
-
Что такое объединение и пересечение множеств А и Б
- Понятие и свойства объединения множеств
- Понятие и свойства пересечения множеств
- Правила нахождения пересечений и объединений, формулы
- Исследование множеств с помощью координатной прямой
-
Как определить пересечение и объединение при помощи изображений числовых множеств
- Изображение пересечения
- Изображение объединения
-
Основные законы операций объединения и пересечения множеств
- Закон коммутативности
- Закон ассоциативности
- Закон дистрибутивности
Что такое объединение и пересечение множеств А и Б
Множество — это совокупность объединенных по какому-либо признаку объектов любой природы.
Оно может состоять из чисел, букв, прямых, точек, слов и т.д. Эти объекты, которые совокупно образуют данное множество, являются его элементами или точками.
Для обозначения множеств применяют заглавные буквы латинского алфавита. А их элементы обозначают строчными буквами. Например, запись\( x\in K\) означает, что х является элементом множества \(К.\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Множество называется подмножеством, когда оно возникает не как самостоятельный объект, а когда оно является частью другого множества, и все его элементы также являются элементами другого множества. Записывается как \(А\;\subset\;Б.\)
Если множества А и Б содержат одинаковые элементы, то они равны:
\(А\;\subset\;Б\) и \(Б\;\subset\;А.\)
Если множество не содержит в себе ни одного элемента, то оно называется пустым и является подмножеством любого множества.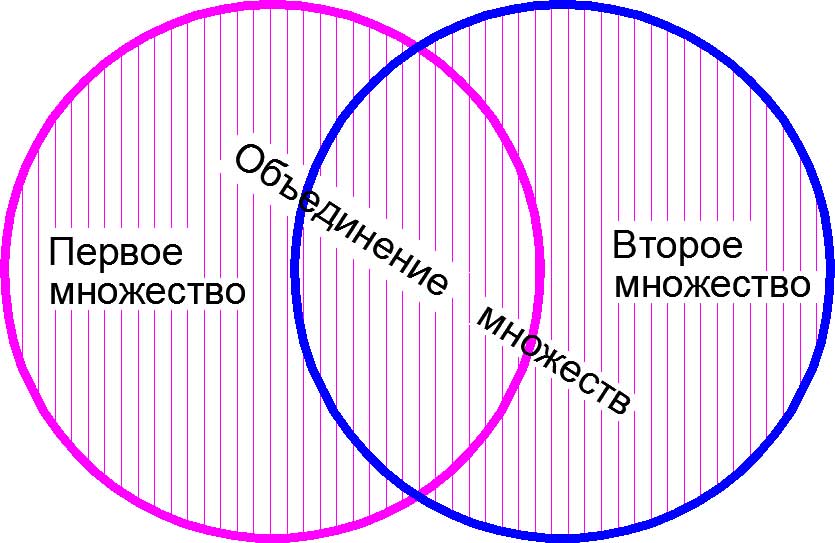 Оно обозначается символом \(Ø.\)
Оно обозначается символом \(Ø.\)
Если пустое множество пересекается с другим, то их общее множество будет так же пустым:
\(A\;\cap\;Б\;=\;\varnothing.\)
Если множества равны, то всякий элемент х, принадлежащий правой части равенства, принадлежит и левой, и наоборот.
Основные операции с множествами подразделяются на:
- пересечение;
- объединение;
- вычитание;
Понятие и свойства объединения множеств
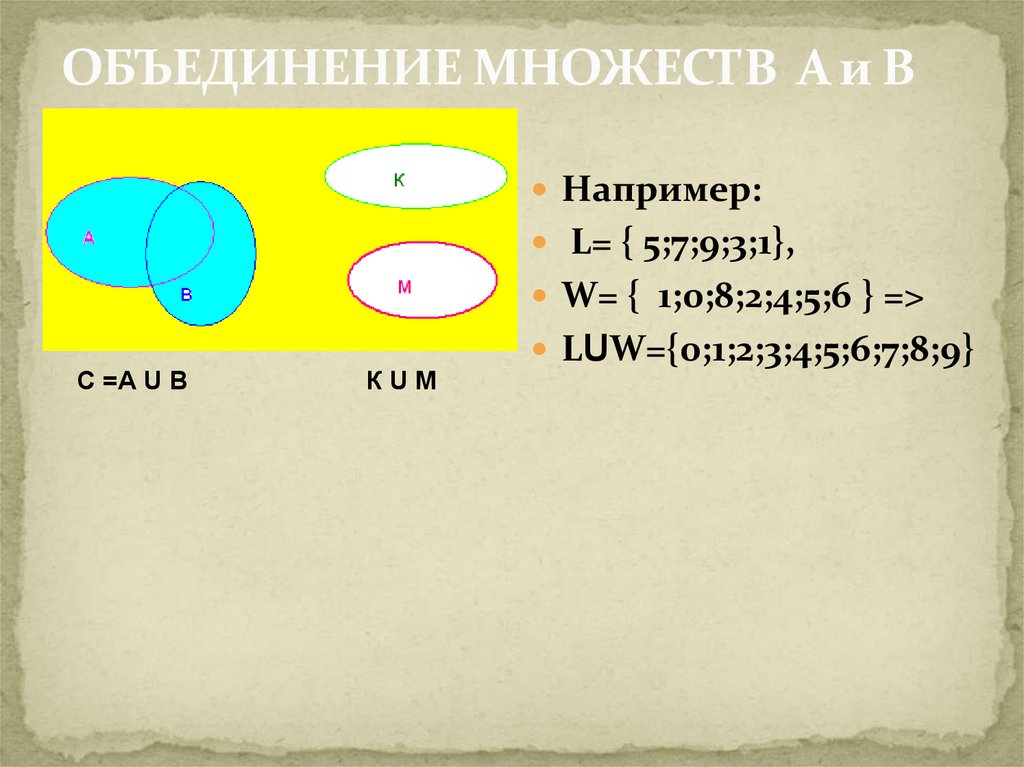
Множество С называют объединением (или суммой) множеств А и Б, если его элементы принадлежат хотя бы одному из указанных множеств. То есть в множестве С содержатся элементы как А, так и Б, и любое множество, которое будет обладать этим свойством, будет содержать С.
Объединение С множеств А и Б обозначается таким образом:
\(C=A\cup Б\)
\(A\;\cap\;Б\;=\;\left\{\left.х\right|\;х\in\;А\;или\;х\;\in\;Б\right\}.\)
Пример
Пусть имеется два множества:
A = {2; 3; 6; 8} и Б = {4; 6; 8; 9}.
Тогда их объединением будет служить множество С = {2; 3; 4; 6; 8; 9}.
Свойства объединений:
Некоторые свойства операции объединений напоминают по своему принципу привычную операцию «сложения» чисел. При этом некоторые свойства объединения, которые соответствуют определенным операциям сложения чисел, будут иметь свои особенности.
Свойства объединения, которые справедливы для любых множеств A, Б и C:
A U Б = Б U A; A U (Б U C) = (A U Б) U C.
\(А\subset А\cup Б\;и\;Б\subset А\cup Б.\)
Кроме того, из включения \(А\subset Б\) следует включение:
\(А\cup С\subset Б\cup С.\)
В частности, любому множеству A соответствует равенство:
\(А\cup А=А.\)
Это равенство означает идемпотентность объединения, то есть повторное осуществление операции по отношению к объекту будет давать тот же результат, что и в первый раз.
А также равенство:
\(А\cup\varnothing=А.\)
Если у множеств А и Б есть общие элементы, то каждый из этих элементов не повторяется в объединении, и входят в него один раз.
Понятие и свойства пересечения множеств
Пересечением множеств А и Б является множество С, включающее в себя элементы, принадлежащие одновременно и А, и Б, то есть элементов, общих для этих множеств.
Пресечение множеств обозначают символом \(∩\):
\(С=А\cap Б\)
\(А\cap Б=\left\{\left.х\right|\;х\in А\;и\;х\in Б\right\}.\)
Пример
Пусть имеется два множества:
A = {2; 3; 6; 8} и Б = {4; 6; 8; 9}; тогда их пересечением будет являться C = {6; 8}.
Свойства пересечений:
Некоторые свойства операции пересечений напоминают по своему принципу привычную операцию «умножения» чисел. При этом некоторые свойства пересечения, которые соответствуют определенным операциям умножения чисел, будут иметь свои особенности.
Свойства пересечения, которые справедливы для любых множеств A, B и C:
A ∩ Б = Б ∩ A; A ∩ (Б ∩ C) = (A ∩ Б) ∩ C.
\(А\cap Б\subset А\;и\;А\cap Б\subset Б.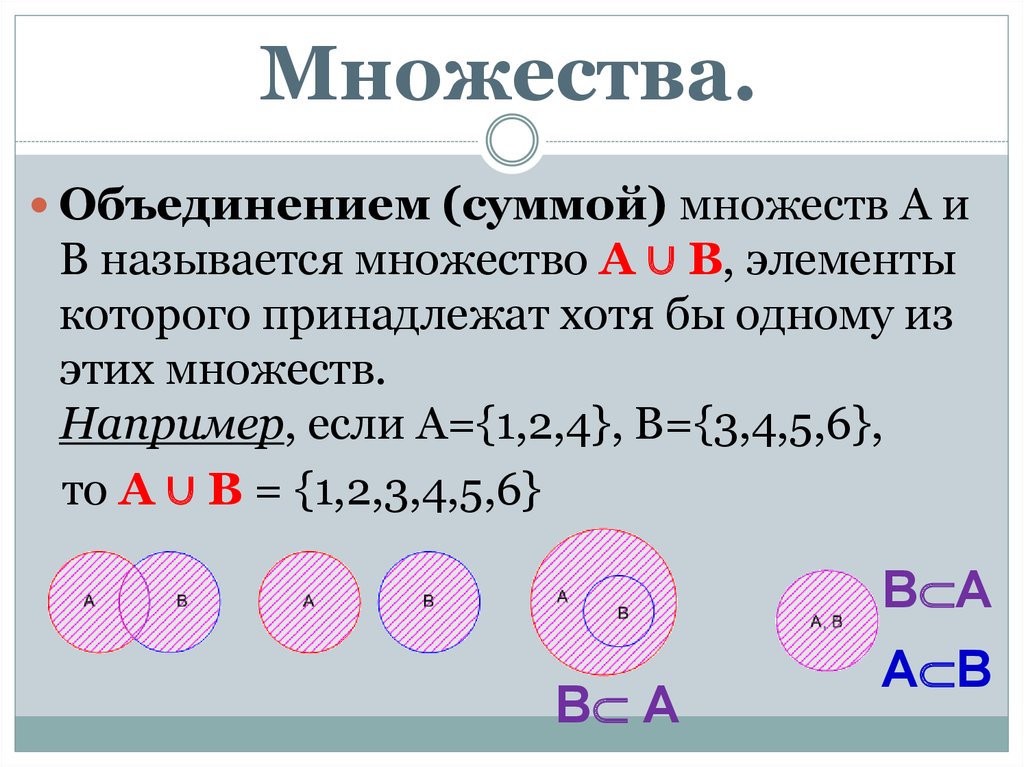 \)
\)
Если у множеств А и Б нет общих элементов, то их пересечением является пустое множество, иначе говорят, что они не пересекаются.
Кроме того, из включения \(А\subset Б\) следует включение:
\(А\cap С\subset Б\cap С.\)
В частности, для любого множества A имеет место равенство\( А\cap\varnothing=\varnothing.\)
Также верно равенство \(А\cap А=А.\)
Здесь, как и в объединении, встречается свойство идемпотентности пересечения. Поэтому здесь не говорят о возведении множества в степени в том привычном смысле, какое применимо к степени числа. Этим операция пересечения отличается от операции умножения чисел, что легко доказывается на различных множествах.
Для произвольной совокупности множеств \(А_\alpha\), где α относится ко всем элементам множества I, \(А_\alpha,\;\alpha\in I\), пишут в случае объединения:
\(C=\underset{\alpha\in I}\cup A_\alpha=\underset\alpha\cup A_\alpha;\)
в случае пересечения:
\(C=\underset\alpha\cap A_\alpha.\)
Правила нахождения пересечений и объединений, формулы
Конечное множестве А обладает мощностью, представляющей собой число элементов.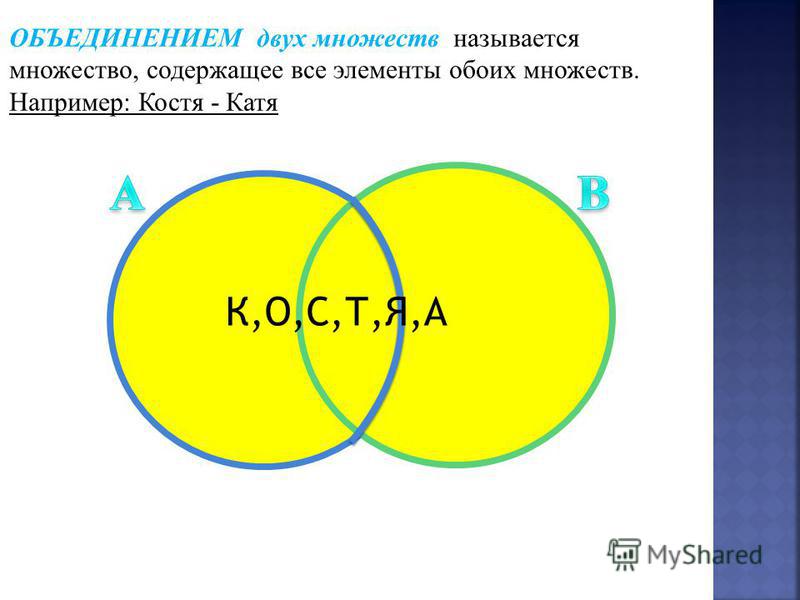 Его обозначают как \(|А|\) или #А.
Его обозначают как \(|А|\) или #А.
Если известны мощности каждого множества и их пересечений, то по следующей формуле можно найти мощность объединения:
\(\left|А\cup Б\right|=\left|А\right|+\left|Б\right|-\left|А\cap Б\right|;\)
\(\left|А\cup Б\cup С\right|=\left|А\right|+\left|Б\right|+\left|С\right|-\left|А\cap Б\right|-\left|А\cap С\right|-\left|Б\cap С\right|+\left|А\cap Б\cap С\right|.\)
Вообще \(\left|А_1\cup…\cup А_n\right|\) равно
\(\sum_i\left|A_i\right|-\sum_{i<J}\left|A_i\cap A_j\right|+\sum_{i<J<k}\left|A_i\cap A_j\cap A_k\right|-….\)
Она называется формулой включений и исключений.
Доказательство
Чтобы доказать это утверждение зафиксируем произвольное множество К. Его подмножествами являются \(A_1,…,A_n.\) Функция \(X_x\) является характеристической функцией множества \(X\subset K\). На элементах Х она равна 1, а на остальных элементах К — равна нулю. Проводимые над подмножествами множества К операции соответствуют операциям с их характеристическими функциями.
В частности, произведение характеристических функций соответствует пересечению множеств:
\(X_{A\cap B}(u)=X_A(u)X_B(u).\)
Если Х является характеристической функцией исходного множества, то дополнению (до К) соответствует функция 1 — Х.
Запишем в виде суммы значений характеристической функции число элементов множества:
\(\left|x\right|=\sum_uX_x(u).\)
Объединение \(A_1\cup…\cup A_n\) представим в виде дополнения к пересечению дополнений множеств \(A_i.\)
Опираясь на термины характеристических функций, получим:
\(X_{A_1\cup…\cup A_n}=1-(1-X_{A_1})…(1-X_{A_n}).\)
Раскроем скобки в правой части:
\(\sum_iX_{A_i}-\sum_{i<j}X_{A_i}X_{A_j}+\sum_{i<j<k}X_{A_i}X_{A_j}X_{A_k}-….\)
Получим формулу включений и исключений, просуммировав правую и левую части по всем элементам К. которые являются функциями на К.
Исследование множеств с помощью координатной прямой
Координатная прямая — прямая линия, содержащая начало отсчета, единичный отрезок и направление.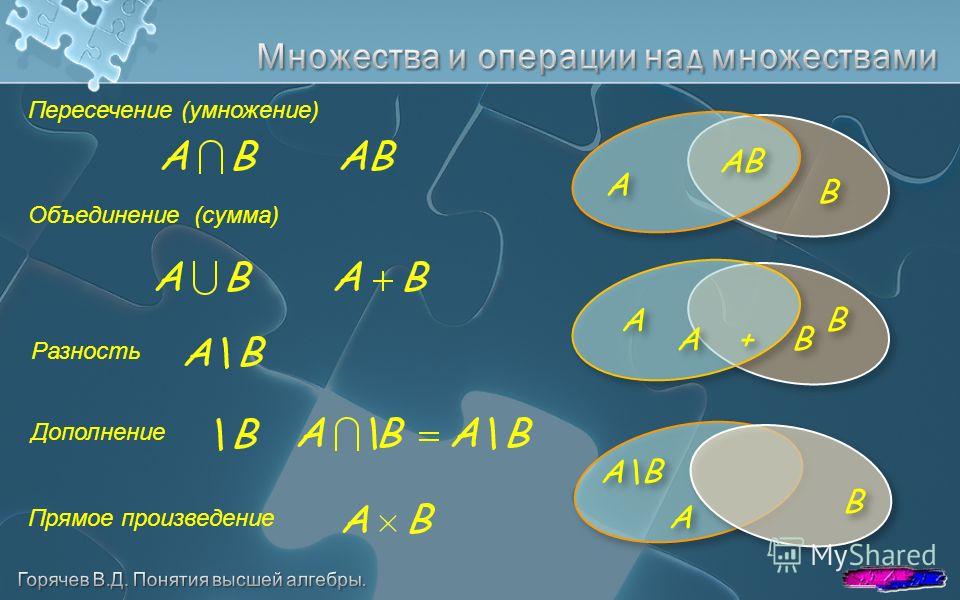
Для любого натурального числа на координатной прямой можно выбрать соответствующую только ему единственную точку. Каждому числу на данной прямой можно подобрать противоположное число, которое расположено симметрично относительно начала отсчета и отличается от другого только знаком.
Также каждому действительному (рациональному или иррациональному) на координатной прямой соответствует единственная точка и, наоборот, для каждой ее точки есть единственное действительное число. Это называется взаимно однозначным соответствием. С учетом этого соответствия,множество R действительных чисел и множество точек координатной прямой часто объединяют общим термином — «числовая прямая».
Ось Оу образована множеством точек х = 0, поэтому ось Оу является графиком уравнения х — 0.
Ось Ох образована множеством точек у = 0, поэтому ось Ох является графиком уравнения у — 0.
Множество точек у = х образует прямую, которая проходит через начало координат и делит I и III квадранты пополам.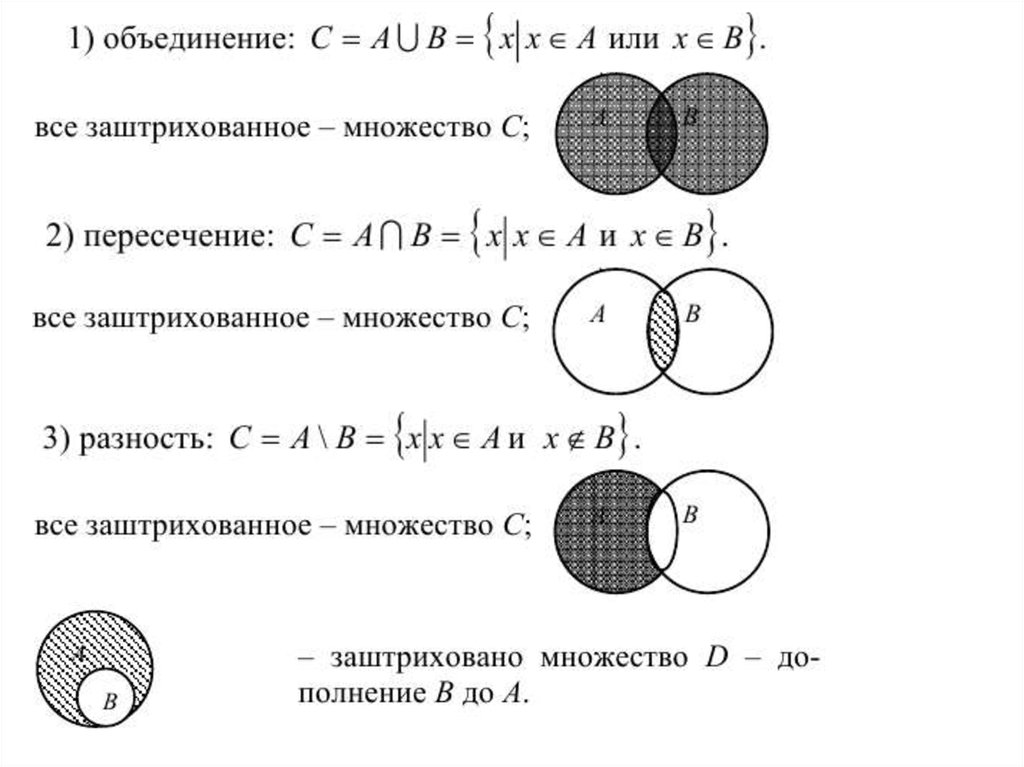
В математике есть важное понятие упорядоченной пары (х, у), которое представлено либо элементами одного и того же множества, либо элементами разных множеств Х и У.
Свойством упорядоченных пар является то, что две упорядоченные пары (\(x_1, y_1)\) и \( (x_2)\) и \((y_2)\) будут называться равными, когда \( x_1=x_2\ и\ y_1=y_2.\)
Первой компонентой (координатой) пары (х, у) является элемент х, второй компонентой (координатой) той же пары — элемент у.
Понятие упорядоченной пары поваляет ввести дополнительную операцию над множествами — прямое или декартово умножение, имеющее вид:
\(X\times Y=\left\{\left.(x,y)\right|\;x\in X,\;y\in Y\right\}\;.\)
Декартово произведение между двумя пересекающимися различными прямыми может быть отождествлено с проходящей через эти прямые плоскостью по правилу \(А = (х, у)\). Это свойство объясняет название умножения и является основой метода координат, который Рене Декартом предложил для решения геометрических задач.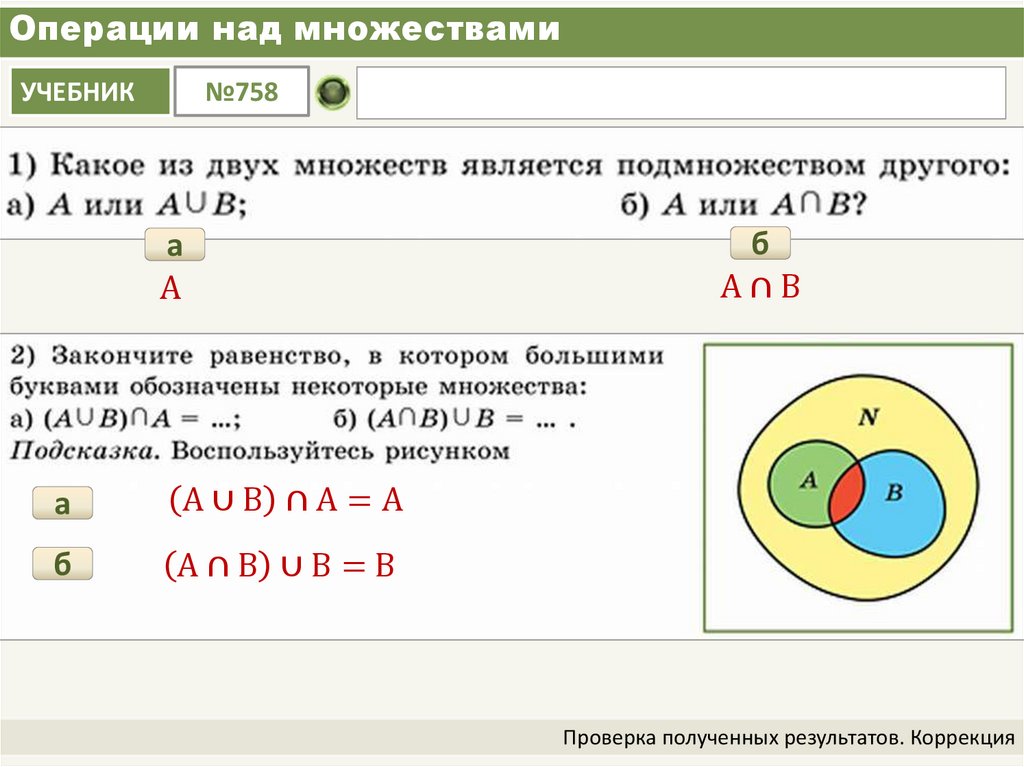
Для определения упорядоченного набора n+1 элементов применяется метод математической индукции:
\((x_1,\;x_2,\;…,\;x_{n+1})=((x_1,\;x_2,\;…,\;x_n),\;x_{n+1}),\;n\geq2.\)
Отсюда выводится произведение множеств:
\(X_1\times X_2\times…X_{n+1}=(X_1\times X_2\times…\times X_n)\times X_{n+1}.\)
Чтобы установить между точками координатной прямой соответствие и между множеством натуральных чисел, на прямой выбирают произвольную точку 0, а затем с помощью единичного отрезка отмечают на ней точки, которым соответствуют натуральные числа.
Пример
Отметим точки 1, 2, 3 и укажем относительно точки 0 соответствующие им симметричные точки. Обозначим их через -1, -2, -3. Числа 1 и -1, 2 и -2 и т. д. на координатной прямой расположены симметрично. Эти числа называются противоположными, то есть они отличаются друг от друга только знаком, а на координатной прямой расположены относительно точки отсчета на одинаковом расстоянии.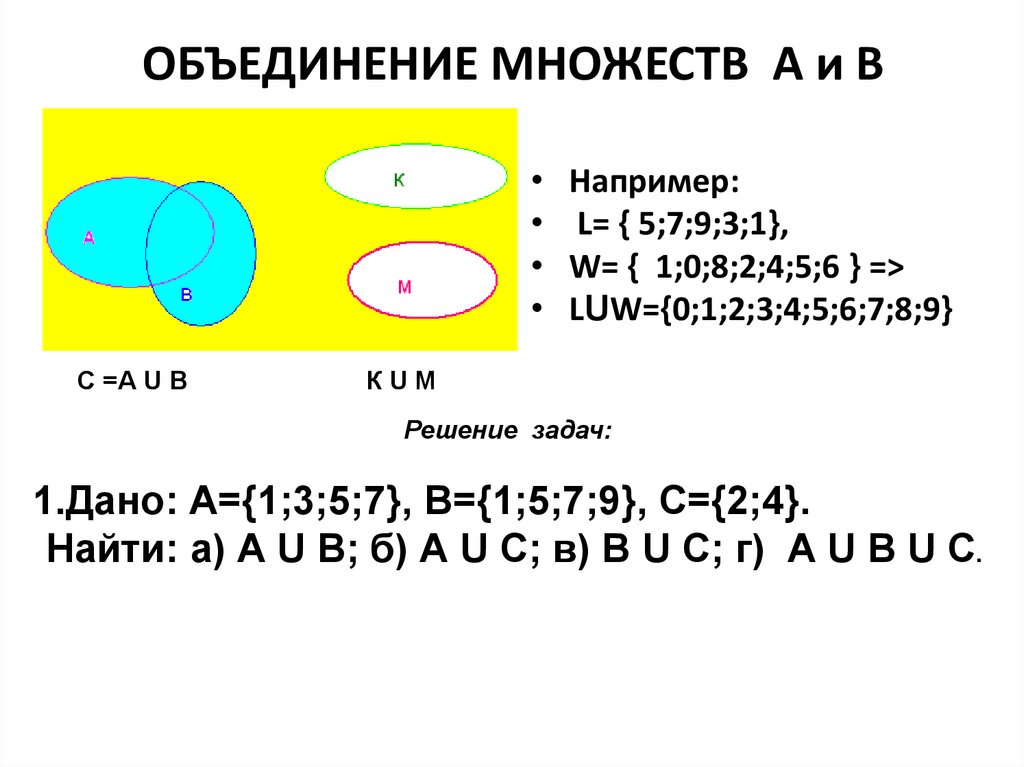
Соответственно, чем правее число расположено на координатной прямой, тем оно больше.
Отсюда следует:
- всякое отрицательное число меньше числа, которое является положительным и больше нуля;
- всякое отрицательное число всегда меньше нуля;
- из двух отрицательных чисел меньше то, модуль которого больше, и наоборот. Например, -4,8 > -6,2, так как|-4,8| < |-6,2|.
Числовые промежутки на координатной прямой имеют обозначения:
- \([a; b] = {x \in R | a ≤ x ≤ b}\) — замкнутый промежуток (или отрезок) с началом а и концом b.
- \((a; b) = {x \in R | a < x < b}\) — открытый промежуток (или интервал).
- \((a;\;b\rbrack=\{x\in R\vert\;a<x\leq b\};\;\lbrack a;\;b)\;=\;\{x\in R\vert\;a\leq x<b\}\) — полуоткрытые промежутки.
- \((a;\;+\infty\rbrack=\{x\in R\vert\;x\geq a\};\;\lbrack-\infty;\;b)\;=\;\{x\in R\vert\;x\leq b\}\) — лучи.
- \((a;\;+\infty)=\{x\in R\vert\;x>a\};\;(-\infty;\;b)\;=\;\{x\in R\vert\;x<b\}\) — открытые лучи.

- \((-\infty;\;+\infty)\;=R\) — числовая прямая.
Как определить пересечение и объединение при помощи изображений числовых множеств
Взаимоотношения и операции между множествами можно наглядно проиллюстрировать, применяя диаграммы Эйлера-Венна. Множества в этих диаграммах чаще всего изображаются в виде кругов и их внутренностями, а в виде прямоугольника изображено универсальное множество U.
В диаграммах Эйлера-Венна имеет значение взаимное расположение, а не их относительный размер.
Изображение пересечения
Рисунки демонстрируют диаграммы Эйлера-Венна, описывающие два множества A и B в случаях, когда \(A\cap B\neq\varnothing\;и\;A\subset B\), соответственно. Множеству \(A\cap B\) на этих рисунках соответствуют части диаграмм со штриховкой.
Рисунок правее демонстрирует что, если A подмножество множества B,\( A\subset B,\;то\;A\cap B=A\), поскольку все элементы множества A будут общими для множеств A и B.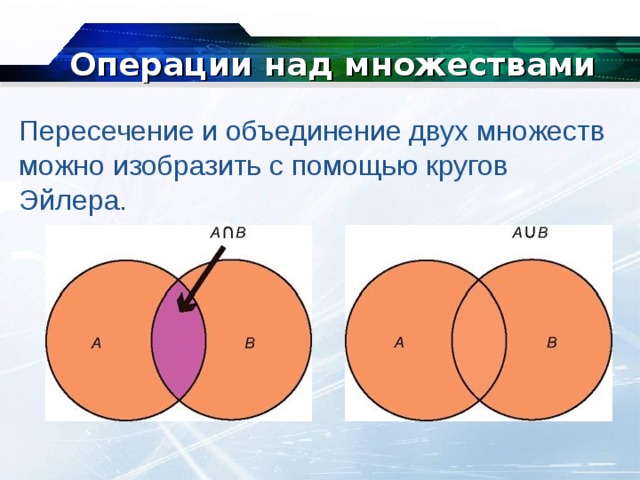
Изображение объединения
На рисунке представлены диаграммы Эйлера-Венна для двух множеств A и B в случаях, когда \(A\cap B\neq\varnothing,\;A\subset B\). Часть диаграммы со штрихами соответствует множеству \(A\cup B.\)
Рисунок демонстрирует, что если A подмножество множества B, т.е.
\(A\subset B,\;то\;A\cup B=B, \)
то раз включать элементы множества А в объединение не требуется, поскольку его элементы принадлежат и множеству B.
Основные законы операций объединения и пересечения множеств
Закон коммутативности
\(A\cup B=B\cup A,\;A\cap B=B\cap A.\)
Коммутативный закон показывает, что изменение порядка множеств в указанных операциях не влияет на их итог. Действительно, множества \(A\cup B\;и\;B\cup A\;\) состоят из элементов, которые относятся хотя бы к одному из множеств A или B, и не содержат никаких других элементов. А множества \(A\cap B\;и\;B\cap A\) включают в себя все элементы, относящиеся к каждому из множеств A и B.
Закон ассоциативности
\(A\cup(B\cup C)=(A\cup B)\cup C,\;A\cap(B\cap C)=(A\cap B)\cap C.\)
Ассоциативность указанных операций позволяет опускать фиксацию посредством скобок порядка проведения операций. Действительно, множества \(A\cup(B\cup C)\;и\;(A\cup B)\cup C\) состоят из всех элементов, входящих хотя бы в одно из множеств A, B и C и не содержат никаких других элементов, а множества \(A\cap(B\cap C)\;и\;(A\cap B)\cap C\) состоят только из общих элементов множеств A, B и C. Заметим, что по закону ассоциативности конечный результат не зависит от порядка действий. Но промежуточные результаты — зависят.
Закон дистрибутивности
\(A\cup(B\cap C)=(A\cup B)\cap(A\cup C),\;A\cap(B\cup C)=(A\cap B)\cup(A\cap C).\)
В числовом случае дистрибутивность умножения относительно сложения позволяет осуществлять вынос общего множителя за скобку и проводить раскрытие скобок. В случае множеств это так же справедливо, при этом соотношений такого рода больше.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Пересечение и объединение множеств
Вы знаете, ученик третьего класса Максим очень хотел объяснить вам эту тему, но немного приболел и прийти сегодня не смог. Но, благодаря Интернету, мы можем с ним связаться.
̶ Здравствуй Максим!
̶ Здравствуйте! Проверьте, чтобы ваши соседи по парте были готовы к уроку. И мы начинаем.
Прослушайте название пар множеств и попытайтесь заметить, что повторяется в каждой паре.
Животные и герои мультфильмов;
Рыбы и птицы;
Материки и части света;
Звёзды и планеты.
Ну, что заметили? Конечно, повторялся слово «и».
Если
в названии множества есть союз «И», то каждый его элемент должен находиться
на пересечении двух множеств, т.е. находиться одновременно в двух
множествах.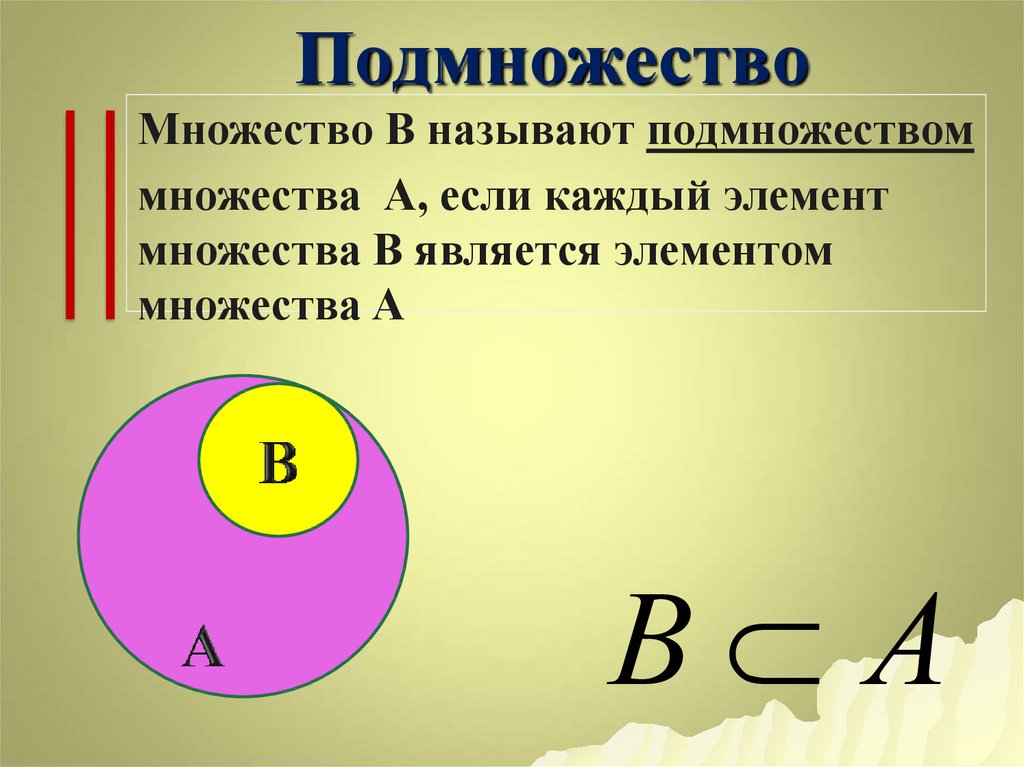 Другими словами мы можем сказать, что пересечение множеств
– это их общая часть.
Другими словами мы можем сказать, что пересечение множеств
– это их общая часть.
А теперь задание.
Необходимо разместить элементы по своим множествам.
Давайте посмотрим, что за элементы. Так это имена мальчиков и девочек: Коля, Ваня, Даша, Игорь, Катя, Саша, Дима, Юля, Ира, Женя. Будем размещать имена мальчиков в синий прямоугольник, а девочек – в розовый. Ага! Так ведь Сашей и Женей могут звать как мальчиков, так и девочек. Значит, эти два имени будут находиться сразу в двух множествах, т.е. на пересечении двух множеств.
Итак,
Коля, Ваня – это мальчики, помещаем эти элементы во множество имён мальчиков.
Даша – имя девочки, помещаем в розовый прямоугольник, где находятся имена
девочек. Игорь – имя мальчика, Катя – имя девочки. Саша, так могут звать и
мальчика, и девочку, значит, этот элемент будет находиться на пересечении
двух множеств. Дима – элемент из множества имён мальчиков. Юля, Ира,
конечно элементы из множества имён девочек. И последнее имя, Женя, это имя
могут иметь как девочки, так и мальчики. Значит, этот элемент будет находиться на
пересечении двух множеств.
Дима – элемент из множества имён мальчиков. Юля, Ира,
конечно элементы из множества имён девочек. И последнее имя, Женя, это имя
могут иметь как девочки, так и мальчики. Значит, этот элемент будет находиться на
пересечении двух множеств.
Теперь все имена находятся в своих множествах.
А сейчас я прочитаю названия ещё нескольких пар множеств, а вы попытайтесь заметить, что повторяется в этих парах.
Яблоки или груши;
Полевые или садовые цветы;
Попугаи или морские свинки;
Рабочие или выходные дни.
Заметили, что повторялось в парах множеств? Конечно, это слово «или».
Посмотрите ещё раз на названия множеств.
Например, яблоки или груши. А ведь эти множества можно объединить в одно с общим названием «фрукты» и все элементы будут располагаться в одном новом множестве.
Попугаи или морские свинки. Их можно объединить во множество с названием
«домашние
животные» и все попугаи, и все морские свинки будут находиться в новом
множестве.
Значит, если в названии множества есть слово «или», то его элемент может находиться в любом множестве и тогда происходит объединение множеств, т.е. эти множества объединяются.
Давайте рассмотрим два множества: домашние животные, дикие животные.
Множество домашние животные содержат следующие элементы: собака, кошка, морская свинка, попугай.
Множество дикие животные состоит из следующих элементов: бегемот, леопард, волк, лев.
Какой общий признак у элементов этих двух множеств? Элементы каждого из них относятся с животному миру. Значит, можно, объединив эти множества, создать новое множество под названием животные. Теперь все элементы находятся в одном множестве.
А теперь, конечно, задание.
Распределить элементы по множествам, объединить их и придумать название для нового множества.
Итак,
смотрим на элементы. Ага, у нас два множества: множество стульев
и множество столов. Распределяем элементы по множествам. Все элементы
стулья во множество стульев, а все элементы столы во множество столов.
Ага, у нас два множества: множество стульев
и множество столов. Распределяем элементы по множествам. Все элементы
стулья во множество стульев, а все элементы столы во множество столов.
Объединяем множества. Какое название будет у нашего нового множества? Множество мебели.
Давайте ещё раз определим разницу между пересечением и объединением множеств.
Если в названии множества есть слово «И», то это пересечение, и каждый элемент должен находиться на пересечении двух множеств.
Если в названии множества есть слово «или», то его элемент может находиться в любо области объединённых множеств.
Я надеюсь, что вы поняли разницу между пересечением и объединением множеств. А давайте проверим?
Итак, перед вами рисунок с тремя множествами.
Множество
учеников, которые любят математику, множество учеников, которые любят
информатику и множество всех учеников.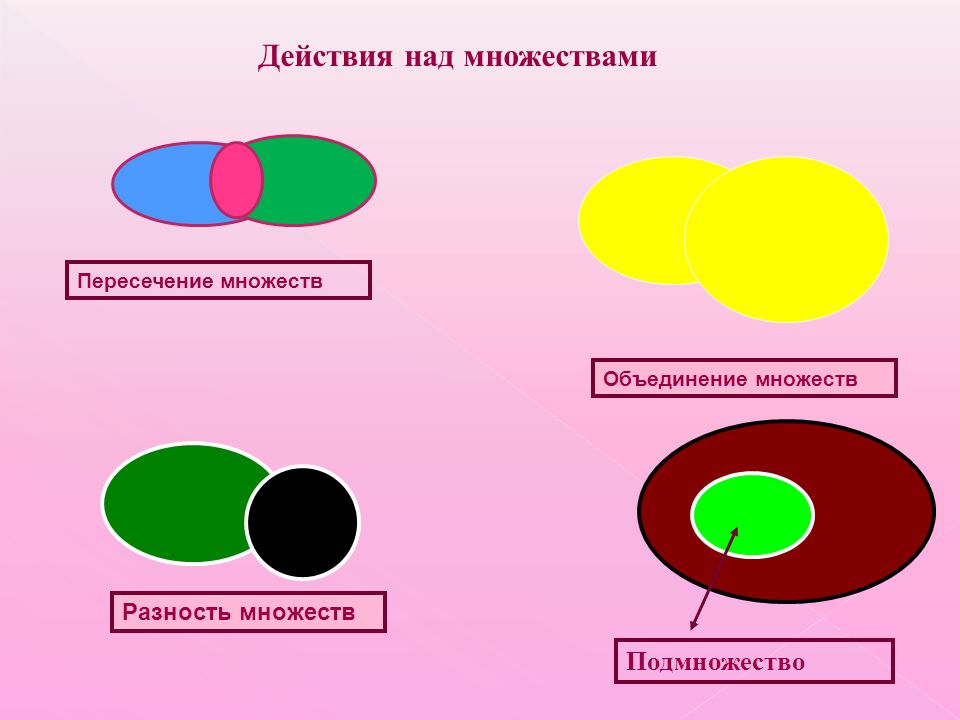 Но, среди учеников есть и такие, которые
любят и математику и информатику. Значит, эти два множества пересекаются
и одновременно они являются подмножеством множества всех
учеников. А теперь появляются элементы во множествах.
Но, среди учеников есть и такие, которые
любят и математику и информатику. Значит, эти два множества пересекаются
и одновременно они являются подмножеством множества всех
учеников. А теперь появляются элементы во множествах.
Используя полученные знания сегодня на уроке, будем отвечать на вопросы. А все ответы хранятся на этом рисунке, главное внимательно слушать вопросы и внимательно смотреть на рисунок.
Первый вопрос:
Сколько учеников любят математику? Считаем их во множестве учеников, которые любят математику, и не забываем посчитать тех учеников, которые находятся на пересечении двух множеств учеников, которые любят и математику, и информатику. Считаем. Их шесть.
Сколько
учеников любят информатику? Считаем их во множестве учеников, которые любят
информатику и опять считаем тех учеников, которые находятся на пересечении
двух множеств.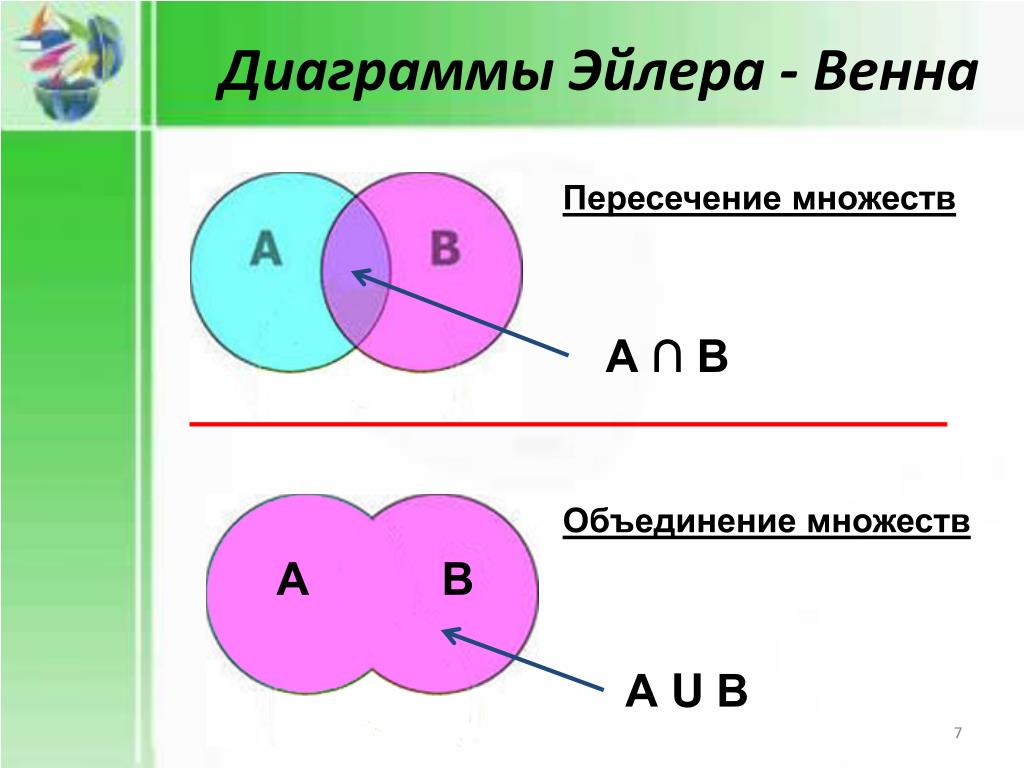 Считаем. Их пять.
Считаем. Их пять.
Сколько учеников любят и математику, и информатику? Будем считать тех учеников, которые находятся на пересечении двух множеств. Их три.
Сколько учеников любят или математику или информатику? Если используется слово «или», значит элементы находятся в любом месте множеств за исключением любителей двух предметов сразу. Значит, считаем учеников и в первом множестве и во втором, но не включаем тех, кто находится в пересечении. Их пять.
Сколько учеников любят только математику? Любят математику только те, которые находятся во множестве учеников, которые любят математику. Ученики, которые находятся на пересечении двух множеств, сюда относится не будут, т.к. они любят и математику, и информатику. Итак, считаем и получается, что 3 ученика любят только математику.
Сколько
учеников любят только информатику? Опять, учеников, которые находятся на пересечении
двух множеств, считать не будем.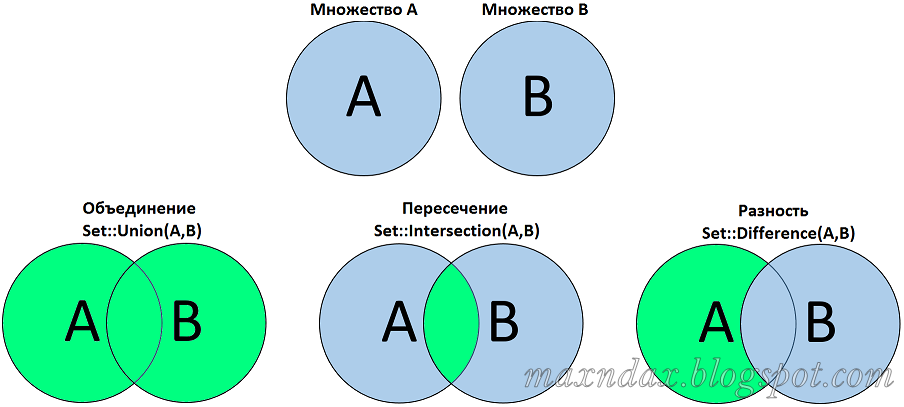 Любителей информатики двое.
Любителей информатики двое.
Сколько учеников не любят математику? Надо посчитать их во множестве учеников, которые любят информатику, кроме тех, которые находятся на пересечении множеств, т.к. эти ученики любят информатику и математику. А так же надо посчитать тех учеников, которые находятся во множестве всех учеников, т.к. они не любят математику. Их всего 5.
Всем спасибо за отличную работу. Теперь я точно понял, что хочу быть учителем!
Тебе спасибо, Максим. Тему объяснил хорошо. До свидания! А мы ещё сделаем выводы.
Итак.
Множество – это объединение некоторых объектов (элементов) в группу по определённым признакам.
Множество может быть подмножеством другого множества. Например: множество собак является подмножеством множества домашние животные.
Множества
могут пересекаться. Например: множество чисел, которые делятся на
2, и множество чисел, которые делятся на 3, пересекаются, т.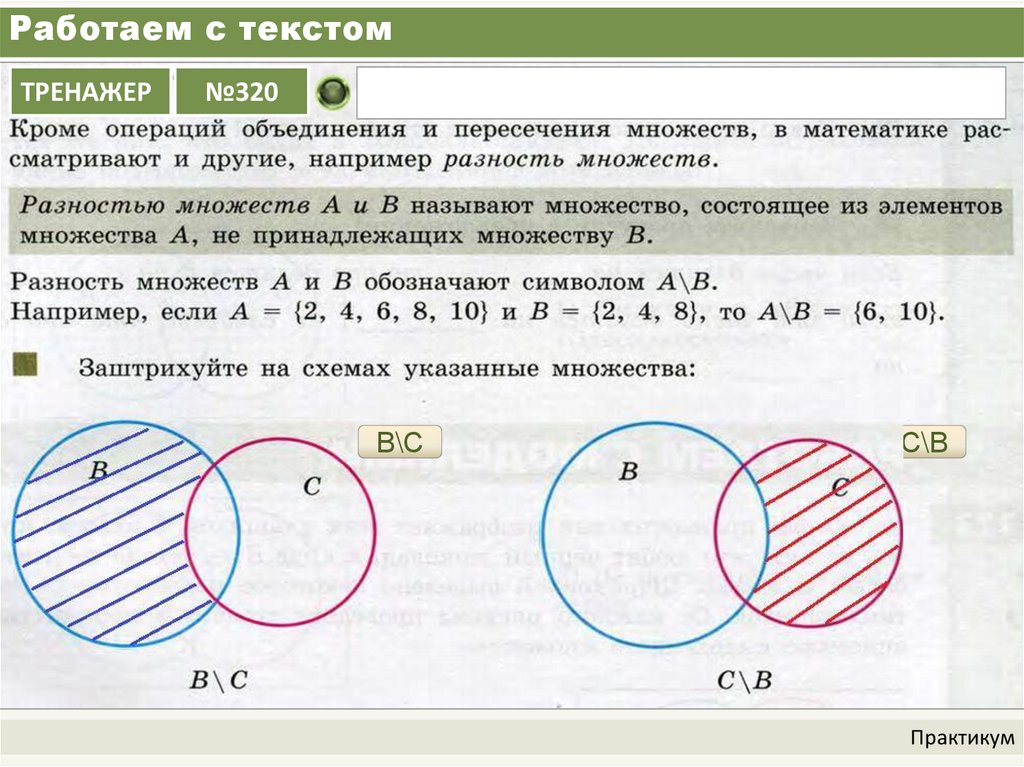 к. числа, например,
6 и 12 делится и на 2, и на 3.
к. числа, например,
6 и 12 делится и на 2, и на 3.
Множества могут и не пересекаться. Например: множество телефонов и множество цветов.
И множества могут объединяться. Например: множество рабочих дней недели и множество выходных можно объединить в одно множество дней недели.
Выводы сделаны, и я желаю вам успехов при выполнении заданий!
Объединение множеств — формула, значение, примеры
Объединение множеств — одна из операций над множествами, используемая в теории множеств. Помимо объединения множеств, другими операциями над множествами являются разность и пересечение. Все операции над множествами представлены с помощью уникального оператора. Объединение множеств аналогично арифметическому сложению. Объединение двух заданных множеств — это множество, содержащее все элементы, присутствующие в обоих множествах. Символом объединения множеств является «∪». Для любых двух множеств A и B объединение A ∪ B (читается как объединение A B) перечисляет все элементы множества A, а также множества B. Таким образом, для два заданных набора, Set A = {1,2,3,4,5} и Set B = {3,4,6,8}, A ∪ B = {1,2,3,4,5,6,8 }
Таким образом, для два заданных набора, Set A = {1,2,3,4,5} и Set B = {3,4,6,8}, A ∪ B = {1,2,3,4,5,6,8 }
В этой статье вы узнаете об объединении множеств, его определении, свойствах с решенными примерами.
| 1. | Что такое Союз наборов? |
| 2. | Диаграмма Венна объединения наборов |
| 3. | Свойства объединения наборов |
| 4. | Объединение наборов Примеры |
| 5. | Часто задаваемые вопросы по Union of Sets |
Что такое объединение наборов?
Объединение любых двух или более наборов приводит к совершенно новому набору, содержащему комбинацию элементов, присутствующих в обоих этих двух или более заданных наборах. Объединение множеств изображается с помощью слова «или». Рассмотрим два множества A и B. Объединение A и B будет содержать все элементы, которые присутствуют в A или B или в обоих множествах.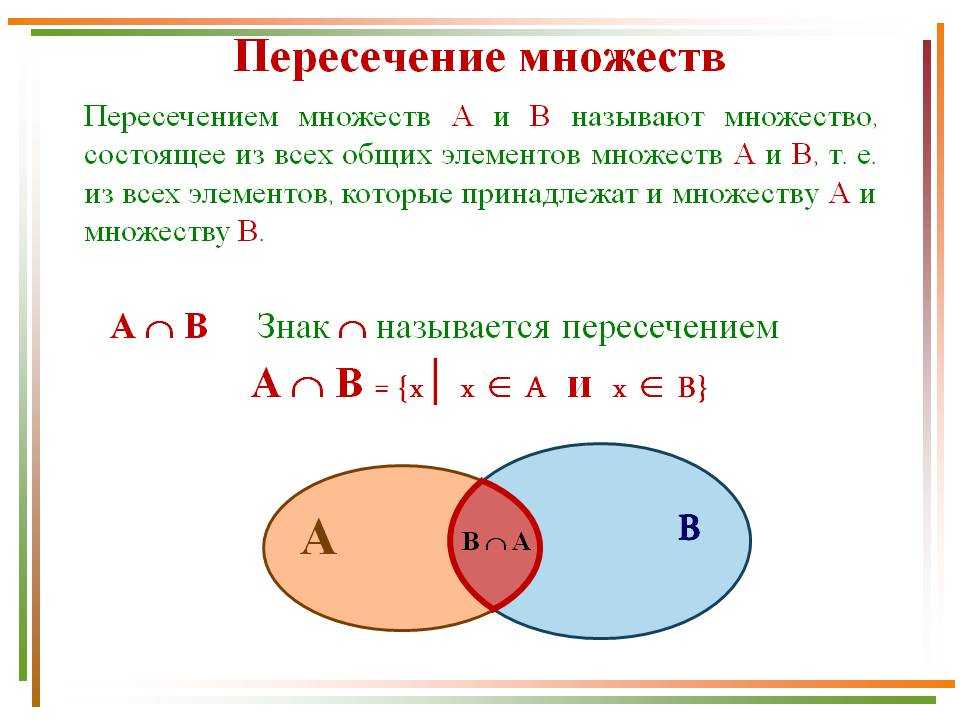 Обозначение множества, используемое для представления объединения множеств, — ∪. Операция множества, то есть объединение множеств, представляется как:
Обозначение множества, используемое для представления объединения множеств, — ∪. Операция множества, то есть объединение множеств, представляется как:
A ∪ B = {x: x ∈ A или x ∈ B}. Здесь x — это элемент, присутствующий в обоих наборах, A и B.
Поиск объединения наборов
Давайте рассмотрим следующий пример, чтобы понять процесс поиска объединения наборов. У нас есть два множества A и B, поскольку A = {a, b, j, k} и B = {h, t, k, c}. Нам нужно найти элементы, присутствующие в объединении A и B.
Согласно определению объединения двух множеств результирующее множество будет включать элементы, присутствующие в A, в B или в обоих множествах. Таким образом, элементами обоих множеств являются a, b, c, j, k, h, t, но так как элемент k присутствует в обоих множествах, то он будет рассмотрен только один раз, так как является общим для обоих заданных множеств. Следовательно, в объединении множеств A и B присутствуют элементы a, b, c, j, k, h, t
Обозначение объединения множеств
Мы используем уникальное математическое обозначение для представления каждой операции с множествами.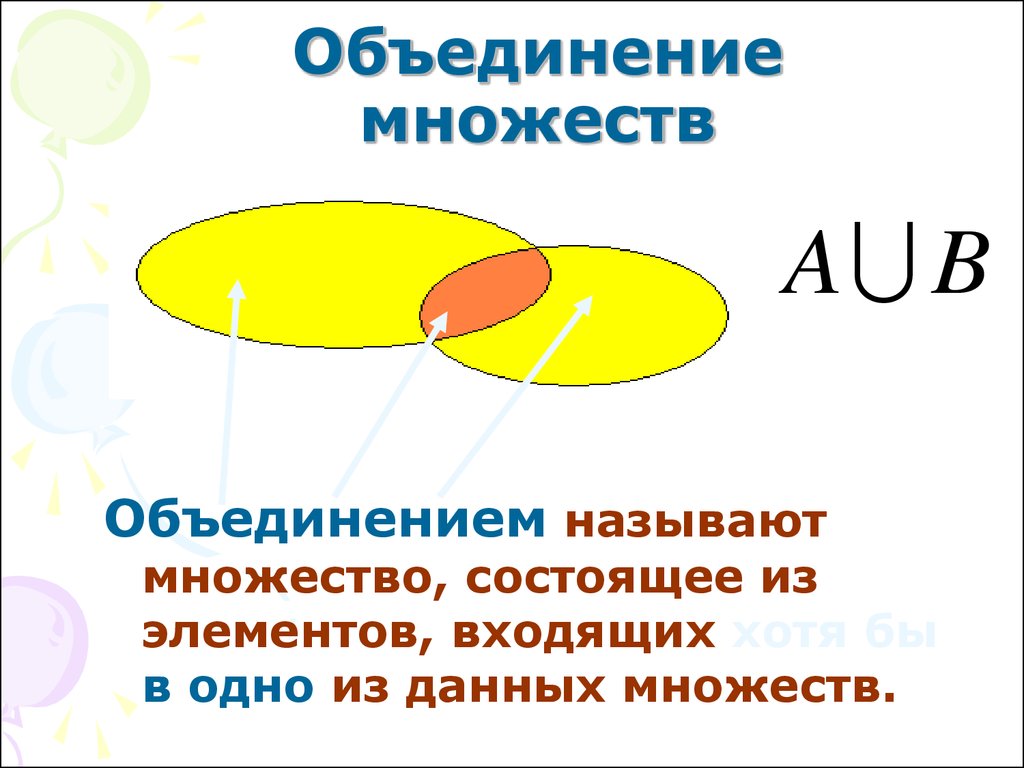 Математическое обозначение, которое используется для представления объединения двух множеств, — «∪». Этот оператор называется инфиксной записью и окружен операндами.
Математическое обозначение, которое используется для представления объединения двух множеств, — «∪». Этот оператор называется инфиксной записью и окружен операндами.
Рассмотрим два множества P и Q, где P = {2,5,7,8} и Q = {1,4,5,7,9}. П ∪ Q = {1,2,4,5,7,8,9}.
Диаграмма Венна объединения наборов
Диаграммы Венна относятся к диаграммам, которые используются для представления или объяснения взаимосвязи между заданными операциями множества. Любая операция множества может быть представлена с помощью диаграммы Венна. Диаграммы Венна представляют каждый набор с помощью кругов. Давайте посмотрим, как использовать диаграмму Венна для представления объединения двух множеств. Для этого нам сначала понадобится универсальное множество, подмножествами которого являются два заданных множества P и Q. Следующая диаграмма Венна представляет собой объединение множеств P и Q.
На приведенной выше диаграмме Венна область синего цвета показывает объединение множеств P и Q.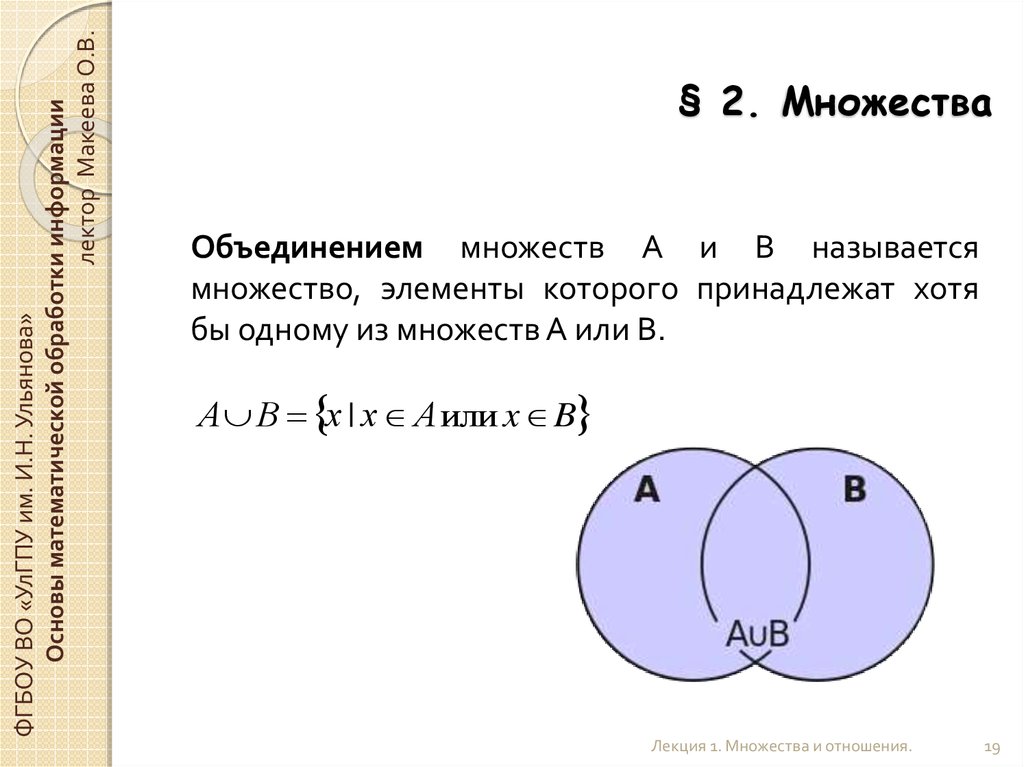 Это также означает, что объединение между этими множествами включает в себя все элементы, присутствующие в P или Q или в обоих множествах. Хотя здесь использовалась операция объединения двух множеств, диаграмма Венна часто используется для представления объединения нескольких множеств при условии, что множества конечны.
Это также означает, что объединение между этими множествами включает в себя все элементы, присутствующие в P или Q или в обоих множествах. Хотя здесь использовалась операция объединения двух множеств, диаграмма Венна часто используется для представления объединения нескольких множеств при условии, что множества конечны.
Свойства объединения наборов
В этом разделе вы узнаете о некоторых важных свойствах объединения множеств. Эти свойства необходимо учитывать при объединении множеств.
| Свойства Союза | Обозначение |
|---|---|
| Коммутативная собственность | А ∪ В = В ∪ А |
| Ассоциативная собственность | (А ∪ В) ∪ С = А ∪ (В ∪ С) |
| Идемпотентное свойство | А ∪ А = А |
| Собственность Ⲫ/ Закон о личности | А ∪ Ⲫ = А |
| Собственность универсального набора | А ∪ U = U |
Переместительное свойство
Согласно свойству перестановочности объединения порядок операционных множеств не влияет на результирующее множество. Это означает, что если изменить положение операндов, решение останется прежним и не изменится. В математических терминах мы можем сказать, что: A ∪ B = B ∪ A
Это означает, что если изменить положение операндов, решение останется прежним и не изменится. В математических терминах мы можем сказать, что: A ∪ B = B ∪ A
Рассмотрим два множества P и Q:
P = {a, m, h, k, j}, Q = {2, 3, 4, 6}
Чтобы доказать коммутативность этих множеств, сначала нужно решить левую часть уравнения, которое имеет вид:
P ∪ Q = {a, m, h, k, j} U {2, 3, 4, 6} = {a, m, h, k, j, 2, 3, 4, 6}
Теперь решим правую часть уравнения:
Q ∪ P = {2, 3, 4, 6} U {a, m, h, k, j} = { a, m, h, k, j, 2, 3, 4, 6}
Теперь мы можем заключить, что свойство коммутативности выполняется для объединения заданных множеств.
Ассоциативное свойство
В соответствии с ассоциативным свойством объединения, когда наборы группируются с помощью круглых скобок, результат не изменяется. Это означает, что когда положение скобок изменяется в любом выражении множеств, включающем объединение, это не повлияет на результирующее множество. В математических терминах
В математических терминах
(A ∪ B) ∪ C = A ∪ (B ∪ C) , где A, B и C — любые конечные множества.
Докажем, что ассоциативность объединения выполняется для следующих множеств:
A = {2, 3, 4}, B = {2, 5, 6}, C = {1, 6, 9}
Решим левую часть приведенного выше уравнения:
(A ∪ B) = {2, 3, 4} U {2, 5, 6} = {2, 3, 4, 5, 6}
(A ∪ B) ∪ C = {2, 3, 4, 5, 6} U {1, 6, 9} = {1, 2, 3, 4, 5, 6, 9}
Теперь решим правую часть уравнения:
(B ∪ C) = {2, 5, 6 } ∪ {1, 6, 9} = {1, 2, 5, 6, 9}
A ∪ (B ∪ C) = {2, 3, 4} ∪ {1, 2, 5, 6, 9} = {1, 2, 3, 4, 5, 6, 9}
Из левой и правой частей уравнений можно заключить, что для данных множеств A, B и C верно ассоциативное свойство объединения.
Свойство идемпотента
Свойство идемпотента утверждает, что объединение любого набора с одним и тем же набором приведет к самому набору. Математически это можно представить как A ∪ A = A .
Докажем это для A = {2,4,6,8,10}
Таким образом, A ∪ A = {2,4,6,8,10} ∪ {2,4,6,8,10} = {2,4,6,8,10} = A
Свойство Ⲫ/ Закона об идентичности
Согласно свойству нулевого набора, объединение любого набора с нулевым набором или пустым набором приведет к поставил себе.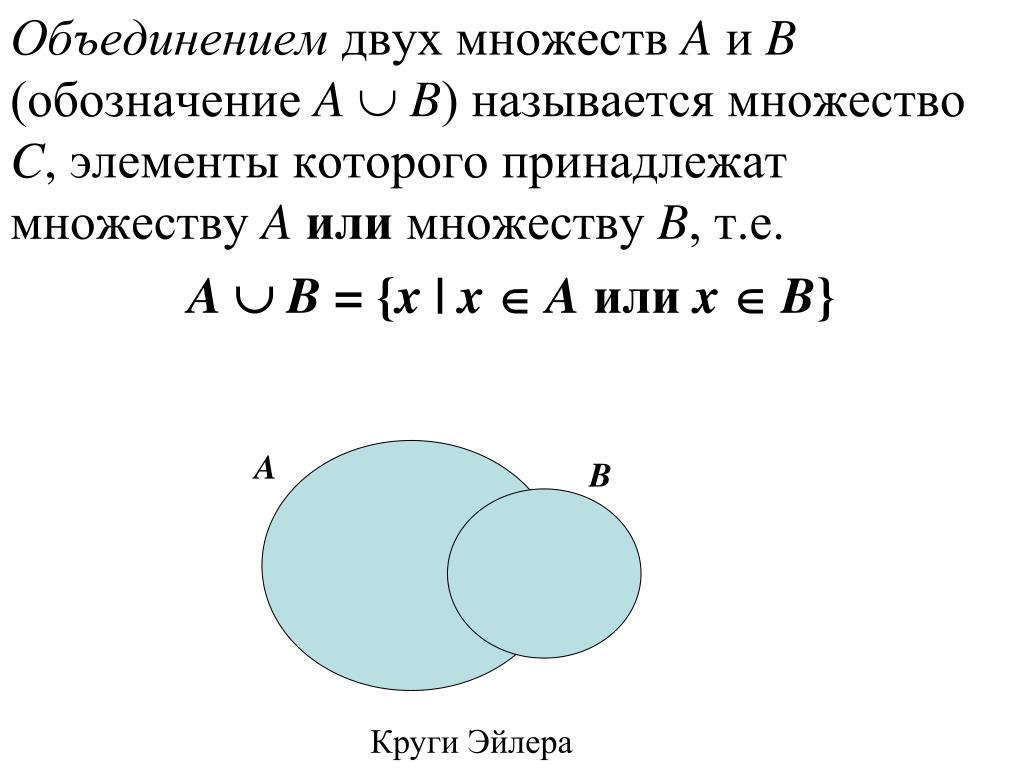 Математически мы можем записать это как А ∪ Ⲫ = А .
Математически мы можем записать это как А ∪ Ⲫ = А .
Докажем это для A = {p,q,r}
Таким образом, A∪∅ = {p,q,r} ∪ {} = {p,q,r}
Свойство универсального множества
As согласно свойству универсального набора, объединение универсального набора с любым набором приводит к универсальному набору. Математически это можно представить как A ∪ U = U .
Докажем это для A = {a,e} и U = {a,b,c,d,e,f,g,h}
, тогда A∪U = {a,e} ∪ {a,b ,c,d,e,f,g,h} = {a,b,c,d,e,f,g,h} = U
Статьи по теме Объединение множеств
Ознакомьтесь со следующими страницами, посвященными объединению множеств
- Конечные и бесконечные множества
- Наборы Формула
Важные замечания по объединению множеств
Вот список нескольких важных моментов, связанных с объединением множеств.
- Объединение любых двух наборов приводит к совершенно новому набору, содержащему элементы, присутствующие в обоих исходных наборах.

- Результирующий набор содержит все элементы, присутствующие в первом наборе, втором наборе или элементы, которые есть в обоих наборах.
- В результате объединения двух непересекающихся множеств получается множество, включающее элементы обоих множеств.
- В соответствии с коммутативным свойством объединения порядок операционных наборов не влияет на результирующий набор.
- Чтобы определить кардинальное число объединения множеств, используйте формулу: n(A ∪ B) = n(A) + n(B) — n(A ∩ B)
Часто задаваемые вопросы по Union of Sets
Что такое объединение множеств в математике?
В математике объединение любых двух множеств представляет собой совершенно новое множество, содержащее элементы, присутствующие в обоих исходных множествах. Результирующий набор представляет собой комбинацию всех элементов, присутствующих в первом наборе, втором наборе или элементов, которые есть в обоих наборах. Например, объединение множеств A = {0,1,2,3,4} и B = {13} можно представить как A ∪ B = {0,1,2,3,4,13}.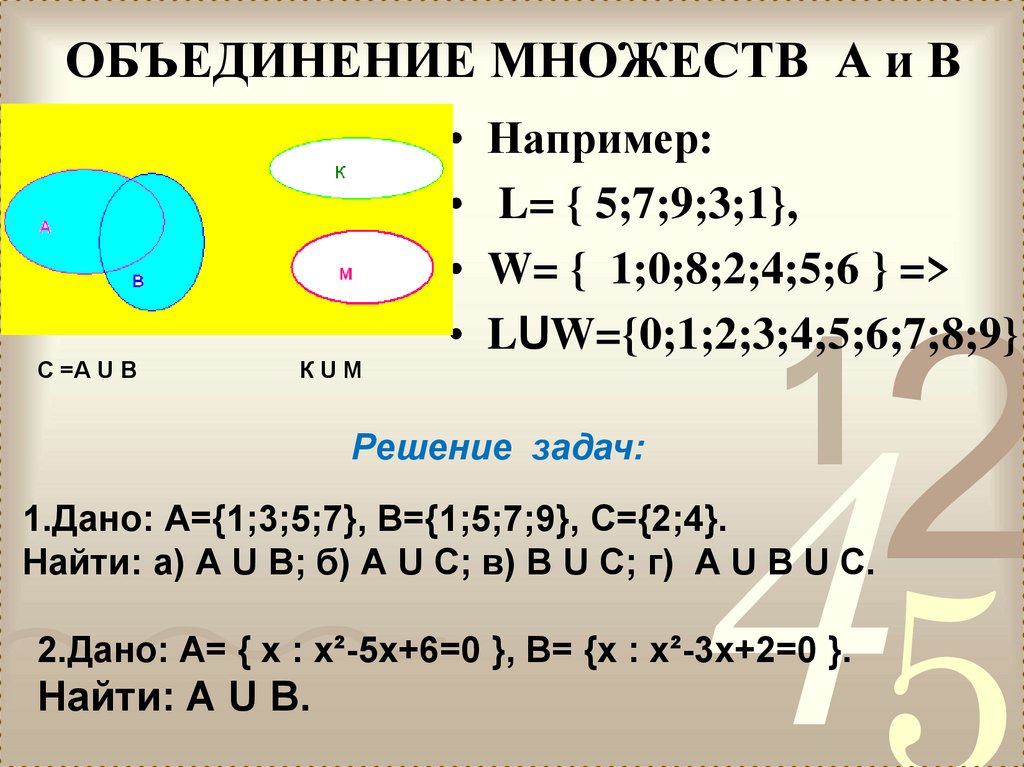
В чем разница между пересечением и объединением множеств?
Объединение любых двух наборов приводит к совершенно новому набору, который содержит элементы, присутствующие в первом наборе, втором наборе или элементы, которые есть в обоих наборах. Принимая во внимание, что пересечение множеств будет содержать элементы, общие для обоих множеств. Рассмотрим два множества A = {1,2} и B = {2,3}. Здесь объединение A и B будет A ∪ B = {1,2,3}, тогда как пересечение A и B будет A ∩ B = {2}.
Что такое символ объединения наборов?
Математическое обозначение, которое используется для представления объединения наборов, — ‘∪’. Этот оператор называется инфиксной записью и окружен операндами.
Что такое коммутативное свойство объединения множеств?
Согласно коммутативному свойству объединения, порядок операционных наборов не влияет на результирующий набор. При изменении положения операндов решение останется прежним, оно не изменится. В математических терминах мы можем сказать, что: A ∪ B = B ∪ A.
Что такое ассоциативное свойство объединения множеств?
В соответствии с ассоциативным свойством объединения, когда наборы группируются с помощью круглых скобок, результирующий набор не изменяется при изменении положения скобок в любом выражении наборов, включающем объединение. Говоря математическим языком, (A ∪ B) ∪ C = A ∪ (B ∪ C), где A, B и C — любые конечные множества.
Что такое Идемпотентное свойство объединения множеств?
Свойство идемпотента указывает, что объединение любого набора с тем же самым набором приведет к самому набору. Математически это можно показать как A ∪ A = A.
Какое свойство Ⲫ в объединении множеств?
Согласно свойству нулевого набора, объединение любого набора с нулевым набором или пустым набором приведет к самому набору. Математически это можно записать как A ∪ Ⲫ = A.
Что такое объединение множеств a и b?
Объединение двух множеств A и B определяется как множество всех элементов, присутствующих в множестве A и множестве B, или обоих элементах в A и B вместе взятых. Объединение множеств a и обозначается как «a ∪ b».
Объединение множеств a и обозначается как «a ∪ b».
Что такое процесс поиска союза?
Объединение двух множеств можно рассматривать как наименьшее множество, состоящее из элементов обоих множеств. Чтобы найти объединение двух множеств, выполните шаги, указанные ниже:
- Шаг 1: Рассмотрим два или более заданных множества.
- Шаг 2: Выберите элементы из двух или более заданных наборов и подготовьте результирующий набор, в котором ни один элемент не повторяется.
- Шаг 3: Представьте объединение множеств с помощью символа ‘∪’.
Например, объединение X = {11,12,13,14,15,16,17,18,19,20} и Y = {13,17,21} = X∪Y = {11,12 ,13,14,15,16,17,18,19,20,21}.
Какова мощность объединения множеств A и B?
Для конечных множеств A и B количество элементов подсчитывается с использованием однозначного соответствия, но дубликаты не учитываются. Например, если объединение множеств = {3, 2, 1, 2, 3}, то оно имеет мощность 3.
Функция Union() в Python — GeeksforGeeks
Python set Union() Метод возвращает новый набор, содержащий все элементы исходного набора.
Объединение двух данных множеств — это множество, содержащее все элементы обоих множеств. Объединение двух данных множеств A и B — это множество, состоящее из всех элементов A и всех элементов B, таких, что ни один элемент не повторяется.
Синтаксис метода Python set Union():Символ для обозначения объединения наборов ‘U’
Python set Union() Пример метода:Синтаксис: set1.union(set2, set3, set4….)
Параметры: ноль или более наборов
Возврат: набор2, набор3…) с набором1. Он возвращает копию set1, только если параметр не передан.
Python3
|
Output:
A U B: {2, 4, 5, 6, 7, 8} Example 1: Working with
Python set Union() methodsPython3
|
Выход
набор1 U набор2 : {2, 4, 5, 6, 7, 8}
набор1 U набор2 U набор3 : {2, 4, 5, 6, 7, 8, 9, 10} Вывод:
набор1 U набор2 : {2, 4, 5, 6, 7, 8}
set1 U set2 U set3 : {2, 4, 5, 6, 7, 8, 9, 10} Пример 2. Объединение множеств Python с использованием | Оператор
Мы можем использовать «|» Оператор нахождения объединения множеств.
Python3
|
Выход
набор1 U набор2 : {2, 4, 5, 6, 7, 8}
набор1 U набор2 U набор3 : {2, 4, 5, 6, 7, 8, 9, 10} Вывод:
набор1 U набор2 : {2, 4, 5, 6, 7, 8}
набор1 U набор2 U набор3 : {2, 4, 5, 6, 7, 8, 9, 10} Example 3 : Python Set Union() Method on String Python3
|
Output
A U B: {'za', 'ab', ' dd', 'dz', 'ba', 'cd'} Пример 4. Метод Python Set Union() для нескольких наборов (с 3 наборами). Python3
|
14.4 Соединение и пересечение | Вероятность
Предыдущий 14.3 Диаграммы Венна | Следующий 14.5 Вероятностные тождества |
14.4 Объединение и пересечение (EMA7Z)
временный текст- Союз
Объединение двух множеств — это новое множество, содержащее все элементы, находящиеся в хотя бы один из двух наборов. Объединение записывается как \(A \cup B\) или «\(A \text{ или } B\)».
- Перекресток
Пересечение двух множеств — это новое множество, содержащее все элементы, в обоих наборах.
 Пересечение записывается как \(A \cap B\) или «\(A \text{
и } В\)”.
Пересечение записывается как \(A \cap B\) или «\(A \text{
и } В\)”.
На рисунке ниже показаны объединение и пересечение для различных конфигураций двух событий в демонстрационное пространство с использованием диаграмм Венна.
Рисунок 14.1: Объединения и пересечения различных событий. Обратите внимание, что в В среднем столбце пересечение \(A \cap B\) пусто, так как два набора не совпадают. перекрывать. В последнем столбце объединение \(A \cup B\) равно \(A\) и пересечение, \(A \cap B\), равно \(B\), так как \(B\) полностью содержится в \(А\).
Учебник Упражнение 14.4
Группе учащихся дается следующая диаграмма Венна:
Пример пространства может быть описан как \(\{ n:n \text{ } \epsilon
\text{ } \mathbb{Z}, \text{ } 1 \leq n \leq 15 \}\).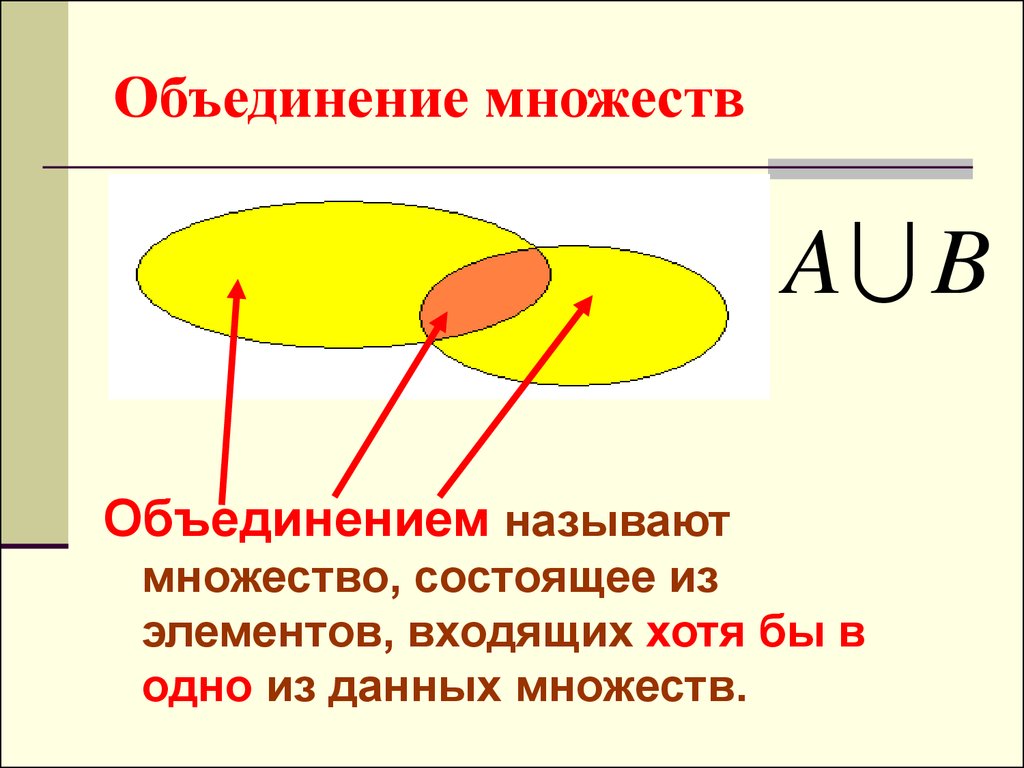
Их просят определить набор событий пересечения между набор событий \(A\) и набор событий \(B\), также записываемый как \(A \cap Б\). Они застревают, и вы предлагаете помочь им найти его.
Какой набор лучше всего описывает набор событий \(A \cap B\)?
- \(\{7;10;11\}\)
- \(\{1;2;3;4;5;6;7;9;10;11\}\)
- \(\{1;2;3;4;5;6;7;9;10\}\)
- \(\{7;10\}\)
Пересечение множества событий \(A\) и множества событий \(B\), а также записывается как \(A \cap B\), может быть заштриховано следующим образом:
Таким образом, набор событий \(\{7;10\}\) лучше всего описывает набор событий
\(А \шапка Б\).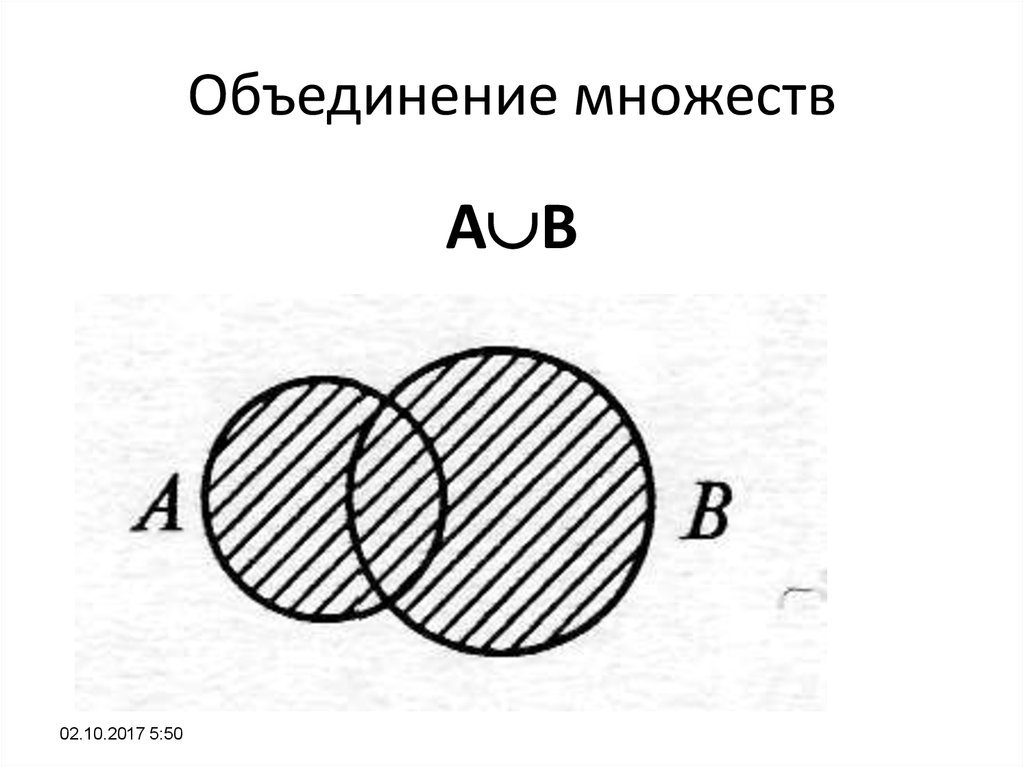
Группе учащихся дается следующая диаграмма Венна:
Пример пространства может быть описан как \(\{ n:n \text{ } \epsilon \text{ } \mathbb{Z}, \text{ } 1 \leq n \leq 15 \}\)
Их просят идентифицировать набор событий союза между событиями набор \(A\) и набор событий \(B\), также обозначаемый как \(A \cup B\). Они застревают, и вы предлагаете помочь им найти его.
Какой набор лучше всего описывает набор событий \(A \cup B\)?
- \(\{1;6;7;10;15\}\)
- \(\{1;2;4;5;6;7;8;9;10;11;12;13;14;15\}\)
- \(\{2;4;5;9;10;11;12;13;14\}\)
- \(\{3\}\)
Объединение между набором событий \(A\) и набором событий \(B\), также записывается как \(A \cup B\), можно заштриховать следующим образом:
Следовательно, набор событий \(\{1;2;4;5;6;7;8;9;10;11;12;13;14;15\}\)
лучше всего описывает набор событий \(A \cup B\).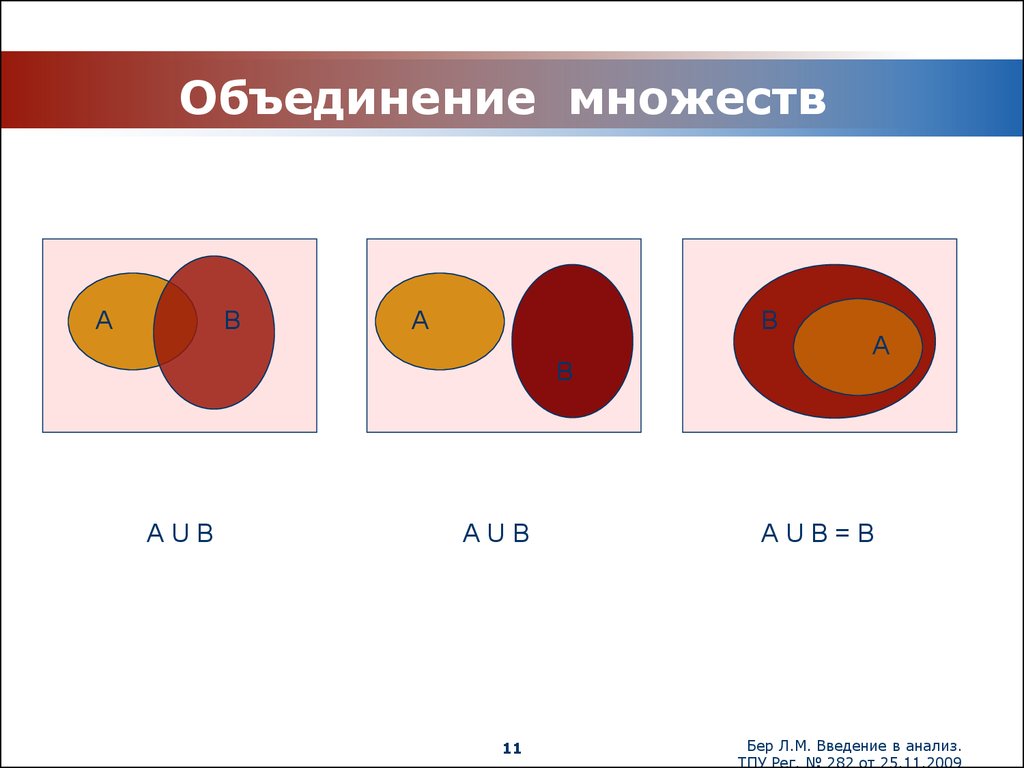

 = B
A.symmetric_difference_update(B)
= B
A.symmetric_difference_update(B)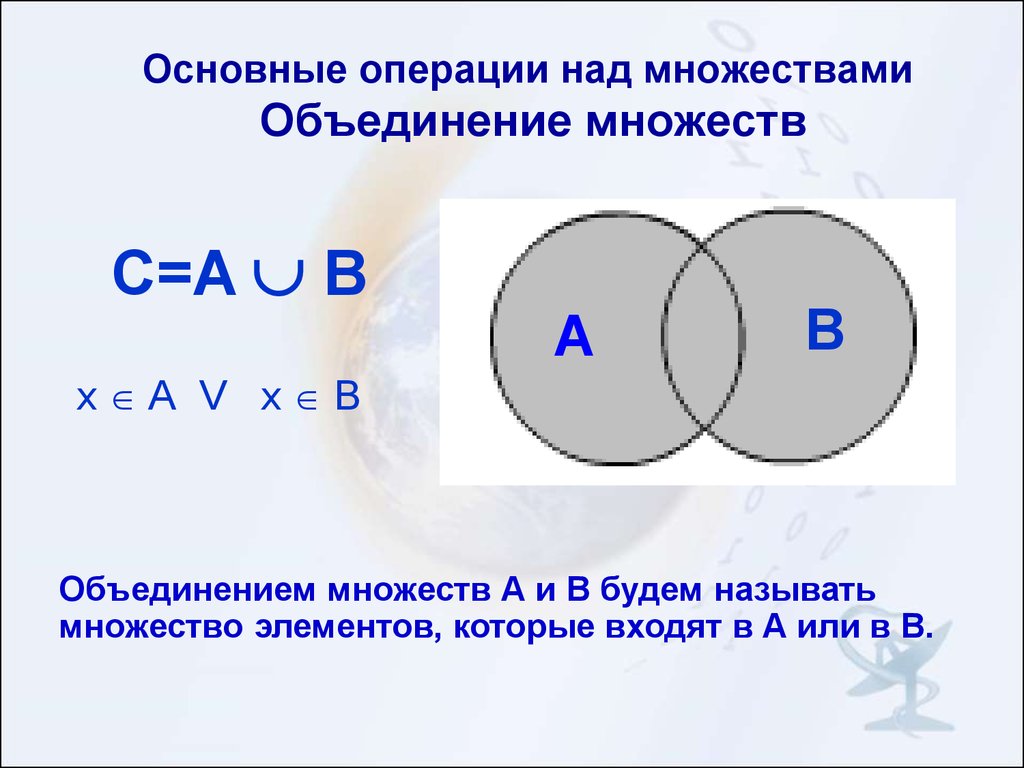

 union(B))
union(B)) 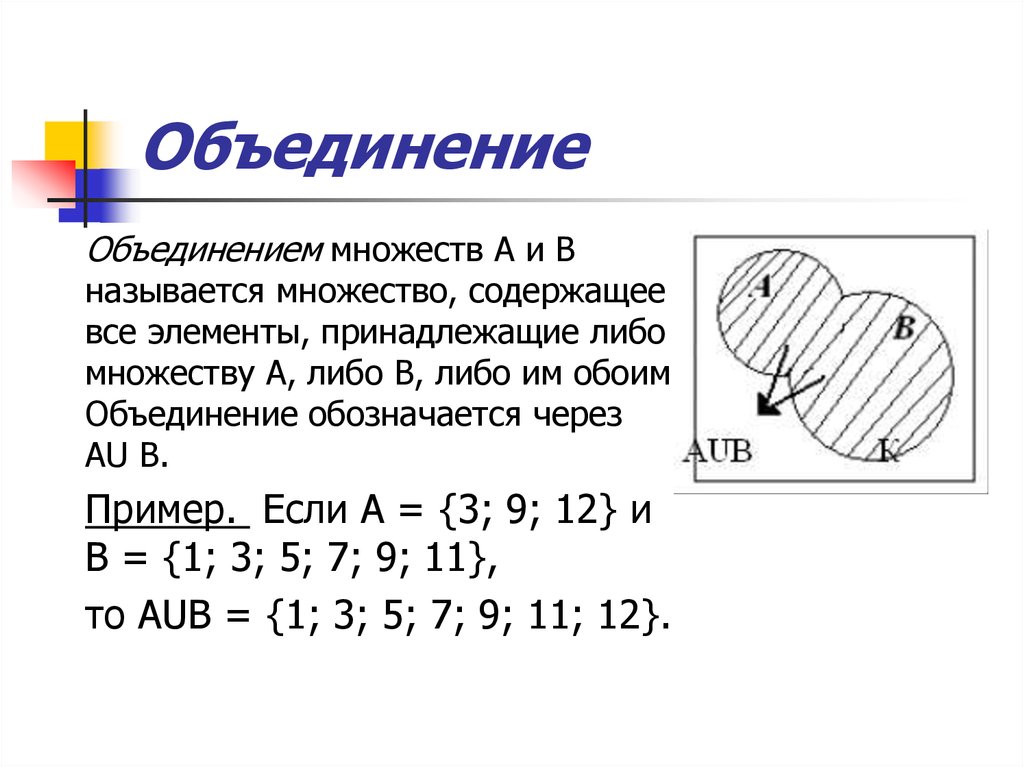 union(set2))
union(set2)) 
 union(B))
union(B)) 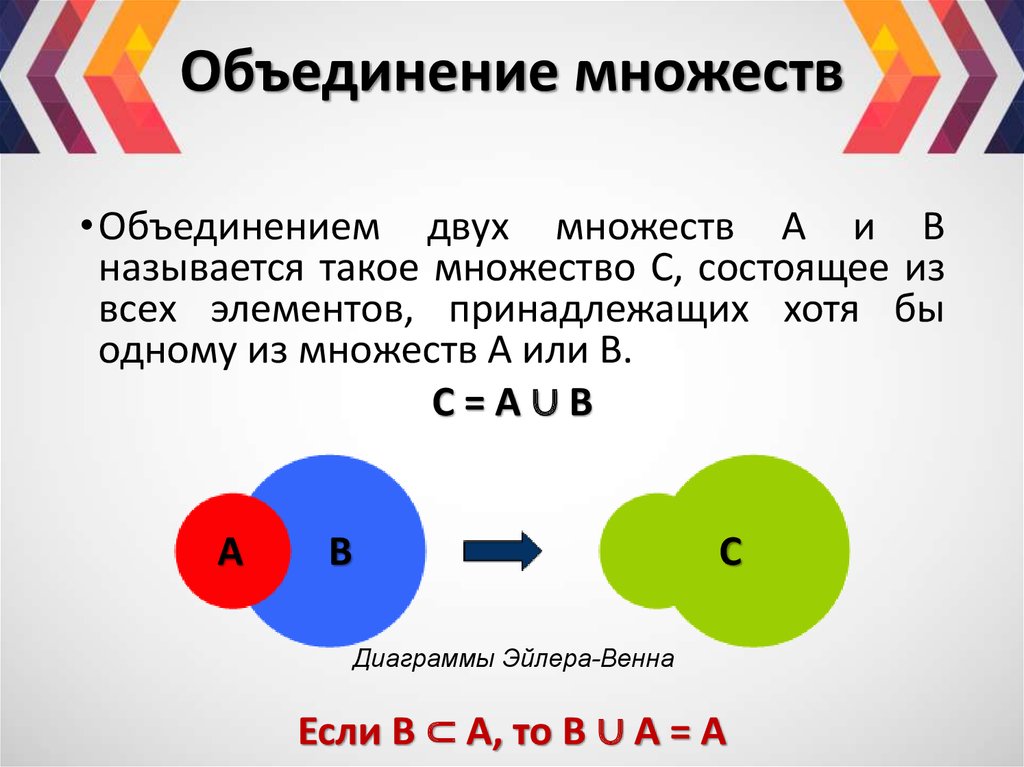 union(B).union(c))
union(B).union(c))  Пересечение записывается как \(A \cap B\) или «\(A \text{
и } В\)”.
Пересечение записывается как \(A \cap B\) или «\(A \text{
и } В\)”.