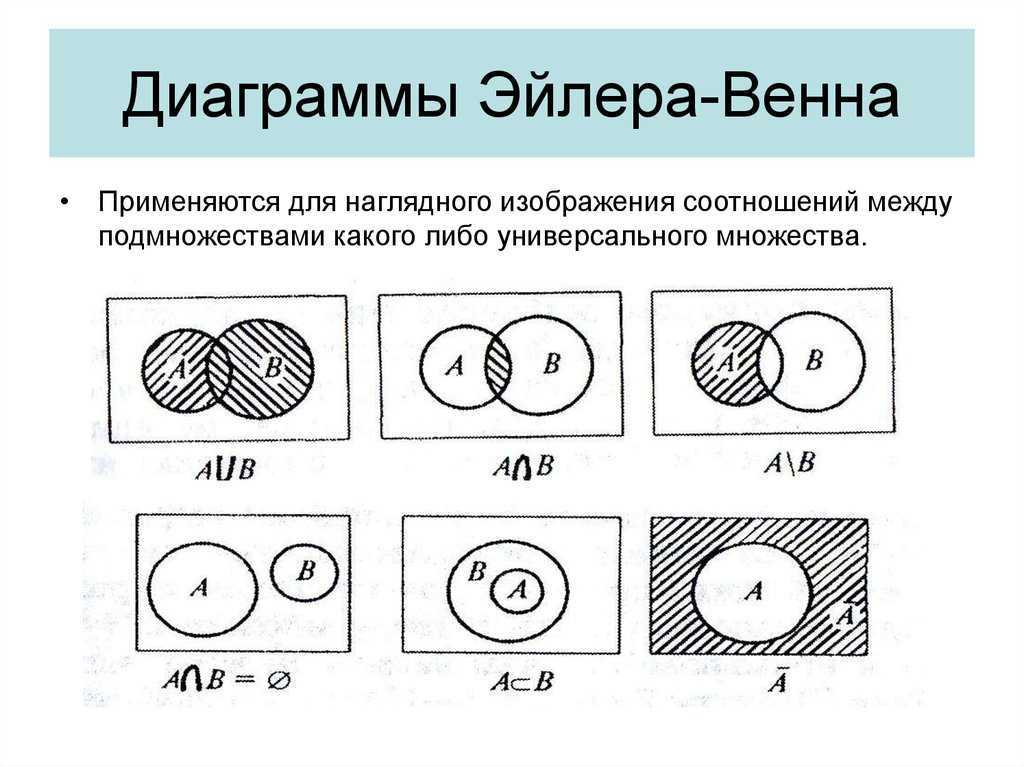
Объединением множеств a и b называется: Пересечение и объединение множеств — урок. Алгебра, 9 класс.

Содержание

Объединение множеств

Объединением множеств А и В называют множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств А и В. Объединение множеств А и В обозначается символом , т.е. .

Определение объединения множеств можно записать как

1.6

Объединение множеств иногда называют суммой множеств и обозначают А+В. Однако свойства объединения множеств несколько отличаются от свойств суммы при обычном арифметическом понимании. Поэтому термином сумма пользоваться не рекомендуется.

Примеры.

Пусть А={4,5,8,12,16,21}; B={1,2,5,7,12,17,21,30}. Тогда

={1,2,4,5,7,8,12,16,17, 21,30}.

Пусть A={a,b,c,d}; B={a,d,e,f,g}. Тогда ={a,b,c,d,e,f,g}.

Е сли множества А и В представить в виде точек, ограниченных окружностями А и В соответственно, то объединение множеств представляет собой закрашенную область, ограниченную обоими кругами, как это показано на рис. 1.1.

Понятие объединения множеств можно распространить и на большее число множеств. Пусть М={X₁, X₂,…. X_n} – совокупность n множеств X₁, X₂, … X_n, называемую системой множеств. Объединение этих множеств представляет собой множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств системы М.

1.7

Для объединения множеств справедливы коммутативный и ассоциативный законы:

; 1.

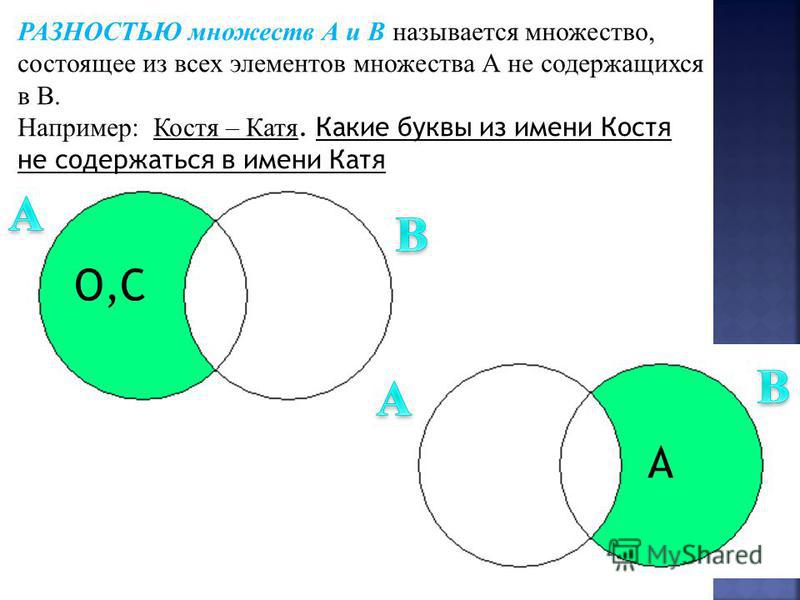
. 1.9

Вполне очевидно, что . 1.10

Пересечением множеств А и В называют множество, состоящее только их тех и только тех элементов, которые принадлежат как множеству А, так и множеству В. Пересечение множеств обозначается символом , т.е. . Определение пересечения может быть записано как

1.11

Пересечение множеств иногда называют произведением множеств, что некорректно.

Примеры.

Если А={4,5,8,12,16,21}; B={1,2,5,7,12,17,21,30}, то ={5,12,21}.
Если A={a,b,c,d}; B={a,d,e,f,g}, то ={a,d}.

Если А – множество левого круга, В – множество правого круга, то пересечение множеств представляет собой закрашенную область, являющуюся общей частью обоих кругов, как это показано на рис.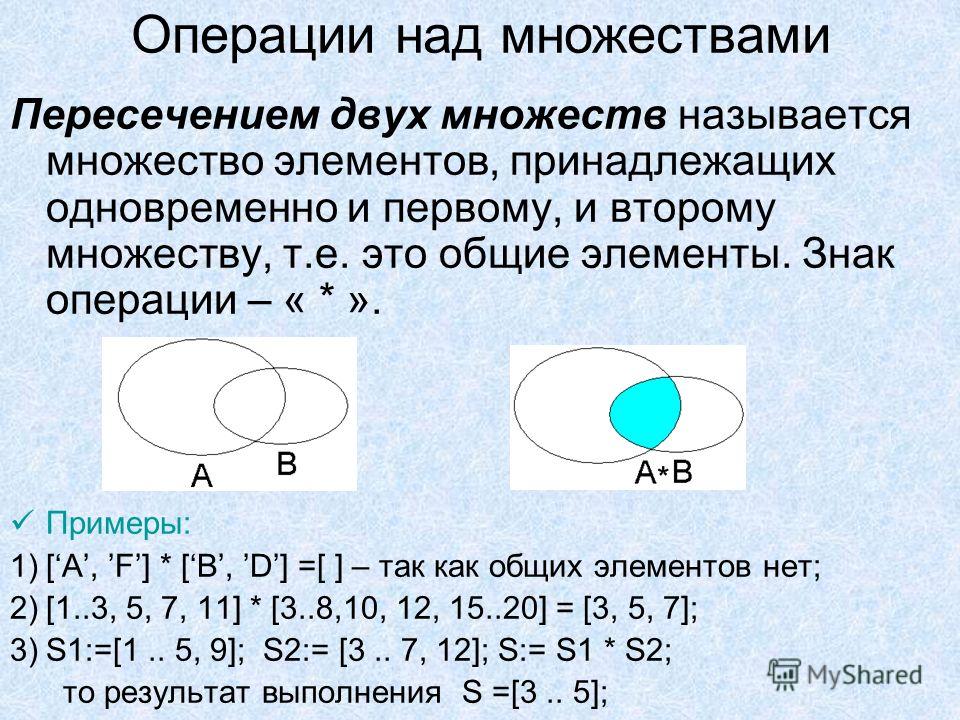 1.2.

Множества А и В называются непересекающимися, если они не имеют общих элементов, т.е. =.

Пример. Пусть А={3,4,5}, B={2,6,7}. Тогда =.

Множества А и В находятся в общем положении, если выполняются три условия:

Существует элемент множества А, не принадлежавший множеству В;
Существует элемент множества В, не принадлежавший множеству А;
Существует элемент, принадлежащий как множеству А, так и множеству В.

Пересечение распространяется и на большее количество множеств. Пусть имеем систему множеств М={X₁, X₂,…. X_n}. Множество

1.12

представляет собой множество, элементы которого принадлежат каждому из множеств системы М.

Пересечение множеств обладает свойством коммутативности

1.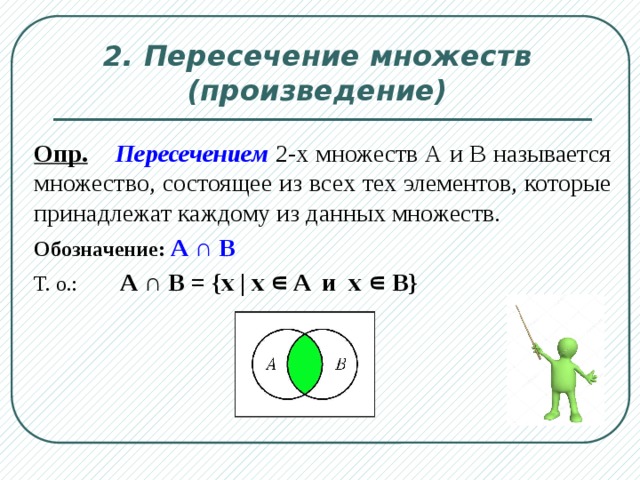 13

и ассоциативности

1.14

Кроме того имеет место соотношение: . 1.15

МНОЖЕСТВ ТЕОРИЯ • Большая российская энциклопедия

МНО́ЖЕСТВ ТЕО́РИЯ, раздел математики, в котором изучаются свойства множеств, преим. бесконечных. Понятие множества, или совокупности, принадлежит к числу исходных математич. понятий; оно формально не определяется, но может быть пояснено при помощи примеров. Так, можно говорить о множестве всех книг, составляющих данную библиотеку, множестве всех точек данной линии, множестве всех решений данного уравнения. Книги данной библиотеки, точки данной линии, решения данного уравнения являются элементами соответствующего множества. Чтобы определить множество, достаточно указать характеристич.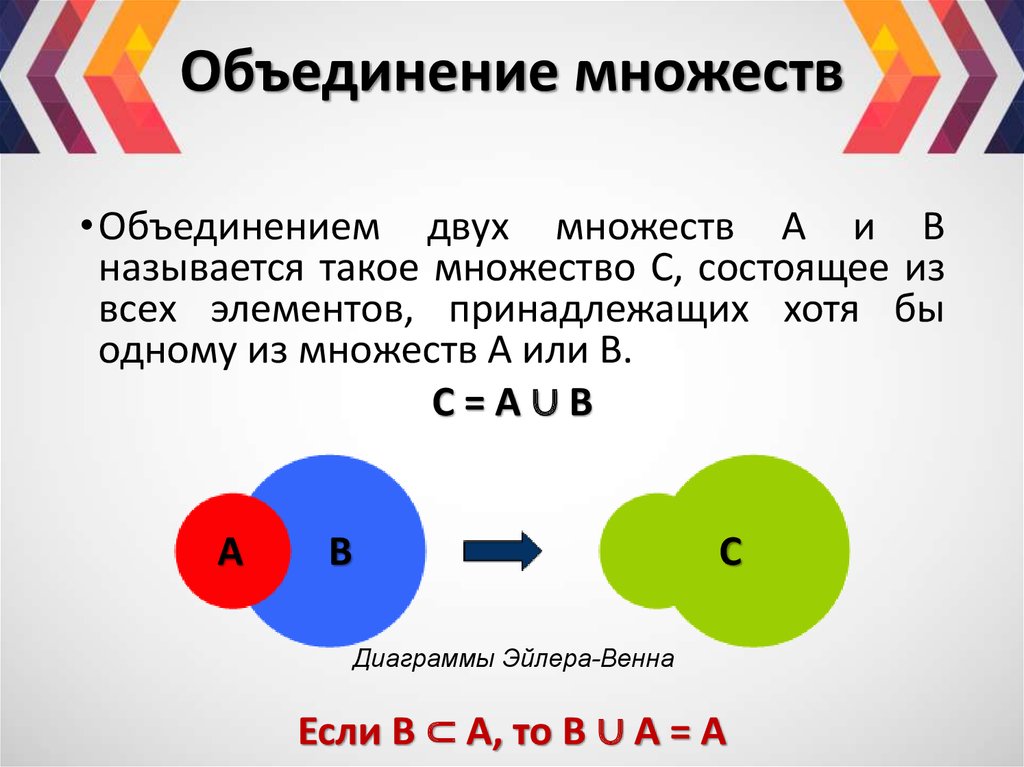 свойство его элементов, т. е. такое свойство, которым обладают все элементы этого множества и только они. Может случиться, что данным свойством не обладает вообще ни один объект; тогда говорят, что это свойство определяет пустое множество. То, что данный объект $x$ есть элемент множества $M$, записывают как $x∈М$.

Если каждый элемент множества $A$ является в то же время элементом множества $B$, то множество $A$ называется подмножеством множества $B$. Это записывают как $A⊂B$ или $B⊃A$. Подмножеством данного множества $B$ является и само множество $B$. Если $A⊂B$ и $A⊃B$, то множества $А$ и $B$ называют равными и пишут $A=B$. Пустое множество, по определению, считают подмножеством любого множества. Всякое непустое подмножество $A$ данного множества $B$, отличное от всего множества $B$, называют правильной частью последнего (вместо символа включения $⊂$ иногда используют символ включения $⊆$; в этом случае запись $A⊂B$ означает, что $A$ есть правильная часть $B$).

Мощность множеств

Первым вопросом, возникшим в применении к бесконечным множествам, был вопрос о возможности их сравнения между собой. Ответ на этот и близкие вопросы дал в кон. 1870-х гг. Г. Кантор, основавший М. т. как математич. науку. Возможность сравнительной оценки множеств опирается на понятие взаимно однозначного соответствия между двумя множествами. Пусть каждому элементу множества $A$ поставлен в соответствие с помощью к.-л. правила или закона некоторый определённый элемент множества $B$; если при этом каждый элемент множества $B$ оказывается поставленным в соответствие одному и только одному элементу множества $A$, то говорят, что между множествами $A$ и $B$ установлено взаимно однозначное соответствие. Между двумя конечными множествами можно установить взаимно однозначное соответствие тогда и только тогда, когда оба множества состоят из одинакового числа элементов. Обобщая этот факт, определяют эквивалентность или равномощность двух бесконечных множеств как возможность установить между ними взаимно однозначное соответствие.

Ещё до создания М. т. Б. Больцано владел, с одной стороны, вполне точно сформулированным понятием взаимно однозначного соответствия, с др. стороны, считал несомненным существование бесконечностей разл. ступеней; однако он не только не сделал взаимно однозначное соответствие основой установления равносильности множеств, но решительно возражал против этого. Больцано останавливало то, что бесконечное множество может находиться во взаимно однозначном соответствии со своей правильной частью. Напр., если каждому натуральному числу $n$ поставить в соответствие натуральное число $2n$, то получается взаимно однозначное соответствие между множеством всех натуральных и множеством всех чётных чисел.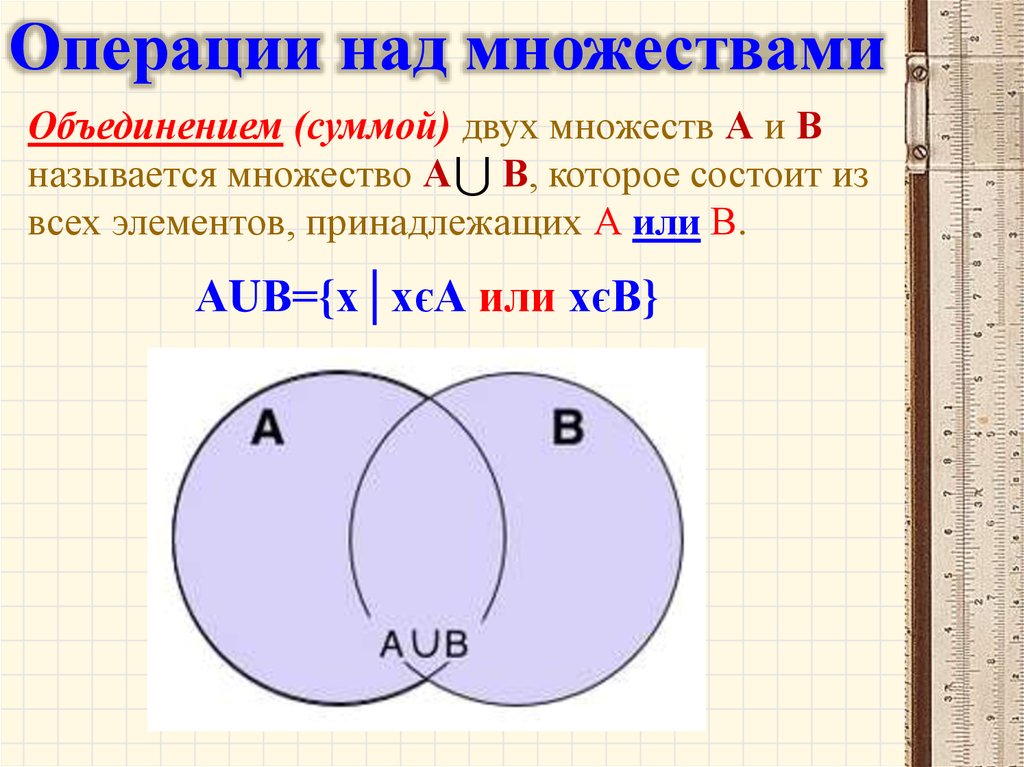 Вместо того чтобы в применении к бесконечным множествам отказаться от положения, состоящего в том, что часть меньше целого, Больцано отказался от взаимной однозначности как критерия равномощности. В каждом бесконечном множестве $M$ имеется правильная часть, равномощная всему множеству $M$, тогда как ни в одном конечном множестве такой правильной части не существует. Поэтому наличие правильной части, равномощной целому, можно принять за определение бесконечного множества.

Для двух бесконечных множеств $A$ и $B$ возможны следующие 3 случая: либо в $A$ есть правильная часть, равномощная $B$, но в $B$ нет правильной части, равномощной $A$; либо, наоборот, в $B$ есть правильная часть, равномощная $A$, а в $A$ нет правильной части, равномощной $B$; либо, наконец, в $A$ есть правильная часть, равномощная $B$, и в $B$ есть правильная часть, равномощная $A$. Доказывается, что в 3-м случае множества $A$ и $B$ равномощны (теорема Кантора – Бернштейна). В 1-м случае говорят, что мощность множества $A$ больше мощности множества $B$, во 2-м – что мощность множества $B$ больше мощности множества $A$. Формально возможный 4-й случай – в $A$ нет правильной части, равномощной $B$, а в $B$ нет правильной части, равномощной $A$, – в действительности для бесконечных множеств осуществиться не может.

Ценность понятия мощности множества связана с существованием неравномощных бесконечных множеств. Напр., множество всех подмножеств данного множества $M$ имеет мощность бо́льшую, чем множество $M$. Множество, равномощное множеству всех натуральных чисел, называется счётным множеством. Мощность счётных множеств есть наименьшая мощность, которую может иметь бесконечное множество; всякое бесконечное множество содержит счётную правильную часть. Кантор доказал, что множество всех рациональных и даже всех алгебраических чисел счётно, тогда как множество всех действительных чисел несчётно. Из этого следует, в частности, доказательство существования т. н. трансцендентных чисел, т. е. действительных чисел, не являющихся корнями никакого алгебраич. уравнения с целыми коэффициентами (и даже несчётность множества таких чисел). Мощность множества всех действительных чисел называется мощностью континуума. Множеству всех действительных чисел равномощны множество всех подмножеств счётного множества, множество всех комплексных чисел и, следовательно, множество всех точек плоскости, а также множество всех точек $n$-мерного пространства при любом $n$. Кантор высказал гипотезу о том, что всякое множество, состоящее из действительных чисел, либо конечно, либо счётно, либо равномощно множеству всех действительных чисел; по поводу этой гипотезы и о связанных с нею результатах см. Континуум-гипотеза, Континуума проблема.

Отображения множеств

В М. т. понятие функции, геометрич. понятие отображения или преобразования фигуры приводят к общему понятию отображения одного множества в другое. Пусть даны два множества $X$ и $Y$ и каждому элементу $x∈X$ поставлен в соответствие некоторый определённый элемент $y=f(x)$ множества $Y$; тогда говорят, что имеется отображение множества $X$ в множество $Y$ или что имеется функция, аргумент $x$ которой пробегает множество $X$, а значения $y$ принадлежат множеству $Y$; при этом для каждого данного $x∈X$ элемент $y=f(x)$ множества $Y$ называется образом элемента $x$ при данном отображении или значением данной функции для данного значения $x$ её аргумента.

Примеры.

1) Пусть в плоскости с данной на ней прямоугольной системой координат задан квадрат с вершинами $(0; 0), (0; 1), (1; 0), (1; 1)$ и этот квадрат спроектирован, напр. 3$, то тем самым будет установлено отображение множества $X$ в себя.

3) Пусть $X$ – множество всех действительных чисел; если для каждого $x∈X$ положить $y=f(x)=\text {arctg}$ $x$, то этим будет установлено отображение множества $X$ в интервал $(-π/2, π/2)$.

Взаимно однозначное соответствие между двумя множествами $X$ и $Y$ есть такое отображение множества $X$ в множество $Y$, при котором каждый элемент множества $Y$ является образом одного и только одного элемента множества $X$. Отображения примеров 2) и 3) взаимно однозначны, примера 1) – нет.

Операции над множествами

Суммой, или объединением, конечного или бесконечного множества множеств называется множество всех тех элементов, каждый из которых есть элемент хотя бы одного из данных множеств-слагаемых. Объединение множеств $A$ и $B$ обозначается $A∪B$. Пересечением любого конечного или бесконечного множества множеств называется множество всех элементов, принадлежащих всем данным множествам.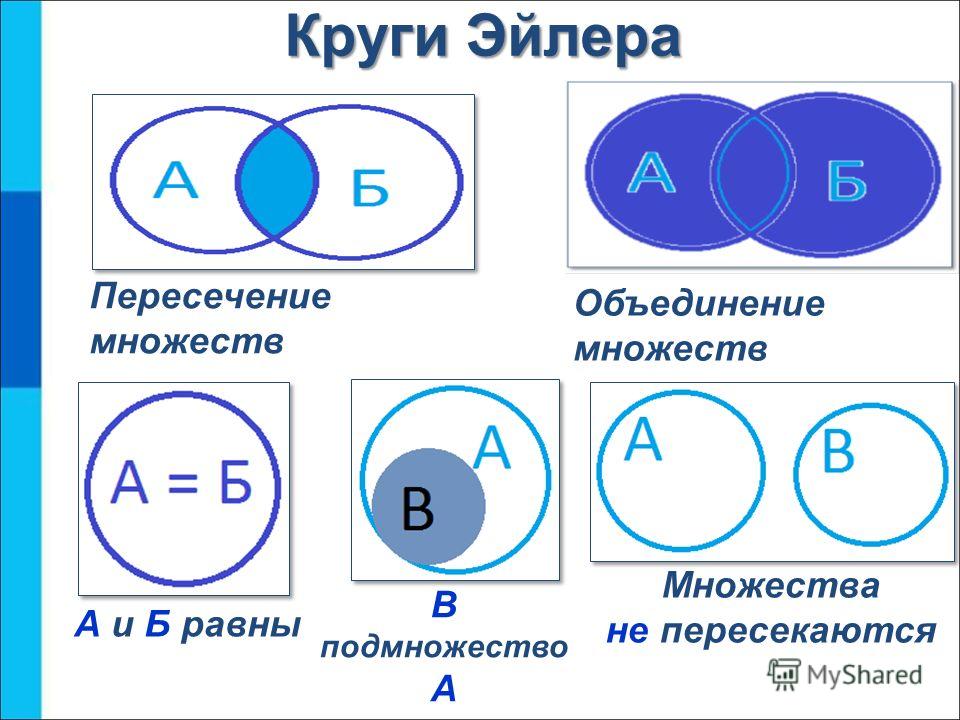 Пересечение множеств $A$ и $B$ обозначается $A∩B$. Пересечение непустых множеств может быть пустым. Разностью между множеством $B$ и множеством $A$ называется множество всех элементов из $B$, не являющихся элементами из $A$; эта разность обозначается $BA$; разность между множеством $B$ и его частью $A$ называется дополнением множества $A$ в множестве $B$ и обозначается .

Операции сложения и пересечения множеств обладают ассоциативностью и коммутативностью. Операция пересечения, кроме того, обладает дистрибутивностью по отношению к сложению и вычитанию. Если эти операции производить над множествами, являющимися подмножествами одного и того же множества $M$, то и результат будет подмножеством множества $M$. Указанным свойством не обладает т. н. внешнее умножение множеств, внешним произведением множеств $X$ и $Y$ или прямым произведением множеств $X$ и $Y$ называется множество $X×Y$ всевозможных пар $(x, y)$, где $x∈X, y∈Y$.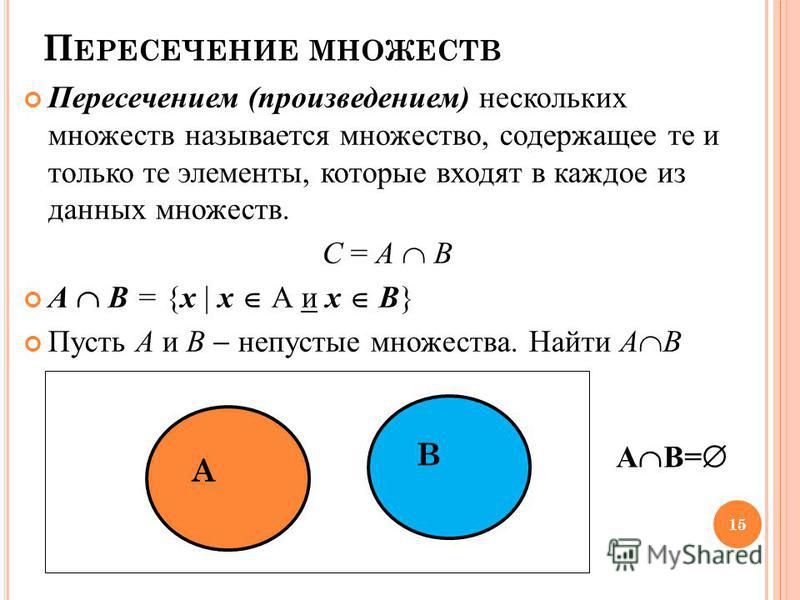 X$, что в случае конечных множеств согласуется с умножением и возведением в степень натуральных чисел. Аналогично определяется сумма мощностей как мощность суммы попарно непересекающихся множеств с заданными мощностями.

Упорядоченные множества

В данном множестве $X$ можно установить порядок, т. е. определить для некоторых пар $x′, x″$ элементов этого множества к.-л. правило предшествования (следования), выражаемое словами элемент $x′$ предшествует элементу $x″$ (или, что то же, элемент $x″$ следует за элементом $x’$ ), что записывается $x′≺x″$; при этом предполагается, что для данного отношения порядка выполнено условие транзитивности, т. е. если $x≺x′$ и $x′≺x″$, то $x≺x″$. Множество, рассматриваемое вместе с к.-л. установленным в нём порядком, называется частично упорядоченным множеством; иногда – упорядоченным множеством. Однако чаще упорядоченным множеством называется частично упорядоченное множество, в котором порядок удовлетворяет следующим дополнит. требованиям (линейного порядка): 1) никакой элемент не предшествует самому себе; 2) из всяких двух разл. элементов $x, x′$ один предшествует другому, т. е. если $x≠x′$, то или $x≺x′$, или $x″≺x$.

Примеры.

1) Любое множество, элементами которого являются некоторые множества $x$, является частично упорядоченным по включению, если считать, что $x≺x′$, если $x⊂x′$.

2) Любое множество функций $f$, определённых на числовой прямой, становится частично упорядоченным, если считать, что $f_1≺f_2$, тогда и только тогда, когда для каждого действительного числа $x$ справедливо неравенство $f_1(x)⩽f_2(x)$.

3) Любое множество действительных чисел линейно упорядочено, если считать, что меньшее из двух чисел предшествует большему.

Два упорядоченных множества называются подобными, или имеющими один и тот же порядковый тип, если между ними можно установить взаимно однозначное соответствие, сохраняющее порядок. Элемент упорядоченного множества называется первым, если он предшествует всем остальным элементам; аналогично определяется и последний элемент. Напр., в упорядоченном множестве всех действительных чисел нет ни первого, ни последнего элемента; в упорядоченном множестве всех неотрицательных чисел нуль есть первый элемент, а последнего элемента нет; в упорядоченном множестве всех действительных чисел $x$, удовлетворяющих неравенствам $a⩽x⩽b$, число $a$ есть первый элемент, $b$ – последний.

Упорядоченное множество называется вполне упорядоченным, если оно само и всякое его правильное подмножество имеют первый элемент. Порядковые типы вполне упорядоченных множеств называются порядковыми, или ординальными, числами.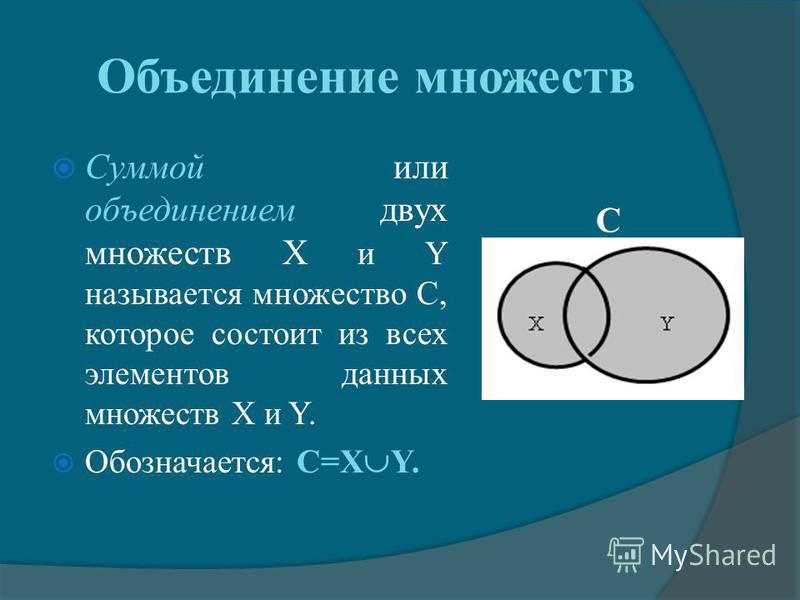 Если вполне упорядоченное множество конечно, то его порядковое число есть натуральное число. Порядковый тип бесконечного вполне упорядоченного множества называется трансфинитным числом.

Точечные множества

Теория точечных множеств, т. е. множеств, элементами которых являются действительные числа (точки числовой прямой), а также точки многомерных пространств, основана Г. Кантором, который ввёл понятие предельной точки множества и связанные с ним понятия замкнутого множества и пр. Развитие теории точечных множеств привело к понятиям метрического пространства и топологического пространства, изучением которых занимается общая топология. Самостоятельно существует дескриптивная теория множеств, основанная франц. математиком Р. Бэром и А. Лебегом в связи с классификацией разрывных функций (1905). Дескриптивная теория множеств началась с изучения и классификации т.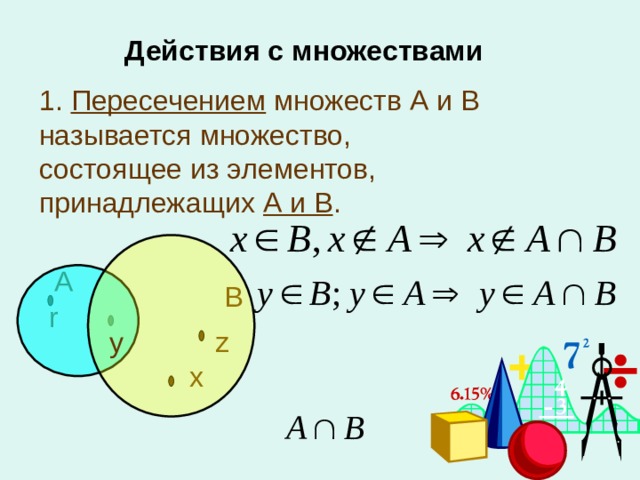 н. борелевских множеств ($B$-множеств). Борелевские множества определяются как множества, которые могут быть построены, отправляясь от замкнутых множеств, применением операций объединения и пересечения в любых комбинациях, но каждый раз к конечному или к счётному множеству множеств. Дальнейшее развитие дескриптивной теории множеств осуществлялось преим. рус. и польск. математиками, особенно московской математич. школой, созданной Н. Н. Лузиным (П. С. Александров, А. Н. Колмогоров, М. А. Лаврентьев, П. С. Новиков, М. Я. Суслин). Александров доказал (1916), что всякое бесконечное несчётное борелевское множество имеет мощность континуума. Аппарат этого доказательства был применён Суслиным для построения теории т. н. $A$-множеств, охватывающих как частный случай борелевские или $B$-множества, считавшиеся до того единственными множествами, которые могут встретиться в математич. 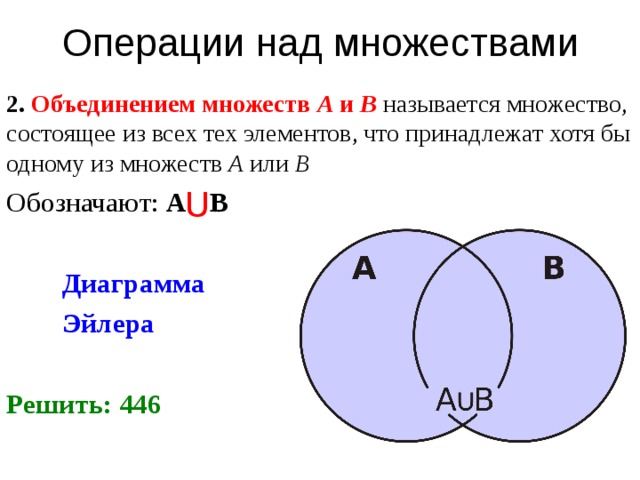анализе. Суслин показал, что множество, дополнительное к $A$-множеству $M$, является само $A$-множеством только в том случае, когда множество $M$ – борелевское (дополнение к борелевскому множеству всегда есть борелевское множество). При этом оказалось, что $A$-множества совпадают с непрерывными образами множества всех иррациональных чисел. Теория $A$-множеств в течение нескoльких лет оставалась в центре внимания дескриптивной теории множеств до того, как Лузин пришёл к общему определению проективных множеств, которые могут быть получены, отправляясь от множества всех иррациональных чисел при помощи повторного применения операций вычитания и непрерывного отображения. К теории $A$-множеств и проективных множеств относятся также работы Новикова и др. Дескриптивная теория множеств тесно связана с исследованиями по основаниям математики (с вопросами эффективной определимости математич. объектов и разрешимости математич. проблем).

Роль теории множеств в развитии математики

Влияние М. т. на развитие совр. математики очень велико. Прежде всего М. т. явилась фундаментом ряда математич. дисциплин, напр. теории функций действительного переменного, общей топологии, общей алгебры, функционального анализа. Теоретико-множественные методы применяются и в классич. разделах математики. Напр., они широко применяются в качественной теории дифференциальных уравнений, вариационном исчислении, теории вероятностей. М. т. оказала глубокое влияние на понимание самого предмета математики, в частности, таких её разделов, как геометрия. Только М. т. позволила отчётливо сформулировать понятие изоморфизма систем объектов, заданных вместе со связывающими их отношениями, и привела к пониманию того, что каждая математич. теория в её чистой абстрактной форме изучает ту или иную систему объектов лишь с точностью до изоморфизма, т. е. может быть без всяких изменений перенесена на любую систему объектов, изоморфную той, для изучения которой теория была первоначально создана. В вопросах обоснования математики, т. е. создания строгого, логически безупречного построения математич. теорий, следует иметь в виду, что сама М. т. нуждается в обосновании применяемых в ней методов рассуждения. Более того, все логич. трудности, связанные с понятием бесконечности, при переходе на точку зрения общей М. т. приобретают бо́льшую отчётливость.

Объединение множеств

Этот урок объяснит, как найти объединение множеств. Начнем с определения объединения двух множеств.

Определение: Для двух множеств A и B объединение множеств A и B — это множество, содержащее элементы или объекты, принадлежащие либо A, либо B, либо обоим.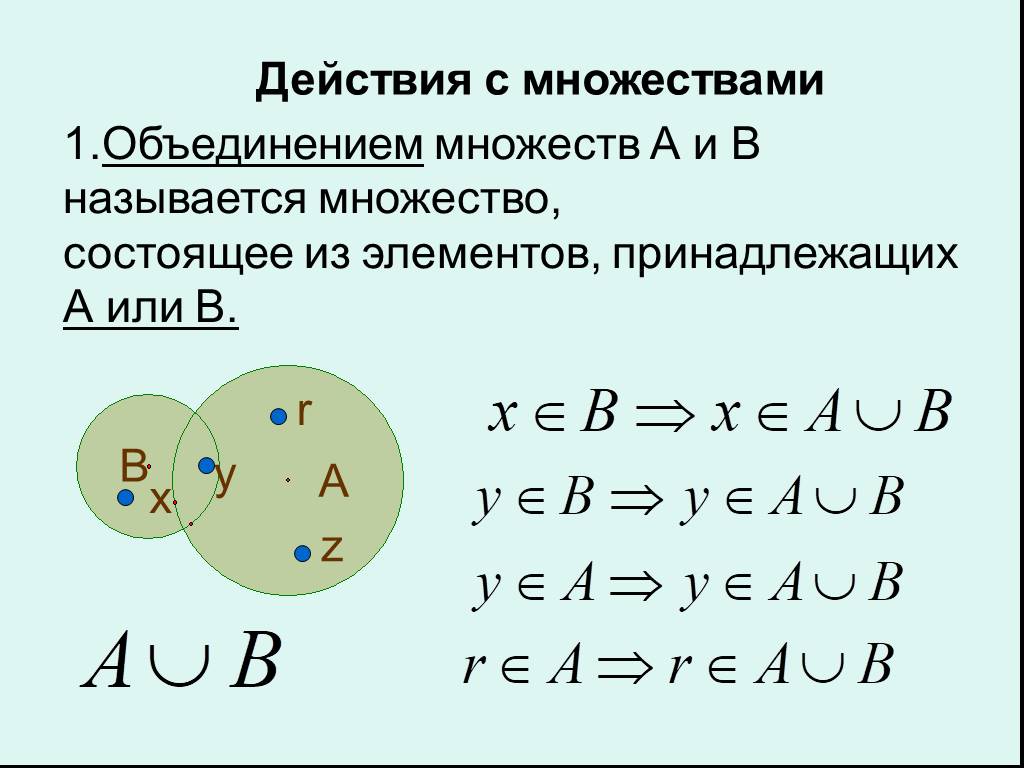

Мы пишем A ∪ B, а A ∪ B читается как A union B.

По сути, мы находим A ∪ B, складывая вместе все элементы A и B. Далее проиллюстрируем примерами.

Пример #1

Пусть A = {1 апельсин, 1 ананас, 1 банан, 1 яблоко} и B = {1 ложка, 1 нож, 1 вилка}

A ∪ B = {1 апельсин, 1 ананас, 1 банан, 1 яблоко, 1 ложка, 1 нож, 1 вилка}

Пример #2

Найти объединение A и B

A = {1, 2, 4, 6} и B = {4, a, b, c, d, f}

A ∪ B = {1, 2, 4, 6, 4, a, b, c, d, f} = {1, 2, 4, 6 , a, b, c, d, f}

Обратите внимание, что вполне нормально написать 4 один или два раза.

Пример #3

A = {x / x число больше 4 и меньше 8}

B = {x / x положительное число меньше 7}

A = {5, 6, 7} и B = {1, 2, 3, 4, 5, 6}

A ∪ B = {1, 2, 3, 4, 5, 6, 7}

Или A ∪ B = { x / x — число больше 0 и меньше 8}

Опять же, обратите внимание, что 5 и 6 были написаны только один раз, хотя было бы совершенно нормально написать их дважды.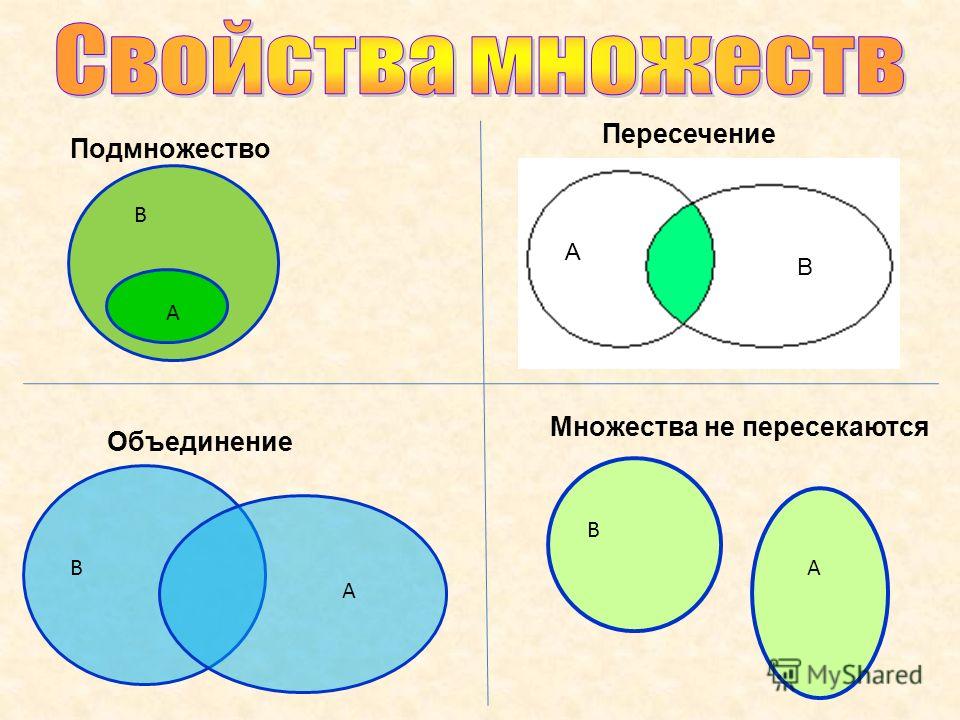

Пример #4

A = {x / x — страна в Азии}

B = {x / x — страна в Африке}

A ∪ B = {x / x — страна в Азии и Африке} = {все стран Азии и Африки}

Технически, используя определение, мы должны были бы сказать A ∪ B = {x / x — страна либо в Азии, либо в Африке, либо в обеих странах}

Однако в реальной жизни это не так. как мы говорим. Говоря обо всех странах Азии и Африки, в повседневных разговорах обычно понимают, что мы говорим обо всех странах Азии и всех странах Африки.

Пример #5

A = {#, %, &, * , $ }

B = { }

A ∪ B = {#, %, &,* , $} B — это пустое множество, также называемое нулевым множеством. Объединение любого множества с пустым множеством есть само множество.

Вы наверняка замечали, что объединение множеств находится просто путем складывания элементов множеств, желательно без повторения.

Определение объединения трех множеств

Для трех множеств A, B и C объединение представляет собой множество, содержащее элементы или объекты, принадлежащие либо A, B, либо C, либо всем трем.

Мы пишем A ∪ B ∪ C

По сути, мы находим A ∪ B ∪ C, складывая вместе все элементы A, B и C.

A = {1, 2, 4, 6}, B = {a, b, c,} и C = A = {#, %, &, * , $}

A ∪ B ∪ C = { 1, 2, 4, 6, a, b, c,#, %, &, * , $}

На первом графике в начале этого урока показана заштрихованная область объединения двух множеств.

На приведенном ниже графике показана заштрихованная область объединения трех наборов.

Свойства объединения множеств

Коммутативный закон

A ∪ B = B ∪ A

Пример

A = {a, b, c, d}

B = {e, f, g0}

A ∪ B = {a, b, c, d, e, f, g}

B ∪ A = {a, b, c, d, e, f, g}

Ассоциативный закон

(A ∪ B) ∪ C = A ∪ (B ∪ C)

Пример

A = {a, b, c, d}

B = {e, f, g}

C = {h, i}

А ∪ В = {а, б, в, г, д, е, г}

(A ∪ B) ∪ C = {a, b, c, d, e, f, g} ∪ {h, i}

(A ∪ B) ∪ C = {a, b, c, d, e, f, g, h, i}

B ∪ C = {e, f, g} ∪ {h, i} = {e, f, g, h, i}

A ∪ (B ∪ C) = {a, b, c, d} ∪ {e, f, g, h, i}

A ∪ (B ∪ C) = {a, b, c, d, e, f, g , h, i}

Закон идемпотента

A ∪ A = A

Пример

A = {x, y, z}

A ∪ A = {x, y, z} ∪ {x, y, z} , z}

A ∪ A = {x, y, z}

Опять же, нет необходимости повторять элементы, которые есть в обоих наборах. По этой причине мы также говорим, что объединение множеств — это наименьшее множество , содержащее все элементы всех множеств.

Закон тождества

Пусть ∅ или { } будет пустым набором } ∪ { }

A ∪ ∅ = {Maserati, BMW, Mercedes}

Закон о доминировании

Пусть U — универсальное множество или множество, содержащее элементы.

A ∪ U = U

A = {0, 1, 2}

U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

A ∪ U = { 0, 1, 2} ∪ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

A ∪ U = {0, 1, 2, 3, 4, 5, 6, 7 , 8, 9}

На этом урок об объединении множеств заканчивается. Если у вас есть какие-либо вопросы об объединении наборов, я буду более чем счастлив ответить на них.

Пройди тест ниже, чтобы узнать, насколько хорошо ты умеешь находить объединение множеств

Квадратичная формула: простые шаги
26, 23 января 11:44
Узнайте о квадратной формуле, дискриминанте, важных определениях, связанных с формулой, и приложениях.
Подробнее
Формула площади — список важных формул
25, 23 января 05:54
Что такое формула площади для двумерной фигуры? Вот список тех, которые вы должны знать!
Подробнее

Терминология, связанная с множествами — Mathstopia

Есть много технических терминов, которые нам необходимо понять, чтобы улучшить наше изучение теории множеств. Некоторые из них описаны ниже:

Наборы
Универсальный набор
Диаграммы Венна
Пересечение наборов
Союз наборов
Непересекающиеся наборы
Разница наборов
Дополнительные наборы
Дополнение к набору
Количество подмножеств из набора

Наборы — это совокупность различных объектов, имеющих хотя бы одно или несколько общих свойств.

Наборы могут состоять из ни одного элемента, нескольких элементов или бесконечного числа элементов. Примеры набора: Набор планет Солнечной системы, Набор континентов, Набор созвездий и т. д.

Концепция наборов может быть очень полезна для понимания, анализа и интерпретации различных отношений между несколькими группами данных/информации.

Примеры наборов:

а. Набор гор Непала высотой 8000 м и выше.

 { Эверест, Канченджанга, Лхоцзе, Макалу, Чо-Ойю, Дхаулагири, Манаслу, Аннапурна}

b. Набор натуральных чисел меньше 8

 { 1, 2, 3, 4, 5, 6, 7}

c. Набор президентов США 21 века:

 { Билл Клинтон, Джордж Буш-младший, Барак Обама }

d. Набор канцлеров Германии с 1980 года:

 {Гельмут Шмидт, Гельмут Коль, Герхард Шредер, Ангела Меркель}

эл. Набор стран СААРК:

 {Непал, Шри-Ланка, Индия, Бутан, Афганистан, Пакистан, Мальдивы, Бангладеш}

f. Набор цветов радуги:

 { Красный, оранжевый, желтый, зеленый, синий, индиго, фиолетовый}

Универсальный набор — это набор, состоящий из всех элементов, рассматриваемых в конкретном случае.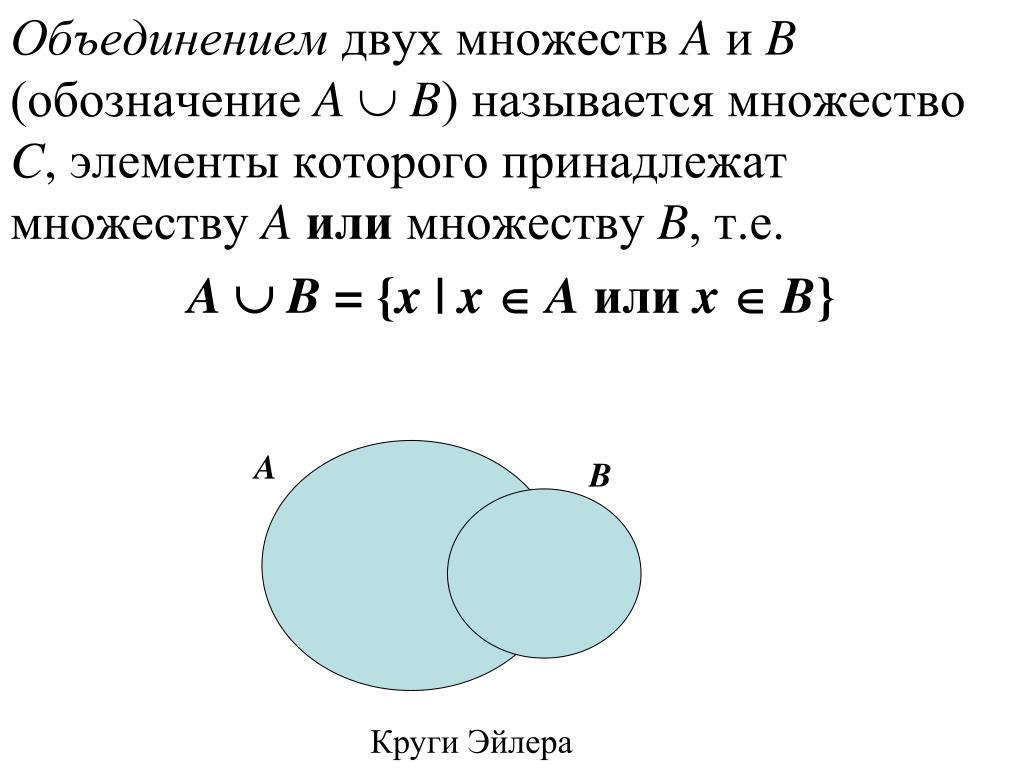 Вот некоторые из соответствующих универсальных наборов для приведенного выше обсуждения:

Набор	Универсальный набор
Горы Непала	Горы
Номера до 100	Целые числа
Президенты США с 1900 г.	президентов США до даты
Канцлеры Германии с 1900 г.	канцлеров Германии до даты
Страны Азии	Страны мира
Цвета, присутствующие в теле Павлина	Первичные и вторичные цвета

Диаграммы Венна — это способ визуального представления наборов и их взаимосвязей.

В диаграммах Венна универсальное множество представлено прямоугольником, а остальные множества представлены кружками или овалами, элементы расположены внутри этих кругов таким образом, чтобы точно описать их принадлежность.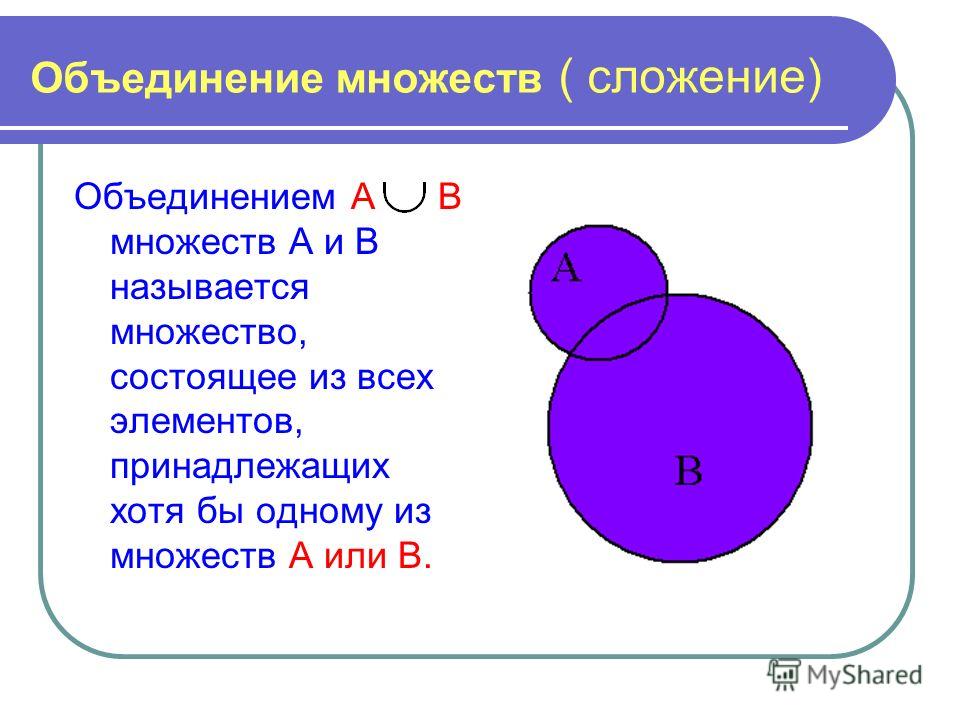

Диаграммы Венна для некоторых наборов, рассмотренных выше:

Множество, образованное путем взятия только тех элементов, которые присутствуют в каждом из рассматриваемых множеств, известно как пересечение множеств.

Рассмотрим универсальный набор
U = {Натуральные числа меньше 20} со следующими наборами:
A = {Натуральные числа меньше 10}
B = {Четные числа меньше 20}

Тогда диаграмма Венна для пересечения A и B (т. е. A $bigcap$ B) будет выглядеть так:

хотя бы одно из рассматриваемых множеств. Символ Союза представлен буквой U. Другими словами,

Набор, состоящий из каждого элемента, одного, некоторых или всех рассматриваемых наборов, известен как Союз наборов.

Объединение некоторых определенных наборов содержит все члены/элементы, которые есть в любом из его наборов элементов.

Тогда диаграмма Венна для объединения множеств A и B (т. е.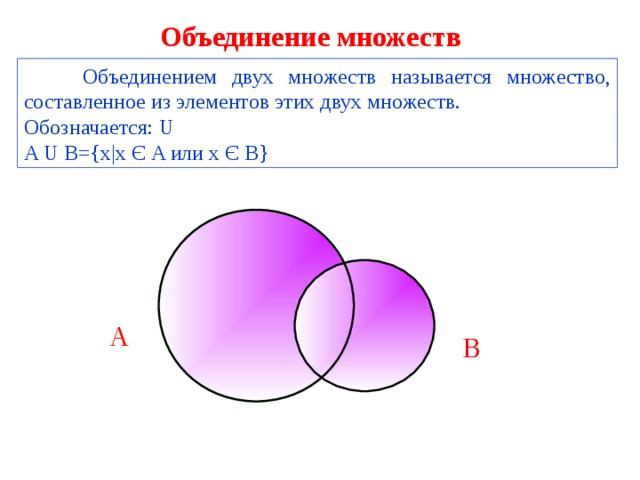 A $bigcup$ B) будет выглядеть так:

Два множества называются непересекающимися, если они не имеют общих элементов.

Рассмотрим универсальный набор
U = {Натуральные числа меньше 20} со следующими наборами:
A = {Натуральные числа меньше 10}
B = {Натуральные числа больше 13 и меньше 20}

Тогда диаграмма Венна для них будет:

Группа элементов набора, исключающая другие элементы другого набора, называется разностью двух наборов.

Если у нас есть два набора A и B, группа элементов A, которые не являются элементами B, называется A-B (читается как «A минус B» или «Разность B»)

Например:

Рассмотрим универсальный набор
U = {Натуральные числа меньше 20} со следующими наборами:
A = {Натуральные числа меньше 10}
E = {Четные числа меньше 20}

Тогда диаграмма Венна для разности A и B (т. е. A – B) будет:

Аналогично, диаграмма Венна для (B – A) станет: некоторые или все элементы из другого набора известны как подмножество.

Если A= {кратные 4, которые меньше 20} и B = {кратные 2, которые меньше 20}
Затем,
А = {4, 8, 12, 16}
B = {2, 4, 6, 8, 10, 12, 14, 16, 18}

$Rightarrow$ A $subset$ B

Правильное подмножество

Если подмножество не содержит всех элементов другого множества, то говорят, что первое множество является правильным подмножеством второго множества.

например:

Рассмотрим универсальный набор
U = {Натуральные числа меньше 20} со следующими наборами:
B = {Натуральные числа меньше 10} и,
A = { Натуральные числа меньше 5}

Здесь, поскольку все элементы A также присутствуют в B, A является подмножеством B. Но поскольку не все элементы B присутствуют в A, A далее называется правильным подмножеством д.

A $subset$ B

Неверное подмножество

Если подмножество содержит все элементы другого множества, то говорят, что первое множество является неправильным подмножеством второго множества.
No related posts.

Объединение множеств

МНОЖЕСТВ ТЕОРИЯ • Большая российская энциклопедия

Мощность множеств

Отображения множеств

Операции над множествами

Упорядоченные множества

Точечные множества

Роль теории множеств в развитии математики

Объединение множеств

Определение объединения трех множеств

Свойства объединения множеств

Коммутативный закон

Ассоциативный закон

Закон идемпотента

Закон тождества

Закон о доминировании

Пройди тест ниже, чтобы узнать, насколько хорошо ты умеешь находить объединение множеств

Квадратичная формула: простые шаги

Формула площади — список важных формул

Терминология, связанная с множествами — Mathstopia

Примеры наборов:

Правильное подмножество

Неверное подмножество

Добавить комментарий Отменить ответ