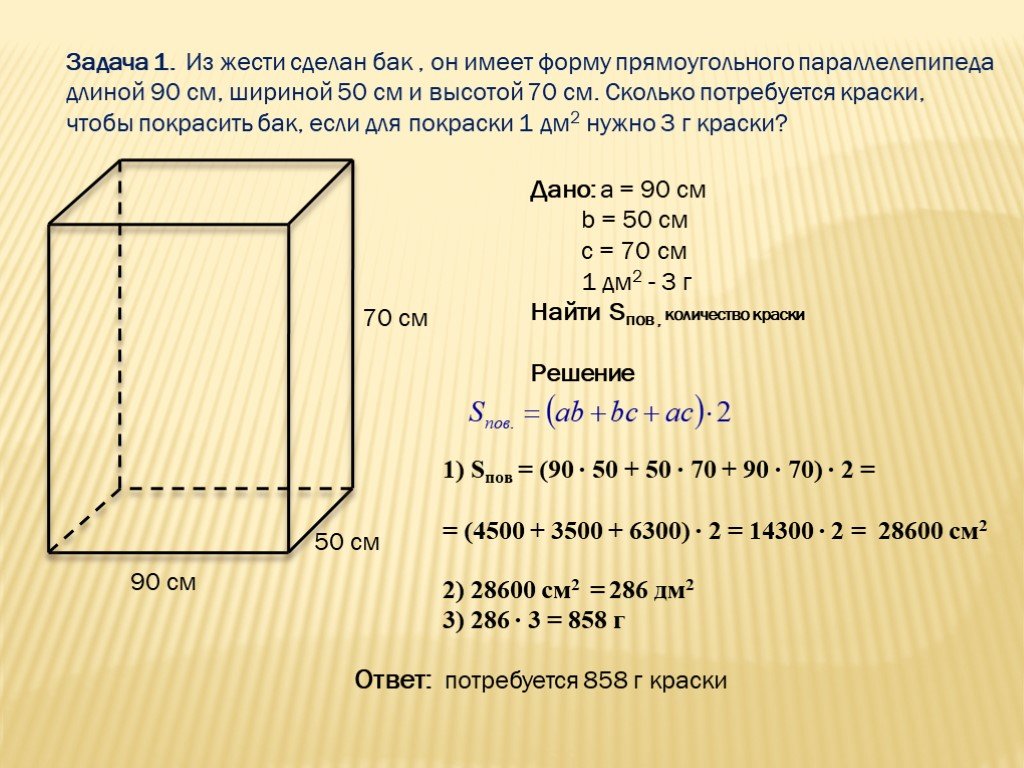
Формула объём прямоугольного параллелепипеда | План-конспект урока по математике (3 класс) по теме:
Конспект урока по «Математике»
3 класс
Тема: «Формула объема прямоугольного параллелепипеда».
Используемые технологии:
• информационно-коммуникативные;
- развивающее обучение;
• технология сотрудничества;
• гуманно-личностные;
Автор: Кошелкина Татьяна Андреевна
учитель начальных классов
ГБОУ школа №212 Фрунзенского района
Санкт-Петербурга
Тип урока: открытие новых знаний.
Тема: «Формула объема прямоугольного параллелепипеда».
Цели:
1)Уточнить представления у учащихся о прямоугольном параллелепипеде и его элементах – ребрах, гранях, вершинах.
2) Познакомить учащихся с кубом как частным случаем прямоугольного параллелепипеда.
3) Познакомить учащихся с формулой объема прямоугольного параллелепипеда.
4) Тренировать навыки устного счета, умения решать задачи на нахождение объема прямоугольного параллелепипеда и куба.
Ход урока:
1. Мотивация к учебной деятельности.
Что вы видите на доске? (формулы)
– Что такое формула? (Формулой называют верное равенство, устанавливающее взаимосвязь между величинами).
— С какими формулами мы вчера работали? (С формулами площади и периметра прямоугольника).
2. Актуализация знаний и фиксация затруднений в пробном учебном действии.
Давайте их повторим, применив при решении задач.
Вычисли, пользуясь формулами:
а) площадь прямоугольника со сторонами 9 м и 40 м;
б) периметр прямоугольника со сторонами 9 м и 10 м
в) сторону прямоугольника, вторая сторона которого равна 20 м, а площадь— 180 м²
г) сторону прямоугольника, вторая сторона которого равна 3см, а периметр- 20 см.
д) объём прямоугольного параллелепипеда с измерениями 6 см, 9 см, 2см;
3. Выявление места и причины затруднения.
Почему не удаётся вычислить объём прямоугольного параллелепипеда? (нет формулы)
Сформулируйте тему урока.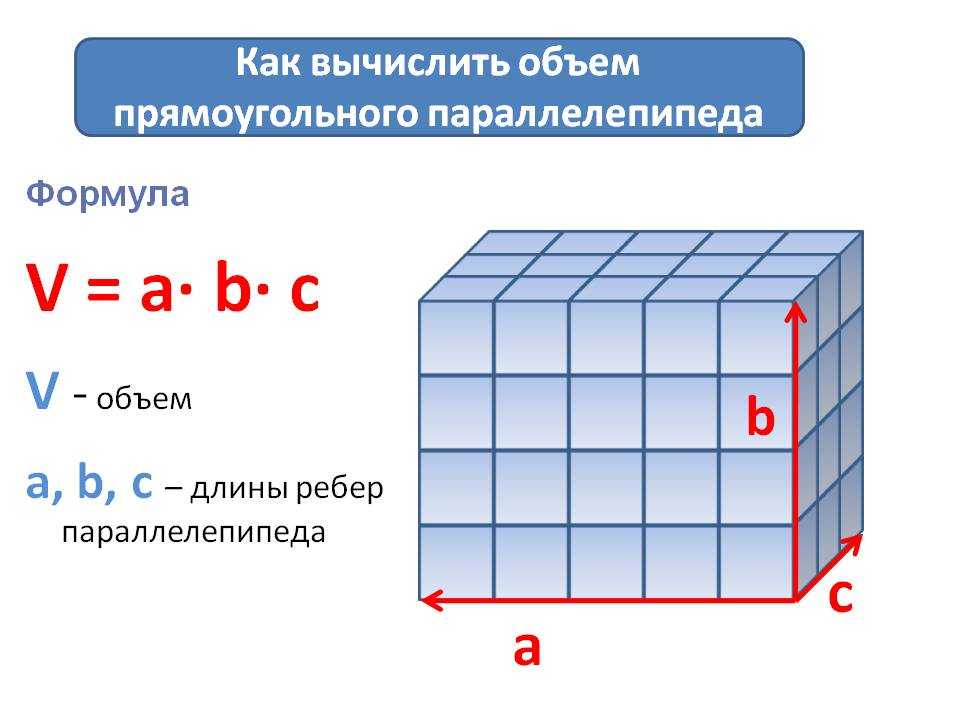
Какую цель мы должны перед собой поставить?
Уточнение представления о плоских и объемных фигурах.
На доске – фигуры:
— Назовите фигуры. (Прямоугольник, параллелепипед, квадрат, куб.)
— На какие группы можно разбить фигуры? (На доске фиксируются слова «Плоские» и «Объемные» фигуры.)
Найдите среди фигур прямоугольный параллелепипед.
Я предлагаю вспомнить всё, об этой фигуре выполнив практическую работу.
Работать будем в группах
— Возьмите в руки модель параллелепипеда и рассмотрите ее. (Учащиеся работают с моделью)
Начнём отвечать на вопросы вместе
— Какими фигурами ограничен параллелепипед? (Прямоугольниками.)
— Назовите отличия данной фигуры от прямоугольника. (Объемная, пространственная.)
— Давайте уточним, какую фигуру называют прямоугольным параллелепипедом?
На доске открывается запись с пропусками:
Прямоугольный параллелепипед – это ______________________ фигура, ограниченная __________________________.
«Прямоугольный параллелепипед – это пространственная фигура, ограниченная прямоугольниками».
— Далее исследование фигуры продолжим в группах. Выполните задание на карточках.
1) Найдите на моделях элементы параллелепипеда, посчитайте и запишите их количество:
граней — ________
вершин — ________
ребер — ________
2) Измерьте длину всех ребер. Запишите все измерения:___________________________________________________________
Сколько различных измерений у вас получилось? Запиши:___________________
При проверке дети на моделях показывают элементы фигуры, все понятия уточняются.
— А куб является параллелепипедом? В чем его особенности? (Куб – это особый параллелепипед, у него равны все ребра и грани; грани являются квадратами.)
Задание для пробного действия.
— Какая величина характеризует параллелепипед в силу того, то это пространственная фигура? (Объем.)
— В математике принято обозначать объем латинской буквой «V»
Что предстоит нам сделать, чтобы мы могли вычислять объём? (Вывести формулу для нахождения объема прямоугольного параллелепипеда. )
)
4. Построение проекта выхода из затруднения.
Составим план действий.
— Какие данные необходимы для формулы? (Измерения.)
— Где вы будете находить измерения параллелепипеда? (На модели параллелепипеда.)
— Что вам поможет установить связь между измерениями? (Арифметические действия.)
-К какому результату вы должны прийти? (Вывести формулу объема прямоугольного параллелепипеда.)
Учитель на доске фиксирует план действий.
1) Определить по модели параллелепипеда измерения.
2) Выбрать арифметическое действие.
3) Записать формулу для нахождения объёма прямоугольного параллелепипеда
5. Реализация построенного проекта.
Рассмотрите ещё одну модель пр. пар.
Что вы видите?
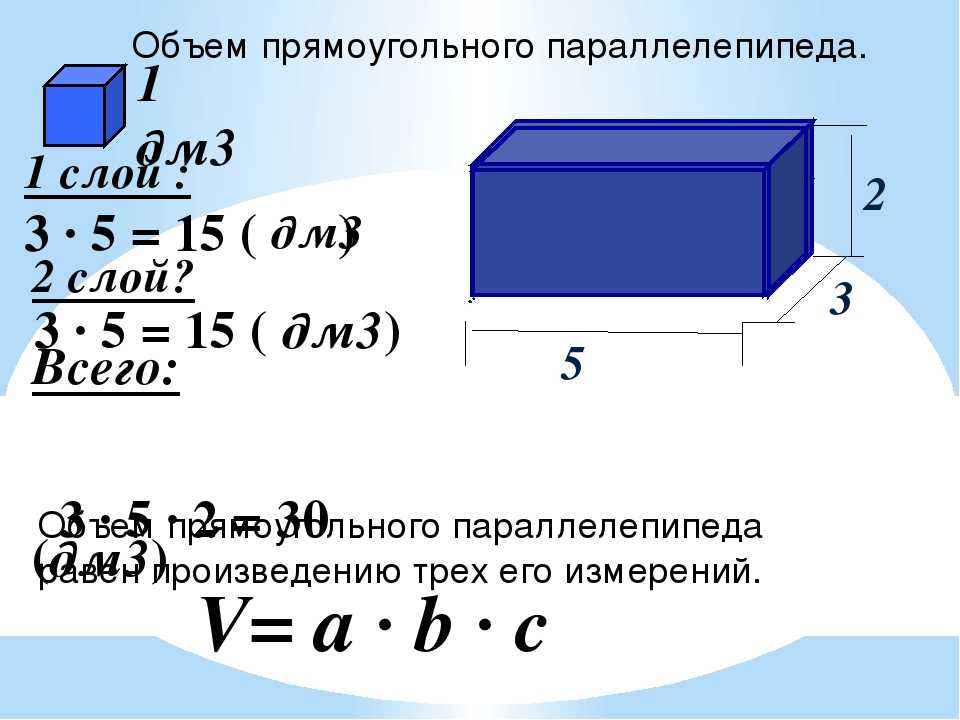
Выложите кубики на дно данной модели.
Сосчитайте количество кубиков удобным способом.
Что мы нашли? (площадь прямоугольника в основании пр пар)
-Назовите формулу? S = a *b (длину умножить на ширину)
-Какой буквой обозначена длина «а», какой ширина «b», а ещё у параллелепипеда есть высота, обозначим её буквой «с».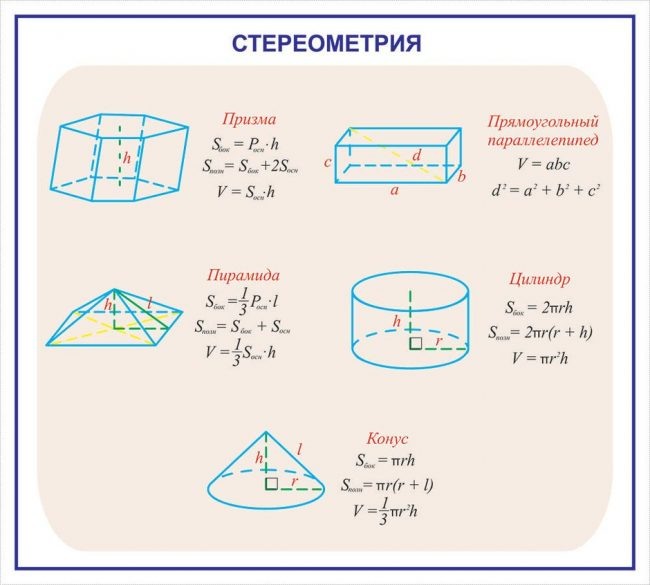
— Ребята площадь основания мы нашли, сколько таких оснований будет в параллелепипеде? ( «с» штук)
-И так ребята, чтобы найти площадь основания нужно а*b,
-А чтобы найти объём нужно а*b и умножить на что? (на с)
— Обратитесь к выводам в учебнике на с. 89.
Дети читают вслух правило нахождения объема параллелепипеда.
— Совпал ли ваш вывод с выводом учебника? (Да, мы сделали правильный вывод.)
— Как найти объема параллелепипеда? (V = a • b • с)
На доске фиксируется формула
V = a • b • с
— Формулу объема можно читать разными способами.
Учебник с.90
Что мы с вами сейчас сделали ? (вывели формулу нахождения объёма прямоугольного парал.)
Сможем мы теперь вернуться к задаче, вспомнить, где возникло затруднение и его преодолеть?
Единицы измерения объёма:
6. Первичное закрепление с проговариванием во внешней речи.
Где может нам пригодиться формула?
Попробуем ей воспользоваться
№4 с.90
№5
7.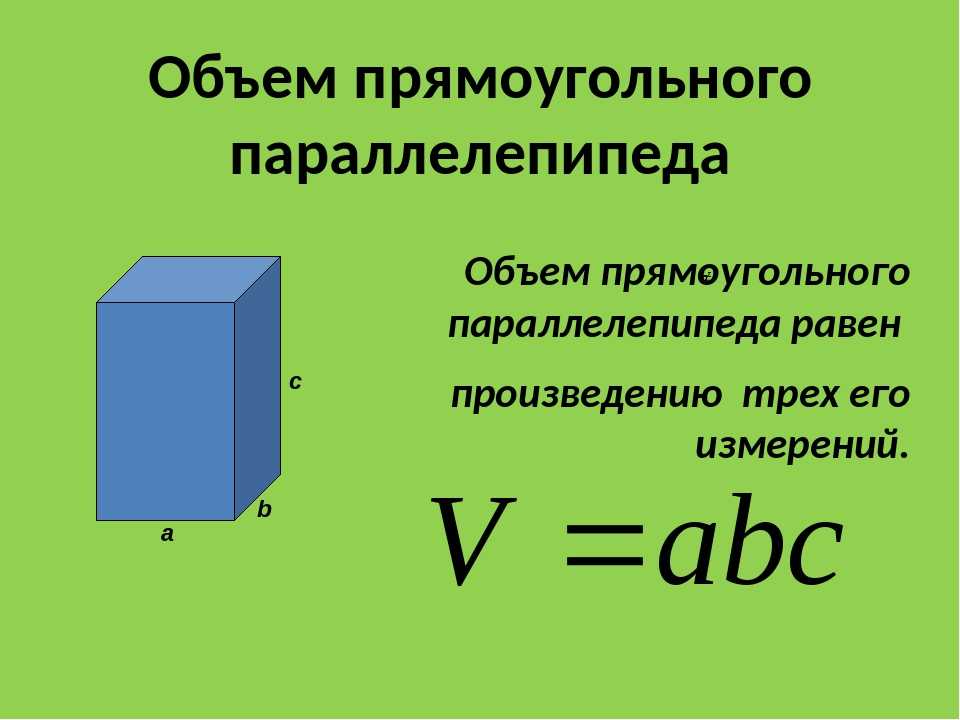 Самостоятельная работа
Самостоятельная работа
№ 4 Б) , №5 Б)
9. Рефлексия учебной деятельности на уроке.
– Какую цель вы перед собой ставили? (…)
– Достигли цели? Докажите. (Мы открыли формулу объема параллелепипеда.)
— Вспомним формулу. (Дети проговаривают еще раз V = a • b • с)
— Научились ли использовать новый способ?
Конспект урока» Формула объема прямоугольного параллелепипеда»
Урок математики в 3 классе « Формула объема прямоугольного параллелепипеда»
Никаньшина Н.И., учитель начальных классов,
МБОУ « Гимназия №102 им.М.С.Устиновой», г.Казань, РТ
Цели: — углубить и расширить знания о применении формул в математике;
— познакомить с формулой объема прямоугольного параллелепипеда;
— совершенствовать вычислительные навыки;
— развивать математическую речь.
Планируемые результаты: учащиеся научатся находить объем прямоугольного параллелепипеда по формуле; понимать учебную задачу урока и стремиться к ее выполнению; осуществлять самоконтроль и самооценку, взаимоконтроль; слушать собеседника и вести диалог.
Ход урока
I.Организационный момент.
Сегодня настроение хорошее с утра? (Да)
Друг друга видеть рады? (ДА)
Готовы считать, размышлять, узнать? (Да)
А пятерки получать? (да)
Сегодня предлагаю вам самостоятельно оценивать каждый этап урока и закрашивать 5! (рисунок 1)
Рисунок 1 Самооценка.
А сейчас разминка для ума!
II. Актуализация знаний.
Устный счет.
Ребята, у вас на столе листочки на которых отмечены точки с цифрами (рисунок 1). Выполните задания математического диктанта, найдите точки с правильным ответами и последовательно соедините их отрезками.
(6 +9) • 3 (45)
(50ˑ9) +30 (480)
(160 – 70) -25 (65)
(720:90) •8 (64)
Найдите площадь прямоугольника со сторонами 9 и 5 см. (45 кв.см)
Найдите периметр квадрата со стороной 12 см. (48 см)
Чему равна длина прямоугольника, если его площадь 180 кв. м, а ширина 9м. (20м)
м, а ширина 9м. (20м)
Найдите площадь прямоугольника со сторонами 13 и 5 мм. (65 кв.мм)
Рисунок 2 Устный счет.
III.Самоопределение к деятельности.
-Какая фигура у вас получилась? (прямоугольный параллелепипед)
-Где в жизни вы встречались с такой фигурой? (коробки, бассейн….)
-Какая это фигура? (объемная)
— Что мы можем вычислить у этой фигуры? (объем)
— Как вычислить объем? (не знаем формулы)
-Кто может сформулировать тему урока?
Формула объема прямоугольного параллелепипеда.
-Какие цели мы поставим? (вывести формулу объема, использовать формулу при решении задач)
— Как мы получили параллелепипед? (соединили точки)
-Выделите точки. Сколько их (8)
-Как они называются? (вершины)
-Из чего состоит поверхность параллелепипеда? (из прямоугольников)
-Как они называются? (грани)
-Сколько их? (6)
-Как называются стороны граней? (ребра)
-Сколько их? (12)-Что интересного заметили? (противоположные грани равны)
-Обведите длинную сторону основания и все равные ей зеленым цветом.
— Обведите короткую сторону основания и все равные ей красным цветом.
— Что лежит в основании прямоугольного параллелепипеда? (прямоугольник)
-Закрасьте его.
— Что можем измерить у прямоугольника? (длину и ширину)
— Что можем найти? (площадь)
— А что еще есть у параллелепипеда, что мы не обвели? (высота)
— Кто уже догадался, как найти объем?
a ˑ b ˑ c = V
Первичное закрепление.
-Можем сейчас найти объем получившегося параллелепипеда? (да)
— Что мы должны сделать? (измерить длину, ширину, высоту и перемножить)
Работа в тетрадях.
а = 6см
b = 2 см
c = 3см
V = ? V = 6 • 2 • 3=36 (куб.см)
— В каких единицах измеряется V?
V. Физминутка.
Ребята, я сейчас буду показывать карточки с единицами измерения, если это единицы измерения периметра P – 1 раз хлопаем в ладоши, если S – ходьба на 1и2, если V – 3 прыжка. (см, кв.дм, куб.м, мм и т.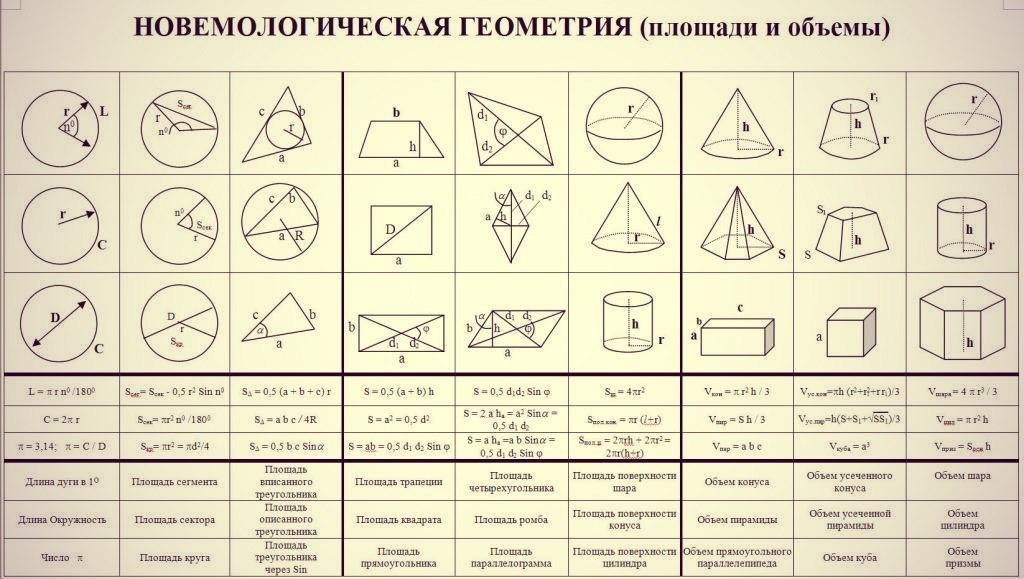 д.).
д.).
VI.Закрепление изученного материала.
1.- Ребята, мы немного отдохнули. А где вы любите отдыхать летом? (на реке, на море) А можем мы кусочек моря поместить у себя дома? (да). Как? (в аквариуме)
-Вычислите V аквариумов?
1 вариант а =5дм, в = 4дм, с = 3дм. ( 60 куб.дм)
2 вариант а =6дм, в = 4 дм, с = 7 дм (168 куб.дм)
Дети работают самостоятельно. Проверка в парах.
-Сравните на сколько один аквариум больше другого. (работа в парах)
168-60=108 (куб.дм)
— Кого можем поселить в 1 аквариум? (черепашку, рыбок), а во второй? (хамелеона). Чем мы должны заполнить аквариум для рыбок? (водой)
2.С понятием V вы еще часто будете встречаться. Игра «Выдумка» (ребята читают 3 высказывания и ищут среди них выдумку).
— Объем памяти человека гораздо больше объема памяти самого современного компьютера.
— Оранжевый цвет визуально увеличивает объем предметов.
— Объем луны больше объема воды в Тихом океане.
(ложь 3 ,они равны)
3. Самостоятельная работа.
Самостоятельная работа.
1.Ученые проводят много экспериментов. А вы хотите побывать в роли экспертов?(да)
Задача: Согласно санитарным нормам в классе на 1 ученика должно приходиться 5 куб. метров воздуха. Соответствует ли норме количество учеников нашего класса, если ширина кабинета 8м, длина 6м, высота 4м?
V = 6 • 8 •4 = 192 куб.м
192 : 32 =6куб.м
6 5 соответствует
3. Тест
1) Сколько у прямоугольного параллелепипеда вершин, граней,ребер?
а) 8, 6, 12
б) 6, 8, 12
в) 12, 8 ,6
2) Найди формулу объема
а) (а + в)• 2
б) а• в
в) а • в • с
3) В каких единицах измеряется объем?
а) см
б) кв.см
в) куб.см
4)Найдите объем прямоугольного параллелепипеда со сторонами 8м,6м,10м.
а) 480 м
б)480 куб.м
в) 4800 куб.м
5) Найдите объем фигуры со сторонами 30 дм,20дм,50дм.
а)30000куб дм
б)3000 куб.дм
в) 3000л
VII. Рефлексия.
-Кто полностью закрасил поверхность 5? (на каждом этапе урока после проверки ребята закрашивали ту часть 5 , где было отмечено задание). Не закрашенные участки показывают, над чем вам еще нужно поработать.
— Раньше я думал что……, теперь думаю.
VIII. Домашнее задание.
Составить и решить задачу на нахождение объема.
7
Объем твердого вещества: значение, формула и примеры
Вы любите печь? Каждый раз, когда вы измеряете ингредиенты в своем рецепте, вы используете расчеты объема, даже не осознавая этого! Вы когда-нибудь задумывались, сколько воды нужно, чтобы наполнить бассейн? Вы можете использовать расчет объема, чтобы узнать, сколько вам потребуется.
Твердые тела представляют собой трехмерные (3D) формы. Их можно встретить повсюду в повседневной жизни и иногда вам нужно будет найти объем этих фигур. Существует множество различных типов твердых тел, и каждый из них узнаваем по внешнему виду. Вот несколько примеров:
Рис. 1 – Примеры тел
1 – Примеры тел
Объем тела в математике
Может быть полезно найти объем этих тел. При измерении объема твердого тела вы рассчитываете объем пространства, которое занимает твердое тело. Например, если полный кувшин может вместить 500 мл, объем этого кувшина будет 500 мл.
Чтобы найти объем твердого тела, нужно подумать о самой форме. Чтобы найти площадь поверхности твердого тела , вы будете использовать длина вместе с шириной , это дает вам квадратных единиц . Чтобы найти объем твердого тела , вам также необходимо учитывать высоту твердого тела, это даст вам кубических единиц .
Чтобы узнать больше о площади поверхности твердого тела, посетите страницу Поверхность твердых тел.
Существуют различные формулы, которые можно использовать для определения объема твердого тела. Эти формулы связаны с формулами, которые можно использовать для нахождения площади поверхности твердого тела.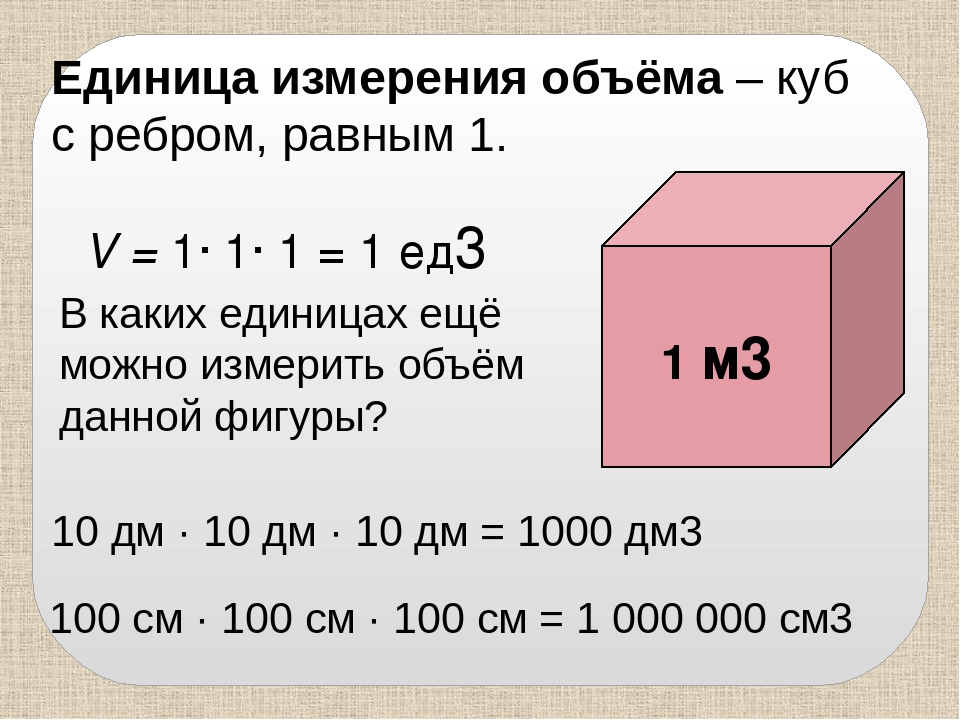 92h.\]
92h.\]
Формулы для объема твердого тела
Поскольку для каждого твердого тела используется своя формула, помогающая найти объем, важно уметь идентифицировать каждую форму и распознавать необходимую формулу.
Объем твердотельной призмы
Призма представляет собой тип твердого тела, которое имеет два основания, параллельные друг другу . Существуют различные типы призм, и они названы в честь формы основания;
Прямоугольная призма
Треугольная призма
Пятиугольная призма
Шестиугольная призма
Правая призма — это призма, в которой соединяемые ребра и грани перпендикулярны базовым граням.
Все призмы на картинке ниже правильные.
Рис. 2 – Примеры призм
Полезно иметь метки для частей призмы. Так что звоните:
\( B\) площадь основания призмы;
\(h\) высота призмы;
\(V\) объем призмы,
Тогда формула для объема прямой призмы равна
\[ V = B\cdot h.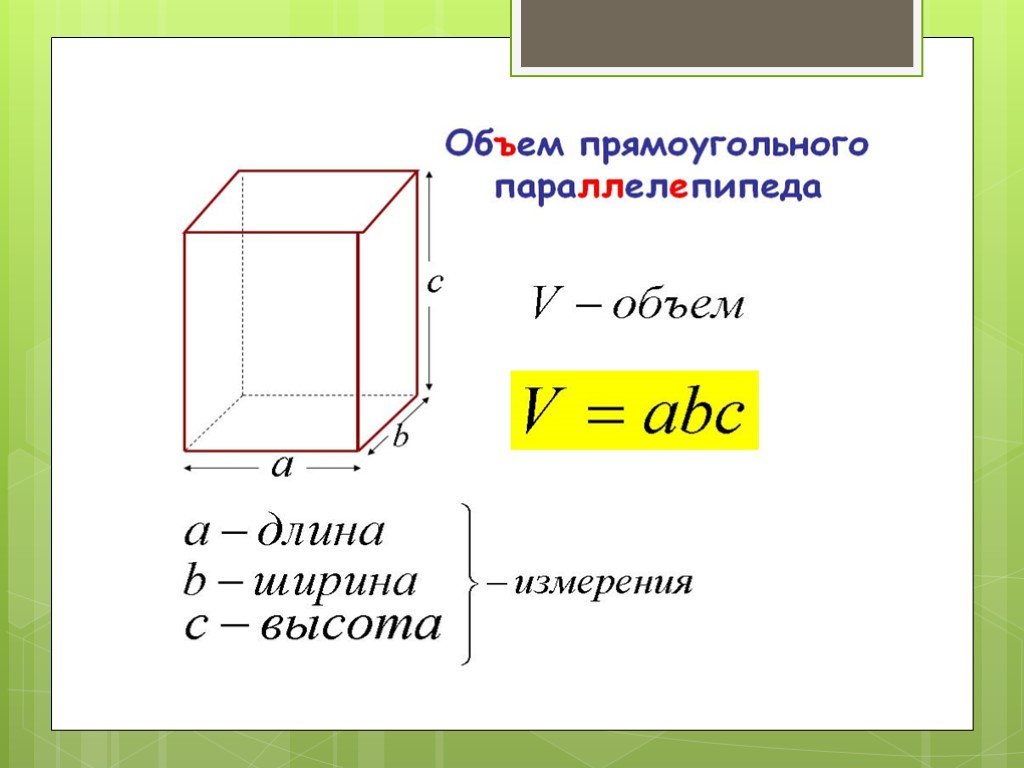 \]
\]
Возьмем посмотрите, как использовать формулу.
Найдите объем следующего твердого тела.
Рис. 3 – Пример объема призмы.
Ответ :
Обратите внимание, что это правильная призма, поэтому вы можете использовать формулу, чтобы найти объем.
Во-первых, вы можете начать с просмотра формулы и записи того, что вы знаете из диаграммы выше. Вы знаете, что высота призмы равна \(9\, см\). Это означает, что в формуле объема прямой призмы \(h = 9\).
Вам нужно рассчитать площадь основания. Вы можете видеть, что треугольник, который составляет основание, имеет одну сторону длины \(4\, см\) и другую сторону длины \( 5\, см\). 93 \end{align}\]
Как насчет наклонной призмы?
В наклонной призме одно основание не находится непосредственно над другим, или соединяемые ребра не перпендикулярны основанию.
Вот пример того, как может выглядеть сплошная наклонная призма.
Рис. 4 — Наклонная призма.
Если вам дана наклонная призма, вы можете использовать наклонную высоту тела, чтобы найти объем.
Чтобы узнать больше о призмах, посетите Volume of Prisms.
Объем твердого цилиндра
Цилиндр представляет собой тип твердого тела, которое имеет два основания и изогнутую кромку . Обычно они выглядят так, как показано на рис. 5.
Рис. 5 — Пример сплошного цилиндра.
Полезно иметь этикетки для частей цилиндра. Так звоните:
\(В\) площадь основания цилиндра;
\(h\) высота цилиндра; и
\(r\) радиус цилиндра. 92h.\]
Чтобы узнать больше о цилиндрах, посетите Volume of Cylinders.
Объем твердотельной пирамиды
Пирамида — это тип твердого тела, которое имеет одно основание . Форма основания определяет тип вашей пирамиды. В пирамиде все грани представляют собой треугольники, которые сходятся в одной вершине.
 Некоторые различные типы пирамид включают в себя:
Некоторые различные типы пирамид включают в себя:Квадратная пирамида
Прямоугольная пирамида
Шестиугольная пирамида
Вот пример квадратной пирамиды.
Рис. 6 – Пример квадратной пирамиды.
Метки пирамид:
\(B\) площадь основания пирамиды;
\(h\) высота пирамиды; и
\(V\) объем пирамиды,
Существует формула, которая поможет вам найти объем пирамиды ;
\[V=\frac{1}{3}Bh.\]
Вы можете заметить, что пирамида и конус — это две очень похожие формы, причем конус — это разновидность пирамиды с круглым основанием. Вот почему вы также можете увидеть сходство в формуле, которую можно использовать для нахождения объема фигур.
Чтобы узнать больше о пирамидах, посетите Том Пирамид.
Объем твердого конуса
Подобно пирамиде, твердый конус имеет только одно основание : круг.
 У конуса только одна грань и вершина. Они выглядят так; 92ч.\]
У конуса только одна грань и вершина. Они выглядят так; 92ч.\]Чтобы узнать больше о конусах, посетите Том конусов.
Объем твердой сферы
Сфера — это тип твердого тела, у которого нет оснований . Это как 3D мяч, например, футбольный. Сфера имеет центральную точку; расстояние между центральной точкой и внешним краем дает радиус сферы.
Рис. 8 – Пример сплошной сферы.
Полезно иметь этикетки для частей этого твердого тела. Так что звоните:
93.\]Чтобы узнать больше о сферах, посетите Том сфер.
Объем прямоугольного твердого тела
Прямоугольное твердое тело представляет собой тип трехмерной формы, где все основания и грани фигуры являются прямоугольниками . Их можно считать особым типом прямой призмы.
Рис. 9 – Пример прямоугольного твердого тела.
Чтобы найти объем прямоугольного тела, вы можете умножить длину на ширину на высоту фигуры .
 Это можно записать в следующую формулу:
Это можно записать в следующую формулу:\[V=L\cdot W\cdot H.\]
Давайте рассмотрим пример использования формулы.
Найдите объем следующего твердого тела.
Рис. 10 – Рабочий пример.
Ответ:
Для начала определите каждую из меток фигуры, чтобы вы знали, где ввести переменную в формулу.
\[L=5cm, \space \space W=7cm, \space \space H=10cm\]
Теперь вы можете ввести переменные в формулу для нахождения объема прямоугольного тела.
\[\begin{align} V&=L\cdot W\cdot H\\ \\ V&=5\cdot 7\cdot 10\\ \\ V&=350cm \end{align}\]
Объем Composite Solid
Составное тело — это тип трехмерного тела, состоящего из двух или более тел . Возьмем, к примеру, дом, здание можно рассматривать как составное твердое тело с призматическим основанием и пирамидальной крышей.
Рис. 11 – Пример составного твердого тела.
Чтобы найти объем составного тела, вам нужно разбить фигуру на отдельные тела и найти объем каждого из них.

Возвращаясь к примеру с домом, вы можете сначала найти объем призмы, а затем объем пирамиды. Чтобы найти объем всего дома, вы должны сложить два отдельных объема вместе.
Объем твердых примеров
Рассмотрим еще несколько примеров.
Вычислите объем пирамиды с квадратным основанием, длиной сторон \(6\,см\) и высотой \(10\,см\).
Ответ:
Для начала вам нужно найти правильную формулу для использования, так как это пирамида, вам понадобится эта конкретная формула:
\[V=\frac{1}{3}Bh\]
Теперь вам нужно найти каждую часть формулы для расчета объема. Поскольку основание пирамиды представляет собой квадрат со стороной \(6\,см\), чтобы найти площадь основания \((B)\), вы можете умножить \(6\) на \(6\ ):
\[B=6\cdot 6=36\]
Теперь вы знаете площадь основания и высоту пирамиды из вопроса, что означает, что теперь вы можете использовать формулу:
\[ \begin{align} V&=\frac{1}{3}(36)(10) \\ \\ V&=120\,см^3 \end{align}\] 93 \end{align}\]
Давайте рассмотрим пример другого типа.

Нарисуйте конус высотой \(10\,см\) и радиусом \(9\,см\).
Ответ:
Чтобы ответить на этот вопрос, вам нужно вычертить твердое тело в соответствии с заданными размерами.
В этом вопросе вас попросили нарисовать конус высотой \(10\,см\) и радиусом \(9\,см\). Это означает, что высота будет \(10\,см\), а радиус круглого основания будет \(9\,см\), то есть ширина будет \(18\,см\).
Рис. 12 – Рабочий пример с конусом.
Рисуя собственную схему, не забудьте указать размеры!
Давайте посмотрим еще на один.
Вычислить объем конуса с радиусом \(9\,м\) и высотой \(11\,м\).
Ответ:
Для начала вам нужно найти правильную формулу для использования, так как это конус, вам понадобится конкретная формула: 93\)
Как рассчитать объем — математика GCSE
Здесь мы научимся рассчитывать объем трехмерных фигур , включая кубы, прямоугольные параллелепипеды, призмы, цилиндры, пирамиды, конусы и сферы.
Существуют также рабочие листы тома , основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое объем?
Объем трехмерной формы — это объем пространства внутри формы.
Чтобы вычислить объем фигуры в трех измерениях, мы можем использовать соответствующую формулу объема.
The table below shows the formulae that we can use for some of the most common 3D shapes:
Cuboid
Prism
Cylinder
Pyramid
Cone
Sphere
93 (кубических миллиметра). Объем также может быть измерен в имперских единицах, включая кубические футы или кубические дюймы. Его также можно описать, используя единицы измерения емкости, такие как миллилитры, литры, пинты или галлоны.
Объем также может быть измерен в имперских единицах, включая кубические футы или кубические дюймы. Его также можно описать, используя единицы измерения емкости, такие как миллилитры, литры, пинты или галлоны.
Что такое объем?
Объем составного твердого тела
Вас могут попросить рассчитать объем трехмерной фигуры, состоящей из 2 или более отдельных фигур. Этот тип формы известен как составная форма . Объем каждой из фигур можно найти, а затем сложить. 93
Как рассчитать объем
Чтобы рассчитать объем:
- Запишите формулу.
- Подставьте значения в формулу.
- Завершите расчет.
- Напишите ответ, включая единицы измерения.
Объясните, как рассчитать объем
Рабочий лист тома
Получите бесплатный рабочий лист с более чем 20 вопросами и ответами. Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксРабочий лист тома
Получите бесплатный рабочий лист с более чем 20 вопросами и ответами. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Примеры объемов
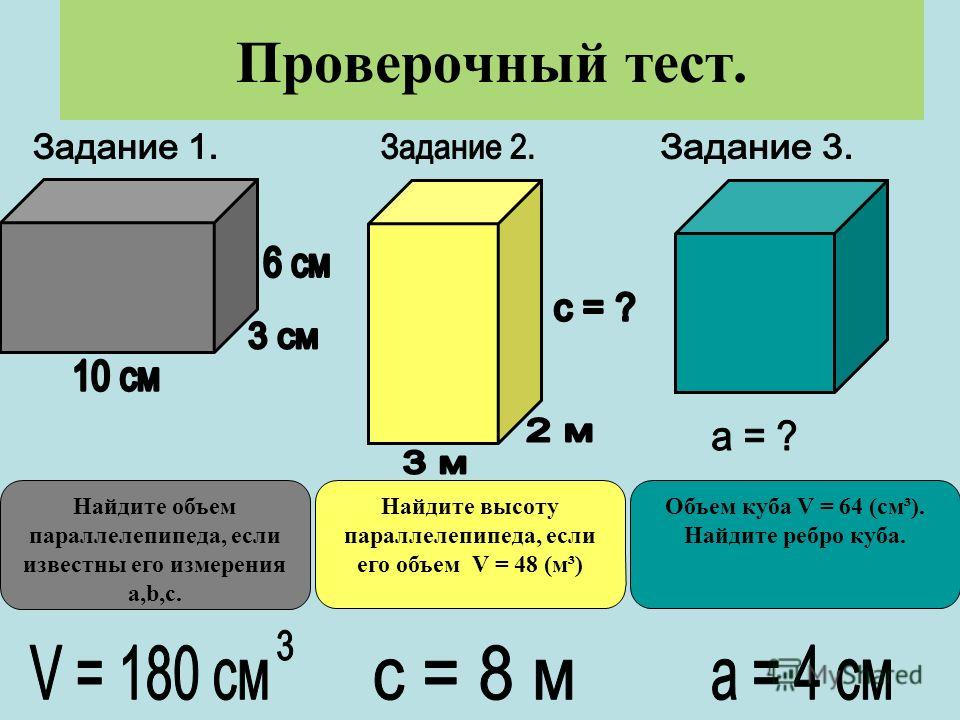
Пример 1: объем прямоугольного параллелепипеда
Вычислите объем параллелепипеда ниже:
- Запишите формулу.
Объем (V) прямоугольного параллелепипеда равен объему прямоугольной призмы или объему коробки. 93
Пример 2: объем призмы
Вычислите объем этой треугольной призмы:
Запишите формулу.
\text{Объем призмы } = \text{Площадь сечения} \times \text{Глубина}
Подставляем значения в формулу.
Во-первых, нам нужно найти площадь поперечного сечения треугольника:
\begin{aligned} \text{Площадь треугольника}&=\frac{1}{2}\times b \times h\\\\ &=\frac{1}{2}\times 2 \times 7\\\\ &=7\text{ m}^2 \end{aligned} 93 и т.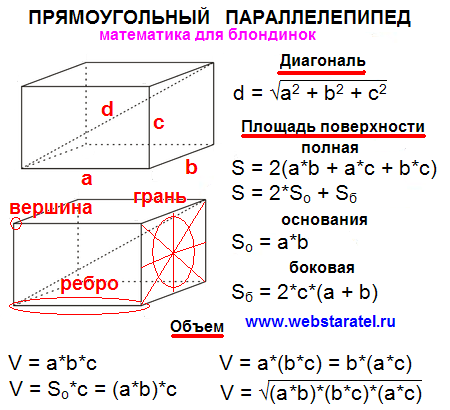 д.)
д.)
- Расчет в других единицах измерения
Перед вычислением объема необходимо убедиться, что все измерения приведены в одних и тех же единицах измерения. (Например, у вас не может быть некоторых измерений в см, а некоторых в м).
- Убедитесь, что вы ввели правильную формулу
Убедитесь, что вы используете правильную формулу для объема трехмерной фигуры.
- Не округляйте слишком рано 93
\end{align}
(1)
2. (a) Вычислите объем этого контейнера
, внутри каждой из которых находится три сферы радиусом
, (b) контейнер. Какой процент пространства в контейнере занимают сферы?
(5 баллов)
Показать ответ
(a)
\text{Площадь поперечного сечения: } \frac{1}{2}(1,4+2)\times 1,2=2,04 9{3}(1)
\text{Объем B: } 15 \times 7 \times h(1)
9025 { 9025} 15 \times 7 \times{h}&=420\\\\ 105ч&=420 \ end {выровнен}
(1)
H = 4 см(1)
Учебный контроль
У вас уже научились:
- 555555555555.

- 555555555555.

 Некоторые различные типы пирамид включают в себя:
Некоторые различные типы пирамид включают в себя: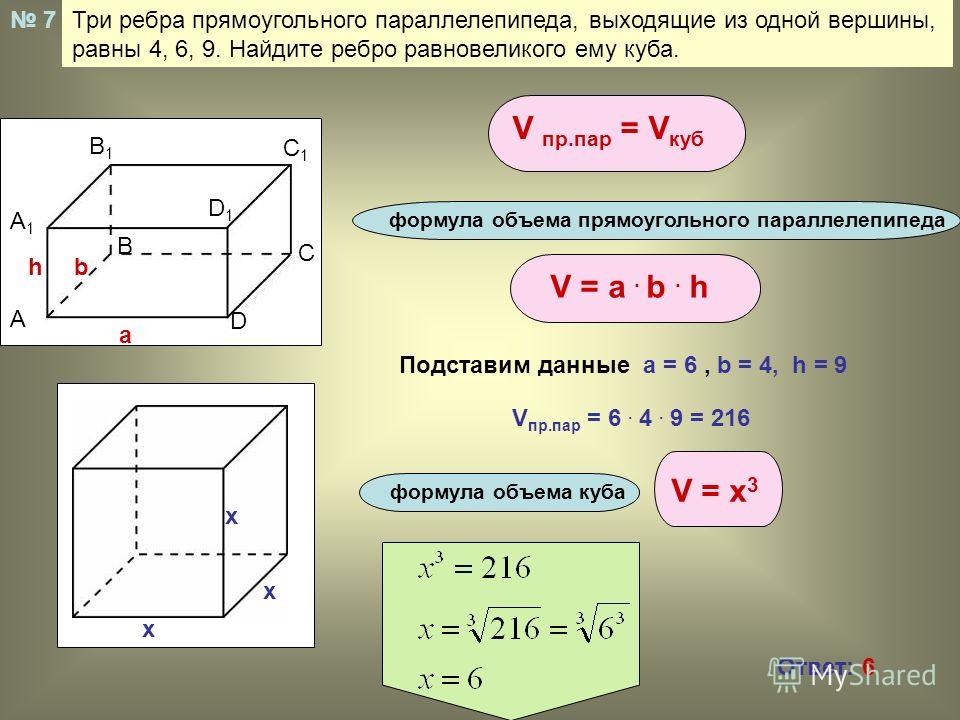 У конуса только одна грань и вершина. Они выглядят так; 92ч.\]
У конуса только одна грань и вершина. Они выглядят так; 92ч.\] Это можно записать в следующую формулу:
Это можно записать в следующую формулу: