Объёма шара: формула, найти через онлайн-калькулятор
Умелая работа с шаром в Древней Греции наравне с другими геометрическими фигурами позволяла использовать его при строительстве. В те времена уже умели рассчитывать объем геометрического тела и площадь его поверхности. Знания в области геометрии
Знания в области геометрии в настоящее время являются неотъемлемой частью в жизни общества. Например, в строительстве нельзя обойтись без проведения точных расчетов необходимого объема строительных материалов для возведения объекта. Чаще всего специалисты в области строительства сталкиваются с вычислениями объема данного геометрической фигуры. Например, в автомобилестроении при создании передней подвески используют шаровые опоры, соединяющие ступицы колес и рычаги. Именно от правильности и точности вычисления объема шаровых зависит надежность, долговечность и правильность работы.
Широко применяются шариковые подшипники, обеспечивающие вращение и надежное крепление осей неподвижных частей узлов и агрегатов. Важным условием при их расчете специалистами является высокая точность результата. Очень часто шары используют:
Важным условием при их расчете специалистами является высокая точность результата. Очень часто шары используют:
- В архитектурном строительстве. Например, в качестве различных декоративных элементов при украшении зданий.
- В игре под названием “бильярд”.
- Елочные украшения также часто представляют собой шарообразные игрушки.
- В шариковые ручки в стержень вставляются маленькие металлические шарики.
При этом любое изделие в форме шара требует проведения точных расчетов. А формула расчета объема геометрического тела позволит произвести необходимые расчеты. Онлайн калькулятор позволит получить точные данные. Пользователю достаточно лишь ввести в поле базовые показатели и нажать на кнопку “рассчитать”.
Шаром (сферу) называют геометрическую фигуру, которая состоит из многочисленных точек пространства, расположенных от цента на расстоянии не больше заданного. Такое расстояние и называется радиусом шара. При этом построить фигуру можно путем вращения круга вокруг своей оси, которая называется диаметром.
Существует несколько методов вычисления объема шара:
- через его радиус;
- через его диаметр;
- через длину его окружности.
Расчет объема шара через радиус
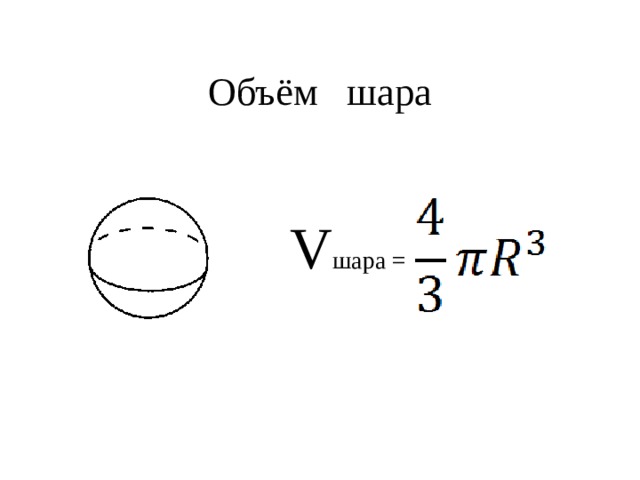
При расчете объема шара через его радиус используется следующая формула:
V = 4/3 × π × R3
В данной формуле:
- V – искомый объем шара;
- π – константа, равная 3,14;
- R – радиус.
Пример расчета 1
Необходимо найти объем шара, радиус которого равен 3 м. Для получения результата имеющийся показатель следует подставить в формулу и произвести вычисления:
V = 4/3 * π * R3 = 4/3 * π * 33 = 4/3 * 3.14 * 27 = 113.0973
Пример расчета 2
Чему будет равен объем шара (сферы) в кубических сантиметрах, радиус которого равняется 4 см.? Используя формулу V = 4/3 * π * R3, получается следующее:
V = 4/3 * π * R3 = 4/3 * 3. 14 * 43 = 4/3 * 3.14 * 64 = 267.9466
14 * 43 = 4/3 * 3.14 * 64 = 267.9466
Расчет объема шара через диаметр
Диаметр шара (сферы) – отрезок, который проходит через центр шара и соединяет две точки, расположенные напротив друг друга на шаровой поверхности. Диаметр шара всегда будет равняться двум его радиусам. И наоборот – радиус равен 1/2 диаметра шара (R = d/2)., где R – радиус, а d – диаметр.
При расчете объема шара через диаметр используется следующая формула:
V = 1/6 × π × d 3
В формуле применяются следующие значения:
- V – объем шара;
- π – математическая постоянная, равная 3,14;
- d – диаметр.
Пример расчета
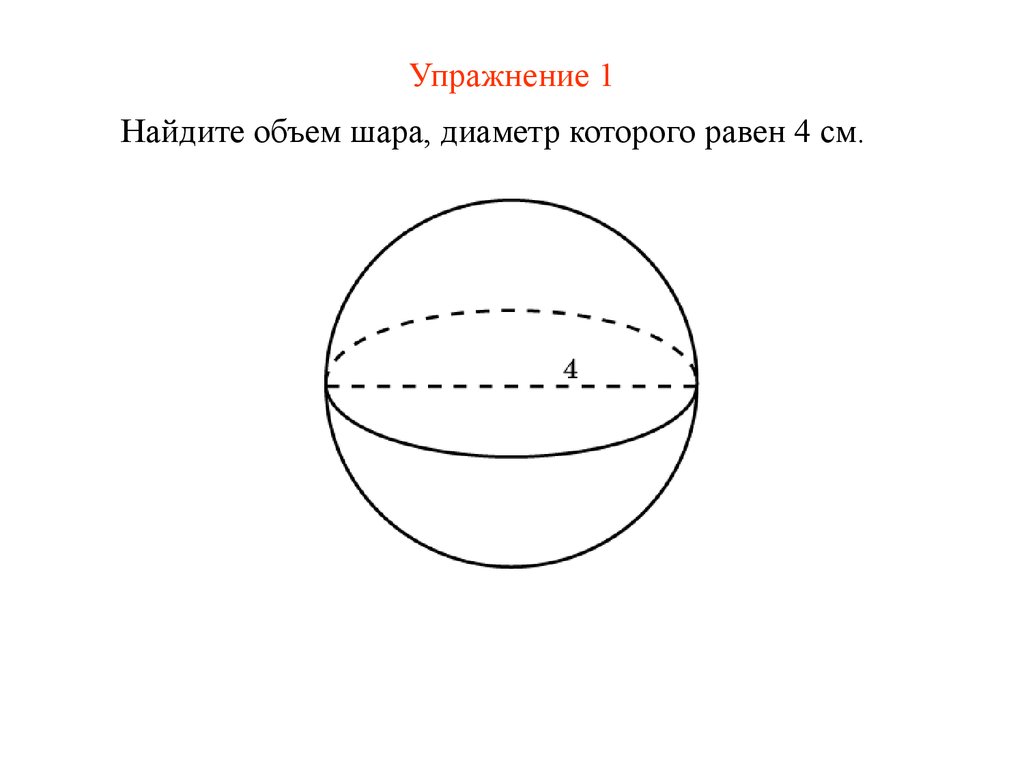
Как найти объем шара, диаметр которого равен 16 см.? При помощи калькулятора, вычислить значение объема шара не составит труда. В данном случае известен показатель – диаметр (d), значение которого следует подставить в формулу, и произвести нужные вычисления:
V = 1/6 * π * d 3 = 1/6 * π * 163 = 1/6 * 3. 14 * 4096 = 2143.57
14 * 4096 = 2143.57
Расчет объема шара через длину окружности
Определить объем шара можно, если имеется показатель длины окружности. Для решения задачи потребуется внести в калькулятор имеющийся показатель значения L.
Расчет объема шара через длину окружности производится по следующей формуле:
V = L3/6 × π2
Для определения длины окружности используется формула: L = 2 *π * R = π * d
Где:
- L – длина окружности;
- π – константа, равная 3.14;
- R – радиус; d – диаметр.
Пример расчета
Требуется рассчитать объем шара через длину его окружности, если радиус шара равен 2 см.
Первым делом следует рассчитать диаметр шара: d = 2 * R = 2 * 2 = 4 см.
Далее определяется длина окружности шара: L = 2 * π * R = π * d = 3.14 * 4 = 12.56 см.
Определив длину окружности, можно высчитывать объем шара: V = L3/6 * π2 = 12. 563/6 * 3.142 = 33.459 см3.
563/6 * 3.142 = 33.459 см3.
Расчет объема шара через площадь поверхности
Узнать, чему равен объем шара через площадь поверхности можно при помощи следующей формулы:
V = √S3/3×6π
- V – объем шара;
- S – площадь поверхности шара;
- π – математическая постоянная (3.14).
Пример расчета 1:
Определить объем шара в см3, если площадь его поверхности равна 113 см2.
Подставляем в формулу известные значения и получаем результат: V = √S3/36π = √1133/36*3.14 = 112.951 см3.
Пример расчета 2:
Рассчитать объем шара (сферы) через площадь поверхности, если радиус шара равен 7 мм.
Первым делом следует рассчитать площадь поверхности геометрического тела. Для вычислений используется формула: S = 4 * π * R2
Подставляем известные данные и получаем: S = 4 * 3. 14 * 49 = 615,75
14 * 49 = 615,75
Далее определяем объем шара: V = √ S3/36π = √615.753/36*3.14 = √233460419.48/36*3.14 = 4512.53
Пользователю доступны некоторые преимущества при использовании онлайн калькулятора:
- экономится время благодаря автоматизации подсчета;
- возможность определить объем шара, имея показатель диаметра тела;
- простой и удобный интерфейс калькулятора.
Таким образом, при использовании онлайн калькулятора не требуется самостоятельно производить все расчеты формул и значений, что существенно экономит время. К тому же, онлайн калькулятор выдает максимально точные расчеты. Главным критерием его использования является лишь наличие интернета.
Объем фигур | Онлайн калькулятор
Многие сложные детали (конструкции) можно представить совокупностью различных элементов, объем которых можно вычислить, воспользовавшись набором online-калькуляторов с данной страницы.
Представлены программы для расчета объемов фигур, базисом которых является квадрат или прямоугольник, а также имеющих в основании окружность: цилиндра, конуса и шаровых элементов.
В конструкторской работе при различных расчетах возникает потребность использования значений объема элементарных фигур: параллелепипеда, куба, призмы и пр. В частности это может иметь место при расчете заполнения вагонов и платформ упакованной в транспортную тару готовой продукцией. Такой расчет требует учета многих факторов, в том числе боковой ветровой нагрузки, смещения центра тяжести и пр.
Если неправильно рассчитать объем тары подлежащего отгрузке упакованного товара, можно не вместить в вагон заявленное количество изделий. В результате предприятие потерпит убытки. Онлайн калькуляторы нашего сайта позволят избежать проблемных ситуаций. Расчеты объемов различных фигур выполняются с большой точностью.
Вычислить, найти объем геометрических тел, фигур
| Объем пирамиды найти объем треугольной, четырехугольной, правильной пирамиды | Объем куба онлайн формула объема куба |
| Объем цилиндра найти чему равен объем цилиндра | Объем конуса вычислить объем конуса |
| Объем шара онлайн формула объема сферы | Объем параллелепипеда чему равен объем параллелепипеда |
| Объем призмы как найти чему равняется объем призмы | Объем октаэдра онлайн калькулятор объема октаэдра |
| Объем тетраэдра как найти объем тетраэдра | Объем усеченной пирамиды онлайн калькулятор для нахождения объема усеченной пирамиды |
| Объем усеченного конуса формула объема усеченного конуса | Объем шарового слоя формула объема шарового слоя онлайн |
| Объем шарового сектора как вычислить объем шарового сектора формула | Объем шарового сегмента формула объема шарового сегмента |
Select rating12345
Рейтинг: 4 (Голосов 2)
Сообщить об ошибке
Вам помог этот калькулятор?
Предложения и пожелания пишите на [email protected]
Поделитесь этим калькулятором на форуме или в сети!
Это помогает делать новые калькуляторы.
НЕТ
Смотрите также
| Площадь фигур | Математика | Периметр фигур | Радиус фигур | Единицы измерения объема |
| Конвертеры | Размеры одежды | Теоремы | Угол | Cколько лет кошке |
Sphere Calculator — онлайн-калькулятор сфер
Сфера определяется как трехмерная фигура, совершенно симметричная и круглая по форме, такая как шар или глобус. В геометрии сфера — это трехмерная твердая фигура круглой формы. С математической точки зрения это комбинация набора точек, соединенных одной общей точкой на равных расстояниях в трех измерениях.
Что такое калькулятор сфер?
‘ Калькулятор сфер ‘ представляет собой онлайн-инструмент, который помогает рассчитать площадь поверхности и объем сферы. Калькулятор сфер поможет вам рассчитать площадь поверхности и объем сферы за несколько секунд.
Калькулятор сфер
Как пользоваться калькулятором сфер?
Чтобы использовать калькулятор, выполните следующие действия:
- Шаг 1: Выберите раскрывающийся список, чтобы найти значение площади поверхности и объема сферы.

- Шаг 2: Введите радиус в соответствующие поля ввода.
- Шаг 3: Нажмите кнопку » Вычислить «, чтобы найти значение площади поверхности и объема сферы.
- Шаг 4: Нажмите кнопку » Сбросить «, чтобы очистить поле и ввести новые значения.
Как найти площадь поверхности и объем сферы?
Площадь поверхности сферы — это количество единичных квадратов, которые могут вместиться в нее, и измеряется в квадратных единицах. Площадь поверхности сферы рассчитывается по формуле:
Площадь поверхности сферы = 4πr 2
Где r – радиус сферы.
Объем сферы – это емкость сферы или мера занимаемого ею пространства. Объем сферы можно рассчитать по формуле:
Объем сферы = 4/3 × π × r 3
Где «r» – радиус сферы.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
С Cuemath находите решения простыми и легкими шагами.
Записаться на бесплатный пробный урок
Решенные примеры на калькуляторе сферПример 1:
Найдите площадь поверхности и объем сферы, если радиус равен 3 единицам, и проверьте его с помощью онлайн-калькулятора сфер .
Решение:
Дано: радиус = 3 единицы
Площадь поверхности сферы = 4πr 2
= 4 × 3,14 × 3 2
= 4 × 3,14 ×
0002 = 113,04 квадратных единицОбъем сферы = 4/3 × π × r 3
= 4/3 × 3,14 × 3 3
= 4 × 3,14 ×
= 113,04 Кубик Unit
Пример 2:
Найдите площадь поверхности и объем сферы, если радиус равен 6 единицам, и проверьте это с помощью онлайн-калькулятора сфер.
Дано: Радиус = 6 единиц
Площадь поверхности сферы = 4πr 2
= 4 × 3,14 × 6 2
= 4 × 3,14 × 36
= 452,16 квадратных единиц
Объем сферы = 4/3 × π × R 3
= 4/3 × 3,14 × 6 3
= 4/3 × 3,14 × 6 3
= 4/3 /3 × 3,14 × 216
= 904,32 кубических единиц
Точно так же вы можете попробовать онлайн-калькулятор сфер, чтобы найти площадь поверхности и объем сферы для
- Радиус = 7 единиц
- Радиус = 11 единиц
- Периметр
- Зона
Плотность в зависимости от удельного веса и удельного веса
Плотность определяется как масса на единицу объема .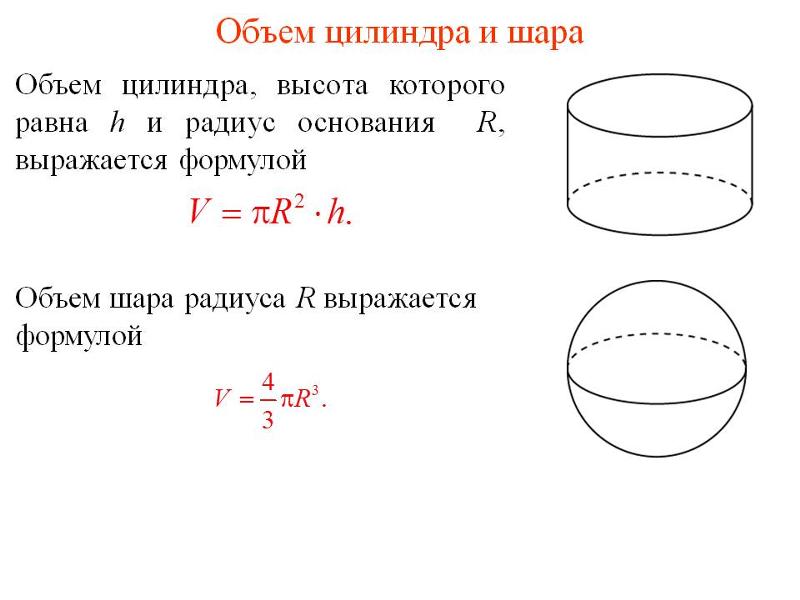 Масса — это свойство, а единицей плотности в системе СИ является [ кг/м 3 ].
Масса — это свойство, а единицей плотности в системе СИ является [ кг/м 3 ].
Плотность может быть выражена как0002 где
ρ = плотность [кг/м 3 ], [слаг/фут 3 ]
m = масса [кг], [слаг]
V = объем [м 3 ], [фут 3 ]
ν = удельный объем [м 3 /кг], [фут 3 /слаг]
- Что такое вес и что такое масса? — разница между весом и массой
Имперские (США) единицы измерения плотности составляют слизней/фут 3 , но фунтов массы на кубический фут — фунтов м /ft 3 — часто используется. Обратите внимание, что существует разница между фунт-силой (фунт f ) и фунт-масса (фунт м ) . Слизней можно умножить на 32,2 , чтобы получить примерное значение в фунтах массы (фунт м ) .
- 1 slug = 32.
 174 lb m = 14.594 kg
174 lb m = 14.594 kg - 1 kg = 2.2046 lb m = 6.8521×10 -2 slugs
- density of water: 1000 kg/m 3 , 1,938 слаг/фут 3
См. также Конвертер единиц – масса и Конвертер единиц – плотность
На атомарном уровне – частицы плотнее упакованы внутри вещества с более высокой плотностью. Плотность — это физическое свойство, постоянное при данной температуре и давлении, которое может быть полезно для идентификации веществ.
Ниже на этой странице: Удельный вес (относительная плотность), Удельный вес для газов, Удельный вес, Примеры расчета
См. также: Плотность некоторых распространенных материалов
Вода – плотность, удельный вес и коэффициент теплового расширения – изменение в зависимости от температуры при 1, 68 и 680 атм, единицы СИ и британские единицы
Воздух – плотность, удельный вес и коэффициент теплового расширения – изменение с температурой и давлением, единицами СИ и имперскими единицами
Как измерить плотность жидких нефтепродуктов
Пример 1. Плотность мяча для гольфа
Плотность мяча для гольфа
Пример 2: Использование плотности для идентификации материала
Пример 3: Плотность для расчета объемной массы
Удельный вес (относительная плотность) — SG — безразмерное отношение единиц плотности, определяемое как единица плотности вещества к плотности воды — при заданной температуре и может быть выражена как
SG = ρ вещества / ρ h3O [2]
, где
SG = удельный вес вещества
ρ вещество = плотность жидкости или вещества [кг/м 3 ]
ρ h3O = плотность воды – обычно при температуре 4 o C [ кг/м 3 ]
Плотность воды при 4 o C (39 o F) обычно используется в качестве эталона, так как вода в этой точке имеет самую высокую плотность 1000 кг/м 3 или 1,940 порций/фут 3 .
Поскольку удельный вес — SG — безразмерный, он имеет одинаковое значение в системе СИ и в имперской английской системе (BG). SG жидкости имеет то же числовое значение, что и ее плотность, выраженная в г/мл или Мг/м 3 . Вода обычно также используется в качестве эталона при расчете удельного веса твердых веществ.
См. также Теплофизические свойства воды — Плотность, Температура замерзания, Температура кипения, Скрытая теплота плавления, Скрытая теплота испарения, Критическая температура …
Example 4: Specific Gravity of Iron
Specific Gravity for some common Materials
| Substance | Specific Gravity — SG — |
|---|---|
| Acetylene | 0.0017 |
| Air, dry | 0.0013 |
| Alcohol | 0.82 |
| Aluminum | 2.72 |
| Brass | 8.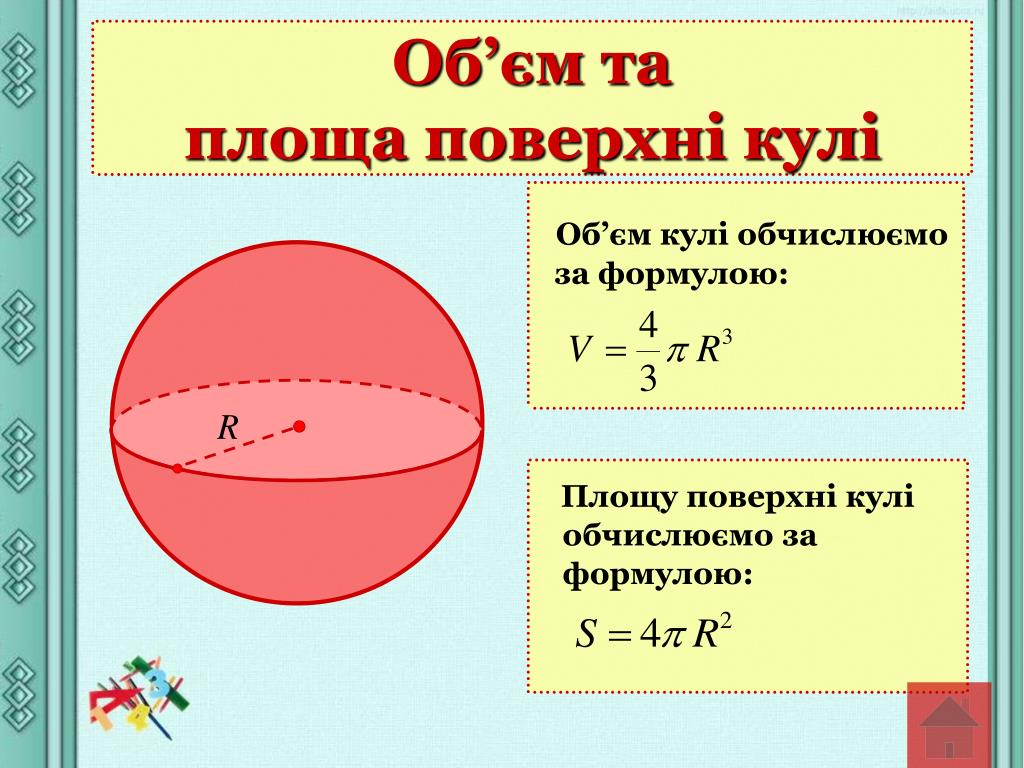 48 48 |
| Cadmium | 8.57 |
| Chromium | 7.03 |
| Copper | 8.79 |
| Carbon dioxide | 0.00198 |
| Carbon monoxide | 0.00126 |
| Cast iron | 7.20 |
| Водород | 0,00009 |
| Свинец | 11,35 |
| Ртуть | 13.59 |
| Nickel | 8.73 |
| Nitrogen | 0.00125 |
| Nylon | 1.12 |
| Oxygen | 0.00143 |
| Paraffin | 0.80 |
| Petrol | 0.72 |
| ПВХ | 1,36 |
| Резина | 0,96 |
| Сталь | 9 7,820356 |
| Tin | 7.28 |
| Zinc | 7. 12 12 |
| Water (4 o C) | 1.00 |
| Water, sea | 1.027 |
| Wood , Дуб | 0,77 |
Вернуться к началу
Удельный вес газов обычно рассчитывается по отношению к воздуху и определяется как отношение плотности газа к плотности воздуха — при заданной температуре и давлении.
Специфический вес можно рассчитать как
]SG = ρ GAS / ρ Воздух [3]
, где
SG = специфический вес газа
ρ GAS = DENCES GAS / M
40180 GAS = DENCES of GAS / M
ρ . 3
ρ воздух = плотность воздуха (обычно при NTP — 1,204 [кг/м 3 ])
- NTP — нормальная температура и давление — определяется как 20 o C (293,15 K, 68 o F) и 1 атм (101,325 кН/м2, 101,325 кПа, 14,7 фунтов на квадратный дюйм, 0 фунтов на кв.
 дюйм, 30 дюймов ртутного столба, 760 торр) плотности газа и воздуха оцениваются при одинаковых давлении и температуре.
дюйм, 30 дюймов ртутного столба, 760 торр) плотности газа и воздуха оцениваются при одинаковых давлении и температуре.См. также Теплофизические свойства воздуха — плотность, вязкость, критическая температура и давление, тройная точка, энтальпы и энтропии, теплопроводность и диффузность, ……
Вернуться к началу
Удельный вес определяется как вес на единицу объема . Вес составляет сила . Единицей СИ для удельного веса является [Н/м 3 ]. Имперская единица измерения [lb/ft 3 ].
Удельный вес (или сила на единицу объема) может быть выражен как
γ = ρ a g [4]
, где
γ = удельный вес (N/M 3 ], [LB. /ft 3 ]
ρ = плотность [кг/м 3 ], [слаг/фут 3 ]
a г = ускорение свободного падения (9,807 [м/с 2 ], 32,174 [фут/с 2 ] при нормальных условиях) 3 7- Что такое вес и что такое масса? — разница между весом и массой
Пример 5: Удельный вес воды
Удельный вес некоторых распространенных материалов
Продукт Удельный вес
— γ —
Imperial Units
(lb/ft 3 )SI Units
(kN/m 3 )Aluminum 172 27 Brass 540 84.  5
5Carbon tetrachloride 99.4 15.6 Copper 570 89 Ethyl Alcohol 49.3 7.74 Gasoline 42.5 6.67 Glycerin 78.6 12.4 Kerosene 50 7.9 Mercury 847 133,7 Моторное масло SAE 20 57 8,95 Морская вода 6,0359 10.03 Stainless Steel 499 — 512 78 — 80 Water 62.4 9.81 Wrought Iron 474 — 499 74 — 78 - Свойства материала
Вернуться к началу
Примеры
Пример 1.
 Плотность мяча для гольфа
Плотность мяча для гольфа Мяч для гольфа имеет диаметр 42 мм и массу 45 г. Объем мяча для гольфа можно рассчитать как
V = (4/3) π (42 [мм] * 0,001 [м/мм]/2) 3 = 3,8 10 -5 [м 3 ]
Плотность мяча для гольфа затем рассчитывается как
ρ = 45 [г] * 0,001 [кг/г] / 3,8 10 -5 [м 3 ] = 1184 [кг/м 3 ]
Вернуться к началу
3
3 Пример 2: Использование плотности для идентификации материала
Неизвестное жидкое вещество имеет массу 18,5 г и занимает объем 23,4 мл (миллилитр).
Плотность вещества можно рассчитать как
ρ = (18,5 [г] /1000 [г/кг]) / (23,4 [мл] /(1000 [мл/л] * 1000[л/м 3 ]))
= 18,5 10 -3 [кг] /23,4 10 -6 [м 3 ] = 790 [кг/м 3 ]
3 Для некоторых обычных жидкостей мы находим, что этиловый спирт — или этанол — имеет плотность 789 кг/м 3 . Жидкость может быть этиловым спиртом!
Жидкость может быть этиловым спиртом!Пример 3: Плотность для расчета объемной массы
Плотность титана составляет 4507 кг/м 3 . Массу 0,17 м 3 объема титана можно рассчитать как
м = 0,17 [м 3 ] * 4507 [кг/м 3 ] = 766,2 [кг]
2 Примечание!
— имейте в виду, что существует разница между «объемной плотностью» и фактической «плотностью твердого вещества или материала». Это может быть неясно в описании товаров. Всегда дважды проверяйте значения с другими источниками перед важными расчетами.Вернуться к началу
Пример 4: Удельный вес железа
Плотность железа 7850 кг/м 3 . Удельный вес железа по отношению к воде с плотностью 1000 кг/м 3 равен
SG(железо) = 7850 [кг/м 3 ] / 1000 [кг/м 3 ] = 7,85
0302 Пример 5: Удельный вес воды
Плотность воды составляет 1000 кг/м3 при 4 °C (39 °F).

 174 lb m = 14.594 kg
174 lb m = 14.594 kg  дюйм, 30 дюймов ртутного столба, 760 торр) плотности газа и воздуха оцениваются при одинаковых давлении и температуре.
дюйм, 30 дюймов ртутного столба, 760 торр) плотности газа и воздуха оцениваются при одинаковых давлении и температуре.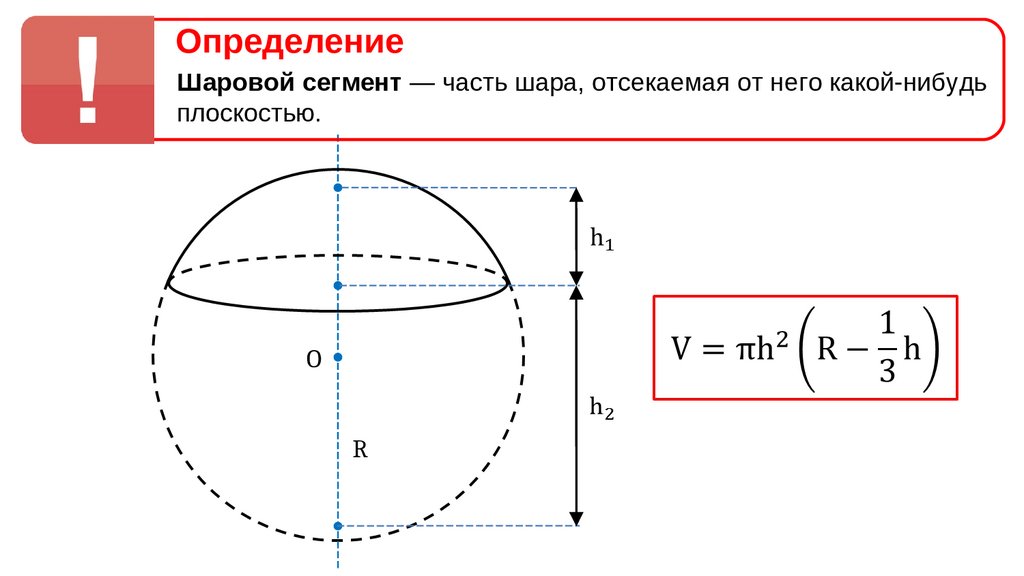 5
5 Плотность мяча для гольфа
Плотность мяча для гольфа  Жидкость может быть этиловым спиртом!
Жидкость может быть этиловым спиртом!