Объем тела вращения онлайн: Объем тела вращения | Онлайн калькулятор

Mathway | Популярные задачи

1	Trovare la Derivata — d/dx	квадратный корень x
2	Trovare la Derivata — d/dx	натуральный логарифм x
3	Вычислим интеграл	интеграл натурального логарифма x по x
4	Trovare la Derivata — d/dx	e^x
5	Вычислим интеграл	интеграл e^(2x) относительно x
6	Trovare la Derivata — d/dx	1/x
7	Trovare la Derivata — d/dx	x^2
8	Вычислим интеграл	интеграл e^(-x) относительно x
9	Trovare la Derivata — d/dx	1/(x^2)
10	Trovare la Derivata — d/dx	sin(x)^2
11	Trovare la Derivata — d/dx	sec(x)
12	Вычислим интеграл	интеграл e^x относительно x
13	Вычислим интеграл	интеграл x^2 относительно x
14	Вычислим интеграл	интеграл квадратного корня x по x
15	Вычислить	натуральный логарифм 1
16	Вычислить	e^0
17	Вычислить	sin(0)
18	Trovare la Derivata — d/dx	cos(x)^2
19	Вычислим интеграл	интеграл 1/x относительно x
20	Вычислить	cos(0)
21	Вычислим интеграл	интеграл sin(x)^2 относительно x
22	Trovare la Derivata — d/dx	x^3
23	Trovare la Derivata — d/dx	sec(x)^2
24	Trovare la Derivata — d/dx	1/(x^2)
25	Вычислим интеграл	интеграл arcsin(x) относительно x
26	Вычислим интеграл	интеграл cos(x)^2 относительно x
27	Вычислим интеграл	интеграл sec(x)^2 относительно x
28	Trovare la Derivata — d/dx	e^(x^2)
29	Вычислим интеграл	интеграл в пределах от 0 до 1 кубического корня 1+7x по x
30	Trovare la Derivata — d/dx	sin(2x)
31	Вычислим интеграл	интеграл натурального логарифма x по x
32	Trovare la Derivata — d/dx	tan(x)^2
33	Вычислим интеграл	интеграл e^(2x) относительно x
34	Вычислим интеграл	интеграл 1/(x^2) относительно x
35	Trovare la Derivata — d/dx	2^x
36	График	натуральный логарифм a
37	Вычислить	e^1
38	Вычислим интеграл	интеграл 1/(x^2) относительно x
39	Вычислить	натуральный логарифм 0
40	Trovare la Derivata — d/dx	cos(2x)
41	Trovare la Derivata — d/dx	xe^x
42	Вычислим интеграл	интеграл 1/x относительно x
43	Вычислим интеграл	интеграл 2x относительно x
44	Trovare la Derivata — d/dx	( натуральный логарифм x)^2
45	Trovare la Derivata — d/dx	натуральный логарифм (x)^2
46	Trovare la Derivata — d/dx	3x^2
47	Вычислить	натуральный логарифм 2
48	Вычислим интеграл	интеграл xe^(2x) относительно x
49	Trovare la Derivata — d/dx	2e^x
50	Trovare la Derivata — d/dx	натуральный логарифм 2x
51	Trovare la Derivata — d/dx	-sin(x)
52	Вычислить	tan(0)
53	Trovare la Derivata — d/dx	4x^2-x+5
54	Trovare la Derivata — d/dx	y=16 корень четвертой степени 4x^4+4
55	Trovare la Derivata — d/dx	2x^2
56	Вычислим интеграл	интеграл e^(3x) относительно x
57	Вычислим интеграл	интеграл cos(2x) относительно x
58	Вычислим интеграл	интеграл cos(x)^2 относительно x
59	Trovare la Derivata — d/dx	1/( квадратный корень x)
60	Вычислим интеграл	интеграл e^(x^2) относительно x
61	Вычислить	sec(0)
62	Вычислить	e^infinity
63	Вычислить	2^4
64	Trovare la Derivata — d/dx	x/2
65	Вычислить	4^3
66	Trovare la Derivata — d/dx	-cos(x)
67	Trovare la Derivata — d/dx	sin(3x)
68	Вычислить	натуральный логарифм 1/e
69	Вычислим интеграл	интеграл x^2 относительно x
70	Упростить	1/( кубический корень от x^4)
71	Trovare la Derivata — d/dx	1/(x^3)
72	Вычислим интеграл	интеграл e^x относительно x
73	Вычислим интеграл	интеграл tan(x)^2 относительно x
74	Вычислим интеграл	интеграл 1 относительно x
75	Trovare la Derivata — d/dx	x^x
76	Trovare la Derivata — d/dx	x натуральный логарифм x
77	Вычислим интеграл	интеграл sin(x)^2 относительно x
78	Trovare la Derivata — d/dx	x^4
79	Оценить предел	предел (3x-5)/(x-3), если x стремится к 3
80	Вычислим интеграл	интеграл от x^2 натуральный логарифм x по x
81	Trovare la Derivata — d/dx	f(x) = square root of x
82	Trovare la Derivata — d/dx	x^2sin(x)
83	Вычислим интеграл	интеграл sin(2x) относительно x
84	Trovare la Derivata — d/dx	3e^x
85	Вычислим интеграл	интеграл xe^x относительно x
86	Trovare la Derivata — d/dx	y=x^2
87	Trovare la Derivata — d/dx	квадратный корень x^2+1
88	Trovare la Derivata — d/dx	sin(x^2)
89	Вычислим интеграл	интеграл e^(-2x) относительно x
90	Вычислим интеграл	интеграл натурального логарифма квадратного корня x по x
91	Вычислить	2^5
92	Trovare la Derivata — d/dx	e^2
93	Trovare la Derivata — d/dx	x^2+1
94	Вычислим интеграл	интеграл sin(x) относительно x
95	Вычислить	2^3
96	Trovare la Derivata — d/dx	arcsin(x)
97	Оценить предел	предел (sin(x))/x, если x стремится к 0
98	Вычислить	e^2
99	Вычислим интеграл	интеграл e^(-x) относительно x
100	Вычислим интеграл	интеграл 1/x относительно x

Mathway | Популярные задачи

1	Trovare la Derivata — d/dx	квадратный корень x
2	Trovare la Derivata — d/dx	натуральный логарифм x
3	Вычислим интеграл	интеграл натурального логарифма x по x
4	Trovare la Derivata — d/dx	e^x
5	Вычислим интеграл	интеграл e^(2x) относительно x
6	Trovare la Derivata — d/dx	1/x
7	Trovare la Derivata — d/dx	x^2
8	Вычислим интеграл	интеграл e^(-x) относительно x
9	Trovare la Derivata — d/dx	1/(x^2)
10	Trovare la Derivata — d/dx	sin(x)^2
11	Trovare la Derivata — d/dx	sec(x)
12	Вычислим интеграл	интеграл e^x относительно x
13	Вычислим интеграл	интеграл x^2 относительно x
14	Вычислим интеграл	интеграл квадратного корня x по x
15	Вычислить	натуральный логарифм 1
16	Вычислить	e^0
17	Вычислить	sin(0)
18	Trovare la Derivata — d/dx	cos(x)^2
19	Вычислим интеграл	интеграл 1/x относительно x
20	Вычислить	cos(0)
21	Вычислим интеграл	интеграл sin(x)^2 относительно x
22	Trovare la Derivata — d/dx	x^3
23	Trovare la Derivata — d/dx	sec(x)^2
24	Trovare la Derivata — d/dx	1/(x^2)
25	Вычислим интеграл	интеграл arcsin(x) относительно x
26	Вычислим интеграл	интеграл cos(x)^2 относительно x
27	Вычислим интеграл	интеграл sec(x)^2 относительно x
28	Trovare la Derivata — d/dx	e^(x^2)
29	Вычислим интеграл	интеграл в пределах от 0 до 1 кубического корня 1+7x по x
30	Trovare la Derivata — d/dx	sin(2x)
31	Вычислим интеграл	интеграл натурального логарифма x по x
32	Trovare la Derivata — d/dx	tan(x)^2
33	Вычислим интеграл	интеграл e^(2x) относительно x
34	Вычислим интеграл	интеграл 1/(x^2) относительно x
35	Trovare la Derivata — d/dx	2^x
36	График	натуральный логарифм a
37	Вычислить	e^1
38	Вычислим интеграл	интеграл 1/(x^2) относительно x
39	Вычислить	натуральный логарифм 0
40	Trovare la Derivata — d/dx	cos(2x)
41	Trovare la Derivata — d/dx	xe^x
42	Вычислим интеграл	интеграл 1/x относительно x
43	Вычислим интеграл	интеграл 2x относительно x
44	Trovare la Derivata — d/dx	( натуральный логарифм x)^2
45	Trovare la Derivata — d/dx	натуральный логарифм (x)^2
46	Trovare la Derivata — d/dx	3x^2
47	Вычислить	натуральный логарифм 2
48	Вычислим интеграл	интеграл xe^(2x) относительно x
49	Trovare la Derivata — d/dx	2e^x
50	Trovare la Derivata — d/dx	натуральный логарифм 2x
51	Trovare la Derivata — d/dx	-sin(x)
52	Вычислить	tan(0)
53	Trovare la Derivata — d/dx	4x^2-x+5
54	Trovare la Derivata — d/dx	y=16 корень четвертой степени 4x^4+4
55	Trovare la Derivata — d/dx	2x^2
56	Вычислим интеграл	интеграл e^(3x) относительно x
57	Вычислим интеграл	интеграл cos(2x) относительно x
58	Вычислим интеграл	интеграл cos(x)^2 относительно x
59	Trovare la Derivata — d/dx	1/( квадратный корень x)
60	Вычислим интеграл	интеграл e^(x^2) относительно x
61	Вычислить	sec(0)
62	Вычислить	e^infinity
63	Вычислить	2^4
64	Trovare la Derivata — d/dx	x/2
65	Вычислить	4^3
66	Trovare la Derivata — d/dx	-cos(x)
67	Trovare la Derivata — d/dx	sin(3x)
68	Вычислить	натуральный логарифм 1/e
69	Вычислим интеграл	интеграл x^2 относительно x
70	Упростить	1/( кубический корень от x^4)
71	Trovare la Derivata — d/dx	1/(x^3)
72	Вычислим интеграл	интеграл e^x относительно x
73	Вычислим интеграл	интеграл tan(x)^2 относительно x
74	Вычислим интеграл	интеграл 1 относительно x
75	Trovare la Derivata — d/dx	x^x
76	Trovare la Derivata — d/dx	x натуральный логарифм x
77	Вычислим интеграл	интеграл sin(x)^2 относительно x
78	Trovare la Derivata — d/dx	x^4
79	Оценить предел	предел (3x-5)/(x-3), если x стремится к 3
80	Вычислим интеграл	интеграл от x^2 натуральный логарифм x по x
81	Trovare la Derivata — d/dx	f(x) = square root of x
82	Trovare la Derivata — d/dx	x^2sin(x)
83	Вычислим интеграл	интеграл sin(2x) относительно x
84	Trovare la Derivata — d/dx	3e^x
85	Вычислим интеграл	интеграл xe^x относительно x
86	Trovare la Derivata — d/dx	y=x^2
87	Trovare la Derivata — d/dx	квадратный корень x^2+1
88	Trovare la Derivata — d/dx	sin(x^2)
89	Вычислим интеграл	интеграл e^(-2x) относительно x
90	Вычислим интеграл	интеграл натурального логарифма квадратного корня x по x
91	Вычислить	2^5
92	Trovare la Derivata — d/dx	e^2
93	Trovare la Derivata — d/dx	x^2+1
94	Вычислим интеграл	интеграл sin(x) относительно x
95	Вычислить	2^3
96	Trovare la Derivata — d/dx	arcsin(x)
97	Оценить предел	предел (sin(x))/x, если x стремится к 0
98	Вычислить	e^2
99	Вычислим интеграл	интеграл e^(-x) относительно x
100	Вычислим интеграл	интеграл 1/x относительно x

Калькулятор нахождения объема тела вращения. Как вычислить объем тела вращения с помощью определенного интеграла

Меню

• Мода и стиль
• Работа
• Лицо
• Семья
• Дети
• Советы

• Мода и стиль
• Работа
• Лицо
• Семья
• Дети
• Советы
• Психология
• Маникюр
• Макияж
• Волосы
• Красота
• Личность
• Обувь
• Аксессуары
• Отношения
• Одежда

вычислить объем тела вращения онлайн калькулятор

Расчет площади и объема геометрических фигур

Цилиндр представляет собой простое геометрическое тело, получаемое при вращении прямоугольника вокруг одной из его сторон. Другое определение: цилиндр — это геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают.

объем цилиндра формула

Если вы хотите знать, как вычислить объем цилиндра,то все, что вам нужно сделать — найти высоту (h) и радиус (r) и и подставить их в формулу:

Если внимательно посмотреть на эту формулу, то можно заметить, что {\pi r^2} — это формула площади круга, а в нашем случае — площадь основания.

Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:

Произвести расчет объема цилиндра вам поможет наш калькулятор онлайн. Просто введите указанные параметры цилиндра и получите его объем.

Ваша оценка

[Оценок: 168 Средняя: 3.4]

Объем цилиндра Автор mnogof средний рейтинг 3.4/5 — 168 рейтинги пользователей

Просмотров страницы: 45 055

Объем цилиндра формула (через радиус основания и высоту)

{V=\pi r^2 h}, где

r — радиус основания цилиндра,

h — высота цилиндра

Объем цилиндра формула (через площадь основания и высоту)

{V=S h}, где

S — площадь основания цилиндра,

h — высота цилиндра

Объем цилиндра калькулятор онлайн

Как найти объём тела вращения с помощью интеграла

С помощью определённого интеграла можно вычислять не только площади плоских фигур, но и объёмы тел, образованных вращением этих фигур вокруг осей координат.

Тело, которое образуется вращением вокруг оси Ox криволинейной трапеции, ограниченной сверху графиком функции y= f(x), имеет объём

.

(1)

Аналогично объём v тела, полученного вращением вокруг оси ординат (Oy) криволинейной трапеции выражается формулой

. (2)

При вычислении площади плоской фигуры мы узнали, что площади некоторых фигур могут быть найдены как разность двух интегралов, в которых подынтегральные функции — те функции, которые ограничивают фигуру сверху и снизу. Похоже обстоит дело и с некоторыми телами вращения, объёмы которых вычисляются как разность объёмов двух тел, такие случаи разобраны в примерах 3, 4 и 5.

Пример 1.

Найти объём тела, образованного вращением вокруг оси абсцисс (Ox) фигуры, ограниченной гиперболой , осью абсцисс и прямыми , .

Решение. Объём тела вращения найдём по формуле (1), в которой , а пределы интегрирования a = 1, b = 4:

Пример 2.

Найти объём шара радиуса R.

Решение. Рассмотрим шар как тело, получащееся при вращении вокруг оси абсцисс полукруга радиуса R с центром в начале координат. Тогда в формуле (1) подынтегральная функция запишется в виде , а пределами интегрирования служат -R и R. Следовательно,

Нет времени вникать в решение?

Можно заказать работу!

Пример 3. Найти объём тела, образованного вращением вокруг оси абсцисс (Ox) фигуры, заключённой между параболами и .

Решение.

Представим искомый объём как разность объёмов тел, полученных вращением вокруг оси абсцисс криволинейных трапеций ABCDE и ABFDE. Объёмы этих тел найдём по формуле (1), в которой пределы интегрирования равны и — абсциссам точек B и D пересечения парабол. Теперь можем найти объём тела:

Пример 4.

Вычислить объём тора (тором называется тело, получающееся при вращении круга радиуса a вокруг оси, лежащей в его плоскости на расстоянии b от центра круга ().

Форму тора имеет, например, баранка).

Решение. Пусть круг вращается вокруг оси Ox (рис.

Формулы площадей и объёмов геометрических фигур

20). Объём тора можно представить как разности объёмов тел, полученных от вращения криволинейных трапеций ABCDE и ABLDE вокруг оси Ox.

Уравнение окружности LBCD имеет вид

причём уравнение кривой BCD

а уравнение кривой BLD

Используя разность объёмов тел, получаем для объёма тора v выражение

Пример 5.

Найти объём тела, образованного вращением вокруг оси ординат (Oy) фигуры, ограниченной линиями и .

Решение.

Представим искомый объём как разность объёмов тел, полученных вращением вокруг оси ординат треугольника OBA и криволинейной трапеции OnBA.

Объёмы этих тел найдём по формуле (2). Пределами интегрирования служат и — ординаты точек O и B пересечения параболы и прямой.

Таким образом, получаем объём тела:

К началу страницы

Пройти тест по теме Интеграл

Начало темы «Интеграл»

Неопределённый интеграл: основные понятия, свойства, таблица неопределённых интегралов

Найти неопределённый интеграл: начала начал, примеры решений

Метод замены переменной в неопределённом интеграле

Интегрирование подведением под знак дифференциала

Метод интегрирования по частям

Интегрирование дробей

Интегрирование рациональных функций и метод неопределённых коэффициентов

Интегрирование некоторых иррациональных функций

Интегрирование тригонометрических функций

Определённый интеграл

Площадь плоской фигуры с помощью интеграла

Несобственные интегралы

Вычисление двойных интегралов

Длина дуги кривой с помощью интеграла

Площадь поверхности вращения с помощью интеграла

Определение работы силы с помощью интеграла

Лучшая кроватка в математике. Качественный. Ничего лишнего.

Объем геометрической фигуры — количественная характеристика пространства, занимаемого телом или веществом. Объем тела или емкости судна определяется его формой и линейными размерами.

Объем куба

Объем куба равна кубу длины ее лица.

Формула Куб

где — объем куба,
— длина куба.

Область призмы

Область призмы равна произведению поверхности дна призмы на высоту.

Формула объема призмы

где — степень призмы,

так

— основание призмы,

час

— высота призмы.

Объем паралелепипедов

Объем паралелепипедов равна произведению поверхности основания относительно высоты.

Объем формулы паралелепипеда

где — объем паралелепипедов,

так

— базовая площадь,

час

— высота высота.

Объем прямоугольного параллелепипеда

Объем прямоугольного параллелепипеда это то же самое, что и произведение его длины, ширины и высоты.

Формула для объема прямоугольного параллелепипеда

где — объем прямоугольного параллелепипеда,
— длина,

б

— ширина

час

— высота.

Объем пирамиды

Объем пирамиды составляет одну треть продукта в базовой области по высоте.

Формула объема пирамиды

где — объем пирамиды,

так

— основание основания пирамиды,

час

— длина пирамиды.

Объем правильного тетраэдра

Формула для объема правильного тетраэдра

1.9. Объём тела вращения для «чайников»



Рассмотрим ещё одно распространённое приложение определённого интеграла.

Представьте некоторую плоскую фигуру на координатной плоскости. Представили? … интересно, кто что представил… 🙂 Её площадь мы уже находили. Но, кроме того, данную фигуру можно ещё и вращать: вокруг оси  или вокруг оси .
В рамках данного курса я остановлюсь на стандартном варианте:

Пример 17
Вычислить объем тела, полученного вращением фигуры, ограниченной линиями ,  вокруг оси  .

Решение: как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. Да, с точно такого же чертежа:

Искомая плоская фигура заштрихована серым цветом, именно она и вращается вокруг оси . В результате получается такое… загадочное яйцо.

Объем тела вращения можно вычислить по формуле:
, где  – неотрицательная или неположительная функция, график которой ограничивает плоскую фигуру на отрезке . Заметьте, что здесь не нужно думать, над осью расположена криволинейная трапеция или под осью, т.к. возведение в квадрат стирает разницу между функциями  и .

В нашей задаче:

Интеграл почти всегда получается простой, главное, быть ВНИМАТЕЛЬНЫМ.

Ответ:  (кубических единиц — «кубиков» единичного объема)

Напоминаю, что , обычно принимают  либо .

Пример 18
Найти объем тела, образованного вращением вокруг оси  фигуры, ограниченной линиями , ,

Тренируемся и переходим к более содержательному случаю:

Пример 19
Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями , ,  и .

Решение: изобразим на чертеже плоскую фигуру, ограниченную линиями , , , , не забывая, что уравнение  задаёт ось :

Искомая фигура заштрихована синим цветом. При её вращении вокруг оси  получается такой сюрреалистический бублик с четырьмя углами. Объем этого бублика вычислим как разность объёмов с помощью стандартной формулы .

1) Фигура, обведённая красным цветом ограничена сверху прямой , поэтому:

2) Фигура, обведенная зеленым цветом ограничена сверху прямой , поэтому:

3) Объем искомого тела вращения:

Ответ:

Решение можно оформить и короче, примерно в таком духе:
., но, как вы уже поняли, за скорость приходится расплачиваться повышенным риском допустить ошибку.

И ещё хочу вас предостеречь от оценки результата «на глазок». При вычислении объёмов этого делать НЕ НАДО. Дело в том, что человек склонен неверно оценивать объёмы. Посмотрите на плоскую фигуру в прорешанной задаче – она вроде бы невелика по площади, а объем тела вращения составил чуть более 50 «кубиков», что кажется слишком большим. Кстати, среднестатистический человек за всю свою жизнь выпивает жидкость объемом с комнату площадью 18 квадратных метров, что, наоборот, кажется слишком маленьким объемом.

И после лирического отступления уместно решить изящную и, конечно же, важную;) задачу:

Пример 20
Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями , ,

Дополнительные примеры можно найти в соответствующей статье сайта, в том числе вращение вокруг оси , ну а сейчас есть более срочный материал:

1.10. Интеграл от чётной функции по симметричному относительно нуля отрезку

1.8. Как вычислить площадь фигуры с помощью определённого интеграла?

| Оглавление |



Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Конспекты по математике на тему «Тела вращения. Объемы тел вращения»

Конспекты занятий по математике для студентов первого курса теме «Тела вращения. Объемы тел вращения».

Тела вращения— объёмные тела, полученные при вращении плоской фигуры вокруг своей оси или стороны.

Примеры тел вращения: цилиндр, конус, шар, сфера.

1. Цилиндр

Цили́ндр (от греч. kýlindros, валик, каток) — геометрическое тело, образованное вращением прямоугольника вокруг одной из сторон.

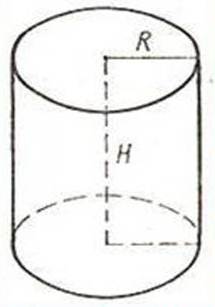
Цилиндр состоит из двух параллельных кругов, не лежащих в одной плоскости, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, — образующими цилиндра.

Примеры тел, имеющих цилиндрическую форму: часть водопроводной трубы, консервная банка.

Элементы цилиндра:

Радиусом цилиндра называется радиус его основания.

Высотой цилиндра называется расстояние между его основаниями.

Осью цилиндра называется прямая, проходящая через центр оснований, параллельно образующим.

Осевое сечение – сечение цилиндра плоскостью, проходящей через его ось.

Поверхность цилиндра состоит из оснований и боковой поверхности.

Боковая поверхность составлена из образующих.

Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.

Свойства цилиндра:

1. Основания цилиндра равны и параллельны.

2. Образующие цилиндра равны и параллельны.

2. Конус

Ко́нус — тело вращения, образованное вращением прямоугольного треугольника, вокруг одного из его катетов.

Конус состоит из круга – основания конуса, вершины конуса — точки, не лежащей в плоскости основания,   и всех отрезков, соединяющих вершину конуса с точками основания.

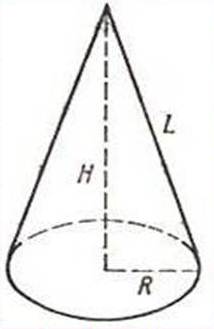
Примеры тел, имеющих форму конуса: воронка для наливания жидкости, чум — жилье народов севера, мороженое-рожок.

Элементы конуса:

Отрезок, соединяющий вершину и границу основания, называется образующей конуса.

Боковая поверхность конуса — объединение образующих конуса.

Отрезок, опущенный перпендикулярно из вершины на плоскость основания, называется высотой конуса.

Конус называется прямым, если прямая (ось конуса), соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.

Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением.

Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом.

3. Шар

Шар — тело вращения, полученное вращением полукруга около его неподвижного диаметра.

Примеры тел, имеющих форму шара или сферы: мыльный пузырь, земля, футбольный и теннисный мячи.

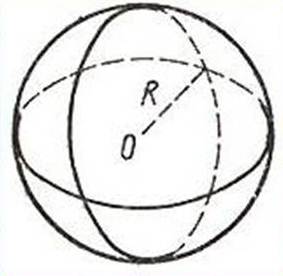
Элементы шара:

Любой отрезок, соединяющий центр шара с точкой его поверхности, называется радиусом.

Сфера это поверхность шара.

Отрезок, соединяющий две точки шаровой поверхности и проходящей через центр шара, называется диаметром.

Концы любого диаметра называются диаметрально противоположными точками шара.

Диаметр называется осью шара, а его оба конца — полюсами шара.

Плоскость, проходящая через центр шара, называется диаметральной плоскостью.

Плоскость, проходящая через точку А шаровой поверхности и перпендикулярная радиусу, проведенному в точку А, называется касательной плоскостью. Точка А называется точкой касания.

Если секущая плоскость проходит через центр шара, то сечение шара называется большим кругом. Другие плоские сечения шара называются малыми кругами.

Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).

Уравнение шара

1. Уравнение шара с радиусом R и центром в начале декартовой системе координат:

x² + y² + z² ≤ R²

2. Уравнение шара с радиусом R и центром в точке с координатами (x₀, y₀, z₀) в декартовой системе координат:

(x — x₀)² + (y — y₀)² + (z — z₀)² ≤ R²

4. Сфера

Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Уравнение сферы

1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:

x² + y² + z² = R²

2. Уравнение сферы с радиусом R и центром в точке с координатами (x₀, y₀, z₀) в декартовой системе координат:

(x — x₀)² + (y — y₀)² + (z — z₀)² = R²

Формулы объема цилиндра, конуса и шара.

1.Объем цилиндра.

Цилиндр — это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.

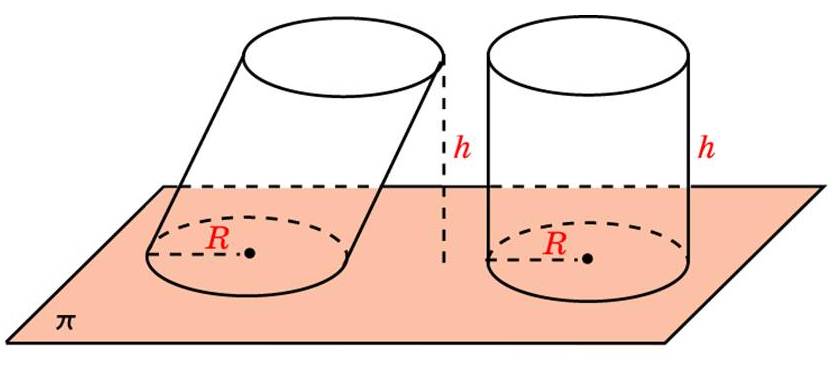
Объем прямого цилиндра равен произведению площади основания на высоту: V= S_оснh, т.к. в основании цилиндра лежит круг, то S_осн=S_круга=πR². Тогда формула объема цилиндра примет вид: V= πR²h.

 2.Объем конуса.

Конус — геометрическое тело, образованное вращением прямоугольного треугольника около одного из его катетов.

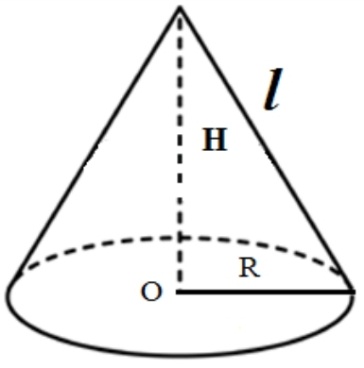
Объем конуса равен одной трети произведения площади основания на высоту V=  S_оснh, т.к. в основании конуса лежит круг, то S_осн=S_круга=πR². Тогда формула объема цилиндра примет вид: V=  πR²h.

3. Объем усеченного конуса.

Усеченный конус — часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию.

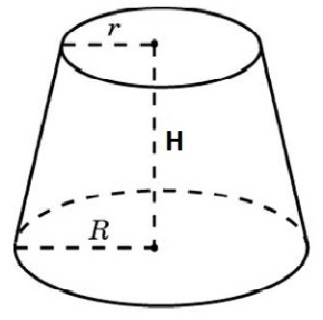
 Объем усеченного конуса вычисляется по формуле V=  πh (R² +Rr + r²).

4.Объем шара. 

Шар — это геометрическое тело, состоящее из точек пространства, которые удалены от центра O на одинаковое расстояние R. 

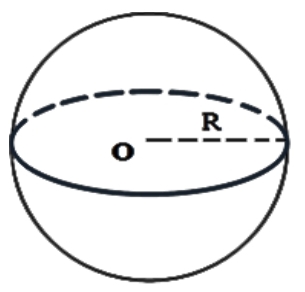
Объем шара радиуса R равен V=  πR³.

Объем вращением с использованием интеграции

Нахождение объема твердого оборота — это метод расчета объема 3D-объект, образованный повернутой областью 2D-пространства. Поиск громкости очень похож на поиск области, но с дополнительным компонентом поворота области вокруг линия симметрии — обычно ось x или y.

(1) Вспомните поиск области под кривой.Найдите площадь определенного интегральный

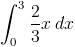
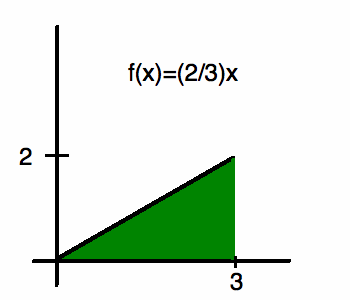
Интегрировать по [0,3]:

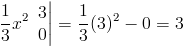
Теперь давайте повернем эту область на 360 градусов вокруг оси x. У нас будет 3D твердое тело это выглядит так:

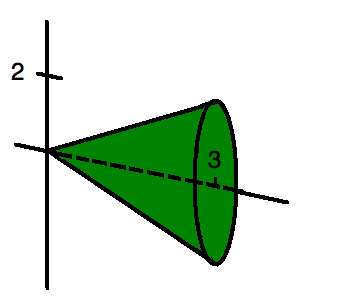
Чтобы найти этот объем, мы могли бы сделать вертикальные срезы твердого тела (каждый dx шириной и f (x) высотой) и сложите их.

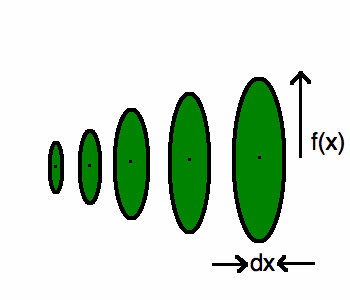
Это довольно утомительно, но, к счастью, у нас есть расчет! Поскольку интегрированная зона вращается вокруг оси под кривой, мы можем использовать , интеграцию диска найти объем. Поскольку область вращается на полный круг, мы можем использовать формулу для площади цилиндра, чтобы найти наш объем.

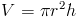
Объем цилиндра

Мы можем объединить формулу для объема цилиндра и наш определенный интеграл, чтобы найти объем нашего твердого тела.Радиус нашего цилиндра будет функцией f (x) а высота нашего цилиндра будет расстоянием до каждого диска: dx

Объем каждого среза будет

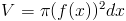
Если сложить объемы дисков с бесконечно малым dx, получится формула

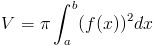
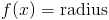
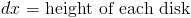
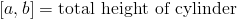
Используя нашу функцию, мы получили бы это подынтегральное выражение для объема

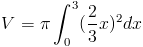
Вычисляя интеграл, получаем

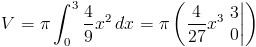
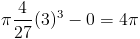
В качестве нашего объема мы получили 4Π единиц ³ .Поскольку наша функция линейна а радиус меняется с постоянной скоростью, это легко проверить, вставив в значениях к формуле для объема конуса.

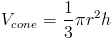
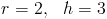
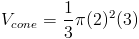
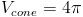
Ответы те же.Поскольку наша функция была линейной и имела форму конуса, когда вращаясь вокруг оси x, можно было использовать формулу объема для конуса. Много из объемов, с которыми мы будем работать, не имеют формы конуса, поэтому мы не можем просто подставьте значения в формулу. Хотя алгебра может позаботиться о красивой прямой линий, исчисление заботится о не очень хороших кривых.

Объем с вращением примеров

(2) Теперь попробуем повернуть ту же область вокруг оси y.

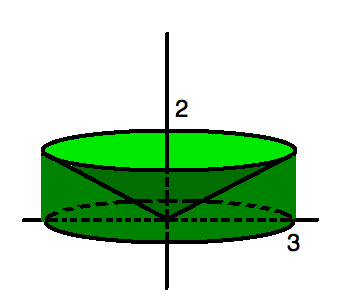
Первое повернутое тело было проинтегрировано по x, чтобы найти площадь, и повернуто вокруг ось x . Точно так же это твердое тело также интегрируется через x для область, но теперь она вращается вокруг оси y . Обратите внимание, что это твердое тело может получается вычитанием конуса радиуса 3 при y = 2 из цилиндра, образованного от радиуса 3 и высоты 2.

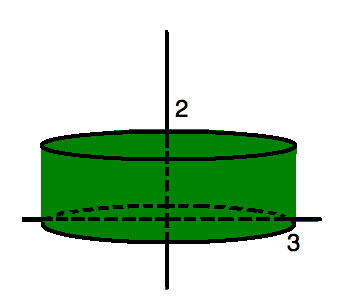
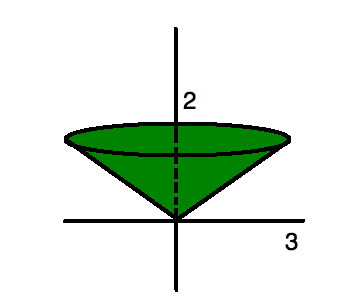
Объем цилиндра — объем конуса

= площадь вращения вокруг оси y.

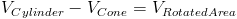
Найти этот том можно тремя способами. Мы можем сделать это к (а) , используя объем формулы для конуса и цилиндра, (b) , объединяющие два разных твердых тела и взяв разницу, или (c) , используя интеграцию оболочки (вращая область вокруг оси, отличной от оси, которой касается область).Попробуем все три методы.

(a) Используя формулы объема, мы имели бы

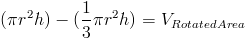
Радиус цилиндра и конуса будет равен 3, а высота — 2.

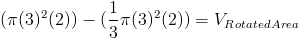
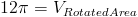
Объем 12Π шт. ³ .Проверим с интеграцией.

(b) При интегрировании находим площадь от кривой до оси. С тех пор, как мы вращаются вокруг оси y, нам нужно интегрировать по y. Для Цилиндр, наша область до поворота будет выглядеть так:

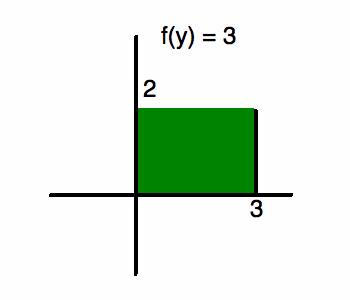
Функция y равна f (y) = 3 из [0,2].Теперь мы можем настроить наш интеграл.

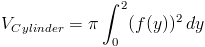
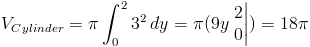
Теперь о конусе. Поскольку он вращается вокруг оси y, нам нужно интегрировать исходная функция по y. Все, что нам нужно сделать, это решить наш исходный функция для x вместо y, что делает ее функцией y. Функция y будет выглядят так:

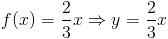
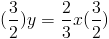
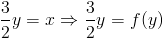
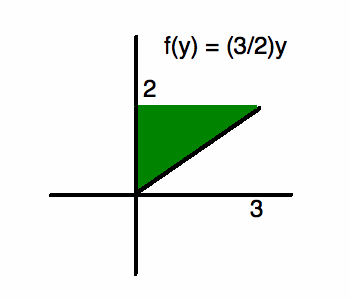
Функция y: f (y) = ( ³ ⁄ ₂ ) y из [0,2].Настроим наш интеграл.

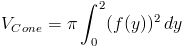
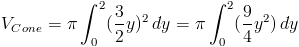
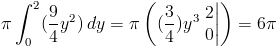
Теперь вычтем объем конуса из объема цилиндра. Мы получаем тот же ответ.

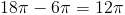
Наконец, выполним интеграцию оболочки.

(c) Обратите внимание, что при интеграции диска область была повернута вокруг той же оси что эта область была интегрирована. Другими словами, ось, которой коснулась область, была ось вращения. В интеграции с оболочкой все наоборот. Обратите внимание, что область касается оси x , а твердое тело вращается вокруг оси y .

Формула интегрирования оболочки определяется как:

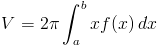
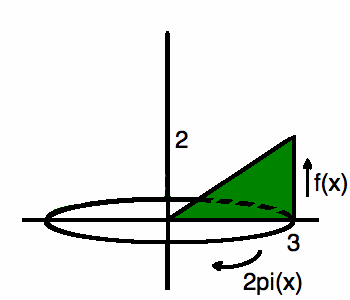
где x — расстояние до оси y или радиус, а f (x) теперь высота оболочки.

Простая замена f (x) даст нам

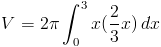
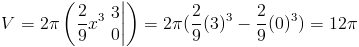
Кажется, что просто использовать формулы объема было лучшим методом, но давайте сделаем несколько разных примеров, когда это не так.

(3) Найдите объем следующей функции, повернутой вокруг оси x из [0,2Π]

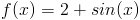
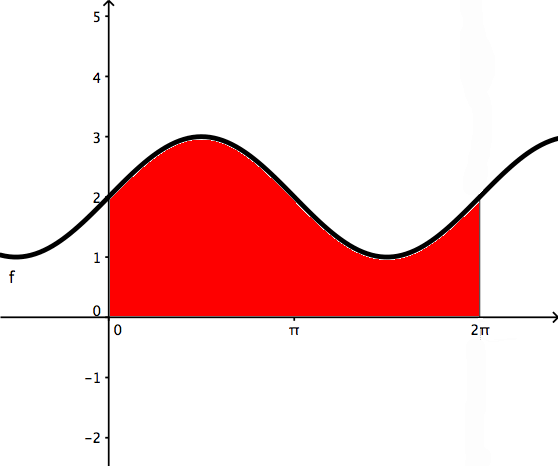
Повернутая область будет выглядеть так:

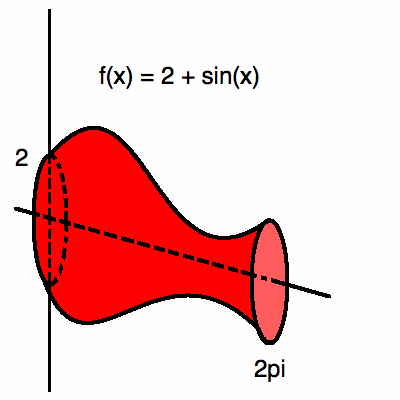
Если вы не знаете формулу для определения объема вазы, мы должны использовать интеграцию найти этот том.Мы не можем использовать формулу для каких-либо простых трехмерных геометрические фигуры как в первых двух примерах. Вращая это твердое тело вокруг x оси, мы должны сделать то же самое, что и в примере (1), и установить интеграл по формуле для объема цилиндра. Радиус цилиндра — это кривая, поэтому мы бы вставьте f (x) для радиуса, и тогда высота будет dx, которая составляет от 0 до 2Π.

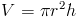
Объем цилиндра

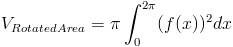
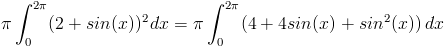
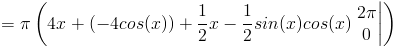
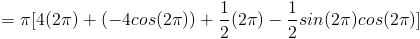
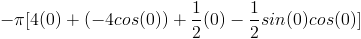
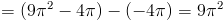
Общий объем твердого 9Π ² шт. ³ .

Что, если бы мы хотели найти объем области, повернутой вокруг оси x та же функция, но с небольшим пространством посередине? Такой тип фигуры называется стиральная машина или пончик. Они похожи на диски, потому что они круглые, но есть пространство посередине.

Рассмотрим ту же функцию с f (x) = 1.

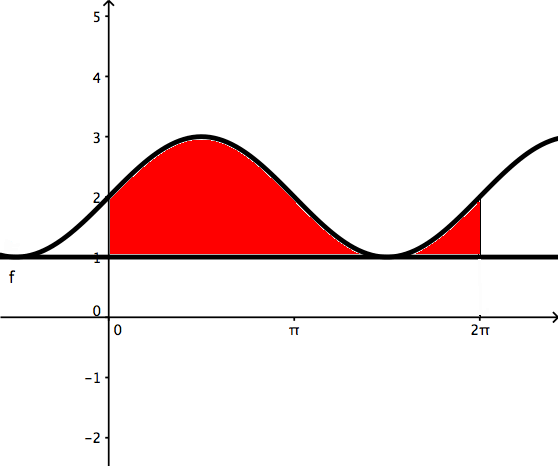
При повороте он будет похож на наш предыдущий поворот, но с цилиндром. удален посередине.

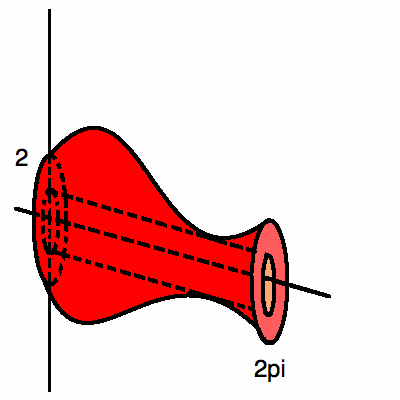
Чтобы найти объем, мы просто берем разницу нашей исходной площади и площади площади в центре.

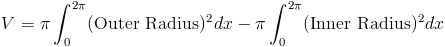
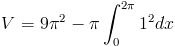
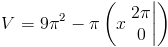
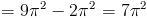
(4) Также было бы полезно поговорить о твердом теле, которое не вращается. на полные 360 градусов.Подумайте о части круга, который был заштрихован.

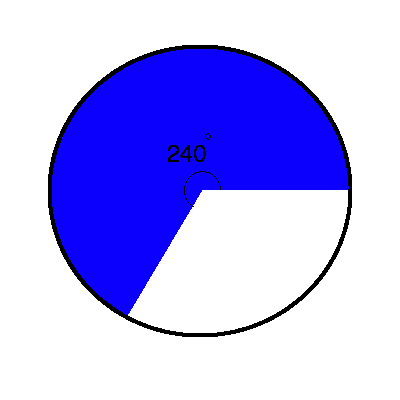
Этот круг закрашен на 240 градусов из 360. Как найти область? Мы просто возьмите долю от общей площади, в данном случае ²⁴⁰ ⁄ ₃₆₀ , или две трети.

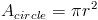
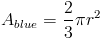
Так обстоит дело с объемом.Если у нас есть повернутая часть площади, мы находим Вывести объем твердого тела из общего объема, если его повернуть на 360 градусов.

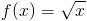
Это твердое тело также повернуто на 240 градусов вокруг оси x. Какой бы объем быть?

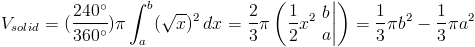
Это объем для повернутой части графика на интервале [a, b].

В предыдущих примерах мы вращали области вокруг оси x или y. Что, если бы мы повернулись их около произвольной оси?

При вращении вокруг оси g (x) мы должны учитывать изменение радиуса. Формулы для интеграции диска и оболочки будут следующими:

.

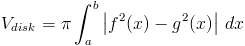
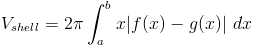
Calculus I — Объемы вращения твердых тел / Метод цилиндров

Онлайн-заметки Павла

Ноты Быстрая навигация Скачать

• Перейти к
• Ноты
• Проблемы с практикой
• Проблемы с назначением
• Показать / Скрыть
• Показать все решения / шаги / и т. Д.
• Скрыть все решения / шаги / и т. Д.

• Разделы
• Объемы тел вращения / Метод колец
• Больше проблем с объемом
• Разделы
• Интегралы
• Дополнительно
• Классы
• Алгебра
• Исчисление I
• Исчисление II
• Исчисление III
• Дифференциальные уравнения
• Дополнительно
• Алгебра и триггерный обзор
• Распространенные математические ошибки
• Праймер комплексных чисел
• Как изучать математику
• Шпаргалки и таблицы
• Разное
• Свяжитесь со мной
• Справка и настройка MathJax
• Мои студенты

• Notes Загрузки
• Полная книга
• Текущая глава
• Текущий раздел
• Practice Problems Загрузок
• Полная книга — Только проблемы
• Полная книга — Решения
• Текущая глава — Только проблемы
• Текущая глава — Решения
• Текущий раздел — Только проблемы
• Текущий раздел — Решения
• Проблемы с назначением Загрузок
• Полная книга
• Текущая глава
• Текущий раздел
• Прочие товары
• Получить URL для загружаемых элементов

• Распечатать страницу в текущем виде (по умолчанию)
• Показать все решения / шаги и распечатать страницу
• Скрыть все решения / шаги и распечатать страницу

• Дом
• Классы
• Алгебра
  • Отборочные
    • Целочисленные экспоненты
    • Рациональные экспоненты
    • Радикалы
    • Полиномы
    • Факторинговые многочлены
    • Рациональные выражения
    • Комплексные числа
  • Решение уравнений и неравенств
    • Решения и наборы решений
    • Линейные уравнения
    • Приложения линейных уравнений
    • Уравнения с более чем одной переменной
    • Квадратные уравнения — Часть I
    • Квадратные уравнения — Часть II
    • Квадратные уравнения: сводка
    • Приложения квадратных уравнений
    • Уравнения, сводимые к квадратичным в форме
    • Уравнения с радикалами
    • Линейные неравенства
    • Полиномиальные неравенства
    • Рациональные неравенства
    • Уравнения абсолютных значений
    • Неравенства абсолютных значений
  • Графики и функции
    • График
    • Строки
    • Круги
    • Определение функции
    • Графические функции
    • Комбинирование функций
    • Обратные функции
  • Общие графы
    • Прямые, окружности и кусочные функции
    • Параболы

.

Определение объема твердого тела вращения — исчисление

Исчисление

Наука

• Анатомия и физиология
• Астрономия
• Астрофизика
• Биология
• Химия
• наука о планете Земля

.

Вращательное движение жесткого тела

Дверь легче открыть, нажав на край, наиболее удаленный от петель, чем посередине. Интуитивно понятно, что величина приложенной силы и расстояние от точки приложения до петли влияют на склонность двери к повороту. Это физическая величина, крутящий момент , — это t = r × F sin θ, где F — приложенная сила, r — это расстояние от точки приложения до центра вращения, а θ — угол от r до F .

Подставьте второй закон Ньютона в определение крутящего момента с θ 90 градусов (прямой угол между F и r ) и используйте соотношение между линейным ускорением и тангенциальным угловым ускорением, чтобы получить t = r F = rma = mr ² ( a / r ) = mr ² α. Величина mr ² определяется как момент инерции точечной массы относительно центра вращения.

Представьте себе два объекта одинаковой массы с разным распределением этой массы. Первым объектом может быть тяжелое кольцо, поддерживаемое стойками на оси, подобной маховику. Второй объект мог иметь массу, близкую к центральной оси. Несмотря на то, что массы двух объектов равны, интуитивно понятно, что маховик будет труднее нажимать на большое количество оборотов в секунду, потому что не только количество массы, но и распределение массы влияет на легкость запуска. вращение для твердого тела.Общее определение момента инерции, также называемого инерцией вращения, для твердого тела составляет I = ∑ м _i r _i ² и измеряется в единицах СИ, килограмм-метрах. ² .

Моменты инерции для различных правильных форм показаны на рисунке 2.

Рисунок 2

Моменты инерции для различных правильных форм.

Проблемы механики часто включают как линейные, так и вращательные движения.

Пример 1: Рассмотрим рисунок 3, где груз висит на веревке, обернутой вокруг шкива. Падающая масса (м) заставляет шкив вращаться, и больше нет необходимости требовать, чтобы шкив был безмассовым. Присвойте шкиву массу ( M ) и рассматривайте его как вращающийся диск с радиусом (R) . Какое ускорение падающей массы и каково натяжение веревки?

Рисунок 3

Висящая масса вращает шкив.

Уравнение силы для падающей массы: T — мг = — ma . Натяжение каната — это сила, приложенная к краю шкива, заставляющая его вращаться. Таким образом, t = I α, или TR = (1/2) MR ² ( ^a / R), что сокращается до T = (1/2) млн лет , где угловое ускорение было заменено на ^a / R, поскольку шнур не скользит, а линейное ускорение блока равно линейному ускорению обода диска.Объединение первого и последнего уравнения в этом примере приводит к

Решение:

Угловой момент — это вращательный момент, который сохраняется так же, как и линейный момент. Для твердого тела угловой момент (L) является произведением момента инерции и угловой скорости: L = I ω. Для точки массы угловой момент может быть выражен как произведение количества движения и радиуса ( r ): L = mvr . L измеряется в килограммах-метрах ² в секунду или, чаще, в джоуль-секундах. Закон сохранения углового момента может быть утвержден, что угловой момент системы объектов сохраняется, если на систему не действует внешний чистый крутящий момент.

Аналогично закону Ньютона (F = Δ ( mv ) / Δ т ) существует вращательный аналог для вращательного движения: т = Δ L / Δ т , или крутящий момент — скорость изменения углового момента.

Рассмотрим пример ребенка, который бежит по касательной к краю карусели на игровой площадке со скоростью v _o и прыгает дальше, пока карусель неподвижна. Единственными внешними силами являются сила тяжести и контактные силы, создаваемые опорными подшипниками, ни одна из которых не вызывает крутящий момент, потому что они не прикладываются, чтобы вызвать горизонтальное вращение. Рассматривайте массу ребенка как точку массы, а карусель — как диск с радиусом R и массой M .По закону сохранения полный угловой момент ребенка до взаимодействия равен полному угловому моменту ребенка и карусели после столкновения: mrv _o = mrv ′ + I ω, где r — радиальное расстояние от центра карусели до места удара ребенка. Если ребенок прыгает на край, (r = R) и угловая скорость ребенка после столкновения может быть заменена на линейную скорость, mRv _o = mR ( R ω ) + (1/2) Руководство по ремонту ² .Если даны значения масс и начальной скорости ребенка, можно рассчитать конечную скорость ребенка и карусели.

У одиночного объекта может измениться угловая скорость из-за сохранения углового момента, если изменяется распределение массы твердого тела. Например, когда фигуристка тянет вытянутые руки, ее момент инерции уменьшается, вызывая увеличение угловой скорости. Согласно закону сохранения углового момента I _o (ω _o ) = I _f (ω _f ), где I _o — момент инерции фигуристки с вытянутыми руками, I _f — ее момент инерции с руками, расположенными близко к ее телу, ω _o — ее исходная угловая скорость, а ω _f — ее конечная угловая скорость.

Кинетическая энергия вращения, работа и мощность. Кинетическая энергия, работа и мощность определены в единицах вращения как K . E = (1/2) I ω ² , W = т θ, P = т ω.

Сравнение уравнений динамики линейного и вращательного движения. Приведены динамические соотношения для сравнения уравнений линейного и вращательного движения (см. Таблицу).

.