Тройной интеграл. Замена переменных в 3-ом интеграле. Тройной интеграл в сферических координатах
Тройной интеграл.
Пусть задана ф-ия 3-х переменных U=¦(x;y;z) в некоторой ограниченной области Т-трехмерного пространства, тогда интеграл от этой ф-ии по области Т записывается след. образом:
Получается след. образом.
Выполним разбиение области Т на элементарные объёмы DV1, …, DVn.
Выберем в каждом элементарном объёме точку М(xk;yk;zk) ®DVk
k=1,n.
Построим сумму вида:
Эта сумма называется интегральной для заданной ф-ии если существует ее придел при неограниченном увеличении числа разбиений области Т на элементарные объёмы, то он является тройным интегралом от ф-ии и записывается таким образом:
Расстановка пределов интегрирования в тройном интеграле.
Пусть
область интегрирования Т удовлетворяет след. условиям.
условиям.
1.Любая прямая L ï ïOz и проходящая через область Т пересекает границу области только в двух
точках:Z
2.Проекция тела Т на пл-ть XoY является правильной областью в направлении оси Oy (или Ox), тогда тройной интеграл в повторной записи будет выглядеть:
Zвх=Z1(x;y)
Zвых=Z2(x;y) a£ x £b
Yвх=Y1(x;y)
Yвых=Y2(x;y)
Таким образом 3-й интеграл сводится к 2-у интегрированию по проекции D.
Замечание: Если подинтегральная ф-ия f(x;y;z) принимает только неотрицательные значения, то тройной интеграл по области Т дает нам массу тела Т т.е.
где f(x;y;z) –плотность распределения массы по телу Т т.е. f(x;y;z)dV=dm.
Замечание: Если подинтегральная ф-ия f(x;y;z)=1, то тройной интеграл по области Т дает нам объем тела Т т.е
Пример: Вычислить тройной интеграл
По телу Т ограниченного плоскостями : x=0;y=0;z=0;x+y+z=1
Решение.
Область Т является пирамидой
ZВХ: Z=0
ZВЫХ: X+Y+Z=1
ZВХ=0
ZВЫХ=1-X-Y
YВХ=0
YВЫХ=1-X
0 £ X £1
Замена переменных в 3-ом интеграле.
Пусть задана непрерывная замена: удовлетворяющая условиям:
1.) Эта замена имеет непрерывные частные производные первого порядка.
2.) Эта замена область Т в координатах x,y,z взаимно однозначно переводит в область Т1 в координатах U,V,W.
3.) Якобиан перехода при этой замене сохраняет постоянный знак в области Т т.е.
Тогда справедлива формула перехода в тройном интеграле от декартовых координат x,y,z к другим U,V,W.
Тройной интеграл в цилиндрическихкоординатах
Цилиндрическими координатами называется тройка чисел , такая что:
Вычислим якобиан перехода к цилиндрическим координатам.
Для этого пологаем U=r ,V=j , W=z
Якобиан перехода к цилиндрическим координатам совпадает с полярным радиусом: I=r, а тогда формула перехода для тройного интеграла запишется таким образом:
Заметим, то что элемент объема в цилиндрических координатах будет вычислятся по формуле:
а в дикартовых
Тройной интеграл в сферических координатах.
Тройка чисел (), называется сферическими координатами, если любая точка М в декартовых координатах связана следующими соотношениями:
Якобиан перехода при сферической замене равен:
Якобиан перехода в сферических координатах имеет вид:
И тогда интеграл:
где элемент объема в сферических координатах:
Тройной интеграл(найти объем тела) : Чулан (М)
| tikho |
| ||
14/10/07 |
| ||
| |||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| tikho |
| ||
14/10/07 |
| ||
| |||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| tikho |
| ||
14/10/07 |
| ||
| |||
| Yu_K |
| ||
02/11/08 |
| ||
| |||
| tikho |
| ||
14/10/07 |
| ||
| |||
| Yu_K |
| ||
02/11/08 |
| ||
| |||
| tikho |
| ||
14/10/07 |
| ||
| |||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| tikho |
| ||
14/10/07 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 11 ] |
Модераторы: Модераторы Математики, Супермодераторы
Нахождение объема из тройных интегралов — Криста Кинг Математика
Установка тройного интеграла для определения объема
Мы можем использовать тройные интегралы для определения объема твердого трехмерного объекта. Формула объема:
Формула объема:
???V=\int\int\int_Ef(x,y,z)\ dV???
где ???Е??? представляет твердый объект. Мы закончим замену ???dV??? с ???dx???, ???dy??? и ???дз???.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать больше.
Мы можем интегрировать в любом порядке, поэтому мы попробуем интегрировать в том порядке, в котором проще всего, в зависимости от пределов интегрирования, которые мы обнаружим, проанализировав объект ???E???.
Имейте в виду, что когда дело доходит до пределов интегрирования, вам нужны предельные значения переменных, которые необходимо интегрировать. Например, если мы решим интегрировать сначала по ???z???, затем ???y???, затем ???x???, то наш объемный интеграл будет выглядеть как
???V=\int\int\int_Ef(x,y,z)\ dz\ dy\ dx???
Так как мы будем интегрировать ???z??? во-первых, это означает, что мы не будем интегрироваться по ???y??? или ???х??? тем не менее, что означает, что мы хотим, чтобы наши пределы интегрирования для ???z??? быть в терминах ???x??? и ???y???, или константы.
Аналогично, поскольку мы еще не интегрировали по ???x??? когда мы делаем интегрирование для ???y???, мы хотим, чтобы наши пределы интегрирования для ???y??? быть в терминах ???x???, или констант.
С ???х??? является последней переменной, которую нужно интегрировать, мы хотим, чтобы наши пределы интегрирования для ???x??? быть постоянными.
Использование тройных интегралов для нахождения объема твердого тела
Пройти курс
Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. 🙂
Учить больше
Нахождение объема тетраэдра, заключенного в координатные плоскости
Пример
Используйте тройной интеграл, чтобы найти объем тетраэдра, заключенного в ???3x+2y+z=6??? и координатные плоскости.
Самый традиционный порядок интегрирования: ???z???, затем ???y???, затем ???x???, вот что мы здесь сделаем. Это означает, что нам понадобятся следующие пределы интегрирования:
Это означает, что нам понадобятся следующие пределы интегрирования:
Поскольку тетраэдр опирается на координатные плоскости, мы знаем, что нижний предел интегрирования для ???x???, ???y??? и ???з??? будет ???0???.
Чтобы найти верхний предел интегрирования для ???x??? (константа), мы установим ???y=0??? и ???z=0??? в ???3x+2y+z=6??? а затем решить для ???x???.
???3x+2y+z=6???
???3x+2(0)+0=6???
???3x=6???
???х=2???
Это означает, что пределы интегрирования для ???x??? ???[0,2]???.
Чтобы найти верхний предел интегрирования для ???y??? (значение в терминах ???x???), мы установим ???z=0??? а затем переставьте ???3x+2y+z=6??? так что это решено для ???y??? в пересчете на ???x???.
???3x+2y+z=6???
???3x+2y+0=6???
???3x+2y=6???
???2y=6-3x???
???y=3-\frac32x???
Это означает, что пределы интегрирования для ???y??? ???[0,3-(3/2)x]???.
Чтобы найти верхний предел интегрирования для ???z??? (значение с точки зрения ???x??? и ???y???), мы решим ???3x+2y+z=6??? для ???z???.
???3x+2y+z=6???
???z=6-3x-2y???
Это означает, что пределы интегрирования для ???z??? составляют ???[0,6-3x-2y]???. 9{6-3x-2y}_01\dz\dy\dx???
Так как мы находим объем самой формы и наши пределы интегрирования находятся в терминах формы, функция, которую мы интегрируем, будет просто ???f(x,y,z)=1???.
Имейте в виду, что когда дело доходит до пределов интегрирования, вам нужны пределы, которые представляют собой переменные, оставшиеся для интегрирования.
Мы всегда интегрируем изнутри наружу, поэтому сначала будем интегрировать по ???z???, рассматривая все остальные переменные как константы. 93}{4}\справа]???
???V=18-\frac{36}{2}+\frac{24}{4}???
???V=18-18+6???
???V=6???
Объем твердого тела ???6??? кубических единиц.
Получить доступ к полному курсу Calculus 3
Начать
Learn mathКриста Кинг математика, выучить онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление 3, исчисление iii, исчисление iii, множественные интегралы, тройные интегралы, объем с тройными интегралами, тройной интегральный объем, порядок интеграция
0 лайковЧем полезны тройные интегралы | by Mike Beneschan
Photo by Tommaso Urli on UnsplashВы можете почувствовать ужас в комнате, когда студенты осознают, что существуют двойных интеграла и тройных интеграла . Интегралы, которые многие студенты помнят только как «странно выглядящие S-элементы», уже были достаточно сложными. Из 5 стадий математической скорби первой является отрицание: они умоляют: «Это ошибка, верно? Почему два этих странных S? После этого наступает второй этап, гнев: «Когда нам когда-нибудь понадобится использовать это в реальной жизни!?» (Третий этап — торг, когда они спрашивают меня об ответах на их тест по математике.)
Я здесь, чтобы объяснить, зачем нам в реальной жизни нужны тройные интегралы (и интегралы вообще).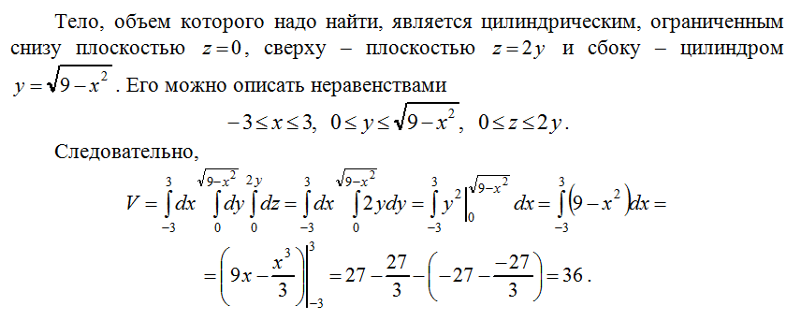 Когда я впервые взялся за многомерное исчисление, меня тоже парализовал страх перед страшной тройкой S, и я понимаю, что поначалу концепция кажется абстрактной чепухой. Но тройные интегралы действительно полезны! Сначала мы собираемся разобрать это, объяснив, почему нам нужны одиночные интегралы, затем двойные интегралы, а затем тройные интегралы.
Когда я впервые взялся за многомерное исчисление, меня тоже парализовал страх перед страшной тройкой S, и я понимаю, что поначалу концепция кажется абстрактной чепухой. Но тройные интегралы действительно полезны! Сначала мы собираемся разобрать это, объяснив, почему нам нужны одиночные интегралы, затем двойные интегралы, а затем тройные интегралы.
Для простых фигур у нас есть четкие формулы для нахождения площади:
Изображение автораНо как мы должны найти площадь этих фигур?
Изображение автораОтвет заключается в том, что мы можем использовать интеграл. Один простой способ описать интеграл состоит в том, что это площадь под некоторой кривой, и обычно мы используем интеграл, чтобы найти площадь странных форм.
Допустим, мы хотим найти область под странной кривой, которая выглядит так:
Изображение автораИзмерить точную площадь сложно, поэтому вы можете решить, что лучше вместо этого аппроксимировать площадь под кривой.
Когда вы ломаете голову над тем, как примерно определить площадь, вы можете мечтать о более простых формах, таких как прямоугольники. Ах да, прямоугольники с их легко вычисляемыми площадями высоты, умноженной на ширину.
Ах да, прямоугольники с их легко вычисляемыми площадями высоты, умноженной на ширину.
«Подождите, — думаете вы, — почему бы нам не приблизить площадь под кривой, нарисовав кучу прямоугольников под кривой, найдя площади этих прямоугольников и сложив все маленькие площади, вот так :”
Изображение автораЭто хорошая идея и приличное приближение. Наша приблизительная площадь будет равна сумме площадей всех зеленых прямоугольников.
Каждый прямоугольник будет иметь одинаковую ширину для облегчения вычислений. Ширина равна величине, которую мы назовем Δx (концептуально Δx — это изменение x). Высота каждого прямоугольника разная, но она задается функцией f(x), представленной изогнутой черной линией в верхней части диаграммы.
Чтобы было понятно, что все высоты разные, мы можем сказать, что 1-й прямоугольник слева имеет высоту f(x₁), 2-й прямоугольник имеет высоту f(x₂) и так далее. В общем случае i-й прямоугольник имеет высоту f(xᵢ).
Площадь прямоугольника равна произведению высоты на ширину, поэтому площадь одного из прямоугольников равна f(xᵢ)*Δx. Если просуммировать все площади прямоугольников, то получим приблизительную площадь под кривой.
Если просуммировать все площади прямоугольников, то получим приблизительную площадь под кривой.
Но наша аппроксимация не настолько точна — между нашими прямоугольниками и кривой есть куча промежутков. Мы могли бы сделать аппроксимацию более точной, увеличив количество прямоугольников, например так:
Изображение автораОбратите внимание, что Δx, изменение x, теперь меньше. Кроме того, эта сумма является более точной, чем предыдущая. Мы можем продолжать делить график на все более тонкие прямоугольники, чтобы сделать нашу сумму еще более точной. В конце концов, когда количество прямоугольников приближается к бесконечности (и ширина каждого прямоугольника приближается к 0), приблизительная область приближается к фактической области . То, что начиналось как грубое приближение, теперь очень точно!
Эта сумма называется интегралом . Интеграл записывается так:
Символ интеграла ∫ выглядит как большая буква S, потому что, когда немецкий чувак по имени Готфрид Лейбниц разрабатывал исчисление, он думал об интеграле как о бесконечной сумме . «dx» представляет Δx, ширину каждого прямоугольника, которая теперь бесконечно мала. «dx» называется дифференциал . f(x) — это просто та же функция, что и раньше (черная линия).
«dx» представляет Δx, ширину каждого прямоугольника, которая теперь бесконечно мала. «dx» называется дифференциал . f(x) — это просто та же функция, что и раньше (черная линия).
Вот как мы используем один интеграл. Мы интегрируем по 1 переменной, в данном случае x. Двигаясь вдоль оси X, мы получаем сумму множества невероятно тонких прямоугольников. Чем меньше ширина, тем точнее наша аппроксимация. Вот как мы находим площадь под кривой.
Для двумерных фигур у нас есть площадь , а для трехмерных фигур у нас есть объем . Как и прежде, у нас есть красивые, аккуратные формулы для объемов некоторых трехмерных фигур:
Изображение автораНо найти объемы этих трехмерных фигур гораздо сложнее:
Изображение автора Излишне говорить, что нелегко найти объем собаки, похожего на губку предмета и/или какой-то голубой сдутый волейбольный мяч. Как мы должны найти объем этих странных фигур? Чтобы найти объем, мы будем использовать двойной интеграл .
Допустим, я хочу найти объем этой буханки ананасового хлеба:
Изображение с Викисклада. xyz-axes добавлены мной. Кокосовая стружка добавлена пекарем.Как и прежде, мы можем начать с аппроксимации громкости. Вместо того, чтобы делить график на прямоугольники, мы могли бы начать с деления этой толстой буханки на ломтики по оси Y:
Изображение автораКаждый ломтик имеет одинаковую ширину; назовем эту ширину Δy. Если сложить площади всех ломтиков, то получится примерный объем батона. И, как и раньше, по мере того, как мы делим буханку на все более тонкие ломтики (по мере того, как Δy становится все ближе и ближе к 0), аппроксимация объема буханки становится все более и более точной.
Итак, нам просто нужно сложить площади всех ломтиков хлеба. Единственная проблема в том, что вычислить объем ломтика хлеба не так-то просто. Если мы посмотрим на отдельный срез, вы заметите, что он сам по себе довольно странной формы:
Изображение с Викисклада. Ось Y выглядит как точка, потому что с этой точки зрения ось Y идет прямо к вам. Вы также заметите, что вместо ломтика ананасового хлеба я использую ломтик цельнозернового пшеничного хлеба без потери универсальности.
Вы также заметите, что вместо ломтика ананасового хлеба я использую ломтик цельнозернового пшеничного хлеба без потери универсальности.Нам нужно приблизительно определить площадь этого ломтика хлеба, и мы можем сделать это, разделив его на несколько прямоугольников. Другими словами, чтобы найти площадь одного ломтика, мы должны выполнить один интеграл, как в предыдущем разделе:
Чтобы найти площадь одного ломтика хлеба, мы интегрируем по оси x, складывая крошечные прямоугольники. Затем, возвращаясь к буханке, мы интегрируем по оси Y, чтобы сложить площади всех ломтиков.
По существу, чтобы найти объем буханки ананасового хлеба, мы возьмем интеграл интегралов: мы возьмем сумму ломтиков, где каждый ломтик представляет собой сумму прямоугольников. Конечно, «интеграл от интегралов» писать неуклюже, поэтому мы просто назовем его 9.0143 двойной интеграл , и пишем его так:
Воу! Это двойной интеграл, во всем. Что это значит? «dy» — это ширина ломтика хлеба (поскольку каждый ломтик расположен вдоль оси y), а «dx» — ширина прямоугольника внутри ломтика хлеба (поскольку каждый прямоугольник в ломтике расположен по оси x). -ось). f(x,y) относится к верхней части буханки. Это связано с тем, что высота буханки в некоторой точке (координата z) является функцией от координаты x этой точки и y-координата , так что это f(x,y).
-ось). f(x,y) относится к верхней части буханки. Это связано с тем, что высота буханки в некоторой точке (координата z) является функцией от координаты x этой точки и y-координата , так что это f(x,y).
Итак, теперь самое интересное: тройные интегралы. Мы уже рассмотрели одинарные и двойные интегралы. Надеюсь, понятно, почему они могут быть полезны: хотя это не единственное их применение, они могут помочь нам найти площади и объемы неправильных 2-D и 3-D форм!
Вы можете догадаться, что здесь есть образец, который выглядит примерно так:
- С одинарными интегралами мы интегрируем по одному измерению, чтобы найти площадь двумерной фигуры.
- С помощью двойных интегралов мы интегрируем по двум измерениям, чтобы найти объем трехмерной фигуры.
- С помощью тройных интегралов мы интегрируем по трем измерениям, чтобы найти объем… четырехмерной формы?
И вы были бы правы! Тройной интеграл используется для нахождения объема четырехмерной фигуры. Это звучит невозможно. «Мы не живем в четырехмерном пространстве, Марк», — можете сказать вы. «Как они могут быть полезны, если четырехмерных форм не существует!» Ну, во-первых, меня зовут Майк, а не Марк. Но во-вторых, я могу объяснить, как тройные интегралы полезны в реальном мире. Чтобы увидеть это, нам нужно изменить то, как мы думаем об измерениях.
Это звучит невозможно. «Мы не живем в четырехмерном пространстве, Марк», — можете сказать вы. «Как они могут быть полезны, если четырехмерных форм не существует!» Ну, во-первых, меня зовут Майк, а не Марк. Но во-вторых, я могу объяснить, как тройные интегралы полезны в реальном мире. Чтобы увидеть это, нам нужно изменить то, как мы думаем об измерениях.
Сколько измерений в фотографии?
Вернемся ненадолго к двойным интегралам. Вы когда-нибудь видели термограмму? Это одна из тех фотографий, сделанных с помощью тепловизионной камеры, где разные цвета представляют разные температуры. Обложка альбома Брокхэмптона Iridescence представляет собой термограмму. Есть еще термограмма кота.
Фотографии являются двухмерными, но каждая точка на термографическом фото имеет связанное с ней «тепло». Поскольку тепло измеряется численно (с температурой), мы можем точно сказать, что каждой точке на термографической фотографии соответствует число: 9.0005 Легенда относится к температуре (Изображение автора).
Как видно из легенды справа, голубые пятна могут иметь теплотворную способность «15», а более красные пятна могут иметь теплотворную способность «28».
Мы даже можем превратить это фото в 3D-график, где высота (координата z) соответствует теплу (так что 30-градусная точка на фотографии будет выше, чем 15-градусная точка):
Изображение автораИтак, вот вопрос: как мне найти общее количество тепла по всей этой фотографии? Ответ заключается в том, что мы используем двойной интеграл! Мы интегрируем по оси x и оси y и суммируем температуру по всей фотографии. Общее количество теплоты равно том трехмерного графика выше.
Это может показаться запутанным, поскольку фотография двумерная, а, как упоминалось ранее, для нахождения объема трехмерной формы используются двойные интегралы. Но нам нужно изменить то, как мы думаем об «измерениях». Обычно мы думаем об измерениях как о пространственных измерениях: на вашей кухне вы можете перемещаться в трех пространственных измерениях. Однако «размер» на самом деле просто относится к значению, связанному с точкой. Измерение не обязательно должно быть направлением в пространстве. Например, взгляните на этот график количества пассажиров рейса с 1949–1961:
Однако «размер» на самом деле просто относится к значению, связанному с точкой. Измерение не обязательно должно быть направлением в пространстве. Например, взгляните на этот график количества пассажиров рейса с 1949–1961:
Эта гистограмма имеет два измерения, но это не совсем x и y. Два измерения — «Дата» и «Пассажиры», и так уж получилось, что дата откладывается по оси x, а количество пассажиров — по оси y.
В термограмме есть 2 пространственных измерения, а также 3-е измерение тепла. Тепло — это секрет 3-го измерения, что означает, что мы можем рассматривать фотографию как трехмерный объект и использовать двойной интеграл.
Тройные интегралы в реальном мире
Итак, вернемся к тройным интегралам. Допустим, у вас есть спальня в форме коробки. Вентиляционное отверстие может находиться только в одном углу комнаты, чтобы тепло не распространялось равномерно по всей комнате. Температура будет высокой возле вентиляционного отверстия, низкой в углу, противоположном вентиляционному отверстию, и так далее. Тепло в любой заданной точке комнаты определяется некоторой функцией f(x,y,z) (это функция координат x, y и z некоторой точки комнаты).
Тепло в любой заданной точке комнаты определяется некоторой функцией f(x,y,z) (это функция координат x, y и z некоторой точки комнаты).
Если я хочу добавить все тепло в номер , как бы я это сделал?
Очевидно, что в комнате есть 3 пространственных измерения. Но опять же, температура также считается измерением, поскольку это число, связанное с точкой. Итак, эта задача имеет место в 4 измерениях: ширина, длина, высота и температура .
Так как есть 4 измерения, мы будем использовать тройной интеграл!
Начнем с визуализации комнаты. Вот как может выглядеть трехмерная термограмма трехмерной комнаты:
Каждая сторона этой «комнаты» на самом деле представляет собой двухмерную термограмму, сделанную ранее. Я отредактировал его, чтобы он выглядел как трехмерная термограмма комнаты. Как было сказано ранее, если вы посмотрите на прямоугольник, то увидите, что температура является функцией точных координат x, y и z точки внутри прямоугольника. Эта функция есть f(x,y,z).
Эта функция есть f(x,y,z).
Начнем с интегрирования по оси Z, разделив коробку на множество срезов, параллельных земле: , но помните, температура это тоже измерение. На самом деле я взял комнату и нарезал ее на кучу двухмерных термограмм. И как мы уже говорили, двухмерную термограмму можно превратить в трехмерный график:
Изображение автораДалее мы проинтегрируем по y, разделив термограмму на множество маленьких кусочков, как мы сделали с буханкой ананасового хлеба:
Изображение автораНаконец, мы возьмем каждый кусочек и разделим его на части. маленьких прямоугольников вдоль оси X:
Изображение автора Делая это, мы можем точно суммировать все тепло в этой квадратной комнате. Разбиваем помещение на термограммы по оси z, затем делим термограммы на срезы по оси y, затем делим срезы на прямоугольники по оси x. Берем сумму суммы сумм, интеграл интегралов интегралов (удачи говорят, что в 3 раза быстрее). Мы называем это тройной интеграл . Записывается так:
Записывается так:
«dz» — это изменение z, «dy» — изменение y, а «dx» — изменение x. Функция f(x,y,z) — это функция, которая сообщает вам температуру в некоторой точке комнаты.
Используя этот тройной интеграл, мы можем найти общее количество тепла в трехмерной комнате. Если «размерность» может означать что-то иное, чем пространственное измерение, мы понимаем, что у тройных интегралов есть множество применений. Мы могли бы найти полную инерцию над некоторым трехмерным объектом или гравитационное притяжение баскетбольного мяча.
Вкратце:
- Измерение в математических целях не обязательно должно относиться к пространству. Он может относиться к любому числовому значению, такому как температура, инерция или влажность.
- В одном интеграле мы интегрируем по 1 переменной, чтобы найти площадь двумерной фигуры.
- В двойном интеграле мы интегрируем две переменные, чтобы найти объем трехмерной фигуры.
- В тройном интеграле мы интегрируем по 3 переменным, чтобы найти объем четырехмерной фигуры.


 11.2008, 11:30
11.2008, 11:30  11.2008, 11:34
11.2008, 11:34 
 11.2008, 22:11
11.2008, 22:11 
 В сферических проще — рекомендации же были про сферические.
В сферических проще — рекомендации же были про сферические. 11.2008, 13:29
11.2008, 13:29  11.2008, 13:37
11.2008, 13:37 