Область определения функции нескольких переменных: Функции нескольких переменных

Дифференциальное и интегральное исчисления для втузов, т.1

Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов, т.1: Учебное пособие для втузов.— 13-е изд.— М.: Наука. Главная редакция физико-математической литературы, 1985. — 432 с. Хорошо известное учебное пособие по математике для втузов с достаточно широкой математической подготовкой. Первый том включает разделы: введение в анализ, дифференциальное исчисление (функций одной и нескольких переменных), неопределенный и определенный интегралы. Настоящее издание не отличается от предыдущего (1978 г.). Для студентов высших технических учебных заведений. Оглавление ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА I. ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ § 1. Действительные числа. § 2. Абсолютная величина действительного числа § 3. Переменные и постоянные величины § 4. Область изменения переменной величины § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина § 6. Функция § 7. Способы задания функции § 8. Основные элементарные функции. Элементарные функции § 9. Алгебраические функции § 10. Полярная система координат Упражнения к главе I ГЛАВА II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ § 1. Предел переменной величины. Бесконечно большая переменная величина § 2. Предел функции § 3. Функция, стремящаяся к бесконечности. Ограниченные функции § 4. Бесконечно малые и их основные свойства § 5. Основные теоремы о пределах § 6. Предел функции (sin x)/x при x->0 § 7. Число e § 8. Натуральные логарифмы § 9. Непрерывность функций § 10. Некоторые свойства непрерывных функций § 11. n при n целом и положительном § 6. Производные от функций y = sinx; y = cosx § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного § 8. Производная логарифмической функции § 9. Производная от сложной функции § 10. Производные функций y = tgx, y = ctgx, y = ln|x| § 11. Неявная функция и ее дифференцирование § 12. Производные степенной функции при любом действительном показателе, показательной функции, сложной показательной функции § 13. Обратная функция и ее дифференцирование § 14. Обратные тригонометрические функции и их дифференцирование § 15. Таблица основных формул дифференцирования § 16. Параметрическое задание функции § 17. Уравнения некоторых кривых в параметрической форме § 18. Производная функции, заданной параметрически § 19. Гиперболические функции § 20. Дифференциал § 21. Геометрическое значение дифференциала Рассмотрим функцию § 22. Производные различных порядков § 23. x, sin x, cos x Упражнения к главе IV ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ § 2. Возрастание и убывание функции § 3. Максимум и минимум функций § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной § 5. Исследование функции на максимум и минимум с помощью второй производной § 6. Наибольшее и наименьшее значения функции на отрезке § 7. Применение теории максимума и минимума функций к решению задач § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора § 9. Выпуклость и вогнутость кривой. Точки перегиба § 10. Асимптоты § 11. Общий план исследования функций и построения графиков § 12. Исследование кривых, заданных параметрически Упражнения к главе V ГЛАВА VI. КРИВИЗНА КРИВОЙ § 1. Длина дуги и ее производная § 2. Кривизна § 3. Вычисление кривизны § 4. Вычисление кривизны линии, заданной параметрически § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах § 6. Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента § 7. Свойства эволюты § 8. Приближенное вычисление действительных корней уравнения Упражнения к главе VI ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ § 1. Комплексные числа. Исходные определения § 2. Основные действия над комплексными числами § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа § 4. Показательная функция с комплексным показателем и ее свойства § 5. Формула Эйлера. Показательная форма комплексного числа § 6. Разложение многочлена на множители § 7. О кратных корнях многочлена § 8. Разложение многочлена на множители в случае комплексных корней § 9. Интерполирование. Интерполяционная формула Лагранжа § 10. Интерполяционная формула Ньютона § 11. Численное дифференцирование § 12. О наилучшем приближении функций многочленами. Теория Чебышева Упражнения к главе VII ГЛАВА VIII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. Определение функции нескольких переменных § 2. Геометрическое изображение функции двух переменных § 3. Частное и полное приращение функции § 4. Непрерывность функции нескольких переменных § 5. Частные производные функции нескольких переменных § 6. Геометрическая интерпретация частных производных функции двух переменных § 7. Полное приращение и полный дифференциал § 8. Применение полного дифференциала в приближенных вычислениях § 9. Приложение дифференциала к оценке погрешности при вычислениях § 10. Производная сложной функции. Полная производная. Полный дифференциал сложной функции § 11. Производная от функции, заданной неявно § 12. Частные производные различных порядков § 13. Поверхности уровня § 14. Производная по направлению § 15. Градиент § 16. Формула Тейлора для функции двух переменных § 17. Максимум и минимум функции нескольких переменных § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы) § 19. Получение функции на основании экспериментальных данных по методу наименьших квадратов § 20. Особые точки кривой Упражнения к главе VIII ГЛАВА IX. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ § 1. Уравнения кривой в пространстве § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости § 3. Правила дифференцирования векторов (векторных функций) § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении § 5. Соприкасающаяся плоскость. Бинормаль. Кручение. § 6. Касательная плоскость и нормаль к поверхности Упражнения к главе IX ГЛАВА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Первообразная и неопределенный интеграл § 2. Таблица интегралов § 3. Некоторые свойства неопределенного интеграла § 4. Интегрирование методом замены переменной или способом подстановки § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен § 6. Интегрирование по частям § 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование § 8. Разложение рациональной дроби на простейшие § 9. Интегрирование рациональных дробей § 10. Интегралы от иррациональных функций § 11. Интегралы вида … § 12. Интегрирование некоторых классов тригонометрических функций § 13. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок § 14. О функциях, интегралы от которых не выражаются через элементарные функции Упражнения к главе X ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Постановка задачи. Нижняя и верхняя интегральные суммы § 2. Определенный интеграл. Теорема о существовании определенного интеграла § 3. Основные свойства определенного интеграла § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница § 5. Замена переменной в определенном интеграле § 6. Интегрирование по частям § 7. Несобственные интегралы § 8. Приближенное вычисление определенных интегралов § 9. 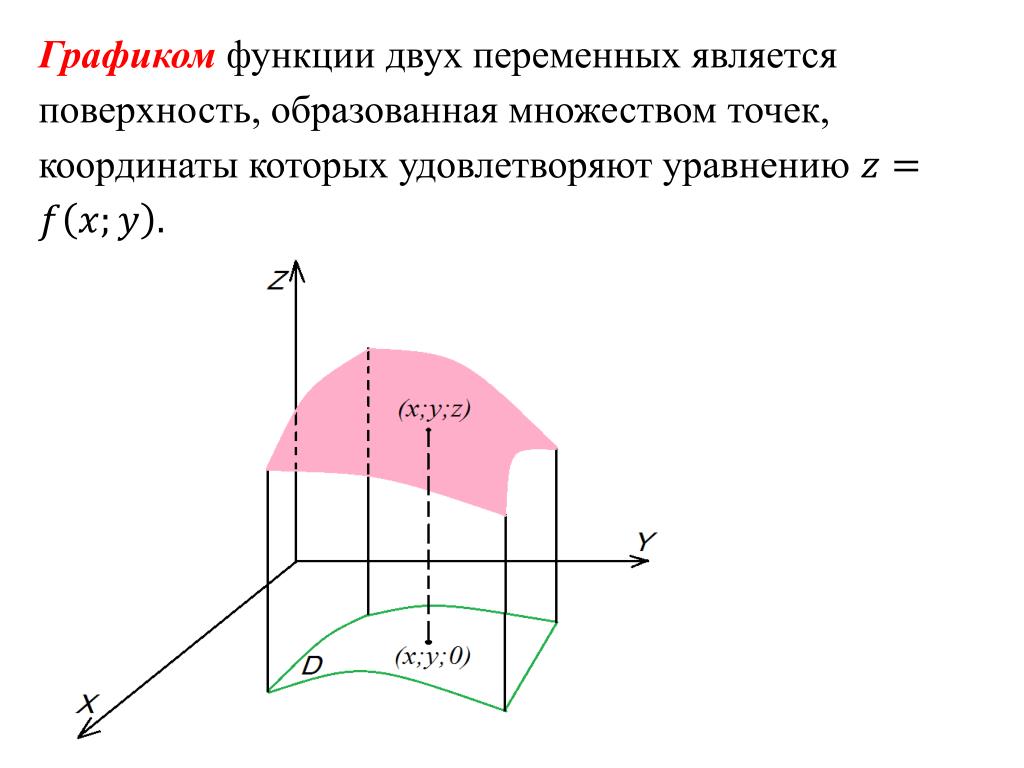Формула Чебышева § 10. Интегралы, зависящие от параметра. Гамма-функция § 11. Интегрирование комплексной функции действительной переменной Упражнения кглаве XI ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. Вычисление площадей в прямоугольных координатах § 2. Площадь криволинейного сектора в полярных координатах § 3. Длина дуги кривой § 4. Вычисление объема тела по площадям параллельных сечений § 5. Объем тела вращения § 6. Площадь поверхности тела вращения § 7. Вычисление работы с помощью определенного интеграла § 8. Координаты центра масс § 9. Вычисление момента инерции линии, круга и цилиндра с помощью определенного интеграла Упражнения к главе XII

1.1. Понятие функций нескольких переменных

В науке и технике часто приходится встречаться с одновременным, совместным изменением нескольких переменных, связанных между собой некоторыми условиями. Так площадь прямоугольника изменяется с изменением длин его сторон и , объем цилиндра изменяется с изменением радиуса основания и высоты цилиндра .

Пусть дано некоторое множество пар чисел .

Функцией двух переменных называется соответствие, при котором каждой паре чисел соответствует единственное число .

При этом и называются Независимыми переменными (или Аргументами), — Зависимой переменной (или Функцией), множество -­ Областью определения функции, а — множеством значений функции.

Обозначения функции двух переменных аналогичны обозначениям функции одной переменной: , , и т. д.

При нахождении частного значения функции , которое она принимает при заданных численных значениях аргументов и , пишут или . Например, если , то .

Так как каждой паре чисел соответствует единственная точка плоскости и обратно, каждой точке соответствует единственная пара чисел , то функцию двух переменных можно рассматривать как функцию точки .

Поэтому вместо записи пишут . в этом случае областью определения функции является некоторое множество точек плоскости .

В основном мы будем рассматривать функции двух переменных, однако все сказанное целиком переносится и на функции любого числа переменных, которые определяются аналогичным образом.

Функцией трех переменных называют соответствие, при котором каждой тройке соответствует единственное число .

При этом , и Называют Независимыми переменными (или Аргументами), — Зависимой переменной (или Функцией), множество — областью определения функции, а — множеством значений функции.

Функцию трех переменных обозначаются так же, как и функции одной или двух переменных: , и т. д.

Функцию трех переменных можно рассматривать как функцию точки , имеющей координаты , , в пространственной системе координат .

Область определения функции есть некоторое множество точек в пространстве.

Аналогично можно ввести Понятие функции четырех, пять и вообще переменных.

Функцию переменных также рассматривают как функцию точки — мерного пространства и пишут .

Если функция задана аналитическим выражением, причем область определения функции заранее не указана, то в качестве области определения принимают совокупность всех тех точек , для которых данное аналитическое выражение имеет конечное действительное значение.

Пример 1. Найти область определения функции

.

Решение. Областью определения этой функции является множество всех точек, для которых выражение определено, т. е. множество точек, для которых , или , т. е. внутренность круга с центром в начале координат и радиусом, равным 1 (рис. 1).

Пример 2. Найти область определения функции .

Решение. Областью определения этой функции является множество точек, удовлетворяющих условию , или , т. е. все точки плоскости за исключением точек прямой (рис. 2).

Пример 3. Найти область определения функции

.

Решение. Функция будет принимать действительные значения при условии, что , или . То есть область определения функции является шар радиуса 2 с центром в начале координат. Точки граничной шаровой поверхности относятся к области определения функции.

Пусть функция определена в некоторой области на плоскости . Тогда каждой точке будет соответствовать точка трехмерного пространства.

Множество всех таких точек , , называется Графиком функции . В общем случае графиком функции является Поверхность в пространстве.

В аналитической геометрии уже рассматривались некоторые поверхности, которые являются графиками функций двух переменных.

Например, эллиптический параболоид является графиком функции .

Линией уровня называется множество точек на плоскости , в которых функция принимает данное постоянное значение . Эту линию можно также получить, пересекая график функции плоскостью , параллельной плоскости , и проектируя линию пересечения ортогонально на плоскость (рис. 3).

Система линий уровня , где , позволяет судить о ходе изменения функции. Там, где линии уровня располагаются густо, функция изменяется быстро, а где линии уровня расположены редко, функция изменяется медленно.

Пример 4. Найти линии уровня функции .

Решение. Рассмотрим

,

Т. е. линиями уровня является семейство парабол.

Для функции трех переменных рассматривают Поверхности уровня – множество точек пространства, в которых функция принимает данное постоянное значение.

Следующая >

Переменные и константы в Go

В Go существует множество способов определения переменных. Это потому, что разработчики хотели сделать язык максимально гибким.

Решение о том, какой из них использовать, обычно основывается на области действия переменной и ее предполагаемом использовании.

Мы будем говорить об области видимости переменных параллельно, пока будем обсуждать различные способы определения переменных.

Содержание

• Переменные локальной области видимости
• Сокращенное объявление
• Длинное объявление — var и const
• Объявление без присвоения
• Объявление групповой переменной
• Глобальные переменные
• Правила доступа
• Объявление глобальной переменной .

  Кроме того, существует область действия блока, в которой переменные, определенные внутри блока (if, for, switch и т. д.), не видны за пределами этого блока.

  Сокращенное объявление

  Самый простой способ определить локальную переменную — использовать сокращенный синтаксис ‘:=’. Требуется только указать имя переменной и значение.

  Это предпочтительный способ определения небольшой переменной области видимости, которой:

  • может быть немедленно присвоено значение
  • давно не используется

  Тип переменной выводится из присвоенного ей значения. Это известно как вывод типа.

  Давайте посмотрим на примере:

   основная функция () {
      // Сокращенное объявление
      а := "Привет"
      б := получитьИмя()
      fmt. Println(a, b) // Привет, мир
  }
  функция getName() строка {
      вернуть "Мир"
  }
   

  Длинное объявление — var и const

  Поскольку объем использования превышает несколько строк, рекомендуется использовать синтаксис длинного объявления.

  Требуется использование ключевого слова var для определения имени и типа переменной или ключевого слова const для определения константы.

  Синтаксис для определения константы или переменной:

  [ключевое слово] [имя] [тип] = [значение].

  Мы будем читать это как

  «определить [переменную/константу] с именем [имя] типа [тип] со значением [значение]».

  Сначала проверим объявление const. Вот несколько моментов, о которых следует помнить:

  • Константы нельзя переназначать.
  • Константам необходимо присвоить буквальное значение во время объявления.
  • Мы не можем использовать вызовы функций или переменные в качестве значений.
  • Объявление типа необязательно, так как он всегда выводится из присвоенного ему значения.

   основная функция () {
      константа = "Привет"
      const b строка = "Мир"
      fmt.Println(a, b) // Привет, мир
  }
   

  Теперь давайте посмотрим, как определить переменные, используя var .

   основная функция () {
      вар а = "Привет"
      var b строка = getName()
      fmt.Println(a, b) // Привет, мир
  }
  функция getName() строка {
      вернуть "Мир"
  }
   

  Как видно из переменной ‘a’, при присвоении значения во время объявления тип выводится из значения, и нам не нужно его указывать.

  Здесь рекомендуется объявлять тип, если у вас нет веских причин не делать этого (например, при присвоении литерального значения). Это упрощает определение типа без необходимости проверять тип назначенной переменной или вызова функции.

  Объявление без присвоения

  Как и в других языках, мы можем объявить переменную без присвоения ей значения. Есть несколько способов сделать это.

  Это предпочтительный способ объявления переменных, которые предназначены для использования в течение длительного времени и их значения часто меняются.

   основная функция () {
      var a, b строка
      переменная с интервалом
      а = "Привет"
      б = получитьИмя()
      с = 10
      fmt.Println(a, b, c) // Привет, мир 10
  }
  функция getName() строка {
      вернуть "Мир"
  }
   

  Если имеется несколько переменных одного типа, мы можем объявить их в одной строке с помощью оператора запятая.

  Есть несколько важных моментов, о которых следует помнить при объявлении переменных без присваивания:

  1. Тип всегда необходимо указывать.
  2. Каждая определенная переменная должна использоваться позже. Если вы забудете использовать переменную, компилятор выдаст вам ошибку. Это сделано для того, чтобы вы не забыли использовать переменную.
  3. Ни одна переменная не является нулевой. Каждой объявленной переменной автоматически присваивается «нулевое» значение указанного типа. Например, строковые переменные инициализируются пустой строкой «», а целочисленные переменные инициализируются значением 0,9.0010

  Объявление групповой переменной

  В дополнение к этим способам мы также можем использовать групповое объявление для одновременного объявления нескольких переменных.

   основная функция () {
      вар (
          а, б строка
          c инт
      )
      а = "Привет"
      б = "Мир"
      с = 10
      fmt.Println(a, b, c) // Привет, мир 10
  }
   

  Мы также можем использовать сокращенный синтаксис объявления для одновременного объявления нескольких переменных.

   основная функция () {
      а, б, в = "Привет", "Мир", 10
      fmt.Println(a, b, c) // Привет, мир 10
  }
   

  Группировка объявлений переменных — хороший способ сократить количество строк кода, необходимых для объявления нескольких переменных.

  Это также хороший способ сгруппировать переменные, которые имеют сходное использование. Его также можно использовать для группировки всех переменных, которые используются в одной функции, чтобы упростить понимание кода.

  Глобальные переменные

  Переменные, определенные вне функций, называются глобальными переменными. Давайте немного поговорим о правилах доступа, прежде чем мы рассмотрим синтаксис.

  Правила доступа

  Go имеет только два типа доступа к глобальным переменным и функциям:

  1. Общий доступ — переменные и функции, начинающиеся с заглавной буквы, являются общедоступными (автоматически экспортируются пакетом) и могут использоваться в любом месте программы.
  2. Доступ к пакету — Переменные и функции, начинающиеся со строчной буквы, являются частными и могут использоваться только внутри пакета, где они определены.

  Если вы не знакомы с пакетами в Go, вы можете думать о пакете как о наборе файлов с одинаковым именем пакета в первой строке файла.

  Объявление глобальной переменной

  Давайте рассмотрим синтаксис объявления глобальной переменной или константы.

   пакет основной
  константа = "Привет"
  const b строка = "Мир"
  константа PI = 3,14
  константа (
      аа = "Привет"
      bb строка = "Мир"
  )
  переменная с интервалом
  var d строка
  вар (
      е = "Привет"
      f строка = "Мир"
      г инт
  )
   

  Несколько важных моментов, о которых следует помнить:

  1. Константы определяются по тем же правилам, что и внутри функции.
  2. Константа PI начинается с заглавной буквы и, следовательно, может быть доступна вне пакета с помощью «main.PI». Другие написаны строчными буквами и доступны только внутри пакета.
  3. Группировка разрешена для глобальных переменных и констант.
  4. Определение типа переменной является необязательным, если присвоенное ей значение является буквальным значением. Присвоение значения необязательно, но тогда необходимо указать тип.
  5. Сокращенное объявление не разрешено для глобальных переменных и констант.

  ---

  Какова область действия переменных в Python?

  Onyejiaku Theophilus Chidalu

  Обзор

  Область переменной — это место, где мы можем обнаружить переменную и получить к ней доступ, если это необходимо. Переменную можно найти в том месте, где она была создана, что является ее областью действия.

  Типы областей

  В Python существует два типа областей:

  1. Локальная область/локальные переменные
  2. Глобальная область/глобальные переменные

  Локальная область/локальные переменные

  Термин локальные переменные или локальная область описывает ситуацию, когда переменная создается внутри функции. Эта переменная принадлежит к локальной области , потому что она доступна только внутри функции, которую она создала.

  Пример кода

   
   # определение функции 
   
   # создание переменной x внутри функции 
   
   def function1(): 
   
   x = 10 
   
   print(x) 
   
   # вызов функции 
   
   function1() 
   

  Пример кода для локальной области видимости переменной

  Код пояснения
• 2 код выше, что переменная x была определена внутри функции, то есть function1() . Этот тип переменной существует только в этой области (в функции, в которой она была создана). Поэтому он упоминается как локальная область действия 9.0056 и переменная является локальной переменной .

  Стоит отметить, что доступ к локальной переменной из функции внутри другой функции можно получить следующим образом:

   
   # определение функции 
   
   # создание переменной x внутри функции 
   
   def function1(): 
   
   x = 10 
   
   # создание внутренней функции 
   
   def innerfunction(): 
   
   print(0x) 
   innerfunction() 
   
   # вызов функции 
   
   function1() 
   

  Пример кода внутренней функции, вызывающей локальную переменную внешней функции

  Глобальная область/глобальная переменная

  созданный вне функции. Функция создается в основной части кода Python, поэтому она называется глобальной областью видимости , а переменная — глобальной переменной .

  Пример кода

   
   # создание глобальной переменной
   
   
   х = 10
   
   
   # определение функции
   
   
   функция определения1():
   
   
   печать(х)
   
   
   # вызов функции
   
   
   функция1()
   
   
   # печать х
   
   
   print(x) 
   

  Пример кода для глобальной области действия переменной

  Объяснение кода

  Мы создаем глобальную переменную с именем x и вызываем ее внутри и вне функции.

  No related posts.