Обращение матриц: Обратная матрица онлайн

ОБРАЩЕНИЕ МАТРИЦЫ | это… Что такое ОБРАЩЕНИЕ МАТРИЦЫ?

— алгоритм, применяемый при численном нахождении обратной матрицы. Как и в задаче решения линейных систем, методы численного обращения подразделяются на прямые и итерационные; однако итерационные методы вследствие их трудоемкости играют здесь существенно меньшую роль.

Большинство прямых методов О. м. основано на идее разложения заданной матрицы в произведение легко обращаемых сомножителей. Если

— такое разложение, то

Типичным (и одним из наиболее употребительных) прямых методов О. м. является метод Жордана (см. [1]).

Пусть А- невырожденная матрица порядка п. Построение обратной матрицы А ^-1 происходит в пшагов; результатом k-го шага будет матрица , первые кстолбцов к-рой совпадают с одноименными столбцами единичной матрицы. Переход от (пусть А=А ₀ )к с матричной точки зрения эквивалентен умножению .слева на матрицу , к-рая отличается от единичной лишь (k+1)-м столбцом.

Из соотношений

вытекает

и

Получение факторизованного представления (1) для обратной матрицы требует примерно операций умножения и примерно операций сложения. Приблизительно такое же число дополнительных операций необходимо для того, чтобы перемножить матрицы в (1) и получить явный вид . Во многих приложениях операции О. м. использование факторизованной формы (1) столь же удовлетворительно, что и явного вида. Напр., вычисление произведения , где b- вектор-столбец, требует одинаковой арифметич. работы в обоих случаях. Одинаковы и требования к памяти при реализации на ЭВМ.

В приведенном описании метода Жордана предполагалось для простоты, что все элементы (называемые ведущими элементами) отличны от нуля. В действительности метод Жордана, как и методы типа Гаусса для решения линейных систем, как правило, применяется с той или иной схемой выбора ведущих элементов.

Невязкой, соответствующей приближенной обратной матрице Xдля А, наз. матрица . Имеет место оценка

Таким образом, норма невязки является оценкой относительной точности приближенной обратной матрицы X. В этом состоит важное отличие задачи численного О. м. от задачи решения линейных систем, где (напр., в ортогональных методах или методах типа Гаусса) невязка обычно мала, а качество полученного решения зависит от обусловленности системы.

Обращение ряда важных классов матриц может быть достигнуто значительно более экономичными, чем в общем случае, методами. Таковы теплицевы, ганкелевы, ленточные (и, в частности, трехдиагональные) матрицы, блочные матрицы, имеющие теплицеву структуру или структуру кронекерова произведения, и т. д. Напр., пусть Т- теплицева матрица порядка n+1 с элементами из Rили С:

Предполагается, что не только Т, но и ее главная подматрица порядка пневырождены. Тогда для матрицы уже, вообще говоря, не являющейся теплицевой, справедливо представление (см. [2]):

При этом векторы

суть соответственно первый и последний столбцы Таким образом, Тполностью определяется заданием первого и последнего столбцов. При необходимости из (2)могут быть последовательно вычислены все элементы

Это вычисление требует арифметич. операций.

В экономичных алгоритмах обращения теплицевых. матриц (см., напр., [3]) вычисление проводится по рекуррентным формулам и также требует операций. Условие невырожденности главных подматриц может быть ослаблено с сохранением порядка О( п ² )необходимой арифметич. работы.

Иногда операцию О. м. используют с тем, чтобы решать линейные системы по формуле В случае матрицы общего вида такой образ действий имеет мало смысла, т. к. сопровождается проигрышем и в арифметич. работе, и в численной устойчивости по-сравнению с прямым решением линейной системы. Для теплицевых (и родственных им) матриц ситуация иная. Как показывает представление (2), вычисление сводится к выполнению четырех умножений, теплицевых матриц на векторы и вычитанию векторов. Существуют экономичные алгоритмы умножения теплицевой матрицы на вектор, требующие (для порядка

Предварительное О. м. может быть оправданным и в случае многократного решения линейных систем с одной и той же матрицей общего вида на ЭВМ с большим; числом параллельно работающих процессоров. Причина в том, что по сравнению с операцией умножения матрицы на вектор прямые методы решения линейных систем не имеют столь же удобного распараллеливания.

где считается отличным от нуля.

С точки зрения теории вычислительной сложности задача О. м. общего вида имеет (на последовательной машине) сложность того же порядка, что и задача решения линейной системы (при выполнении нек-рых естественных условий на скорость роста сложности обеих задаче увеличением их порядка [5]). Эта сложность имеет порядок, не превышающий n^log₂⁷.

С. Д. Икрамов.

Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.

Обращение матриц — функции inv, pinv MatLab

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях.

1023 0

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

• Главная
/
• База знаний
/
• CAD / CAM
/
• MatLab

Урок 11. Матричные операции линейной алгебры
Вычисление нормы и чисел обусловленности матрицы
Определитель и ранг матрицы
Определение нормы вектора
Определение ортонормированного базиса матрицы

Обращение матриц — одна из наиболее распространенных операций матричного анализа. -1=Е/Х. Следующие функции обеспечивают реализацию данной операции:

 inv(X) — возвращает матрицу, обратную квадратной матрице X. Предупреждающее сообщение выдается, если X плохо масштабирована или близка к вырожденной.

» inv(rand(4,4)) 

ans =

2.2631 -2.3495-0.4696-0.6631

-0.76201.2122 1.7041 -1.2146

-2.04081.4228 1.5538 1.3730 

1.3075 -0.0183-2.54830.6344

На практике вычисление явной обратной матрицы не так уж необходимо. Чаще операцию обращения применяют при решении системы линейных уравнений вида Ах=b. Один из путей решения этой системы — вычисление x=inv(A)*b. Но лучшим с точки зрения минимизации времени расчета и повышения точности вычислений является использование оператора матричного деления х=А\b. Эта операция использует метод исключения Гаусса без явного формирования обратной матрицы.

В = pinv(A) — возвращает матрицу, псевдообратную матрице А (псевдообращение матрицы по Муру-Пенроузу). Результатом псевдообращения матрицы по Муру-Пенроузу является матрица В того же размера, что и А’, и удовлетворяющая условиям А*В*А=А и В*А*В=В. Вычисление основано на использовании функции svd(A) и приравнивании к нулю всех сингулярных чисел, меньших величины tol;

В = pinv (A. tol) — возвращает псевдообратную матрицу и отменяет заданный по умолчанию порог, равный max(size(A))*norm(A)*eps.

Пример:

» pinv(rand(4,3))

ans =

-1. 3907-0.0485-0.24931.8640

-0.87751.1636 0.6605 -0.0034 

2.0906 -0.5921-0.2749-0.5987

Нравится

Твитнуть

Теги MatLab САПР

Сюжеты MatLab

Знакомство с матричной лабораторией MATLAB MatLab

8079 0

Визуализация и графические средства MatLab

9572 0

Техническая документация по системе MatLab

6105 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster.ru

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2278 s

Инверсия матриц — библиотека ALGLIB, C++ и C#

Руководство пользователя ALGLIB — Операции с матрицами и разложение — Инверсия матриц

Обратная матрица A ^-1 определяется как решение B по AB = BA = I . Традиционная инверсия определена только для квадратных матриц NxN, а некоторые квадратные матрицы (называемые вырожденными или сингулярными) вообще не имеют обратной. Кроме того, существуют так называемые плохо обусловленные матрицы, которые являются обратимыми, но их обратное значение трудно вычислить численно с достаточной точностью.

В пакете ALGLIB есть процедуры для обращения нескольких различных типов матриц, включая обращение действительных и комплексных матриц, общих и симметричных положительно определенных матриц. ALGLIB также может инвертировать матрицы, заданные их треугольными факторизациями: LU или разложения Холецкого. Все версии ALGLIB (C++, C# или другие версии) предоставляют одинаковый набор функций обращения матриц.

Содержимое

1 Алгоритмы обращения матриц
           Обращение треугольной матрицы
           General matrix inversion (LU-based inversion)
           Positive definite matrix inversion (Cholesky-based inversion)
           Examples
    2 Benchmarks
           Comparison with other free C# libraries
           Comparing C#, C++ and SIMD implementations
    3 Additional notes
           Avoiding explicit calculation of обратная матрица
           Несколько заметок о кеше ЦП и производительности
    4 Раздел загрузок

Треугольные матрицы, такие как верхняя треугольная U и верхняя однотреугольная U ₁ приведены ниже (и, конечно, их нижние треугольные аналоги L и L ₁ ) могут быть достаточно эффективно инвертированы за O(N ³ ) времени. Кроме того, поскольку обратная треугольная матрица также является треугольной, можно выполнить инверсию на месте — без выделения места для временной копии У / л .

Вы можете использовать следующие функции подпакета matinv для инвертирования треугольных матриц:

• rmatrixtrinverse для инвертирования real верхние/нижние треугольные матрицы (с поддержкой унитреугольных матриц)
• cmatrixtrinverse для инвертирования комплекс верхняя/нижняя треугольные матрицы (с поддержкой унитреугольных матриц)

Во всех случаях результат инверсии перезаписывает исходную матрицу. Другой треугольник входной матрицы оставляем без изменений. И если вы скажете ALGLIB, что матрица унитреугольная (т.е. имеет единичную диагональ), тогда диагональные элементы входной матрицы также будут игнорироваться.

Рассмотренная выше треугольная функция обращения матриц может служить основой для более общих алгоритмов обращения матриц. Любую общую вещественную/комплексную матрицу A можно разложить на множители как A=P·L·U , где P — матрица перестановок. (используется для улучшения численной устойчивости всего алгоритма), L — нижняя треугольная, а U — верхняя треугольная матрица (традиционно либо L , либо U нормализуются, чтобы иметь единичную диагональ; соглашение ALGLIB заключается в нормализации л ). Такое представление называется LU-разложением.

Таким образом, любую общую матрицу можно инвертировать с помощью трехэтапного процесса: 1) вычислить ее LU-факторизацию, 2) решить последовательность треугольных задач обращения для вычисления общей (нетреугольной) обратной матрицы, 3) счет матрицы перестановок P .

Вы можете использовать следующие функции подпакета matinv для инвертирования общих матриц:

• rmatrixinverse to инвертировать real матрица
• cmatrixinverse to инвертировать комплекс матрица

Упомянутые выше функции внутренне вычисляют LU-разложение входной матрицы A . Если у вас уже есть эта декомпозиция под рукой, вы можете сэкономить значительное количество времени, повторно используя ее. Следующие функции ALGLIB могут использовать уже рассчитанное разложение LU:

• rmatrixluinverse для инвертирования реальной матрицы, заданной ее факторизацией LU
• cmatrixluinverse для инвертирования сложная матрица , заданная ее факторизацией LU

Во всех случаях обратная матрица перезаписывает исходный ввод. Все подпрограммы проверяют номер условия перед началом инверсии. Если матрица вырождена (один из треугольных множителей имеет нулевой элемент на диагонали) или плохо обусловленный (номер состояния настолько высок, что существует риск переполнения во время инверсии) затем подпрограмма возвращает код ошибки -3 и нулевую матрицу.

Симметричный положительно определенный (для сложного случая: Эрмитова положительно определенная) матрица конечно, можно инвертировать с помощью того же алгоритма общего назначения на основе LU. Однако для таких матриц существует лучшая альтернатива — факторизация Холецкого, что представляет собой матрицу SPD A как A = L·L ^T с нижним треугольником L (или, что то же самое, A = U ^T ·U ), с верхним треугольником U ).

Инверсия матрицы на основе Холецкого имеет несколько преимуществ по сравнению с инверсией на основе LU. Во-первых, вместо двух множителей ( L и U ) теперь у нас есть только один треугольный множитель для инвертирования. Меньше факторов = меньше работы. Во-вторых, больше нет матрицы перестановки строк P . Перестановки строк необходимы для стабильности разложения LU, но факторизация Холецкого совершенно стабильна даже без них (если ваша матрица строго положительно определена). Эти перестановки значительно увеличивают время выполнения алгоритма по двум причинам: а) они уничтожают кеш ЦП нелокальным доступом к памяти, и б) они ухудшают потенциал параллелизма, добавляя в алгоритм еще одну точку синхронизации.

Вы можете использовать следующие функции подпакета matinv для инвертирования матриц SPD/HPD:

• spdmatrixinverse to инвертировать вещественная симметричная положительно определенная матрица
• hpdmatrixinverse to convert комплексная Эрмитова положительно определенная матрица

Упомянутые выше функции внутренне вычисляют разложение Холецкого входной матрицы A . Если у вас уже есть эта декомпозиция под рукой, вы можете сэкономить значительное количество времени, повторно используя ее. В таких случаях звоните:

• spdmatrixcholeskyinverse для инвертирования матрицы SPD, заданной ее реальной факторизацией Холецкого
• hpdmatrixcholeskyinverse, чтобы инвертировать матрицу HPD, заданную ее комплексной факторизацией Холецкого

Во всех случаях обратная матрица перезаписывает исходный ввод. Все подпрограммы проверяют номер условия перед началом инверсии. Если матрица вырождена (один из треугольных множителей имеет нулевой элемент на диагонали) или плохо обусловленный (номер состояния настолько высок, что существует риск переполнения во время инверсии) затем подпрограмма возвращает код ошибки -3 и нулевую матрицу.

В Справочном руководстве ALGLIB есть несколько примеров обращения матриц (на всех языках программирования, поддерживаемых библиотекой):

• matinv_d_r1 — пример обращения реальной матрицы
• matinv_d_spd1 — пример инверсии вещественной симметричной положительно определенной матрицы
• matinv_d_c1 — пример обращения сложной матрицы
• matinv_d_hpd1 — пример обращения эрмитовой симметричной положительно определенной матрицы

В этом разделе мы сравниваем производительность следующих бесплатных библиотек C#:

• ALGLIB 3. 12.0 для C# (бесплатная версия) — чистая версия C# нашего продукта
• Math.NET Numerics 3.20.0 (серверная часть C#) — хорошо известная бесплатная числовая библиотека, скомпилированная с реализацией C# серверной части линейной алгебры
• Accord 3.8.0 — еще одна бесплатная числовая библиотека, полностью написанная на C#

Как Math.NET, так и ALGLIB для C# могут использовать ядра линейной алгебры с поддержкой SIMD (скажем, Intel MKL в качестве серверной части), поскольку в этом тесте мы оцениваем производительность 100% NET-реализаций. Во-первых, интересно узнать, насколько быстр C#. Во-вторых, в некоторых случаях приходится использовать 100% управляемую реализацию. Таким образом, производительность реализации NET является важным фактором.

Наше первое сравнение включает однопоточную инверсию реальной матрицы 1024×1024. Этот тест был выполнен на процессоре Intel x64 с тактовой частотой 2,3 ГГц под управлением операционной системы Windows.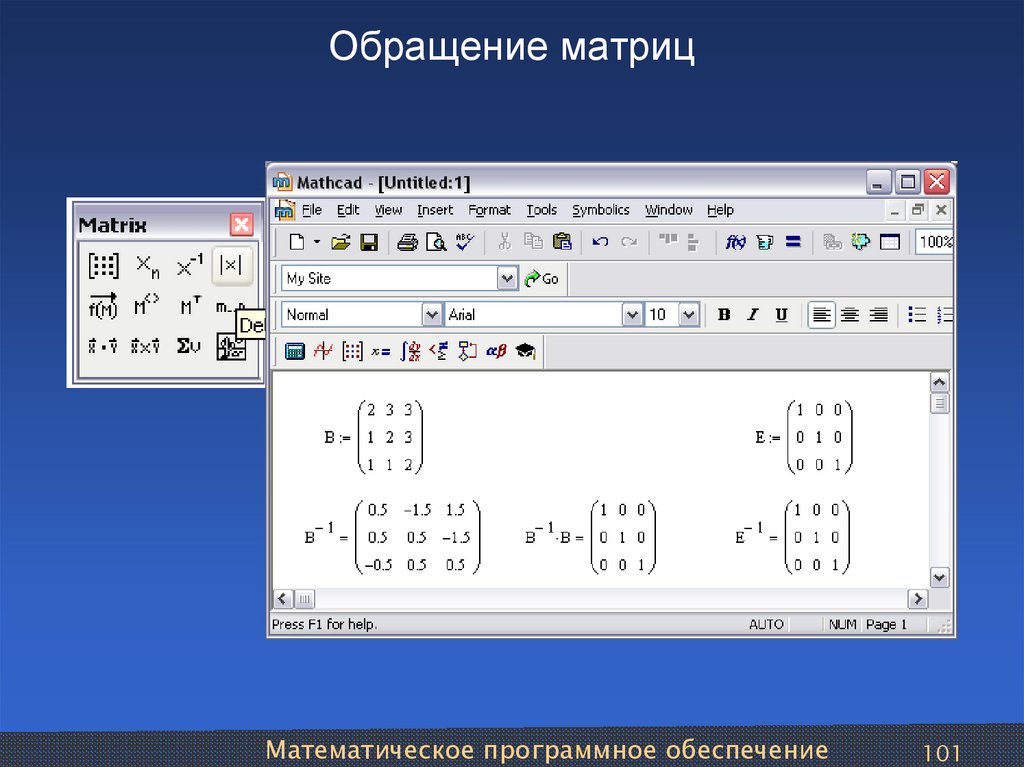 ALGLIB был скомпилирован с помощью компилятора Microsoft C#, для других продуктов мы использовали предварительно скомпилированные сборки NET 4.5.

Вы можете видеть, что ALGLIB показывает наилучшие результаты (по нашему опыту — наилучшие результаты возможны при реализации на чистом C#). Accord.NET в 3 раза медленнее, и (очень странный результат) Math.NET примерно в 20 раз (!) раз медленнее, чем ALGLIB. Мы полагаем, что такая низкая производительность реализации Math.NET Numerics как-то связана с большим размером матрицы. Их код, кажется, оптимизирован для небольших задач.

ALGLIB имеет несколько различных реализаций функций линейной алгебры, все со 100% идентичными API:

• 100% управляемая реализация C# — используется ALGLIB для C#
• универсальная реализация C/C++ , которую можно использовать на платформах без высокопроизводительных ядер с поддержкой SIMD (например, встроенные системы)
• Реализация HPC — высокооптимизированная версия библиотеки, которую можно использовать с C++ и C#, с ассемблерным кодом для компонентов, требующих высокой производительности (включая реализации поставщиков, таких как Intel MKL)

Очевидно, что последняя реализация должна быть самой быстрой 🙂 Но все же очень интересно сравнить производительность разных сред программирования (NET, универсальный C, SIMD-совместимый C). Наше первое сравнение включает однопоточную инверсию реальной матрицы 2048×2048. Этот тест был выполнен на процессоре Intel x64 с тактовой частотой 2,3 ГГц под управлением операционной системы Windows.

Вы можете видеть, что на платформе x64 производительность чистого кода C# примерно в 2 раза ниже, чем у универсального кода C/C++. Наша реализация инверсии матриц на C# максимально оптимизирована, но все же она медленнее, чем общий код C. И, в свою очередь, код с поддержкой SIMD, использующий Intel MKL, во много раз быстрее, чем его общий аналог C.

Во многих случаях можно избежать явного вычисления обратной матрицы. Скажем, если вы хотите решить линейное уравнение A·x=b , вы можете сделать это, вычислив обратную матрицу A ^-1 и путем умножения матрицы на вектор. Но гораздо лучшим подходом является использование функций подпакета плотнорешателя. который может решить линейную систему без явного формирования A ^-1 . Вам все еще нужно выполнить разложение LU/Cholesky, но, по крайней мере, вы можете пропустить фазу обращения матрицы. Другой вариант — использовать функции TRSV/TRSM (треугольный вектор решения/матрица решения) подпакета ablas.

Общее правило таково, что если вам не нужны коэффициенты A ^-1 , а просто его произведение на некоторую матрицу/вектор, обычно существует лучший способ, чем явный расчет A ^-1 .

Наивная реализация алгоритма обращения матрицы включает три вложенных цикла, с внутренним, последовательно обращающимся ко всем элементам в строке/столбце. Однако такая базовая реализация имеет серьезные проблемы с эффективностью при работе с матрицами размером более 64×64 из-за проблем с кэшем ЦП. Производительность алгоритма может составлять всего 10% от общего потенциала ЦП, при этом большая часть времени тратится на промахи кэша.

Лучшим решением является использование блочно-матричного подхода, который разбивает большую матрицу на более мелкие блоки:

Такое разбиение более крупной задачи на несколько более мелких может выполняться многократно несколько раз, пока операнды не поместятся в кэш L1 вашего процессора. Если вы выполняете декомпозицию рекурсивным способом, когда оба операнда имеют одинаковый размер, это называется «подход без учета кеша». И если вы предпочитаете разложить на множители небольшой фрагмент размером 32×32 (или аналогичного размера) в начале/конце задачи, это называется «блочно-матричным подходом». ALGLIB сочетает в себе оба подхода для обеспечения максимально возможной производительности.

Эта статья лицензирована только для личного использования.

Обратная матрица — APL Wiki

Из APL Wiki

(перенаправлено с обратной матрицы) простой числовой массив ранга 2 или ниже. Некоторые диалекты автоматически применяют его к подмассивам ранга 2 аргументов более высокого ранга. Он разделяет глиф Quad Divide 9.0008 ⌹ (часто называемый Domino ) с диадической функцией Matrix Divide.

 ⎕ ←M ←2 2⍴3 4 4 5
3 4
4 5
      ⎕ ←R ←⌹M
¯5 4
 4 ¯3
      Р+.×М
1 0
0 1
      ⌹2 2⍴0
ОШИБКА ДОМЕНА
 ⌹2 2⍴0
 ∧
 

 (⌹2)(⌹2J1)
0,5 0,4Дж¯0,2
      ÷2 2J1
0,5 0,4Дж¯0,2
      (⌹3 1)(⌹2 1 1J2)
┌───────┬────────────────┐
│0,3 0,1│0,2 0,1 0,1J¯0,2│
└───────┴────────────────┘
      {(+⍵)÷⍵+.×+⍵}¨ (3 1) (2 1 1J2)
┌───────┬────────────────┐
│0,3 0,1│0,2 0,1 0,1J¯0,2│
└───────┴────────────────┘
      (⌹3 1)(⌹2 1 1J2) +.

No related posts.