Образуют ли вектора базис | Онлайн калькулятор
Онлайн калькулятор для проверки, образуют ли вектора базис.
Этот онлайн калькулятор позволит вам очень просто проверить образует ли заданный набор векторов базис (проверить линейную независимость векторов).
Линейная независимость векторов
Данный онлайн сервис позволяет определить, могут ли введенные векторы быть базисом. Необходимым и достаточным условием образования базиса является линейная независимость векторов, когда ни один из них не может быть выражен через комбинацию оставшихся. Именно на этом принципе строится решение данной задачи в данном калькуляторе. Имеется удобный интерфейс по вводу векторов, заданных либо по координатам векторов, либо по кординатам точек начала и конца векторов, а также возможность в больших пределах изменять пространство векторов: от 2 до 6.
В n-мерном пространстве, если заданы n базисных векторов, через них могут выражаться любые другие вектора пространства, поэтому правильно выбрать базис очень важно.
«,»className»,»ramka»,»
| A = | ‘,» | «,» | «,» |
«,»m1″,»»,»;»,» maxLength=8 class=mvect>»,»v1″,’
a‘,»
= {‘,» maxLength=8 class=mvect1> x«,» + «,» = «,» maxLength=8 class=mvect1>
| ‘,»showzn»,»m»,» | «,'»/>‘,»
| «,»«,» = «,»clear»,»
| B= | «,» | |
| ‘,» | ||
| «,» |
| X= |
«,»
|
Линейная зависимость и независимость системы векторов калькулятор.
 Что значит «линейная зависимость»
Что значит «линейная зависимость»В аудитории находится тележка с шоколадками, и каждому посетителю сегодня достанется сладкая парочка – аналитическая геометрия с линейной алгеброй. В данной статье будут затронуты сразу два раздела высшей математики, и мы посмотрим, как они уживаются в одной обёртке. Сделай паузу, скушай «Твикс»! …блин, ну и чушь спорол. Хотя ладно, забивать не буду, в конце концов, на учёбу должен быть позитивный настрой.
Линейная зависимость векторов , линейная независимость векторов , базис векторов и др. термины имеют не только геометрическую интерпретацию, но, прежде всего, алгебраический смысл . Само понятие «вектор» с точки зрения линейной алгебры – это далеко не всегда тот «обычный» вектор, который мы можем изобразить на плоскости или в пространстве. За доказательством далеко ходить не нужно, попробуйте нарисовать вектор пятимерного пространства . Или вектор погоды, за которым я только что сходил на Гисметео: – температура и атмосферное давление соответственно.
Нет, я не собираюсь грузить вас теорией, линейными векторными пространствами, задача состоит в том, чтобы понять определения и теоремы. Новые термины (линейная зависимость, независимость, линейная комбинация, базис и т.д.) приложимы ко всем векторам с алгебраической точки зрения , но примеры будут даны геометрические. Таким образом, всё просто, доступно и наглядно. Помимо задач аналитической геометрии мы рассмотрим и некоторые типовые задания алгебры . Для освоения материала желательно ознакомиться с уроками Векторы для чайников и Как вычислить определитель?
Линейная зависимость и независимость векторов плоскости.Базис плоскости и аффинная система координат
Рассмотрим плоскость вашего компьютерного стола (просто стола, тумбочки, пола, потолка, кому что нравится). Задача будет состоять в следующих действиях:
Задача будет состоять в следующих действиях:
1) Выбрать базис плоскости . Грубо говоря, у столешницы есть длина и ширина, поэтому интуитивно понятно, что для построения базиса потребуется два вектора. Одного вектора явно мало, три вектора – лишка.
2) На основе выбранного базиса задать систему координат (координатную сетку), чтобы присвоить координаты всем находящимся на столе предметам.
Не удивляйтесь, сначала объяснения будут на пальцах. Причём, на ваших. Пожалуйста, поместите указательный палец левой руки на край столешницы так, чтобы он смотрел в монитор. Это будет вектор . Теперь поместите
, ну, или наоборот: , где – некоторое число, отличное от нуля.

Картинку сего действа можно посмотреть на уроке Векторы для чайников , где я объяснял правило умножения вектора на число.
Будут ли ваши пальчики задавать базис на плоскости компьютерного стола? Очевидно, что нет. Коллинеарные векторы путешествуют туда-сюда по одному направлению, а у плоскости есть длина и ширина.
Такие векторы называют линейно зависимыми .
Справка: Слова «линейный», «линейно» обозначают тот факт, что в математических уравнениях, выражениях нет квадратов, кубов, других степеней, логарифмов, синусов и т.д. Есть только линейные (1-й степени) выражения и зависимости.
Два вектора плоскости линейно зависимы тогда и только тогда , когда они коллинеарны .
Скрестите пальцы на столе, чтобы между ними был любой угол, кроме 0 или 180 градусов. Два вектора плоскости линейно не зависимы в том и только том случае, если они не коллинеарны . Итак, базис получен. Не нужно смущаться, что базис получился «косым» с неперпендикулярными векторами различной длины. Очень скоро мы увидим, что для его построения пригоден не только угол в 90 градусов, и не только единичные, равные по длине векторы
Очень скоро мы увидим, что для его построения пригоден не только угол в 90 градусов, и не только единичные, равные по длине векторы
Любой вектор плоскости единственным образом раскладывается по базису :
, где – действительные числа . Числа называют координатами вектора в данном базисе.
Также говорят, что вектор
Например, можно сказать, что вектор разложен по ортонормированному базису плоскости , а можно сказать, что он представлен в виде линейной комбинации векторов .
Сформулируем определение базиса формально: Базисом плоскости называется пара линейно независимых (неколлинеарных) векторов , , при этом любой вектор плоскости является линейной комбинацией базисных векторов.
Существенным моментом определения является тот факт, что векторы взяты в определённом порядке . Базисы – это два совершенно разных базиса! Как говорится, мизинец левой руки не переставишь на место мизинца правой руки.
Базисы – это два совершенно разных базиса! Как говорится, мизинец левой руки не переставишь на место мизинца правой руки.
С базисом разобрались, но его недостаточно, чтобы задать координатную сетку и присвоить координаты каждому предмету вашего компьютерного стола. Почему недостаточно? Векторы являются свободными и блуждают по всей плоскости. Так как же присвоить координаты тем маленьким грязным точкам стола, которые остались после бурных выходных? Необходим отправной ориентир. И таким ориентиром является знакомая всем точка – начало координат. Разбираемся с системой координат:
Начну со «школьной» системы. Уже на вступительном уроке Векторы для чайников я выделял некоторые различия между прямоугольной системой координат и ортонормированным базисом . Вот стандартная картина:
Когда говорят о прямоугольной системе координат , то чаще всего имеют в виду начало координат, координатные оси и масштаб по осям. Попробуйте набрать в поисковике «прямоугольная система координат», и вы увидите, что многие источники вам будут рассказывать про знакомые с 5-6-го класса координатные оси и о том, как откладывать точки на плоскости.
С другой стороны, создается впечатление, что прямоугольную систему координат вполне можно определить через ортонормированный базис . И это почти так. Формулировка звучит следующим образом:
началом координат , и ортонормированный базис задают декартову прямоугольную систему координат плоскости . То есть, прямоугольная система координат однозначно определяется единственной точкой и двумя единичными ортогональными векторами . Именно поэтому, вы видите чертёж, который я привёл выше – в геометрических задачах часто (но далеко не всегда) рисуют и векторы, и координатные оси.
Думаю, всем понятно, что с помощью точки (начала координат) и ортонормированного базиса ЛЮБОЙ ТОЧКЕ плоскости и ЛЮБОМУ ВЕКТОРУ плоскости можно присвоить координаты. Образно говоря, «на плоскости всё можно пронумеровать».
Обязаны ли координатные векторы быть единичными? Нет, они могут иметь произвольную ненулевую длину. Рассмотрим точку и два ортогональных вектора произвольной ненулевой длины:
Такой базис называется ортогональным . Начало координат с векторами задают координатную сетку, и любая точка плоскости, любой вектор имеют свои координаты в данном базисе. Например, или . Очевидное неудобство состоит в том, что координатные векторы в общем случае имеют различные длины, отличные от единицы. Если длины равняются единице, то получается привычный ортонормированный базис.
Начало координат с векторами задают координатную сетку, и любая точка плоскости, любой вектор имеют свои координаты в данном базисе. Например, или . Очевидное неудобство состоит в том, что координатные векторы в общем случае имеют различные длины, отличные от единицы. Если длины равняются единице, то получается привычный ортонормированный базис.
! Примечание : в ортогональном базисе, а также ниже в аффинных базисах плоскости и пространства единицы по осям считаются УСЛОВНЫМИ . Например, в одной единице по оси абсцисс содержится 4 см, в одной единице по оси ординат 2 см. Данной информации достаточно, чтобы при необходимости перевести «нестандартные» координаты в «наши обычные сантиметры».
И второй вопрос, на который уже на самом деле дан ответ – обязательно ли угол между базисными векторами должен равняться 90 градусам? Нет! Как гласит определение, базисные векторы должны быть лишь неколлинеарными . Соответственно угол может быть любым, кроме 0 и 180 градусов.
Точка плоскости, которая называется началом координат , и неколлинеарные векторы , , задают аффинную систему координат плоскости :
Иногда такую систему координат называют косоугольной системой. В качестве примеров на чертеже изображены точки и векторы:
Как понимаете, аффинная система координат ещё менее удобна, в ней не работают формулы длин векторов и отрезков, которые мы рассматривали во второй части урока Векторы для чайников , многие вкусные формулы, связанные со скалярным произведением векторов . Зато справедливы правила сложения векторов и умножения вектора на число, формулы деления отрезка в данном отношении , а также ещё некоторые типы задач, которые мы скоро рассмотрим.
А вывод таков, что наиболее удобным частным случаем аффинной системы координат является декартова прямоугольная система. Поэтому её, родную, чаще всего и приходится лицезреть. …Впрочем, всё в этой жизни относительно – существует немало ситуаций, в которых уместна именно косоугольная (или какая-набудь другая, например, полярная ) система координат. Да и гуманоидам такие системы могут прийтись по вкусу =)
Да и гуманоидам такие системы могут прийтись по вкусу =)
Переходим к практической части. Все задачи данного урока справедливы как для прямоугольной системы координат, так и для общего аффинного случая. Сложного здесь ничего нет, весь материал доступен даже школьнику.
Как определить коллинеарность векторов плоскости?Типовая вещь. Для того чтобы два вектора плоскости были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны .По существу, это покоординатная детализация очевидного соотношения .
Пример 1
а) Проверить, коллинеарны ли векторы .
б) Образуют ли базис векторы ?
Решение:
а) Выясним, существует ли для векторов коэффициент пропорциональности , такой, чтобы выполнялись равенства :
Обязательно расскажу о «пижонской» разновидности применения данного правила, которая вполне прокатывает на практике. Идея состоит в том, чтобы сразу составить пропорцию и посмотреть, будет ли она верной:
Составим пропорцию из отношений соответствующих координат векторов:
Сокращаем:
, таким образом, соответствующие координаты пропорциональны, следовательно,
Отношение можно было составить и наоборот, это равноценный вариант:
Для самопроверки можно использовать то обстоятельство, что коллинеарные векторы линейно выражаются друг через друга. В данном случае имеют место равенства . Их справедливость легко проверяется через элементарные действия с векторами:
В данном случае имеют место равенства . Их справедливость легко проверяется через элементарные действия с векторами:
б) Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы). Исследуем на коллинеарность векторы . Составим систему:
Из первого уравнения следует, что , из второго уравнения следует, что , значит, система несовместна (решений нет). Таким образом, соответствующие координаты векторов не пропорциональны.
Вывод : векторы линейно независимы и образуют базис.
Упрощённая версия решения выглядит так:
Составим пропорцию из соответствующих координат векторов :
, значит, данные векторы линейно независимы и образуют базис.
Обычно такой вариант не бракуют рецензенты, но возникает проблема в тех случаях, когда некоторые координаты равны нулю. Вот так: . Или так: . Или так: . Как тут действовать через пропорцию? (действительно, на ноль же делить нельзя). Именно по этой причине я и назвал упрощенное решение «пижонским».
Ответ: а) , б) образуют.
Небольшой творческий пример для самостоятельного решения:
Пример 2
При каком значении параметра векторы будут коллинеарны?
В образце решения параметр найден через пропорцию .
Существует изящный алгебраический способ проверки векторов на коллинеарность., систематизируем наши знания и пятым пунктом как раз добавим его:
Для двух векторов плоскости эквивалентны следующие утверждения :
2) векторы образуют базис;
3) векторы не коллинеарны;
+ 5) определитель, составленный из координат данных векторов, отличен от нуля .
Соответственно, эквивалентны следующие противоположные утверждения :
1) векторы линейно зависимы;
2) векторы не образуют базиса;
3) векторы коллинеарны;
4) векторы можно линейно выразить друг через друга;
+ 5) определитель, составленный из координат данных векторов, равен нулю .
Я очень и очень надеюсь, что на данный момент вам уже понятны все встретившиеся термины и утверждения.
Рассмотрим более подробно новый, пятый пункт: два вектора плоскости коллинеарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю :. Для применения данного признака, естественно, нужно уметь находить определители .
Решим Пример 1 вторым способом:
а)
, значит, данные векторы коллинеарны.
б) Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы). Вычислим определитель, составленный из координат векторов :
, значит, векторы линейно независимы и образуют базис.
Ответ: а) , б) образуют.
Выглядит значительно компактнее и симпатичнее, чем решение с пропорциями.
С помощью рассмотренного материала можно устанавливать не только коллинеарность векторов, но и доказывать параллельность отрезков, прямых. Рассмотрим пару задач с конкретными геометрическими фигурами.
Пример 3
Даны вершины четырёхугольника . Доказать, что четырёхугольник является параллелограммом.
Доказательство : Чертежа в задаче строить не нужно, поскольку решение будет чисто аналитическим. Вспоминаем определение параллелограмма:
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.
Таким образом, необходимо доказать:
1) параллельность противоположных сторон и ;
2) параллельность противоположных сторон и .
Доказываем:
1) Найдём векторы:
Вычислим определитель, составленный из координат векторов :
2) Найдём векторы:
Получился один и тот же вектор («по школьному» – равные векторы). Коллинеарность совсем очевидна, но решение таки лучше оформить с толком, с расстановкой. Вычислим определитель, составленный из координат векторов :
, значит, данные векторы коллинеарны, и .
Вывод : Противоположные стороны четырёхугольника попарно параллельны, значит, он является параллелограммом по определению. Что и требовалось доказать .
Больше фигур хороших и разных:
Пример 4
Даны вершины четырёхугольника . Доказать, что четырёхугольник является трапецией.
Для более строгой формулировки доказательства лучше, конечно, раздобыть определение трапеции, но достаточно и просто вспомнить, как она выглядит.
Это задание для самостоятельного решения. Полное решение в конце урока.
А теперь пора потихонечку перебираться из плоскости в пространство:
Как определить коллинеарность векторов пространства?Правило очень похоже. Для того чтобы два вектора пространства были коллинеарны, необходимо и достаточно , чтобы их соответствующие координаты были пропорциональны .
Пример 5
Выяснить, будут ли коллинеарны следующие векторы пространства:
а) ;
б)
в)
Решение:
а) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов:
Система не имеет решения, значит, векторы не коллинеарны.
«Упрощёнка» оформляется проверкой пропорции . В данном случае:
– соответствующие координаты не пропорциональны, значит, векторы не коллинеарны.
Ответ: векторы не коллинеарны.
б-в) Это пункты для самостоятельного решения. Попробуйте его оформить двумя способами.
Существует метод проверки пространственных векторов на коллинеарность и через определитель третьего порядка, данный способ освещен в статье Векторное произведение векторов .
Аналогично плоскому случаю, рассмотренный инструментарий может применяться в целях исследования параллельности пространственных отрезков и прямых.
Добро пожаловать во второй раздел:
Линейная зависимость и независимость векторов трехмерного пространства.Пространственный базис и аффинная система координат
Многие закономерности, которые мы рассмотрели на плоскости, будут справедливыми и для пространства. Я постарался минимизировать конспект по теории, поскольку львиная доля информации уже разжёвана. Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия.
Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия.
Теперь вместо плоскости компьютерного стола исследуем трёхмерное пространство. Сначала создадим его базис. Кто-то сейчас находится в помещении, кто-то на улице, но в любом случае нам никуда не деться от трёх измерений: ширины, длины и высоты. Поэтому для построения базиса потребуется три пространственных вектора. Одного-двух векторов мало, четвёртый – лишний.
И снова разминаемся на пальцах. Пожалуйста, поднимите руку вверх и растопырьте в разные стороны большой, указательный и средний палец . Это будут векторы , они смотрят в разные стороны, имеют разную длину и имеют разные углы между собой. Поздравляю, базис трёхмерного пространства готов! Кстати, не нужно демонстрировать такое преподавателям, как ни крути пальцами, а от определений никуда не деться =)
Далее зададимся важным вопросом, любые ли три вектора образуют базис трехмерного пространства ? Пожалуйста, плотно прижмите три пальца к столешнице компьютерного стола. Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являются компланарными и, совершенно очевидно, что базиса трёхмерного пространства не создают.
Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являются компланарными и, совершенно очевидно, что базиса трёхмерного пространства не создают.
Следует отметить, что компланарные векторы не обязаны лежать в одной плоскости, они могут находиться в параллельных плоскостях (только не делайте этого с пальцами, так отрывался только Сальвадор Дали =)).
Определение : векторы называются компланарными , если существует плоскость, которой они параллельны. Здесь логично добавить, что если такой плоскости не существует, то и векторы будут не компланарны.
Три компланарных вектора всегда линейно зависимы , то есть линейно выражаются друг через друга. Для простоты снова представим, что они лежат в одной плоскости. Во-первых, векторы мало того, что компланарны, могут быть вдобавок ещё и коллинеарны, тогда любой вектор можно выразить через любой вектор. Во втором случае, если, например, векторы не коллинеарны, то третий вектор выражается через них единственным образом: (а почему – легко догадаться по материалам предыдущего раздела).
Справедливо и обратное утверждение: три некомпланарных вектора всегда линейно независимы , то есть никоим образом не выражаются друг через друга. И, очевидно, только такие векторы могут образовать базис трёхмерного пространства.
Определение : Базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов , взятых в определённом порядке , при этом любой вектор пространства единственным образом раскладывается по данному базису , где – координаты вектора в данном базисе
Напоминаю, также можно сказать, что вектор представлен в виде линейной комбинации базисных векторов.
Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки и любых трёх линейно независимых векторов:
началом координат , и некомпланарные векторы , взятые в определённом порядке , задают аффинную систему координат трёхмерного пространства :
Конечно, координатная сетка «косая» и малоудобная, но, тем не менее, построенная система координат позволяет нам однозначно определить координаты любого вектора и координаты любой точки пространства. Аналогично плоскости, в аффинной системе координат пространства не будут работать некоторые формулы, о которых я уже упоминал.
Аналогично плоскости, в аффинной системе координат пространства не будут работать некоторые формулы, о которых я уже упоминал.
Наиболее привычным и удобным частным случаем аффинной системы координат, как все догадываются, является прямоугольная система координат пространства :
Точка пространства, которая называется началом координат , и ортонормированный базис задают декартову прямоугольную систему координат пространства . Знакомая картинка:
Перед тем, как перейти к практическим заданиям, вновь систематизируем информацию:
Для трёх векторов пространства эквивалентны следующие утверждения :
1) векторы линейно независимы;
2) векторы образуют базис;
3) векторы не компланарны;
4) векторы нельзя линейно выразить друг через друга;
5) определитель, составленный из координат данных векторов, отличен от нуля.
Противоположные высказывания, думаю, понятны.
Линейная зависимость / независимость векторов пространства традиционно проверяется с помощью определителя (пункт 5). Оставшиеся практические задания будут носить ярко выраженный алгебраический характер. Пора повесить на гвоздь геометрическую клюшку и орудовать бейсбольной битой линейной алгебры:
Оставшиеся практические задания будут носить ярко выраженный алгебраический характер. Пора повесить на гвоздь геометрическую клюшку и орудовать бейсбольной битой линейной алгебры:
Три вектора пространства компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю :.
Обращаю внимание на небольшой технический нюанс: координаты векторов можно записывать не только в столбцы, но и в строки (значение определителя от этого не изменится – см. свойства определителей). Но гораздо лучше в столбцы, поскольку это выгоднее для решения некоторых практических задач.
Тем читателям, которые немножко позабыли методы расчета определителей, а может и вообще слабо в них ориентируются, рекомендую один из моих самых старых уроков: Как вычислить определитель?
Пример 6
Проверить, образуют ли базис трёхмерного пространства следующие векторы:
Решение : Фактически всё решение сводится к вычислению определителя.
а) Вычислим определитель, составленный из координат векторов (определитель раскрыт по первой строке):
, значит, векторы линейно независимы (не компланарны) и образуют базис трёхмерного пространства.
Ответ : данные векторы образуют базис
б) Это пункт для самостоятельного решения. Полное решение и ответ в конце урока.
Встречаются и творческие задачи:
Пример 7
При каком значении параметра векторы будут компланарны?
Решение : Векторы компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов равен нулю:
По существу, требуется решить уравнение с определителем. Налетаем на нули как коршуны на тушканчиков – определитель выгоднее всего раскрыть по второй строке и сразу же избавиться от минусов:
Проводим дальнейшие упрощения и сводим дело к простейшему линейному уравнению:
Ответ : при
Здесь легко выполнить проверку, для этого нужно подставить полученное значение в исходный определитель и убедиться, что , раскрыв его заново.
В заключение рассмотрим ещё одну типовую задачу, которая носит больше алгебраический характер и традиционно включается в курс линейной алгебры. Она настолько распространена, что заслуживает отдельного топика:
Доказать, что 3 вектора образуют базис трёхмерного пространстваи найти координаты 4-го вектора в данном базисе
Пример 8
Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе.
Решение : Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора вполне могут образовывать новый базис . И первый этап полностью совпадает с решением Примера 6, необходимо проверить, действительно ли векторы линейно независимы:
Вычислим определитель, составленный из координат векторов :
, значит, векторы линейно независимы и образуют базис трехмерного пространства.
! Важно : координаты векторов обязательно записываем в столбцы определителя, а не в строки. Иначе будет путаница в дальнейшем алгоритме решения. – координаты вектора метод Крамера здесь – совсем не айс;-)
И, как я уже отмечал, задание носит алгебраический характер. Векторы, которые были рассмотрены – это не обязательно те векторы, которые можно нарисовать в пространстве, а, в первую очередь, произвольные векторы курса линейной алгебры . Для случая двумерных векторов можно сформулировать и решить аналогичную задачу – решение будет технически намного проще, и поэтому я прошёл мимо него в предыдущем параграфе.
Такая же задача с трёхмерными векторами для самостоятельного решения:
Пример 9
Даны векторы . Показать, что векторы образуют базис и найти координаты вектора в этом базисе. Систему линейных уравнений решить методом Крамера.
Полное решение и примерный образец чистового оформления в конце урока.
Аналогично можно рассмотреть четырёхмерное, пятимерное и т.д. векторные пространства , где у векторов соответственно 4, 5 и более координат. Для данных векторных пространств тоже существует понятие линейной зависимости, линейной независимости векторов, существует базис, в том числе, ортонормированный, разложение вектора по базису. Да, такие пространства невозможно нарисовать геометрически, но в них работают все правила, свойства и теоремы двух и трех мерных случаев – чистая алгебра.…Хотя, кто его знает, может быть и не чистая…, однако закругляемся – о философских вопросах меня уже пробивало поговорить в статье Частные производные функции трёх переменных , которая появилась раньше данного урока.
Любите векторы, и векторы полюбят вас!
Линейная зависимость и независимость векторов
Определения линейно зависимой и независимой систем векторов
Определение 22
Пусть имеем систему из n-векторови имеем набор чисел , тогда
(11)
называется линейной
комбинацией данной системы векторов
с данным набором коэффициентов.
Определение 23
Система векторовназываетсялинейно зависимой, если существует такой набор коэффициентов, из которых хотя бы один не равен нулю, что линейная комбинация данной системы векторов с этим набором коэффициентов равна нулевому вектору:
Пусть , тогда
Определение 24 (через представление одного вектора системы в виде линейной комбинации остальных)
Система векторов называетсялинейно зависимой, если хотя бы один из векторов этой системы можно представить в виде линейной комбинации остальных векторов этой системы.
Утверждение 3
Определения 23 и 24 эквивалентны.
Определение 25 (через нулевую линейную комбинацию)
Система векторов называетсялинейно независимой, если нулевая линейная комбинация этой системы возможна лишь при всехравных нулю.
Определение 26 (через невозможность представления одного вектора системы в виде линейной комбинации остальных)
Система векторов
называетсялинейно
независимой, если не один из векторов
этой системы нельзя представить в виде
линейной комбинации других векторов
этой системы.
Свойства линейно зависимой и независимой систем векторов
Теорема 2 (нулевой вектор в системе векторов)
Если в системе векторов имеется нулевой вектор, то система линейно зависима.
Пусть, тогда.
Получим , следовательно, по определению линейно зависимой системы векторов через нулевую линейную комбинацию(12) система линейно зависима.
Теорема 3 (зависимая подсистема в системе векторов)
Если в системе векторов имеется линейно зависимая подсистема, то и вся система линейно зависима.
Пусть- линейно зависимая подсистема, среди которых хотя бы одно не равно нулю:
Значит, по определению 23, система линейно зависима.
Теорема 4
Любая подсистема линейно независимой системы линейно независима.
От
противного. Пусть система линейно
независима и в ней имеется линейно
зависимая подсистема. Но тогда по теореме
3 вся система будет также линейно
зависимой. Противоречие. Следовательно,
подсистема линейно независимой системы
не может быть линейно зависимой.
Следовательно,
подсистема линейно независимой системы
не может быть линейно зависимой.
Геометрический смысл линейной зависимости и независимости системы векторов
Теорема 5
Два вектора илинейно зависимы тогда и только тогда, когда.
Необходимость.
и- линейно зависимы, что выполняется условие. Тогда, т.е..
Достаточность.
линейно зависимы.
Следствие 5.1
Нулевой вектор коллинеарен любому вектору
Следствие 5.2
Для того чтобы два вектора были линейно независимы необходимо и достаточно, чтобы был не коллинеарен .
Теорема 6
Для того чтобы система из трёх векторов была линейно зависима необходимо и достаточно, чтобы эти векторы были компланарными.
Необходимость.
Линейно зависимы, следовательно, один вектор можно представить в виде линейной комбинации двух других.
где
и.
По правилу параллелограммаесть диагональ параллелограмма со
сторонами,
но параллелограмм – плоская фигуракомпланарны- тоже компланарны.
Достаточность .
Компланарны. Приложим три вектора к точке О:
– линейно зависимы
Следствие 6.1
Нулевой вектор компланарен любой паре векторов.
Следствие 6.2
Для того чтобы векторы были линейно независимы необходимо и достаточно, чтобы они были не компланарны.
Следствие 6.3
Любой вектор плоскости можно представить в виде линейной комбинации любых двух неколлинеарных векторов этой же плоскости.
Теорема 7
Любые четыре вектора в пространстве линейно зависимы.
Рассмотрим 4 случая:
Проведем плоскость через векторы , затем плоскость через векторы и плоскость через векторы . Затем проведем плоскости, проходящие через точкуD, параллельные парам векторов ; ; соответственно. По линиям пересечения плоскостей строим параллелепипедOB 1 D 1 C 1 ABDC .
Рассмотрим OB 1 D 1 C 1 – параллелограмм по построению по
правилу параллелограмма.
Рассмотрим OADD 1 – параллелограмм (из свойства параллелепипеда), тогда
EMBED Equation.3 .
По теореме 1 такие, что. Тогда, и по определению 24 система векторов линейно зависимая.
Следствие 7.1
Суммой трёх некомпланарных векторов в пространстве является вектор, совпадающий с диагональю параллелепипеда, построенного на этих трёх векторах, приложенных к общему началу, причём начало вектора суммы совпадает с общим началом этих трёх векторов.
Следствие 7.2
Если в пространстве взять 3 некомпланарных вектора, то любой вектор этого пространства можно разложить в линейную комбинацию данных трёх векторов.
Задача 1. Выяснить, является ли система векторов линейно независимой. Систему векторов будем задавать матрицей системы, столбцы которой состоят из координат векторов.
Решение. Пусть линейная комбинация равна нулю. Записав это равенство в координатах, получим следующую систему уравнений:
Такая система уравнений называется треугольной. Она имеет единственное решение . Следовательно, векторы линейно независимы.
Она имеет единственное решение . Следовательно, векторы линейно независимы.
Задача 2. Выяснить, является ли линейно независимой система векторов.
Решение. Векторы линейно независимы (см. задачу 1). Докажем, что вектор является линейной комбинацией векторов . Коэффициенты разложения по векторам определяются из системы уравнений
Эта система, как треугольная, имеет единственное решение.
Следовательно, система векторов линейно зависима.
Замечание . Матрицы, такого вида, как в задаче 1, называются треугольными , а в задаче 2 – ступенчато-треугольными . Вопрос о линейной зависимости системы векторов легко решается, если матрица, составленная из координат этих векторов, является ступенчато треугольной. Если матрица не имеет специального вида, то с помощью элементарных преобразований строк , сохраняющих линейные соотношения между столбцами, её можно привести к ступенчато-треугольному виду.
Элементарными преобразованиями строк матрицы(ЭПС) называются следующие операции над матрицей:
1) перестановка строк;
2) умножение строки на отличное от нуля число;
3) прибавление к строке другой строки, умноженной на произвольное число.
Задача 3. Найти максимальную линейно независимую подсистему и вычислить ранг системы векторов
Решение. Приведем матрицу системы с помощью ЭПС к ступенчато-треугольному виду. Чтобы объяснить порядок действий, строчку с номером преобразуемой матрицы обозначим символом . В столбце после стрелки указаны действия над строками преобразуемой матрицы, которые надо выполнить для получения строк новой матрицы.
Очевидно, что первые два столбца полученной матрицы линейно независимы, третий столбец является их линейной комбинацией, а четвертый не зависит от двух первых. Векторы называются базисными. Они образуют максимальную линейно независимую подсистему системы , а ранг системы равен трем.
Базис, координаты
Задача 4. Найти базис и координаты векторов в этом базисе на множестве геометрических векторов, координаты которых удовлетворяют условию .
Решение . Множество является плоскостью, проходящей через начало координат. Произвольный базис на плоскости состоит из двух неколлинеарных векторов. Координаты векторов в выбранном базисе определяются решением соответствующей системы линейных уравнений.
Координаты векторов в выбранном базисе определяются решением соответствующей системы линейных уравнений.
Существует и другой способ решения этой задачи, когда найти базис можно по координатам.
Координаты пространства не являются координатами на плоскости , так как они связаны соотношением , то есть не являются независимыми. Независимые переменные и (они называются свободными) однозначно определяют вектор на плоскости и, следовательно, они могут быть выбраны координатами в . Тогда базис состоит из векторов, лежащих в и соответствующих наборам свободных переменных и , то есть .
Задача 5. Найти базис и координаты векторов в этом базисе на множестве всех векторов пространства , у которых нечетные координаты равны между собой.
Решение . Выберем, как и в предыдущей задаче, координаты в пространстве .
Так как , то свободные переменные однозначно определяют вектор из и, следовательно, являются координатами. Соответствующий базис состоит из векторов .
Задача 6. Найти базис и координаты векторов в этом базисе на множестве всех матриц вида , где – произвольные числа.
Решение . Каждая матрица из однозначно представима в виде:
Это соотношение является разложением вектора из по базису с координатами .
Задача 7. Найти размерность и базис линейной оболочки системы векторов
Решение. Преобразуем с помощью ЭПС матрицу из координат векторов системы к ступенчато-треугольному виду.
Столбцы последней матрицы линейно независимы, а столбцы линейно выражаются через них. Следовательно, векторы образуют базис , и .
Замечание . Базис в выбирается неоднозначно. Например, векторы также образуют базис .
Важнейшим понятием в теории линейных пространств является линейная зависимость векторов. Прежде чем определить это понятие, рассмотрим несколько примеров.
Примеры. 1. Дана следующая система трех векторов из пространства Тк:
Легко заметить, что или
2. Возьмем теперь другую систему векторов из
Соотношение, аналогичное равенству (1), для этой системы векторов непосредственно усмотреть затруднительно. Однако нетрудно проверить, что
Однако нетрудно проверить, что
Коэффициенты 4, -7,5 соотношения (2) можно было бы найти следующим образом. Обозначим их через считая неизвестными, будем решать векторное уравнение:
Произведя указанные операции умножения и сложения и переходя к равенству компонент векторов в (2), получаем однородную систему линейных уравнений относительно
Одним из решений этой системы является:
3. Рассмотрим систему векторов:
Равенство
приводит к системе уравнений, имеющей единственное — нулевое — решение. (Проверьте!) Таким образом, из равенства (3) следует,
что Иначе говоря, равенство (3) выполняется только при
Системы векторов в примерах 1-2 являются линейно зависимыми, система примера 3 — линейно независимой.
Определение 3. Система векторов линейного пространства над полем называется линейно зависимой, если существуют не все равные нулю числа поля Я, такие, что
Если же для векторов равенство имеет место только при то система векторов называется линейно независимой.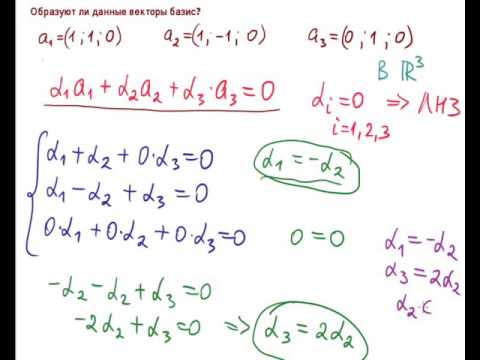
Заметим, что свойство линейной зависимости и независимости является свойством системы векторов. Однако в литературе широко используют те же прилагательные в применении непосредственно к самим векторам и говорят, допуская вольность речи, «система линейно независимых векторов» и даже «векторы линейно независимы».
Если в системе имеется всего один вектор а, то при по свойству 6 (§ 2) из следует Значит, система, состоящая из одного ненулевого вектора, линейно независима. Напротив, любая система векторов содержащая нулевой вектор 0, линейно зависима. Например, если то
Если система двух векторов линейно зависима, то имеет место равенство при (или . Тогда
т. е. векторы пропорциональны. Верно и обратное, так как из следует Значит, система двух векторов линейно зависима тогда и только тогда, когда векторы пропорциональны.
Пропорциональные векторы из лежат на одной прямой; в связи с этим и в общем случае пропорциональные векторы иногда называют коллинеарными.
Отметим некоторые свойства линейной зависимости векторов.
Свойство 1. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.
Пусть линейно зависима подсистема
Тогда существуют не все равные нулю числа такие, что
Добавив в левую часть этого равенства остальные векторы данной системы с нулевыми коэффициентами, получим требуемое.
Из свойства 1 следует, что всякая подсистема линейно независимой системы векторов линейно независима.
Свойство 2. Если система векторов
линейно независима, а система векторов
линейно зависима, то вектор линейно выражается через векторы системы (4).
Так как система векторов (5) линейно зависима, то существуют не все равные нулю числа такие, что
Если то и тогда ненулевые коэффициенты будут среди что означало бы линейную зависимость системы (4). Значит, и
Свойство 3. Упорядоченная система ненулевых векторов
линейно зависима тогда и только тогда, когда некоторый вектор является линейной комбинацией предшествующих векторов.
Пусть система линейно зависима. Так как то вектор линейно независим. Обозначим через наименьшее натуральное число, при котором система линейно зависима. (Такое существует: в крайнем случае, если системы линейно независимы, то Тогда существуют не все равные нулю числа такие, что выполняется равенство
Так как то вектор линейно независим. Обозначим через наименьшее натуральное число, при котором система линейно зависима. (Такое существует: в крайнем случае, если системы линейно независимы, то Тогда существуют не все равные нулю числа такие, что выполняется равенство
Если бы то ненулевые коэффициенты были бы среди и выполнялось бы равенство
что означало бы линейную зависимость системы но это противоречило бы выбору числа Значит, и потому
Обратно, из равенства (7) по свойству 1 следует линейная зависимость системы
Из свойства 3 легко следует, что система векторов тогда и только тогда линейно зависима, когда хотя бы один ее вектор линейно выражается через остальные. В этом смысле и говорят, что понятие линейной зависимости эквивалентно понятию линейной выражаемости.
Свойство 4. Если вектор х линейно выражается через векторы системы
а вектор линейно выражается через остальные векторы системы (8), то вектор также линейно выражается через эти векторы системы (8).
В самом деле,
Теперь можно доказать одну из важнейших теорем о линейной зависимости векторов.
Теорема 1. Если каждый вектор линейно независимой системы
есть линейная комбинация векторов
то Другими словами, в линейно независимой системе векторов, являющихся линейными комбинациями векторов число векторов не может быть больше
Доказательство. 1-й шаг. Построим систему
По условию каждый вектор системы (9), в частности вектор линейно выражается через векторы (10), а потому система (11) линейно зависима. По свойству 3 в системе (11) некоторый вектор где линейно выражается через предшествующие векторы, а потому и через векторы системы
полученной из (11) удалением вектора Отсюда по свойству 4 имеем: каждый вектор системы (9) линейно выражается через векторы системы (12).
2-й шаг. Применяя те же рассуждения, что и на шаге, к системам векторов
и (12) и учитывая, что система векторов линейно независима, мы получим систему векторов
через которые линейно выражаются все векторы системы (9).
Если допустить, что то, продолжая этот процесс, мы через шагов исчерпаем все векторы и получим систему
такую, что каждый вектор системы (9), в частности линейно выражается через векторы системы (14). Тогда система (9) оказывается линейно зависимой, что противоречит условию. Остается принять, что
Рассмотрим теперь, что означает линейная зависимость векторов в различных пространствах.
1. Пространство Если система двух векторов линейно зависима, то или т. е. векторы коллинеарны. Верно и обратное. Система трех векторов пространства линейно зависима тогда и только тогда, когда они лежат в одной плоскости. (Докажите!) Система четырех векторов пространства всегда линейно зависима. В самом деле, если какая-либо подсистема нашей системы линейно зависима, то и вся система линейно зависима. Если же никакая собственная подсистема не является линейно зависимой, то по предыдущему это означает, что никакие три вектора нашей системы не лежат на одной плоскости. Тогда из геометрических соображений следует существование вещественных чисел таких, что параллелепипед с ребрами-векторами будет иметь диагональ т. е. в равенстве
е. в равенстве
Пусть — поле скаляров и F — его основное множество. Пусть — -мерное арифметическое пространство над — произвольная система векторов пространства
ОПРЕДЕЛЕНИЕ. Линейной комбинацией системы векторов называется сумма вида где . Скаляры называются коэффициентами линейной комбинации. Линейная комбинация называется нетривиальной, если хотя бы один ее коэффициент отличен от нуля. Линейная комбинация называется тривиальной, если все ее коэффициенты равны нулю.
ОПРЕДЕЛЕНИЕ. Множество всех линейных комбинаций векторов системы называется линейной оболочкой этой системы и обозначается через . Линейной оболочкой пустой системы считается множество, состоящее из нулевого вектора.
Итак, по определению,
Легко видеть, что линейная оболочка данной системы векторов замкнута относительно операций сложения векторов, вычитания векторов и умножений векторов на скаляры.
ОПРЕДЕЛЕНИЕ. Система векторов называется линейно независимой, если для любых скаляров из равенства следуют равенства . Пустая система векторов
Пустая система векторов
считается линейно независимой.
Другими словами, конечная система векторов линейно независима в том и только в том случае, когда всякая нетривиальная линейная комбинация векторов системы не равна нулевому вектору.
ОПРЕДЕЛЕНИЕ. Система векторов называется линейно зависимой, если существуют скаляры не все равные нулю, такие, что
Другими словами, конечная система векторов называется линейно зависимой, если существует нетривиальная линейная комбинация векторов системы, равная нулевому вектору.
Система векторов
называется системой единичных векторов векторного пространства Эта система векторов линейно независима. В самом деле, для любых скаляров из равенства следует равенство и, значит, равенства
Рассмотрим свойства линейной зависимости и независимости системы векторов.
СВОЙСТВО 1.1. Система векторов, содержащая нуле вой вектор, линейно зависима.
Доказательство. Если в системе векторов один из векторов, например вектор нулевой, то линейная комбинация векторов системы, все коэффициенты которой нулевые, за исключением коэффициента при равна нулевому вектору. Следовательно, такая система векторов линейно зависима.
Следовательно, такая система векторов линейно зависима.
СВОЙСТВО 1.2. Система векторов линейно зависима, если какая-нибудь ее подсистема линейно зависима.
Доказательство. Пусть — линейно зависимая подсистема системы причем хотя бы один из коэффициентов отличен от нуля. Тогда Следовательно, система векторов линейно зависима.
СЛЕДСТВИЕ. Любая подсистема линейно независимой системы линейно независима.
СВОЙСТВО 1.3. Система векторов
в которой линейно зависима тогда и только тогда, когда хотя бы один из векторов является линейной комбинацией предшествующих векторов.
Доказательство. Пусть система (1) линейно зависима и Тогда существуют скаляры не все равные нулю, такие, что
Обозначим через k наибольшее из чисел удовлетворяющее условию Тогда равенство (2) можно записать в виде
Отметим, что ибо в противном случае следовательно, поскольку . Из (3) следует равенство
Предположим теперь, что вектор есть линейная комбинация предшествующих ему векторов, т. е. Тогда , т. е. подсистема системы (1) линейно зависима. Следовательно, по свойству 1.2, линейно зависима и исходная система (1).
е. Тогда , т. е. подсистема системы (1) линейно зависима. Следовательно, по свойству 1.2, линейно зависима и исходная система (1).
СВОЙСТВО 1.4. Если система векторов линейно независима, а система векторов
линейно зависима, то вектор v линейно выражается через векторы
и притом единственным образом.
Доказательство. По условию система (2) линейно зависима, т. е. существуют скаляры не все равные нулю, такие, что
При этом так как при что противоречит линейной независимости системы (1). Из (3) следует равенство
В силу линейной независимости системы (1) отсюда следует, что
СВОЙСТВО 1.5. Если и
Доказательство. Условие означает что найдутся такие скаляры что
Условие означает, что существуют такие скаляры что
В силу (1) и (2) получаем
ТЕОРЕМА 1.2. Если
то система векторов линейно зависима. Доказательство (проводится индукцией по ).
Найти разложение вектора онлайн. Базис. Разложение вектора по векторам. Разложение вектора по базису
В векторном исчислении и его приложениях большое значение имеет задача разложения, состоящая в представлении данного вектора в виде суммы нескольких векторов, называемых составляющими данного
вектора. Эта задача, имеющая в общем случае бесчисленное множество решений, становится вполне определенной, если задать некоторые элементы составляющих векторов.
Эта задача, имеющая в общем случае бесчисленное множество решений, становится вполне определенной, если задать некоторые элементы составляющих векторов.
2. Примеры разложения.
Рассмотрим несколько весьма часто встречающихся случаев разложения.
1. Разложить данный вектор с на два составляющих вектора из которых один, например а, задан по величине и направлению.
Задача сводится к определению разности двух векторов. Действительно, если векторы являются составляющими вектора с, то должно выполняться равенство
Отсюда определяется второй составляющий вектор
2. Разложить данный вектор с на два составляющих, из которых один должен лежать в заданной плоскости а второй должен лежать на заданной прямой а.
Для определения составляющих векторов перенесем вектор с так, чтобы его начало совпало с точкой пересечения заданной прямой с плоскостью (точка О — см. рис. 18). Из конца вектора с (точка С) проведем прямую до
пересечения с плоскостью {В — точка пересечения), а затем из точки С проведем прямую параллельно
Векторы и будут искомыми, т. е. Естественно, что указанное разложение возможно, если прямая а и плоскость не параллельны.
е. Естественно, что указанное разложение возможно, если прямая а и плоскость не параллельны.
3. Даны три компланарных вектора а, b и с, причем векторы не коллинеарны. Требуется разложить вектор с по векторам
Приведем все три заданных вектора к одной точке О. Тогда в силу их компланарности они расположатся в одной плоскости. На данном векторе с как на диагонали построим параллелограмм, стороны которого параллельны линиям действия векторов (рис. 19). Это построение всегда возможно (если только векторы не коллинеарны) и единственно. Из рис. 19 видно, что
В аудитории находится тележка с шоколадками, и каждому посетителю сегодня достанется сладкая парочка – аналитическая геометрия с линейной алгеброй. В данной статье будут затронуты сразу два раздела высшей математики, и мы посмотрим, как они уживаются в одной обёртке. Сделай паузу, скушай «Твикс»! …блин, ну и чушь спорол. Хотя ладно, забивать не буду, в конце концов, на учёбу должен быть позитивный настрой.
Линейная зависимость векторов , линейная независимость векторов , базис векторов и др. термины имеют не только геометрическую интерпретацию, но, прежде всего, алгебраический смысл . Само понятие «вектор» с точки зрения линейной алгебры – это далеко не всегда тот «обычный» вектор, который мы можем изобразить на плоскости или в пространстве. За доказательством далеко ходить не нужно, попробуйте нарисовать вектор пятимерного пространства . Или вектор погоды, за которым я только что сходил на Гисметео: – температура и атмосферное давление соответственно. Пример, конечно, некорректен с точки зрения свойств векторного пространства, но, тем не менее, никто не запрещает формализовать данные параметры вектором. Дыхание осени….
термины имеют не только геометрическую интерпретацию, но, прежде всего, алгебраический смысл . Само понятие «вектор» с точки зрения линейной алгебры – это далеко не всегда тот «обычный» вектор, который мы можем изобразить на плоскости или в пространстве. За доказательством далеко ходить не нужно, попробуйте нарисовать вектор пятимерного пространства . Или вектор погоды, за которым я только что сходил на Гисметео: – температура и атмосферное давление соответственно. Пример, конечно, некорректен с точки зрения свойств векторного пространства, но, тем не менее, никто не запрещает формализовать данные параметры вектором. Дыхание осени….
Нет, я не собираюсь грузить вас теорией, линейными векторными пространствами, задача состоит в том, чтобы понять определения и теоремы. Новые термины (линейная зависимость, независимость, линейная комбинация, базис и т.д.) приложимы ко всем векторам с алгебраической точки зрения , но примеры будут даны геометрические. Таким образом, всё просто, доступно и наглядно. Помимо задач аналитической геометрии мы рассмотрим и некоторые типовые задания алгебры . Для освоения материала желательно ознакомиться с уроками Векторы для чайников и Как вычислить определитель?
Помимо задач аналитической геометрии мы рассмотрим и некоторые типовые задания алгебры . Для освоения материала желательно ознакомиться с уроками Векторы для чайников и Как вычислить определитель?
Базис плоскости и аффинная система координат
Рассмотрим плоскость вашего компьютерного стола (просто стола, тумбочки, пола, потолка, кому что нравится). Задача будет состоять в следующих действиях:
1) Выбрать базис плоскости . Грубо говоря, у столешницы есть длина и ширина, поэтому интуитивно понятно, что для построения базиса потребуется два вектора. Одного вектора явно мало, три вектора – лишка.
2) На основе выбранного базиса задать систему координат (координатную сетку), чтобы присвоить координаты всем находящимся на столе предметам.
Не удивляйтесь, сначала объяснения будут на пальцах. Причём, на ваших. Пожалуйста, поместите указательный палец левой руки на край столешницы так, чтобы он смотрел в монитор. Это будет вектор . Теперь поместите мизинец правой руки на край стола точно так же – чтобы он был направлен на экран монитора. Это будет вектор . Улыбнитесь, вы замечательно выглядите! Что можно сказать о векторах ? Данные векторы коллинеарны , а значит, линейно выражаются друг через друга:
Это будет вектор . Теперь поместите мизинец правой руки на край стола точно так же – чтобы он был направлен на экран монитора. Это будет вектор . Улыбнитесь, вы замечательно выглядите! Что можно сказать о векторах ? Данные векторы коллинеарны , а значит, линейно выражаются друг через друга:
, ну, или наоборот: , где – некоторое число, отличное от нуля.
Картинку сего действа можно посмотреть на уроке Векторы для чайников , где я объяснял правило умножения вектора на число.
Будут ли ваши пальчики задавать базис на плоскости компьютерного стола? Очевидно, что нет. Коллинеарные векторы путешествуют туда-сюда по одному направлению, а у плоскости есть длина и ширина.
Такие векторы называют линейно зависимыми .
Справка: Слова «линейный», «линейно» обозначают тот факт, что в математических уравнениях, выражениях нет квадратов, кубов, других степеней, логарифмов, синусов и т.д. Есть только линейные (1-й степени) выражения и зависимости.
Два вектора плоскости линейно зависимы тогда и только тогда , когда они коллинеарны .
Скрестите пальцы на столе, чтобы между ними был любой угол, кроме 0 или 180 градусов. Два вектора плоскости линейно не зависимы в том и только том случае, если они не коллинеарны . Итак, базис получен. Не нужно смущаться, что базис получился «косым» с неперпендикулярными векторами различной длины. Очень скоро мы увидим, что для его построения пригоден не только угол в 90 градусов, и не только единичные, равные по длине векторы
Любой вектор плоскости единственным образом раскладывается по базису :
, где – действительные числа . Числа называют координатами вектора в данном базисе.
Также говорят, что вектор представлен в виде линейной комбинации базисных векторов . То есть, выражение называют разложением вектора по базису или линейной комбинацией базисных векторов.
Например, можно сказать, что вектор разложен по ортонормированному базису плоскости , а можно сказать, что он представлен в виде линейной комбинации векторов .
Сформулируем определение базиса формально: Базисом плоскости называется пара линейно независимых (неколлинеарных) векторов , , при этом любой вектор плоскости является линейной комбинацией базисных векторов.
Существенным моментом определения является тот факт, что векторы взяты в определённом порядке . Базисы – это два совершенно разных базиса! Как говорится, мизинец левой руки не переставишь на место мизинца правой руки.
С базисом разобрались, но его недостаточно, чтобы задать координатную сетку и присвоить координаты каждому предмету вашего компьютерного стола. Почему недостаточно? Векторы являются свободными и блуждают по всей плоскости. Так как же присвоить координаты тем маленьким грязным точкам стола, которые остались после бурных выходных? Необходим отправной ориентир. И таким ориентиром является знакомая всем точка – начало координат. Разбираемся с системой координат:
Начну со «школьной» системы. Уже на вступительном уроке Векторы для чайников я выделял некоторые различия между прямоугольной системой координат и ортонормированным базисом . Вот стандартная картина:
Вот стандартная картина:
Когда говорят о прямоугольной системе координат , то чаще всего имеют в виду начало координат, координатные оси и масштаб по осям. Попробуйте набрать в поисковике «прямоугольная система координат», и вы увидите, что многие источники вам будут рассказывать про знакомые с 5-6-го класса координатные оси и о том, как откладывать точки на плоскости.
С другой стороны, создается впечатление, что прямоугольную систему координат вполне можно определить через ортонормированный базис . И это почти так. Формулировка звучит следующим образом:
началом координат , и ортонормированный базис задают декартову прямоугольную систему координат плоскости . То есть, прямоугольная система координат однозначно определяется единственной точкой и двумя единичными ортогональными векторами . Именно поэтому, вы видите чертёж, который я привёл выше – в геометрических задачах часто (но далеко не всегда) рисуют и векторы, и координатные оси.
Думаю, всем понятно, что с помощью точки (начала координат) и ортонормированного базиса ЛЮБОЙ ТОЧКЕ плоскости и ЛЮБОМУ ВЕКТОРУ плоскости можно присвоить координаты. Образно говоря, «на плоскости всё можно пронумеровать».
Обязаны ли координатные векторы быть единичными? Нет, они могут иметь произвольную ненулевую длину. Рассмотрим точку и два ортогональных вектора произвольной ненулевой длины:
Такой базис называется ортогональным . Начало координат с векторами задают координатную сетку, и любая точка плоскости, любой вектор имеют свои координаты в данном базисе. Например, или . Очевидное неудобство состоит в том, что координатные векторы в общем случае имеют различные длины, отличные от единицы. Если длины равняются единице, то получается привычный ортонормированный базис.
! Примечание : в ортогональном базисе, а также ниже в аффинных базисах плоскости и пространства единицы по осям считаются УСЛОВНЫМИ . Например, в одной единице по оси абсцисс содержится 4 см, в одной единице по оси ординат 2 см. Данной информации достаточно, чтобы при необходимости перевести «нестандартные» координаты в «наши обычные сантиметры».
Данной информации достаточно, чтобы при необходимости перевести «нестандартные» координаты в «наши обычные сантиметры».
И второй вопрос, на который уже на самом деле дан ответ – обязательно ли угол между базисными векторами должен равняться 90 градусам? Нет! Как гласит определение, базисные векторы должны быть лишь неколлинеарными . Соответственно угол может быть любым, кроме 0 и 180 градусов.
Точка плоскости, которая называется началом координат , и неколлинеарные векторы , , задают аффинную систему координат плоскости :
Иногда такую систему координат называют косоугольной системой. В качестве примеров на чертеже изображены точки и векторы:
Как понимаете, аффинная система координат ещё менее удобна, в ней не работают формулы длин векторов и отрезков, которые мы рассматривали во второй части урока Векторы для чайников , многие вкусные формулы, связанные со скалярным произведением векторов . Зато справедливы правила сложения векторов и умножения вектора на число, формулы деления отрезка в данном отношении , а также ещё некоторые типы задач, которые мы скоро рассмотрим.
Зато справедливы правила сложения векторов и умножения вектора на число, формулы деления отрезка в данном отношении , а также ещё некоторые типы задач, которые мы скоро рассмотрим.
А вывод таков, что наиболее удобным частным случаем аффинной системы координат является декартова прямоугольная система. Поэтому её, родную, чаще всего и приходится лицезреть. …Впрочем, всё в этой жизни относительно – существует немало ситуаций, в которых уместна именно косоугольная (или какая-набудь другая, например, полярная ) система координат. Да и гуманоидам такие системы могут прийтись по вкусу =)
Переходим к практической части. Все задачи данного урока справедливы как для прямоугольной системы координат, так и для общего аффинного случая. Сложного здесь ничего нет, весь материал доступен даже школьнику.
Как определить коллинеарность векторов плоскости?Типовая вещь. Для того чтобы два вектора плоскости были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны . По существу, это покоординатная детализация очевидного соотношения .
По существу, это покоординатная детализация очевидного соотношения .
Пример 1
а) Проверить, коллинеарны ли векторы .
б) Образуют ли базис векторы ?
Решение:
а) Выясним, существует ли для векторов коэффициент пропорциональности , такой, чтобы выполнялись равенства :
Обязательно расскажу о «пижонской» разновидности применения данного правила, которая вполне прокатывает на практике. Идея состоит в том, чтобы сразу составить пропорцию и посмотреть, будет ли она верной:
Составим пропорцию из отношений соответствующих координат векторов:
Сокращаем:
, таким образом, соответствующие координаты пропорциональны, следовательно,
Отношение можно было составить и наоборот, это равноценный вариант:
Для самопроверки можно использовать то обстоятельство, что коллинеарные векторы линейно выражаются друг через друга. В данном случае имеют место равенства . Их справедливость легко проверяется через элементарные действия с векторами:
б) Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы). Исследуем на коллинеарность векторы . Составим систему:
Исследуем на коллинеарность векторы . Составим систему:
Из первого уравнения следует, что , из второго уравнения следует, что , значит, система несовместна (решений нет). Таким образом, соответствующие координаты векторов не пропорциональны.
Вывод : векторы линейно независимы и образуют базис.
Упрощённая версия решения выглядит так:
Составим пропорцию из соответствующих координат векторов :
, значит, данные векторы линейно независимы и образуют базис.
Обычно такой вариант не бракуют рецензенты, но возникает проблема в тех случаях, когда некоторые координаты равны нулю. Вот так: . Или так: . Или так: . Как тут действовать через пропорцию? (действительно, на ноль же делить нельзя). Именно по этой причине я и назвал упрощенное решение «пижонским».
Ответ: а) , б) образуют.
Небольшой творческий пример для самостоятельного решения:
Пример 2
При каком значении параметра векторы будут коллинеарны?
В образце решения параметр найден через пропорцию .
Существует изящный алгебраический способ проверки векторов на коллинеарность., систематизируем наши знания и пятым пунктом как раз добавим его:
Для двух векторов плоскости эквивалентны следующие утверждения :
2) векторы образуют базис;
3) векторы не коллинеарны;
+ 5) определитель, составленный из координат данных векторов, отличен от нуля .
Соответственно, эквивалентны следующие противоположные утверждения :
1) векторы линейно зависимы;
2) векторы не образуют базиса;
3) векторы коллинеарны;
4) векторы можно линейно выразить друг через друга;
+ 5) определитель, составленный из координат данных векторов, равен нулю .
Я очень и очень надеюсь, что на данный момент вам уже понятны все встретившиеся термины и утверждения.
Рассмотрим более подробно новый, пятый пункт: два вектора плоскости коллинеарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю :. Для применения данного признака, естественно, нужно уметь находить определители .
Для применения данного признака, естественно, нужно уметь находить определители .
Решим Пример 1 вторым способом:
а) Вычислим определитель, составленный из координат векторов :
, значит, данные векторы коллинеарны.
б) Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы). Вычислим определитель, составленный из координат векторов :
, значит, векторы линейно независимы и образуют базис.
Ответ: а) , б) образуют.
Выглядит значительно компактнее и симпатичнее, чем решение с пропорциями.
С помощью рассмотренного материала можно устанавливать не только коллинеарность векторов, но и доказывать параллельность отрезков, прямых. Рассмотрим пару задач с конкретными геометрическими фигурами.
Пример 3
Даны вершины четырёхугольника . Доказать, что четырёхугольник является параллелограммом.
Доказательство : Чертежа в задаче строить не нужно, поскольку решение будет чисто аналитическим. Вспоминаем определение параллелограмма:
Вспоминаем определение параллелограмма:
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.
Таким образом, необходимо доказать:
1) параллельность противоположных сторон и ;
2) параллельность противоположных сторон и .
Доказываем:
1) Найдём векторы:
2) Найдём векторы:
Получился один и тот же вектор («по школьному» – равные векторы). Коллинеарность совсем очевидна, но решение таки лучше оформить с толком, с расстановкой. Вычислим определитель, составленный из координат векторов :
, значит, данные векторы коллинеарны, и .
Вывод : Противоположные стороны четырёхугольника попарно параллельны, значит, он является параллелограммом по определению. Что и требовалось доказать .
Больше фигур хороших и разных:
Пример 4
Даны вершины четырёхугольника . Доказать, что четырёхугольник является трапецией.
Для более строгой формулировки доказательства лучше, конечно, раздобыть определение трапеции, но достаточно и просто вспомнить, как она выглядит.
Это задание для самостоятельного решения. Полное решение в конце урока.
А теперь пора потихонечку перебираться из плоскости в пространство:
Как определить коллинеарность векторов пространства?Правило очень похоже. Для того чтобы два вектора пространства были коллинеарны, необходимо и достаточно , чтобы их соответствующие координаты были пропорциональны .
Пример 5
Выяснить, будут ли коллинеарны следующие векторы пространства:
а) ;
б)
в)
Решение:
а) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов:
Система не имеет решения, значит, векторы не коллинеарны.
«Упрощёнка» оформляется проверкой пропорции . В данном случае:
– соответствующие координаты не пропорциональны, значит, векторы не коллинеарны.
Ответ: векторы не коллинеарны.
б-в) Это пункты для самостоятельного решения. Попробуйте его оформить двумя способами.
Существует метод проверки пространственных векторов на коллинеарность и через определитель третьего порядка, данный способ освещен в статье Векторное произведение векторов .
Аналогично плоскому случаю, рассмотренный инструментарий может применяться в целях исследования параллельности пространственных отрезков и прямых.
Добро пожаловать во второй раздел:
Линейная зависимость и независимость векторов трехмерного пространства.Пространственный базис и аффинная система координат
Многие закономерности, которые мы рассмотрели на плоскости, будут справедливыми и для пространства. Я постарался минимизировать конспект по теории, поскольку львиная доля информации уже разжёвана. Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия.
Теперь вместо плоскости компьютерного стола исследуем трёхмерное пространство. Сначала создадим его базис. Кто-то сейчас находится в помещении, кто-то на улице, но в любом случае нам никуда не деться от трёх измерений: ширины, длины и высоты. Поэтому для построения базиса потребуется три пространственных вектора. Одного-двух векторов мало, четвёртый – лишний.
Поэтому для построения базиса потребуется три пространственных вектора. Одного-двух векторов мало, четвёртый – лишний.
И снова разминаемся на пальцах. Пожалуйста, поднимите руку вверх и растопырьте в разные стороны большой, указательный и средний палец . Это будут векторы , они смотрят в разные стороны, имеют разную длину и имеют разные углы между собой. Поздравляю, базис трёхмерного пространства готов! Кстати, не нужно демонстрировать такое преподавателям, как ни крути пальцами, а от определений никуда не деться =)
Далее зададимся важным вопросом, любые ли три вектора образуют базис трехмерного пространства ? Пожалуйста, плотно прижмите три пальца к столешнице компьютерного стола. Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являются компланарными и, совершенно очевидно, что базиса трёхмерного пространства не создают.
Следует отметить, что компланарные векторы не обязаны лежать в одной плоскости, они могут находиться в параллельных плоскостях (только не делайте этого с пальцами, так отрывался только Сальвадор Дали =)).
Определение : векторы называются компланарными , если существует плоскость, которой они параллельны. Здесь логично добавить, что если такой плоскости не существует, то и векторы будут не компланарны.
Три компланарных вектора всегда линейно зависимы , то есть линейно выражаются друг через друга. Для простоты снова представим, что они лежат в одной плоскости. Во-первых, векторы мало того, что компланарны, могут быть вдобавок ещё и коллинеарны, тогда любой вектор можно выразить через любой вектор. Во втором случае, если, например, векторы не коллинеарны, то третий вектор выражается через них единственным образом: (а почему – легко догадаться по материалам предыдущего раздела).
Справедливо и обратное утверждение: три некомпланарных вектора всегда линейно независимы , то есть никоим образом не выражаются друг через друга. И, очевидно, только такие векторы могут образовать базис трёхмерного пространства.
Определение : Базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов , взятых в определённом порядке , при этом любой вектор пространства единственным образом раскладывается по данному базису , где – координаты вектора в данном базисе
Напоминаю, также можно сказать, что вектор представлен в виде линейной комбинации базисных векторов.
Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки и любых трёх линейно независимых векторов:
началом координат , и некомпланарные векторы , взятые в определённом порядке , задают аффинную систему координат трёхмерного пространства :
Конечно, координатная сетка «косая» и малоудобная, но, тем не менее, построенная система координат позволяет нам однозначно определить координаты любого вектора и координаты любой точки пространства. Аналогично плоскости, в аффинной системе координат пространства не будут работать некоторые формулы, о которых я уже упоминал.
Наиболее привычным и удобным частным случаем аффинной системы координат, как все догадываются, является прямоугольная система координат пространства :
Точка пространства, которая называется началом координат , и ортонормированный базис задают декартову прямоугольную систему координат пространства . Знакомая картинка:
Знакомая картинка:
Перед тем, как перейти к практическим заданиям, вновь систематизируем информацию:
Для трёх векторов пространства эквивалентны следующие утверждения :
1) векторы линейно независимы;
2) векторы образуют базис;
3) векторы не компланарны;
4) векторы нельзя линейно выразить друг через друга;
5) определитель, составленный из координат данных векторов, отличен от нуля.
Противоположные высказывания, думаю, понятны.
Линейная зависимость / независимость векторов пространства традиционно проверяется с помощью определителя (пункт 5). Оставшиеся практические задания будут носить ярко выраженный алгебраический характер. Пора повесить на гвоздь геометрическую клюшку и орудовать бейсбольной битой линейной алгебры:
Три вектора пространства компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю :.
Обращаю внимание на небольшой технический нюанс: координаты векторов можно записывать не только в столбцы, но и в строки (значение определителя от этого не изменится – см. свойства определителей). Но гораздо лучше в столбцы, поскольку это выгоднее для решения некоторых практических задач.
свойства определителей). Но гораздо лучше в столбцы, поскольку это выгоднее для решения некоторых практических задач.
Тем читателям, которые немножко позабыли методы расчета определителей, а может и вообще слабо в них ориентируются, рекомендую один из моих самых старых уроков: Как вычислить определитель?
Пример 6
Проверить, образуют ли базис трёхмерного пространства следующие векторы:
Решение : Фактически всё решение сводится к вычислению определителя.
а) Вычислим определитель, составленный из координат векторов (определитель раскрыт по первой строке):
, значит, векторы линейно независимы (не компланарны) и образуют базис трёхмерного пространства.
Ответ : данные векторы образуют базис
б) Это пункт для самостоятельного решения. Полное решение и ответ в конце урока.
Встречаются и творческие задачи:
Пример 7
При каком значении параметра векторы будут компланарны?
Решение : Векторы компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов равен нулю:
По существу, требуется решить уравнение с определителем. Налетаем на нули как коршуны на тушканчиков – определитель выгоднее всего раскрыть по второй строке и сразу же избавиться от минусов:
Налетаем на нули как коршуны на тушканчиков – определитель выгоднее всего раскрыть по второй строке и сразу же избавиться от минусов:
Проводим дальнейшие упрощения и сводим дело к простейшему линейному уравнению:
Ответ : при
Здесь легко выполнить проверку, для этого нужно подставить полученное значение в исходный определитель и убедиться, что , раскрыв его заново.
В заключение рассмотрим ещё одну типовую задачу, которая носит больше алгебраический характер и традиционно включается в курс линейной алгебры. Она настолько распространена, что заслуживает отдельного топика:
Доказать, что 3 вектора образуют базис трёхмерного пространстваи найти координаты 4-го вектора в данном базисе
Пример 8
Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе.
Решение : Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора вполне могут образовывать новый базис . И первый этап полностью совпадает с решением Примера 6, необходимо проверить, действительно ли векторы линейно независимы:
Какой это базис – нас не интересует. А интересует следующая вещь: три вектора вполне могут образовывать новый базис . И первый этап полностью совпадает с решением Примера 6, необходимо проверить, действительно ли векторы линейно независимы:
Вычислим определитель, составленный из координат векторов :
, значит, векторы линейно независимы и образуют базис трехмерного пространства.
! Важно : координаты векторов обязательно записываем в столбцы определителя, а не в строки. Иначе будет путаница в дальнейшем алгоритме решения.
Rn,
(МАТЕМАТИКА В ЭКОНОМИКЕ)
Разложение вектора
Разложение вектора а на составляющие — операция замены вектора а несколькими другими векторами аь а2, а3 и т. д., которые при их сложении образуют начальный вектор а; в этом случае векторы db а2, а3 и т. д. называются составляющими вектора а. Иными словами, разложение любого. ..
..(ФИЗИКА)
Базис и ранг системы векторов
Рассмотрим систему векторов (1.18) Максимально независимой подсистемой системы векторов (1.I8) называется частичный набор векторов этой системы, удовлетворяющий двум условиям: 1) векторы этого набора линейно независимы; 2) любой вектор системы (1.18) линейно выражается через векторы этого набора….(МАТЕМАТИКА В ЭКОНОМИКЕ)
Представление вектора в разных системах координат.
Рассмотрим две ортогональные прямолинейные координатные системы с наборами ортов (i, j, к) и (i j», k») и представим в них вектор a . Условно примем, что орты со штрихами отвечают новой системе координат, а без штрихов — старой. Представим вектор в виде разложения по осям как старой, так и новой систем…Разложение вектора в ортогональном базисе
Рассмотрим базис пространства Rn, в котором каждый вектор ортогонален остальным векторам базиса: Ортогональные базисы известны и хорошо представимы на плоскости и в пространстве (рис. 1.6). Базисы такого вида удобны прежде всего тем, что координаты разложения произвольного вектора определяются…
1.6). Базисы такого вида удобны прежде всего тем, что координаты разложения произвольного вектора определяются…(МАТЕМАТИКА В ЭКОНОМИКЕ)
Векторы и их представления в координатных системах
Понятие вектора связывается с определенными физическими величинами, которые характеризуются своей интенсивностью (величиной) и направлением в пространстве. Такими величинами являются, например, сила, действующая на материальное тело, скорость определенной точки этого тела, ускорение материальной частицы…(МЕХАНИКА СПЛОШНОЙ СРЕДЫ: ТЕОРИЯ НАПРЯЖЕНИЙ И ОСНОВНЫЕ МОДЕЛИ)
Простейшие аналитические представления произвольной эллиптической функции
Представление эллиптической функции в виде суммы простейших элементов. Пусть / (z) есть эллиптическая функция порядка s с простыми полюсами jjt, $s, лежащими в параллелограме периодов. Обозначая через Bk вычет функции относительно полюса мы имеем, что 2 ?л = 0 (§ 1»п. 3, теорема…(ВВЕДЕНИЕ В ТЕОРИЮ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО)
⇐ ПредыдущаяСтр 2 из 2 Правило очень похоже. Пример 5 Выяснить, будут ли коллинеарны следующие векторы пространства: а) ; Решение: Система не имеет решения, значит, векторы не коллинеарны. «Упрощёнка» оформляется проверкой пропорции . В данном случае: Ответ: векторы не коллинеарны. б-в) Это пункты для самостоятельного решения. Попробуйте его оформить двумя способами. Существует метод проверки пространственных векторов на коллинеарность и через определитель третьего порядка, данный способ освещен в статье Векторное произведение векторов. Аналогично плоскому случаю, рассмотренный инструментарий может применяться в целях исследования параллельности пространственных отрезков и прямых. Добро пожаловать во второй раздел:
Линейная зависимость и независимость векторов трехмерного пространства. Многие закономерности, которые мы рассмотрели на плоскости, будут справедливыми и для пространства. Я постарался минимизировать конспект по теории, поскольку львиная доля информации уже разжёвана. Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия. Теперь вместо плоскости компьютерного стола исследуем трёхмерное пространство. Сначала создадим его базис. Кто-то сейчас находится в помещении, кто-то на улице, но в любом случае нам никуда не деться от трёх измерений: ширины, длины и высоты. Поэтому для построения базиса потребуется три пространственных вектора. Одного-двух векторов мало, четвёртый – лишний. И снова разминаемся на пальцах. Пожалуйста, поднимите руку вверх и растопырьте в разные стороны болՌ鍈젾ѯ쓐縠嬵顒ғ嚷Ұ䙂ельный и средний палец. Далее зададимся важным вопросом, любые ли три вектора образуют базис трехмерного пространства? Пожалуйста, плотно прижмите три пальца к столешнице компьютерного стола. Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являютсякомпланарными и, совершенно очевидно, что базиса трёхмерного пространства не создают. Следует отметить, что компланарные векторы не обязаны лежать в одной плоскости, они могут находиться в параллельных плоскостях (только не делайте этого с пальцами, так отрывался только Сальвадор Дали =)). Определение: три вектора называются компланарными, если существует плоскость, которой они параллельны. Компланарные векторы всегда линейно зависимы, то есть линейно выражаются друг через друга. Для простоты снова представим, что они лежат в одной плоскости. Во-первых, векторы мало того, что компланарны, могут быть вдобавок ещё и коллинеарны, тогда любой вектор можно выразить через любой вектор. Во втором случае, если, например, векторы не коллинеарны, то третий вектор выражается через них единственным образом: (а почему – легко догадаться по материалам предыдущего раздела). Справедливо и обратное утверждение:три некомпланарных вектора всегда линейно независимы, то есть никоим образом не выражаются друг через друга. И, очевидно, только такие векторы могут образовать базис трёхмерного пространства. Определение: Базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов , взятых в определённом порядке, при этом любой вектор пространства единственным образом раскладывается по данному базису , где – координаты вектора в данном базисе Напоминаю, также можно сказать, что вектор представлен в виде линейной комбинации базисных векторов. Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки и любых трёх линейно независимых векторов: Точка пространства, которая называетсяначалом координат, и некомпланарныевекторы , взятые в определённом порядке, задаютаффинную систему координат трёхмерного пространства: Конечно, координатная сетка «косая» и малоудобная, но, тем не менее, построенная система координат позволяет нам однозначно определить координаты любого вектора и координатной любой точки пространства. Аналогично плоскости, в аффинной системе координат пространства не будут работать некоторые формулы, о которых я уже упоминал. Наиболее привычным и удобным частным случаем аффинной системы координат, как все догадываются, является прямоугольная система координат пространства: Точка пространства, которая называетсяначалом координат, иортонормированныйбазис задаютдекартову прямоугольную систему координат пространства. Перед тем, как перейти к практическим заданиям, вновь систематизируем информацию: Для трёх векторов пространства эквиваленты следующие утверждения: Противоположные высказывания, думаю, понятны. Линейная зависимость / независимость векторов пространства традиционно проверяется с помощью определителя (пункт 5). Оставшиеся практические задания будут носить ярко выраженный алгебраический характер. Пора повесить на гвоздь геометрическую клюшку и орудовать бейсбольной битой линейной алгебры: Три вектора пространства компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю: . Обращаю внимание на небольшой технический нюанс: координаты векторов можно записывать не только в столбцы, но и в строки (значение определителя от этого не изменится – см. Тем читателям, которые немножко позабыли методы расчета определителей, а может и вообще слабо в них ориентируются, рекомендую один из моих самых старых уроков: Как вычислить определитель? Пример 6 Проверить, образуют ли базис трёхмерного пространства следующие векторы: а) Решение: Фактически всё решение сводится к вычислению определителя. а) Вычислим определитель, составленный из координат векторов (определитель раскрыт по первой строке): Ответ: данные векторы образуют базис б) Это пункт для самостоятельного решения. Полное решение и ответ в конце урока. Встречаются и творческие задачи: Пример 7 При каком значении параметра векторы будут компланарны? Решение: Векторы компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов равен нулю: По существу, требуется решить уравнение с определителем. Проводим дальнейшие упрощения и сводим дело к простейшему линейному уравнению: Ответ: при Здесь легко выполнить проверку, для этого нужно подставить полученное значение в исходный определитель и убедиться, что , раскрыв его заново. В заключение рассмотрим ещё одну типовую задачу, которая носит больше алгебраический характер и традиционно включается в курс линейной алгебры. Она настолько распространена, что заслуживает отдельного топика: Доказать, что 3 вектора образуют базис трёхмерного пространства Пример 8 Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе. Решение: Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Вычислим определитель, составленный из координат векторов : ! Важно: координаты векторов обязательно записываем в столбцыопределителя, а не в строки. Иначе будет путаница в дальнейшем алгоритме решения. Теперь вспомним теоретическую часть: если векторы образуют базис, то любой вектор можно единственным способом разложить по данному базису: , где – координаты вектора в базисе . Поскольку наши векторы образуют базис трёхмерного пространства (это уже доказано), то вектор можно единственным образом разложить по данному базису: По условию и требуется найти координаты . Для удобства объяснения поменяю части местами: . В целях нахождения следует расписать данное равенство покоординатно: По какому принципу расставлены коэффициенты? Все коэффициенты левой части в точности перенесены из определителя , в правую часть записаны координаты вектора . Получилась система трёх линейных уравнений с тремя неизвестными. Обычно её решают по формулам Крамера, часто даже в условии задачи есть такое требование. Главный определитель системы уже найден: Дальнейшее – дело техники: Таким образом: Ответ: Как я уже отмечал, задача носит алгебраический характер. Векторы, которые были рассмотрены – это не обязательно те векторы, которые можно нарисовать в пространстве, а, в первую очередь, абстрактные векторы курса линейной алгебры. Для случая двумерных векторов можно сформулировать и решить аналогичную задачу, решение будет намного проще. Такая же задача с трёхмерными векторами для самостоятельного решения: Пример 9 Даны векторы . Показать, что векторы образуют базис и найти координаты вектора в этом базисе. Систему линейных уравнений решить методом Крамера. Полное решение и примерный образец чистового оформления в конце урока. Аналогично можно рассмотреть четырёхмерное, пятимерное и т.д. векторные пространства, где у векторов соответственно 4, 5 и более координат. Для данных векторных пространств тоже существует понятие линейной зависимости, линейной независимости векторов, существует базис, в том числе, ортонормированный, разложение вектора по базису. Да, такие пространства невозможно нарисовать геометрически, но в них работают все правила, свойства и теоремы двух и трех мерных случаев – чистая алгебра. Собственно, о философских вопросах меня уже пробивало поговорить в статье Частные производные функции трёх переменных, которая появилась раньше данного урока. Пример 2:Решение: составим пропорцию из соответствующих координат векторов: Пример 4:Доказательство:Трапециейназывается четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Пример 5:Решение: Пример 6:Решение: б) Вычислим определитель, составленный из координат векторов (определитель раскрыт по первой строке): Пример 9:Решение:Вычислим определитель, составленный из координат векторов : Ответ:Векторы образуют базис,
⇐ Предыдущая12 ©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов. |
Решение высшей математики онлайн
‹— Назад
Базис и размерность пространства
Так как в линейном пространстве векторы можно складывать и умножать на числа, то из них можно составлять линейные комбинации и можно ввести понятия линейной зависимости и линейной независимости системы векторов так же, как это было сделано в разделе «Линейная зависимость векторов». На случай произвольного линейного пространства определения 10.14 и 10.15 переносятся дословно. Предложения 10.6, 10.7, 10.8 переносятся дословно вместе с доказательствами.
На случай произвольного линейного пространства определения 10.14 и 10.15 переносятся дословно. Предложения 10.6, 10.7, 10.8 переносятся дословно вместе с доказательствами.
На основе линейной зависимости в линейном пространстве вводится определение базиса. Оно почти дословно совпадает с определением 10.16.
Определение 18.2 Базисом линейного пространства называется такая конечная упорядоченная линейно независимая система векторов, что любой вектор пространства является линейной комбинацией этих векторов.
В отличие от трехмерного пространства векторов, в некоторых линейных пространствах базис не существует.
Пример 18.2 Пусть — линейное пространство всех многочленов с веществеными коэффициентами. Покажем, что в этом пространстве базис не существует.
Предположим противное. Пусть векторы образуют в этом пространстве базис.
Каждый вектор пространства — это многочлен. Пусть
Пусть
Из степеней многочленов выберем наибольшую и обозначим ее буквой . Возьмем многочлен . Так как и векторы образуют базис, то , где — вещественные числа. Следовательно, является суммой многочленов степеней меньших, чем , и поэтому его степень должна быть меньше, чем . С другой стороны, по определению, многочлен имеет степень . Получили противоречие. Значит, предположение о существовании базиса неверно.
Теорема 18.1 В линейном пространстве любые два базиса содержат одинаковое число векторов.
Доказательство теоремы мы приводить не будем. Желающие могут найти его в любом учебнике по линейной алгебре, например в [1].
Определение 18.3 Линейное пространство , в котором существует базис, состоящий из векторов, называется -мерным линейным или векторным пространством. Число называется размерностью пространства и обозначается . Линейное пространство, в котором не существует базис, называется бесконечномерным.
Число называется размерностью пространства и обозначается . Линейное пространство, в котором не существует базис, называется бесконечномерным.
Примером бесконечномерного пространства является пространство всех многочленов с вещественными коэффициентами. Как показано в примере 18.2 в этом пространстве базис отсутствует.
Предложение 18.1 Пространство столбцов из элементов, являющихся вещественными числами, имеет рамерность .
Доказательство. Возьмем систему векторов
Покажем, что эта система линейно независима. Составим линейную комбинацию и приравняем ее к нулю:
Преобразуем левую часть:
Следовательно,
откуда , , . Итак, система векторов — линейно независима.
Пусть — произвольный вектор пространства, Очевидно, что
Следовательно, вектор является линейной комбинацией векторов . Тем самым доказано, что векторы образуют базис в пространстве столбцов из элементов. Размерность пространства равна числу векторов в базисе. Следовательно, пространство — -мерное.
Пространство столбцов из элементов, являющихся вещественными числами, обозначается .
Предложение 18.2 Пространство столбцов из элементов, являющихся комплексными числами, имеет размерность .
Доказательство такое же, как и в предыдущем предложении. Это пространство обозначается .
Пример 18.3 Пространство решений однородной системы линейных уравнений имеет базис из решений, где — число неизвестных, а — ранг матрицы . Этим базисом служит фундаментальная система решений (см. определение 15.5 и теорему 15.3).
Этим базисом служит фундаментальная система решений (см. определение 15.5 и теорему 15.3).
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Линейная комбинация векторов — определение с примерами
Содержание:
- Линейная комбинация векторов
- Зависимость векторов
Линейной комбинацией векторов с действительными коэффициентами называют вектор
Коллинеарными называют два вектора линейная комбинация которых с некоторыми действительными числами принимает вид , причем не равны одновременно нулю. Геометрический смысл: векторы параллельны одной прямой.
Геометрический смысл: векторы параллельны одной прямой.
Компланарными называют три вектора линейная комбинация которых с некоторыми действительными числами
принимает вид причем не равны одновременно нулю. Геометрический смысл: векторы параллельны одной плоскости.
Линейно независимыми векторами на плоскости называются два вектора, если они не коллинеарные, а в трехмерном пространстве — три вектора, если они не компланарные.
Два или три ортогональных (перпендикулярных) вектора являются линейно независимыми и образуют двойку или тройку линейно независимых векторов.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Если три единичных взаимно перпендикулярных вектора образуют правую тройку векторов, то эти векторы являются базой прямоугольной декартовой системы координат (рис.
1.6). Такие векторы называются ортами координат.
Система координат называется правой потому, что векторы имеют такую же ориентацию, как соответственно большой, указательный и средний пальцы правой руки. Для определения правого направления системы координат может быть использовано правило правого винта: если винт вкручивается в ось Oz со стороны нуля, то отвертка вращается от
Вектор в прямоугольной декартовой системе координат записывается в виде где — прямоугольные декартовы координаты вектора или проекции этого вектора на соответствующие оси.
Линейная комбинация векторов
Пусть дано несколько векторов. например три вектора Тогда всякий вектор, имеющий вид — некоторые скаляры, называется линейной комбинацией векторов а, Ь. с; говорят также, что d линейно выражается через а, Ь, с, т. е. получается из них с помощью линейных действий. Например, такими линейными комбинациями являются и т. д. Заданные векторы называются линейно зависимыми, если какой-либо из этих векторов линейно выражается через остальные; в противном случае эти векторы называются линейно независимыми (между собой).
Возможно вам будут полезны данные страницы:
Линейная зависимость векторов |
Умножение векторов: пример решения |
Найти угол между векторами: пример решения |
Длина вектора по координатам |
Зависимость векторов
Два вектора линейно зависимы тогда и только тогда, если они параллельны друг другу. Действительно, из определения п. 7.4 вытекает, что если Наоборот, если два вектора параллельны, то один из них всегда может растянуть во столько раз, чтобы получить второй (если векторы направлены противоположно друг другу, то коэффициент растяжения отрицательный). Три вектора линейно зависимы тогда и только тогда, когда они параллельны одной плоскости (говорят также: компланарны).
Действительно, пусть ; отнесем все три вектора а, Ь, с к одному началу и проведем через векторы а и b плоскость (Р). Тогда векторы будут лежать в плоскости (Р), а потому и их сумма, т. е. с, лежит в той же плоскости. Значит, и в исходном положении векторы а, Ь, с были параллельны плоскости (Р). Наоборот, пусть дано, что векторы а, Ь, с параллельны одной плоскости; если тогда их отнести к одному началу, то они все будут лежать в одной плоскости (Р). Если то представление с в виде линейной комбинации а и b показано на рис. 7.11; оно называется разложением вектора в плоскости по двум непараллельным векторам. Если же то согласно предыдущему абзацу уже из двух векторов а, b один (например, а) линейно выражается через другой (b), т. е. а выражается через b и с.
Тогда векторы будут лежать в плоскости (Р), а потому и их сумма, т. е. с, лежит в той же плоскости. Значит, и в исходном положении векторы а, Ь, с были параллельны плоскости (Р). Наоборот, пусть дано, что векторы а, Ь, с параллельны одной плоскости; если тогда их отнести к одному началу, то они все будут лежать в одной плоскости (Р). Если то представление с в виде линейной комбинации а и b показано на рис. 7.11; оно называется разложением вектора в плоскости по двум непараллельным векторам. Если же то согласно предыдущему абзацу уже из двух векторов а, b один (например, а) линейно выражается через другой (b), т. е. а выражается через b и с.
Четыре или более векторов всегда линейно зависимы. Действительно, пусть даны четыре вектора a, b, с, d; отнесем их к одному началу. Если после этого векторы а, Ь, с окажутся лежащими в одной плоскости,
то по предыдущему абзацу один из них линейно выражается через остальные и т. д. (как в конце предыдущего абзаца). Пусть теперь а, Ь, с не лежат в одной плоскости (рис. 7.12). Тогда проводим через точку D (конец вектора d) прямую, параллельную вектору с до пересечения с плоскостью векторов а и Ь в точке С; затем через С проводим прямую, параллельную вектору Ь, до пересечения с прямой, на которой лежит вектор а, в точке В. Тогда
7.12). Тогда проводим через точку D (конец вектора d) прямую, параллельную вектору с до пересечения с плоскостью векторов а и Ь в точке С; затем через С проводим прямую, параллельную вектору Ь, до пересечения с прямой, на которой лежит вектор а, в точке В. Тогда
Это представление называется разложением вектора по трем векторам, не параллельным одной плоскости’, оно же называется разложением вектора по трем осям (на рис. 7.12 по осям ). Такое разложение часто применяется в теоретической механике и в других дисциплинах при разложении силы потрем направлениям и т. п. Каждое из слагаемых называется составляющей или, что то же, компонентой вектора d по (вдоль) соответствующей оси. Компонента вдоль каждой оси определяется не только направлением этой оси, но и направлениями остальных осей. Однако от ориентации осей, т. е. от указания на них положительного направления, а также от модулей векторов а, Ь и с компоненты не зависят.
Иногда применяется разложение вектора по оси и не параллельной ей плоскости. Это разложение показано на рис. 7.13.
Это разложение показано на рис. 7.13.
Разложение (7.1) возможно осуществить лишь единственным образом. В самом деле, если бы наряду с (7.1) существовало другое разложение d то. приравнивая правые части, мы получим откуда вытекает линейная зависимость векторов а, Ь, с (почему?). Если дано более четырех векторов, то уже из первых четырех векторов один линейно выражается через все остальные, т. е. векторы линейно зависимы.
Совокупность линейно независимых векторов, по которым производится разложение остальных векторов, называется базисом. Из сказанного выше следует, что в плоскости базисом могут служить любые два непараллельных вектора, а в пространстве — любые три вектора, не параллельных одной плоскости.
Если а, Ь. с —такой базис, то в формуле разложения (7.1) набор чисел однозначно определяется вектором d и, наоборот, однозначно определяет его; эти числа являются координатами вектора d в базисе а, Ь, с (относительно базиса а, Ь, с).
Коротко формулу (7. 1) записывают так: , однако надо помнить, что координаты вектора зависят не только от него самого, но и от выбора базиса. Если все рассматриваемые векторы имеют одинаковую размерность, то координаты — числа, и упорядоченная (т. е. взятая в определенном порядке) тройка чисел называется числовым вектором.
1) записывают так: , однако надо помнить, что координаты вектора зависят не только от него самого, но и от выбора базиса. Если все рассматриваемые векторы имеют одинаковую размерность, то координаты — числа, и упорядоченная (т. е. взятая в определенном порядке) тройка чисел называется числовым вектором.
Знание координат векторов в фиксированном базисе позволяет производить действия над ними по простым правилам:
Векторы на плоскости имеют две координаты, и в приведенных правилах третья координата отсутствует.
База и измерение
Цели
- Понять определение базиса подпространства.
- Поймите основную теорему.
- Рецепты: основа для столбцового пространства, основа для нулевого пространства, основа для спана.
- Рисунок: базис подпространства R2 или R3.
- Теорема : базисная теорема .
- Основные словарные слова: основа , измерение .

Как мы обсуждали в разделе 2.6, подпространство — это то же самое, что и отрезок, за исключением того, что мы не имеем в виду набор остовных векторов. Существует бесконечно много вариантов остовных множеств для ненулевого подпространства; чтобы избежать избыточности, обычно удобнее всего выбирать остовный набор с минимальным числом векторов в нем. Это идея, лежащая в основе понятия базиса.
Определение
Пусть V — подпространство в Rn. Базис V — это набор векторов {v1,v2,…,vm} в V, таких что:
- V=Span{v1,v2,…,vm} и
- множество {v1,v2,…,vm} линейно независимо.
Напомним, что набор векторов является линейно независимым тогда и только тогда, когда при удалении любого вектора из набора отрезок уменьшается (теорема 2.5.12). Другими словами, если {v1,v2,…,vm} является базисом подпространства V, то никакое собственное подмножество {v1,v2,…,vm} не будет охватывать V: это минимальных охватный набор. Любое подпространство допускает базис по этой теореме из раздела 2.6.
Любое подпространство допускает базис по этой теореме из раздела 2.6.
Ненулевое подпространство имеет бесконечно много различных оснований, но все они содержат одинаковое количество векторов.
Мы оставляем в качестве упражнения доказательство того, что любые два основания имеют одинаковое количество векторов; возможно, вы захотите подождать, пока не изучите теорему об обратимой матрице в разделе 3.5.
Определение
Пусть V — подпространство в Rn. Количество векторов в любом базисе V называется размерностью V и пишется dimV.
Пример (основа R2)
Пример (все базы R2)
Пример (Стандартный базис Rn)
Пример
Из предыдущего примера следует, что любой базис Rn содержит n векторов. Пусть v1,v2,…,vn — векторы в Rn, а A — матрица размера n×n со столбцами v1,v2,…,vn.
- Утверждение, что {v1,v2,…,vn} охватывает Rn, означает, что A имеет точку поворота в каждой строке : см.
 эту теорему в разделе 2.3.
эту теорему в разделе 2.3. - Сказать, что {v1,v2,…,vn} линейно независима, означает, что A имеет точку поворота в каждой 9-й точке.0010 столбец : см. это важное примечание в Разделе 2.5.
Поскольку матрица A является квадратной, она имеет точку опоры в каждой строке тогда и только тогда, когда она имеет точку опоры в каждом столбце. В разделе 3.5 мы увидим, что два приведенных выше условия эквивалентны обратимости матрицы A.
Пример
Теперь мы покажем, как найти основания для пространства столбцов матрицы и нулевого пространства матрицы. Чтобы найти основу для данного подпространства, обычно лучше всего сначала переписать подпространство как пространство столбца или нулевое пространство: см. это важное примечание в разделе 2.6.
Основа для пространства столбца
Сначала мы покажем, как вычислить базис для пространства столбцов матрицы.
Теорема
Опорные столбцы матрицы A образуют основу для Col(A).
Доказательство
Это переформулировка теоремы из раздела 2.5.
Вышеупомянутая теорема относится к опорным столбцам в исходной матрице , а не к ее уменьшенной ступенчатой форме строк. Действительно, матрица и ее сокращенная эшелонированная форма строк обычно имеют разные пространства столбцов. Например, в матрице A ниже:
A=120-1-2-345240-2FGRREF—→10-8-701430000FGpivotcolumns=basispivotcolumnsinRREFсводными столбцами являются первые два столбца, поэтому базисом для Col(A) является
.DB1-22C, B2-34CE.
Первые два столбца редуцированной эшелонированной формы строк определенно охватывают другое подпространство, так как
SpanDB100C, B010CE = DBab0CAAAa, binRE = (плоскость xy),
, но Col(A) содержит векторы, последняя координата которых отлична от нуля.
Следствие
Размерность Col(A) — это количество точек опоры A.
Основа пролета
Вычисление основы для диапазона выполняется так же, как вычисление основы для пространства столбца. В самом деле, длина конечного числа векторов v1,v2,…,vm равна пространству столбцов матрицы, а именно матрицы A, столбцами которой являются v1,v2,…,vm:
В самом деле, длина конечного числа векторов v1,v2,…,vm равна пространству столбцов матрицы, а именно матрицы A, столбцами которой являются v1,v2,…,vm:
A=B|||v1v2···vm|||C.
Пример (основа пролета)
Пример (другая основа того же промежутка)
Основа для нулевого пространства
Чтобы вычислить базис нулевого пространства матрицы, нужно найти параметрическую векторную форму решений однородного уравнения Ax=0.
Теорема
Векторы, присоединенные к свободным переменным в параметрической векторной форме набора решений Ax=0, образуют основу Nul(A).
Доказательство теоремы состоит из двух частей. Первая часть заключается в том, что каждое решение лежит в промежутке заданных векторов. Это происходит автоматически: векторы выбираются точно так, чтобы каждое решение представляло собой линейную комбинацию этих векторов. Вторая часть состоит в том, что векторы линейно независимы. Эта часть обсуждалась в этом примере в Разделе 2. 5.
5.
Базис общего подпространства
Как упоминалось в начале этого подраздела, когда задано подпространство, записанное в другой форме, для вычисления базиса обычно лучше всего переписать его как пространство столбца или пустое пространство матрицы.
Пример (базис подпространства)
Напомним, что {v1,v2,…,vn} образует базис для Rn тогда и только тогда, когда матрица A со столбцами v1,v2,…,vn имеет центральную точку в каждой строке и столбце (см. этот пример ). Поскольку A представляет собой матрицу размера n × n, эти два условия эквивалентны: векторы охватывают тогда и только тогда, когда они линейно независимы. Базисная теорема — это абстрактная версия предыдущего утверждения, применимая к любому подпространству.
Основная теорема
Пусть V — подпространство размерности m. Тогда:
- Любые m линейно независимых векторов в V образуют базис для V.
- Любые m векторов, которые охватывают V, образуют основу для V.

Доказательство
Предположим, что B={v1,v2,…,vm} — набор линейно независимых векторов в V. Чтобы показать, что B является базисом для V, мы должны доказать, что V=Span{ v1,v2,…,vm}. Если нет, то существует некоторый вектор vm+1 в V, не содержащийся в Span{v1,v2,…,vm}. По возрастающему критерию размаха в разделе 2.5 множество {v1,v2,…,vm,vm+1} также линейно независимо. Продолжая в том же духе, мы продолжаем выбирать векторы, пока в конце концов не получим линейно независимый остовный набор: скажем, V=Span{v1,v2,…,vm,…,vm+k}. Тогда {v1,v2,…,vm+k} является базисом для V, откуда следует, что dim(V)=m+k>m. Но мы предполагали, что V имеет размерность m, поэтому B уже должна была быть базисом.
Теперь предположим, что B={v1,v2,…,vm} покрывает V. Если B не является линейно независимым, то по этой теореме из раздела 2.5 мы можем удалить некоторое количество векторов из B, не уменьшая его последовательность. После переупорядочения мы можем считать, что мы удалили последние k векторов, не уменьшая диапазон, и что мы не можем удалить больше. Другими словами, если вы уже знаете, что dimV=m, и если у вас есть набор из m векторов B={v1,v2,…,vm} в V, то вам нужно проверить только один из: для того, чтобы B было основой V. Если вы еще не знали, что dimV=m, то вам нужно было бы проверить оба свойства . Другими словами, предположим, что у нас есть набор векторов B={v1,v2,…,vm} в подпространстве V. Тогда, если любые два из следующих утверждений верны, третье также должно быть истинным : Например, если V — плоскость, то любые два неколлинеарных вектора в V образуют базис. Комментарии, исправления или предложения? (Требуется бесплатная учетная запись GitHub) Мы говорили о смене баз со стандартной базы на альтернативную и наоборот. Привет! Я Криста. Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее. Теперь мы хотим поговорить об особом виде базиса, называемом ортонормированным базисом, в котором каждый вектор в базисе равен ???1??? единица длины и ортогонален каждому из других базисных векторов. 92=1???. А если каждый вектор в наборе ???\vec{v}_i??? ортогонален любому другому вектору в наборе ???\vec{v}_j???, то ???\vec{v}_i\cdot \vec{v}_j=0??? для ???i\ne j???. Поймите также, что если набор векторов ортонормирован, это означает, что все векторы в наборе также линейно независимы. Теперь V=Span{v1,v2,…,vm-k}, и {v1,v2,…,vm-k} является базисом для V, поскольку он линейно независим. Отсюда следует, что dimV=m−k
Теперь V=Span{v1,v2,…,vm-k}, и {v1,v2,…,vm-k} является базисом для V, поскольку он линейно независим. Отсюда следует, что dimV=m−k Пример (Два неколлинеарных вектора образуют основу плоскости)
Пример (Нахождение основы путем проверки)
Как найти ортонормированный базис для набора векторов — Krista King Math
Что такое ортонормированный базис?

Как найти ортонормированный базис для набора векторов
Пройти курс
Хотите узнать больше о линейной алгебре? У меня есть пошаговый курс для этого. 🙂
Проверка ортонормированности набора векторов
Пример
Проверка набора векторов ???V=\{\vec{v}_1,\vec{v}_2\}??? является ортонормированным множеством, если ???\vec{v}_1=(0,0,1)??? и ???\vec{v}_2=(0,1,0)???. n???.
n???.
Принимая во внимание тот факт, что стандартные базисные векторы очень легко использовать в качестве базиса, должно быть понятно, что ортонормированные базисы вообще являются хорошими базисами.
Например, чтобы преобразовать вектор из стандартного базиса в альтернативный базис ???B???, обычно мы решаем матричное уравнение вида
Это означает, что мы должны создать расширенную матрицу, поместить ее в rref и из этой rref-матрицы извлечь компоненты ???[\vec{x}]_B???.
Но если мы конкретно конвертируем в ортонормированный базис, это означает, что векторы-столбцы ???v_1???, ???v_2???, ???v_3??? образуют ортонормированный набор векторов. Ортогональная матрица — это квадратная матрица, столбцы которой образуют ортонормированный набор векторов. Если матрица прямоугольная, но ее столбцы по-прежнему образуют ортонормированный набор векторов, то мы называем ее ортонормированной матрицей.
Когда матрица ортогональна, мы знаем, что ее транспонирование такое же, как и обратное. Итак, учитывая ортогональную матрицу ???A???, 9{-1}???
Итак, учитывая ортогональную матрицу ???A???, 9{-1}???
Ортогональные матрицы всегда квадратные (ортонормированная матрица может быть прямоугольной, но если мы называем матрицу ортогональной, мы специально подразумеваем, что это квадратная матрица), поэтому ее обратную можно определить, предполагая, что квадратная матрица обратима.
Использование ортонормированного базиса упрощает многие из изученных нами операций и формул. Здесь, если векторы-столбцы ???v_1???, ???v_2???, ???v_3??? в
образуют ортонормированный набор, тогда матричная задача упрощается до задачи скалярного произведения. В частности, приведенное выше уравнение становится 9{3}???, матричная задача становится нерешаемой без компьютера. Но с ортонормированным набором матричная задача превращается в задачу скалярного произведения, что значительно упрощает вычисления.
Поймите также, что если набор векторов ортонормирован, это означает, что все векторы в наборе также линейно независимы.
Пример
Преобразование ???\vec{x}=(5,6,-1)??? со стандартной базы на альтернативную базу ???B=\{\vec{v_1},\vec{v_2},\vec{v_3}\}???. 92=\frac{1}{4}+\frac24+\frac{1}{4}=1???
Подтвердите, что каждый вектор ортогонален другим.
???\vec{v}_1\cdot\vec{v}_2=\frac{1}{\sqrt2}\left(\frac12\right)+0\left(\frac{\sqrt2}{2 }\right)-\frac{1}{\sqrt2}\left(\frac12\right)=\frac{1}{2\sqrt2}+0-\frac{1}{2\sqrt2}=0?? ?
???\vec{v}_1\cdot\vec{v}_3=\frac{1}{\sqrt2}\left(\frac12\right)+0\left(-\frac{\sqrt2}{ 2}\right)-\frac{1}{\sqrt2}\left(\frac12\right)=\frac{1}{2\sqrt2}+0-\frac{1}{2\sqrt2}=0? ??
???\vec{v}_2\cdot\vec{v}_3=\frac{1}{2}\left(\frac12\right)+\frac{\sqrt2}{2}\left(- \ frac {\ sqrt2} {2} \ right) + \ frac {1} {2} \ left (\ frac12 \ right) = \ frac14- \ frac {2} {4} + \ frac {1} {4} =0???
Каждый из векторов ???\vec{v}_1???, ???\vec{v}_2??? и ???\vec{v}_3??? имеет длину ???1??? и ортогонален другим векторам в наборе, поэтому набор ортонормирован.
Поскольку множество ортонормировано, вектор ???\vec{x}=(5,6,-1)??? можно преобразовать в альтернативную основу ???B??? с точечными произведениями. Другими словами, вместо решения
, что потребовало бы от нас преобразования расширенной матрицы в уменьшенную форму строки-эшелона, мы можем просто взять скалярные произведения, чтобы получить значение ???[\vec{x}]_B???.
???[\vec{x}]_B=\begin{bmatrix}\frac{1}{\sqrt2}(5)+0(6)-\frac{1}{\sqrt2}(-1) \\ \frac12(5)+\frac{\sqrt2}{2}(6)+\frac{1}{2}(-1)\\ \frac12(5)-\frac{\sqrt2}{2} (6)+\frac{1}{2}(-1)\end{bmatrix}???
???[\vec{x}]_B=\begin{bmatrix}\frac{5}{\sqrt2}+0+\frac{1}{\sqrt2}\\ \frac52+3\sqrt2-\ frac{1}{2}\\ \frac52-3\sqrt2-\frac{1}{2}\end{bmatrix}???
???[\vec{x}]_B=\begin{bmatrix}\frac{6}{\sqrt2}\\ 2+3\sqrt2\\ 2-3\sqrt2\end{bmatrix}???
???[\vec{x}]_B=\begin{bmatrix}\frac{6\sqrt2}{2}\\ 2+3\sqrt2\\ 2-3\sqrt2\end{bmatrix}?? ?
???[\vec{x}]_B=\begin{bmatrix}3\sqrt2\\ 2+3\sqrt2\\ 2-3\sqrt2\end{bmatrix}???
Этот результат говорит нам, что ???\vec{x}=(5,6,-1)??? может быть выражено в альтернативной основе ???B??? как
???[\vec{x}]_B=\begin{bmatrix}3\sqrt2\\ 2+3\sqrt2\\ 2-3\sqrt2\end{bmatrix}???
Получите доступ к полному курсу линейной алгебры
Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, линейная алгебра, ортонормированный базис, альтернативный базис, ортонормированный базис для векторного набора, поиск ортонормированного базиса, проверка того, что набор ортонормирован, преобразование в ортонормированный базис
0 лайковКалькулятор линейной независимости — Найдите независимые векторы
Онлайн-калькулятор линейной независимости поможет вам определить линейную независимость и зависимость между векторами. Это очень важная идея в линейной алгебре, которая включает в себя понимание концепции независимости векторов. В этой статье мы разберем, что такое зависимые и независимые переменные, и объясним, как определить, являются ли векторы линейно независимыми?
Что такое линейная зависимость и независимость? В векторных пространствах, если существует нетривиальная линейная комбинация векторов, равная нулю, то набор векторов называется линейно зависимым. Вектор называется линейно независимым, если не существует линейной комбинации.
Вектор называется линейно независимым, если не существует линейной комбинации.
Если уравнение имеет вид \( a_1 * v_1 + a_2 * v_2 + a_3 * v_3 + a_4 * v_4 + … + a_{n – 1} * v_{n – 1} + a_n * v_n = 0 \), то \(v_1, v_2, v_3, v_4, …, v_{n – 1}, v_n \) — линейно независимые векторы.
Здесь ноль (0) — это вектор с во всех координатах выполняется тогда и только тогда, когда \( a_1 + a_2 + a_3 + a_4 + … + a_{n-1} + a_n = 0 \). В противном случае можно сказать, что векторы линейно зависимы.
Единственная комбинация линейных векторов, дающая нулевой вектор, называется тривиальной. Например, v = (2, -1), тогда также возьмем \( e_1 = (1, 0), e_2 = (0, 1) \). Тогда \( 1 * e_2 + (-2) * e_1 + 1 * v = 1 * (0, 1) + (-2) * (1, 0) + 1 * (2, -1) = (0, 1 ) + (-2 ,0) + (2, -1) = (0, 0) \), значит, мы нашли нетривиальную комбинацию векторов, дающую ноль. Следовательно, они линейно зависимы. Кроме того, мы видим, что \( e_1 и e_2 \) без проблемного вектора v являются линейно независимыми векторами.
Однако онлайн-калькулятор Вронскиана поможет вам определить Вронскиан заданного набора функций.
Как проверить линейную зависимость?Для проверки линейной зависимости меняем значения с векторных на матричные. Например, три вектора в двумерном пространстве: \( v (a_1, a_2), w (b_1, b_2), v (c_1, c_2) \), то запишите их координаты в виде одной матрицы, где каждая строка соответствует одной векторов.
&& M = |D|= \left|\begin{array}{ccc}a_1 & a_1 & \\b_1 & b_2\\c_1 & c_2\end{массив}\right| $$
Тогда ранг матрицы равен максимальному числу независимых векторов среди w, v и u.
Чтобы проверить, являются ли векторы линейно независимыми, онлайн-калькулятор линейной независимости может сказать о любом наборе векторов, если они линейно независимы. Если вы хотите проверить это вручную, то следующие примеры помогут вам лучше понять.
Пример 1:
Найдите значения h, для которых векторы линейно зависимы, если векторы \( h_1 = {1, 1, 0}, h_2 = {2, 5, -3}, h_3 = { 1, 2, 7} \) в 3-х измерениях, то найдите они линейно независимые или нет?
Решение:
Векторы A, B, C линейно зависимы, если их определитель равен нулю. т. е. |D|=0
т. е. |D|=0
$$ A = (1, 1, 0), B = (2, 5, −3), C = (1, 2, 7) $$
$$ |D|= \left|\begin{массив}{ccc}1 & 1 & 0\\2 & 5 & -3\\1 & 2 & 7\end{массив}\right| $$
$$|D|= 1 \times \left|\begin{array}{cc}5 & -3\\2 & 7\end{array}\right| – (1) \times \left|\begin{array}{cc}2 & -3\\1 & 7\end{array}\right| + (0) \times \left|\begin{array}{cc}2 & 5\\1 & 2\end{array}\right|$$
$$ |D|= 1 × ((5) × (7) − (−3) × (2)) − (1) × ((2) × (7) − ( − 3) × (1) ) + (0) × ((2) × (2) − (5) × (1)) $$
$$ |D|= 1 × ((35) − (- 6)) − (1) × ((14) − (− 3)) + (0) × ((4) − (5)) $$
$$ |D|=1 × (41) − (1) × (17) + (0 ) × (− 1) $$
$$ |D = (41) − (17) + (0) $$
$$ |D|= 24 $$
$$|D|= 24 ≠ 0 $$
Так как |D|≠ 0, то векторы A, B, C линейно независимы.
Пример 2:
Определите, образуют ли столбцы матрицы линейно независимый набор, когда трехмерные векторы равны \( v_1 = {1, 1, 1}, v_2 = {1, 1, 1}, v_3 = {1, 1, 1} \), затем определите, являются ли векторы линейно независимыми.
Решение:
Если их определитель равен нулю. т. е. |D|=0, затем проверить линейную независимость векторов A, B, C.
$$ A = (1, 1, 1), B = (1, 1, 1), C = (1, 1, 1) $$
$$ |D|= \left|\begin{array}{ccc}1 & 1 & 1\\1 & 1 & 1\\1 & 1 & 1\end{массив}\right| $$
$$ |D|=1×|1111|−(1)×|1111|+(1)×|1111| $$
$$|D|= 1 \times \left|\begin{array}{cc}1 & 1\\1 & 1\end{array}\right| – (1) \times \left|\begin{array}{cc}1 & 1\\1 & 1\end{array}\right| + (1) \times \left|\begin{array}{cc}1 & 1\\1 & 1\end{array}\right|$$
$$ |Д| = 1 × ((1) − (1)) − (1) × ((1) − (1)) + (1) × ((1) − (1)) $$
$$ |D|= 1 × (0) − (1) × (0) + (1) × (0) $$
$$ |D| = (0) − (0) + (0) $$
$$ |D|= 0 $$
Так как |D|= 0, то векторы A, B, C линейно зависимы.
Однако онлайн-калькулятор Якоби позволяет найти определитель набора функций и матрицы Якоби.
Как работает калькулятор линейной независимости?Онлайн-калькулятор линейной зависимости проверяет, являются ли заданные векторы зависимыми или независимыми, выполнив следующие действия:
Ввод:- Сначала выберите количество векторов и координат из выпадающего списка.

- Теперь замените указанные значения или вы можете добавить случайные значения во все поля, нажав кнопку «Создать значения».
- Нажмите кнопку расчета.
- Линейно-независимый калькулятор сначала сообщает, являются ли векторы независимыми или зависимыми.
- Затем линейно-независимый матричный калькулятор находит определитель векторов и предоставляет комплексное решение.
Если определитель векторов A, B, C равен нулю, то векторы линейно зависимы. Кроме того, если определитель векторов не равен нулю, то векторы линейно зависимы.
Как узнать, является ли матрица линейно независимой? Изначально нам нужно привести матрицу в редуцированный эшелонный вид. Если мы получаем единичную матрицу, то данная матрица линейно независима.
Используйте этот онлайн-калькулятор линейной независимости, чтобы определить определитель заданных векторов и проверить, являются ли все векторы независимыми или нет. Если доступных векторов больше, чем измерений, то все векторы линейно зависимы. Несомненно, определение природы вектора является сложной задачей, но этот рекомендуемый калькулятор поможет студентам и преподавателям найти зависимость и независимость векторов.
Артикул:Из источника Википедии: Оценка линейной независимости, Бесконечный случай, Нулевой вектор, Линейная зависимость и независимость двух векторов, Векторы в R2.
Из источника Libre Text: Линейная независимость и вронскиан, определитель соответствующей матрицы, линейные дифференциальные уравнения, аффинная независимость.
Из источника Корнельского университета: Линейная независимость значений G-функций, Альтернативный метод с использованием определителей, Больше векторов, чем размерностей, Естественные базисные векторы, Линейная независимость функций, Пространство линейных зависимостей.
Из источника Lumen Learning: Независимая переменная, Линейная независимость функций, Пространство линейных зависимостей, Аффинная независимость.
Основы математики для науки о данных: основа и изменение основы | by Hadrien Jean
Понимание концепции базиса линейной алгебры, полезной для собственного разложения и SVD
(Изображение автора)В этой статье вы узнаете о концепции базиса, которая представляет собой интересный способ понять методы матричной факторизации как собственное разложение или разложение по сингулярным значениям (SVD).
Базис — это система координат, используемая для описания векторных пространств (наборов векторов). Это ссылка, которую вы используете для связи чисел с геометрическими векторами.
Чтобы считаться базой, набор векторов должен:
- Быть линейно независимым.
- Охватите пространство.
Каждый вектор в пространстве представляет собой уникальную комбинацию базисных векторов. Размерность пространства определяется как размер базисного набора. Например, есть два базисных вектора в ℝ² (соответствует x и по оси Y в декартовой плоскости), или три в ℝ³ .
Размерность пространства определяется как размер базисного набора. Например, есть два базисных вектора в ℝ² (соответствует x и по оси Y в декартовой плоскости), или три в ℝ³ .
Как показано в разделе 7.4 Essential Math for Data Science, если количество векторов в наборе больше, чем размеры пространства, они не могут быть линейно независимыми. Если набор содержит меньше векторов, чем количество измерений, эти векторы не могут охватывать все пространство.
Векторы можно представить в виде стрелок, идущих от начала координат к точке в пространстве. Координаты этой точки можно сохранить в виде списка. Геометрическое представление вектора в декартовой плоскости подразумевает, что мы берем точку отсчета: направления, заданные двумя осями х и у .
Базисные векторы — это векторы, соответствующие этой ссылке. В декартовой плоскости базисные векторы представляют собой ортогональные единичные векторы (длина единицы), обычно обозначаемые как i и j .
Например, на рисунке 1 базисные векторы i и j указывают в направлении оси x и y соответственно. Эти векторы дают стандартный базис. Если вы поместите эти базисные векторы в матрицу, вы получите следующую единичную матрицу (дополнительную информацию о единичных матрицах см. в разделе 6.4.3 в Essential Math for Data Science):
Таким образом, столбцы I ₂ диапазон ℝ² . Таким же образом столбцы I ₃ охватывают ℝ³ и так далее.
Ортогональный базис
Базисные векторы могут быть ортогональными, поскольку ортогональные векторы независимы. Однако обратное не обязательно верно: неортогональные векторы могут быть линейно независимыми и, таким образом, образовывать базис (но не стандартный базис).
Основа вашего векторного пространства очень важна, потому что значения координат, соответствующие векторам, зависят от этой основы. Кстати, вы можете выбрать разные базисные векторы, как, например, на рисунке 2.
Рис. 2. Еще один базис в двумерном пространстве. (Изображение автора)Имейте в виду, что векторные координаты зависят от неявного выбора базисных векторов.
Любой вектор в векторном пространстве можно рассматривать как линейную комбинацию базисных векторов.
Например, возьмем следующий двумерный вектор v :
Рис. 3. Компоненты вектора 𝒗. (Изображение автора) Компоненты вектора v являются проекциями на 9по оси 0010 x и по оси y ( v_x и v_y , как показано на рисунке 3). Вектор v соответствует сумме своих компонент: v = v_x + v_y , и эти компоненты можно получить путем масштабирования базисных векторов: v_x = 2 1 3 v_y = -0,5 j . Таким образом, вектор v , показанный на рис. 3, можно рассматривать как линейную комбинацию двух базисных векторов i и j :
Таким образом, вектор v , показанный на рис. 3, можно рассматривать как линейную комбинацию двух базисных векторов i и j :
Столбцы единичных матриц — не единственный случай линейно независимых вектор-столбцов. Можно найти другие наборы из n векторов, линейно независимых в ℝⁿ .
Например, давайте рассмотрим следующие векторы в ℝ² :
и
Рисунок 4: Другой базис в двумерном пространстве. (Изображение автора)Из приведенного выше определения векторы v и w являются базисом, потому что они линейно независимы (вы не можете получить одно из них из комбинаций других) и охватывают пространство (все пространство можно получить из линейных комбинаций этих векторов).
Важно помнить, что при использовании компонентов векторов (например, v_x и v_y компоненты x и y вектора v ), значения относятся к выбранному вами базису. Если вы используете другую основу, эти значения будут другими.
Если вы используете другую основу, эти значения будут другими.
В главах 09 и 10 книги «Основы математики для науки о данных» вы увидите, что способность изменять основания является фундаментальной в линейной алгебре и является ключом к пониманию разложения по собственным числам или разложения по сингулярным значениям.
Вы видели, что для связывания геометрических векторов (стрелок в пространстве) с координатными векторами (массивами чисел) вам нужна ссылка. Эта ссылка является основой вашего векторного пространства. По этой причине вектор всегда должен определяться относительно базиса.
Возьмем следующий вектор:
Значения компонентов x и y соответственно равны 2 и -0,5. Стандартная основа используется, если она не указана.
Вы можете написать IV , чтобы указать, что эти числа соответствуют координатам относительно стандартного базиса. В этом случае I называется изменением базовой матрицы .
Вы можете определить векторы относительно другого базиса, используя другую матрицу, чем я .
Векторные пространства (множество возможных векторов) характеризуются относительно базиса. Выражение геометрического вектора в виде массива чисел подразумевает, что вы выбираете основу. При разном базисе одному и тому же вектору v соответствуют разные числа.
Вы видели, что базис представляет собой набор линейно независимых векторов, охватывающих пространство. Точнее, набор векторов является базисом, если каждый вектор из пространства может быть описан как конечная линейная комбинация компонентов базиса и если набор линейно независим.
Рассмотрим следующий двумерный вектор:
В декартовой плоскости ℝ² можно рассматривать v как линейную комбинацию стандартных базисных векторов i ,
3 9 как1 ,3 9 Рисунок 5: Вектор v может быть описан как линейная комбинация базисных векторов i и Дж . (Изображение автора)
(Изображение автора) Но если вы используете другую систему координат, v связаны с новыми числами. На рис. 6 показано представление вектора v в новой системе координат ( i ’ и j ’ ).
Рисунок 6: Вектор v относительно координат нового базиса. (Изображение автора)В новом базисе v новый набор чисел:
Вы можете использовать изменение базовой матрицы для перехода от одного базиса к другому. Чтобы найти матрицу, соответствующую новым базисным векторам, вы можете выразить эти новые базисные векторы ( i ‘ и j ‘ ) как координаты в старом базисе ( i1 j ).
Вернемся к предыдущему примеру. У вас есть:
и
Это показано на рисунке 7.
, так как они являются базисными векторами, I ‘ и J ‘ могут быть выражены в виде линейных комбинаций I и 111111111111111111111111111111111111111111111111111111111111111111111111111111111111134.
Запишем эти уравнения в матричной форме (подробнее о матричной форме систем уравнений в главе 08 Essential Math for Data Science):
Чтобы базисные векторы были столбцами, необходимо транспонировать матрицы. Вы получаете:
Эта матрица называется матрицей изменения базиса. Назовем его C :
Как вы можете заметить, каждый столбец матрицы изменения базиса является базисным вектором нового базиса. Далее вы увидите, что вы можете использовать матрицу изменения базиса C для преобразования векторов из выходного базиса во входной базис.
Изменение базиса в сравнении с линейным преобразованием
Разница между сменой базиса и линейным преобразованием носит концептуальный характер. Иногда полезно рассматривать действие матрицы как изменение базиса; иногда вы получаете больше информации, когда думаете об этом как о линейном преобразовании.
Либо вы перемещаете вектор, либо перемещаете его ссылку. Вот почему вращение системы координат имеет обратный эффект по сравнению с вращением самого вектора.
Для собственного разложения и SVD оба эти вида обычно используются вместе, что поначалу может сбивать с толку. Помнить об этом различии будет полезно на протяжении всей книги.
Основное техническое различие между ними заключается в том, что изменение базиса должно быть обратимым, что не требуется для линейных преобразований.
Нахождение матрицы изменения базиса
Матрица изменения базиса сопоставляет входной базис с выходным базисом. Назовем входной базис B ₁ с базисными векторами i и j , а выходной базис B00010 ₂ с базисными векторами i ’ и j ’ . У вас есть:
У вас есть:
и
Из уравнения изменения базиса вы имеете:
Если вы хотите найти матрицу изменения базиса, заданную B ₁ и B 1 90 , вам нужно вычислить обратное число B ₁ , чтобы изолировать C 9{-1} , который содержит входные базисные векторы в виде столбцов) на выходную базисную матрицу ( B ₂ , которая содержит выходные базисные векторы в виде столбцов).
Будьте осторожны, это изменение базовой матрицы позволяет вам конвертировать векторы из B ₂ в B ₁ , а не наоборот. Интуитивно это происходит потому, что перемещение объекта противоположно перемещению ссылки. Таким образом, перейти от 9{-1} .
Обратите внимание, что если входной базис является стандартным базисом ( B ₁= I ), то изменение базисной матрицы является просто выходной базисной матрицей:
Поскольку базисные векторы линейны независимы, столбцы C линейно независимы, и, таким образом, как указано в разделе 7. 4 Essential Math for Data Science, C является обратимым.
4 Essential Math for Data Science, C является обратимым.
Поменяем основу вектора v , снова используя геометрические векторы, представленные на рисунке 6.
Обозначение
Вы измените базис v со стандартного базиса на новый. Обозначим стандартный базис как B ₁ и новый базис как B ₂ . Помните, что базис — это матрица, содержащая базисные векторы в виде столбцов. У вас есть:
и
Обозначим вектор V По сравнению с базой B ₁ AS [ V ] B ₁ :
Цель находит координат 3333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333н3н . базис B ₂ , обозначаемый как [ v ] B ₂ .
Обозначение в квадратных скобках
Чтобы различать основу, используемую для определения вектора, вы можете указать имя основы (например, B ₁) в нижнем индексе после имени вектора, заключенного в квадратные скобки. Однако из-за ограничений среднего нижнего индекса мы напишем, например, [ v ] B ₁ в тексте, чтобы обозначить вектор v относительно базиса B ₁. Его также называют представлением v по отношению к B ₁.
Использование линейных комбинаций
Представим вектор v в виде линейной комбинации входного и выходного базисных векторов: и d₂ взвешивают линейную комбинацию выходных базисных векторов. Вы можете объединить два уравнения:
Теперь давайте запишем это уравнение в матричной форме:
Вектор, содержащий скаляры C₁ и C₂ соответствует [ V ] B ₁ и вектор, содержащий скаляры D₁ и D₂ , соответствует [ V и D₂ . ₂ . У вас есть:
₂ . У вас есть:
Хорошо, это уравнение с членом, который вы хотите найти: [ v ] B ₂ . Вы можете изолировать его, умножив каждую сторону на B 9{-1} allows you to convert vectors from an input basis B ₁ to an output basis B ₂ and C from B ₂ to В ₁ .
В контексте этого примера, поскольку B ₁ является стандартным основанием, оно упрощается до:
Это означает, что, применяя матрицу B 9{-1} to [ v ] B _1 позволяет изменить его основу на B ₂ .
Let’s code this:
array([ 0.86757991, -1.00456621])
These values are the coordinates of the vector v relative to the basis B ₂ . Это означает, что если вы перейдете на 0,86757991 i ’ — 1,00456621 j ‘ вы достигаете позиции (2, 1) в стандартном базисе, как показано на рисунке 6. разложение (также называемое матричной факторизацией ), как собственное разложение или разложение по сингулярным значениям (SVD). В этих терминах вы можете думать о матричной декомпозиции как о поиске базиса, в котором матрица, связанная с преобразованием, имеет определенные свойства: факторизация — это изменение базовой матрицы, новая матрица преобразования и, наконец, обратная замена базовой матрицы на вернуться к исходному базису (подробнее в главе 09).и 10 из Essential Math for Data Science).
Этот пост является образцом моей книги Essential Math for Data Science !
Получите книгу здесь: https://bit. ly/2WVf4CR!
ly/2WVf4CR!
Как определить, является ли вектор линейной комбинацией других векторов
Идея линейной комбинации векторов очень важна для изучения линейной алгебры. Мы можем использовать линейные комбинации для понимания остовных множеств, пространства столбцов матрицы и многих других тем. Одним из самых полезных навыков при работе с линейными комбинациями является определение того, когда один вектор является линейной комбинацией заданного набора векторов.
реклама
Предположим, что у нас есть вектор \(\vec{v}\) и мы хотим узнать ответ на вопрос «является ли \(\vec{v}\) линейной комбинацией векторов \(\vec{ a}_{1}\), \(\vec{a}_{2}\) и \(\vec{a}_{3}\)?». Используя определение линейной комбинации векторов, этот вопрос можно сформулировать следующим образом:
Существуют ли скаляры \(x_{1}\), \(x_{2}\) и \(x_{3}\) такие, что:
\(\vec{v} = x_1\vec{a}_{ 1 }+x_2\vec{a}_{2}+ x_3\vec{a}_{3}\)?
9n\) для некоторого \(n\), то на этот вопрос можно ответить, используя эквивалентную расширенную матрицу:
\(\left[ \begin{array}{ccc|c} \vec{a}_1 & \vec{a}_2 & \vec{a}_3 & \vec{v} \\ \end{array} \right ]\)
Если эта матрица представляет собой непротиворечивую систему уравнений, то мы можем сказать, что \(\vec{v}\) является линейной комбинацией других векторов.
Пример
Определить, является ли вектор \(\begin{bmatrix} 5 \\ 3 \\ 0 \\ \end{bmatrix}\) линейной комбинацией векторов:
\(\begin{bmatrix} 2 \\ 0 \\ 1 \\ \end{bmatrix}\), \(\begin{bmatrix} 1 \\ 4 \\ 3 \\ \end{bmatrix}\), \ (\begin{bmatrix} 8 \\ 1 \\ 1 \\ \end{bmatrix}\) и \(\begin{bmatrix} -4 \\ 6 \\ 1 \\ \end{bmatrix}\)
Решение
Помните, что это означает, что мы хотим найти константы \(x_{1}\), \(x_{2}\), \(x_{3}\) и \(x_{4}\) так что:
\(\begin{bmatrix} 5 \\ 3 \\ 0 \\ \end{bmatrix} = x_{1}\begin{bmatrix} 2 \\ 0 \\ 1 \\ \end{bmatrix} + x_{2} \begin{bmatrix} 1 \\ 4 \\ 3 \\ \end{bmatrix} + x_{3}\begin{bmatrix} 8 \\ 1 \\ 1 \\ \end{bmatrix} + x_{4}\begin {bmatrix}-4\6\1\\end{bmatrix}\)
Это векторное уравнение эквивалентно расширенной матрице. Составляя эту матрицу и уменьшая количество строк, мы находим, что:
\(\left[ \begin{array}{cccc|c} 2 & 1 & 8 & -4 & 5 \\
0 & 4 & 1 & 6 & 3 \\
1 & 3 & 1 & 1 & 0 \ \
\ конец {массив} \ справа]
\)
Эквивалент:
\(\left[ \begin{array}{cccc|c} 1 & 0 & 0 & -\dfrac{103}{29} & -\dfrac{74}{29} \\
0 & 1 & 0 & \ дфрак{42}{29} & \dfrac{13}{29} \\
0 & 0 & 1 & \dfrac{6}{29} & \dfrac{35}{29} \\
\end{массив}\right]\)
Хотя это и некрасиво, но эта матрица НЕ содержит такой строки, как \(\begin{bmatrix} 0 & 0 & 0 & 0 & c \\ \end{bmatrix}\), где \(c \neq 0 \), что указывало бы на то, что базовая система несовместима. Следовательно, основная система непротиворечива (имеет решение), что означает, что векторное уравнение также непротиворечиво.
Следовательно, основная система непротиворечива (имеет решение), что означает, что векторное уравнение также непротиворечиво.
Итак, мы можем сказать, что \(\begin{bmatrix} 5 \\ 3 \\ 0 \\ \end{bmatrix}\) является линейной комбинацией других векторов.
Пошаговый процесс
В общем, если вы хотите определить, является ли вектор \(\vec{u}\) линейной комбинацией векторов \(\vec{v}_{1}\) , \(\vec{v}_{2}\), … , \(\vec{v}_{p}\) (для любого целого числа \(p > 2\)) вы сделаете следующее.
Шаг 1
Настройка расширенной матрицы
\(\left[ \begin{array}{cccc|c} \vec{v}_1 & \vec{v}_2 & \cdots & \vec{v}_p & \vec{u} \\ \end{array } \right]\)
и уменьшить строку.
Шаг 2
Используйте сокращенную форму матрицы, чтобы определить, представляет ли расширенная матрица непротиворечивую систему уравнений. Если это так, то \(\vec{u}\) является линейной комбинацией остальных. В противном случае это не так.
На втором этапе важно помнить, что система уравнений непротиворечива, если существует одно решение ИЛИ много решений. Количество решений не важно, главное, чтобы было хотя бы одно решение. Это означает, что существует по крайней мере один способ записать данный вектор как линейную комбинацию других.
Количество решений не важно, главное, чтобы было хотя бы одно решение. Это означает, что существует по крайней мере один способ записать данный вектор как линейную комбинацию других.
Запись вектора в виде линейной комбинации других векторов
Иногда вас могут попросить записать вектор в виде линейной комбинации других векторов. Это требует той же работы, что и выше, с еще одним шагом. Вам нужно использовать решение векторного уравнения, чтобы написать, как векторы комбинируются, чтобы создать новый вектор.
Давайте начнем с более простого случая, чем тот, который мы делали раньше, а затем вернемся к нему, так как он немного сложнее.
Пример
Запишите вектор \(\vec{v} = \begin{bmatrix} 2 \\ 4 \\ 2 \\ \end{bmatrix}\) в виде линейной комбинации векторов:
\(\begin{bmatrix} 2 \ \ 0 \\ 1 \\ \end{bmatrix}\), \(\begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix}\) и \(\begin{bmatrix} -2 \ \ 0 \\ 0 \\ \end{bmatrix}\)
Решение
Шаг 1
Мы настраиваем нашу расширенную матрицу и уменьшаем ее по строкам.
\(
\left[ \begin{array}{ccc|c} 2 & 0 & -2 & 2 \\
0 & 1 & 0 & 4 \\
1 & 0 & 0 & 2 \\
\end{массив} \right]
\)
эквивалентно
\(
\left[ \begin{array}{ccc|c} 1 & 0 & 0 & 2 \\
0 & 1 & 0 & 4 \\
0 & 0 & 1 & 1 \\
\end{array } \справа]
\)
Шаг 2
Определяем, представляет ли матрица непротиворечивую систему уравнений.
На основе сокращенной матрицы базовая система непротиворечива. Опять же, это потому, что нет строк со всеми нулями в коэффициентной части матрицы и единственного ненулевого значения в дополнении. (вы также можете использовать количество опорных точек, чтобы привести аргумент.)
В отличие от предыдущего, мы не только хотим убедиться, что у нас есть линейная комбинация. Мы хотим показать саму линейную комбинацию. Это означает, что нам нужно реальное решение. В данном случае есть только один:
\(x_1 = 2\), \(x_2 = 4\), \(x_3 = 1\)
Используя эти значения, мы можем записать \(\vec{v}\) как:
\(\vec{v} = \begin{bmatrix} 2 \\ 4 \\ 2 \\ \end{bmatrix} = (2)\begin{bmatrix} 2 \\ 0 \\ 1 \\ \end{bmatrix} + (4)\begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix} + (1)\begin{bmatrix} -2 \\ 0 \\ 0 \\ \end{bmatrix}\)
Теперь вернемся к нашему первому примеру (с сумасшедшими дробями), но немного изменим инструкции.
Пример
Запишите вектор \(\vec{v} = \begin{bmatrix} 5 \\ 3 \\ 0 \\ \end{bmatrix}\) в виде линейной комбинации векторов:
\(\begin{bmatrix} 2 \ \ 0 \\ 1 \\ \end{bmatrix}\), \(\begin{bmatrix} 1 \\ 4 \\ 3 \\ \end{bmatrix}\), \(\begin{bmatrix} 8 \\ 1 \\ 1 \\ \end{bmatrix}\), и \(\begin{bmatrix} -4 \\ 6 \\ 1 \\ \end{bmatrix}\)
Когда мы сделали шаг 1, у нас была следующая работа. Это показало, что эквивалентное векторное уравнение было непротиворечивым, и подтвердило, что \(\vec{v}\) является линейной комбинацией других векторов.
\(\left[ \begin{array}{cccc|c} 2 & 1 & 8 & -4 & 5 \\
0 & 4 & 1 & 6 & 3 \\
1 & 3 & 1 & 1 & 0 \ \
\ конец {массив} \ справа]
\)
Эквивалент:
\(\left[ \begin{array}{cccc|c} 1 & 0 & 0 & -\dfrac{103}{29} & -\dfrac{74}{29} \\
0 & 1 & 0 & \ dfrac{42}{29} & \dfrac{13}{29} \\
0 & 0 & 1 & \dfrac{6}{29} & \dfrac{35}{29} \\
\end{массив} \Правильно]\)
Что, если бы мы захотели записать линейную комбинацию. Этот пример отличается от предыдущего тем, что существует бесконечно много решений векторного уравнения.
Этот пример отличается от предыдущего тем, что существует бесконечно много решений векторного уравнения.
Присмотревшись к этой расширенной матрице, мы увидим, что имеется одна свободная переменная \(x_{4}\). Если мы выпишем уравнения, то получим:
\(x_1 – \left(\dfrac{103}{29}\right)x_4 = -\dfrac{74}{29}\)
\(x_2 + \left(\dfrac{42}{29}\right)x_4 = \dfrac{13}{29}\)
\(x_3 + \влево(\dfrac{6}{29}\right)x_4 = \dfrac{35}{29}\)
Поскольку \(x_{4}\) — свободная переменная, мы можем присвоить ей любое значение и найти решение этой системы уравнений. Действительно «хорошее» значение было бы равно нулю. Если \(x_4 = 0\), то:
\(x_1 – \dfrac{103}{29}(0) = -\dfrac{74}{29}\)
\(x_2 + \dfrac{42}{29}(0) = \dfrac{13}{29}\)
\(x_3 + \dfrac{6}{29}(0) = \dfrac{35}{29}\)
Используя это решение, мы можем записать \(\vec{v}\) как линейную комбинацию других векторов.
\(\vec{v} = \begin{bmatrix} 5 \\ 3 \\ 0 \\ \end{bmatrix} = \left(-\dfrac{72}{29}\right)\begin{bmatrix} 2 \ \ 0 \\ 1 \\ \end{bmatrix} + \left(\dfrac{13}{29}\right)\begin{bmatrix} 1 \\ 4 \\ 3 \\ \end{bmatrix} + \left( \dfrac{35}{29}\right)\begin{bmatrix} 8 \\ 1 \\ 1 \\ \end{bmatrix} + (0)\begin{bmatrix} -4 \\ 6 \\ 1 \\ \ конец{bматрица}\)
Это было бы одно решение, но поскольку \(x_4\) бесплатен, их бесконечно много. Для каждого возможного значения \(x_4\) у вас есть другой правильный способ записать \(\vec{v}\) как линейную комбинацию других векторов. Например, если \(x_4 = 1\):
Для каждого возможного значения \(x_4\) у вас есть другой правильный способ записать \(\vec{v}\) как линейную комбинацию других векторов. Например, если \(x_4 = 1\):
\(\begin{align}x_1 &= -\dfrac{74}{29} + \dfrac{103}{29} \\ &= \dfrac{29}{29} \\ &= 1\end{align} \)
\(\begin{align}x_2 &= \dfrac{13}{29} – \dfrac{42}{29}\\ &= -\dfrac{29}{29} \\ &= -1\end{align }\)
\(\begin{align}x_3 &= \dfrac{35}{29} – \dfrac{6}{29}\\ &= \dfrac{29}{29} \\ &= 1\end{align}\ )
Используя это, мы также можем написать:
\(\vec{v} = \begin{bmatrix} 5 \\ 3 \\ 0 \\ \end{bmatrix} = (1)\begin{bmatrix} 2 \\ 0 \\ 1 \\ \end{bmatrix} + (-1)\begin{bmatrix} 1 \\ 4 \\ 3 \\ \end{bmatrix} + (1)\begin{bmatrix} 8 \\ 1 \\ 1 \\ \end{bmatrix} + (1 )\begin{bmatrix} -4 \\ 6 \\ 1 \\ \end{bmatrix}\)
Как хорошо? (примечание: обычно мы не записываем 1 в уравнении, показывающем линейную комбинацию. Я оставил его там, чтобы вы могли видеть, где оказалось каждое число из решения).
Опять же, у подобной задачи бесконечно много ответов. Все, что вам нужно сделать, это выбрать значение для свободных переменных, и у вас будет одно конкретное решение, которое вы сможете использовать при написании линейной комбинации.
Все, что вам нужно сделать, это выбрать значение для свободных переменных, и у вас будет одно конкретное решение, которое вы сможете использовать при написании линейной комбинации.
Когда вектор НЕ является линейной комбинацией других
Стоит рассмотреть один пример, когда вектор не является линейной комбинацией некоторых заданных векторов. Когда это произойдет, мы получим расширенную матрицу, указывающую на противоречивую систему уравнений.
Пример
Определить, является ли вектор \(\begin{bmatrix} 1 \\ 2 \\ 1 \\ \end{bmatrix}\) линейной комбинацией векторов:
\(\begin{bmatrix} 1 \\ 1 \\ 0 \\ \end{bmatrix}\), \(\begin{bmatrix} 0 \\ 1 \\ -1 \\ \end{bmatrix}\), и \(\begin{bmatrix} 1\\ 2 \\ — 1 \\ \end{bmatrix}\).
Решение
Шаг 1
Мы настраиваем нашу расширенную матрицу и уменьшаем ее по строкам.
\(
\left[ \begin{array}{ccc|c} 1 & 0 & 1 & 1 \\
1 & 1 & 2 & 2 \\
0 & -1 & -1 & 1 \\
\end{массив} \right]
\)
эквивалентно:
\(
\left[ \begin{array}{ccc|c} 1 & 0 & 1 & 0 \\
0 & 1 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{array } \справа]
\)
Шаг 2
Определяем, представляет ли матрица непротиворечивую систему уравнений.
Учитывая форму последней строки, эта матрица представляет собой противоречивую систему уравнений. Это означает, что нет никакого способа записать этот вектор как линейную комбинацию других векторов. Вот именно — больше нечего сказать! Это будет наш вывод каждый раз, когда сокращение строки приводит к строке с нулями и ненулевым значением в увеличении.
Учебное пособие – линейные комбинации и пролет
Нужно больше практики с линейными комбинациями и пролетом? Это 40-страничное учебное пособие поможет! Он включает в себя объяснения, примеры, практические задачи и полные пошаговые решения.
Получить учебное пособие
Подпишитесь на нашу рассылку!
Мы всегда публикуем новые бесплатные уроки и добавляем дополнительные учебные пособия, руководства по калькуляторам и наборы задач.
Подпишитесь, чтобы время от времени получать электронные письма (раз в пару или три недели), чтобы узнавать о новинках!
Диапазон и нулевое пространство матрицы
Все ресурсы линейной алгебры
4 Диагностические тесты 108 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по линейной алгебре » Операции и свойства » Диапазон и нулевое пространство матрицы
Вычислите нулевое пространство следующей матрицы.
Возможные ответы:
Пустого пространства нет
Правильный ответ: 95723
0 Объяснение:Первым шагом является создание расширенной матрицы со столбцом нулей.
Следующий шаг — добавить это в RREF.
Мы можем упростить до
3
.
Теперь нам нужно записать это в виде линейной комбинации.
Тогда нулевое пространство равно
Сообщить об ошибке
Найдите основу для диапазона пространства преобразования, заданного матрицей .
Возможные ответы:
Ни один из других ответов.
Правильный ответ:
Ни один из других ответов.
Объяснение:
Сначала мы можем найти основу для пространства диапазона , найдя основу для пространства столбцов его сокращенной эшелонированной формы строк.
С помощью калькулятора или редукции строк получаем
для сокращенной эшелонированной формы строки.
При осмотре видно, что четвертый столбец в этой матрице представляет собой линейную комбинацию трех других столбцов, поэтому он не включен в наш базис. Следовательно, первые три столбца образуют основу для пространства столбцов редуцированной эшелонированной формы строки , и, следовательно, первые три столбца образуют основу для его пространства диапазона.
.
Сообщить об ошибке
Найти основу для пространства диапазона преобразования, заданного матрицей .
Возможные ответы: 9
Правильный ответ:
Объяснение:
Сначала мы можем найти основу для пространства диапазона , найдя основу для пространства столбцов его сокращенной эшелонированной формы строк.
С помощью калькулятора или редукции строк получаем
для сокращенной эшелонированной формы строки.
При осмотре видно, что второй столбец в этой матрице является линейной комбинацией первого столбца, поэтому он не включен в наш базис для . Следовательно, первый и третий столбцы образуют основу для пространства столбцов , и, следовательно, первый и третий столбцы формируют основу для пространства диапазона .
Сообщить об ошибке
Найдите основу для пространства диапазона преобразования, заданного матрицей .
Возможные ответы:
Ни один из других ответов
Правильный ответ:
3 Объяснение:Сначала мы можем найти основу для пространства диапазона , найдя основу для пространства столбцов его сокращенной эшелонированной формы строк.
С помощью калькулятора или сокращения строк получаем
для ступенчатой формы уменьшенного ряда.
При осмотре видно, что четвертый столбец в этой матрице является линейной комбинацией первых трех столбцов, поэтому он не включен в нашу основу для . Следовательно, первые три столбца формируют основу для пространства столбцов , и, следовательно, первые три столбца формируют основу для пространства диапазонов .
Сообщить об ошибке
Найти основу для нулевого пространства матрицы .
Возможные ответы:
Другие ответы отсутствуют
Объяснение:
Пустое пространство матрицы – это множество решений уравнения
.
Мы можем решить приведенную выше систему путем сокращения строк используя либо сокращение строк, либо калькулятор, чтобы найти ее сокращенную форму эшелона строк. После этого наша система становится
Следовательно, базой для нулевого пространства является просто нулевой вектор;
.
Сообщить об ошибке
Найти нулевое пространство матричного оператора.
Возможные ответы:
Нет других ответов Объяснение:
Пустое пространство оператора представляет собой множество решений уравнения
.
Мы можем решить приведенную выше систему, сократив нашу матрицу по строкам, используя либо сокращение по строкам, либо калькулятор, чтобы найти ее ступенчатую форму с сокращенными строками. После этого наша система становится
Следовательно, нулевое пространство состоит только из нулевого вектора.
Сообщить об ошибке
Найти нулевое пространство матрицы.
Возможные ответы:
Ни один из других ответов
Правильный ответ:
Объяснение:
Пустое пространство матрицы – это множество решений уравнения
.
Мы можем решить приведенную выше систему путем сокращения строк, используя либо сокращение строк, либо калькулятор, чтобы найти ее сокращенную форму эшелона строк. После этого наша система становится
Умножение этого вектора на избавляется от дроби и не влияет на наш ответ, так как за ним стоит произвольная константа.
Следовательно, нулевое пространство состоит из всех векторов, натянутых на ;
.
Сообщить об ошибке
Найти нулевое пространство матрицы.
Возможные ответы:
Правильный ответ:
Объяснение:
Пустое пространство матрицы – это множество решений уравнения
.
Мы можем решить приведенную выше систему путем сокращения строк, используя либо сокращение строк, либо калькулятор, чтобы найти ее сокращенную форму эшелона строк. После этого наша система становится
После этого наша система становится
Следовательно, нулевое пространство состоит из всех векторов, натянутых на ;
.
Сообщить об ошибке
Каков максимально возможный ранг матрицы?
Возможные ответы:
Нет других ответов Объяснение:
Ранг равен размерности пространства строки и пространства столбца (оба пространства всегда имеют одинаковую размерность). Эта матрица состоит из трех строк и пяти столбцов, что означает, что максимально возможное количество векторов в основе пространства строк матрицы равно , поэтому это максимально возможный ранг.
Сообщить об ошибке
Какова наименьшая возможная недействительность матрицы?
Возможные ответы:
Ни один из других ответов
Правильный ответ:
33 Объяснение:
Согласно теореме ранг + недействительность,
Поскольку матрица имеет столбцы, мы можем изменить уравнение, чтобы получить
Итак, чтобы сделать недействительность как можно меньше, нам нужно сделать ранг как можно больше.

 «,»ch»,»inv»,»r»,»>A-1 =
«,»ch»,»inv»,»r»,»>A-1 = «,»search»,»,»,»replace»,»split»,»length»,»t»,»add»,»add1″,»
«,»search»,»,»,»replace»,»split»,»length»,»t»,»add»,»add1″,»