1.2.1. Обыкновенные дроби
Глава 1. Арифметика
1.2.
1.2.1.
Можно еще больше расширить числовое множество – так, чтобы операция деления над натуральными числами была выполнима всегда. Для этого введем понятие дроби.
|
Обыкновенной дробью называется число вида где m и n – натуральные числа. Число m называется числителем этой дроби, а число n – её знаменателем. |
||
Если n = 1, то дробь имеет вид
и её часто записывают просто m. Отсюда, в частности, следует, что любое натуральное число представимо в виде обыкновенной дроби со знаменателем 1.
Отсюда, в частности, следует, что любое натуральное число представимо в виде обыкновенной дроби со знаменателем 1.
|
Две дроби и называются равными, если |
||
Например, так как Из этого определения следует, что дробь равна любой дроби вида где m – натуральное число. В самом деле, так как то Итак, мы готовы сформулировать следующее правило.
| Основное свойство дроби Если числитель и знаменатель данной дроби умножить или разделить на одно и то же число, неравное нулю, то получится дробь, равная данной. |
С помощью основного свойства дроби можно заменить данную дробь другой дробью, равной данной, но с меньшими числителем и знаменателем. Такая замена называется сокращением дроби. Например, (здесь числитель и знаменатель разделили сначала на 2, а потом ещё на 2). Сокращение дроби можно провести тогда и только тогда, когда её числитель и знаменатель не являются взаимно простыми числами. Если же числитель и знаменатель данной дроби взаимно просты, то дробь сократить нельзя, например, – несократимая дробь.
|
Модель 1.5. Сокращение обыкновенных дробей |
|
Обыкновенная дробь
называется правильной, если её числитель меньше её знаменателя, то есть m < n. |
||
Справедливо следующее утверждение (его мы докажем ниже):
Всякую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби. |
Из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше. Например,
Из двух дробей с одинаковыми числителями больше та дробь, знаменатель которой меньше. Например,
Чтобы сравнить две дроби с разными числителями и знаменателями, нужно преобразовать обе дроби так, чтобы их знаменатели стали одинаковыми. Такое преобразование называется приведением дробей к общему знаменателю.
|
Модель 1.6. Сравнение обыкновенных дробей |
Теперь знаменатели этих дробей одинаковы, значит,
Следовательно,
Ясно, что две дроби можно привести не к единственному общему знаменателю. Так, в нашем примере дроби и
можно привести к знаменателю 56. В самом деле:
 Однако обычно стараются привести дроби к наименьшему общему знаменателю, который равен наименьшему общему кратному знаменателей двух данных дробей.
Пример 1
Однако обычно стараются привести дроби к наименьшему общему знаменателю, который равен наименьшему общему кратному знаменателей двух данных дробей.
Пример 1Привести дроби к наименьшему общему знаменателю: и
Решение
|
Найдём сперва наименьшее общее кратное чисел 15 и 20. НОК (15, 20) = 60. Так как 60 : 15 = 4, то числитель и знаменатель дроби
нужно умножить на 4:
Поскольку 60 : 20 = 3, то числитель и знаменатель второй дроби нужно умножить на 3:
Итак, дроби приведены к общему знаменателю:
Ответ. |
В рассмотренном примере числа 4 и 3 называют дополнительными множителями для первой и второй дроби соответственно.
Теперь мы можем определить арифметические действия с дробями.
Сложение. Если знаменатели дробей одинаковы, то чтобы сложить эти дроби, нужно сложить их числители; знаменатель остаётся прежним, то есть
Вычитание. Если две дроби имеют одинаковые знаменатели, то
|
Модель 1. |
Умножение. Произведение двух дробей равно дроби, числитель которой равен произведению числителей данных дробей, а знаменатель равен произведению их знаменателей, то есть
Деление. Деление дробей осуществляют следующим образом:
В случае умножения и деления смешанных чисел всегда удобно переходить к неправильным дробям.
|
Модель 1.8. Умножение и деление обыкновенных дробей |
Пример 2
Сложить две дроби
и
Ответ представить в виде неправильной дроби.
Показать решение
Пример 3
Сложить две дроби и Ответ представить в виде неправильной дроби.
Показать решение
Теперь можно показать, что любую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби (или в виде натурального числа, если дробь такова, что число m кратно n, например, ).
Пример 4
Представить неправильную дробь в виде суммы натурального числа и правильной дроби: 1) 2)
Показать решение
Всякую неправильную дробь можно представить в виде смешанного числа (или в виде натурального числа). Понятно также, что верно и обратное: всякое смешанное число может быть представлено в виде неправильной дроби. Например,
Пример 5
Выполнить действия.
Показать решение
Главная Онлайн учебники База репетиторов России Тренажеры по математике Подготовка к ЕГЭ 2017 онлайн |
||||||||
|
||||||||
|
|
||||||||
Дроби которые нужно запомнить. Обыкновенные дроби
Примеры с дробями – один из основных элементов математики. Существует много разных типов уравнений с дробями. Ниже приведена подробная инструкция по решению примеров такого типа.
Как решать примеры с дробями – общие правила
Для решения примеров с дробями любых типов, будь то сложение, вычитание, умножение или деление, необходимо знать основные правила:
- Для того чтобы сложить дробные выражения с одинаковым знаменателем (знаменатель – число, находящееся в нижней части дроби, числитель – в верхней), нужно сложить их числители, а знаменатель оставить тем же.
- Для того чтобы вычесть от одного дробного выражения второе (с одинаковым знаменателем), нужно вычесть их числители, а знаменатель оставить тем же.

- Для того чтобы сложить или вычесть дробные выражения с разными знаменателями, нужно найти наименьший общий знаменатель.
- Для того чтобы найти дробное произведение, нужно перемножить числители и знаменатели, при этом, если есть возможность, сократить.
- Для того чтобы разделить дробь на дробь, нужно умножить первую дробь на перевернутую вторую.
Как решать примеры с дробями – практика
Правило 1, пример 1:
Вычислить 3/4 +1/4.
Согласно правилу 1, если у дробей двух (или больше) одинаковый знаменатель, нужно просто сложить их числители. Получим: 3/4 + 1/4 = 4/4. Если у дроби числитель и знаменатель одинаковы, такая дробь будет равна 1.
Ответ: 3/4 + 1/4 = 4/4 = 1.
Правило 2, пример 1:
Вычислить: 3/4 – 1/4
Пользуясь правилом номер 2, для решения этого уравнения нужно от 3 отнять 1, а знаменатель оставить тем же. Получаем 2/4. Так как два 2 и 4 можно сократить, сокращаем и получаем 1/2.
Ответ: 3/4 – 1/4 = 2/4 = 1/2.
Правило 3, Пример 1
Вычислить: 3/4 + 1/6
Решение: Пользуясь 3-м правилом, находим наименьший общий знаменатель. Наименьшим общим знаменателем называется такое число, которое делится на знаменатели всех дробных выражений примера. Таким образом, нам нужно найти такое минимальное число, которое будет делиться и на 4, и на 6. Таким числом является 12. Записываем в качестве знаменателя 12. 12 делим на знаменатель первой дроби, получаем 3, умножаем на 3, записываем в числителе 3*3 и знак +. 12 делим на знаменатель второй дроби, получаем 2, 2 умножаем на 1, записываем в числителе 2*1. Итак, получилась новая дробь со знаменателем, равным 12 и числителем, равным 3*3+2*1=11. 11/12.
Ответ: 11/12
Правило 3, Пример 2:
Вычислить 3/4 – 1/6. Этот пример очень схож с предыдущим. Проделываем все те же действия, но в числителе вместо знака +, пишем знак минус. Получаем: 3*3-2*1/12 = 9-2/12 = 7/12.
Ответ: 7/12
Правило 4, Пример 1:
Вычислить: 3/4 * 1/4
Пользуясь четвертым правилом, умножаем знаменатель первой дроби на знаменатель второй и числитель первой дроби на числитель второй. 3*1/4*4 = 3/16.
3*1/4*4 = 3/16.
Ответ: 3/16
Правило 4, Пример 2:
Вычислить 2/5 * 10/4.
Данную дробь можно сократить. В случае произведения сокращаются числитель первой дроби и знаменатель второй и числитель второй дроби и знаменатель первой.
2 сокращается с 4. 10 сокращается с 5. получаем 1 * 2/2 = 1*1 = 1.
Ответ: 2/5 * 10/4 = 1
Правило 5, Пример 1:
Вычислить: 3/4: 5/6
Пользуясь 5-м правилом, получим: 3/4: 5/6 = 3/4 * 6/5. Сокращаем дробь по принципу предыдущего примера и получаем 9/10.
Ответ: 9/10.
Как решать примеры с дробями – дробные уравнения
Дробными уравнениями называются примеры, где в знаменателе есть неизвестное. Для того чтобы решить такое уравнение нужно пользоваться определенными правилами.
Рассмотрим пример:
Решить уравнение 15/3x+5 = 3
Вспомним, нельзя делить на ноль, т.е. значение знаменателя не должно равняться нулю. При решении таких примеров, это нужно обязательно указывать. Для этого существует ОДЗ (область допустимых значений).
Таким образом, 3x+5 ≠ 0.
Отсюда: 3x ≠ 5.
x ≠ 5/3
При x = 5/3 уравнение просто не имеет решения.
Указав ОДЗ, наилучшим способом решить данное уравнение будет избавиться от дробей. Для это сначала представим все не дробные значения в виде дроби, в данном случае число 3. Получим: 15/(3x+5) = 3/1. Чтобы избавиться от дроби нужно умножить каждую из них на наименьший общий знаменатель. В данном случае таковым будет (3x+5)*1. Последовательность действий:
- Умножаем 15/(3x+5) на (3x+5)*1 = 15*(3x+5).
- Раскрываем скобки: 15*(3x+5) = 45x + 75.
- То же самое проделываем с правой частью уравнения: 3*(3x+5) = 9x + 15.
- Приравниваем левую и правую часть: 45x + 75 = 9x +15
- Переносим иксы влево, числа вправо: 36x = – 50
- Находим x: x = -50/36.
- Сокращаем: -50/36 = -25/18
Ответ: ОДЗ x ≠ 5/3 . x = -25/18.
Как решать примеры с дробями – дробные неравенства
Дробные неравенства по типу (3x-5)/(2-x)≥0 решаются при помощи числовой оси. Рассмотрим данный пример.
Рассмотрим данный пример.
Последовательность действий:
- Приравниваем числитель и знаменатель к нулю: 1. 3x-5=0 => 3x=5 => x=5/3
2. 2-x=0 => x=2 - Чертим числовую ось, расписывая на ней получившиеся значения.
- Под значение рисуем кружок. Кружок бывает двух типов – заполненный и пустой. Заполненный кружок означает, что данное значение входит в ареал решений. Пустой круг говорит о том, что данное значение не входит в ареал решений.
- Так как знаменатель не может быть равным нулю, под 2-ой будет пустой круг.
- Чтобы определить знаки, подставляем в уравнение любое число больше двух, например 3. (3*3-5)/(2-3)= -4. значение отрицательное, значит над областью после двойки пишем минус. Затем подставляем вместо икса любое значение интервала от 5/3 до 2, например 1. Значение опять отрицательное. Пишем минус. То же самое повторяем с областью, находящейся до 5/3. Подставляем любое число, меньшее чем 5/3, например 1. Опять минус.

- Так как нас интересуют значения икса, при котором выражение будет больше или равно 0, а таких значений нет (везде минусы), это неравенство не имеет решения, то есть x = Ø (пустое множество).
Ответ: x = Ø
Действия с дробями. В этой статье разберём примеры, всё подробно с пояснениями. Рассматривать будем обыкновенные дроби. В дальнейшем разберём и десятичные. Рекомендую посмотреть весь и изучать последовательно.
1. Сумма дробей, разность дробей.
Правило: при сложении дробей с равными знаменателями, в результате получаем дробь – знаменатель которой остаётся тот же, а числитель её будет равен сумме числителей дробей.
Правило: при вычислении разности дробей с одинаковыми знаменателями получаем дробь – знаменатель остаётся тот же, а из числителя первой дроби вычитается числитель второй.
Формальная запись суммы и разности дробей с равными знаменателями:
Примеры (1):
Понятно, что когда даны обыкновенные дроби, то всё просто, а если смешанные? Ничего сложного…
Вариант 1 – можно перевести их в обыкновенные и далее вычислять.
Вариант 2 – можно отдельно «работать» с целой и дробной частью.
Примеры (2):
Ещё:
А если будет дана разность двух смешанных дробей и числитель первой дроби будет меньше числителя второй? Тоже можно действовать двумя способами.
Примеры (3):
*Перевели в обыкновенные дроби, вычислили разность, перевели полученную неправильную дробь в смешанную.
*Разбили на целые и дробные части, получили тройку, далее представили 3 как сумму 2 и 1, при чём единицу представили как 11/11, далее нашли разность 11/11 и 7/11 и вычислили результат. Смысл изложенных преобразований заключается в том, чтобы взять (выделить) единицу и представить её в виде дроби с нужным нам знаменателем, далее от этой дроби мы уже можем вычесть другую.
Ещё пример:
Вывод: имеется универсальный подход – для того, чтобы вычислить сумму (разность) смешанных дробей с равными знаменателями их всегда можно перевести в неправильные, далее выполнить необходимое действие.
После этого если в результате получаем неправильную дробь переводим её в смешанную.
Выше мы рассмотрели примеры с дробями, у которых равные знаменатели. А если знаменатели будут отличаться? В этом случае дроби приводятся к одному знаменателю и выполняется указанное действие. Для изменения (преобразования) дроби используется основное свойство дроби.
Рассмотрим простые примеры:
В данных примерах мы сразу видим каким образом можно преобразовать одну из дробей, чтобы получить равные знаменатели.
Если обозначить способы приведения дробей к одному знаменателю, то этот назовём СПОСОБ ПЕРВЫЙ .
То есть, сразу при «оценке» дроби нужно прикинуть сработает ли такой подход – проверяем делится ли больший знаменатель на меньший. И если делится, то выполняем преобразование — домножаем числитель и знаменатель так чтобы у обеих дробей знаменатели стали равными.
Теперь посмотрите на эти примеры:
К ним указанный подход не применим. Существуют ещё способы приведения дробей к общему знаменателю, рассмотрим их.
Существуют ещё способы приведения дробей к общему знаменателю, рассмотрим их.
Способ ВТОРОЙ .
Умножаем числитель и знаменатель первой дроби на знаменатель второй, а числитель и знаменатель второй дроби на знаменатель первой:
*Фактически мы приводим дроби к виду, когда знаменатели становятся равными. Далее используем правило сложения робей с равными знаменателями.
Пример:
*Данный способ можно назвать универсальным, и он работает всегда. Единственный минус в том, что после вычислений может получится дробь которую необходимо будет ещё сократить.
Рассмотрим пример:
Видно что числитель и знаменатель делится на 5:
Способ ТРЕТИЙ.
Необходимо найти наименьшее общее кратное (НОК) знаменателей. Это и будет общий знаменатель. Что это за число такое? Это наименьшее натуральное число, которое делится на каждое из чисел.
Посмотрите, вот два числа: 3 и 4, есть множество чисел, которые делятся на них – это 12, 24, 36, … Наименьшее из них 12. Или 6 и 15, на них делятся 30, 60, 90 …. Наименьшее 30. Вопрос – а как определить это самое наименьшее общее кратное?
Или 6 и 15, на них делятся 30, 60, 90 …. Наименьшее 30. Вопрос – а как определить это самое наименьшее общее кратное?
Имеется чёткий алгоритм, но часто это можно сделать и сразу без вычислений. Например, по указанным выше примерам (3 и 4, 6 и 15) никакого алгоритма не надо, мы взяли большие числа (4 и 15) увеличили их в два раза и увидели, что они делятся на второе число, но пары чисел могут быть и другими, например 51 и 119.
Алгоритм. Для того, чтобы определить наименьшее общее кратное нескольких чисел, необходимо:
— разложить каждое из чисел на ПРОСТЫЕ множители
— выписать разложение БОЛЬШЕГО из них
— умножить его на НЕДОСТАЮЩИЕ множители других чисел
Рассмотрим примеры:
50 и 60 => 50 = 2∙5∙5 60 = 2∙2∙3∙5
в разложении большего числа не хватает одной пятёрки
=> НОК(50,60) = 2∙2∙3∙5∙5 = 300
48 и 72 => 48 = 2∙2∙2∙2∙3 72 = 2∙2∙2∙3∙3
в разложении большего числа не хватает двойки и тройки
=> НОК(48,72) = 2∙2∙2∙2∙3∙3 = 144
* Наименьшее общее кратное двух простых чисел равно их произведению
Вопрос! А чем полезно нахождение наименьшего общего кратного, ведь можно пользоваться вторым способом и полученную дробь просто сократить? Да, можно, но это не всегда удобно. Посмотрите, какой получится знаменатель для чисел 48 и 72, если их просто перемножить 48∙72 = 3456. Согласитесь, что приятнее работать с меньшими числами.
Посмотрите, какой получится знаменатель для чисел 48 и 72, если их просто перемножить 48∙72 = 3456. Согласитесь, что приятнее работать с меньшими числами.
Рассмотрим примеры:
*51 = 3∙17 119 = 7∙17
в разложении большего числа не хватает тройки
=> НОК(51,119) = 3∙7∙17
А теперь применим первый способ:
*Посмотрите какая разница в вычислениях, в первом случае их минимум, а во втором нужно потрудиться отдельно на листочке, да ещё и дробь которую получили сократить необходимо. Нахождение НОК упрощает работу значительно.
Ещё примеры:
*Во втором примере и так видно, что наименьшее число, которое делится на 40 и 60 равно 120.
ИТОГ! ОБЩИЙ АЛГОРИТМ ВЫЧИСЛЕНИЙ!
— приводим дроби к обыкновенным, если есть целая часть.
— приводим дроби к общему знаменателю (сначала смотрим делится ли один знаменатель на другой, если делится то умножаем числитель и знаменатель этой другой дроби; если не делится действуем посредством других указанных выше способов).
— получив дроби с равными знаменателями, выполняем действия (сложение, вычитание).
— если необходимо, то результат сокращаем.
— если необходимо, то выделяем целую часть.
2. Произведение дробей.
Правило простое. При умножении дробей умножаются их числители и знаменатели:
Примеры:
Одним из самых сложных разделов математики по сей день считаются дроби. История дробей насчитывает не одно тысячелетие. Умение делить целое на части возникло на территории древнего Египта и Вавилона. С годами усложнялись операции, проделываемые с дробями, менялась форма их записи. У каждого были свои особенности во «взаимоотношениях» с этим разделом математики.
Что такое дробь?
Когда возникла необходимость делить целое на части без лишних усилий, тогда и появились дроби. История дробей неразрывна связана с решением утилитарных задач. Сам термин «дробь» имеет арабские корни и происходит от слова, обозначающего «ломать, разделять». С древних времен в этом смысле мало что изменилось. Современное определение звучит следующим образом: дробь — это часть или сумма частей единицы. Соответственно, примеры с дробями представляют собой последовательное выполнение математических операций с долями чисел.
Современное определение звучит следующим образом: дробь — это часть или сумма частей единицы. Соответственно, примеры с дробями представляют собой последовательное выполнение математических операций с долями чисел.
Сегодня различают два способа их записи. возникли в разное время: первые являются более древними.
Пришли из глубины веков
Впервые оперировать дробями начали на территории Египта и Вавилона. Подход математиков двух государств имел значительные отличия. Однако начало и там и там было положено одинаково. Первой дробью стала половина или 1/2. Дальше возникла четверть, треть и так далее. Согласно данным археологических раскопок, история возникновения дробей насчитывает около 5 тысяч лет. Впервые доли числа встречаются в египетских папирусах и на вавилонских глиняных табличках.
Древний Египет
Виды обыкновенных дробей сегодня включают в себя и так называемые египетские. Они представляют собой сумму нескольких слагаемых вида 1/n. Числитель — всегда единица, а знаменатель — натуральное число. Появились такие дроби, как ни трудно догадаться, в древнем Египте. При расчетах все доли старались записывать в виде таких сумм (например, 1/2 + 1/4 + 1/8). Отдельными обозначениями обладали только дроби 2/3 и 3/4, остальные разбивались на слагаемые. Существовали специальные таблицы, в которых доли числа представлялись в виде суммы.
Появились такие дроби, как ни трудно догадаться, в древнем Египте. При расчетах все доли старались записывать в виде таких сумм (например, 1/2 + 1/4 + 1/8). Отдельными обозначениями обладали только дроби 2/3 и 3/4, остальные разбивались на слагаемые. Существовали специальные таблицы, в которых доли числа представлялись в виде суммы.
Наиболее древнее из известных упоминаний такой системы встречается в Математическом папирусе Ринда, датируемом началом второго тысячелетия до нашей эры. Он включает таблицу дробей и математические задачи с решениями и ответами, представленными в виде сумм дробей. Египтяне умели складывать, делить и умножать доли числа. Дроби в долине Нила записывались с помощью иероглифов.
Представление доли числа в виде суммы слагаемых вида 1/n, характерное для древнего Египта, использовалось математиками не только этой страны. Вплоть до Средних веков египетские дроби применялись на территории Греции и других государств.
Развитие математики в Вавилоне
Иначе выглядела математика в Вавилонском царстве. История возникновения дробей здесь напрямую связана с особенностями системы счисления, доставшейся древнему государству в наследство от предшественника, шумеро-аккадской цивилизации. Расчетная техника в Вавилоне была удобнее и совершеннее, чем в Египте. Математика в этой стране решала гораздо больший круг задач.
История возникновения дробей здесь напрямую связана с особенностями системы счисления, доставшейся древнему государству в наследство от предшественника, шумеро-аккадской цивилизации. Расчетная техника в Вавилоне была удобнее и совершеннее, чем в Египте. Математика в этой стране решала гораздо больший круг задач.
Судить о достижениях вавилонян сегодня можно по сохранившимся глиняным табличкам, заполненным клинописью. Благодаря особенностям материала они дошли до нас в большом количестве. По мнению некоторых в Вавилоне раньше Пифагора открыли известную теорему, что, несомненно, свидетельствует о развитии науки в этом древнем государстве.
Дроби: история дробей в Вавилоне
Система счисления в Вавилоне была шестидесятеричной. Каждый новый разряд отличался от предыдущего на 60. Такая система сохранилась в современном мире для обозначения времени и величин углов. Дроби также были шестидесятеричными. Для записи использовали специальные значки. Как и в Египте, примеры с дробями содержали отдельные символы для обозначения 1/2, 1/3 и 2/3.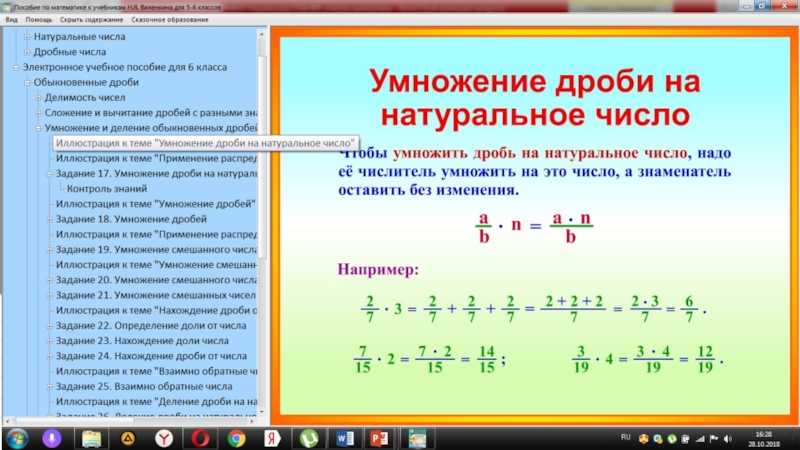
Вавилонская система не исчезла вместе с государством. Дробями, написанными в 60-тиричной системе, пользовались античные и арабские астрономы и математики.
Древняя Греция
История обыкновенных дробей мало чем обогатилась в древней Греции. Жители Эллады считали, что математика должна оперировать лишь целыми числами. Поэтому выражения с дробями на страницах древнегреческих трактатов практически не встречались. Однако определенный вклад в этот раздел математики внесли пифагорейцы. Они понимали дроби как отношения или пропорции, а единицу считали также неделимой. Пифагор с учениками построил общую теорию дробей, научился проводить все четыре арифметические операции, а также сравнение дробей путем приведения их к общему знаменателю.
Священная римская империя
Римская система дробей была связана с мерой веса, называемой «асс». Она делилась на 12 долей. 1/12 асса называлась унцией. Для обозначения дробей существовало 18 названий. Приведем некоторые из них:
семис — половина асса;
секстанте — шестая доля асса;
семиунция — пол-унции или 1/24 асса.
Неудобство такой системы заключалось в невозможности представить число в виде дроби со знаменателем 10 или 100. Римские математики преодолели трудность с помощью использования процентов.
Написание обыкновенных дробей
В Античности дроби уже писали знакомым нам образом: одно число над другим. Однако было одно существенное отличие. Числитель располагался под знаменателем. Впервые так писать дроби начали в древней Индии. Современный нам способ стали использовать арабы. Но никто из названных народов не применял горизонтальную черту для разделения числителя и знаменателя. Впервые она появляется в трудах Леонардо Пизанского, более известного как Фибоначчи, в 1202 году.
Китай
Если история возникновения обыкновенных дробей началась в Египте, то десятичные впервые появились в Китае. В Поднебесной империи их стали использовать примерно с III века до нашей эры. История десятичных дробей началась с китайского математика Лю Хуэя, предложившего использовать их при извлечении квадратных корней.
В III веке нашей эры десятичные дроби в Китае стали применяться при расчете веса и объема. Постепенно они все глубже начали проникать в математику. В Европе, однако, десятичные дроби стали использоваться гораздо позже.
Аль-Каши из Самарканда
Независимо от китайских предшественников десятичные дроби открыл астроном аль-Каши из древнего города Самарканда. Жил и трудился он в XV веке. Свою теорию ученый изложил в трактате «Ключ к арифметике», увидевшем свет в 1427 году. Аль-Каши предложил использовать новую форму записи дробей. И целая, и дробная часть теперь писались в одной строке. Для их разделения самаркандский астроном не использовал запятую. Он писал целое число и дробную часть разными цветами, используя черные и красные чернила. Иногда для разделения аль-Каши также применял вертикальную черту.
Десятичные дроби в Европе
Новый вид дробей начал появляться в трудах европейских математиков с XIII века. Нужно заметить, что с трудами аль-Каши, как и с изобретением китайцев они знакомы не были. Десятичные дроби появились в трудах Иордана Неморария. Затем их использовал уже в XVI веке Французский ученый написал «Математический канон», в котором содержались тригонометрические таблицы. В них Виет использовал десятичные дроби. Для разделения целой и дробной части ученый применял вертикальную черту, а также разный размер шрифта.
Десятичные дроби появились в трудах Иордана Неморария. Затем их использовал уже в XVI веке Французский ученый написал «Математический канон», в котором содержались тригонометрические таблицы. В них Виет использовал десятичные дроби. Для разделения целой и дробной части ученый применял вертикальную черту, а также разный размер шрифта.
Однако это были лишь частные случаи научного использования. Для решения повседневных задач десятичные дроби в Европе стали применяться несколько позже. Произошло это благодаря голландскому ученому Симону Стевину в конце XVI века. Он издал математический труд «Десятая» в 1585 году. В нем ученый изложил теорию использования десятичных дробей в арифметике, в денежной системе и для определения мер и весов.
Точка, точка, запятая
Стевин также не пользовался запятой. Он отделял две части дроби при помощи нуля, обведенного в круг.
Впервые запятая разделила две части десятичной дроби только в 1592 году. В Англии, однако, вместо нее стали применять точку. На территории США до сих пор десятичные дроби пишут именно таким образом.
На территории США до сих пор десятичные дроби пишут именно таким образом.
Одним из инициаторов использования обоих знаков препинания для разделения целой и дробной части был шотландский математик Джон Непер. Он высказал свое предложение в 1616-1617 гг. Запятой пользовался и немецкий ученый
Дроби на Руси
На русской земле первым математиком, изложившим деление целого на части, стал новгородский монах Кирик. В 1136 году он написал труд, в котором изложил метод «счисления лет». Кирик занимался вопросами хронологии и календаря. В своем труде он привел в том числе и деление часа на части: пятые, двадцать пятые и так далее доли.
Деление целого на части применялось при расчете размера налога в XV-XVII веках. Использовались операции сложения, вычитания, деления и умножения с дробными частями.
Само слово «дробь» появилось на Руси в VIII веке. Оно произошло от глагола «дробить, разделять на части». Для названия дробей наши предки использовали специальные слова. Например, 1/2 обозначалась как половина или полтина, 1/4 — четь, 1/8 — полчеть, 1/16 — полполчеть и так далее.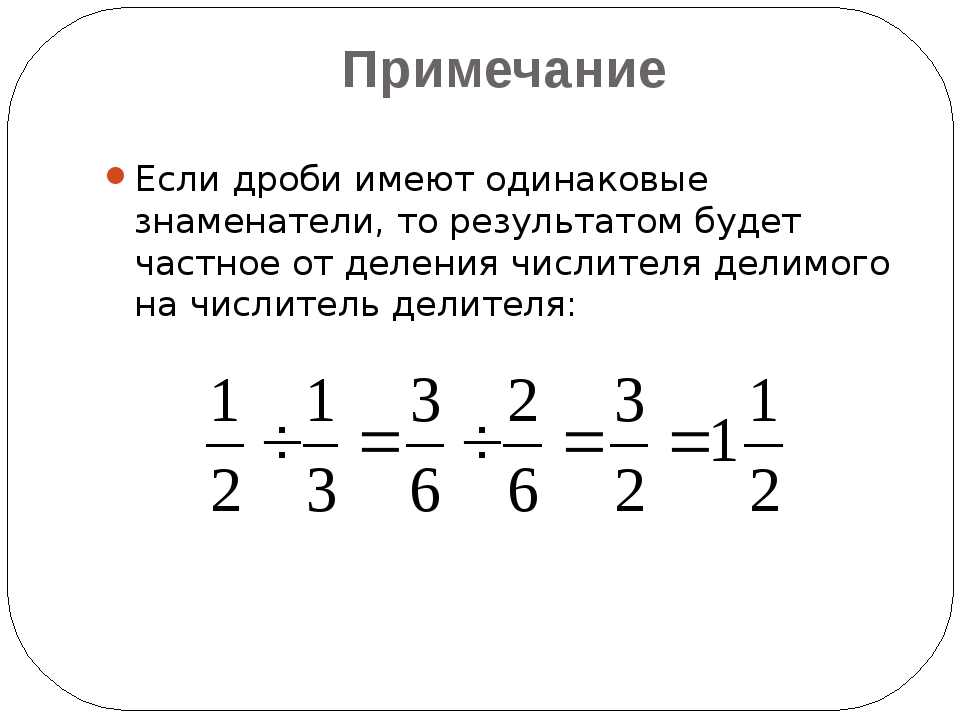
Полная теория дробей, мало чем отличающаяся от современной, была изложена в первом учебнике по арифметике, написанном в 1701 году Леонтием Филипповичем Магницким. «Арифметика» состояла из нескольких частей. О дробях подробно автор рассказывает в разделе «О числах ломаных или с долями». Магницкий приводит операции с «ломанными» числами, разные их обозначения.
Сегодня по-прежнему в числе самых сложных разделов математики называются дроби. История дробей также не была простой. Разные народы иногда независимо друг от друга, а иногда заимствуя опыт предшественников, пришли к необходимости введения, освоения и применения долей числа. Всегда учение о дробях вырастало из практических наблюдений и благодаря насущным проблемам. Необходимо было делить хлеб, размечать равные участки земли, высчитывать налоги, измерять время и так далее. Особенности применения дробей и математических операций с ними зависели от системы счисления в государстве и от общего уровня развития математики. Так или иначе, преодолев не одну тысячу лет, раздел алгебры, посвященный долям чисел, сформировался, развился и с успехом используется сегодня для самых разных нужд как практического характера, так и теоретического.
Изучая царицу всех наук — математику, в определенный момент все сталкиваются с дробями. Хотя это понятие (как и сами виды дробей или математические действия с ними) совсем несложное, к нему нужно относиться внимательно, ведь в реальной жизни за пределами школы оно очень пригодится. Итак, давайте освежим свои знания о дробях: что это, для чего нужно, какие виды их бывают и как совершать с ними различные арифметические действия.
Ее величество дробь: это что такое
Дробями в математике называются числа, каждое из которых состоит из одной или более частей единицы. Такие дроби еще называют обыкновенными, либо простыми. Как правило, они записываются в виде двух чисел, которые разделены горизонтальной или слеш-чертой, она называется «дробной». Например: ½, ¾.
Верхнее, или первое из этих чисел — это числитель (показывает, сколько взято долей от числа), а нижнее, или второе — знаменатель (демонстрирует, на столько частей разделена единица).
Дробная черта фактически выполняет функции знака деления.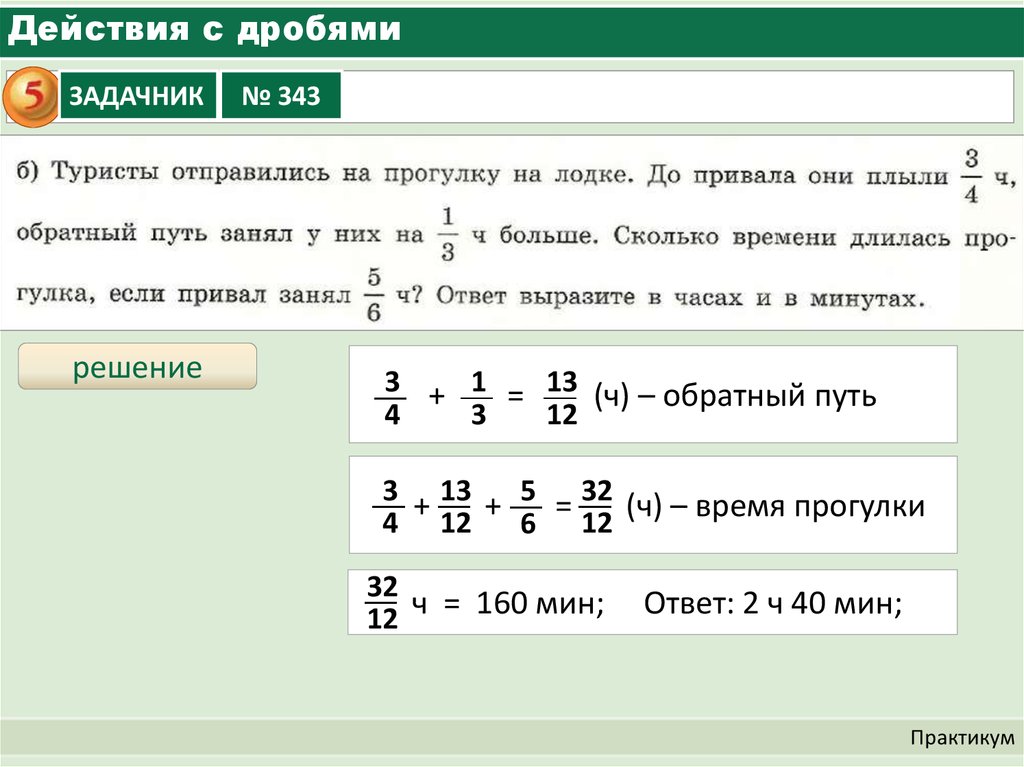 К примеру, 7:9=7/9
К примеру, 7:9=7/9
Традиционно обыкновенные дроби меньше единицы. В то время как десятичные могут быть больше ее.
Для чего нужны дроби? Да для всего, ведь в реальном мире далеко не все числа целые. К примеру, две школьницы в столовой купили в складчину одну вкусную шоколадку. Когда они уже собрались делить десерт, встретили подружку и решили угостить и и ее. Однако теперь необходимо правильно разделить шоколадку, если учесть, что она состоит из 12 квадратиков.
Поначалу девчонки хотели разделить все поровну, и тогда каждой бы досталось по четыре кусочка. Но, раздумав, они решили угостить подружку, не 1/3, а 1/4 шоколадки. А поскольку школьницы плохо изучали дроби, то они не учли, что при подобном раскладе в результате у них останется 9 кусочков, которые очень плохо делятся на двоих. Этот довольно простой пример показывает, насколько важно уметь правильно находить часть от числа. А ведь в жизни подобных случаев гораздо больше.
Виды дробей: обыкновенные и десятичные
Все математические дроби делятся на два больших разряда: обыкновенные и десятичные. Об особенностях первого из них было рассказано в предыдущем пункте, так что теперь стоит уделить внимание второму.
Об особенностях первого из них было рассказано в предыдущем пункте, так что теперь стоит уделить внимание второму.
Десятичной называют позиционную запись дроби числа, которая фиксируется на письме через запятую, без черточки или слеша. Например: 0,75, 0,5.
Фактически десятичная дробь идентична обыкновенной, однако, в ее знаменателе всегда единица с последующими нулями — отсюда произошло и ее название.
Число, предшествующее запятой, — это целая часть, а все находящееся после — дробная. Любую простую дробь можно перевести в десятичную. Так, указанные в предыдущем примере десятичные дроби можно записать как обычные: ¾ и ½.
Стоит отметить, что и десятичные, и обыкновенные дроби могут быть как положительными, так и отрицательными. Если перед ними стоит знак «-«, данная дробь отрицательная, если «+» — то положительная.
Подвиды обыкновенных дробей
Есть такие виды дробей простых.
Подвиды десятичной дроби
В отличие от простой, десятичная дробь делится всего на 2 вида.
- Конечная — получила такое название из-за того, что после запятой у нее ограниченное (конечное) число цифр: 19,25.
- Бесконечная дробь — это число с нескончаемым количеством цифр после запятой. К примеру, при делении 10 на 3 результатом будет бесконечная дробь 3,333…
Сложение дробей
Проводить различные арифметические манипуляции с дробями немного сложнее, чем с обычными числами. Однако, если усвоить основные правила, решить любой пример с ними не составит особого труда.
Например: 2/3+3/4. Наименьшим общим кратным для них будет 12, следовательно, необходимо, чтобы в каждом знаменателе стояло это число. Для этого числитель и знаменатель первой дроби умножаем на 4, получается 8/12, аналогично поступаем со вторым слагаемым, но только множим на 3 — 9/12. Теперь можно легко решить пример: 8/12+9/12= 17/12. Получившаяся дробь — это неправильная величина, поскольку числитель больше знаменателя. Ее можно и нужно пребразовать в правильную смешанную, разделив 17:12= 1 и 5/12.
В случае, если слагаются смешанные дроби, сначала действия совершаются с целыми числами, а потом с дробными.
Если в примере присутствует десятичная дробь и обычная, необходимо, чтобы обе стали простыми, потом привести их к одному знаменателю и сложить. К примеру 3,1+1/2. Число 3,1 можно записать как смешанную дробь 3 и 1/10 или как неправильную — 31/10. Общим знаменателем для слагаемых будет 10, поэтому нужно умножить поочередно числитель и знаменатель 1/2 на 5, получается 5/10. Далее можно легко все высчитать: 31/10+5/10=35/10. Полученный результат — неправильная сократимая дробь, приводим ее в нормальный вид, сократив на 5: 7/2=3 и 1/2, или десятичной — 3,5.
Если слагать 2 десятичные дроби, важно, чтобы после запятой было одинаковое количество цифр. Если это не так, нужно просто дописать необходимое количество нулей, ведь в десятичной дроби это можно сделать безболезненно. Например, 3,5+3,005. Чтобы решить это задание, нужно к первому числу прибавить 2 ноля и далее поочередно слагать: 3,500+3,005=3,505.
Вычитание дробей
Вычитая дроби, стоит поступать так же, как и при сложении: свести к общему знаменателю, отнять один числитель от другого, при необходимости перевести результат в смешанную дробь.
Например: 16/20-5/10. Общим знаменателем будет 20. Нужно привести вторую дробь к этому знаменателю, умножив обе ее части на 2, получается 10/20. Теперь можно решать пример: 16/20-10/20= 6/20. Однако этот результат относится к сократимым дробям, поэтому стоит поделить обе части на 2 и получается результат — 3/10.
Умножение дробей
Деление и умножение дробей — значительно более простые действия, нежели сложение и вычитание. Дело в том, что, выполняя эти задания, нет необходимости искать общий знаменатель.
Чтобы умножить дроби, нужно просто поочередно перемножить между собою оба числителя, а затем и оба знаменателя. Получившийся результат сократить, если дробь — это сократимая величина.
Например: 4/9х5/8. После поочередного умножения получается такой результат 4х5/9х8=20/72. Такая дробь сократима на 4, поэтому конечный ответ в примере — 5/18.
Такая дробь сократима на 4, поэтому конечный ответ в примере — 5/18.
Как делить дроби
Деление дробей — тоже несложное действие, фактически оно все равно сводится к их умножению. Чтобы разделить одну дробь на другую, нужно вторую перевернуть и умножить на первую.
Например, деление дробей 5/19 и 5/7. Чтобы решить пример, нужно поменять местами знаменатель и числитель второй дроби и умножить: 5/19х7/5=35/95. Результат можно сократить на 5 — получается 7/19.
В случае, если необходимо разделить дробь на простое число, методика немного отличается. Изначально стоит записать это число как неправильную дробь, а потом делить по той же схеме. Например, 2/13:5 нужно записать как 2/13: 5/1. Теперь нужно перевернуть 5/1 и умножить получившиеся дроби: 2/13х1/5= 2/65.
Иногда приходится совершать деление дробей смешанных. С ними нужно поступать, как и с целыми числами: превратить в неправильные дроби, перевернуть делитель и умножить все. Например, 8 ½: 3. Превращаем все в неправильные дроби: 17/2: 3/1. Далее следует переворот 3/1 и умножение: 17/2х1/3= 17/6. Теперь следует перевести неправильную дробь в правильную — 2 целых и 5/6.
Далее следует переворот 3/1 и умножение: 17/2х1/3= 17/6. Теперь следует перевести неправильную дробь в правильную — 2 целых и 5/6.
Итак, разобравшись с тем, что такое дроби и как можно с ними совершать различные арифметические действия, нужно постараться не забывать об этом. Ведь люди всегда более склонны делить что-то на части, нежели прибавлять, поэтому нужно уметь делать это правильно.
Рассмотрение данной темы мы начнем с изучения понятия доли в целом, которое даст нам более полное понимание смысла обыкновенной дроби. Дадим основные термины и их определение, изучим тему в геометрическом толковании, т.е. на координатной прямой, а также определим список основных действий с дробями.
Yandex.RTB R-A-339285-1
Доли целого
Представим некий предмет, состоящий из нескольких, совершенно равных частей. Например, это может быть апельсин, состоящий из нескольких одинаковых долек.
Определение 1
Доля целого или доля – это каждая из равных частей, составляющих целый предмет.
Очевидно, что доли могут быть разные. Чтобы наглядно пояснить это утверждение, представим два яблока, одно из которых разрезано на две равные части, а второе – на четыре. Ясно, что размеры получившихся долей у разных яблок будут различаться.
Доли имеют свои названия, которые зависят от количества долей, составляющих целый предмет. Если предмет имеет две доли, то каждая из них будет определяться как одна вторая доля этого предмета; когда предмет состоит из трех долей, то каждая из них – одна третья и так далее.
Определение 2
Половина – одна вторая доля предмета.
Треть – одна третья доля предмета.
Четверть – одна четвертая доля предмета.
Чтобы сократить запись, ввели следующие обозначения долей: половина — 1 2 или 1 / 2 ; треть — 1 3 или 1 / 3 ; одна четвертая доля — 1 4 или 1 / 4 и так далее. Записи с горизонтальной чертой используются чаще.
Понятие доли естественно расширяется с предметов на величины. Так, можно использовать для измерения небольших предметов доли метра (треть или одна сотая), как одной из единиц измерения длины. Аналогичным образом можно применить доли других величин.
Так, можно использовать для измерения небольших предметов доли метра (треть или одна сотая), как одной из единиц измерения длины. Аналогичным образом можно применить доли других величин.
Обыкновенные дроби, определение и примеры
Обыкновенные дробиприменяются для описания количества долей. Рассмотрим простой пример, который приблизит нас к определению обыкновенной дроби.
Представим апельсин, состоящий из 12 долек. Каждая доля тогда будет – одна двенадцатая или 1 / 12 . Две доли – 2 / 12 ; три доли – 3 / 12 и т.д. Все 12 долей или целое число будет выглядеть так: 12 / 12 . Каждая из используемых в примере записей является примером обыкновенной дроби.
Определение 3
Обыкновенная дробь – это запись вида m n или m / n , где m и n являются любыми натуральными числами.
Согласно данному определению, примерами обыкновенных дробей могут быть записи: 4 / 9 , 11 34 , 917 54 . А такие записи: 11 5 , 1 , 9 4 , 3 не являются обыкновенными дробями.
Числитель и знаменатель
Определение 4
Числителем обыкновенной дроби m n или m / n является натуральное число m .
Знаменателем обыкновенной дроби m n или m / n является натуральное число n .
Т.е. числитель – число, расположенное сверху над чертой обыкновенной дроби (или слева от наклонной черты), а знаменатель – число, расположенное под чертой (справа от наклонной черты).
Какой же смысл несут в себе числитель и знаменатель? Знаменатель обыкновенной дроби указывает на то, из скольких долей состоит один предмет, а числитель дает нам информацию о том, каково рассматриваемое количество таких долей. К примеру, обыкновенная дробь 7 54 указывает нам на то, что некий предмет состоит из 54 долей, и для рассмотрения мы взяли 7 таких долей.
Натуральное число как дробь со знаменателем 1
Знаменатель обыкновенной дроби может быть равен единице. В таком случае возможно говорить, что рассматриваемый предмет (величина) неделим, являет собой нечто целое. Числитель в подобной дроби укажет, какое количество таких предметов взято, т.е. обыкновенная дробь вида m 1 имеет смысл натурального числа m . Это утверждение служит обоснованием равенства m 1 = m .
Числитель в подобной дроби укажет, какое количество таких предметов взято, т.е. обыкновенная дробь вида m 1 имеет смысл натурального числа m . Это утверждение служит обоснованием равенства m 1 = m .
Запишем последнее равенство так: m = m 1 . Оно даст нам возможность любое натуральное число использовать в виде обыкновенной дроби. К примеру, число 74 – это обыкновенная дробь вида 74 1 .
Определение 5
Любое натуральное число m возможно записать в виде обыкновенной дроби, где знаменатель – единица: m 1 .
В свою очередь, любая обыкновенная дробь вида m 1 может быть представлена натуральным числом m .
Черта дроби как знак деления
Использованное выше представление данного предмета как n долей является не чем иным, как делением на n равных частей. Когда предмет разделен на n частей, мы имеем возможность разделить его поровну между n людьми – каждый получит свою долю.
В случае, когда мы изначально имеем m одинаковых предметов (каждый разделен на n частей), то и эти m предметов возможно поровну разделить между n людьми, дав каждому из них по одной доле от каждого из m предметов. При этом у каждого человека будет m долей 1 n , а m долей 1 n даст обыкновенную дробь m n . Следовательно, обыкновенную дробь m n можно использовать, чтобы обозначать деление m предметов между n людьми.
При этом у каждого человека будет m долей 1 n , а m долей 1 n даст обыкновенную дробь m n . Следовательно, обыкновенную дробь m n можно использовать, чтобы обозначать деление m предметов между n людьми.
Полученное утверждение устанавливает связь между обыкновенными дробями и делением. И эту связь можно выразить следующим образом: черту дроби возможно иметь в виду в качестве знака деления, т.е. m / n = m: n .
При помощи обыкновенной дроби мы можем записать итог деления двух натуральных чисел. К примеру, деление 7 яблок на 10 человек запишем как 7 10: каждому человеку достанется семь десятых долей.
Равные и неравные обыкновенные дроби
Логичным действием является сравнение обыкновенных дробей, ведь очевидно, что, к примеру, 1 8 яблока отлична от 7 8 .
Результатом сравнения обыкновенных дробей может быть: равны или неравны.
Определение 6
Равные обыкновенные дроби – обыкновенные дроби a b и c d , для которых справедливо равенство: a · d = b · c .
Неравные обыкновенные дроби — обыкновенные дроби a b и c d , для которых равенство: a · d = b · c не является верным.
Пример равных дробей: 1 3 и 4 12 – поскольку выполняется равенство 1 · 12 = 3 · 4 .
В случае, когда выясняется, что дроби не являются равными, обычно необходимо также узнать, какая из данных дробей меньше, а какая – больше. Чтобы дать ответ на эти вопросы, обыкновенные дроби сравнивают, приводя их к общему знаменателю и затем сравнив числители.
Дробные числа
Каждая дробь – это запись дробного числа, что по сути — просто «оболочка», визуализация смысловой нагрузки. Но все же для удобства мы объединяем понятия дроби и дробного числа, говоря просто – дробь.
Все дробные числа, как и любое другое число, имеют свое уникальное месторасположение на координатном луче: существует однозначное соответствие между дробями и точками координатного луча.
Чтобы на координатном луче найти точку, обозначающую дробь m n , необходимо от начала координат отложить в положительном направлении m отрезков, длина каждого из которых составит 1 n долю единичного отрезка. Отрезки можно получить, разделив единичный отрезок на n одинаковых частей.
Отрезки можно получить, разделив единичный отрезок на n одинаковых частей.
Как пример, обозначим на координатном луче точку М, которая соответствует дроби 14 10 . Длина отрезка, концами которого является точка О и ближайшая точка, отмеченная маленьким штрихом, равна 1 10 доле единичного отрезка. Точка, соответствующая дроби 14 10 , расположена в удалении от начала координат на расстояние 14 таких отрезков.
Если дроби равны, т.е. им соответствует одно и то же дробное число, тогда эти дроби служат координатами одной и той же точки на координатном луче. К примеру, координатам в виде равных дробей 1 3 , 2 6 , 3 9 , 5 15 , 11 33 соответствует одна и та же точка на координатном луче, располагающаяся на расстоянии трети единичного отрезка, отложенного от начала отсчета в положительном направлении.
Здесь работает тот же принцип, что и с целыми числами: на горизонтальном, направленном вправо координатном луче точка, которой соответствует большая дробь, разместится правее точки, которой соответствует меньшая дробь. И наоборот: точка, координата которой – меньшая дробь, будет располагаться левее точки, которой соответствует бОльшая координата.
И наоборот: точка, координата которой – меньшая дробь, будет располагаться левее точки, которой соответствует бОльшая координата.
Правильные и неправильные дроби, определения, примеры
В основе разделения дробей на правильные и неправильные лежит сравнение числителя и знаменателя в пределах одной дроби.
Определение 7
Правильная дробь – это обыкновенная дробь, в которой числитель меньше, чем знаменатель. Т.е., если выполняется неравенство m
Неправильная дробь — это обыкновенная дробь, числитель которой больше или равен знаменателю. Т.е., если выполняется неравенство undefined , то обыкновенная дробь m n является неправильной.
Приведем примеры: — правильные дроби:
Пример 1
5 / 9 , 3 67 , 138 514 ;
Неправильные дроби:
Пример 2
13 / 13 , 57 3 , 901 112 , 16 7 .
Также возможно дать определение правильных и неправильных дробей, опираясь на сравнение дроби с единицей.
Определение 8
Правильная дробь – обыкновенная дробь, которая меньше единицы.
Неправильная дробь – обыкновенная дробь, равная или бОльшая единицы.
Например, дробь 8 12 – правильная, т.к. 8 12 1 , а 14 14 = 1 .
Немного углубимся в размышление, почему дроби, в которых числитель больше или равен знаменателю получили название «неправильных».
Рассмотрим неправильную дробь 8 8: она сообщает нам, что взято 8 долей предмета, состоящего из 8 долей. Таким образом, из имеющихся восьми долей мы можем составить целый предмет, т.е. заданная дробь 8 8 по сути представляет целый предмет: 8 8 = 1 . Дроби, в которых числитель и знаменатель равны, полноценно заменяет натуральное число 1 .
Рассмотрим также дроби, в которых числитель превосходит знаменатель: 11 5 и 36 3 . Понятно, что дробь 11 5 сообщает о том, что из нее мы можем составить два целых предмета и еще останется одна пятая доля. Т.е. дробь 11 5 – это 2 предмета и еще 1 5 от него. В свою очередь, 36 3 – дробь, означающая по сути 12 целых предметов.
Указанные примеры дают возможность сделать вывод, что неправильные дроби возможно заменить натуральными числами (если числитель без остатка делится на знаменатель: 8 8 = 1 ; 36 3 = 12) или суммой натурального числа и правильной дроби (если числитель не делится на знаменатель без остатка: 11 5 = 2 + 1 5). Вероятно, потому такие дроби и получили название «неправильных».
Вероятно, потому такие дроби и получили название «неправильных».
Здесь также мы сталкиваемся с одним из важнейших навыков работы с числами.
Определение 9
Выделение целой части из неправильной дроби – это запись неправильной дроби в виде суммы натурального числа и правильной дроби.
Также отметим, что существует тесная взаимосвязь между неправильными дробями и смешанными числами.
Положительные и отрицательные дроби
Выше мы говорили о том, что каждой обыкновенной дроби соответствует положительное дробное число. Т.е. обыкновенные дроби – это положительные дроби. Например, дроби 5 17 , 6 98 , 64 79 – положительные, и, когда необходимо особо подчеркнуть «положительность» дроби, она записывается с использованием знака плюс: + 5 17 , + 6 98 , + 64 79 .
Если же обыкновенной дроби присвоить знак минус, то полученная запись будет являться записью отрицательного дробного числа, и мы говорим в таком случае об отрицательных дробях. Например, — 8 17 , — 78 14 и т. д.
д.
Положительная и отрицательная дроби m n и — m n – противоположные числа.Например, дроби 7 8 и — 7 8 являются противоположными.
Положительные дроби, как и любые положительные числа в целом, означают прибавление, изменение в сторону увеличения. В свою очередь, отрицательные дроби соответствуют расходу, изменению в сторону уменьшения.
Если мы рассмотрим координатную прямую, то увидим, что отрицательные дроби расположены левее точки начала отсчета. Точки, которым соответствуют дроби, являющиеся противоположными (m n и — m n), располагаются на одинаковом расстоянии от начала отсчета координат О, но по разные стороны от нее.
Здесь также отдельно скажем о дробях, записанных в виде 0 n . Такая дробь равна нулю, т.е. 0 n = 0 .
Суммируя все вышесказанное, мы подошли к важнейшему понятию рациональных чисел.
Определение 10
Рациональные числа – это множество положительных дробей, отрицательных дробей и дробей вида 0 n .
Действия с дробями
Перечислим основные действия с дробями.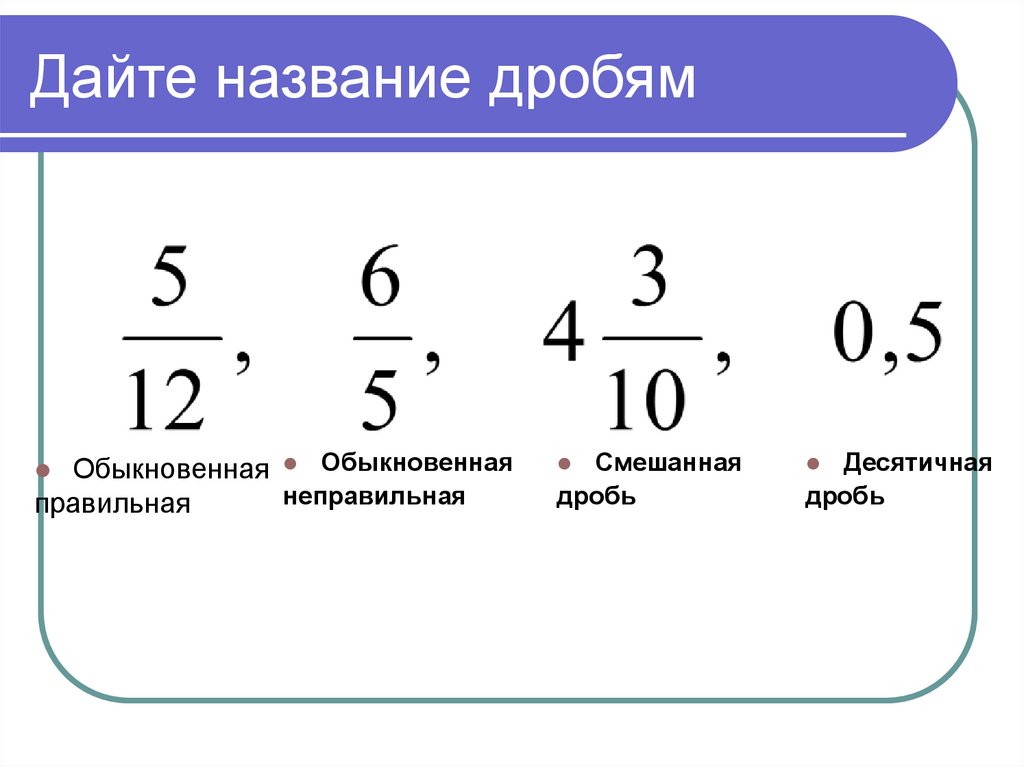 В общем и целом, суть их та же, что имеют соответствующие действия с натуральными числами
В общем и целом, суть их та же, что имеют соответствующие действия с натуральными числами
- Сравнение дробей – данное действие мы рассмотрели выше.
- Сложение дробей – результатом сложения обыкновенных дробей является обыкновенная дробь (в частном случае сокращаемая до натурального числа).
- Вычитание дробей – действие, обратно сложению, когда по одной известной дроби и заданной сумме дробей определяется неизвестная дробь.
- Умножение дробей – это действие можно описать как нахождение дроби от дроби. Результат умножения двух обыкновенных дробей – обыкновенная дробь (в частном случае равная натуральному числу).
- Деление дробей – действие, обратное умножению, когда мы определяем дробь, на которую необходимо умножить заданную, чтобы получить известное произведение двух дробей.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Сложение и вычитание дробей с одинаковыми знаменателями
Скачать 20.
|
С этим файлом связано 18 файл(ов). Среди них: funktsionalnaya gramotnost.pptx, 00067d0a-56b25aca.doc, поурочный 9ю3.docx, 7 класс.pdf, 3kl_fizkult_ 2019-2020.docx, ЕГ_7_Малярия критерии.docx, 2021d6129e3c9 21d3ccd3d959 dd60923.docx, blanki-oge-2021.pdf, Список детей.docx, 11.pdf, 56.pdf, График дежурств учителей МБОУ.docx, рабочая программа 9 класс геометрия (автовосстан овление).docx, ЕГ_7 класс_вариант 2_система оценивания.docx, Анализ воспитательной работы за 1 полугодие 2021-2022.doc, Практическая работа № 1.doc, Практическая работа 4.docx, практическая работа 3.docx и ещё 8 файл(а). Показать все связанные файлы Подборка по базе: Самостоятельная работа по алгебре 8 класс _Сокращение дробей.  Сло, №1.Сложение и вычитание.docx, Самостоятельная работа по теме Сложение и умножение числовых нер, Разработка открытого урока обобщения знаний по теме Умножение и , Самостоятельная работа по теме «Сложение и вычитание смешанных ч, тренажер сложение.docx, Сравнение, сложение и вычитание дробей с разными знаменателями.d, карточка сложение смешаных.docx, с.р. вычитание целых чисел.docx, Задания на сложение и сравнение целых чисел.docx Сло, №1.Сложение и вычитание.docx, Самостоятельная работа по теме Сложение и умножение числовых нер, Разработка открытого урока обобщения знаний по теме Умножение и , Самостоятельная работа по теме «Сложение и вычитание смешанных ч, тренажер сложение.docx, Сравнение, сложение и вычитание дробей с разными знаменателями.d, карточка сложение смешаных.docx, с.р. вычитание целых чисел.docx, Задания на сложение и сравнение целых чисел.docxПлан-конспект открытого урока по математике в 5 классе Тема: Сложение и вычитание дробей с одинаковыми знаменателями Учитель: Хадисов М.Х. – учитель математики МКОУ «Митлиурибская ООШ» Тип урока: урок получения новых знаний Цель урока: формирование навыков сложения и вычитания дробей с одинаковыми знаменателями, развитие умения складывать и вычитать дроби с одинаковыми знаменателями Задачи: Повторить понятие обыкновенной дроби; Сформулировать правила сложения и вычитания обыкновенных дробей с одинаковыми множителями через решение проблемной ситуации; Формировать навыки сложения и вычитания дробей с одинаковыми знаменателями.  Планируемые результаты:учащиеся познакомятся с правилами сложения и вычитания обыкновенных дробей с одинаковыми знаменателями, научаться применять данные правила на практике, при решении задач. Личностные УУД: проявление учебно-познавательного интереса, формирование мотивации к изучению нового материала. Предметные УУД: знать и использовать основные правила работы на уроке; научиться использовать правила сложения и вычитания обыкновенных дробей с одинаковыми знаменателями. Метапредметные УУД: Регулятивные: ставить учебную задачу урока, решать учебную задачу под руководством учителя, определять цель учебного задания, работать в соответствии с планом; находить и исправлять ошибки, отвечать на итоговые вопросы, оценивать свои достижения и работу одноклассников Познавательные: формировать навыки сложения и вычитания дробей с одинаковыми знаменателями; научить правильно читать и записывать выражения, содержащие обыкновенные дроби; формировать умение решать задачи на сложение и вычитание дробей с одинаковыми знаменателями; применять полученные знания при решении задач. Коммуникативные: воспитывать любовь к математике, уважение друг к другу, умение слушать, дисциплинированность, самостоятельность мышления. Репродуктивный (стимулирование учебной деятельности) Наглядный Проблемно – поисковый Эвристическая беседа Формы работы учащихся: Фронтальная Парная Ход урока Организационный момент. Приветствие, проверка готовности учащихся к занятию, организация внимания детей. Здравствуйте, ребята! Пожалуйста, убедитесь в своей готовности к уроку! Я желаю вам успешной и плодотворной работы! Садитесь. Актуализация знаний.  Учитель направляет деятельность учащихся, определяет содержание урока (продолжение изучения обыкновенных дробей). Ребята, на прошлых занятиях мы с Вами уже успели познакомиться и подружиться с понятием обыкновенной дроби. Давайте вспомним всё то, что мы уже знаем об обыкновенных дробях? Ученикам предлагается ответить на вопросы и выполнить ряд заданий: Почему люди стали использовать дробные числа? (Деление целого на равные части привело людей к использованию дробных чисел). Как записывается обыкновенная дробь? (С помощью дробной черты) Как называют число, которое стоит над чертой дроби? Под чертой дроби? Что показывает знаменатель обыкновенной дроби? Что показывает числитель? Какие дроби называются правильными обыкновенными дробями? А какие называются неправильными дробями? Прочитайте дроби. Из представленных на доске дробей, ребята, сидящие на первом варианте, пусть выпишут все неправильные обыкновенные дроби.  Ребята, сидящие на втором варианте – выпишите все правильные дроби. Ребята, сидящие на втором варианте – выпишите все правильные дроби.А теперь расположите выписанные вами дроби в порядке убывания. Учащиеся устно отвечают на вопросы, письменно выполняют два последних задания, повторяют уже изученный материал. Создание проблемной ситуации. Учитель создает проблемную ситуацию, тем самым мотивирует учащихся искать решение, развивая логическое мышление. Рассмотрим задачу: Папа съел 6/12 частей пиццы, мама съела ещё 2/12 частей пиццы, а сын съел 3/12частей пиццы. Кто съел больше всех? Сколько пиццы съедено всего? На сколько папа съел больше, чем мама? Какое действие поможет нам ответить на первый вопрос в задаче? (Сравнение дробей). Какие действия необходимо выполнить, чтобы ответить на остальные вопросы? (Сложение и вычитание). При направляющей помощи учителя ученики отвечают на вопросы, делают выводы. Формулирование проблемы.  Мы уже умеем сравнивать дроби. А чему же нам предстоит научиться сегодня? (Сложению и вычитанию дробей). Правильно! Сегодня мы научимся складывать и вычитать обыкновенные дроби с одинаковыми знаменателями, и с помощью этих знаний мы будем решать задачи. Какую тему урока мы запишем в тетрадь? (Сложение и вычитание дробей с одинаковыми знаменателями). Ученики записывают тему и число. Изучение нового материала. При направляющей помощи учителя дети выполняют задания: По математике задали решить 6 примеров. Вася решил 3 примера и отправился на прогулку. Какую часть домашнего задания по математике выполнил Вася? (3/6). После прогулки Вася решил ещё 2 примера. Какую часть заданий он решил после прогулки? (2/6). Какую часть домашнего задания сделал Вася? (5/6). Как мы определили, что Вася решил именно 5/6 задания? (Дети формулируют правило сложения дробей с одинаковыми знаменателями). Давайте запишем решение данной задачи в тетрадь! Торт разрезали на 6 частей. Откроем учебник на странице 155 и прочтем правила сложения и вычитания дробей. При сложении дробей с одинаковыми знаменателями числители складывают, а знаменатель не меняют. При вычитании дробей с одинаковыми знаменателями числители вычитают, а знаменатель не меняют. Запишем в тетради буквенную запись правил! Эти правила надо выучить! Физминутка (слежение глазами за подвижными объектами) Первичное применение нового знания. Ещё раз вслух повторим правила сложения и вычитания дробей! Молодцы. Давайте вернемся к нашей задаче. Теперь мы сможем ответить на все вопросы? (Да). Ученики отвечают на вопросы. Запишем решение задачи в тетрадь. Самостоятельная работа с учебником. Ребята, теперь попробуйте самостоятельно выполнить задание по учебнику № 1005, № 1006. Рабочая тетрадь №1, №2, №3 Если вы затрудняетесь с решением, я помогу. Справились с заданием? Молодцы! Теперь давайте проверим результаты! Для проверки поменяйтесь тетрадками, ошибки подчеркиваем и оцениваем работу. «5» — задание выполнено без ошибок, 1-2 ошибки – «4», 3 ошибки «3». Рефлексия. Какую тему урока мы сегодня изучали? Какие цели были поставлены? Достигнуты ли они? Что показалось сложным? Повторите правило сложения дробей с одинаковыми знаменателями. Повторите правило вычитание дробей с одинаковыми знаменателями. Домашнее задание. Запишите в дневники домашнее задание: Выучить правила на стр. 155, решить 1041(а-в), №1049 (а). Дата проведения: 31.01.2019г. |
Пошаговое руководство по решению дробей с примерами
Вы ищете лучший способ похудеть? Если да!! Давайте узнаем, как решать дроби. Звучит странно? Да, вы правильно прочитали! Вам нужно знать индекс массы тела (ИМТ), используя дроби, чтобы эффективно похудеть.
Дамы, ювелир дает вам украшения весом 18 или 24 карата? 24 карата считаются чистым золотом, тогда как 18 карат означают 18/24, что равно 75% золота. Вот как вы можете использовать дроби, чтобы узнать чистоту ювелирных изделий.
Этот блог поможет вам понять, как решать дроби, используя различные методы. Кроме того, я перечислил несколько полезных советов по использованию дробей. Итак, чтобы не создавать путаницы, давайте подробно разберемся с концепцией дробей.
Что нужно знать о Fraction!!Содержание
Во-первых, поймите, что такое дробь.
Дробь — это числовая величина или значение, не являющееся целым числом, например, 4/5, 6/7 и т. д.
д.
| Забавный факт: Есть факт, который поможет вам произвести впечатление на учителей и друзей. Это черта или знак деления в дроби, известной как «ВИНКУЛУМ». |
Следующее, что нужно выучить, это термины, используемые для обозначения нарушений. Таким образом, каждая дробь состоит из двух частей.
| -> Первая часть называется числителем , написанным над знаком деления, и это делает количество частей дроби равным. Короче говоря, это означает количество частей, которые мы имеем в дробях. | -> В то время как вторая часть называется знаменателем , написанным под символом деления, она в основном равна общему количеству частей в целом, и поэтому она означает общее количество частей числа в целом. |
Например, В дроби 3/5 3 — числитель, а 5 — знаменатель.
Здесь 3 означает, что это третья часть целого числа, а 5 означает, что целое число состоит из 5 частей.
Второе, что нужно узнать о типах дробей.Мы имеем дело с тремя типами дробей. Давайте проверим каждый из них один за другим.
- Правильная дробь: В этой дроби числитель имеет меньшее значение по сравнению со знаменателем.
| Примечание: Значение правильной дроби всегда меньше 1. | Пример правильной дроби: 3/5, 1/2 и 5/7. |
- Неправильная дробь: В этой дроби числитель всегда больше знаменателя.
| Примечание: Значение неправильной дроби всегда больше 1. | Примером неправильной дроби является 6/3, 50/21 и 16/25. |
- Смешанная дробь: В этой дроби число представлено целым числом, за которым следуют дробные числа.

| Примечание: Смешанная дробь также называется смешанным числом. | Пример смешанной дроби: 6⅘, 2⅔ и 25⅝. |
Давайте разберемся, как решить смешанные дроби до целого числа на примере.
Замените 7⅘ на целое число.
| -> Сначала умножьте целое число на знаменатель дроби. То есть 7*5=35. |
| -> Теперь прибавьте полученное значение к числителю дроби. То есть 35 + 4 = 39. |
| -> Возьмите числитель и подставьте его в исходный знаменатель. То есть 39/5. |
| -> Окончательная целая дробь будет 39/5. |
Самый простой способ превратить дробь в десятичную — просто разделить число. Здесь требуется разделить числитель на знаменатель.
Здесь требуется разделить числитель на знаменатель.
Преобразовать дробь 7/10 в десятичную.
| You need to just divide the numerator 7 by the denominator which is 10. You get the answer that is: |
| 7 /10 => 0.7 |
Для преобразования дроби в процент можно использовать три метода. Ниже я привел три разных метода на примере 7/20.
| Divide the numerator by the denominator and multiply the result by 100. |
| That is: 7/20 = 0.350.35 * 100 = 35% |
| Multiply the числитель на 100 и разделить число на знаменатель. |
| 7 *100 = 700700/20 = 35% |
Разделите числитель на знаменатель и переставьте запятую справа от двух знаков. |
| 7/20 = 0,35 Теперь переместите десятичные точки, чтобы преобразовать их в 35%. |
Предположим, вам нужно добавить 3/4 к 1/4.
Здесь вы видите, что знаменатели одинаковы, так что это самое простое сложение дробей.
Итак, первый шаг в решении дробей сложением — найти общий знаменатель чисел. В этой задаче оба имеют одинаковый знаменатель, поэтому общего между ними всего 4.
Таким образом, вы можете написать уравнение следующим образом –
3/4 + 1/4
= (3+1)/ 4
= 4/4 = 1
Если у вас разные знаменатели, то также вы легко решить дроби. Давайте учиться на другом примере –
Предположим, вам нужно добавить 3/4 к 2/5, тогда у вас будет следующее уравнение –
3/4 + 2/5
Тогда следующий шаг к решению этой дроби в как решать дроби найти любой общий знаменатель.
Поскольку у него нет общего знаменателя, мы умножим оба знаменателя и сложим приведенные выше числа. Посмотрите на ниже, чтобы понять лучше.
= (3+2) / 4×5
= 5/20
= 1/4
Теперь давайте возьмем еще один пример, где мы можем найти общие знаменатели.
Предположим, что нам нужно сложить дроби ¾ и ⅝
= 3/4 + 5/8
Теперь мы найдем наименьший общий множитель, который является НОК, между двумя знаменателями.
Тогда мы получим 8 в виде НОК, и, таким образом, уравнение будет таким: умножит первую дробь на 2, чтобы знаменатель дроби был равен 8; таким образом, уравнение будет
= (6+5)/8
= 11/8
Итак, ответ 11/8.
Теперь давайте научимся вычитать дроби, как решать дроби.Предположим, уравнение 3/2 – 1/2
Итак, мы будем следовать тому же процессу, но сначала выведем общий множитель, поскольку знаменатель в этом уравнении тот же, поэтому такой проблемы нет.
Теперь вы можете напрямую поместить 2 в знаменатель, а затем вычесть 1 из 3. Следуйте инструкциям –
=(3-1)/2
=2/2
= 1
Ответ равен 1.
Другой пример решения дробей5/7 – 2/ 4
Мы не видим общего делителя между знаменателями, поэтому делаем знаменатели одинаковыми, умножая первую дробь на 4, а вторую дробь на 7; тогда мы получим следующее уравнение.
= 5×4/7×4 – 2×7/4×7
Чтобы решить уравнение, мы должны привести к общему знаменателю, так как только тогда мы сможем выполнять операции Лютера в уравнении. Таким образом, мы получим следующий ответ –
= (20-14)/7×4
= 6/28
Теперь мы можем видеть, что 2 является общим как для числителя, так и для знаменателя, поэтому мы можем разделить всю дробь на 2 следующим образом –
= 6\2/28\2
= 3/14
Таким образом, ответ равен 3/14.
Теперь давайте научимся умножать две дроби. Это также очень важно, чтобы научиться решать дроби.
Возьмем следующий пример:
¾ x ⅕
Умножение дробей очень просто, так как вам просто нужно умножить числители друг на друга, а также знаменатели друг на друга.
Тогда вы получите следующий результат –
= 3×1 / 4×5
=3/20
Таким образом, ответ 3/20.
Теперь давайте изучим метод деления на дроби, как решать дроби.Вы можете взять обратную дробь, чтобы разделить дробь. Чтобы было взаимно, нужно поменять знаменатель на числитель, а числитель на знаменатель.
Возьмем пример:
Решите 1/2 ÷ 1/5.
Во-первых, возьмем обратную величину 1/5 как 5/1.
Возьмите обратную дробь и умножьте ее на другое число (числа).
1/2 * 5/1
Чтобы решить, умножьте знаменатели и числители:
2 * 1 = 2 (знаменатель)
1 * 5 = 5 (числитель)
То есть: 1/2 * 5/1 = 5/2 = 2,5
Что нужно понимать, чтобы избежать распространенных ошибок в дробях! Может быть непросто складывать и вычитать дроби с разными знаменателями. Поэтому разные ученики не решают дроби с разными знаменателями и допускают ошибки.
Поэтому разные ученики не решают дроби с разными знаменателями и допускают ошибки.
Для начала рассмотрим пример решения дробей с разными знаменателями .
| => Решите 3/4 + 1/6. -> Первое, что вам нужно сделать, это умножить числитель и знаменатель на противоположное значение знаменателя. -> Это кратное 4 на 6 и 6 на 4. Это даст вам 24 в знаменателе. -> Точно так же умножьте числитель как 3 * 6 = 18 и 1 * 4 = 4. -> Теперь добавьте 18 + 4 = 22. -> Это означает, что 3/4 + 1/6 = 22/24 => 11/12 |
- Неверное понимание требований вопросов, таких как деление вместо умножения и так далее.
- Когда учащимся нужно сложить или вычесть дробь, они забывают изменить знаменатель дроби. [Как и в приведенных выше примерах 4 и 6 меняются на 24].
- Причем заметно, что числитель тоже надо изменить, как и знаменатель.
 [Например, 3 * 6 = 18 и 1 * 4 = 4].
[Например, 3 * 6 = 18 и 1 * 4 = 4]. - Наконец, некоторые ученики не могут упростить уравнение. [Например, 22/24 также пишется как 11/12 после деления числа на 2].
| Творческое занятие, чтобы научить ваших детей дробям!! Вы можете научить своих детей дробям, попросив их нарисовать птицу на бумаге. Дайте им инструкции разрезать бумагу в заданной пропорции. -> Дайте им круг и научите их дробям. -> Разрежьте круг на 8 частей и выучите дроби, такие как 1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8 и 8/8. -> Также позвольте им упростить дроби как 2/8 => 1/4, 4/8 => 1/2, 6/8 => 3/4 и 8/8 => 1. -> Наконец, они должны нарисовать птицу в следующем виде: |
Многие ученики борются с дробями, и дроби на первый взгляд кажутся сложными, но становятся простыми, если вы практикуете их ежедневно.
Если вы также ищете как решать дроби , то мы надеемся, что эта статья помогла вам понять процесс решения дробей. Если все-таки вы столкнулись с трудностями при решении дробей, то вы можете обратиться к нам в любое время. Мы всегда здесь, чтобы помочь вам. Наши специалисты дадут вам консультацию 24/7. Получите лучшую помощь в выполнении домашних заданий по математике от экспертов.
Если все-таки вы столкнулись с трудностями при решении дробей, то вы можете обратиться к нам в любое время. Мы всегда здесь, чтобы помочь вам. Наши специалисты дадут вам консультацию 24/7. Получите лучшую помощь в выполнении домашних заданий по математике от экспертов.
Q1.
Какая формула для дробей? Дробь = выбранное количество частей / общее количество частей
Каждая дробь имеет числитель, который равен выбранному количеству частей, а знаменатель равен общему количеству частей в целом.
Q2.
Что такое А и В в дроби?Во дроби A и B рассматриваются как A/B. Где число А — числитель, а В — знаменатель.
Q3.
Чему равна 1/3 в виде дроби?Дробь 1/3 эквивалентна: 2/6, 3/9, 4/12, 5/15, 6/18, 7/21, 8/24, 9/27, 10/30 и т. д. на.
Как найти общий знаменатель
Быстро, сколько будет 1/4 + 3/4? Если вы помните школьную математику, то наверняка знаете, что ответ равен 1. Как насчет 1/5 + 3/4? На этот раз не так просто, правда? Прибавление 1/4 к 3/4 довольно просто, потому что знаменатели обеих дробей одинаковы. Но прибавить 1/5 к 3/4 не так просто, и все потому, что знаменатели разные. Итак, как мы решаем такие проблемы? Начнем с того, что найдем то, что называется общим знаменателем. Что именно мы и научимся делать сегодня.
Как насчет 1/5 + 3/4? На этот раз не так просто, правда? Прибавление 1/4 к 3/4 довольно просто, потому что знаменатели обеих дробей одинаковы. Но прибавить 1/5 к 3/4 не так просто, и все потому, что знаменатели разные. Итак, как мы решаем такие проблемы? Начнем с того, что найдем то, что называется общим знаменателем. Что именно мы и научимся делать сегодня.
Числители и знаменатели
Прежде чем мы научимся складывать и вычитать дроби, нам нужно научиться находить общий знаменатель. И прежде чем мы это сделаем, нам нужно убедиться, что мы в курсе некоторых основных принципов дроби. В частности, когда мы впервые заговорили о числителях и знаменателях, мы узнали, что знаменатель дроби говорит вам, сколько равных частей в целом — и это может быть целый пирог, целый год, целый iPhone или что-то еще. — разбивается на части, и числитель дроби говорит вам, сколько таких равных частей содержит дробь.
Таким образом, 4 в дроби, такой как 3/4, означает, что мы разбиваем целое число на 4 равные части. Таким образом, 3 из 3/4 говорит нам, что эта дробь представляет собой сумму, которую мы получим, если возьмем 3 из этих 4 равных частей чего-либо. Хорошо, достаточно легко. Теперь давайте посмотрим, что все это означает при простом сложении и вычитании дробей.
Таким образом, 3 из 3/4 говорит нам, что эта дробь представляет собой сумму, которую мы получим, если возьмем 3 из этих 4 равных частей чего-либо. Хорошо, достаточно легко. Теперь давайте посмотрим, что все это означает при простом сложении и вычитании дробей.
Сложение и вычитание дробей
Для начала, что произойдет, если мы захотим взять эти 3/4 чего-то из предыдущего и добавить к 1/4 этого чего-то? Что ж, здравый смысл — и, как мы, к счастью, увидим, математика — подсказывает нам, что в итоге мы получим что-то целое. Как насчет того, чтобы начать с 1 целого чего-то и вычесть из него 1/4 этого чего-то? Конечно, в итоге мы получаем 3/4 того, с чего начали.
Эти основные факты, по сути, стали для нас здравым смыслом после многих часов, которые мы провели, разбираясь и думая о таких вещах, как пицца, пироги и все остальное в мире, которое можно разбить на части. Как многие из нас узнали в свое время, если мы начнем с целого пирога и удалим 1/4 его (предположительно, ртом), у нас останется 3/4 пирога. Если вместо этого мы начнем с 3/4 пирога, а затем каким-то образом (я не уверен, что хочу знать, как) добавим к нему 1/4 пирога, то неудивительно, что мы получим обратно весь наш пирог.
Если вместо этого мы начнем с 3/4 пирога, а затем каким-то образом (я не уверен, что хочу знать, как) добавим к нему 1/4 пирога, то неудивительно, что мы получим обратно весь наш пирог.
Что такое общие знаменатели?
Что делает подобные задачи довольно интуитивными и даже легкими для размышления, так это тот факт, что все дроби записываются в терминах так называемого общего знаменателя. Другими словами, они написаны в терминах одного и того же типа «чего-то» — будь то равные порции яблок, пирогов или чего-то еще. В подобных ситуациях все, что вам нужно сделать, чтобы сложить или вычесть дроби, — это сложить или вычесть их числители (поскольку это говорит нам об общем количестве вещей, которые у вас есть), а затем записать это поверх исходного знаменателя (чтобы вернуть ответ в термины этих вещей).
Например, поскольку обе дроби в 3/4 + 1/4 имеют общий знаменатель 4, мы находим ответ, складывая числители 3 + 1 = 4, а затем записывая это поверх исходного знаменателя 4, чтобы найти, что 3/4 + 1/4 = 4/4. Как мы узнали, говоря об упрощении дробей, эта дробь 4/4 равна 1. Для задачи 2/3 – 1/3, поскольку обе дроби записаны в терминах одного и того же общего знаменателя, мы можем вычесть числители чтобы получить 2 — 1 = 1, и, следовательно, найти, что 2/3 — 1/3 = 1/3.
Как мы узнали, говоря об упрощении дробей, эта дробь 4/4 равна 1. Для задачи 2/3 – 1/3, поскольку обе дроби записаны в терминах одного и того же общего знаменателя, мы можем вычесть числители чтобы получить 2 — 1 = 1, и, следовательно, найти, что 2/3 — 1/3 = 1/3.
Ключевым моментом здесь (поэтому я повторяю это!) является то, что дроби легко складывать, если они записаны в терминах одного и того же общего знаменателя. Естественно возникает вопрос: как привести дроби к общему знаменателю?
Как найти общий знаменатель
Самый простой способ найти общий знаменатель пары дробей — умножить числитель и знаменатель каждой дроби на знаменатель другой. Итак, если вы пытаетесь переписать 1/3 и 1/6 с точки зрения одного и того же общего знаменателя, все, что вам нужно сделать, это умножить верхнюю и нижнюю часть 1/3 на 6 (что является знаменателем 1/6). ) и верхнюю и нижнюю части 1/6 на 3 (что является знаменателем 1/3), чтобы найти, что 1/3 = (1 x 6) / (3 x 6) = 6/18 и 1/6 = ( 1 х 3) / (6 х 3) = 3/18.
Почему это работает? Потому что, как мы знаем из нашего опыта упрощения дробей, 1/3 и 6/18 эквивалентны, как и 1/6 и 3/18. Таким образом, уловка, которую мы изучили, — это не более чем метод быстрого нахождения эквивалентных форм дробей, записанных в терминах одного и того же общего знаменателя. Как обычно, обратите внимание, что после того, как мы переписали эти дроби в терминах общего знаменателя, мы можем легко складывать или вычитать их. Итак, 1/3 + 1/6 = 6/18 + 3/18 = 9/18 (что можно упростить до 1/2), 1/3 – 1/6 = 6/18 – 3/18 = 3/18. (которое можно упростить до 1/6) и так далее.
Хотя этот метод нахождения общего знаменателя всегда будет работать, это не обязательно лучший метод для решения каждой задачи. Почему? Ну, краткий ответ заключается в том, что это часто оставляет вас с большим количеством упрощений. И, как мы узнаем в следующий раз, большей части этого упрощения можно полностью избежать, если быть немного умнее в выборе общего знаменателя.
Подведение итогов
Итак, это все, на что у нас есть время на математику. Не забудьте стать поклонником Math Dude на Facebook, где вы найдете множество отличных материалов по математике, публикуемых в течение недели. Если вы есть в Твиттере, подпишитесь на меня и там. Наконец, пожалуйста, присылайте мне свои вопросы по математике через Facebook, Twitter или по электронной почте [email protected].
Не забудьте стать поклонником Math Dude на Facebook, где вы найдете множество отличных материалов по математике, публикуемых в течение недели. Если вы есть в Твиттере, подпишитесь на меня и там. Наконец, пожалуйста, присылайте мне свои вопросы по математике через Facebook, Twitter или по электронной почте [email protected].
До свидания, это Джейсон Маршалл с «Быстрыми и грязными советами по упрощению математики от чувака-математика». Спасибо за внимание, любители математики!
Сложение дробей
PGSG8gJWt1g
Дробь типа 3 4 говорит, что у нас есть 3 из 4 частей, на которые делится целое.
Чтобы сложить дроби, нужно выполнить три простых шага:
- Шаг 1: убедитесь, что нижние числа (знаменатели ) совпадают
- Шаг 2: Сложите верхние числа ( числители ), поместите этот ответ над знаменателем
- Шаг 3. Упростите дробь (если возможно)
Пример:
1 4 + 1 4
Шаг 1 . Нижние числа (знаменатели) уже одинаковы. Сразу переходите к шагу 2.
Нижние числа (знаменатели) уже одинаковы. Сразу переходите к шагу 2.
Шаг 2 . Сложите верхние числа и поставьте ответ над тем же знаменателем:
1 4 + 1 4 знак равно 1 + 1 4 знак равно 2 4
Шаг 3 . Упростите дробь:
2 4 знак равно 1 2
На картинке это выглядит так:
| 1 4 | + | 1 4 | = | 2 4 | = | 1 2 |
. .. и вы видите, как 2 4 проще, как 1 2 ? (см. Эквивалентные дроби.)
.. и вы видите, как 2 4 проще, как 1 2 ? (см. Эквивалентные дроби.)
Пример:
1 3 + 1 6
Шаг 1 : Нижние числа разные. Видите, как кусочки разного размера?
| 1 3 | + | 1 6 | = | ? | ||
Нам нужно сделать их одинаковыми, прежде чем мы сможем продолжить, потому что мы не может добавить их вот так.
Число «6» в два раза больше, чем «3», поэтому, чтобы сделать нижние числа одинаковыми, мы можем умножить верхнюю и нижнюю части первой дроби на 2 , например:
| × 2 |
| 1 3 | = | 2 6 |
| × 2 |
Важно: вы умножаете как верхнее, так и нижнее на одну и ту же сумму,
, чтобы значение дроби осталось прежним
Теперь дроби имеют одинаковое нижнее число («6»), и наш вопрос выглядит так:
| 2 6 | + | 1 6 | ||||
Нижние числа теперь одинаковы, поэтому мы можем перейти к шагу 2.
Шаг 2 : Сложите верхние числа и поместите их над одним и тем же знаменателем:
2 6 + 1 6 знак равно 2 + 1 6 знак равно 3 6
На картинке это выглядит так:
| 2 6 | + | 1 6 | = | 3 6 | ||
Шаг 3 : Упростить дробь:
3 6 знак равно 1 2
В графической форме весь ответ выглядит так:
| 2 6 | + | 1 6 | = | 3 6 | = | 1 2 |
С ручкой и бумагой
А вот как это сделать ручкой и бумагой (нажмите кнопку воспроизведения):
Играй! Попробуйте сложить дроби. |
Стихотворение, которое поможет вам вспомнить
♫ «Если вашей целью является сложение или вычитание,
Нижние числа должны быть одинаковыми!
♫ «Измените низ, используя умножение или деление,
Но то же самое нужно применить к верху,
♫ » И не забудьте упростить,
Пока не пришло время прощаться»
Пример:
1 3 + 1 5
Опять же, нижние цифры разные (ломтики разного размера)!
| 1 3 | + | 1 5 | = | ? | ||
Но давайте попробуем разделить их на более мелкие, чтобы были одинаковыми :
| 5 15 | + | 3 15 | ||||
Первая дробь: умножив верх и низ на 5, мы получили 5 15 :
| × 5 |
| 1 3 | = | 5 15 |
| × 5 |
Вторая дробь: умножив верх и низ на 3, мы получили 3 15 :
| × 3 |
| 1 5 | = | 3 15 |
| × 3 |
Нижние числа теперь одинаковы, поэтому мы можем добавить верхние числа:
| 5 15 | + | 3 15 | = | 8 15 | ||
Результат уже настолько прост, насколько это возможно, поэтому ответ:
1 3 + 1 5 знак равно 8 15
Уравнивание знаменателей
Откуда в предыдущем примере мы узнали, что нужно разрезать их на 1 / 15 тысяч, чтобы знаменатели совпадали? Мы просто перемножили два знаменателя (3 × 5 = 15).
Прочитать о двух основных способах приведения знаменателей в соответствие можно здесь:
- Метод общего знаменателя или
- Метод наименьшего общего знаменателя
Они оба работают, используйте тот, который вам больше нравится!
Пример: Кексы
Вы хотите испечь и продать кексы:
- Друг может предоставить ингредиенты, если вы им дадите 1 / 3 продаж
- А прилавок на рынке стоит 1 / 4 продаж
Сколько это вообще?
нам нужно добавить 1 / 3 и 1 / 4
1 3 + 1 4 = ? ?
Сначала сделайте нижние числа (знаменатели) одинаковыми.
Умножить верх и низ 1 / 3 на 4 :
1×4 3×4 + 34 90
?
и умноженный верх и дно 1 / 4 на 3 :
1 × 4 3 × 4 + 1 × 3 4 × 3 = ?? ?
Now do the calculations:
4 12 + 3 12 = 4+3 12 = 7 12
Answer: 7 12 сбываний идут в ингридиентах и ценах рынка.


 Обыкновенная дробь называется неправильной, если её числитель больше её знаменателя, то есть m > n.
Обыкновенная дробь называется неправильной, если её числитель больше её знаменателя, то есть m > n. 7.
Сложение и вычитание обыкновенных дробей
7.
Сложение и вычитание обыкновенных дробей



 После этого если в результате получаем неправильную дробь переводим её в смешанную.
После этого если в результате получаем неправильную дробь переводим её в смешанную.
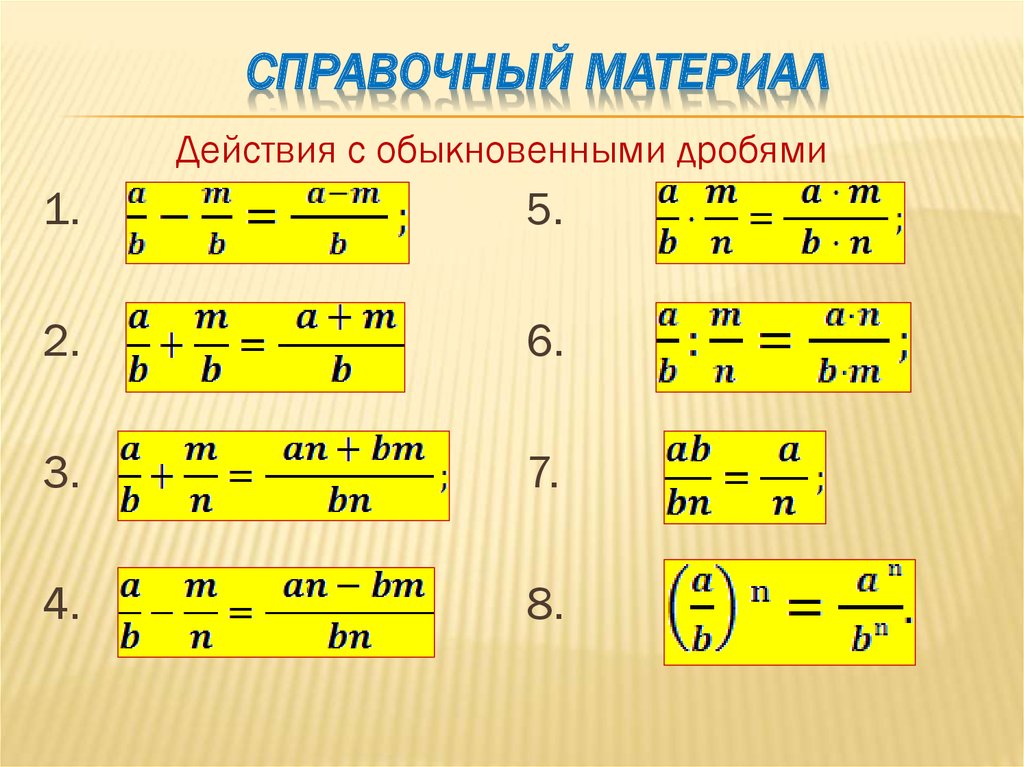 74 Kb.
74 Kb.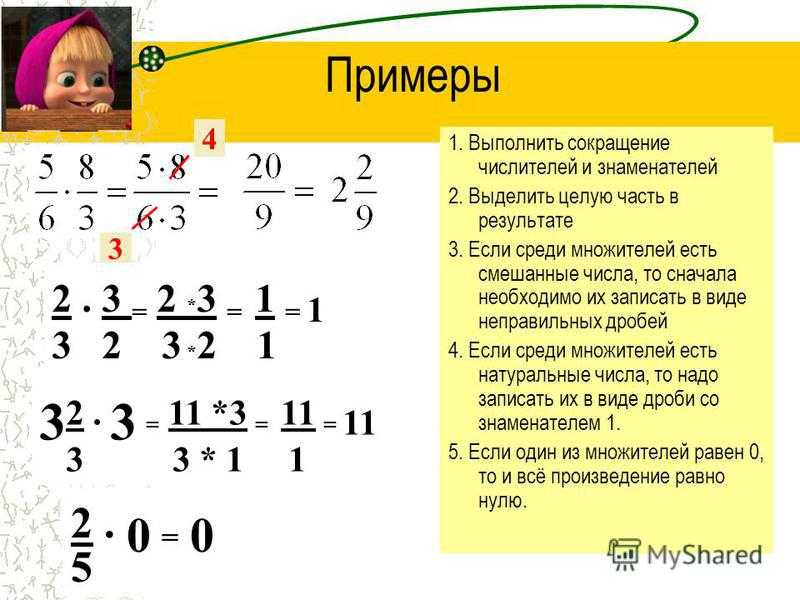
 1/6 часть торта съел Сережа. Сколько частей торта осталось? (5/6). Маша и Даша съели ещё 2/6 торта. Сколько частей торта осталось на тарелке? (3/6). Как нам удалось выполнить вычисления? (Дети формулируют правило вычитания дробей с одинаковыми знаменателями). Запишем решение данной задачи в тетрадь.
1/6 часть торта съел Сережа. Сколько частей торта осталось? (5/6). Маша и Даша съели ещё 2/6 торта. Сколько частей торта осталось на тарелке? (3/6). Как нам удалось выполнить вычисления? (Дети формулируют правило вычитания дробей с одинаковыми знаменателями). Запишем решение данной задачи в тетрадь.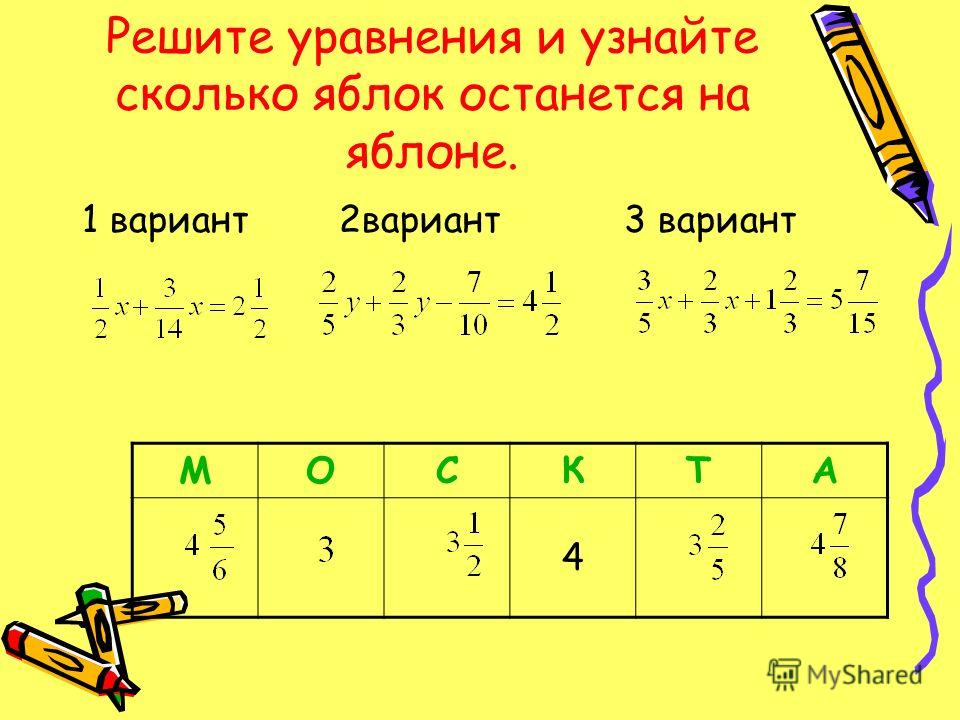
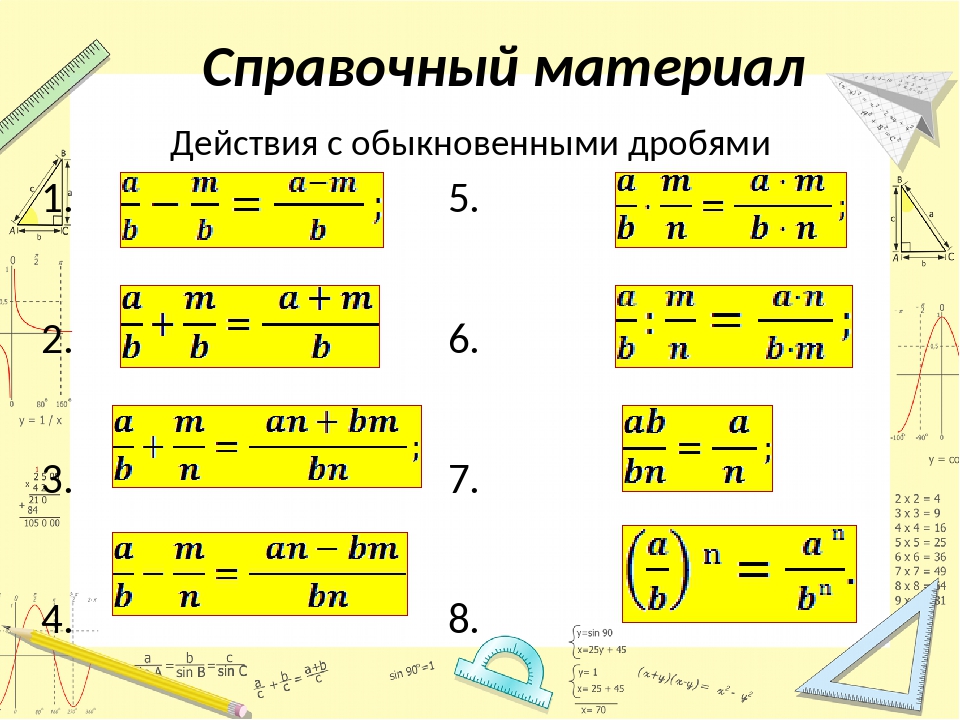 Спасибо за урок!
Спасибо за урок!
 [Например, 3 * 6 = 18 и 1 * 4 = 4].
[Например, 3 * 6 = 18 и 1 * 4 = 4].