Одна Из Тригонометрических Функций, Секанс Дополнительного Угла 8 Букв
Решение этого кроссворда состоит из 8 букв длиной и начинается с буквы К
Ниже вы найдете правильный ответ на Одна из тригонометрических функций, секанс дополнительного угла 8 букв, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.
ответ на кроссворд и сканворд
КОСЕКАНС
предыдущий следующий
ты знаешь ответ ?
ответ:
связанные кроссворды
- Косеканс
- Одна из тригонометрических функций 8 букв
- Тригонометрическая функция 8 букв
- Функция cosec(x) 8 букв
- Собрат синуса и косинуса 8 букв
- Единица, делённая на синус 8 букв
Одна Из Тригонометрических Функций Букв
Решение этого кроссворда состоит из 8 букв длиной и начинается с буквы К
Ниже вы найдете правильный ответ на Одна из тригонометрических функций букв, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.
ответ на кроссворд и сканворд
КОСЕКАНС
предыдущий следующий
ты знаешь ответ ?
ответ:
связанные кроссворды
- Косеканс
- Функция в тригонометрии букв
- Синус, косинус, секанс, 8 букв
- Функция cosec 8 букв
- Косеканс
- Отношение длины гипотенузы к неприлегающему углу катета
- Тригонометрическая функция
- Косеканс
4.
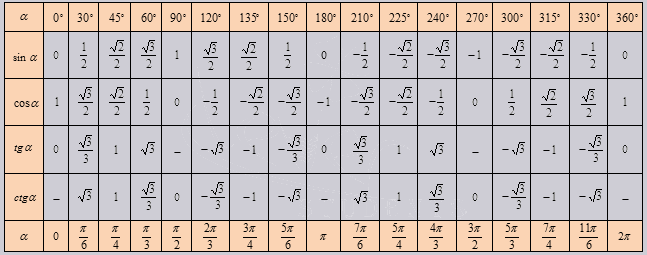1 Тригонометрические функции Когда вы впервые столкнулись с тригонометрическими функциями, вероятно,
в контексте «тригонометрии треугольника», определяя, например,
синус угла как «сторона, противоположная гипотенузе».
Хотя это все еще будет полезно в неофициальном порядке, нам нужно использовать
более широкое определение тригонометрических функций. Сначала
Важное примечание: хотя градусная мера углов иногда удобна
из-за того, что он такой знакомый, он оказывается неподходящим для
математический расчет, поэтому (почти) все, что мы делаем, будет
условия радиана измеряют угла.Чтобы определить систему измерения в радианах, рассмотрим единичную окружность в $xy$-плоскости:
связаны с дугой окружности, которая, как говорят, стягивает угол. На рисунке эта дуга является частью
окружность из точки $(1,0)$ в точку $A$. Длина этой дуги
радианная мера угла $x$; тот факт, что радиан мера
является фактической геометрической длиной, в значительной степени ответственной за
полезность радианной меры.
В то время как угол с определенной мерой может появиться где угодно вокруг круг, нам нужно фиксированное, условное местоположение, чтобы мы могли использовать система координат для определения свойств угла. Стандартное соглашение состоит в том, чтобы поместить начальный радиус для угла на положительной оси $x$ и для измерения положительных углов против часовой стрелки по кругу. На рисунке $x$ является стандартным расположение угла $\pi/6$, то есть длина дуги от От $(1,0)$ до $A$ равно $\pi/6$. Угол $y$ на рисунке равен $-\pi/6$, потому что расстояние от $(1,0)$ до $B$ по окружности также равно $\pi/6$, но по часовой стрелке.
Теперь основные тригонометрические определения таковы:
косинус $x$ и синус $x$ — это первая и вторая
координаты точки $A$, как показано на рисунке. Угол
Показанный $x$ можно рассматривать как угол прямоугольного треугольника, т.
Простые определения треугольника работают только для углов, которые могут «соответствовать» в прямоугольном треугольнике, а именно углы между 0 и $\pi/2$. определения координат, с другой стороны, применимы к любым углам, как на этом рисунке указано:
Щелкните черную точку на окружности, чтобы увидеть соответствующий синус и косинус.
Дуга, граничащая с зеленой областью, изначально имеет длину $7\pi/6$, поэтому угол, который он образует, равен углу $7\pi/6$. Обе координаты красной точки на этом рисунке отрицательны, поэтому синус и косинус $7\pi/6$ отрицательны.
Остальные тригонометрические функции проще всего определить в
члены синуса и косинуса, как обычно:
$$\выравнивание{
\ загар х & = {\ грех х \ над \ соз х} \ кр
\ раскладушка х & = {\ соз х \ над \ грех х} \ кр
\sec x &= {1\over \cos x}\cr
\csc x &= {1\over \sin x}\cr
}$$
а также их можно определить как соответствующие отношения
координаты.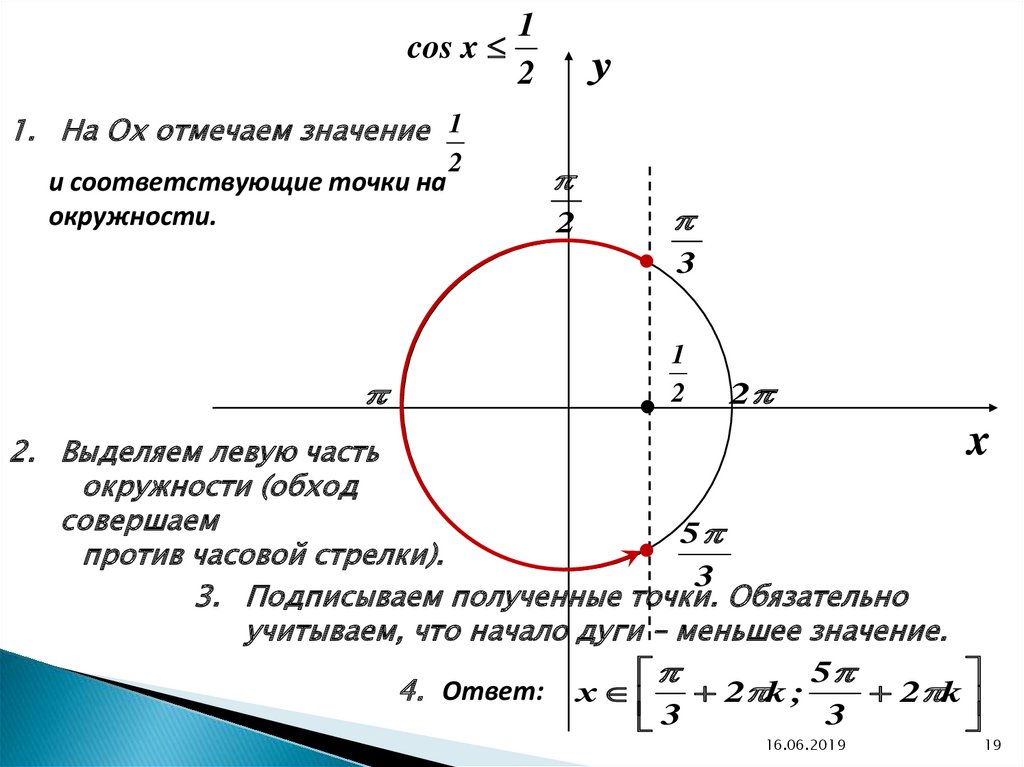
Хотя тригонометрические функции определяются в терминах единицы круг, единичная круговая диаграмма — это не то, что мы обычно считаем график тригонометрической функции. (Единичный круг — это график, ну, круг.) Мы легко можем получить качественно правильное представление о графики тригонометрических функций от единичной окружности диаграмма. Рассмотрим синусоидальную функцию $y=\sin x$. По мере увеличения $x$ от 0 на единичной круговой диаграмме вторая координата точки $A$ изменяется от 0 до максимума 1, затем обратно до 0, затем до минимума $-1$, затем обратно на 0, а затем, очевидно, повторяется. Итак график $y=\sin x$ должен выглядеть примерно так:
Точно так же, когда угол $x$ увеличивается от 0 на единичной круговой диаграмме, первая координата точки $A$ изменяется от 1 до 0, затем до $-1$, обратно к 0 и обратно к 1, поэтому график $y=\cos x$ должен выглядеть что-то вроде этого:
Некоторые полезные тригонометрические тождества находятся в глава 18.
Пример 4.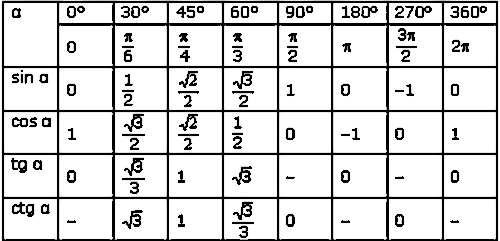
2(t) =0$ в
интервал $[0,2\pi]$.
(отвечать)
Тригонометрические функции
Круговые функции и тригонометрия
Тригонометрия — это изучение отношений между сторонами и углами прямоугольного треугольника. Это понятие впервые было введено греческим математиком Гиппархом.
Что такое тригонометрическая функция?
Круговые функции (также называемые тригонометрическими функциями или тригонометрическими отношениями) — это функции или соотношения, определяющие отношения между углами и сторонами прямоугольного треугольника.
Основные тригонометрические функции (sin, cos, tan, cosec, sec, cot)
Синус (sin), косинус (cos), тангенс (tan), косеканс (cosec), секанс (sec) и котангенс (cot) являются основными тригонометрическими функциями. Из них синус, косек и тангенс являются основными тригонометрическими функциями.
Для определения тригонометрических функций используется диаграмма прямоугольного треугольника, называемая в тригонометрии диаграммой sin-cos-tan.
[Изображения скоро будут загружены]
Гипотенуза — самая длинная сторона прямоугольного треугольника, и она всегда противоположна прямому углу.
Противоположная сторона — это сторона, противоположная углу a.
Прилегающая сторона — сторона, соединяющая угол а с прямым углом.
Определение шести тригонометрических функций
Имея в виду эту схему, мы можем теперь определить основные тригонометрические функции.
1. Синус (sin): Синусоидальная функция угла (тета) представляет собой отношение противолежащего катета к гипотенузе.
2. Косинус (cos): Функция косинуса угла (тета) представляет собой отношение прилежащего катета к гипотенузе.
3. Тангенс (тангенс): функция тангенса угла (тета) представляет собой отношение противоположной стороны к прилежащей стороне.
Следующие функции получены из синуса, косинуса и тангенса и являются обратными значениями.
4.Косеканс (косек): Косеканс является обратной величиной синуса. Cosecθ — это гипотенуза, деленная на противоположную сторону.
5.Секанс (сек): Секанс является обратной величиной косинуса. Secθ — это гипотенуза, деленная на прилежащую сторону.
6.Котангенс (кот): Котангенс является обратной величиной тангенса. Cotθ — это в основном соседняя сторона, разделенная противоположной стороной.
Formulas for Angle θ | Reciprocal Identities | Other Representations | |||||||||||||||
sin θ = Opposite/Hypotenuse | sinθ = 1/cosecθ |
| |||||||||||||||
COS θ = прилегающий/гипотенуза | COSθ = 1/SECθ | ||||||||||||||||
TAN θ = OALPOSOLE/ARDEST 9 TAN θ = OALPOSOSE/ARDED 9 θ = OALPOSOSE/ARDED θ = OALPOSOSE/ARDED 9 . COT θ = соседний/противоположный Cotθ = 1/TANθ COTθ = COSθ .0132 secθ = 1/cosθ cosec θ = Hypotenuse/Opposite cosecθ = 1/sinθ |
/cosθ
You can use the mnemonic SOH -CAH-TOA, чтобы легко запомнить формулы.
[Изображение скоро будет загружено]
Основные значения шести тригонометрических функций, которые нам необходимо знать, приведены ниже.
Значения всех тригонометрических функций
Degrees | Radians | Sin θ | Cos θ | Tan θ | Cot θ | Sec θ | Cosec θ |
0⁰ | 0 | 0 | 1 | 0 | Undefined | 1 | Undefined |
30⁰ | Π/6 | | √3/2 | 1/√3 | √3 | 2/√3 | 2 |
45⁰ | Π/4 | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
60⁰ | Π/3 | √3/2 | 1/ 2 | √3 | 1/√3 | 2 | 2/√3 |
90⁰ | Π/2 | 1 | 0 | Undefined | 0 | Undefined | 1 |
180⁰ | Π | 0 | -1 | 0 | Undefined | -1 | Undefined |
360⁰ | 2/Π | 0 | 1 | 0 | Undefined | 1 | Undefined |
Trigonometric Functions Examples With Solution
Example 1: A bird is sitting on a tree при угле возвышения 20°.