Односторонние углы и соответственные: Углы при пересечении двух прямых

Содержание

Теорема об односторонних углах / Параллельные прямые / Справочник по геометрии 7-9 класс

Главная
Справочники
Справочник по геометрии 7-9 класс
Параллельные прямые
Теорема об односторонних углах

Теорема

Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180⁰.

Дано: , — секущая, 1 и 2 односторонние (Рис.1).

Доказать: 1 + 2 = 180⁰.

Доказательство:

По условию , значит соответственные углы 2 и 3 равны, т. е. 2 =

3 (по теореме о соответственных углах). При этом 1 и 3 — смежные, следовательно, их сумма равна 180⁰, т.е. 1 + 3 = 180⁰.

Из равенств 2 =3 и 1 +3 = 180⁰ следует, что 1 +2 = 180⁰. Что и требовалось доказать.

Советуем посмотреть:

Параллельные прямые

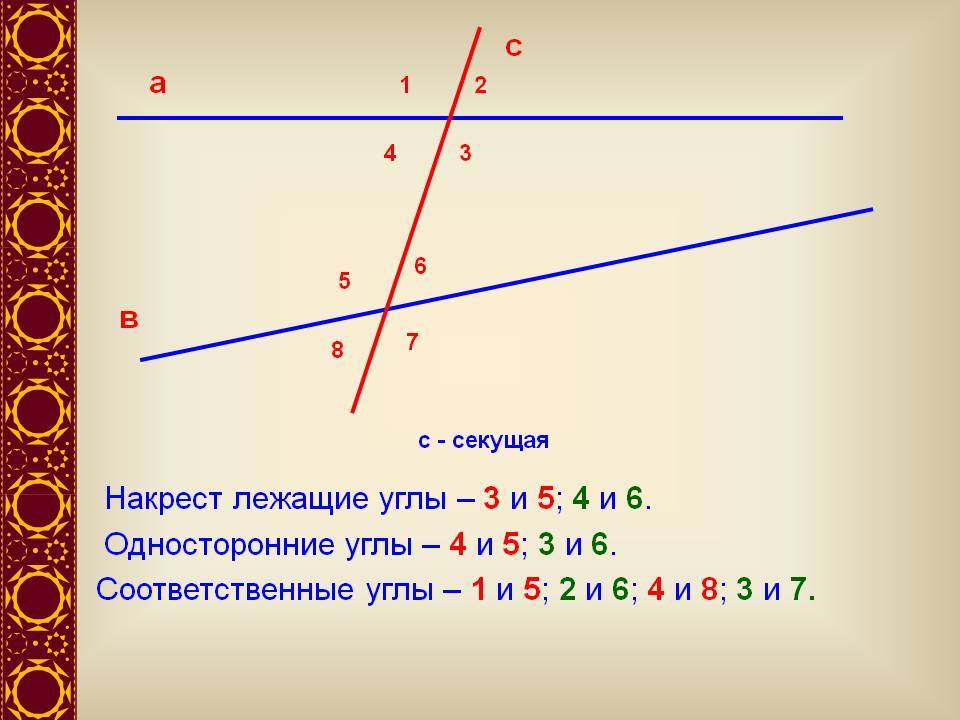
Признаки параллельности двух прямых

Практические способы построения параллельных прямых

Аксиомы геометрии

Аксиома параллельных прямых

Теорема о накрест лежащих углах

Теорема о соответственных углах

Теорема об углах с соответственно параллельными сторонами

Теорема об углах с соответственно перпендикулярными сторонами

Параллельные прямые

Правило встречается в следующих упражнениях:

7 класс

Задание 208, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 17, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 298, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 376, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 387, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 388, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 390, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 391, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 405, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1072, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Углы — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас.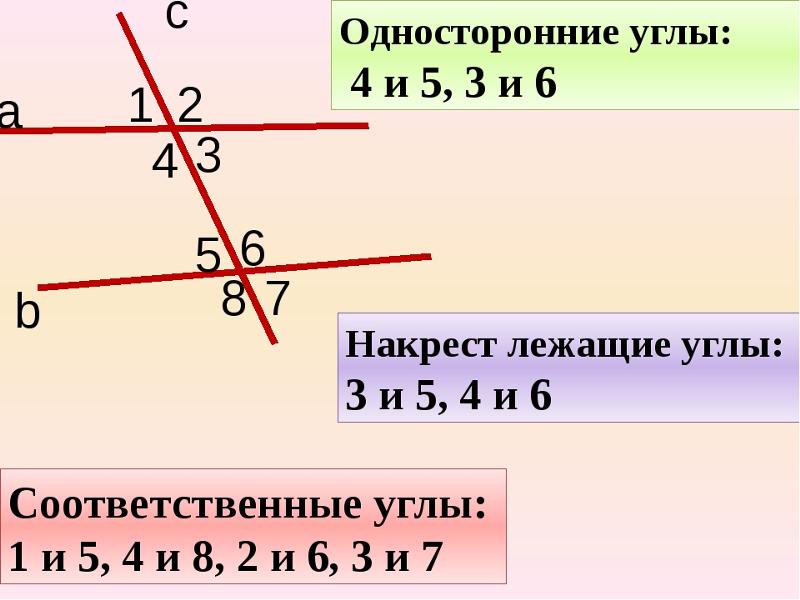 Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. УГЛЫ

У́гол — геометрическая фигура, образованная
двумя лучами (сторонами угла), выходящими из
одной точки (которая называется вершиной угла)

3. По величине

УГЛЫ
ОСТРЫЙ
ТУПОЙ
ПРЯМОЙ
РАЗВЁРНУТЫЙ

5. Центральный угол, угол с вершиной в центре окружности.

Центральный угол,
угол с вершиной в центре окружности.
Величина центрального угла равна
градусной мере дуги, заключённой между
сторонами этого угла.

6. Вписанный угол, угол, вершина которого лежит на окружности, а стороны пересекают эту окружность

Величина вписанного угла равна половине градусной
меры дуги, ограниченной его сторонами.

Все вписанные углы,
опирающиеся на одну и ту же дугу, равны.

7. Сопряжённые углы

Два угла, имеющие общие вершину и обе
стороны, но различающиеся внутренней
областью; они образуют вместе полный
угол; сумма их величин 360°.

8. Смежные углы

два угла с общей вершиной, одна из сторон
которых — общая, а оставшиеся стороны
лежат на одной прямой.
Сумма смежных углов равна 180°.
Биссектрисы смежных углов перпендикулярны.

9. Вертикальные углы

Углы, которые образуются при
пересечении двух прямых, эти углы не
имеют общих сторон.
Вертикальные углы равны.

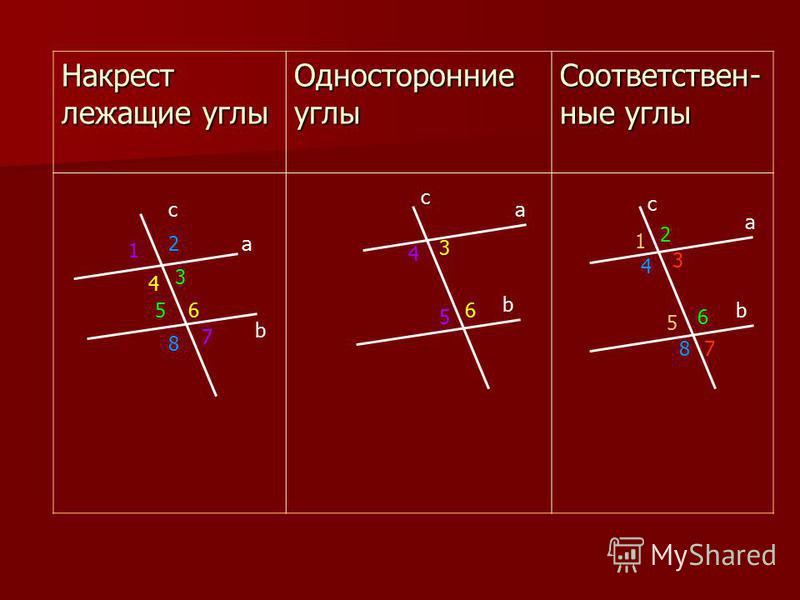
10. Внутренние односторонние углы при параллельных прямых.

Если две параллельные прямые пересечены
третьей прямой, то
сумма внутренних односторонних углов
равна 180°

11. Внутренние накрест лежащие углы при параллельных прямых.

Если две параллельные прямые пересечены
третьей прямой, то
внутренние накрест лежащие углы равны.

12. Соответственные углы при параллельных прямых.

Если две параллельные прямые пересечены
третьей прямой, то
соответственные углы равны.

13. Внешний угол треугольника

при данной вершине — это угол, смежный с
внутренним углом треугольника при этой
вершине.
Внешний угол треугольника равен сумме двух
внутренних углов, не смежных с ним.

14. Устная работа

№1 Найдите : y .
70°
y
a
110°
y — 10°
b
c
d
Ответ : 95°

15. Устная работа

№2 Найдите : x .
c
d
x
120°
a
60°
b
x + 10°
Ответ :85°.
Чему равен угол ВАС=?

18. СУММА УГЛОВ

Сумма внутренних углов
треугольника равна 180°.
Сумма внутренних углов
четырёхугольника равна 360°.
Сумма внутренних углов
n-угольника равна (n — 2)∙180°.
1. 37
2. 60
3. 70
4. 149
1
3
5
2
4
1. 100
2. 60
3. 35
4. 25
5. 65
6. 75
6

21.

ЗадачаВ треугольнике два угла равны 36⁰ и 73⁰.
Найдите его третий угол. Ответ дайте в
градусах.
Решение. Сумма углов треугольника равна
180⁰.
3 180 36 73 71
73⁰
?⁰
36⁰
№ 16
7 1
3
10 х
х

22. Задача

Один из острых углов прямоугольного
треугольника равен 57⁰. Найдите его другой
острый угол. Ответ дайте в градусах.
Решение.
Сумма острых углов прямоугольного
треугольника равна 90⁰.
3 90 57 33
57⁰
?⁰
№ 16
3 3
3
10 х
х

23. Задача

Один из углов равнобедренного треугольника равен
98⁰. Найдите один из других его углов. Ответ дайте в
градусах.
Решение.
Т.к. 98⁰- тупой угол, то это угол при
вершине равнобедренного треугольника,
А
поскольку углы при основании
равнобедренного треугольника
равны, а двух тупых углов у треугольника
быть не может.
А (180 98 ) : 2 41
№ 16
4 1
В
98⁰
3
10 х
С
х

24.

ЗадачаВ треугольнике АВС известно, что ∠ВАС = 64⁰,
AD – биссектриса. Найдите угол BAD. Ответ
дайте в градусах.
Решение.
Биссектриса треугольника
делит угол пополам.
BAD BAC : 2
BAD 64 : 2 32
№ 16
3 2
3
10 х
х
Ответ: 70
25
∠ВСА = 180° — 57° — 117°=6°
Ответ: 6
26
BAC BAL LAC 23 23 46
Ответ: 111
27

28. Четырёхугольники

Ответ: 7
∟А +∟С = ∟В +∟Д
Ответ: 100 и 120.
Углы
выпуклого
четырехугольника
пропорциональны числам 1, 2, 3, 4. Найдите
их.
Ответ: 36о, 72о, 108o, 144o.

35. В угол С величиной 75° вписана окружность, которая касается сторон угла в точках А и В, где О — центр окружности. Найдите угол

АОВ. Ответ дайте в градусах.

36. В окружности с центром О отрезки АС и BD — диаметры. Угол AOD равен 148°. Найдите угол АСВ. Ответ дайте в градусах.

АBCD – прямоугольник; М, K, Р, Т – середины его сторон, АВ =
6 см, AD = 12 см.
Найдите площадь четырехугольника МКРТ.

В
K
6см M
A
C
Р
T
12 см
D

English Русский Правила

Соответствующие углы — определение, теорема и примеры

Соответствующий угол — это угол, который занимает ту же относительную позицию, что и другой угол в другом месте на рисунке. Соответствующие углы в планиметрии образуются при пересечении двух прямых секущими.

Два угла соответствуют или относятся друг к другу, поскольку они находятся на одной стороне поперечной. Один — внешний угол (вне параллельных прямых) и один внутренний угол (внутри параллельных прямых).

Соответствующие углы и поперечное объяснение

Соответствующие углы — это всего лишь один тип пары углов. Углы, лежащие по другую сторону от секущей, называются противоположными углами. У вас могут быть альтернативные внутренние углы и альтернативные внешние углы.

Соответствующие углы никогда не являются смежными углами. Они не соприкасаются, поэтому никогда не могут быть последовательными внутренними углами.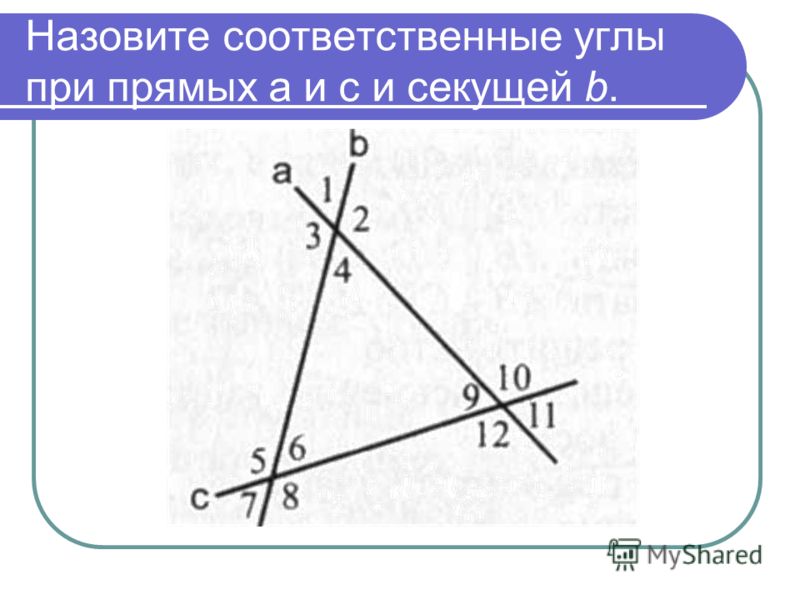

Что такое соответствующие углы

Какие углы являются соответствующими углами?

Можете ли вы найти соответствующий угол для угла 2 на нашем рисунке?

Пример определения соответствующих углов

Вы заметили, что угол 6 соответствует угол 2 ? Это пара соответствующих углов. Сможете ли вы найти все четыре соответствующие пары углов?

Вот четыре пары соответствующих углов:

Углы 1 и 5
Углы 2 и 6
Углы 3 и 7
Углы 4 и 8 пересекает две линии, образуются восемь углов. Теорема о соответствующих углах утверждает, что:
Постулат о соответствующих углах прост, но он обладает преимуществом, поскольку с его помощью вы можете установить отношения для всех восьми углов фигуры.
Теорема о соответствующих углах
Благодаря теореме о соответствующих углах вы уже знаете кое-что о восьми углах, образованных тремя прямыми:
- Если один угол прямой, то все прямые
- Если один острый, четыре острые углы
- Если один тупой, то четыре тупых угла
- Все восемь углов можно классифицировать как смежные углы, вертикальные углы и соответствующие углы
Свойства прямых, известные из теоремы о соответствующих углах
Если у вас есть две параллельные прямые, пересеченные секущей, и один угол ( угол 2 ) помечен 57° , что делает его острым, наша теорема говорит нам, что есть еще три острых угла.
Углы по обе стороны от нашего 57° угла — смежных углов — тупые. Угол 3 – это угол по вертикали к углу 2 . Они имеют общую вершину и находятся друг напротив друга.
Обращение теоремы о соответствующих углах
Интересна также обратная теорема о соответствующих углах:
Обратная теорема позволяет быстро оценить фигуру. Если вам дана фигура, подобная приведенной ниже, но с обозначенными только двумя углами, сможете ли вы по ней что-либо определить?
Обращение теоремы о соответствующих углах
Так как соответствующие углы равны, вы знаете, что две линии, пересекаемые секущей, параллельны.
Если линии, пересекаемые секущей, не параллельны, то соответствующие углы не равны. Они просто соответствуют местоположению. 9Примеры соответственных углов мера?
Теорему о соответствующих углах можно использовать даже без чертежа. Если два соответствующих угла секущей, пересекающей параллельные прямые, прямые, что вы знаете о фигуре?
Можете ли вы провести параллельные прямые с секущей, образующей пару соответствующих углов, каждый из которых имеет размеры 181° ?
Представьте себе поперечное сечение двух линий. Вы узнали, что соответствующие углы не равны. Что это говорит вам о линиях, пересекаемых секущей?

А теперь ответы (постарайтесь сначала!):

Угол 5 также измеряет 123° . Из-за теоремы о вертикальных углах составляют угол 4 и 8 , а также измеряют 123° .
Если два соответствующих угла секущей, пересекающей параллельные прямые, прямые, то все углы прямые, а секущая перпендикулярна параллельным прямым.
Вы не можете провести параллельные прямые с секущей, образующей пару соответствующих углов, каждый из которых имеет размеры 181° .
При поперечном разрезании двух прямых, образующих неконгруэнтные соответствующие углы, вы знаете, что эти две прямые не параллельны.

Соответствующие углы | ChiliMath

Соответствующие углы — это два угла, которые лежат в сходных относительных положениях на одной и той же стороне секущей или на каждом пересечении.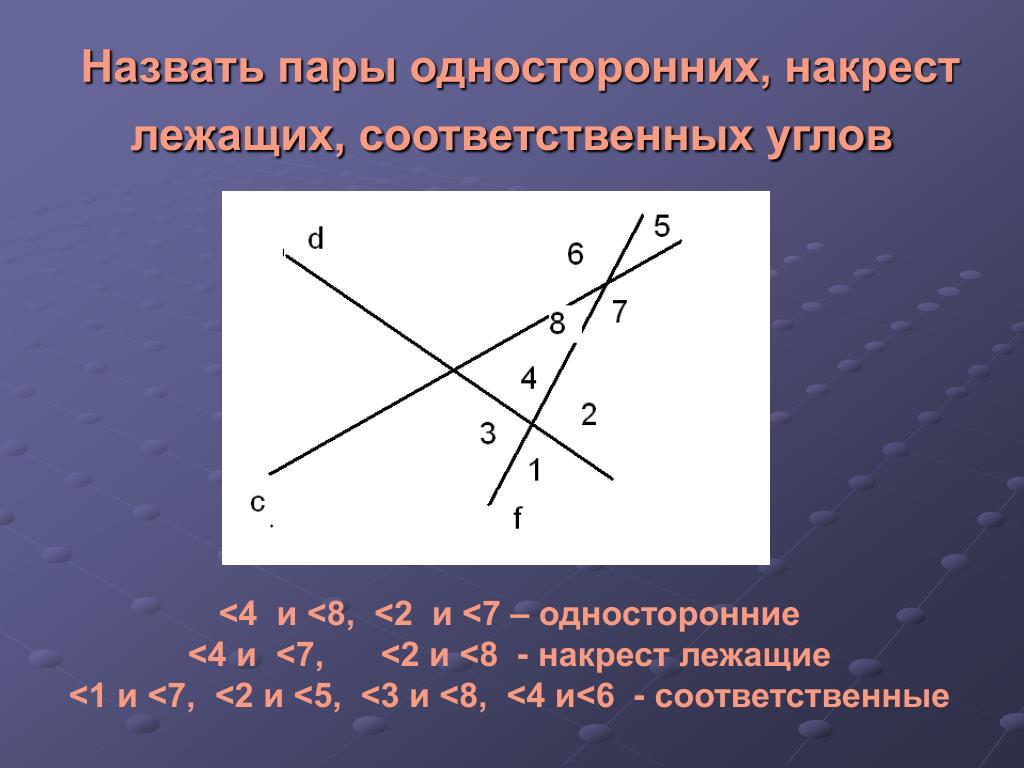 Обычно они образуются при пересечении двух параллельных или непараллельных прямых секущей.

Помните, что поперечная — это линия, пересекающая две или более линий.

На приведенном выше рисунке параллельные прямые a и b пересекаются секущей, в результате чего образуются 4 соответствующих угла. Например, \угол 2 и \угол 6 являются соответствующими углами. Почему? Потому что оба угла расположены в совпадающих углах или соответствующих позициях с правой стороны поперечной. Другими словами, каждый угол расположен на 90 191 выше линии 90 192 и на 90 191 правее 90 192 от секущей.

Вот наши соответствующие углы (должны быть парами) на диаграмме и их расположение.

\angle \textbf{1} и \angle \textbf{5} – над линией, слева от поперечной
\angle \textbf{3} и \angle \textbf{7} – под линией, слева поперечной
\angle \textbf{2} и \angle \textbf{6} – над линией, справа от поперечной
\angle \textbf{4} и \angle \textbf{8} – под линией , справа от поперечной

При работе с соответствующими углами следует помнить несколько вещей.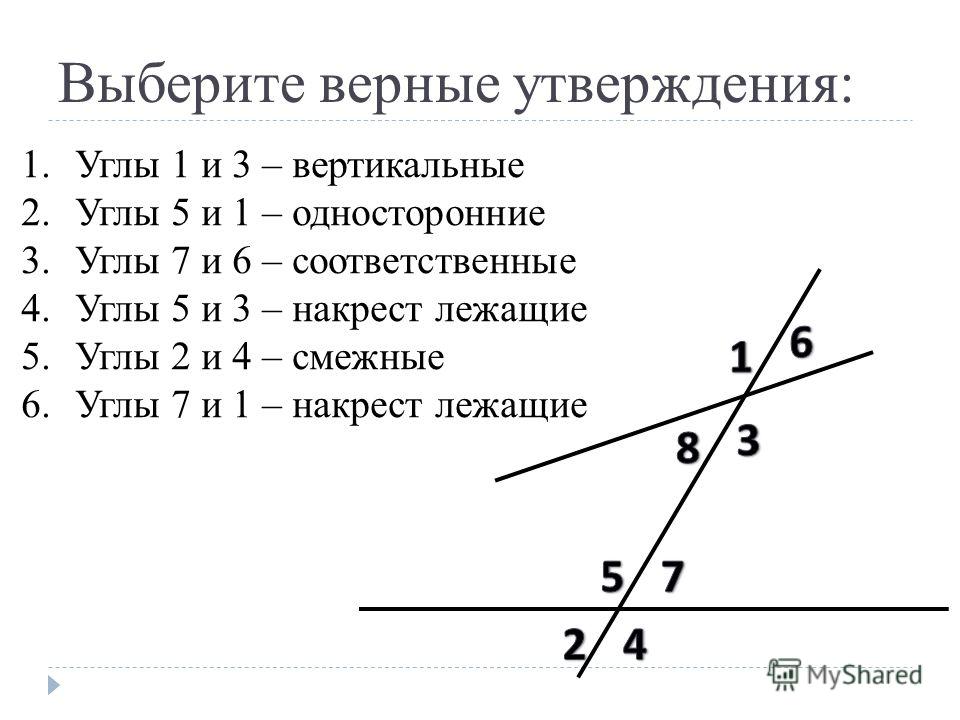 \circ. Следовательно, \угол 1 \конг \угол 5.

С другой стороны, если поперечная пересекается с двумя непараллельными прямыми , образующиеся соответствующие углы не равны и не имеют определенного отношения друг к другу.

Следовательно, \угол a и \угол e являются соответствующими углами, но НЕ конгруэнтными.

Примеры задач с соответствующими углами

Пример 1: Определите соответствующие углы.

Здесь мы имеем две параллельные прямые, прямые k и g, которые пересекаются секущей t. Напомним, что соответствующие углы — это углы, находящиеся в одинаковых положениях по одну и ту же сторону от секущей.

Таким образом, соответствующие углы равны:

\угол 2 и \угол 1
\угол 4 и \угол 3
\угол 6 и \угол 5

\угол 8 и \угол 7

6 Пример 2: Назовите пары соответствующих углов и их расположение.

Как видите, секущая пересекает две непараллельные прямые, образуя 4 соответствующих угла.