Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Справочник по математике | Геометрия (Планиметрия) | Углы |
| Вписанные и центральные углы |
| Углы, образованные хордами, касательными и секущими |
| Доказательства теорем об углах, связанных с окружностью |
Вписанные и центральные углы
Определение 1. Центральным угломназывают угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Рис. 1
Определение 2. Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Рис. 2
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3. Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема |
| Вписанный угол | Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Посмотреть доказательство | |
| Вписанный угол | Вписанные углы, опирающиеся на одну и ту же дугу равны. | |
| Вписанный угол | Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды | |
| Вписанный угол | Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от этой хорды | |
| Вписанный угол | Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр | |
| Окружность, описанная около прямоугольного треугольника | Середина гипотенузы прямоугольного треугольника является центром описанной Посмотреть доказательство |
| Вписанный угол |
Теорема: Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Посмотреть доказательство |
Теорема: Вписанные углы, опирающиеся на одну и ту же дугу равны. |
Теорема: Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды |
Теорема: Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от этой хорды |
Теорема: Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр |
| Окружность, описанная около прямоугольного треугольника |
Теорема: Середина гипотенузы прямоугольного треугольника является центром описанной Посмотреть доказательство |
Теоремы об углах, образованных хордами, касательными и секущими
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами | Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. Посмотреть доказательство | ||
| Угол, образованный секущими, которые пересекаются вне круга | Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство | ||
| Угол, образованный касательной и хордой, проходящей через точку касания | Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами Посмотреть доказательство | ||
| Угол, образованный касательной и секущей | Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство | ||
| Угол, образованный двумя касательными к окружности | Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |
| Угол, образованный пересекающимися хордами хордами |
| Формула: |
Теорема Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. Посмотреть доказательство |
| Угол, образованный секущими секущими, которые пересекаются вне круга |
| Формула: |
Теорема Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |
| Угол, образованный касательной и хордой хордой, проходящей через точку касания |
| Формула: |
Теорема Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами Посмотреть доказательство |
| Угол, образованный касательной и секущей касательной и секущей |
| Формула: |
Теорема Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |
| Угол, образованный двумя касательными касательными к окружности |
| Формулы: |
Теорема Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |
Доказательства теорем об углах, связанных с окружностью
Теорема 1.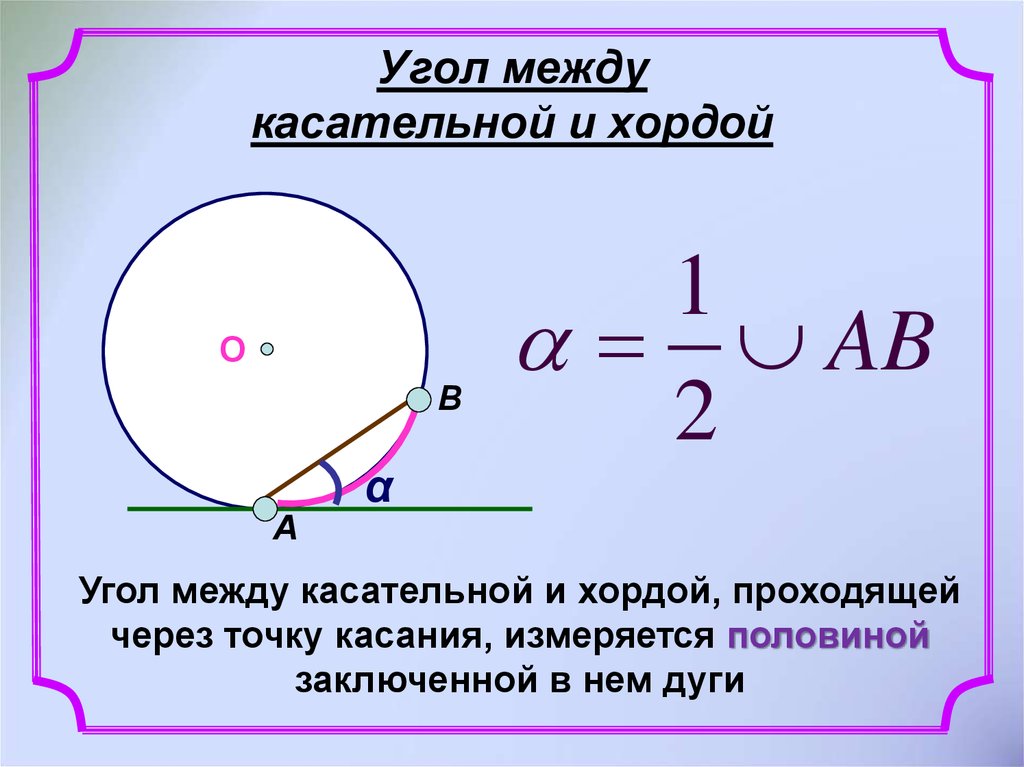 Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
Доказательство. Рассмотрим сначала вписанный угол ABC, сторона BC которого является диаметром окружности диаметром окружности, и центральный угол AOC (рис. 5).
Рис. 5
Так как отрезки AO и BO являются радиусами окружности радиусами окружности, то треугольник AOB – равнобедренный, и угол ABO равен углу OAB. Поскольку угол AOC является внешним углом треугольника AOB, то справедливы равенства
Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.
Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).
Рис. 6
В этом случае справедливы равенства
и теорема 1 в этом случае доказана.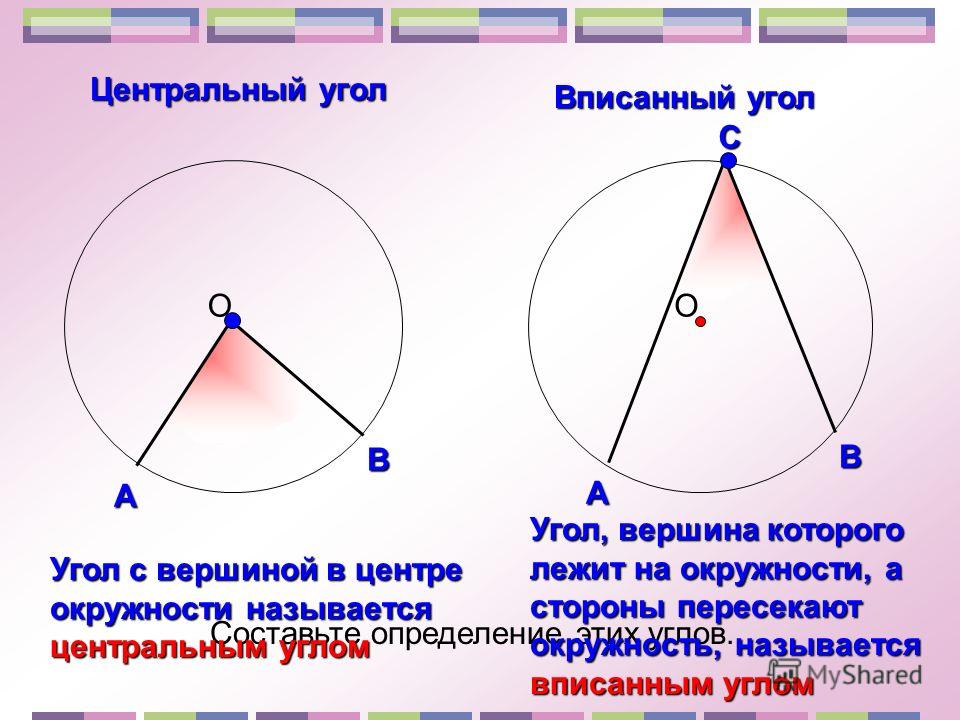
Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).
Рис. 7
В этом случае справедливы равенства
что и завершает доказательство теоремы 1.
Теорема 2. Величина угла, образованного пересекающимися хордами хордами, равна половине суммы величин дуг, заключённых между его сторонами.
Доказательство. Рассмотрим рисунок 8.
Рис. 8
Нас интересует величина угла AED, образованного пересекающимися в точке E хордами AB и CD. Поскольку угол AED – внешний угол треугольника BED, а углы CDB и ABD являются вписанными углами, то справедливы равенства
что и требовалось доказать.
Теорема 3. Величина угла, образованного секущими секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.
Доказательство. Рассмотрим рисунок 9.
Рис. 9
Нас интересует величина угла BED, образованного пересекающимися в точке E секущими AB и CD. Поскольку угол ADC – внешний угол треугольника ADE, а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства
что и требовалось доказать.
Теорема 4. Величина угла, образованного касательной и хордой касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.
Доказательство. Рассмотрим рисунок 10.
Рис. 10
Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр, проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства
что и требовалось доказать
Теорема 5. Величина угла, образованного касательной и секущей касательной и секущей, равна половине разности величин дуг, заключённых между сторонами этого угла.
Величина угла, образованного касательной и секущей касательной и секущей, равна половине разности величин дуг, заключённых между сторонами этого угла.
Доказательство. Рассмотрим рисунок 11.
Рис. 11
Нас интересует величина угла BED, образованного касательной AB и секущей CD. Заметим, что угол BDC – внешний угол треугольника DBE, а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB, в силу теоремы 4, равны. Поэтому справедливы равенства
что и требовалось доказать.
Теорема 6.Величина угла, образованного двумя касательными к окружности касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами.
Доказательство. Рассмотрим рисунок 12.
Рис. 12
Нас интересует величина угла BED, образованного касательными AB и CD. Заметим, что углы BOD и BED в сумме составляют π радиан.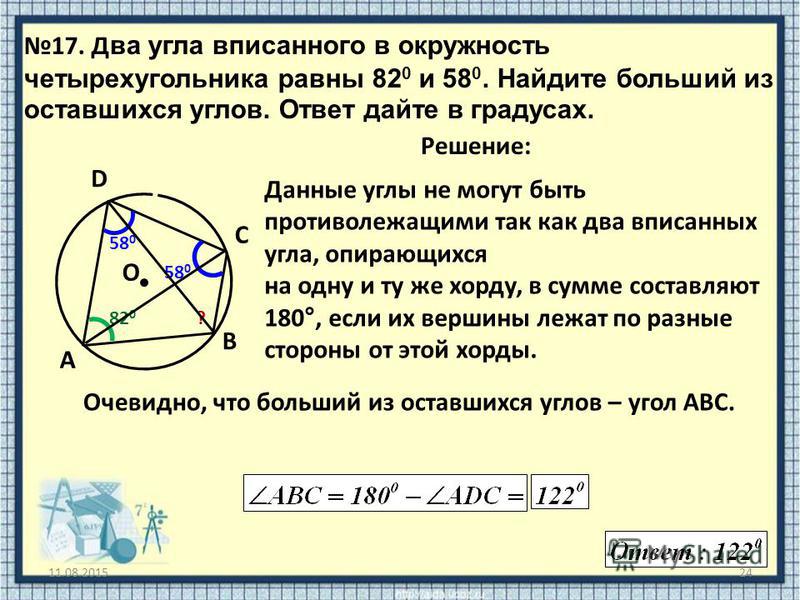 Поэтому справедливо равенство
Поэтому справедливо равенство
α = π – γ .
Далее получаем
что и требовалось доказать.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
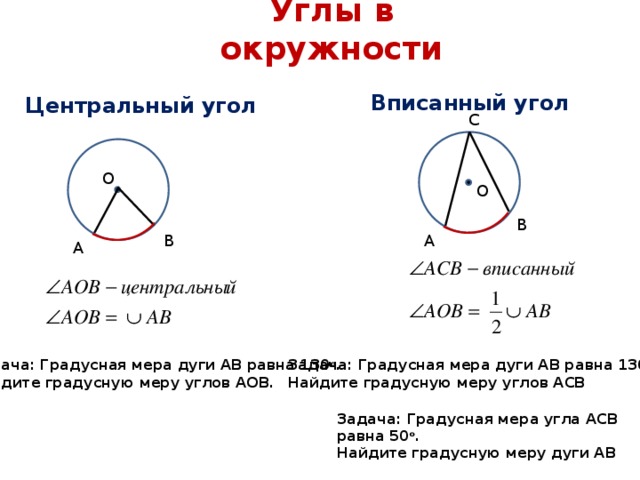
Центральный и вписанный угол, свойства
Центральный угол — это угол, вершина которого находится в центре окружности.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее.
Отрезок, соединяющий две точки окружности, называется хорда.
Самая большая хорда проходит через центр окружности и называется диаметр.
На рисунках — центральные и вписанные углы, а также их важнейшие свойства.
Угол, вершина которого лежит в центре окружности, называется центральным. Величина центрального угла равна угловой величине дуги, на которую он опирается.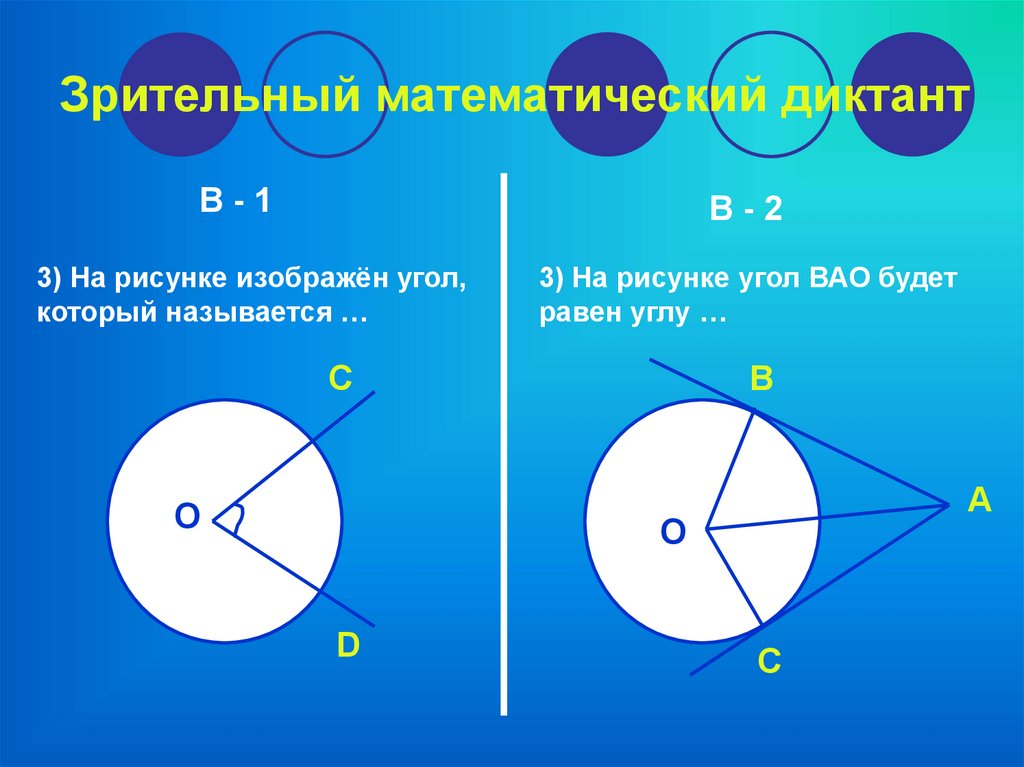 Угол тоже можно назвать центральным. Только он опирается на дугу, которая больше 180
Угол тоже можно назвать центральным. Только он опирается на дугу, которая больше 180
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. Величина вписанного угла равна половине центрального угла, опирающегося на ту же дугу.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на диаметр, — прямой.
Величина центрального угла равна угловой величине дуги, на которую он опирается. Значит, центральный угол величиной в градусов будет опираться на дугу, равную , то есть круга. Центральный угол, равный , опирается на дугу в 60 градусов, то есть на шестую часть круга.
Докажем, что величина вписанного угла в два раза меньше центрального, опирающегося на ту же дугу.
Пусть угол AOC — центральный и опирается на дугу АС, тогда ОА и ОС — радиусы окружности.
Пусть ABC — вписанный угол, опирающийся на дугу АС,
АВ и ВС — хорды окружности.
Первый случай: Точка O лежит на BC, то есть ВС — диаметр окружности.
Треугольник AOB — равнобедренный, АО = ОВ как радиусы. Значит,
— внешний угол а внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Получили, что
Второй случай: Центр окружности точка О не лежит на ВС. Построим диаметр BК
Если точка О лежит внутри вписанного угла АВС, как на рисунке слева, то
Если О лежит вне вписанного угла АВС, как на рисунке справа, то
Мы получили, что в каждом из этих случаев величина центрального угла в два раза больше, чем величина вписанного угла, опирающегося на ту же дугу.
Теорема доказана.
При решении задач по геометрии также применяются следующие теоремы:
1. Равные центральные углы опираются на равные хорды.
2. Равные вписанные углы опираются на равные хорды.
3. Равные хорды стягивают равные дуги.
Докажем теорему 3.
Пусть хорды AB и CD равны. Докажем, что AMB дуги CND имеют одинаковую градусную меру, то есть равны.
Доказательство:
По условию, AB = CD. Соединим концы хорд с центром окружности. Получим: AO = BO = CO = DO = r.
по трем сторонам, отсюда следует, что центральные углы равны, т.е. Значит, и дуги, на которые они опираются, также равны, т.е. дуги AMB и CND имеют одинаковую градусную меру.
Теорема доказана.
Верна и обратная теорема:
Если две дуги окружности равны, то равны и хорды, их стягивающие.
Пусть дуги AMB и CND равны. Тогда как центральные углы, опирающиеся на эти дуги. Значит, треугольники и равны по двум сторонам и углу между ними, и тогда что и требовалось доказать.
Эти две теоремы можно объединить в одну, которая формулируется так:
Хорды окружности равны тогда и только тогда, когда равны дуги, которые они стягивают.
Разберем задачи ЕГЭ и ОГЭ по теме: Окружность, центральный угол, вписанный угол.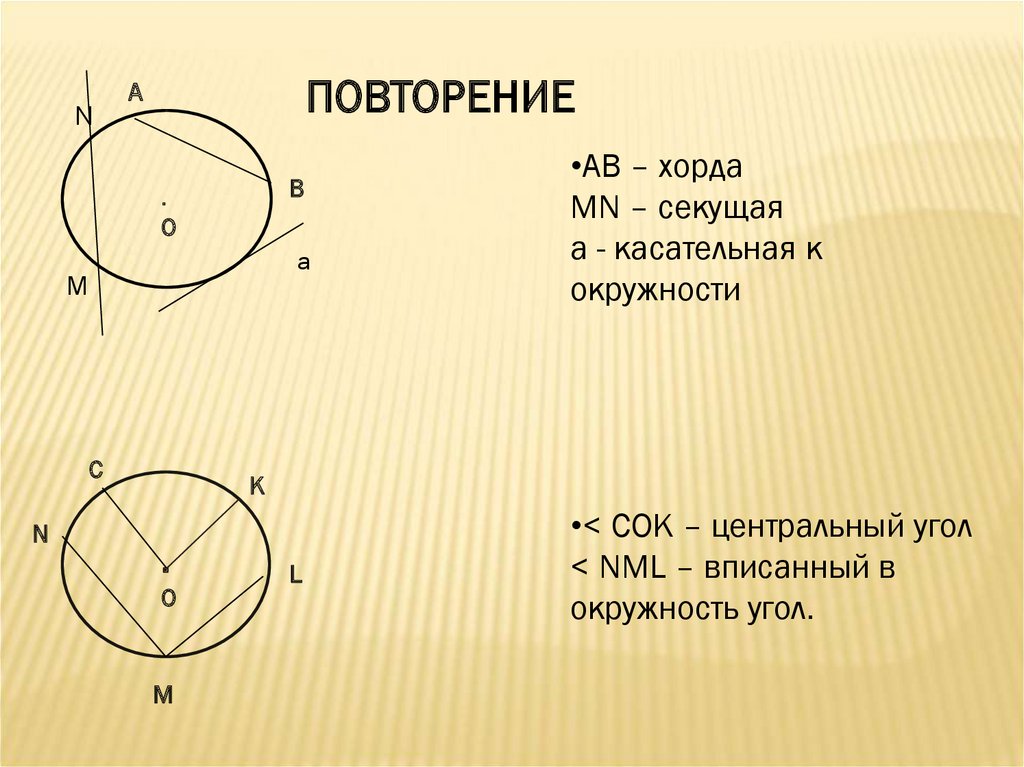
Задача 1, ЕГЭ. Чему равен вписанный угол, опирающийся на диаметр окружности? Ответ дайте в градусах.
Вписанный угол, опирающийся на диаметр, — прямой.
Ответ: 90.
Задача 2, ЕГЭ. Центральный угол на больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.
Решение:
Пусть центральный угол равен x, а вписанный угол, опирающийся на ту же дугу, равен y.
Мы знаем, что
Отсюда
Ответ: 36.
Задача 3, ЕГЭ. Радиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную Ответ дайте в градусах.
Решение:
Пусть хорда AB равна Тупой вписанный угол, опирающийся на эту хорду, обозначим В треугольнике AOB стороны AO и OB равны 1, сторона AB равна Нам уже встречались такие треугольники. Очевидно, что треугольник AOB — прямоугольный и равнобедренный, то есть угол AOB равен 90 Тогда дуга ACB равна 90 а дуга AKB равна Вписанный угол опирается на дугу AKB и равен половине угловой величины этой дуги, то есть 135.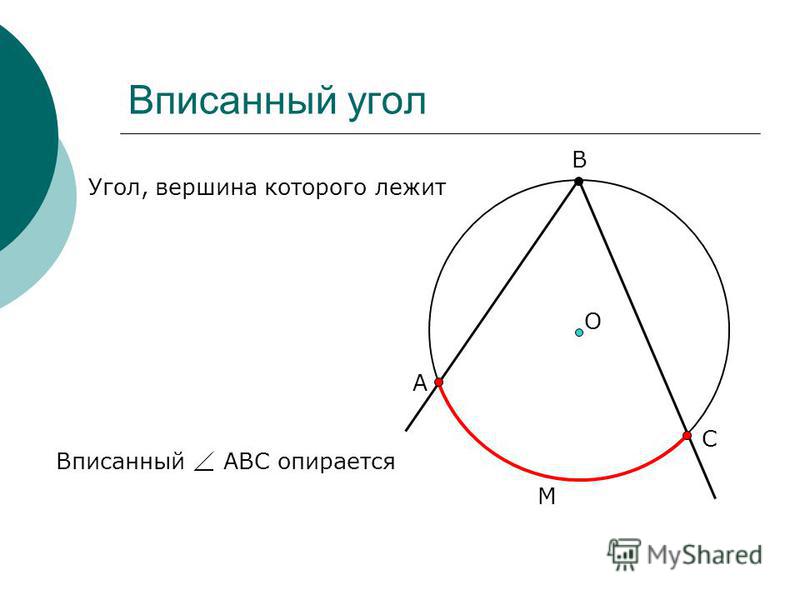
Ответ: 135.
Задача 4, ЕГЭ. Хорда AB делит окружность на две части, градусные величины которых относятся как 5 : 7. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
Решение:
Главное в этой задаче — правильный чертеж и понимание условия. Как вы понимаете вопрос: «Под каким углом хорда видна из точки С?»
Представьте, что вы сидите в точке С и вам необходимо видеть всё, что происходит на хорде AB. Так, как будто хорда AB — это экран в кинотеатре 🙂
Очевидно, что найти нужно угол ACB.
Сумма двух дуг, на которые хорда AB делит окружность, равна то есть
Отсюда и тогда вписанный угол ACB опирается на дугу, равную Величина вписанного угла равна половине угловой величины дуги, на которую он опирается, значит, угол ACB равен
Ответ: 105.
Задача 5, ЕГЭ.
Треугольник ABC вписан в окружность с центром O. Найдите угол BOC, если угол BAC равен 32
Решение:
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
Значит,
Ответ: 64.
Задача 6, ЕГЭ. Найдите центральный угол AOB, если он на больше вписанного угла ACB, опирающегося на ту же дугу. Ответ дайте в градусах.
Решение:
Пусть величина угла АОВ равна х градусов. Величина вписанного угла АСВ равна половине центрального угла, опирающегося на ту же дугу, то есть градусов.
Получим уравнение: откуда
Ответ: 30.
Задача 7, ЕГЭ. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.
Решение.
Рассмотрим треугольник AOB. Он равносторонний, так как AO = OB = AB = R.
Поэтому угол AOB = 60. Вписанный угол ACB равен половине дуги, на которую он опирается, то есть 30
Ответ: 30
Задача 8, ЕГЭ.
Дуга окружности AC, не содержащая точки B, составляет 200 А дуга окружности BC, не содержащая точки A, составляет 80 Найдите вписанный угол ACB. Ответ дайте в градусах.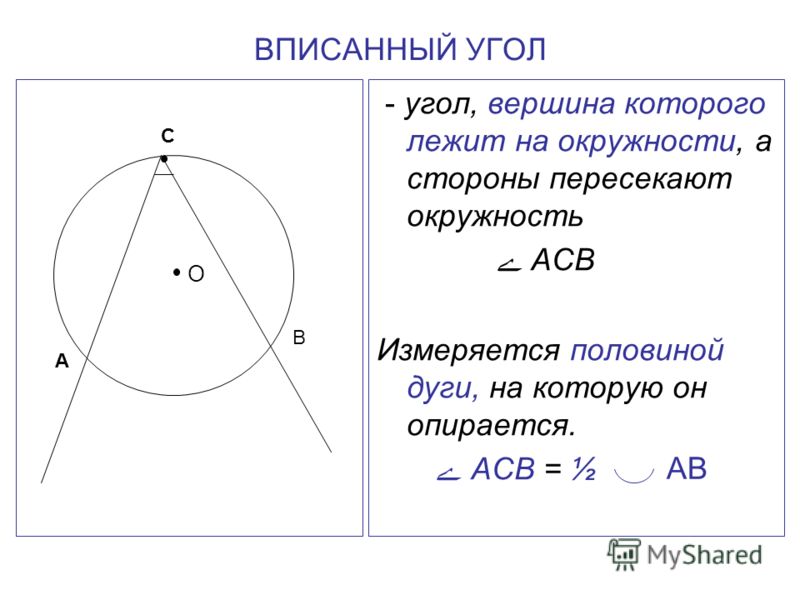
Решение:
Вписанный угол равен половине угловой величины дуги, на которую он опирается. Дуга АВ равна Тогда
Ответ: 40.
Задачи ОГЭ по теме: Центральный и вписанный угол, градусная мера дуги.
Задача 9, ОГЭ. Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен Найдите радиус окружности.
Решение.
Рассмотрим треугольник AOB: он равнобедренный, его боковые стороны равны радиусу окружности.
Углы при основании равнобедренного треугольника равны. Пусть AOB равен x, тогда где Треугольник, у которого все углы равны, — равносторонний треугольник; значит, радиус равен 6.
Ответ: 6.
Задача 10, ОГЭ. В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен Найдите величину угла OAB.
Решение.
Вписанные углы ВСD и ВАD опираются на одну и ту же дугу окружности, поэтому они равны, угол
Ответ: 30.
Задача 11, ОГЭ. Найдите градусную меру центрального MON, если известно, что NP — диаметр, а градусная мера MNP равна 18
Решение:
Треугольник MON — равнобедренный. Тогда −
Ответ: 144.
Задача 12, ОГЭ.
Найдите DEF, если градусные меры дуг DE и EF равны и соответственно.
Решение.
Дуга FD, не содержащая точку Е, равна Вписанный угол DEF, опирающийся на эту дугу, равен половине ее угловой величины,
Ответ: 71.
Задача 13, ОГЭ. В окружности с центром O AC и BD — диаметры. Угол ACB равен Найдите угол AOD. Ответ дайте в градусах.
Решение.
Угол ACB — вписанный, он равен половине центрального угла, опирающегося на ту же дугу, то есть AОВ = 52 Угол ВОD — развернутый, поэтому угол AOD равен
Ответ: 128.
Центральные и вписанные углы» Градусная мера дуги окружности
Центральный угол — угол с вершиной в центре окружности. Центральный угол равен градусной мере дуги, на которую опирается . Вписанный угол — угол, вершина которого лежит на окружности, а обе стороны пересекают эту окружность
Центральный угол равен градусной мере дуги, на которую опирается . Вписанный угол — угол, вершина которого лежит на окружности, а обе стороны пересекают эту окружность
Центральный угол
Это угол с вершиной в центре окружности.
Дуга окружности, соответствующая центральному углу
Это часть окружности, расположенная внутри угла
Градусная мера дуги окружности
Это градусная мера соответствующего центрального угла.
= АОВ
Вписанный угол
Это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Доказательства теорем об углах, связанных с окружностью Теорема 1 . Величина вписанного угла равна половине величины
Так как отрезки AO и BO являются радиусами окружности , то треугольник AOB – равнобедренный, и угол ABO равен углу OAB . Поскольку угол AOC является внешним углом треугольника AOB , то справедливы равенства
Поскольку угол AOC является внешним углом треугольника AOB , то справедливы равенства
Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.
Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла.
и теорема 1 в этом случае доказана.
Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла
В этом случае справедливы равенства
что и завершает доказательство теоремы 1.
Тема урока: Углы, вписанные в окружность. 9 класс.
Цели урока:
Образовательные: познакомиться с понятиями вписанного и центрального углов, теоремой о вписанном угле и ее следствиями. Научиться решать задачи на применение теоремы и ее следствий. Укрепить знания слабоуспевающих учеников, укрепить и расширить знания среднеуспевающих и хорошо успевающих учащихся.
Развивающие: развивать у учащихся способность анализировать, проводить сопоставление, обобщать, строить доказательства, проводить наблюдения, планировать деятельность.
Воспитательные: воспитание культуры математической речи; построение плана ответа; формирование умений осуществлять взаимоконтроль, самоконтроль.
Оборудование:
Мультимедийный проектор
Тест (самостоятельной работой)
Карточки с заданием для работы в группах
Карточки оранжевого и синего цветов.
Ход урока:
Здравствуйте, садитесь. Сегодня у нас важная, новая тема, задания этой темы встречаются в ГИА, ЕГЭ.
Как называется тема урока, и какая цель сегодняшнего урока вы мне скажите чуть позже.
А сейчас повторим некоторые понятия, необходимые для изучения новой темы.
1. Как называется отрезок, соединяющий две точки на окружности и проходящий через центр.
2. Сколько градусов составляет окружность? (слайд)
3. Какую фигуру называют углом?
4. Треугольник вершины, которого лежат на окружности называется……..? (слайд)
5. Какую фигуру называют дугой окружности? (слайд)
6. Каждый угол имеет……..?
Каждый угол имеет……..?
Выполняем задания:
Вычислите градусную меру угла АВС.
С угол АОС = 120 0
Ответы учащихся. Данные задачи стали проблемными.
Обратите внимание, как построен угол, который надо найти. Где лежит вершина угла?
Как проходят стороны угла? Как можно назвать этот угол?
Это новое понятие? Значит тема нашего урока………(ответы учащихся)
Запишем число и тему урока «Углы, вписанные в окружность» (слайд)
Какая цель нашего урока? (ответы учащихся)
Цель урока для учащихся:
Познакомиться с новым понятием вписанный угол; дополнительными понятиями связанными с вписанным углом; научиться вычислять градусную меру вписанного угла; развивать самостоятельность.
Построите вписанный угол и составьте определение.
(ответы учащихся) слайд с определением
Постройте угол вершина которого лежит в центре окружности.
Как можно назвать этот угол? (ответы учащихся) Составьте определение.
Слайд с определением.
Задание . Является ли данные углы центральными или вписанными?
Стороны центрального и вписанного угла разбивают окружность на…….(дуги)
Продлите стороны углов, которые у вас построены и выделите ручкой дуги, находящие внутри угла.
Как вы думаете, дуга имеет градусную меру? Градусной мере, какого угла равна градусная мера дуги? (ответы учащихся) Слайд
Устно выполняем упражнения. Найти х. слайды 5 задач
(дети выходят к экрану и рассказывают решение задач)
Сейчас выполним практическое задание и попытаемся вычислить градусную меру вписанного угла.
С какой фигурой будет связана градусная мера вписанного угла?
Значит центральный и вписанный угол должны опираться на одну дугу.
Выполните построения и произведите вычисление. Сделайте вывод.(ответы учащихся)
Слайд.
Выполним устно упражнение.
Слайды. 6 задач
Практическая работа.
Постройте вписанный угол. Выделите дугу на которую он опирается. Постройте еще несколько вписанных углов, опирающихся на данную дугу. Сделайте измерения и составьте вывод. (ответы учащихся)
Постройте вписанный угол, опирающийся на полуокружность. Вывод.(ответы учащихся)
Слайд.
Решение задач 7-9 на слайдах.
Работа в группах.
Выполняем работу каждый индивидуально, сверяемся с учащимися в группе.
Проверяем.
Повторим материал в учебнике
Вернемся к нашим задачам, которые мы не смогли сделать в начале урока.
Решение задач.
Самостоятельная работа.
Взаимопроверка. Слайд.
Что вы узнали сегодня на уроке? (ответы учащихся)
Если вы сегодня все поняли — оранжевая карточка
Если материал поняли не весь – синяя карточка.
Оценки.
Домашнее задание : п.107 в 13-16 № 48(а), 49. Применение вписанных углов в архитектуре.
Применение вписанных углов в архитектуре.
«Окружность и круг геометрия» — Окружность и круг. Длина окружности. L=2?R. Площадь круга. Окружность. А знаешь ли ты: Круг. Фигура, ограниченная окружностью, называется кругом. Историческая справка.
«Длина окружности» — Окружность. В Древнем Египте считали, что??3,16. Чем больше я знаю, Тем больше умею. Великий математик Эйлер. Эйлер. Великий ученый Древней Греции Архимед. R – радиус окружности. В Древнем Риме считали, что?? 3,12. Древний Египет. Длина окружности. Практическая работа «Измерение кофейных банок». ?? 3,14.
«Уравнение окружности» — Запишите формулу нахождения координат середины отрезка. Повторение. Заполните таблицу. Найдите координаты центра и радиус, если АВ – диаметр данной окружности. Проверьте, лежат ли на окружности, заданной уравнением (х + 3)2 + (у? 4)2 = 25, точки А(1;?1), В(0;8), С(?3;?1). Пусть дана окружность. Запишите формулу нахождения расстояния между точками (длины отрезка).
«Окружность 9 класс» — Задачи.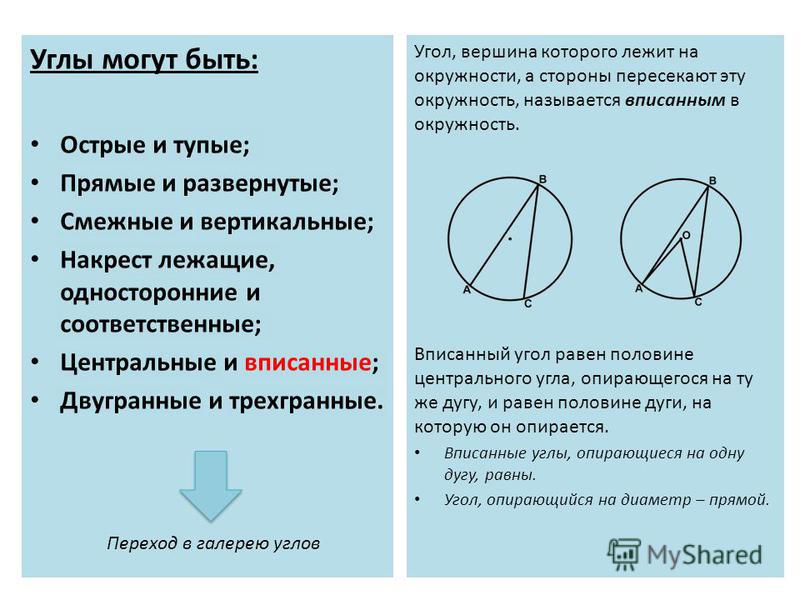 Уравнение окружности. Пусть d – расстояние от центра окружности до заданной точки плоскости, R – радиус окружности. Дано: М (-3; 4) – центр окружности О (0; 0) – точка на окружности. № 2 Вывести уравнение окружности с центром в точке М (-3; 4), проходящей через начало координат. О (хо, уо) – центр окружности, А (х; у) – точка окружности.
Уравнение окружности. Пусть d – расстояние от центра окружности до заданной точки плоскости, R – радиус окружности. Дано: М (-3; 4) – центр окружности О (0; 0) – точка на окружности. № 2 Вывести уравнение окружности с центром в точке М (-3; 4), проходящей через начало координат. О (хо, уо) – центр окружности, А (х; у) – точка окружности.
«Урок Касательная к окружности» — Вычислите длину ВС, если ОD=3см. Обобщающий урок. Решение: Задание 1. Построить равнобедренный треугольник. Провести касательную к данной окружности. Решение задач. Дано: окр.(О;ОМ), МР – касательная, угол КМР=45?. Докажите, что прямая АС является касательной к данной окружности. Практическая работа.
«Числовая окружность» — Числовая окружность. 4. Аналитическая запись дуги числовой окружности. План лекции: Отрицательные числа. 3. «Хорошие» числа на числовой окружности(макет 1 , макет 2). 3. Аналитическая запись дуги числовой окружности. Найдите на числовой окружности точку, которая соответствует заданному числу: Числовая прямая.
Всего в теме 21 презентация
Описание:
Эта презентация представляет собой мультимедийное пособие учебно-методического характера, предназначенное для школьных уроков по геометрии.Вся информация, собранная здесь, наглядно иллюстрирована доступными примерами в виде чертежей, которые способствуют оптимальному освоению и пониманию темы.
Целью этого занятия является введение таких понятий, как вписанный и центральный угол. Учащиеся также знакомятся со свойствами, присущими вписанному углу и теми следствиями, которые вытекают из них.
Представленный здесь материал изложен понятным языком, он оптимально адаптирован для быстрого восприятия учениками школьного уровня, при этом здесь удалось сохранить точность и строгость логических формулировок.
Работа даст возможность для учеников познакомиться с соответствующими понятиями, а также повторить основные виды углов. Кроме того, они смогут разобраться в доказательствах свойств угла, вписанного в окружность, после чего — получить необходимые следствия из данной теоремы. Они также проведут первичное закрепление пройденной темы на задачах, снабженных готовыми чертежами. Работа способствует развитию внимания, наблюдательности и логики.
Они также проведут первичное закрепление пройденной темы на задачах, снабженных готовыми чертежами. Работа способствует развитию внимания, наблюдательности и логики.
Работа состоит из таких блоков:
- Виды углов.
- Свойства вписанного угла.
- Задачи, целью которых является нахождение градусной меры различных углов, которые вписаны в окружность. Они служат для повторения и необходимого закрепления всего пройденного материала.
Категория:
Слайды:
Информация:
- Дата создания материала: 08 Мая 2013 г.
- Слайды: 13 слайдов
- Дата создания файла презентации: 08 Мая 2013 г.
- Размер презентации: 345 Кб
- Тип файла презентации: .rar
- Скачана: 694 раза
- Последний раз скачана: 15 Октября 2019 г., в 16:45
- Просмотров: 2411 просмотров
Теорема о вписанном угле / Окружность / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Окружность
- Теорема о вписанном угле
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают окружность.
На рисунке 1 угол ВАС вписанный, дуга ВLС расположена внутри этого угла. В таком случае говорят, что вписанный угол АВС опирается на дугу ВLC.
Теорема
| Вписанный угол измеряется половиной дуги, на которую он опирается. |
Доказательство
Дано: окружность (О), АВС — вписанный, АС — внутри АВС.
Доказать: АВС = АС.
Доказательство:
1 случай
Луч ВО совпадает с одной из сторон угла АВС.
Пусть ВО совпадает с ВС (Рис. 2).
2).
В данном случае дуга АС меньше полуокружности, следовательно, АОС =АС (т.к. АОС — центральный угол, причем он меньше полуокружности, поэтому градусная мера центрального угла равна градусной мере дуги, на которую он опирается).
АВО — равнобедренный с основанием АВ (т.к. ОА = ОВ — радиусы), 1 = 2 (углы при основании). АОС — внешний угол АВО, АОС = 1 + 2 = 21. Следовательно, учитывая то, что АОС =АС, получим: АС = 2 1, откуда 1 = АС, т.е. АВС = АС.
2 случай
Луч ВО делит угол АВС на два угла.
В данном случае луч ВО пересекает дугу АС в некоторой точке D (Рис. 3).
Точка D разделят дугу АС на две дуги: АD и DС, поэтому АС = АD + DС.
Луч ВD разделяет угол АВС на два угла, поэтому АВС = АВD + DВС.
По доказанному в 1 случае АВD = АD и DВС = DС. Складывая эти равенства, получаем: АВD + DВС = АD + DС или АВD + DВС = (АD + DС).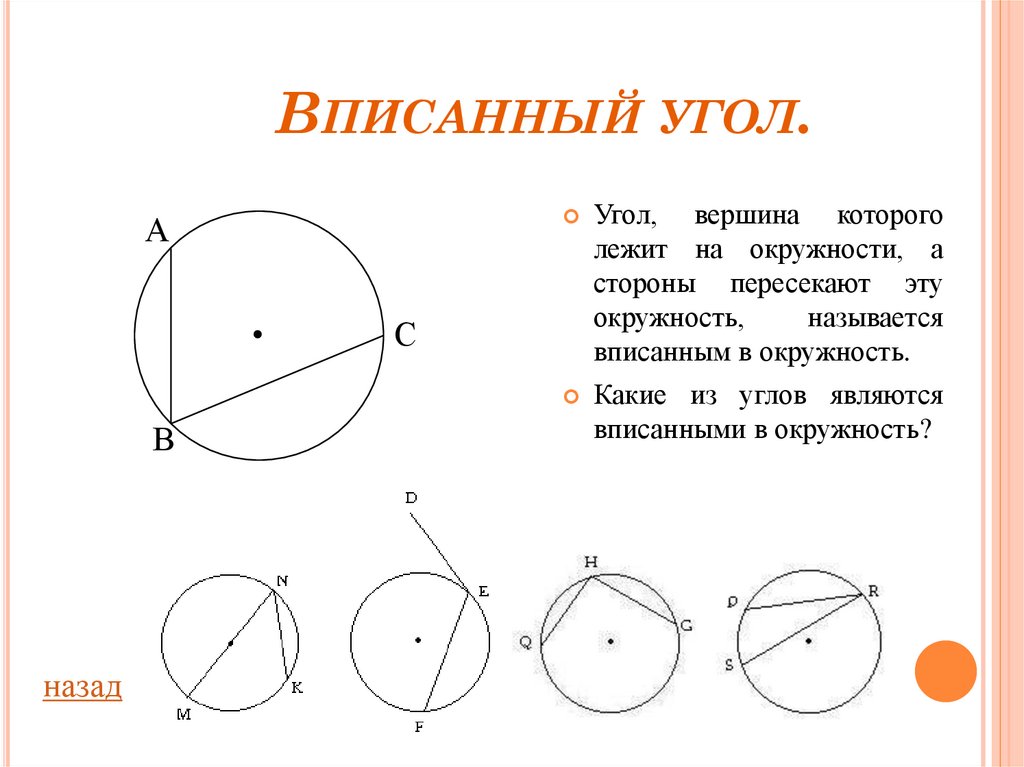 Следовательно, АВС = АС.
Следовательно, АВС = АС.
3 случай
Луч ВО не делит угол АВС на два угла и не совпадает со стороной этого угла.
В данном случае луч ВС пересекает дугу АD в точке С (Рис. 4).
Точка С разделят дугу АD на две дуги: АC и CD, поэтому АD = АC + CD, откуда АC = АD — CD.
Луч ВС разделяет угол АВD на два угла, поэтому АВD = АВC + CВD, откуда АВC = АВD — CВD.
По доказанному в 1 случае АВD = АD и СВD = СD. Вычитая из первого равенства второе, получаем: АВD — СВD = АD — CD или АВD — СВD = (АD — CD). Следовательно, АВС = АС.
Теорема доказана.
Следствия из теоремы о вписанном угле
| 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны (Рис. 5). |
| 2. Вписанный угол, опирающийся на полуокружность, — прямой (рис. 6). |
Теорема
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. |
Доказательство
Дано: окружность, АВ и СD — хорды, АВСD = Е (Рис. 7).
Доказать: АЕВЕ = СЕDЕ.
Доказательство:
В АDЕ и СВЕ: 1 = 2, т.к. они вписанные и опираются на одну и ту же дугу ВD (смотри следствие 1 из теоремы о вписанном угле), 3 = 4 как вертикальные углы, следовательно, треугольники АDЕ и СВЕ подобны (по 1 признаку подобия треугольников). В подобных треугольниках сходственные стороны пропорциональны, поэтому , откуда АЕВЕ = СЕDЕ. Теорема доказана.
Теорема доказана.
Теорема
| Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой этой хордой. |
Доказательство
Дано: окр.(О, ), АВ — хорда, АС — касательная, А — точка касания.
Доказать: ВАС = АВ.
Доказательство:
АОВ — равнобедренный с основанием АВ, т.к. ОА = ОВ = , значит, ОАВ = ОВА (как углы при основании), при этом ОААС (свойство касательной), поэтому ОАВ = ОВА = 900 — ВАС.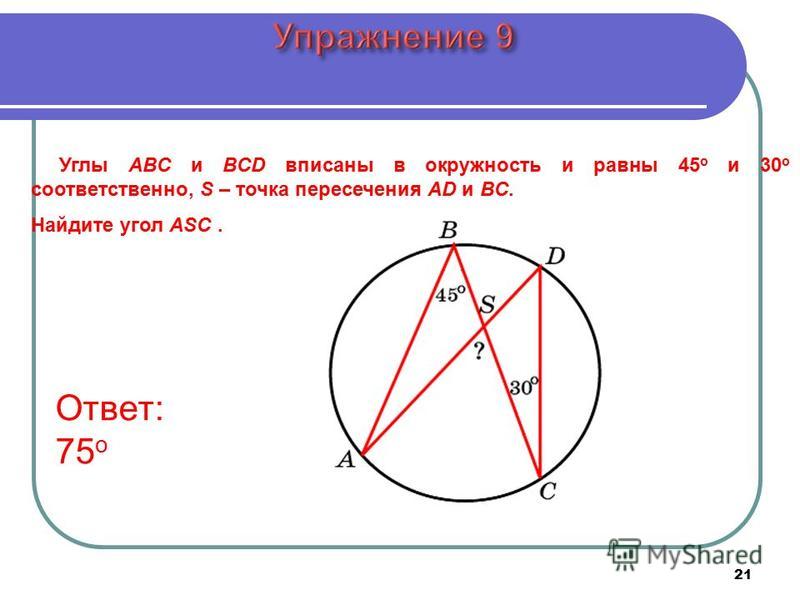 Следовательно, по теореме о сумме углов треугольника: АОВ = 1800 — 2·(900 — ВАС) = 1800 — 1800 + 2ВАС = 2ВАС, откуда ВАС = АОВ. АОВ — центральный, поэтому ВАС = АВ. Теорема доказана.
Следовательно, по теореме о сумме углов треугольника: АОВ = 1800 — 2·(900 — ВАС) = 1800 — 1800 + 2ВАС = 2ВАС, откуда ВАС = АОВ. АОВ — центральный, поэтому ВАС = АВ. Теорема доказана.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Взаимное расположение прямой и окружности
Касательная к окружности
Градусная мера дуги окружности
Свойство биссектрисы угла
Свойства серединного перпендикуляра к отрезку
Теорема о пересечении высот треугольника
Вписанная окружность
Описанная окружность
Окружность
Правило встречается в следующих упражнениях:
7 класс
Задание 654, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 655, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 13, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 717, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 877, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 883, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 887, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 899, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1035, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1133, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Урок математики по теме «Углы, вписанные в окружность».
 9-й класс
9-й класс- Плитина Елена Алексеевна, учитель математики
Разделы: Математика, Конкурс «Презентация к уроку»
Класс: 9
Презентация к уроку
Загрузить презентацию (109 кБ)
Цели и задачи:
- знать определения вписанного и центрального углов, знать теорему о вписанном угле, уметь решать задачи нахождение вписанных, центральных углов и дуг на которые опираются эти углы;
- формирование пространственного мышления;
- воспитание самостоятельности.
На прошлом уроке мы познакомились с понятиями вписанного угла и центрального угла, с теоремой о вписанном угле. Сегодня мы будем применять эти знания для решения задач.
Сегодня мы будем применять эти знания для решения задач.
слайд 1.
- Закончите предложение.
- Центральный угол – это… (угол с вершиной в центре окружности).
- Градусная мера дуги – это… (градусная мера соответствующего центрального угла).
- Угол, вписанный в окружность, – это…(угол, вершина которого лежит на окружности, стороны пересекают ее).
- Угол, вписанный в окружность, равен…(половине соответствующего центрального угла).
- Вписанные углы, опирающиеся на одну и ту же дугу…(равны)
- Вписанные углы, опирающиеся на диаметр… (прямые).
- На доске на рисунке показать и назвать углы и дуги, на которые эти углы опираются.
Рисунок 1.
- центральный угол, ответ: ∠АОD, ∠АОВ, ∠ВОD, ∠КОD, ∠ВОК, ∠АОК.

- вписанный угол, ответ: ∠ВКD, ∠АDК, ∠ВАD
- вписанные углы, опирающиеся на одну и ту же дугу, ответ: ∠ВКD и ∠ВАD
Проверить и разобрать решение задач №71 и №72 из рабочей тетради к учебнику геометрии.
слайд 2.
№71. Начертите окружность и проведите ее радиусы ОА, ОВ и ОС так, чтобы углы АОВ, ВОС и СОА были равны. Вычислите градусные меры образовавшихся дуг АВ, ВС и СА.
Устно разобрать, чему равны градусные меры получившихся дуг.
АВ=ВС= АС =120°.
№77. Точки М, К и Р делят окружность на дуги, градусные меры которых пропорциональны числам 3, 2 и 7 (считая от точки М к точке К). Вычислите градусные меры углов треугольника МКР.
В рабочей тетради в решении дается подсказка: принимаем градусные меры дуг за 3х°, 2х° и __, что подставили? (7х°).
Так как сумма их градусных мер равна 360°, составим уравнение ____________
Какое уравнение получили?
Проверили решение уравнения.
3х+2х+7х=360
12х=360
х=360:12
х=30
МК=3х=90, РК=2х=60, МР=7х=210
Используя свойство вписанных углов, находим величины углов треугольника МКР:
IV. Решение задач∠ Р=45°, ∠ М=30°, ∠К=105°.
1. Задачи по чертежам. слайд 3:
- Решите задачи устно найдите х:
Разобрать, почему в задаче 1 x= 60°, а в задаче 2 x = 80°.
На основании какого свойства? ( свойство вписанного угла: угол, вписанный в окружность, равен половине соответствующего центрального угла).
Постройте в тетради четыре одинаковых окружности.
- Скопируйте задания с рисунков в тетрадь и по данным задач 3 и 4. Презентация слайд 4. См. рисунок 3, найдите х.
Решение задачи 3: 360° – 80° = 280°,
x = 280°:2 = 140°
Решение задачи 4: 360° – 110° = 250°,
x = 250°:2 = 125°
- Скопируйте задания с рисунков в тетрадь и по данным задач 5 и 6.
 слайд 5. См. рисунок 4 найдите х.
слайд 5. См. рисунок 4 найдите х.
Решение задачи 5: ∠С = 90°,
Какое свойство вписанного угла применяем?
(Вписанные углы, опирающиеся на диаметр прямые)
∠А = 90° – 37°= 53°.
Решение задачи 6: в треугольнике АВD∠В = 90°, ∠CВD =30° + 90° = 120°.
2) Задача №79 в рабочей тетради.
Около равнобедренного треугольника АВС описана окружность. Его основание АС стягивает дугу, градусная мера которой равна 140°. Вычислите градусные меры всех углов треугольника АВС.
В рабочей тетради построили чертеж к задаче Рисунок 7.
Решение.
Какой угол треугольника АВС можно найти?
Можно найти ∠B, т.к. это вписанный угол, который опирается на дугу АС.
∠В = 140°:2 = 70°,
Какое свойство равнобедренного треугольника можно применить?
В равнобедренном треугольнике углы при основании равны.
∠А = ∠С = (180° – 70°) : 2 = 110°:2 = 55°.
Ответ: ∠В = 70°, ∠А = ∠С = 55°.
V. Домашнее задание.П.107, повторить теорию по теме «Углы, вписанные в окружность»
Решить задачи №80, 82 в рабочей тетради.
VI. Самостоятельная работа на карточках по готовым чертежам.слайд 6.
Учащиеся получают карточки с заданиями. См. рисунок 5.
VII. Проверка самостоятельной работы.слайд 7.
VIII. Итоги урока.Приложение.
Центральные и вписанные углы — примеры и правила построения » Kupuk.net
В геометрии существует понятие о центральных и вписанных углах в окружность. Для решения задач на данную тематику потребуются некоторые формулы и соотношения. В интернете можно найти информацию, однако она разбросана по всему информационному пространству. В некоторых источниках встречаются погрешности в вычислениях. Специалисты рекомендуют действовать по некоторому алгоритму, позволяющему за короткий промежуток времени достичь высоких результатов.
В интернете можно найти информацию, однако она разбросана по всему информационному пространству. В некоторых источниках встречаются погрешности в вычислениях. Специалисты рекомендуют действовать по некоторому алгоритму, позволяющему за короткий промежуток времени достичь высоких результатов.
Общие сведения
Перед обучением необходимо ознакомиться с основными понятиями об углах, а также подробно разобрать их классификацию. Углом называется геометрическая фигура, состоящая из общей точки и двух исходящих лучей, которые не лежат на одной прямой. Он обозначается символом «∠». Луч — часть прямой линии, ограниченной с одной стороны и неограниченной с другой.
Точкой называется базовая единица геометрии, при помощи которой строятся другие фигуры. Прямая — линия, которая не имеет начала и конца. Следует отметить, что угол может состоять не только из двух лучей, но и из отрезков. Отрезком называется часть прямой или луча, имеющая ограничения с обеих сторон. Однако базовых элементов недостаточно для построения более сложных фигур. В этом случае применяются аксиомы геометрии Евклида.
Однако базовых элементов недостаточно для построения более сложных фигур. В этом случае применяются аксиомы геометрии Евклида.
Аксиомы плоскостной геометрии
Аксиома — утверждение, не требующее доказательств. Оно воспринимается как неоспоримый факт. Плоскостная геометрия называется Евклидовой. Она основана на базовых элементах, аксиомах и теоремах. Теоремой называется гипотеза, которую следует доказать при помощи аксиом или их комбинаций.
В геометрии существует всего 5 базовых утверждений: принадлежности, порядка, равенства (конгруэнтности), параллельности прямых линий и непрерывности. Знать формулировки этих базисов очень важно. Они характеризуются такими определениями:
Для понимания первой аксиомы необходимо представить лист бумаги. Это некоторая плоскость, состоящая из множества точек. Однако для удобства и читабельности их не отмечают, а берут только нужные. Известно, что достаточно всего двух точек, чтобы провести прямую. На листе бумаги можно их отметить и провести ее. Необходимо отметить, что лист бумаги является ограниченной плоскостью.
Что касается второго утверждения, то любая прямая включает в себя простейшие элементы (точки), которые могут лежать между другими. Это свойство позволяет отмечать на искомой фигуре любое количества элементов для выполнения чертежей.
Архимедова аксиома считается сложной для понимания на первоначальных этапах обучения. Однако все очень просто. Следует начертить прямую, и отметить на ней два равных отрезка. Каждый из них поделить на две части, чтобы первая часть одного отрезка была эквивалентна части другого. Пусть первый отрезок АВ = 10 см, а второй — DЕ = 10 см. На первом нужно отметить точку С (АС = 3 и СВ = 7). На втором — отметить точку F, лежащую между D и E (DF = 3 и FE = 7). Следовательно, АС = DF = 3 и СВ = FE = 7.
Классификация треугольников
Углы отличаются между собой по градусной мере. Последняя является главной характеристикой и исчислением его размерности. На основании этого свойства их можно классифицировать таким образом по интервалам:

Запись (90;180) расшифровывается следующим образом: значение принадлежит интервалу от 90 градусов не включительно до 180 не включительно. Смежным является угол, который лежит на одной прямой с основным. Например, на прямой нужно отметить произвольную точку. Затем через нее следует провести луч под углом 60 градусов. Чтобы найти смежный ∠, нужно выполнить такие действия: 180 — 60 = 120. Прямая — развернутый ∠, т. е. его размерность составляет 180. Необходимо также отметить, какими свойствами обладает величина угла:
Для доказательства теорем следует разобрать классификацию треугольников. Она более сложная включает в себя некоторые критерии:
/918870b1bc4a305.s.siteapi.org/img/8aa195e2cfb8b8b18f3ad80023d4eae977f22c8f.jpg)
Сумма углов фигуры эквивалентна 180 градусам. Следовательно, у него бывают только острые, тупой и прямой углы. Если один из них является прямым или тупым, то значит два других — острые. Исходя из этого можно выделить три вида фигур, которые классифицируются по данному параметру (∠): остроугольные, прямоугольные и тупоугольные.
Следующий критерий — стороны. Если у треугольника три стороны не равны между собой, то его принято называть разносторонним. Когда равны две стороны, тогда он является равнобедренным (третья — основание). В случае равенства всех сторон он считается правильным или равносторонним. У него каждый из углов равен 60.
Подобными называются треугольники, у которых прослеживается равенство ∠, а стороны пропорциональны между собой. Соотношение последних зависит от некоторой величины. Ее в геометрии называют коэффициентом подобия. Всего три признака подобия: по всем ∠, по двум ∠ и стороне, а также по двум сторонам и ∠ между ними.
Следует отметить, что для доказательства теорем следует обратить внимание на такие вспомогательные элементы: высоту, медиану и биссектрису. Первый элемент — отрезок, опущенный из произвольной вершины на противоположную сторону под углом 90 градусов. Медианой является луч или отрезок, который соединяет вершину с центром противоположной стороны. Биссектриса — прямая (луч, отрезок), которая делит заданный угол на две равные между собой части. В правильном и равнобедренном треугольниках эти три элемента совпадают.
Информация об окружности
Окружностью называет геометрическое место точек, соединенных между собой и удаленных от центра на равные расстояния. Отрезок, проходящий через ее центр и соединяющий две соседние точки, является диаметром (d). Радиус некоторый отрезок, соединяющий центральную точку с любой из точек на окружности. Его принятое обозначение литерой «R». Если из центра провести два луча (радиуса), то часть окружности, образованная ими, называется дугой.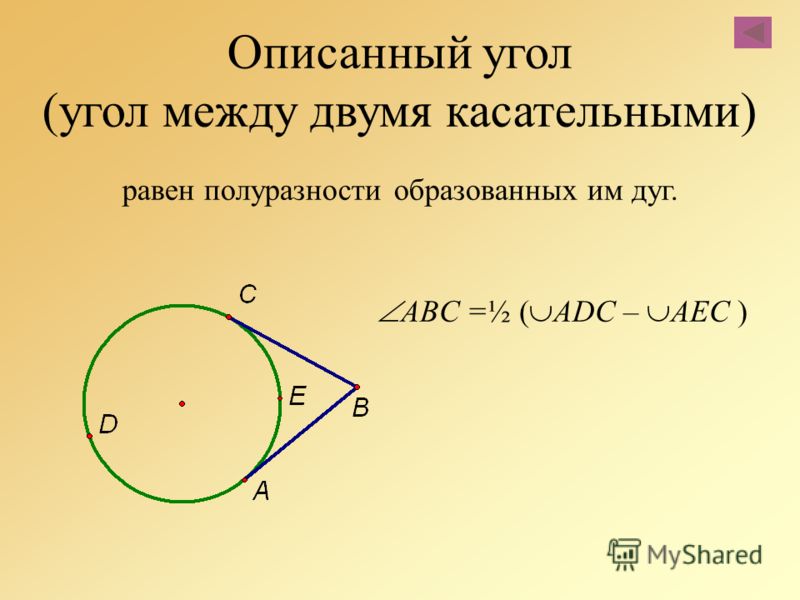
Следует отметить, что любой отрезок, проходящий только через две точки окружности, является хордой. Если последняя проходит через центр, то она является диаметром. Площадью окружности называется произведение квадрата радиуса на число ПИ, которое примерно соответствует значению 3,1416. Формула имеет такой вид: S = ПИ * R 2. Соотношение можно править таким образом: S = (ПИ * d 2 ) / 4. Из соотношения можно сделать вывод, что d = R / 2. Длиной окружности является произведение ПИ на диаметр заданной окружности.
Вписанные углы
Вокруг любого угла можно описать окружность. Он бывает центральным или вписанным. Термины нужно различать между собой, чтобы правильно применять следствия из утверждения. Центральным называется произвольный угол, у которого вершина совпадает с центральной точкой окружности, а его стороны эквивалентны радиусам. Вписанным является любой угол с вершиной, расположенной на окружности и сторонами, пересекающими ее.
Вписанным является любой угол с вершиной, расположенной на окружности и сторонами, пересекающими ее.
Затем следует рассмотреть теоремы о вписанных углах. Кроме того, центральный также является вписанным, но отличие состоит в том, что его вершина совпадает с центром круга. На основании утверждений можно сформулировать некоторые свойства вписанного угла. Последние могут также оказаться полезными при вычислении параметров некоторых фигур.
Основные теоремы
Теоремы применяются для оптимизации вычислений некоторых величин и параметров фигур, образованных углами и описанной окружностью вокруг них. Необходимо отметить, что специалисты классифицируют их на два вида: для вписанных и углов, образованных хордами и касательными. В первом случае утверждения, которые следует доказать, являются следующими:

Необходимо отметить, что вышеописанные теоремы являются также и свойствами. Следует ввести обозначение вписанного ∠ АВС. В первом случае свойство доказывается для двух вариантов. Первый — ∠ АВС лежит на диаметре АВ. Необходимо обозначит центральный ∠ АОС. Следовательно, АО = ВО = R. Треугольник АОВ является равнобедренным, а его ∠ при основании равны (∠ АВО = ∠В АО). Для внешнего ∠ АОС справедливо такое равенство: ∠ АОС = 2 * ∠В АО. Если центральная точка круга лежит внутри ∠ABC. Следует провести биссектрису вписанного ∠, пересекающую окружность в точке D. Тогда ∠ABC = ∠AОC / 2.
Следует провести биссектрису вписанного ∠, пересекающую окружность в точке D. Тогда ∠ABC = ∠AОC / 2.
Другие случаи
Однако бывают и другие случаи, в результате которых образовываются углы внутри окружности. Специалисты выделяют следующие теоремы о них, образованных касательными и хордами:

Как правило, теорем бывает достаточно для доказательства геометрических тождеств. Однако для закрепления материала нужно разобрать пример решения задания.
Пример решения
Для практического применения знаний следует разобрать задачу на данную тематику. Задания состоят из двух частей: исходных данных и неизвестной величины. Например, дана хорда АВ. Она делит окружность на две дуги, градусные меры которых относятся между собой как 5:7. Дана также еще точка, расположенная на дуге меньшей части. Необходимо вычислить вписанный ∠АСВ. Для решения следует воспользоваться следующим алгоритмом:

В седьмом пункте алгоритма было использовано свойство под номером 7. Если его не применять, то решение займет больше времени, поскольку потребует строить треугольник и искать его стороны. После этих операций можно будет найти его ∠ по теореме косинусов или синусов.
Таким образом, для проведения расчетов размерностей углов, которые являются центральными или вписанными, необходимы знания основных теорем и формул.
Углы в круге – Объяснение и примеры
Понятие углов имеет важное значение при изучении геометрии, особенно в кругах. Вы уже видели несколько теорем , связанных с окружностями , и все они включают в себя углы.
Эта статья посвящена исключительно углам окружности.
Вы также узнаете, как найти угол в окружности. Для определения углов и частей окружности вы можете обратиться к предыдущим статьям. Вы также узнаете, что влечет за собой внутренний угол и внешний угол круга.
Что такое угол окружности?
Каков угол окружности? Или, если быть более точным, как мы можем образовать угол внутри фигуры, у которой нет ребер?
Ответ состоит в том, что углы образуются внутри круга с радиусами, хордами и касательными. Посмотрим ниже. Угол окружности — это угол, образованный между радиусами, хордами или касательными окружности.
Различные виды углов мы видели в разделе «Углы» , но в случае с кругом, в основном, есть четыре типа углов. Это центральный, вписанный, внутренний и внешний углы. Давайте рассмотрим каждый из них по отдельности ниже.
Центральный угол образован двумя радиусами, а его вершина лежит в центре окружности.
На приведенной выше диаграмме ∠ AOB = центральный угол
, где дуга AB — это дуга, на которую она опирается.
В окружности сумма центрального угла малого и большого сегментов равна 360 градусам.
С другой стороны, вписанный угол образован между двумя хордами, вершина которых лежит на окружности.
На приведенном выше рисунке ∠ AOB — это вписанный угол.
Как найти угол?
Как найти центральный угол:
Формула для нахождения центрального угла:
Центральный угол = (длина дуги x 360)/2πr
, где r — радиус окружности.
Как найти вписанный угол:
Формула для вписанного угла:
Вписанный угол = ½ дуги, проведенной между точками
Ранее мы изучали внутренние и внешние углы треугольников и многоугольников. Пришло время изучить их и для кругов.
Внутренний угол окружности
Внутренний угол окружности образован на пересечении двух линий, пересекающихся внутри окружности.
На диаграмме выше, если b и a являются дугами, пересекаемыми, то мера внутреннего угла x равна половине суммы дуг.
x = ½ (b + a)
Внешний угол окружности
Внешний угол окружности — это угол, вершина которого находится вне окружности, а стороны угла являются секущими или касательными круг.
Величина внешнего угла равна половине разности величин образуемых дуг.
Формула для наружного угла определяется
Угол внешнего вида, ▲ BOA = ½ (B — A)
Пусть на работу по нескольким примерам:
9000 2 7 70002. Пример 1Найдите центральный угол отрезка, длина дуги которого равна 15,7 см, а радиус 6 см.
Решение
Центральный угол = (длина дуги x 360)/2πr
Центральный угол = (15,7 x 360)/2 x 3,14 x 6
= 5652/37,68
= 150
Следовательно, центральный угол равен 150 градусам.
Пример 2
На приведенной ниже диаграмме пересекаемые дуги составляют 60 градусов и 120 градусов соответственно. Найдите градусную меру внешнего угла x?
Решение
Внешний угол, х = ½ (б – а)
х = ½ (120º – 60º)
х = 90, мера внешнего угла 90, 0 7 0 30 градусов.
Пример 3
Найдите величину недостающего центрального угла в следующем круге.
Решение
Сумма центральных углов окружности = 360°
80° + 120° + x = 360°
Упростить.
200° + x = 360°
Вычесть по 200° с обеих сторон.
x = 160 º
Следовательно, недостающий центральный угол равен 160 градусам.
Пример 4
Какова мера ∠BOA и ∠AOE в круге, показанном ниже? 180°
2x + 60°= 180°
Вычесть 60° с обеих сторон.
2x = 120°
Разделив обе стороны на 2, мы получим
x = 60°
Теперь подставим.
(х + 50) ° = 60° + 50°
= 110°
(x + 10) ° = 60° + 10°
= 70°
Следовательно, мера ∠BOA и ∠AOE составляет 110° и 70° соответственно.
Пример 5
Найдите внутренний угол следующей окружности.
Решение
Дано измерение пересекаемых дуг как 150° и 100°.
Внутренний угол, x = ½ (150° + 100°)
= ½ x 250°
=125°
Таким образом, внутренний угол равен 125°.
Предыдущий урок | Главная страница | Next LessonПредставление трансформаций на плоскости с использованием, например, прозрачных пленок и программного обеспечения для геометрии; описывать преобразования как функции, которые принимают точки на плоскости в качестве входных данных и дают другие точки в качестве выходных данных.
 Сравните преобразования, которые сохраняют расстояние и угол, с теми, которые этого не делают (например, перемещение по сравнению с горизонтальным растяжением). | СС | ГСГ | HSG-СО | HSG-CO.A
Сравните преобразования, которые сохраняют расстояние и угол, с теми, которые этого не делают (например, перемещение по сравнению с горизонтальным растяжением). | СС | ГСГ | HSG-СО | HSG-CO.APopular Tutorials
in Представление преобразований на плоскости с использованием, например, прозрачных пленок и программного обеспечения для геометрии; описывать преобразования как функции, которые принимают точки на плоскости в качестве входных данных и дают другие точки в качестве выходных данных. Сравните преобразования, которые сохраняют расстояние и угол, с теми, которые этого не делают (например, перемещение по сравнению с горизонтальным растяжением).Как вы используете матрицы для перевода фигуры?
Матрицы помогут решить любые проблемы! В этом уроке вы увидите, как использовать матрицу перевода для перемещения фигуры на координатную плоскость.
Что такое преобразование конгруэнтности или изометрия?
Не все преобразования одинаковы! Преобразования конгруэнтности, или изометрии, обладают особым свойством, отличающим их от других преобразований.
 Этот урок покажет вам, что делает их особенными!
Этот урок покажет вам, что делает их особенными!Что такое расширение?
Когда чьи-то глаза расширяются, их зрачки становятся больше или меньше, но они всегда остаются прежними. Расширение в математике очень похоже. Когда вы расширяете фигуру, вы меняете размер фигуры, не изменяя ее формы. Этот урок знакомит вас с дилатацией. Взглянем!
Как вы используете координаты для отражения фигуры по оси X?
Хотите увидеть, как отразить фигуру по оси X? Тогда этот урок создан для вас! В этом уроке вы увидите, как использовать координаты исходной фигуры для отражения фигуры по оси x. Взглянем!
Как вы используете координаты для отражения фигуры по оси Y?
Хотите посмотреть, как отразить фигуру по оси Y? Тогда этот урок создан для вас! В этом уроке вы увидите, как использовать координаты исходной фигуры, чтобы отразить фигуру по оси Y. Взглянем!
Как повернуть фигуру 90 градусов вокруг начала координат?
Вращение фигуры относительно исходной точки может быть немного сложным, но это руководство может помочь! В этом уроке показано, как повернуть координаты исходной фигуры относительно начала координат.
 Затем просто соедините точки, чтобы создать новую фигуру. Посмотрите этот процесс в действии, посмотрев этот урок!
Затем просто соедините точки, чтобы создать новую фигуру. Посмотрите этот процесс в действии, посмотрев этот урок!Как повернуть фигуру на 180 градусов вокруг начала координат?
Вращение фигуры относительно исходной точки может быть немного сложным, но это руководство может помочь! В этом уроке показано, как повернуть координаты исходной фигуры относительно начала координат. Затем просто соедините точки, чтобы создать новую фигуру. Посмотрите этот процесс в действии, посмотрев этот урок!
Как повернуть фигуру на 270 градусов по часовой стрелке вокруг начала координат?
Вращение фигуры относительно исходной точки может быть немного сложным, но это руководство может помочь! В этом уроке показано, как повернуть координаты исходной фигуры относительно начала координат. Затем просто соедините точки, чтобы создать новую фигуру. Посмотрите этот процесс в действии, посмотрев этот урок!
Как вы используете координаты для перемещения фигуры по горизонтали?
Перевести фигуру на координатную плоскость проще, чем вы думаете! В этом руководстве показано, как преобразовать координаты исходной фигуры.
 Затем просто соедините точки, чтобы создать новую фигуру. Этот урок покажет вам, как!
Затем просто соедините точки, чтобы создать новую фигуру. Этот урок покажет вам, как!Как вы используете координаты для перемещения фигуры по вертикали?
Перевести фигуру на координатную плоскость проще, чем вы думаете! В этом руководстве показано, как преобразовать координаты исходной фигуры. Затем просто соедините точки, чтобы создать новую фигуру. Этот урок покажет вам, как!
Что такое отражение?
Когда вы смотрите в зеркало, вы видите свое отражение. В математике вы можете создавать зеркальные изображения фигур, отражая их по заданной линии. Этот урок знакомит вас с отражениями и показывает несколько примеров отражений. Взглянем!
Что такое вращение?
Вы когда-нибудь поворачивали дверную ручку? Вы выполняли вращение! В математике вращения точно такие же! Ознакомьтесь с этим руководством, чтобы узнать о поворотах.
Что такое перевод?
Вы когда-нибудь двигали что-нибудь по столу? Если да, то вы выполнили перевод! В этом уроке вы узнаете определение перевода и увидите несколько действительно отличных примеров.
 Взглянем!
Взглянем!Что такое трансформация?
Трансформации могут быть очень веселыми! Они позволяют изменить или переместить фигуру. В этом уроке вы узнаете обо всех видах преобразований!
Что такое изображение?
Почти все в математике имеет имя! Знаете ли вы, что когда вы имеете дело с трансформациями, новая фигура, которую вы получаете, называется изображением? Посмотрите этот учебник и узнайте об этом математическом термине!
6.16: Углы на окружности и внутри нее
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 5041
Углы, вершины которых лежат на окружности или образованы касательными и хордами.
Когда мы говорим, что угол равен на окружности, мы имеем в виду, что вершина находится на краю окружности. Одним из типов угла на окружности является вписанный угол (см. Вписанные углы в окружности). Другой тип угла на окружность образована касательной и хордой .
Угол хорды/тангенса Теорема : Угол, образованный хордой и касательной, пересекающимися на окружности, равен половине меры перехваченная дуга .
Рисунок \(\PageIndex{1}\)\(m\angle DBA=\dfrac{1}{2}m\widehat{AB}\)
Если два угла с вершинами на окружности опираются на одну и ту же дугу, то углы равны.
Угол находится внутри окружности, если вершина лежит в любом месте внутри окружности.
Угол пересечения хорд Теорема : Мерой угла, образованного двумя хордами, которые пересекают внутри окружности, является среднее значение мер пересекаемых дуг.
\(\begin{align}m\angle SVR&=\dfrac{1}{2}(m\widehat{SR} +m\widehat{TQ} )=m\widehat {SR} +m\widehat{TQ} 2=m\угол TVQ \\ m\угол SVT&=\dfrac{1}{2}(m\widehat{ST} +m\widehat{RQ})=m\widehat {ST} +m\widehat{RQ} 2=m\угол RVQ\конец{выровнено}\)
Что, если бы вам дали окружность с хордой и касательной или с двумя хордами, пересекающимися в одной точке? Как вы могли бы использовать меру дуги, образованной этими частями круга, чтобы найти меру углов, которые они образуют на окружности или внутри нее? 9{\ круг} \) Рисунок \(\PageIndex{14}\)
Найдите \(x\).
- Заполните пробелы в доказательстве теоремы о пересекающихся хордах и углах Рисунок \(\PageIndex{15}\)
Дано : Пересекающиеся хорды \(\overline{AC}\) и \(\overline{BD}\).
Докажите : \(m\angle a=\dfrac{1}{2}(m\widehat{DC}+m\widehat{AB})\)
| Заявление | Причина |
|---|---|
1. Пересекающиеся хорды \(\overline{AC}\) и \(\overline{BD}\). Пересекающиеся хорды \(\overline{AC}\) и \(\overline{BD}\). | 1. |
2. Нарисуйте \(\overline{BC}\) Рисунок \(\PageIndex{16}\) | 2. Строительство |
3. \(m\angle DBC=\dfrac{1}{2}m\widehat{DC}\) \(м\угол ACB=\dfrac{1}{2}м\широкая шляпа{AB}\) | 3. |
| 4. \(m\угол a=m\угол DBC+m\угол ACB\) | 4. |
| 5. \(m\angle a=\dfrac{1}{2}m\widehat{DC}+\dfrac{1}{2}m\widehat{AB}\) | 5. |
Заполните пропуски.
- Если вершиной угла является _______________ окружность, то его мерой является среднее __________________ дуг.

- Если вершина угла — ________ окружность, то его мера — ______________ дуги, на которую она опирается.
Словарь
| Срок | Определение |
|---|---|
| центральный угол | Угол, образованный двумя радиусами, вершина которого находится в центре окружности. |
| хорда | Отрезок, концы которого лежат на окружности. |
| круг | Набор всех точек, находящихся на одинаковом расстоянии от определенной точки, называемой центром . |
| диаметр | Хорда, проходящая через центр окружности. Длина диаметра в два раза больше длины радиуса. Длина диаметра в два раза больше длины радиуса. |
| угол вписанный | Угол с вершиной на окружности и сторонами которого являются хорды. |
| перехваченная дуга | Дуга внутри вписанного угла, концы которой лежат на этом угле. |
| точка касания | Точка, в которой касательная касается окружности. |
| радиус | Расстояние от центра до внешнего края круга. |
| Теорема о хорде и касательном угле | Теорема хорды/касательного угла утверждает, что мера угла, образованного хордой и касательной, которые пересекаются на окружности, равна половине меры дуги, на которую она опирается. |
| Теорема о пересекающихся хордах и углах | Теорема об угле пересекающихся хорд утверждает, что мера угла, образованного двумя хордами, пересекающимися внутри окружности, является средним значением мер пересекающихся дуг. |
Дополнительные ресурсы
Интерактивный элемент
Видео: Углы на окружности и внутри нее. Основные принципы
Задания: Углы на окружности и внутри нее. Углы внутри и внутри круга
Эта страница под названием 6.16: Angles On and Inside a Circle распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
ПОД ЛИЦЕНЗИЕЙ
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- СК12
- Лицензия
- СК-12
- Программа ООР или издатель
- СК-12
- Показать оглавление
- нет
- Теги
- источник@https://www.
 ck12.org/c/geometry
ck12.org/c/geometry
- источник@https://www.
Углы в кругах: значение, правила и взаимосвязь
При выполнении штрафного удара в футболе уровень кривизны определяется углом, образованным между ногой игрока и круглым мячом.
В этой статье мы обсуждаем далее угла в кругах .
Нахождение углов в окружностях
Углы в окружностях — это углы, образованные между радиусами, хордами или касательными окружности.
Углы в окружностях можно построить с помощью радиусов, касательных и хорд. Если говорить о окружностях, то общепринятой единицей измерения углов в окружности являются градусы.
У вас есть 360 градусов в окружности, как показано на рисунке ниже. Присмотревшись к этой фигуре, мы понимаем, что все образованные углы являются частью полного угла, образованного окружностью, который равен 360°.
Рисунок 1. Углы, образованные лучами в окружности, являются частью полного угла, StudySmarter Originals
Например, если вы возьмете луч, находящийся в точке, и другой луч, идущий прямо вверх, как показано на рисунке 2, это составляет одну четвертую окружности круга, поэтому образующийся угол также будет составлять одну четвертую от полного угла. Угол, образованный лучом, идущим прямо вверх с другим лучом, направленным либо влево, либо вправо, обозначается как перпендикулярный (правый) угол.
Угол, образованный лучом, идущим прямо вверх с другим лучом, направленным либо влево, либо вправо, обозначается как перпендикулярный (правый) угол.
Рисунок 2. 90 градусов составляют одну четвертую общего угла, образованного окружностью, StudySmarter Originals
Углы в правилах окружности
решаются углы в окружности. Эти правила будут обсуждаться в нескольких разделах ниже.
Типы углов в окружности
Есть два типа углов, о которых нам нужно знать при работе с углами в окружности.
Центральные углы
Угол при вершине, где вершина находится в центре круга, образует центральный угол.
Когда два радиуса образуют угол, вершина которого находится в центре окружности, говорят о центральном угле.
Рис. 3. Центральный угол образован двумя радиусами, отходящими от центра окружности, StudySmarter Originals
Вписанные углы
Вершина вписанных углов находится на окружности окружности.
Когда две хорды образуют угол на окружности окружности, где обе хорды имеют общий конец, говорят о вписанном угле.
Рисунок 4. Вписанный угол, вершина которого находится на окружности окружности, StudySmarter Originals`
Соотношение углов в окружностях
По сути, взаимосвязь углов, существующая в окружностях, представляет собой взаимосвязь между центральным углом и вписанным углом .
Связь между центральным углом и вписанным углом
Посмотрите на рисунок ниже, на котором центральный угол и вписанный угол изображены вместе.
Связь между центральным углом и вписанным углом заключается в том, что вписанный угол составляет половину центрального угла, опирающегося на центр окружности. Другими словами, центральный угол в два раза больше вписанного угла.
Рисунок 5. Центральный угол в два раза больше вписанного угла, StudySmarter Originals
Посмотрите на рисунок ниже и запишите центральный угол, вписанный угол и уравнение, подчеркивающее связь между двумя углами.
Пример центрального угла и вписанного угла, StudySmarter Originals
Решение:
Поскольку мы знаем, что центральный угол образован двумя радиусами, имеющими вершину в центре окружности, центральный угол для на приведенном выше рисунке принимает вид
Для вписанного угла будут рассматриваться две хорды, имеющие общую вершину на окружности. Итак, для вписанного угла
Итак, для вписанного угла
Вписанный угол составляет половину центрального угла, поэтому для приведенного выше рисунка уравнение можно записать как
Пересекающиеся углы в окружности
Пересекающиеся углы в окружности также известны как хордовый угол . Этот угол образован пересечением двух хорд. На приведенном ниже рисунке показаны две хорды AE и CD, которые пересекаются в точке B. Угол и равны, поскольку они являются вертикальными углами.
На рисунке ниже угол ABC является средним значением суммы дуг AC и DE.
Рисунок 6. Две пересекающиеся хорды, StudySmarter Originals
Найдите углы x и y по рисунку ниже. Все показания даны в градусах.
Пример двух пересекающихся хорд, StudySmarter Originals
Решение:
Мы знаем, что средняя сумма дуг DE и AC составляет Y. Следовательно,
Угол B также равен 82,5° вертикальный угол. Обратите внимание, что углы образуют линейные пары, так как Y + X равно 180°. Итак,
Итак,
Здесь будут использоваться некоторые термины, с которыми вам нужно быть знакомым.
Касательная — — это линия вне круга, которая касается окружности круга только в одной точке. Эта линия перпендикулярна радиусу окружности.
Изображение касательной окружности, StudySmarter Originals
Секущая — это линия, пересекающая окружность и касающаяся окружности в двух точках.
Иллюстрация секущей окружности, StudySmarter Originals
Вершина — это точка, где пересекаются две секущие, две касательные или секущая и касательная. При вершине образуется угол.
Изображение вершины, образованной секущей и касательной, StudySmarter Originals
Внутренние дуги и внешние дуги — внутренние дуги — это дуги, которые ограничивают одну или обе касательные и секущие внутрь. Между тем, внешние дуги ограничивают одну или обе касательные и секущие снаружи.
Иллюстрация внутренней и внешней дуг, StudySmarter Originals
Угол секущей
Предположим, что две секущие линии пересекаются в точке A, ситуация ниже иллюстрируется. Точки B, C, D и E — это точки пересечения окружности, образующие две дуги: внутреннюю и внешнюю дуги. Если мы должны вычислить угол , уравнение составляет половину разницы дуг и .
Точки B, C, D и E — это точки пересечения окружности, образующие две дуги: внутреннюю и внешнюю дуги. Если мы должны вычислить угол , уравнение составляет половину разницы дуг и .
Рисунок 7. Чтобы вычислить угол в вершине секущей, большая и малая дуги вычитаются, а затем делятся пополам, StudySmarter Originals
Найдите на рисунке ниже:
Пример углов секущей-секущей , StudySmarter Originals
Решение:
Из вышеизложенного следует отметить, что это угол секущей секущей. Угол внешней дуги равен , а угол внутренней дуги равен . Следовательно:
Так
Угол секущей-тангенса
Расчет угла секанс-тангенс очень похож на угол секанс-секанс. На рисунке 8 касательная и секущая пересекаются в точке B (вершине). Чтобы вычислить угол B, вам нужно найти разницу между внешней дугой и внутренней дугой , а затем разделить на 2. Итак,
Рис. 8. Секущая-тангенс угла с вершиной в точке B, StudySmarter Originals на рисунке ниже найдите :
Пример правила секущей и касательной, StudySmarter Originals
Решение:
Из вышеизложенного следует отметить, что угол представляет собой секущую и касательную. Угол внешней дуги равен , а угол внутренней дуги равен . Следовательно:
Угол внешней дуги равен , а угол внутренней дуги равен . Следовательно:
Таким образом,
Угол касательной
Для двух касательных на рисунке 9 уравнение для расчета угла P будет иметь вид
Вычислите угол P, если на рисунке ниже большая дуга равна 240°.
Пример углов тангенс-тангенс, StudySmarter Originals
Решение:
Полный круг образует угол 360°, а дуга равна 240°, таким образом,
Используя приведенное выше уравнение для расчета угла P,
Углы в кругах – ключевые выводы
- Полный круг состоит из 360 градусов.
- Когда два радиуса от угла, где вершина находится в центре круга, это центральный угол.
- Две хорды, образующие угол на окружности окружности, где обе хорды имеют общий конец, называются вписанным углом.
- Вписанный угол равен половине центрального угла, опирающегося на центр окружности.
- Для хордового угла угол при вершине рассчитывается как среднее значение суммы противоположных дуг.

- Чтобы вычислить угол при вершине для углов секущая-тангенс, секущая-секущая и тангенс-тангенс, большая дуга вычитается из малой дуги, а затем делится пополам.
Калькулятор центрального угла. Найдите длину дуги, радиус, центральный угол центральный угол?
Вы когда-нибудь задумывались, как найти центральный угол окружности? Калькулятор центрального угла здесь, чтобы помочь; единственные переменные, которые вам нужны, это длина дуги и радиус.
Читайте дальше, чтобы узнать определение центрального угла и как использовать формулу центрального угла.
Что такое центральный угол?
Центральный угол — это угол с вершиной в центре круга, стороны которого выходят на окружность. Вы можете представить, что центральный угол находится на кончике куска пиццы в большой круглой пицце.
Вы можете представить, что центральный угол находится на кончике куска пиццы в большой круглой пицце.
Центральный угол окружности можно найти по формуле:
θ = L / r
где θ — центральный угол в радианах, L — длина дуги, r — длина дуги радиус.
Откуда берется формула центрального угла?
Простота формулы центрального угла проистекает из определения радиана. радиана — это единица углового размера, где 1 радиан определяется как центральный угол (θ), длина дуги которого равна радиусу ( л = r ).
Калькулятор угла окружности в терминах пиццы
Поскольку математика может сделать людей голодными, мы могли бы лучше понять центральный угол в терминах пиццы. Каким был бы центральный угол куска пиццы, если бы длина корки (L) была равна радиусу (r)?
Поскольку задача определяет L = r , и мы знаем, что 1 радиан определяется как центральный угол, когда L = r, мы можем видеть, что центральный угол равен 1 радиану. Мы также могли бы использовать формулу центрального угла следующим образом:
Мы также могли бы использовать формулу центрального угла следующим образом:
θ = L / r
= L / L
= 1 рад
Сколько кусков пиццы с центральным углом в 1 радиан можно отрезать от круглой пиццы?
В полной круглой пицце мы знаем, что центральные углы всех ломтиков в сумме составляют 2π радиан = 360°. Поскольку каждый срез имеет центральный угол в 1 радиан, нам потребуется 2π / 1 = 2π срезов или 6,28 срезов, чтобы заполнить полный круг.
Мы придем к тому же ответу, если рассматривать эту задачу с точки зрения корочки для пиццы: мы знаем, что длина окружности равна 2πr . Поскольку длина корочки = радиусу, то по периметру пиццы поместится 2πr / r = 2π корок.
Теперь, если вы все еще голодны, взгляните на калькулятор площади сектора, чтобы рассчитать площадь каждого кусочка пиццы!
Бонусное задание. Как далеко Земля перемещается в каждое время года?
Попробуйте использовать калькулятор центрального угла в обратном порядке, чтобы решить эту проблему. Земля находится примерно в 149,6 млн км от Солнца. Если Земля проходит около четверти своей орбиты каждый сезон, сколько километров Земля проходит каждый сезон (например, с весны на лето)?
Земля находится примерно в 149,6 млн км от Солнца. Если Земля проходит около четверти своей орбиты каждый сезон, сколько километров Земля проходит каждый сезон (например, с весны на лето)?
Давайте подойдем к этой задаче шаг за шагом:
- Упростим задачу, предположив, что орбита Земли круговая ( Орбита Земли на самом деле эллиптическая и постоянно меняется ). В этой модели Солнце находится в центре круга, а орбита Земли — это окружность.
- Радиус — это расстояние от Земли и Солнца: 149,6 млн км.
- Центральный угол равен четверти окружности:
360° / 4 = 90°. - Используйте калькулятор центрального угла, чтобы найти длину дуги .
Вы можете сами попробовать произвести окончательный расчет, изменив формулу следующим образом:
L = θ * r
Затем переведите центральный угол в радианы: 90° = 1,57 рад и решите уравнение:
L = 1,57 * 149,6 млн км
L = 234,9 млн км .
Если предположить, что по идеально круговой орбите Земля проходит примерно 234,9миллионов км каждый сезон!
Часто задаваемые вопросы
Как найти центральный угол окружности?
Чтобы найти центральный угол окружности, используйте формулу:
θ = L / r
где:
θ — центральный угол в радианах;
L – длина дуги; а
r — радиус.
Чтобы найти центральный угол окружности, нужно вычислить отношение длины дуги к радиусу окружности.
Вы можете представить, что центральный угол находится на кончике куска пиццы в большой круглой пицце.
Как найти радиус по длине дуги и центральному углу?
Чтобы найти радиус по длине дуги и центральному углу, нужно взять отношение длины дуги к центральному углу.
Jasmine J MAH
Длина дуги (L)
Радиус (R)
Диаметр
Центральный угол (θ)
Проверьте 6 аналогичных угловых кальлеров 🕑
Угол между двумя векторами укол сопутствующих Дуги и стягивающие углы | Решенные примеры | Геометрия
В окружности есть различные углы, которые могут быть образованы, соединяя концы дуг, и эти углы называются вытянутыми углами. Существуют разные категории углов, образованных этими дугами, например, углы в одном отрезке, углы в полуокружности, углы на окружности и т.д. Давайте узнаем об этом подробно в этом уроке.
Существуют разные категории углов, образованных этими дугами, например, углы в одном отрезке, углы в полуокружности, углы на окружности и т.д. Давайте узнаем об этом подробно в этом уроке.
| 1. | Как найти угол, образуемый дугой окружности? |
| 2. | Угол, опирающийся на дугу в центре |
| 3. | Углы на одном отрезке окружности равны |
Как найти угол, образуемый дугой окружности?
дуга окружности — это любая часть окружности. Угол , на который опирается дуга в любой точке, — это угол, образованный между двумя отрезками, соединяющими эту точку с конечными точками дуги. На следующем рисунке показанная дуга окружности образует угол α в точке на окружности и угол β в центре O.
Нас интересует соотношение между углом, на который данная дуга опирается в любом месте окружности, и углом, на который эта дуга опирается в центре окружности. Связь между ними проста и чрезвычайно важна.
Связь между ними проста и чрезвычайно важна.
Угол, опирающийся на дугу в центре
В центре круга, если есть два отрезка прямой, исходящие из конечных точек дуги пересечения окружности, этот угол называется углом, опирающимся на дугу в центре. Разберемся с теоремой и ее доказательством на ее основе.
Теорема:
Угол, образуемый дугой окружности в ее центре, в два раза больше угла, который она образует в любой точке окружности.
Доказательство этой теоремы довольно простое и использует теорему о внешнем угле – внешний угол треугольника равен сумме противоположных внутренних углов. Если два противоположных внутренних угла равны, то внешний угол будет вдвое больше любого из противолежащих внутренних углов.
Доказательство:
Рассмотрим следующий рисунок, на котором дуга (или сегмент) AB опирается на ∠AOB в центре O и ∠ACB в точке C на окружности.
Нам нужно доказать, что ∠AOB = 2 × ∠ACB. Проведите линию через О и С и дайте ей снова пересечь окружность в точке D, как показано на рисунке.
Проведите линию через О и С и дайте ей снова пересечь окружность в точке D, как показано на рисунке.
Имеются два треугольника, образованные ΔOAC и ΔOBC. Итак, делаем следующие наблюдения.
1. В ΔOAC ∠OAC = ∠OCA, поскольку OA = OC
2. В ΔOBC ∠OBC = ∠OCB, поскольку OB = OC.
Отсюда, используя теорему о внешнем угле, получаем :
∠AOD+ ∠DOB= 2× (∠ACO+ ∠OCB)
⇒ ∠AOB= 2× ∠ACB
Это завершает доказательство теоремы. Вы можете поэкспериментировать с симуляцией ниже, чтобы понять взаимосвязь между углами, стягиваемыми дугой в центре и в точке на окружности.
Что, если дуга AB такова, что образует рефлекторный угол в центре? Что ж, наше доказательство не меняется, как показано на следующем рисунке.
Теперь вы можете применить точно такие же шаги, как мы делали ранее, и получить тот же результат: ∠AOB= 2× ∠ACB. Другая конфигурация была бы, когда O не лежит в пределах ∠ACB. Сохранится ли результат, как показано на следующем рисунке?
Да, будет. Снова соедините C с O и расширьте его до D по окружности круга. (1)
Снова соедините C с O и расширьте его до D по окружности круга. (1)
20007
Чтобы не загромождать, эти углы не выделены на рисунке, но внимательно их соблюдайте. Вычтем из (1) уравнение (2)
∠BOD− ∠AOD= 2× (∠BCD− ∠ACD)
⇒ ∠AOB= 2× ∠ACB
Эта теорема приводит к интересному следствию, которое обсуждается далее. .
Следствие:
Угол в полуокружности прямой. Рассмотрим рисунок ниже, где AB — диаметр окружности. Нам нужно доказать, что ∠ACB= 90 ∘
Доказательство:
Так как ∠AOB= 180 º , ∠ACB= 1/2× ∠AOB= 90 º 900 Эта теорема также приводит к следующему результату.
Углы на одном отрезке окружности равны
В круге есть два сегмента — большие сегменты и второстепенные сегменты. Углы, образованные концами хорды как на большом, так и на малом отрезках, всегда равны. Давайте разберемся в этой теореме и ее доказательстве в деталях.
Теорема:
Углы одного сегмента окружности равны. Другими словами, дуга окружности образует равные углы в любом месте окружности. Рассмотрим следующий рисунок, на котором показана дуга AB, образующая углы ACB и ADB в двух произвольных точках C и D на окружности. О — центр круга.
Другими словами, дуга окружности образует равные углы в любом месте окружности. Рассмотрим следующий рисунок, на котором показана дуга AB, образующая углы ACB и ADB в двух произвольных точках C и D на окружности. О — центр круга.
Нам нужно доказать, что ∠ACB= ∠ADB.
Доказательство:
Используя нашу предыдущую теорему, мы получаем, что
∠ACB= 1/2× ∠AOB ⋯ (1)
∠ADB= 1/2× ∠AOB ⋯ (2)
Из уравнений (1) и (2) получаем ∠ACB= ∠ADB.
Важные примечания:
- Конгруэнтные дуги окружности образуют равные углы в центре.
- Угол, образуемый дугой в центре, в два раза больше угла, образуемого дугой в любой точке оставшейся части окружности.
- Углы одного сегмента окружности равны.
- Угол в полуокружности является прямым углом.
Аналитический центр:
- Если углы, образуемые хордами окружности в центре, равны, равны ли хорды?
- Хорды конгруэнтных окружностей образуют равные углы в своих центрах.
 Аккорды равны?
Аккорды равны?
Часто задаваемые вопросы по дугам и вытянутым углам
Что означает Subtended?
В геометрии стягиваемый означает продолжение под. Стягивающий угол образуется при пересечении более чем одной линии или лучей, соединяющих конечные точки линии или дуги.
Что такое вытянутый центральный угол?
Вытянутый центральный угол — это угол, образованный в центре окружности, а стороны угла — это радиусы окружности, пересекающие окружность в двух разных точках.
Как найти угол, образуемый дугой в центре?
Чтобы найти значение угла, образуемого дугой в центре, мы должны умножить угол, образованный через те же концы дуги на окружности, на два. Например, если угол, образуемый в любой точке окружности, равен 60 º , это означает, что угол, образуемый той же дугой в центре, равен 120 º .
Что такое центральный угол окружности?
Центральный угол окружности — это угол, вершина которого совпадает с центром окружности.


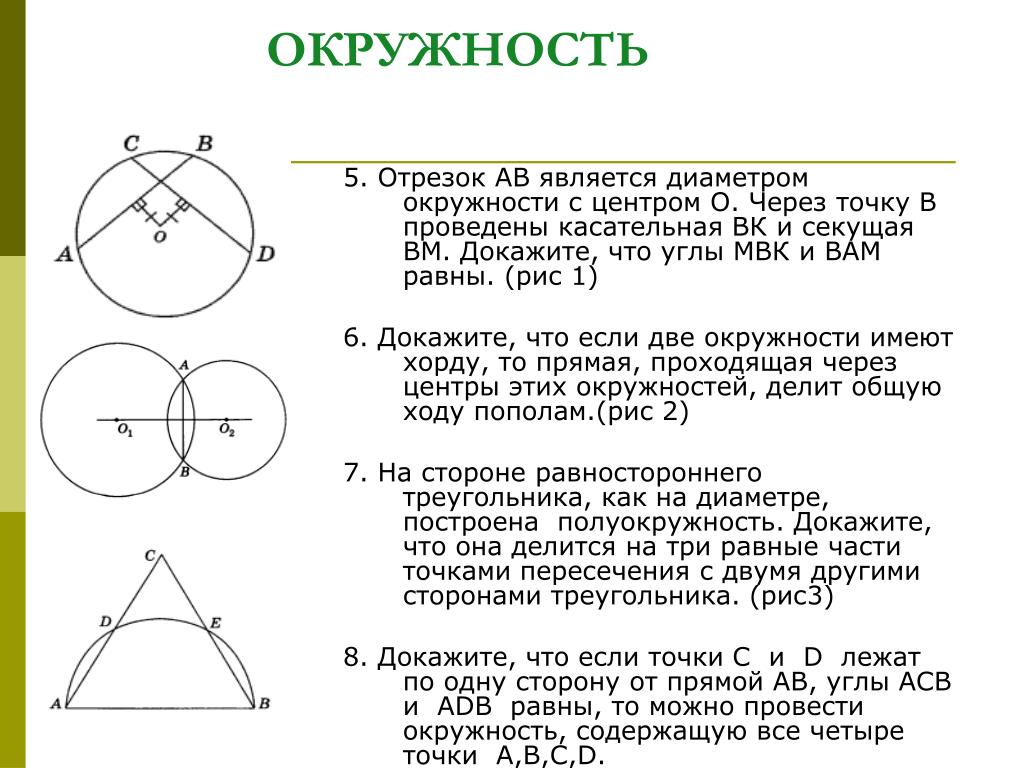

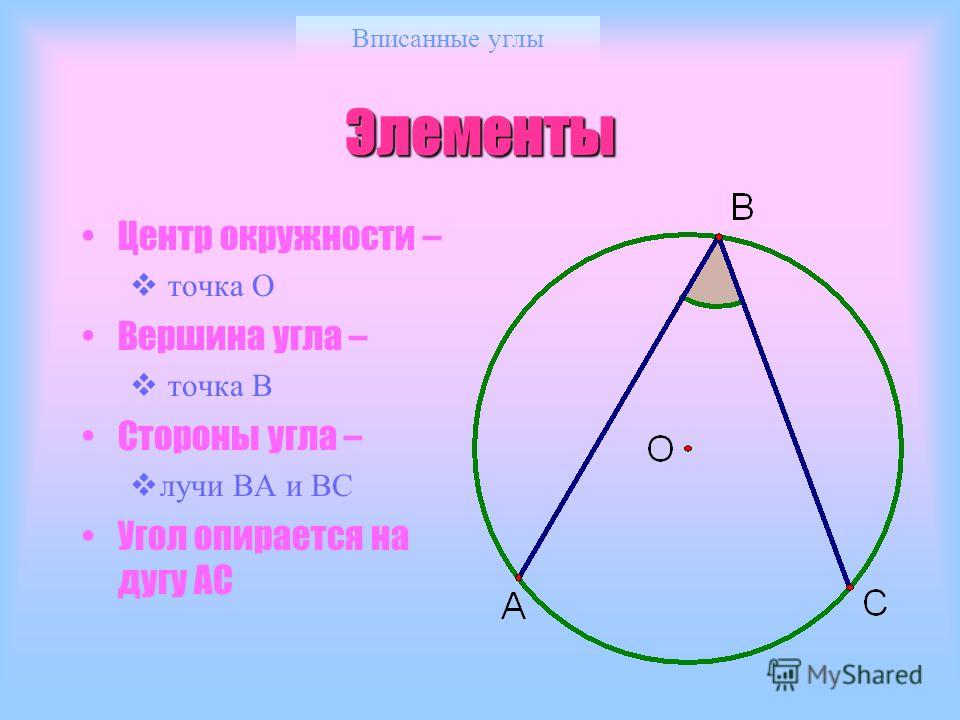
 слайд 5. См. рисунок 4 найдите х.
слайд 5. См. рисунок 4 найдите х. /918870b1bc4a305.s.siteapi.org/img/809187499fcd0edfbd7e361ade849ad26c8b0352.jpg)