2+n-72)=1/(n+9)
2+n-72)=1/(n+9)Координаты точки на окружности — Без Сменки
16 мая, 2022
1 мин
Мтмт 📈
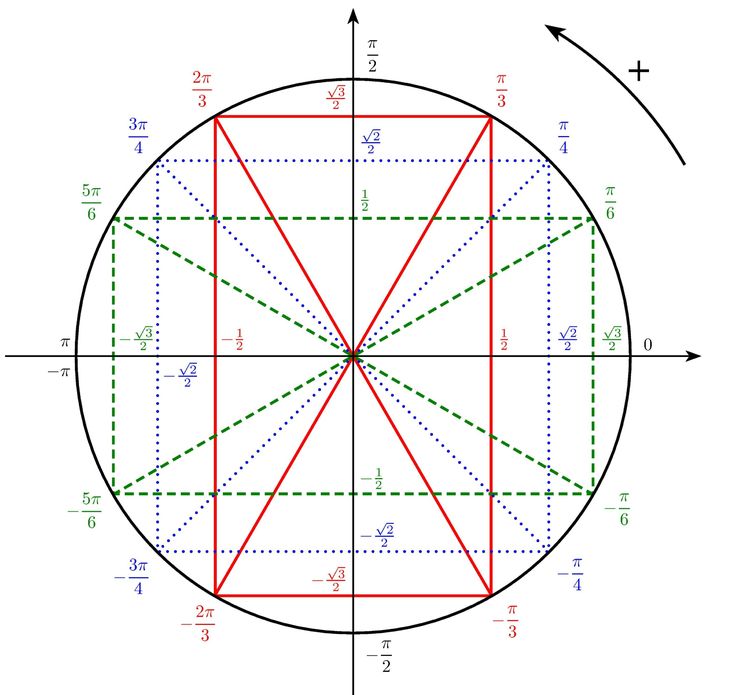
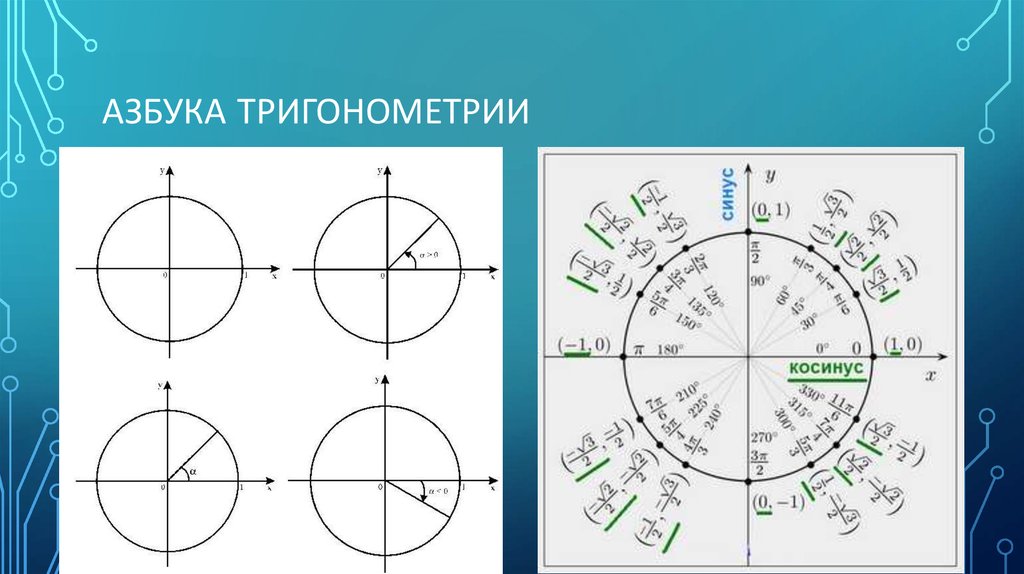
Сегодня поговорим об единичной окружности 🧑🏫
Можно ли найти точку (её координаты) на окружности, зная координаты центра окружности, её радиус и угол поворота?🤔
Ну, конечно, можно! Записывай и запоминай общую формулу для нахождения координат точки:
x=x0+r⋅cos δ
y=y0+r⋅sin δ
x0,y0 — координаты центра окружности;
r — радиус окружности;
δ —угол поворота радиуса вектора.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Редакция Без Сменки
Честно. Понятно. С душой.
Понятно. С душой.
44 подписчиков
+ Подписаться
Редакция Без Сменки
03 июня, 2022
1 мин
Ист 🤴
Культура XVIII века
👉🏻 ЖИВОПИСЬ: В живописи второй половины XVIII века важнейшее место занимал портрет. Обратим…
Редакция Без Сменки
21 марта, 2022
1 мин
Физ 🔬
Механические колебания
Движение, при котором состояния движущегося тела с течением времени повторяются, причём тело.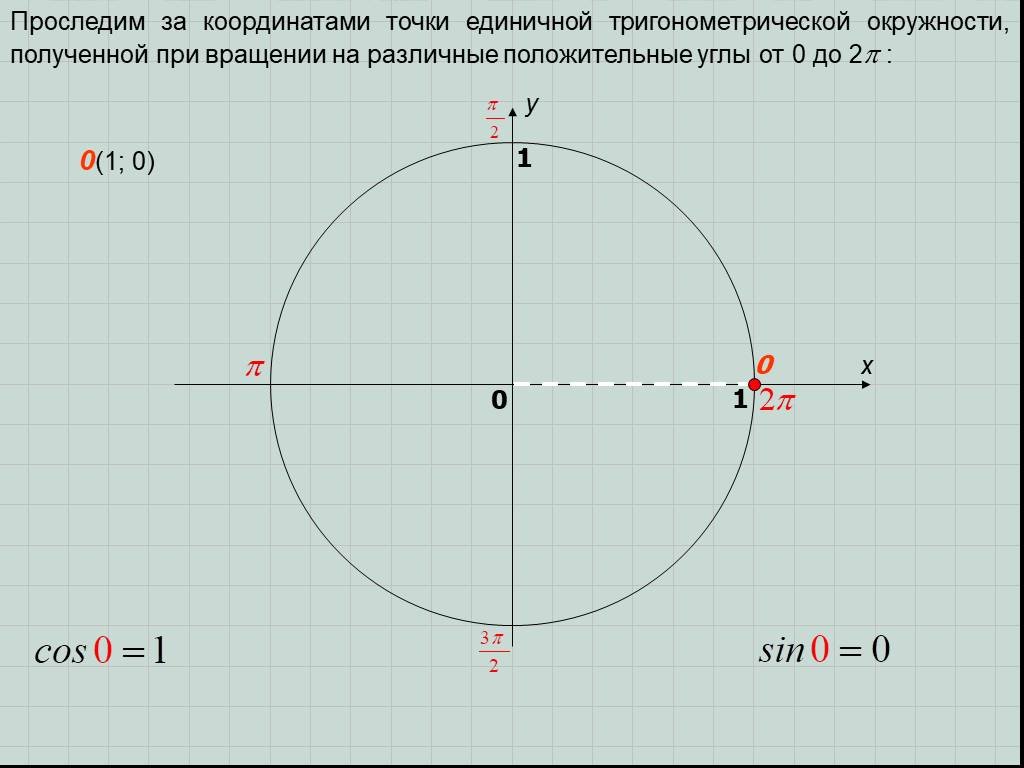 ..
..
Редакция Без Сменки
26 мая, 2022
1 мин
Мтмт 📈
Формулы показательных выражений
Чтобы нормально решать задания на показательные выражения и уравнения, нужно как минимум знать…
Редакция Без Сменки
03 мая, 2022
1 мин
Англ 🇬🇧
Лексика кино
Сегодня готовимся идти в кино и рассказывать на экзамене про лучшие фильмы, которые успели…
Редакция Без Сменки
01 июля, 2022
1 мин
Лит 📚
Авторская позиция
Авторская позиция проявляется в:
❄️ точках зрения на события и героев
❄️чувствах и мыслях.
Редакция Без Сменки
06 июня, 2022
1 мин
Общ 👨👩👧
Власть
Власть появляется одновременно с возникновением человеческого общества, которое не может обойтись…
генерация координат окружности
Быстрый обзор триггера
В прямоугольном треугольнике, показанном ниже (названном так потому, что он имеет
прямой (90 градусов) угол в нем), мы пометили 3 стороны.
Гипотенуза лежит напротив прямого угла треугольника.
Высота — это синяя линия, а основание — красная линия.
Существуют соотношения между углами прямоугольного треугольника и его основание и высота.
Отношение высоты к гипотенузе называется синусом.
Отношение основания к гипотенузе называется косинусом.
Вот забавная демонстрация, показывающая высоту (или основание) треугольника. когда гипотенуза колеблется по кругу, образуя синусоидальную (или косинусоидальную) волну.
Генерация (x,y) координат окружности
Возьмем окружность с центром в точке (0,0).
Радиус окружности равен 1.
На рисунке ниже показаны оси X (горизонтальная) и Y (вертикальная).
Углы измеряются, начиная с оси x.
Если провести линию из точки (0,0) под углом a от оси абсцисс линия пересечет окружность в точке Р .
Мы можем использовать отношения выше, чтобы определить координаты x и y точки P. Вот как:
- Координата x точки P называется косинусом a (записывается так: cos(a))
- Координата y точки P называется синусом a (записывается так: sin(a))
Пристальный взгляд на генерирующие точки по кругу
Чтобы сгенерировать координаты по кругу, начнем
с небольшим примером.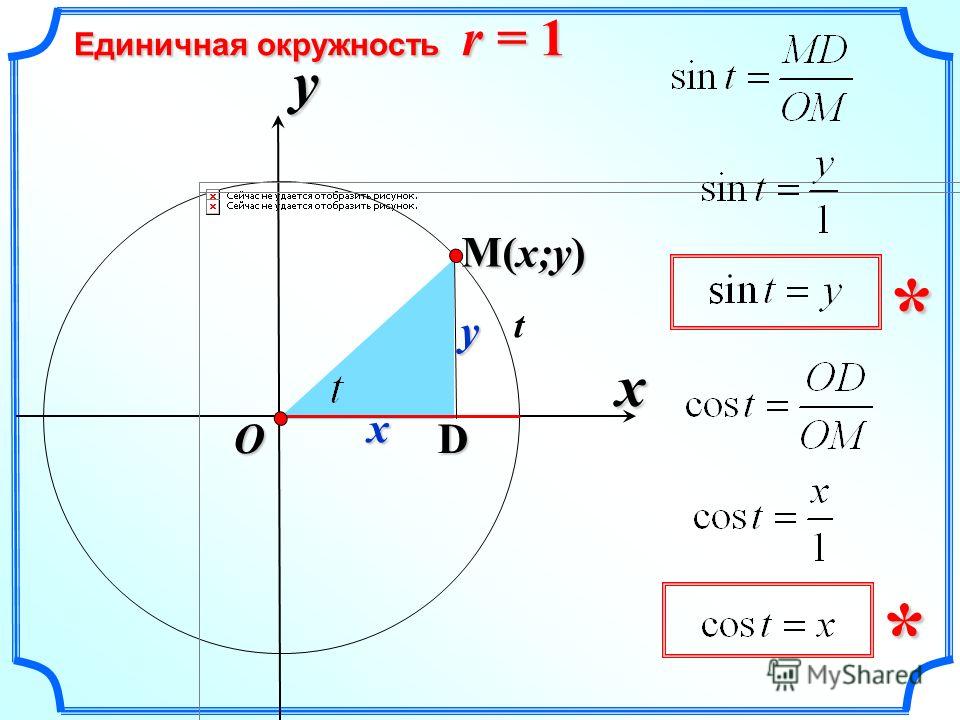
Мы будем использовать r для обозначения
радиус окружности и для обозначения
углы, натянутые, начиная с оси x.
Начнем всего с пяти следующих углов: 0, 90, 180, 270 и 360.
(0 и 360 градусов — это один и тот же угол, а именно положительная ось абсцисс).
r = 1
a = 0, 90, 180, 270, 360 (углы в градусах)
Теперь посмотрим на те же углы, но покажем их в радианах а не градусов.
a = 0, pi/2, pi, 3pi/2, 2pi
(углы в радианах, где полный оборот по окружности равен 2pi)
Затем, чтобы сгенерировать координаты x и y вдоль окружности, мы используем:
x = r * cos(a)
y = r * sin(a)
Для каждого из 5 значений нашего угла a это дает нам:
A = 0 A = PI/2 A = PI A = 3PI/2 A = 2PI/2PI. x =
1 * cos(0) 1 * cos(pi/2) 1* cos(pi) 1* cos(3*pi/2) 1* cos(2*pi) х = 1 * 1 1 * 0 1 * -1 1 * 0 1 * 1 х = 1 0 -1 0 1
И мы делаем аналогичный расчет для координаты y, используя:
у = г * грех (а)
444444444444444444444444444444444444444444444444444444444444444444444449н Эти координаты x и y (в желтых прямоугольниках выше), взятые попарно, действительно дают нам координаты из точек, показанных на рисунке выше (движемся против часовой стрелки):
y = 1 * sin(0) 1 * sin(pi/2) 1* sin(pi) 1* sin(3*pi/2) 1* sin(2*pi) у = 1 * 0 1 * 1 1 * 0 1 * -1 1 * 0 Y = 0 1 0 -1 0 (1, 0)
(0, 1)
(-1, 0)
(0, -1)
(1,0)В приведенных выше примерах мы используем только 4 точки, так что это не выглядит очень похоже на круг еще.
Однако, если мы рассмотрим эти 9 углов:a = 0, пи/4, пи/2, 3пи/4, пи, 5пи/4, 3пи/2, 7пи/8, 2пи
Затем мы можем получить координаты x и y для этих 9 углов:
И если мы перепрыгнем с 9 на 17 углов между 0 и 2pi, мы сможем см. координаты приближаются к круглой форме.
Вернуться к заданию 1
геометрия — Найти координаты точки на окружности
спросил
Изменено 11 месяцев назад
Просмотрено 197 тысяч раз
$\begingroup$
У меня есть такой круг
Учитывая вращение θ
и радиус r , как мне найти координату (x, y)? Имейте в виду, что это вращение может быть где угодно между 0 и 360 градусами.Например, у меня есть радиус 12 и поворот θ на 115 градусов. Как бы вы нашли точку (x, y)?
- геометрия
- тригонометрия
- круги
- вращения
$\endgroup$
2
$\begingroup$
Судя по картинке, ваша окружность имеет центр начала координат и радиус $r$. Вращение, кажется, по часовой стрелке. И вопрос, похоже, в том, где заканчивается точка $(0,r)$ в верхней части круга.
Точка $(0,r)$ заканчивается в $x=r\sin\theta$, $y=r\cos\theta$.
В общем, предположим, что вы вращаетесь вокруг начала координат по часовой стрелке на угол $\theta$. Тогда точка $(s,t)$ оказывается в точке $(u,v)$, где $$u=s\cos\theta+t\sin\theta\qquad\text{and} \qquad v=-s\sin\theta+t\cos\theta.$$
$\endgroup$
3
$\begingroup$
С углом 115° по часовой стрелке, вы можете найти точку (x,y), как показано на диаграмме, с помощью следующей математики:
Любая точка $(x,y)$ на пути окружности равна $x = r*sin(θ), y = r*cos(θ)$
таким образом: $(x,y) = (12*sin(115), 12*cos(115))$
Итак, ваша точка будет примерно будет $(10,876, -5,071)$ (при условии, что верхний правый квадрант равен x+, y+)
$\endgroup$
$\begingroup$
Стандартный круг рисуется с начальной точкой 0 градусов на пересечении круга и оси x с положительным углом, направленным против часовой стрелки.
Таким образом, стандартная параметризация учебника: х=cos т y=sin t
На вашем рисунке показан другой сценарий. Как это нарисовано, начальная точка находится вверху, а градусы увеличиваются по часовой стрелке. Таким образом, стандартная параметризация должна быть изменена в соответствии с вашей ситуацией.
Посмотрите, каково значение x на вашей картинке в начальной точке, а затем, что происходит, когда t увеличивается. x начинается с 0, затем увеличивается до максимума 1, а затем возвращается к 0, когда t = Pi.
Теперь вы хотите сравнить это поведение со стандартным графиком sin и cos, чтобы решить, какой из них соответствует вашим потребностям. X=sin t ведет себя именно так, так что теперь у вас есть параметризация x. Обратите внимание, что это не x = cos t, как учит стандартный учебник по математике, потому что в классе тригонометрии они обычно имеют 0 градусов на пересечении оси x и единичной окружности.
Теперь y на вашем чертеже начинается с 1, а затем уменьшается, пока вы не достигнете 0, а затем -1 в PI.

 x =
x =