Окружность углы: Центральные и вписанные углы — урок. Геометрия, 8 класс.

Вписанный угол, теория и задачи

Вписанный угол, теория задачи. Друзья! В этой статье речь пойдёт о заданиях, для решения которых необходимо знать свойства вписанного угла. Это целая группа задач, они включены в ЕГЭ. Большинство из них решаются очень просто, в одно действие.

Есть задачи посложнее, но и они большой трудности для вас не представят, необходимо знать свойства вписанного угла. Постепенно мы разберём все прототипы задач, приглашаю вас на блог!

Теперь необходимая теория. Вспомним, что такое центральный и вписанный угол, хорда, дуга, на которые опираются эти углы:

Центральным углом в окружности называется плоский угол с вершиной в ее центре.

Часть окружности, расположенная внутри плоского угла, называется дугой окружности.

Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.

Угол, называется вписанным в окружность, если вершина угла лежит на окружности, а стороны угла пересекают эту окружность.

Отрезок соединяющий две точки окружности называется хордой. Самая большая хорда проходит через центр окружности и называется диаметр.

Для решения задач на вписанные в окружность углы, вам необходимо знать следующие свойства:

1. Вписанный угол равен половине центрального, опирающегося на ту же дугу.

2. Все вписанные углы, опирающиеся на одну и ту же дугу, равны. 

3. Все вписанные углы, опирающиеся на одну и ту же хорду, вершины которых лежат по одну сторону от этой хорды, равны.

4. Любая пара углов, опирающихся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180°.

Следствие: противолежащие углы четырёхугольника вписанного в окружность в сумме составляют 180 градусов.

5. Все вписанные углы, опирающиеся на диаметр, прямые.

Вообще, это свойство является следствием из свойства (1), это его частный случай. Посмотрите – центральный угол равен 180 градусам (и этот развёрнутый угол есть не что иное, как диаметр), значит по первому свойству вписанный угол С равен его половине, то есть 90 градусам.

Знание данного свойства помогает в решении многих задач и часто позволяет избежать лишних расчётов. Хорошо усвоив его — вы более половины задач такого типа сможете решать устно. Два следствие, которые можно сделать:

Следствие 1: если в окружность вписан треугольник и одна его сторона совпадает с диаметром этой окружности, то треугольник является прямоугольным (вершина прямого угла лежит на окружности).

Следствие 2: центр описанной около прямоугольного треугольника окружности совпадает с серединой его гипотенузы.

Многие прототипы стереометрических задач также решаются благодаря использованию этого свойства и данных следствий. Запомните сам факт: если диаметр окружности является стороной вписанного треугольника, то этот треугольник прямоугольный (угол лежащий против диаметра равен 90 градусов). Все остальные выводы и следствия вы сможете сделать сами, учить их не надо.

Как правило, половина  задач на вписанный угол даётся с эскизом, но без обозначений. Для понимания процесса рассуждения при решении задач (ниже в статье) введены обозначения вершин (углов). На ЕГЭ вы можете этого не делать. Рассмотрим задачи:

Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

Построим центральный угол для заданного вписанного угла, обозначим вершины:

По свойству вписанного в окружность угла:

Угол АОВ равен 60⁰, так как треугольник АОВ равносторонний, а в равностороннем треугольнике все углы равны по 60⁰. Стороны треугольника равны, так как в условии сказано, что хорда равна радиусу.

Таким образом, вписанный угол АСВ равен 30⁰.

Ответ: 30 

Найдите хорду, на которую опирается угол 30⁰, вписанный в окружность радиуса 3.

Это по сути обратная задача (предыдущей). Построим центральный угол.

Он в два раза больше вписанного, то есть угол АОВ равен 60⁰. От сюда можно сделать вывод, что треугольник АОВ равносторонний. Таким образом, хорда равна радиусу, то есть трём.

Ответ: 3

Радиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную корню из двух. Ответ дайте в градусах.

Построим центральный угол:

Зная радиус и хорду мы можем найти центральный угол  АСВ. Это можно сделать по теореме косинусов. Зная центральный угол мы без труда найдём вписанный угол АСВ.

Теорема косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус  угла между ними.

Следовательно, второй центральный угол равен 360⁰ – 90⁰ = 270⁰.

Угол АСВ по свойству вписанного угла равен его половине, то есть 135 градусам.

Ответ: 135

Найдите хорду, на которую опирается угол 120 градусов, вписанный в окружность радиуса  корень из трёх.

Соединим точки А и В с центром окружности. Обозначим её как О:

Нам известен радиус и вписанный угол АСВ. Мы можем найти центральный угол АОВ (больший 180 градусов), затем найти угол АОВ в треугольнике АОВ. А далее по теореме косинусов вычислить АВ.

По свойству вписанного угла центральный угол АОВ (который больше 180 градусов) будет равен вдвое больше  вписанного, то есть 240 градусам. Значит, угол АОВ в треугольнике АОВ равен  360⁰ – 240⁰ = 120⁰.

По теореме косинусов:

Ответ:3

Найдите вписанный угол, опирающийся на дугу, которая составляет 20% окружности. Ответ дайте в градусах.

По свойству вписанного угла он вдвое меньше центрального угла, опирающегося на ту же дугу, в данном случае речь идёт о дуге АВ.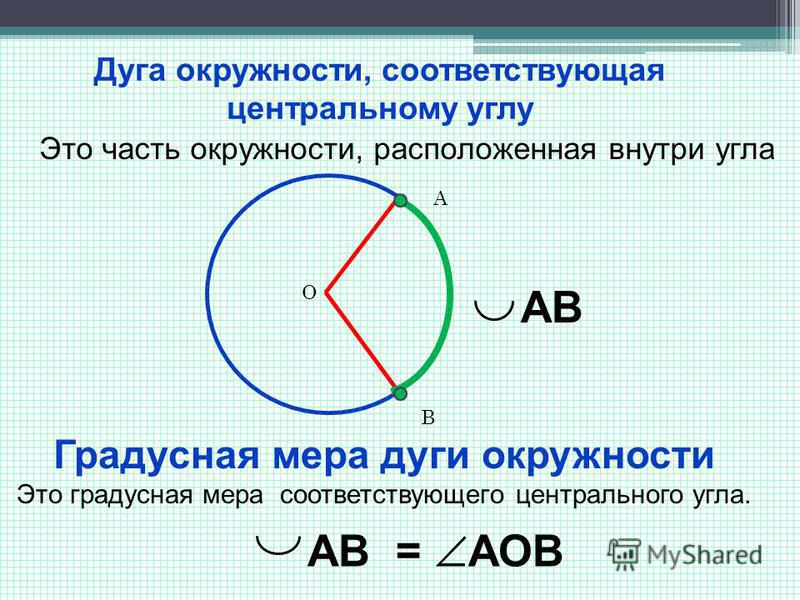

Сказано, дуга АВ составляет 20 процентов от окружности. Это означает, что центральный угол АОВ составляет так же 20 процентов от 360⁰. *Окружность это угол в 360 градусов. Значит,

Таким образом, вписанный угол АСВ равен 36 градусам.

Ответ: 36

Дуга окружности AC, не содержащая точки B, составляет 200 градусов. А дуга окружности BC, не содержащая точки A, составляет 80 градусов. Найдите вписанный угол ACB. Ответ дайте в градусах.

Обозначим для наглядности дуги, угловые меры которых даны. Дуга соответствующая 200 градусам – синий цвет, дуга соответствующая 80 градусам – красный цвет, оставшаяся часть окружности – жёлтый цвет.

Таким образом, градусная мера дуги АВ (жёлтый цвет), а значит и центральный угол АОВ составляет:  360⁰ – 200⁰ – 80⁰ = 80⁰.

Вписанный угол АСВ вдвое меньше центрального угла АОВ,то есть равен 40 градусам.

Ответ: 40

Чему равен вписанный угол, опирающийся на диаметр окружности? Ответ дайте в градусах.

Посмотреть решение

Найдите хорду, на которую опирается угол 90⁰, вписанный в окружность радиуса 1.

Посмотреть решение

Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

Посмотреть решение

Радиус окружности равен 1. Найдите величину острого вписанного угла, опирающегося на хорду, равную корню из двух. Ответ дайте в градусах.

Посмотреть решение

Центральный угол на 36⁰ больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.

Посмотреть решение

Найдите вписанный угол, опирающийся на дугу АВ, которая составляет  0,2 окружности. Ответ дайте в градусах.

Посмотреть решение

Хорда делит окружность на две части, градусные величины которых относятся как 5:7. Под каким углом видна эта хорда из точки, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.

Посмотреть решение

Точки А, В, С, расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1:3:5. Найдите больший угол треугольника АВС. Ответ дайте в градусах.

Посмотреть решение

На что обратить внимание при решении подобных задач?

Необходимо знать свойство вписанного угла; понимать, когда и как необходимо использовать теорему косинусов, подробнее о ней посмотрите здесь.

На этом всё! Успехов Вам!

С уважением, Александр Крутицких

Учительница математики в школе в третьем классе:
— Дети, а скажите мне, сколько будет 6*6?
Дети дружно хором отвечают:
— Семьдесят шесть!
— Ну, что вы, такое говорите детки! Шесть на шесть будет тридцать шесть… ну может быть еще 37, 38, 39… ну максимум 40… но никак не семьдесят шесть!

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.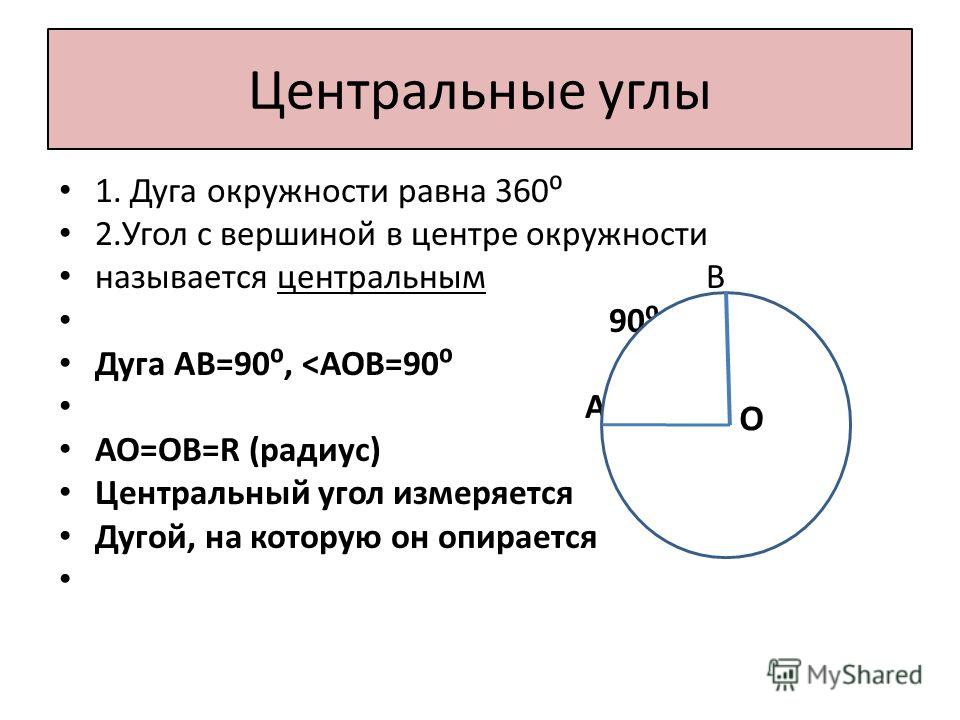

Вписанный угол окружности. Теорема с доказательством

• Теорема о вписанном угле
• Следствия из теоремы

Вписанный угол окружности — это угол, образованный двумя хордами, исходящими из одной точки, то есть вписанным углом называется угол, вершина которого лежит на окружности.

Угол  ABC  — вписанный угол.  ∠ABC  опирается на дугу  AC,  заключённую между его сторонами.

Теорема о вписанном угле

Теорема:

Вписанный угол измеряется половиной дуги, на которую он опирается.

Это следует понимать так: вписанный угол содержит в два раза меньше градусов, чем дуга, на которую он опирается:

∠ABC =	1	AC.
	2

Доказательство:

При доказательстве этой теоремы следует рассмотреть три возможных случая расположения вписанного угла относительно центра окружности.

Первый случай. Сторона вписанного угла проходит через центр окружности.

Соединим точку  A  с центром круга (точкой  O).  Получим равнобедренный треугольник  AOB,  в котором  AO = OB,  как радиусы одной окружности. Следовательно,  ∠A = ∠B,  как углы при основании равнобедренного треугольника.

Так как  ∠AOC  — внешний угол равнобедренного треугольника, то:

∠AOC = ∠A + ∠B,

а так как углы  A  и  B  равны, то

∠B =	1	∠AOC.
	2

Но  ∠AOC — центральный угол, значит  ∠AOC = AC,  следовательно  ∠B  измеряется половиной дуги  AC:

∠ABC = ∠B =	1	AC.
	2

Второй случай. Центр окружности лежит между сторонами вписанного угла.

Проведём диаметр  BD.  Угол  ABC  разбился на два угла:  ∠1  и  ∠2.

Точка  D  разделяет дугу  AC  на две дуги:  AD  и  DC.  По доказательству, рассмотренному в первом случае:

∠1 =	1	AD  и  ∠2 =	1	DC.
	2		2

Следовательно, весь угол  ABC  будет измеряться половиной дуги  AC:

∠1 + ∠2 =	1	AD  +	1	DC
	2		2

или

∠ABC =	1	AC.
	2

Третий случай. Центр окружности лежит вне вписанного угла.

Проведём диаметр  BD.

∠ABC = ∠ABD — ∠CBD.

Но  ∠ABD  измеряется половиной дуги  AD , а  ∠CBD  измеряется половиной дуги  CD.  Следовательно,

∠ABC =	1	(AD — CD),
	2

то есть

∠ABC =	1	AC.
	2

Следствия из теоремы

1. Все вписанные углы, опирающиеся на одну и ту же дугу, равны между собой, так как они измеряются половиной одной и той же дуги.

2. Вписанный угол, опирающийся на диаметр, — прямой, так как он опирается на половину окружности.

Половина окружности содержит  180°,  значит, угол, опирающийся на диаметр, содержит  90°.

Теоремы о круге

Несколько интересных фактов об углах и окружностях

Вписанный угол

Прежде всего, определение:

Вписанный угол : угол, образованный точками, лежащими на окружности окружности.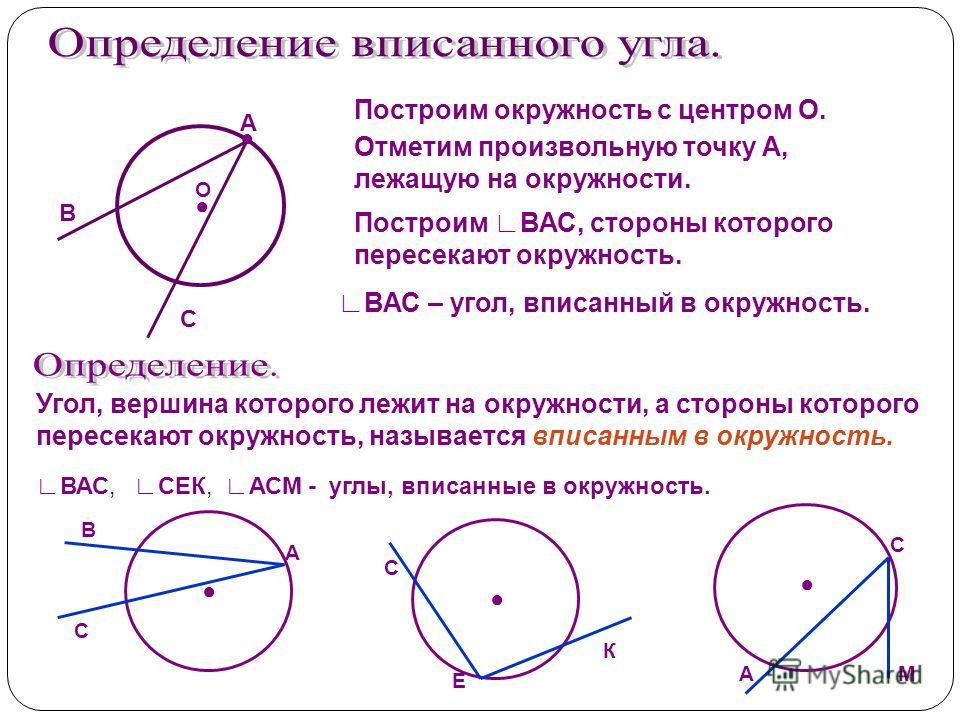

A и C — «конечные точки»
B — «вершина»

Поиграй с этим здесь:

изображений/circle-prop.js?mode=inscribe

Когда вы перемещаете точку «B», что происходит с углом?

Теоремы о вписанном угле

Фиксация конечных точек …

… угол a° равен всегда один и тот же ,
независимо от того, где он находится на той же дуге между конечными точками:

(называется углов, опирающихся на одну и ту же дугу теоремой )

А вписанный угол а° составляет половину центрального угла 2а°

(Называется угол в центре теоремы )

Попробуйте здесь (не всегда точно из-за округления):

изображений/circle-prop.js?mode=inscribe2

Пример: Каков размер Angle POQ? (О — центр окружности)

Угол POQ = 2 × Угол PRQ = 2 × 62° = 124°

Пример: Каков размер Angle CBX?

Угол ADB = 32° также равен углу ACB.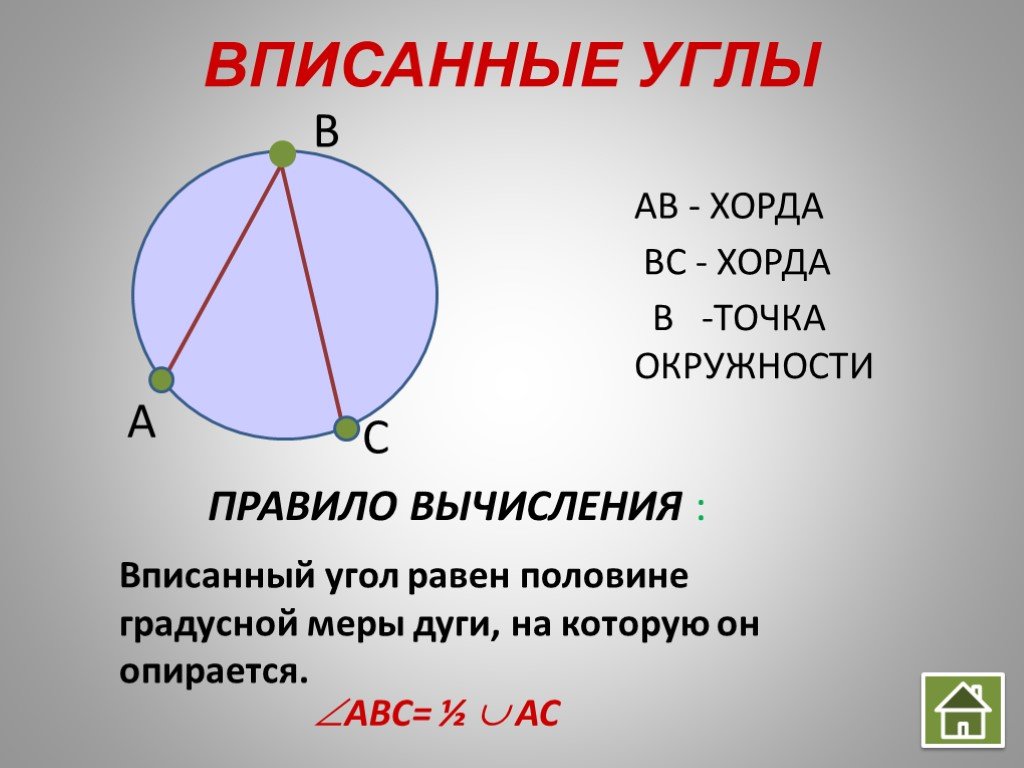

И угол ACB также равен углу XCB.

Таким образом, в треугольнике BXC мы знаем, что угол BXC = 85°, а угол XCB = 32°

Теперь используйте углы треугольника, добавленные к 180° :

Угол CBX + Угол BXC + Угол XCB = 180°

Угол CBX + 85° + 32° = 180°

Угол CBX = 63°

Угол полуокружности (теорема Фалеса)

Угол , вписанный в окружность с диаметром , всегда прямой:

(Конечными точками являются любые концы диаметра круга,
точка вершины может быть где угодно на окружности.)

Поиграй с этим здесь:

изображения/circle-prop.js?mode=thales

Почему? Потому что: Вписанный угол 90° составляет половину центрального угла 180° (с использованием приведенной выше теоремы об угле в центре)

 

Еще одна веская причина, почему это работает

Мы также можем повернуть фигуру на 180°, чтобы получился прямоугольник!

это прямоугольник, потому что все стороны параллельны, а обе диагонали равны.

Итак, все его внутренние углы прямые (90°).

Пример: Каков размер угла BAC?

Теорема об угле в полуокружности говорит нам, что угол ACB = 90°

Теперь используйте углы треугольника, добавленные к 180°, чтобы найти угол BAC:

Угол BAC + 55° + 90° = 180°

Угол ВАС = 35°

 

Итак, поехали! Неважно , где этот угол равен
по окружности, он равен всегда 90°

Нахождение центра круга

Мы можем использовать эту идею, чтобы найти центр круга:

• начертите прямой угол из любой точки окружности круга, затем нарисуйте диаметр в том месте, где две ножки касаются круга
• сделайте это снова, но с другим диаметром

Там, где пересекаются диаметры, находится центр!

Рисование окружности из двух противоположных точек

Когда мы знаем две противоположные точки на окружности, мы можем нарисовать эту окружность.

Вставьте несколько булавок или гвоздей в эти точки и используйте строительный угольник, например:

 

Циклический четырехугольник

«Циклический» четырехугольник имеет каждую вершину на окружности:
В циклическом четырехугольнике противоположных углов составляют 180° : а + с = 180° b + d = 180°

Пример: Каков размер угла WXY?

Сумма противоположных углов вписанного четырехугольника дает 180°

Угол WZY + угол WXY = 180°

69° + угол WXY = 180°

Угол WXY = 111° 3 0 90 9000

Угол касательной

Касательная линия касается окружности только в одной точке.

Всегда образует прямой угол с радиусом окружности.

 

1012, 3240, 1013, 3241, 1014, 3242, 1015, 3243, 1016, 3244

Геометрия — Окружности и углы

Несколько слов

Хорда окружности — это отрезок, концы которого лежат на окружности.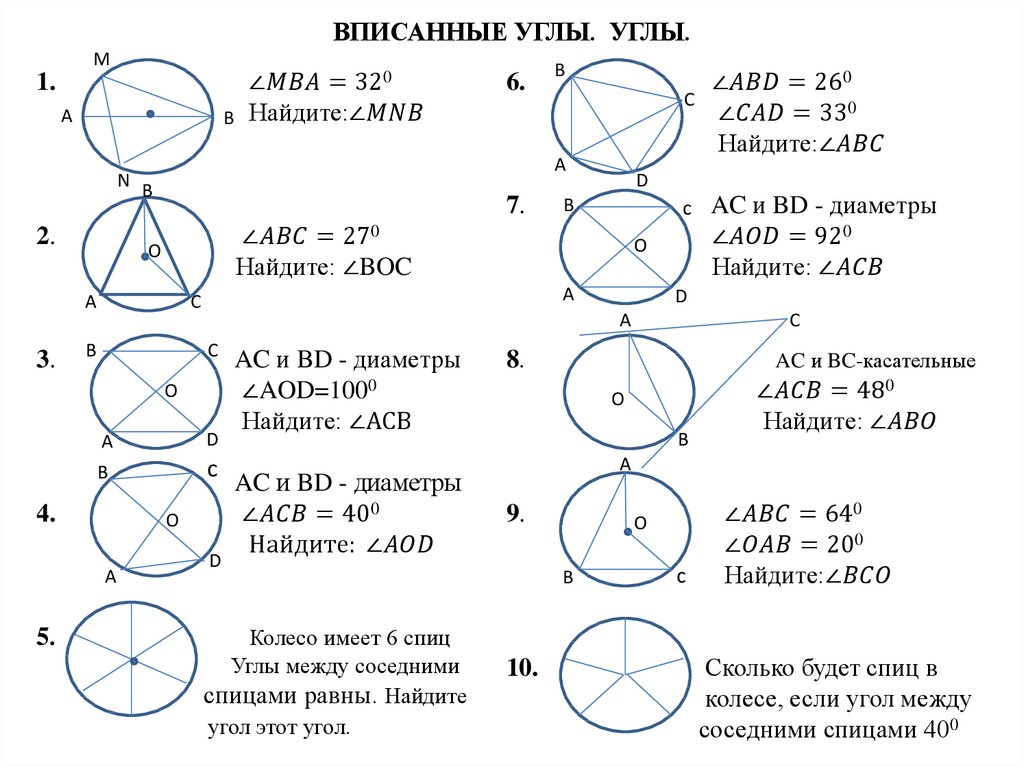

секанс окружности – это прямая, пересекающая окружность в двух точках

Вписанный угол угол, образованный двумя хордами, имеющими общий конец. Другие конечные точки определяют перехватил дугу .

Угол центральный пересекаемой дуги — это угол в середине круга.

На рисунке слева вписанный угол — это угол \(\угол ACB\), а центральный угол равен углу \(\угол AMB\).

задач GeoGebra

Центральный угол и вписанный угол

Какое отношение между центральным углом и вписанным углом дуги?

Сделайте предположение и запишите его. Это должно быть ясно видно из вашей конструкции что ваша гипотеза верна. Сохраните свою конструкцию.

Вписанные углы

Что вы можете сказать о разных углах, вписанных в одну и ту же дугу? Не могли бы вы разобраться без построения? Сделай вывод и напиши вниз. Докажите, что ваша гипотеза верна, либо ссылаясь на конструкцию, или по рассуждениям (или по обоим)

Противоположные углы четырехугольника, вписанного в окружность

Начертите круг и поставьте на него четыре точки. Составьте четырехугольник, используя четыре точки. Что вы можете сказать о противоположных углах четырехугольников?

Сделайте предположение и запишите его. Это должно быть ясно видно из вашей конструкции что ваша гипотеза верна. Сохраните свою конструкцию.

Угол, вписанный в полуокружность

Что вы можете сказать о углах, вписанных в полуокружность? Можете ли вы понять это без создания конструкции? Сделайте предположение и запишите его. Спорить что ваша догадка верна либо ссылкой на конструкцию, либо рассуждениями (или оба).

Пересекающиеся хорды

Нарисуйте окружность с двумя пересекающимися хордами.

Создайте четыре переменные для хранения расстояний, как показано на рисунке слева. \(a=AE\), \(b=EC\), \(c=BE\) и \(d=ED\) (вы можете использовать другие буквы или имена)

Если вы хотите сохранить расстояние между точками \(A\) и \(B\) в переменной с именем a, вы пишете: a=Distance[A,B] в строке ввода. Вы можете также сделайте отрезок между точками \(A\) и \(B\) и используйте значение сегмент.

Убедитесь, что вы не используете имена переменных, уже используемые программой.

Найдите соотношение между четырьмя расстояниями либо в виде отношений, либо в виде произведений.

Сделайте предположение и запишите его. Это должно быть ясно видно из вашей конструкции что ваша гипотеза верна. Сохраните свою конструкцию.

Доказательства

При доказательстве своих догадок разрешается использовать следующие «факты»

Центральный угол и вписанный угол

Гипотеза: Центральный угол вдвое больше вписанного угол, если они оба являются углами на одной и той же пересекающейся дуге.

Доказательство: Есть три случая.

Попробуйте доказать теорему в каком-то из случаев/случаев. 3 случай самый сложный случае вы можете использовать случай 1 и вычитание, чтобы доказать случай 3.