Метод итераций онлайн
Метод итераций онлайнПостроить график функции Точки разрыва функции Построение графика методом дифференциального исчисления Упростить выражение
Примеры решенийМетод Зейделя Метод Ньютона Метод хорд Решение уравненийМетод LU-разложения Метод Гаусса Матрица Гессе Градиент функции Экстремум функции
- Решение онлайн
- Видеоинструкция
F(x) =
Искать в интервале от до .Точность ξ =
Количество интервалов разбиения, n =
Метод решения нелинейных уравнений Метод дихотомииМетод Ньютона (метод касательных)Модифицированный метод НьютонаМетод хордКомбинированный методМетод золотого сеченияМетод итерацийМетод секущих
Решение оформляется в формате Word. (2/3)
(2/3)
Заменим его равносильным уравнением
x=φ(x). (1)
Выберем начальное приближение корня x0 и подставим его в правую часть уравнения (1). Тогда получим некоторое число
x1=φ(x0). (2)
Подставляя теперь в правую часть (2) вместо x0 число x1 получим число x2=φ(x1). Повторяя этот процесс, будем иметь последовательность чисел
xn=φ(xn-1) (n=1,2..). (3)
Если эта последовательность сходящаяся, то есть существует предел , то переходя к пределу в равенстве (3) и предполагая функцию φ(x) непрерывной найдем или ξ=φ(ξ).
Таким образом, предел ξ является корнем уравнения (1) и может быть вычислен по формуле (3) с любой степенью точности.
 Рис. 1а Рис. 1б
Рис. 1а Рис. 1б
Рис. 2. |φ′(x)|>1 — расходящийся процесс
На рис.1а, 1б в окрестности корня |φ′(x)|<1 и процесс итерации сходится. Однако, если рассмотреть случай |φ′(x)|>1, то процесс итерации может быть расходящимся (см. рис.2).
Достаточные условия сходимости метода итерации
Теорема 7. Пусть функция φ(x) определена и дифференцируема на отрезке [a,b], причем все ее значения φ(x)∈[a,b] и пусть |φ′(x)|≤q<1 при x∈[a,b]. Тогда процесс итерации xn = φ(xn-1) сходится независимо от начального значения x0∈[a,b] и предельное значение является единственным корнем уравнения x= φ(x) на отрезке [a,b]. По теореме Лагранжа правая часть может быть представлена как
По теореме Лагранжа правая часть может быть представлена как
φ′(xn)(xn-xn-1)
где xn∈[a,b]Тогда получим
|xn+1-xn|≤φ′(xn)|xn-xn-1|≤q|xn-xn-1|
Полагая n=1,2,…
|x2-x1|≤q|x1-x0|
|x3-x2|≤q|x2-x1|≤q²|x1-x0|
|xn+1-xn≤qn|x1-x0
Из (4) в силу условия q<1 видно, что последовательность {xn} сходится к некоторому числу ξ, то есть , и следовательно,
(в силу непрерывности функции φ(x))
или
ξ= φ(ξ) ч.т.д.
Для погрешности корня ξ можно получить следующую формулу.
Имеем xn=φ(xn-1).
Далее ξ-xn=ξ-φ(xn-1) = φ(ξ)-φ(xn-1) →
Теперь φ(xn-1)=φ(xn)-φ′(c)(xn-xn-1) →
φ(ξ)-φ(xn)+φ′(c)(xn-xn-1)
В результате получим
ξ-xn = φ′(c1)(ξ-xn-1)+φ′(c)(xn-xn-1)
или
|ξ-xn|≤q|ξ-xn|+q|xn-xn-1|
Отсюда
, (5)
откуда видно, что при q близком к 1 разность |ξ -xn
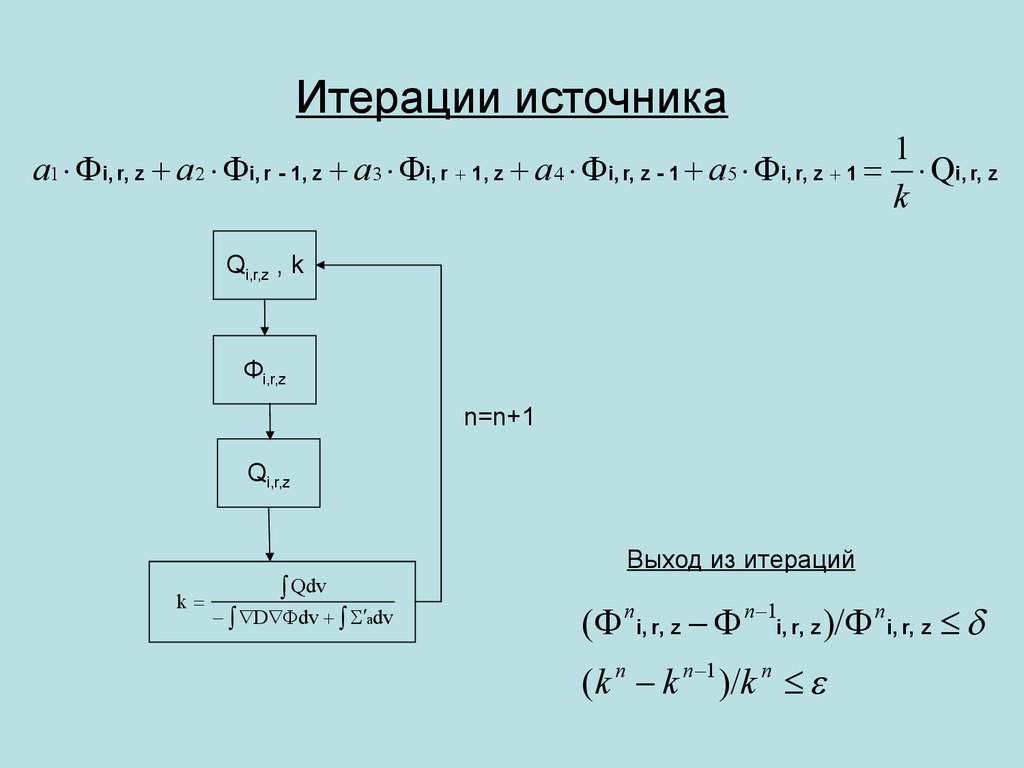 Для того, чтобы вычислить ξ с точностью ε необходимо обеспечить
Для того, чтобы вычислить ξ с точностью ε необходимо обеспечить
. (6)
Тогда подставляя (6) в (5), получим |ξ -xn|<ε.
Если q очень мало, то вместо (6) можно использовать
|xn-xn-1|<ε
Сходимость метода итерации линейная с коэффициентом сходимости α=q. Действительно, имеем
ξ-xn=φ(ξ)-φn-1 = φ′(c)·(ξ-xn-1), отсюда |ξ-xn|≤q·|ξ-xn-1|.
Замечание. Пусть в некоторой окрестности корня ξ∈(a,b) уравнения x= φ(x) производная φ’(x) сохраняет постоянный знак и выполнено неравенство |φ’(x)|≤q<1. Тогда, если φ’(x) положительна, то последовательные приближения x n = φ(xn-1) сходятся к корню монотонно.
Если же φ’(x) отрицательна, то последовательные приближения колеблются около корня.
Рассмотрим способ представления уравнения f(x)=0 в форме x= φ(x).
Функцию φ(x) необходимо задать такую, чтобы |φ’(x)| была малой величиной в окрестности корня.
Пусть известно m1 и M1 — наименьшее и наибольшее значения производной f’(x)
0<m1≤f’(x) ≤M1 (7)
Заменим уравнение f(x)=0 эквивалентным ему уравнением
x = x — λf(x).
Положим φ(x) = x- λf(x). Подберем параметр λ таким образом, чтобы в окрестности корня ξ выполнялось неравенство
0≤|φ′(x)|=|1-λ·f′(x)|≤q≤1
Отсюда на основании (7) получаем
0≤|1-λM
Тогда выбирая λ = 1/M1, получим
q = 1-m1/M1 < 1.
Если λ =1/f’(x), то итерационная формула xn = φ(xn-1) переходит в формулу Ньютона
xn = xn-1 – f(xn)/f’(x).
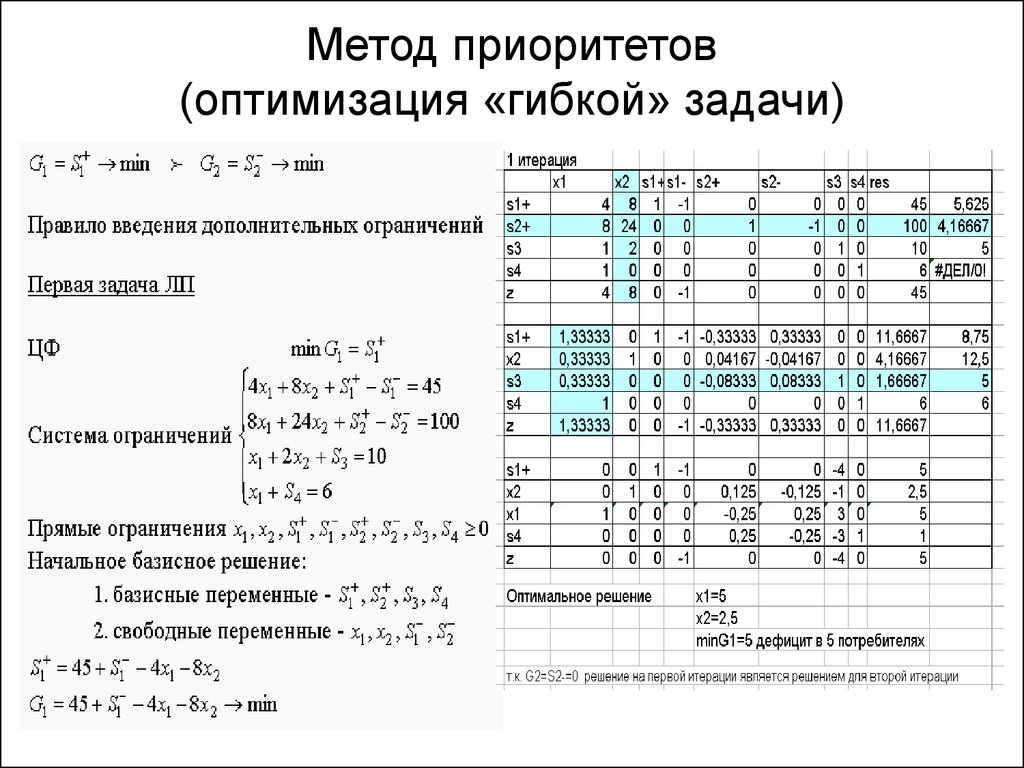
Метод итераций в Excel
В ячейкуB2 заносим начало интервала a, в ячейку B3 заносим конец интервала b. Строку
Строку 4 отводим под заголовок таблицы. Сам процесс итераций организуем в ячейках A5:D5.
Процесс нахождения нулей функции методом итераций состоит из следующих этапов:
- Получить шаблон с омощью этого сервиса.
- Уточнить интервалы в ячейках
B2,B3. - Копировать строки итераций до требуемой точности (столбец
D).
A — номер итерации, столбец B — корень уравнения X, столбец C — значение функции F(X), столбец D — точность eps.
Пример. Найти корень уравнения e-x-x=0, x=∈[0,1], ε=0.001 (8)
Решение.
Представим уравнение (8) в форме x=x-λ(e-x-x)
Найдем максимальное значение производной от функции f(x)= e—x-x.
max f′(x)=max(-(e-x+1)) ≈ -1.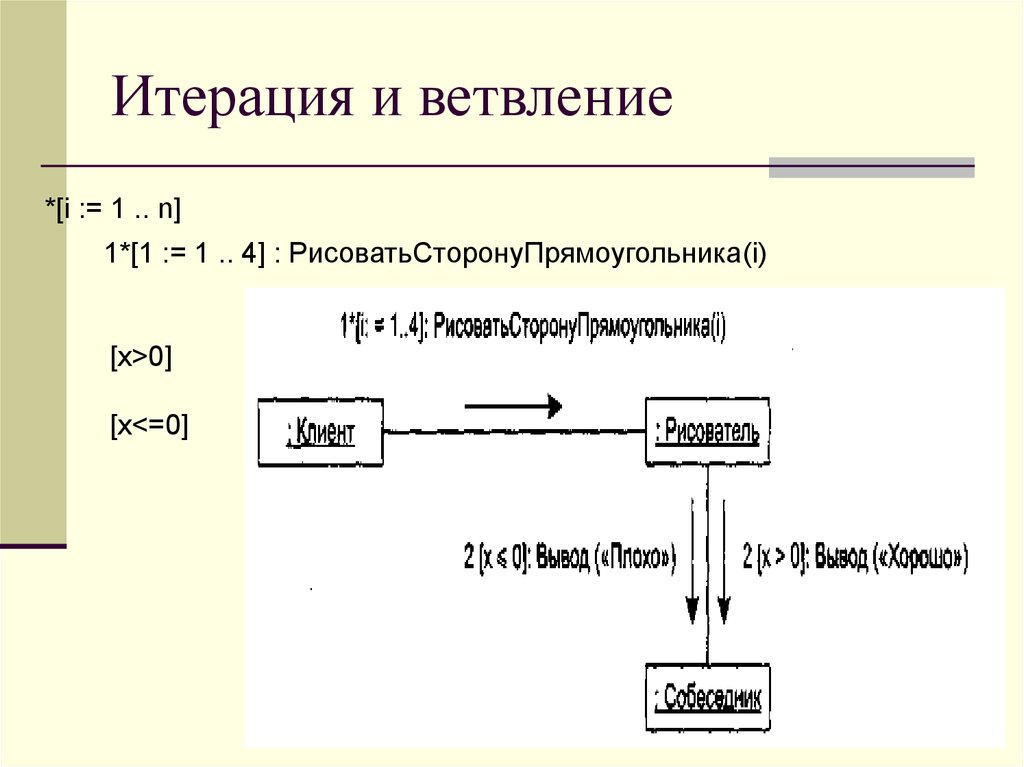 37. Значение . Таким образом, решаем следующее уравнение
37. Значение . Таким образом, решаем следующее уравнение
x=x+0,73(e—x-x)
Значения последовательных приближений даны в таблице.
| xi | f(xi) | |
| 1 | 0.0 | 1.0 |
| 2 | 0.73 | -0.2481 |
| 3 | 0.5489 | 0.0287 |
| 4 | 0.5698 | -0.0042 |
| 5 | 0.5668 | 0.0006 |
- Помощь в решении
- Поиск
- Поддержать проект
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Боремся с бесконечными итерациями – XP Injection
Я решил поучаствовать в разборе кейса, описанного Тимофеем Евграшиным в его блоге. Сначала начал писать комментарий, но потом понял, что он будет слишком большим. Поэтому оформляю в виде отдельной статьи. Вкратце проблема выглядит так – команда никогда не заканчивает все задачи в итерации, перенося их на следующую. В итоге итерации получаются размазанными.
Команда провела анализ и выделила возможные причины такой ситуации. Первая причина в том, что очень 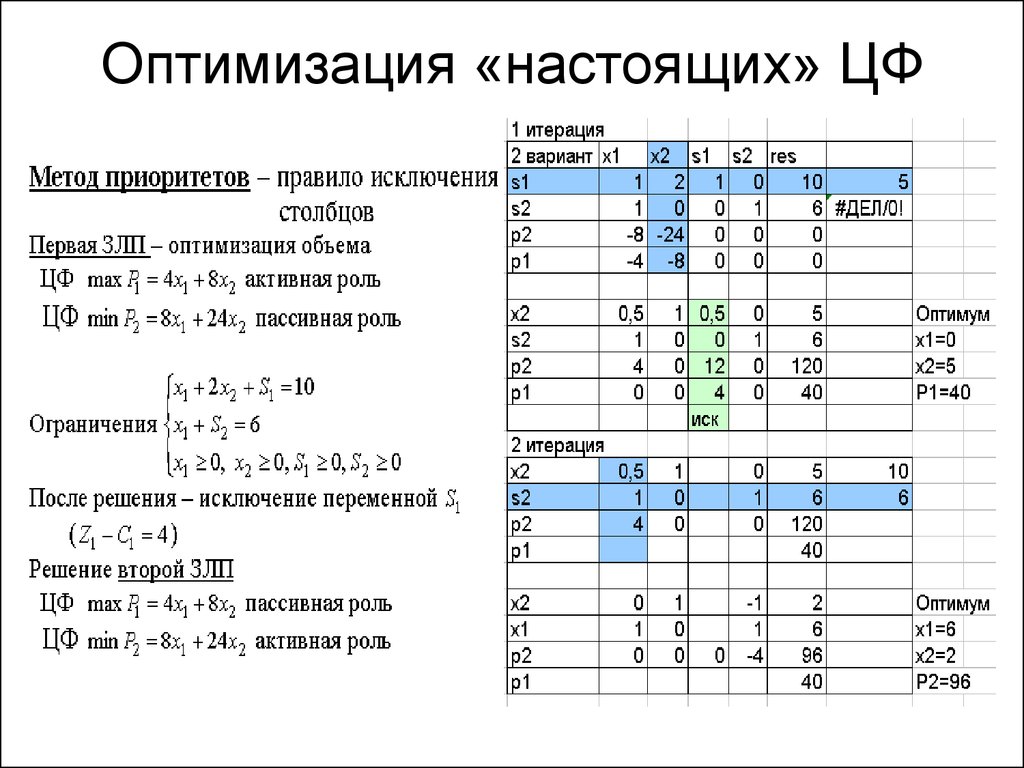 Вторая заключается в том, что циклы тестирования и разработки “натурально” не совпадают и никто не может аргументировать в чем недостатки данной ситуации.
Вторая заключается в том, что циклы тестирования и разработки “натурально” не совпадают и никто не может аргументировать в чем недостатки данной ситуации.
Начну с причин, потому что без их разбора нет смысла давать советы. Мне кажется из первой причины стоило копнуть еще глубже. Почему происходит столько много задержек? Почему команда целый день тратит на ревью результатов спринта, причем сборку надо залить за день до ревью? Откуда берутся многочисленные задержки, которые даже вынудили команду последний день итерации сделать не совсем рабочим? Первопричин может быть много, не берусь судить однозначно. Возможно не полностью автоматизирована сборка и установка приложения, может быть некоторые процедуры делаются по шаблону и из-за этого занимают много времени.
Вторая причина, указанная командой, является очень классической. Она пришла из поэтапного подхода к разработке, когда тестирование делается после завершения кодирования. При этом часто задачи на кодирование требуют несколько дней, что еще больше откладывает тестирование.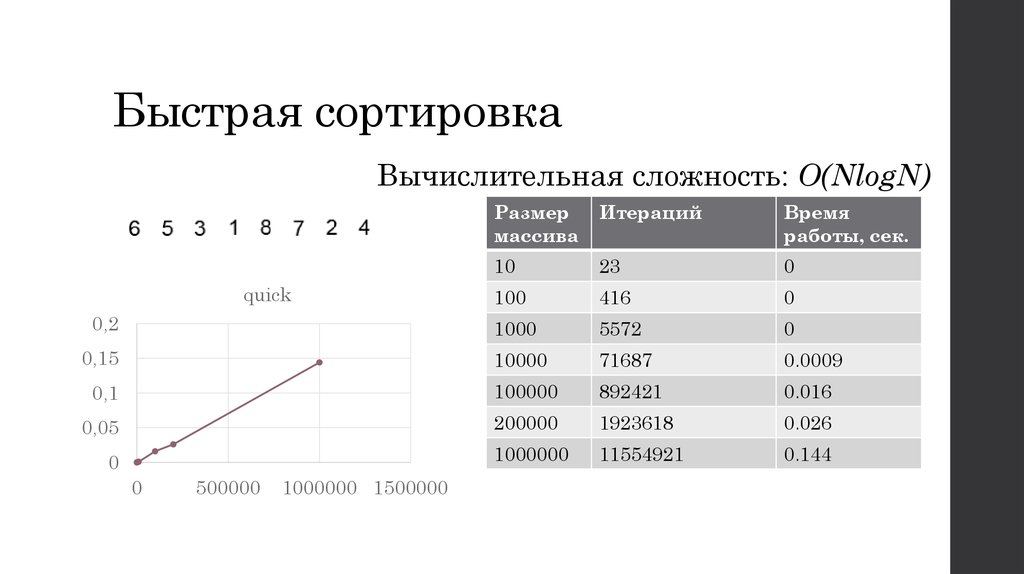 И не меняя подхода, нереально ничего поменять.
И не меняя подхода, нереально ничего поменять.
Scrum предлагает комбинировать итерационный и инкрементальный подходы. А это значит, что в итерации команда делает одну фичу и только потом переходит на следующую. Такой подход заставляет распределять работу между членами команды и концентрироваться на достижении результата. Что делать тестировщикам пока нечего тестировать? Писать автоматизированные тесты, собирать тестовые данные, подготавливать необходимые процедуры и артефакты. Как только что-то готово, сразу передавать разработчику. Как только у разработчика что-то готово, сразу отдавать тестировщику. Таким образом, после завершения работы над задачей требуется минимальное время на ее тестирование.
Но самый главный вопрос – это вопрос понимания цели самих итераций. Итерации нужны для предсказуемости, налаженного ритма выполнения обязательств и слаженной деятельности без помех извне. Если задачи могут легко переноситься на следующую итерацию, то предсказуемость теряется. Никто не знает сколько задач завершит команда в очередной итерации. Ритм тут же теряется тоже, потому что ни у кого нет ощущения законченности выполненной работы и старта новой итерации с чистого листа. Вместо этого тянется тестирование и другие активности из прошлого. Пока все в команде не осознают этого, менять что-то почти бессмысленно.
Никто не знает сколько задач завершит команда в очередной итерации. Ритм тут же теряется тоже, потому что ни у кого нет ощущения законченности выполненной работы и старта новой итерации с чистого листа. Вместо этого тянется тестирование и другие активности из прошлого. Пока все в команде не осознают этого, менять что-то почти бессмысленно.
Теперь разберемся, что же со всем этим делать. Задачи понятны. Я бы посоветовал реализовать следующие подходы:
- Планируйте ровно на столько, сколько вы можете полностью закончить в итерацию. Не тратьте время на планирование остального. Это и сэкономит вам время и не будет никому давать несбыточных обещаний. Лучше возьмите еще работы, если все закончите в срок. Это будет гораздо приятнее и команде и заказчику, чем в очередной раз получить часть обещанного не готовым.
- Для более плотной командной работы над задачами и инкрементальности внутри итерации установите лимиты на количество задач, которые находятся в прогрессе.
 Причем жесткие и непоколебимые лимиты. Они будут вас заставлять помогать друг другу, делить большие задачи на маленькие, автоматизировать ручную работу и не распыляться на много задач сразу. Это повысит вашу эффективность.
Причем жесткие и непоколебимые лимиты. Они будут вас заставлять помогать друг другу, делить большие задачи на маленькие, автоматизировать ручную работу и не распыляться на много задач сразу. Это повысит вашу эффективность. - Для решения проблем с циклом тестирования внедряйте активно автоматизацию. Причем не просто автоматизацию, а различные вариации TDD (Test Driven Development). Чем больше тестов будет написано до завершения реализации задачи, тем меньше времени уйдет на тестирование. Еще одна практика, которая очень сильно может помочь – Slicing Development. Не разрабатывайте по несколько дней целиком готовую фичу. Вместо этого выкатывайте несколько промежуточных реализаций с урезанной функциональностью и отдавайте на тестирование.
- Ну и последний совет очевиднее всех – проведите ретроспективу и разберитесь в том, что происходит. Если команда или руководство не понимают зачем это все нужно, то все предыдущие усилия будут просто бесполезны.
 Возможно, в результате разбора окажется, что Scrum в вашем случае совершенно не подходит. Такое тоже бывает. Scrum – не серебряная пуля.
Возможно, в результате разбора окажется, что Scrum в вашем случае совершенно не подходит. Такое тоже бывает. Scrum – не серебряная пуля.
Ну и конечно же не опускайте руки. Из любой ситуации есть выход, его надо только поискать. 🙂 Удачи этой команде и всем, кто сталкивается с подобными проблемами!
ИТЕРАЦИЙ
Прямая трансляция
Пятница 9.12.2022
Четверг 8.12.2022
●Как последние технологические разработки позволяют производителям создавать новые творческие возможности? Как будет развиваться ландшафт творческого кодирования в ближайшие несколько лет? Эти вопросы будут рассмотрены на симпозиуме по творческому программированию ITERATIONS. Делая акцент на инклюзивности, мы пригласили международную группу разработчиков из разных дисциплин, чтобы рассказать о том, как они используют код в качестве творческого средства. В форме презентаций, интерактивных сессий и мастер-классов мы обсудим темы: машинное обучение, построение мира и творческое образование.
Делая акцент на инклюзивности, мы пригласили международную группу разработчиков из разных дисциплин, чтобы рассказать о том, как они используют код в качестве творческого средства. В форме презентаций, интерактивных сессий и мастер-классов мы обсудим темы: машинное обучение, построение мира и творческое образование.
Вы можете присоединиться к симпозиуму физически в Havenloods в Утрехте, посмотреть интересные арты в параллельной программе artmachines.nl или посмотреть доклады онлайн бесплатно. Некоторые мастер-классы также будут проводиться онлайн.
Динамики
Аймерик Мансу + Брендан Хауэлл
Бабузи Ньони
Минди Сеу онлайн
Оливия Джек онлайн
Сун Мэнсюань
Тега Мозг онлайн
Семинары
Искусство, алгоритмы и искусственный интеллект
Андреас Рефсгаард (онлайн)
На этом практическом семинаре художник и дизайнер взаимодействия Андреас Рефсгаард продемонстрирует, как использовать алгоритмы машинного обучения в игровой и поэтической форме.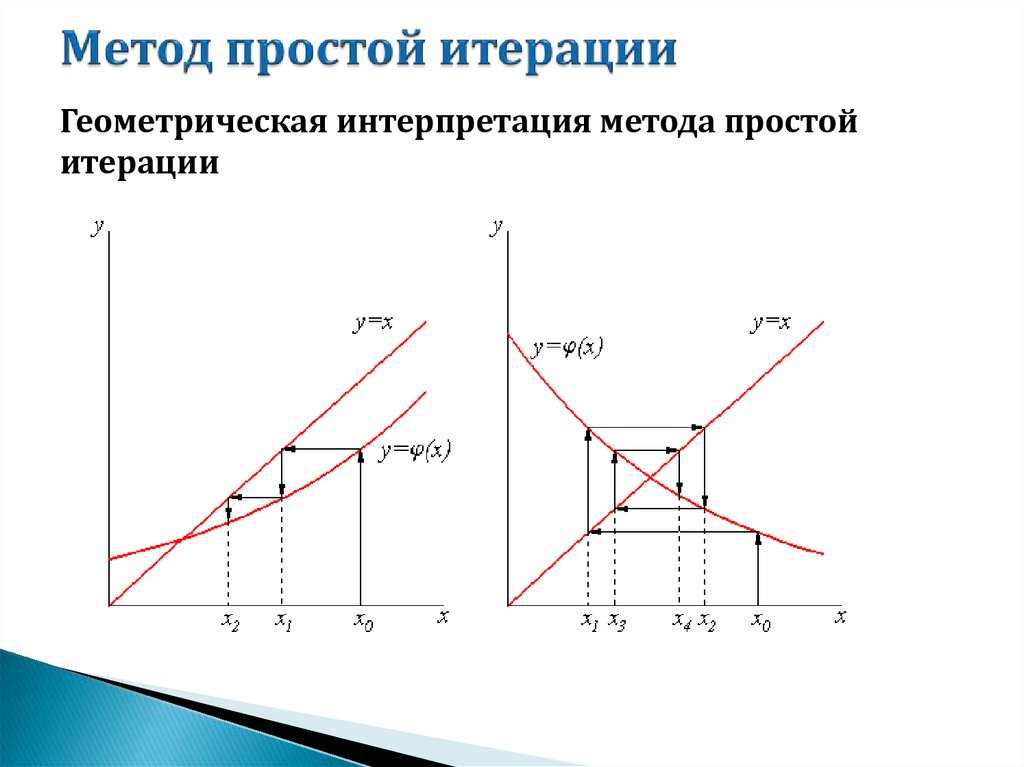 Участники будут собирать данные и обучать свой собственный классификатор изображений, генерировать изображения и алгоритмическую поэзию и многое другое!
Участники будут собирать данные и обучать свой собственный классификатор изображений, генерировать изображения и алгоритмическую поэзию и многое другое!
Семинар подходит для людей без опыта работы с кодом или машинным обучением, которые заинтересованы в получении познакомиться с творческим потенциалом этих технологий.
Макс. 35
Что взять с собой ноутбук с работающей веб-камерой.
Доступ Ссылка на Zoom будет отправлена участникам
Билеты €8,50 / €5
Танцы в метавселенной Бабузи Ньони
(гибрид)
Присоединяйтесь к метавселенной, превратив себя в 3D-аватар с помощью машинного обучения. Испытайте что-то совершенно новое, управляя своим аватаром, используя танцевальные движения в реальной жизни во время мини-танцевальной вечеринки!
Макс. 20
Что взять с собой компьютер, зарядное устройство и заряженный смартфон
Технические требования Для этого упражнения на вашем компьютере должна быть установлена обновленная версия современного браузера, такого как Chrome или Firefox.
Производственные требования Если вы присоединяетесь онлайн, убедитесь, что у вас есть хорошее освещение и, если оно есть, динамик.
Доступ Онлайн-участникам будет отправлена ссылка на Zoom. Физические участники приветствуются на месте проведения.
Билеты €8,50 / €5
Расписание (CET)
Четверг 8.12.2022
11:00–13:00 Билеты на семинар Андреаса Рефсгаарда
10:00–13:00 Билеты на семинар Babusi Nyoni
13:00–14:00 Перерыв
14:00 Открытие симпозиума
14:00–14:45 Бабуси Ниони
14:45–15:00 Перерыв
15:00–15:45 Оливия Джек (онлайн)
15:45–16:00 Перерыв
16:00–16:45 Тега Мозг (онлайн)
16:45–17:00 Завершение первого дня
17:15–20:00 Напитки и закуски
Пятница 9.12.2022
14:00 Открытие симпозиума
14:00–14:45 Сунь Мэнсюань
14:45–15:00 Перерыв
15:00–15:45 Эмерик Мансу и Брендан Хауэлл
15:45–16:00 Перерыв
16:00–16:45 Минди Сеу (онлайн)
16:45–17:00 Подведение итогов симпозиума
17:15–20:00 Напитки и закуски
Билеты
Семинары
Искусство, алгоритмы и искусственный интеллект
Андреас Рефсгаард 8,50 € / 5 €, четверг 8. 12.22, 11:00 – 13:00 (онлайн)
12.22, 11:00 – 13:00 (онлайн)
Танцы в метавселенной
Babusi Nyoni 8,50 € / 5 €, пт 9.12.22, 10:00 – 13:00 (гибрид)
Симпозиум
Симпозиум Четверг€17,50 / €10
Симпозиум Пятница€17,50 / €10
Полный симпозиум €25 / €15
Полный симпозиум + ART MACHINES €40 / €15
В сети Бесплатно
Предыдущая версия
2021
Colophon
Организация
Vera van de Seyp
Creative Coding Utrecht
Поддержан
Фонд креативной индустрии NL
Identity
Tipefep New Edge TM Шарлотта Роде
Times Now Ян-Хенрик Арнольд
Production
Anne-Linde Munstermann
Werner de Valk
Social Media
Anne-Linde Munstermann
Vera van de Seyp
Audio & Video Production
Studio Schilp
Moderation
Rosa Wevers
Online calculator: Метод итераций с фиксированной точкой
Исследование Математика
Этот онлайн-калькулятор вычисляет фиксированные точки итерируемых функций, используя метод итераций с фиксированной точкой (метод последовательных приближений).
В численном анализе итерация с фиксированной точкой — это метод вычисления фиксированных точек повторяемых функций. Более конкретно, если задана функция, определенная на действительных числах с действительными значениями, и задана точка в области , итерация с фиксированной точкой равна
Это дает начало последовательности , которая, как ожидается, сойдется к точке . Если непрерывно, то можно доказать, что полученное является неподвижной точкой – т. е. . 1
Этот метод является разновидностью метода последовательных приближений — метода решения математических задач с помощью последовательности приближений, сходящихся к решению и строящейся рекурсивно, т. е. каждое новое приближение вычисляется на основе предыдущего приближения; выбор начального приближения до некоторой степени произволен. Метод используется для аппроксимации корней алгебраических и трансцендентных уравнений. Он также используется для доказательства существования решения и для аппроксимации решений дифференциальных, интегральных и интегродифференциальных уравнений.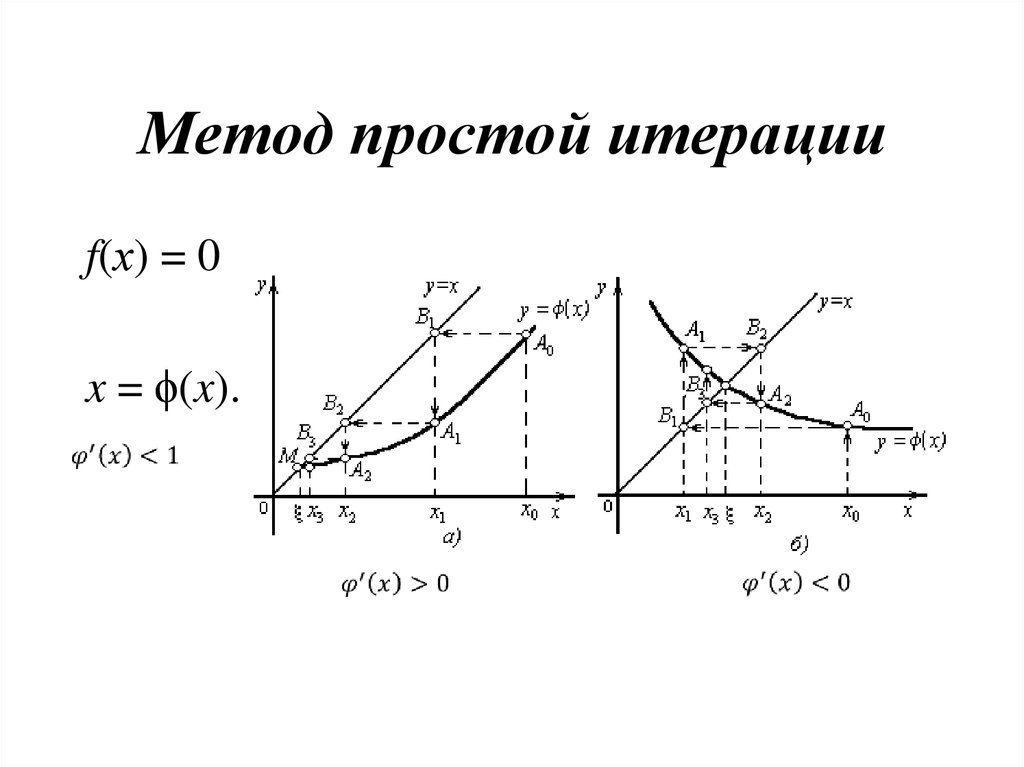
Использование этого метода довольно простое:
– принять приблизительное значение переменной (начальное значение)
– найти переменную
– использовать ответ как второе приблизительное значение и снова решить уравнение
– повторять этот процесс до тех пор, пока достигается желаемая точность для переменной
Это именно то, что делает приведенный ниже калькулятор. Он выполняет итерационные вычисления x по заданной формуле и останавливается, когда два последовательных значения отличаются меньше заданной точности.
Также стоит упомянуть, что функция, использованная в качестве примера, т. е.
,
, представляет собой итерированную функцию для вычисления квадратного корня из a. Это, возможно, первый алгоритм, используемый для аппроксимации квадратного корня. Он известен как «вавилонский метод», названный в честь вавилонян, или «метод Героя», названный в честь греческого математика первого века Героя Александрийского, который дал первое подробное описание метода.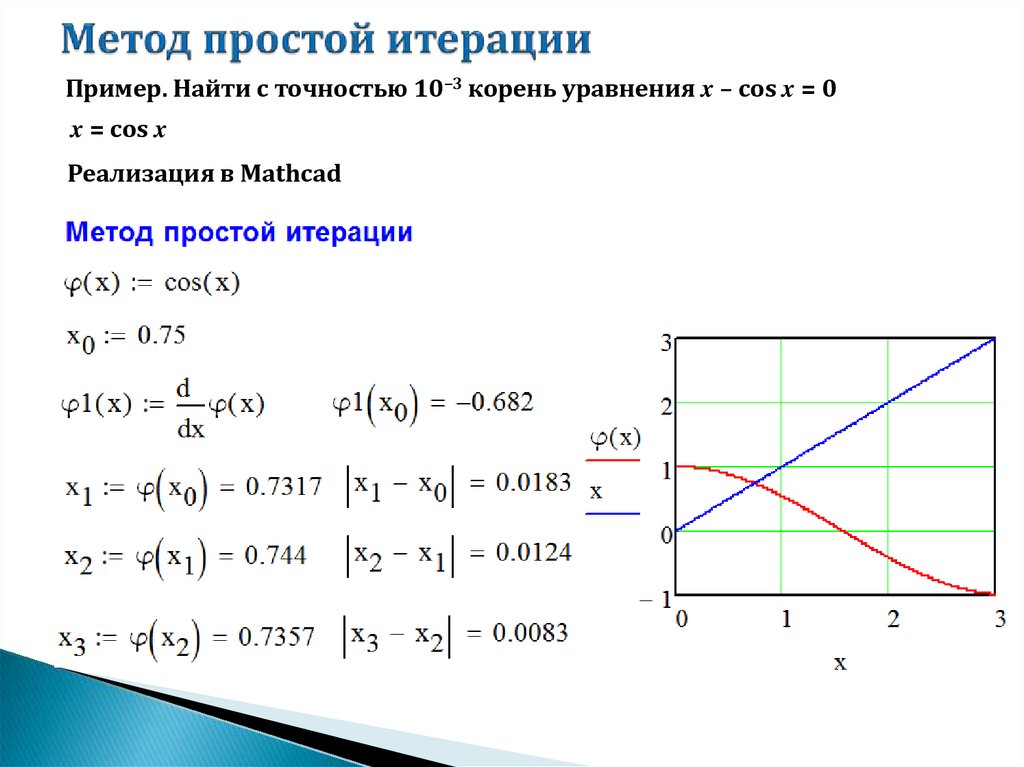

 Причем жесткие и непоколебимые лимиты. Они будут вас заставлять помогать друг другу, делить большие задачи на маленькие, автоматизировать ручную работу и не распыляться на много задач сразу. Это повысит вашу эффективность.
Причем жесткие и непоколебимые лимиты. Они будут вас заставлять помогать друг другу, делить большие задачи на маленькие, автоматизировать ручную работу и не распыляться на много задач сразу. Это повысит вашу эффективность. Возможно, в результате разбора окажется, что Scrum в вашем случае совершенно не подходит. Такое тоже бывает. Scrum – не серебряная пуля.
Возможно, в результате разбора окажется, что Scrum в вашем случае совершенно не подходит. Такое тоже бывает. Scrum – не серебряная пуля.