Умножение матриц — Онлайн калькулятор
- Справочник
- Онлайн-калькуляторы
- Тесты с ответами
Умножение матриц онлайн-калькулятором пригодится студентам технических специальностей и учащимся, для которых математика в числе непрофильных предметов. Школьники старших классов с углубленным изучением математики в целях повышения своего уровня и подготовки к олимпиадам могут осуществлять самоконтроль при решении задач.
При перемножении матриц онлайн должно соблюдаться условие равенства числа столбцов в первом множителе числу строк во втором. В таком случае форма матриц согласована. Умножение матрицы на матрицу онлайн выполнимо всегда, если множители имеют один и тот же порядок.
Чтобы умножить матрицы онлайн, соблюдайте последовательность действий:
- выберите количество строк и столбцов для первого и второго множителей соответственно;
- нажмите кнопку «Рассчитать»;
- изучите подробный расчет или воспользуйтесь быстрым ответом на пример.

Умножение матриц
Как произвести умножение матриц с помощью онлайн-калькулятора:
- Задайте две матрицы. Для этого сначала укажите размерность для каждой из них. Калькулятор позволяет производить вычисления с матрицами размерностью от 2х2 до до 7х7.
Калькулятор особенно удобен, когда нужно оперировать матрицами больших размерностей. В качестве примера возьмем матрицы 3х3 и 3х4. - В полях ниже введите значения элементов матриц:
Значения могут быть положительными и отрицательными, целыми и дробными: - Когда матрицы заданы, нажмите рассчитать, и ознакомьтесь в решением:
Материалы, которые помогут вам лучше разобраться в теме:
- Матрицы (раздел)
- Умножение матриц: примеры, алгоритм действий, свойства произведения
- Определитель матрицы: алгоритм и примеры вычисления определителя матрицы
- Равенство матриц: как доказать и проверить?
- Действия над матрицами.
 Сложение и вычитание
Сложение и вычитание - Нахождение ранга матрицы
Ответ:
Решение
Ответ:
Похожие калькуляторы:
- Найти определитель матрицы
- Найти обратную матрицу
- Возведение матрицы в степень
- Умножение матрицы на число
- Транспонирование матрицы
- Сложение и вычитание матриц
- Ранг матрицы
Умножение матриц онлайн
Сервис создан для помощи студентам в освоении учебного материала.
Умножение матриц – одна из ключевых операций линейной алгебры. Применяется для решения системы линейных уравнений, доказательства теорем и др. Вычислить результат понадобится в сферах электроники и строительства – при анализе электронных схем, расчете прочности строительных сооружений.
При возникновении сложностей в теме умножения матриц или других, обратитесь к консультанту для выполнения работы на заказ.
Понравился калькулятор? Поделись с друзьями!
Разделы калькуляторов
- Решение матриц
- Точка, прямая, плоскость
- Конвертеры
- Объем фигур
- Калькуляторы площади фигур
- Решение уравнений
- Операции над векторами
- Периметр фигур
Поможем с любой работой
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Решение задач
- Отчеты по практике
Все наши услуги
Узнай бесплатно стоимость работыНе получается написать работу самому?
Доверь это кандидату наук!
Калькулятор умножения матриц — MathCracker.
 com
comРешатели Алгебра
Инструкции: Используйте этот пошаговый калькулятор для вычисления умножения двух матриц. Следите за тем, чтобы количество столбцов первой матрицы совпадало с количеством строк второй матрицы.
При необходимости измените размер матриц, указав количество строк и количество столбцов.
Number of Rows B = Number of Cols B =
The number of rows and columns provided needs to be integers that are greater than 1. The maximum number of rows is 8, and the maximum number of columns is 8
\(A\) = \begin{bmatrix} & \\ & \end{bmatrix}
\(B\) = \begin{bmatrix} & \\ & \end{bmatrix}
Матрицы часто появляются в линейной алгебре из-за их тесной связи с линейными функциями. Но помимо этой связи матрицы — это объекты, которые во многом похожи на числа. Действительно, вы можете складывать, вычитать и умножать матрицы при условии, что размеры совместимы.
Например, чтобы
добавить две матрицы
нужно, чтобы они имели одинаковые габариты. Это же требование необходимо, когда
вы хотите вычесть матрицы
.
Это же требование необходимо, когда
вы хотите вычесть матрицы
.
Как умножать матрицы?
Умножение матриц представляет собой другую проблему, поскольку его определение менее интуитивно понятно, чем способ сложения и вычитания матриц. Кроме того, подходящие размерности для умножения не требуют, чтобы матрицы имели одинаковые размеры, но все же были в другом состоянии.
Итак, начнем с этого: чтобы можно было перемножать матрицы, количество столбцов первой матрицы должно совпадать с количеством строк второй матрицы. n A_{ik} B_{kj}\]
n A_{ik} B_{kj}\]
Часто эту формулу трудно усвоить, но лучший способ сделать это — думать о ней так: элемент матрицы произведения, который находится в строке i и столбце j, вычисляется путем вычисления скалярного произведения между i- -я строка первой матрицы и j-й столбец второй матрицы.
Что такое свойство единичной матрицы умножения матриц?
Единичная матрица является очень особенным с точки зрения матричного умножения. Действительно, матрица А вообще не меняется при умножении на Единичная матрица (при условии, что размеры допустимы для проведения умножения)
Это калькулятор умножения матриц с шагами?
Да, это так. Все, что вам нужно сделать, это указать матрицы, которые вы хотите перемножить, а калькулятор сделает все остальное. Калькулятор начинает с двух пустых матриц 2×2. Таким образом, вам может потребоваться настроить размеры матриц, чтобы ввести нужные вам матрицы.
Все, что вам нужно сделать, это указать матрицы, которые вы хотите перемножить, а калькулятор сделает все остальное. Калькулятор начинает с двух пустых матриц 2×2. Таким образом, вам может потребоваться настроить размеры матриц, чтобы ввести нужные вам матрицы.
Это калькулятор умножения 3-х матриц?
Не напрямую. Этот калькулятор вычислит произведение двух матриц. Если вы хотите умножить три функции, то вам нужно сначала вычислить умножение первых двух, а затем результат умножить на третью.
калькулятор умножения матриц Калькулятор умножения матриц Калькулятор умножения двух матриц
Матрицы: основные операции OTUS
В математике и информатике полно разнообразных объектов, с которыми нужно уметь работать. Некоторые из них изучаются в школьных программах, а какие-то в университетах. В данной статье будет рассказано о том, что такое матрица. А еще – как найти произведение двух матриц, умножить соответствующий объект на число, выполнить иные основные операции.
Некоторые из них изучаются в школьных программах, а какие-то в университетах. В данной статье будет рассказано о том, что такое матрица. А еще – как найти произведение двух матриц, умножить соответствующий объект на число, выполнить иные основные операции.
Определение термина
Матрица – это некий математический объект. Он представлен таблицей чисел, которая включает в себя определенное количество столбцов и срок.
Под матрицами принято понимать прямоугольную или квадратную табличку элементов, в которой строчки получают нумерацию по направлению «сверху-вниз», а столбцы – «слева-направо».
При помощи таких математических объектов можно решать разного рода задачи. С рассматриваемыми компонентами должен уметь справляться любой математик. Программистам и работникам сферы IT тоже пригодятся подобные навыки.
Основные операции
Стоит запомнить, что с матричными объектами удается выполнять разнообразные действия. В основном – алгебраического характера:
- перемножать между собой;
- находить обратные матрицы и транспонированные;
- складывать;
- вычитать;
- обнаруживать произведение матрицы на число.

Также человек сможет отыскать детерминант при необходимости. Все это удается сделать как вручную, так и через специальные онлайн калькуляторы.
Сложение
Правило сложения матриц напоминает принцип сложения в линейных уравнениях (примерах). Но соответствующая операция доступна только относительно объектов с одинаковым количеством чисел. На выходе получится мат. объект аналогичного «объема».
Для сложения нескольких матричных составляющих, необходимо просто сложить их соответствующие элементы.
Вычитание
Перед тем, как умножать заданные матрицы, рекомендуется изучить более простые операции над ними. Все это пригодится в будущем каждому.
В случае с вычитанием действует точно такое же правило, как и со сложением – манипуляции возможны над объектами одинакового размера. На выходе получим результат с таким же количеством составляющих. И для этого достаточно от чисел матрицы a отнять соответствующие элементы матрицы b.
Обнаружение транспонированной матрицы
Для некоторых задач в математике имеет смысл транспонирование. Это – операция, при которой строки и столбцы заданного объекта будут меняться местами. Столбик станет строкой и наоборот.
Это – операция, при которой строки и столбцы заданного объекта будут меняться местами. Столбик станет строкой и наоборот.
Умножение на число
Теперь можно задуматься над тем, как умножать заданные изначально задачей матрицы. Первый вариант – на число.
С этой операцией проблем возникнуть не должно. Каждый элемент имеющихся матриц нужно просто последовательно умножить на заданное число. Принцип здесь точно такой же, как и в обычных алгебраических примерах.
Друг с другом
Умножать (cdot) матричные объекты можно не всегда. Здесь необходимо запомнить следующие моменты:
- удастся найти результат умножения рассматриваемых объектов, когда количество у первой матрицы количество строк точно такое же, как и количество столбцов у второй матрицы;
- результатом перемножения (cdot) матричного объекта A размером m cdot n и B с параметрами n*k будет C «объемом» m*k;
- каждый компонент в C будет равен сумме произведений элементов i-строки матрицы A на соответствующие составляющие в j-строке от матрицы B.

Найти произведение рассматриваемых мат. объектов можно, осуществив cdot (умножение) строк на столбцы.
Пошаговый алгоритм
Для того, чтобы у матрицы умножение на «себе подобную» прошло успешно, стоит соблюдать следующий алгоритм действий:
- Определить размеры каждого матричного объекта.
- Сравнить строки и столбцы в оных.
- Если соблюдено правило перемножения – применить cdot (умножение) строки матрицы на столбец.
- Записать результаты и сложить их, согласно действующим принципам математики.
Это – самый верный вектор направления по изучению рассматриваемой тематики. Если в процессе возникли какие-то проблемы, можно воспользоваться разнообразными онлайн-калькуляторами. В режиме реального времени они помогут перемножить между собой разного рода матричные объекты, а также осуществить с ними иные операции. Там нередко рассматриваемая манипуляция помечена как cdot.
Определители
После того, как у матриц умножение оказалось позади, можно рассмотреть связанные с этим действием операции. Первое, что должен знать математик после изученного материала – это нахождение определителя.
Первое, что должен знать математик после изученного материала – это нахождение определителя.
Здесь актуальны следующие моменты:
- определитель носит название детерминанта;
- это – численная характеристика заданного квадратного матричного объекта;
- помогает решать разного рода задачи;
- вычисляется путем разности произведений элементов главной и побочных диагоналей.
В случае единичной матрицы результатом будет служить единственный элемент мат. объекта. Когда разговор заходит о более крупных составляющих, ситуация меняется. Здесь предстоит вспомнить принципы cdot.
Для матричного объекта размером 3 на 3 детерминантом станет сумма произведений элементов главной диагонали, а также произведений компонентов на треугольниках с гранью которая идет параллельно главной. После этого от последней нужно отнять произведение (cdot) побочной диагонали и результат умножения числовых составляющих, лежащих на треугольниках с гранью параллельной побочной диагонали.
На практике искать детерминант крупных рассматриваемых элементов требуется редко. Если с этим процессом возникли затруднения, cdot сможет выполнить практически любой специализированный онлайн калькулятор. В нем достаточно выставить команду «определитель» или «детерминант», после чего ввести изначальные параметры.
Обратные
Для каждого числа a, не равного нулю, существует обратное a-1. Если к ним применить cdot, результатом послужит единица. Запись данного правила: a cdot a-1 = 1 = E. Соответствующее утверждение актуально и для матричных квадратных компонентов.
Нужно запомнить, что:
- A-1 – обратная к A, если при cdot ее на соответствующую матрицу, как справа, так и слева, будет единица.
- Не у каждой матрицы есть обратная ей.
- Когда a не равно 0 – это условие, которое является достаточным и необходимым для существования a-1, для получения A-1 требованием будет условие, что модуль A не равен 0.

Транспонирование и обратные матричные элементы, а также cdot – это база, без которой более сложные задачи решать не выйдет. Особенно тогда, когда речь заходит об уравнениях.
О минорах
Вектор направления в рассматриваемой теме в основном крутится вокруг cdot. Это – элементарная, но очень важная операция, с которой предстоит столкнуться не только математику, но и работнику в IT-сфере. Особенно если он хочет попытаться составить собственный калькулятор.
Для более полного раскрытия темы необходимо изучить миноры и алгебраические дополнения:
- Минор – это детерминант (n-1) порядка, который получается из определителя n-го порядка. В последнем нужно вычеркнуть i-строку и k-столбец, на пересечении которых находится aik. Обозначение минора – Mik.
- Алгебраическое дополнение – это минор с определенным знаком. Последний зависит от четности суммы i+k номеров строки и столбца, на пересечении которых находится aik.

- Обозначение алгебраического дополнения: Aik = (-1)i+k cdot Mik.
- Если у детерминанта n-го порядка все элементы последней строки/столбца, исключая составляющую, которая находится в правом нижнем углу, равны 0, то определителем будет cdot этого значения на минор.
- Когда определитель состоит из нулей за исключением одного компонента – детерминантом будет cdot соответствующего значения на алгебраическое дополнение.
В этой теории без матриц, умножение которых было рассмотрено ранее, разобраться не получится. Миноры и алгебраические дополнения тоже иногда удается получить через специализированные онлайн калькуляторы.
Об уравнениях
Математика – точная наука, в которой иногда требуется не только нарисовать вектор или фигуру, совершить элементарные операции, но и обнаружить неизвестное. В рассматриваемой теме речь зайдет о матрицах и уравнениях с ними.
Без cdot справиться с этой задачей не получится, ведь существуют различные варианты развития событий. В них может потребоваться воспользоваться перемножением строки одного компонента на второй, а также cdot на число. В некоторых ситуациях нужно искать обратные мат. составляющие.
В них может потребоваться воспользоваться перемножением строки одного компонента на второй, а также cdot на число. В некоторых ситуациях нужно искать обратные мат. составляющие.
Для матричных уравнений будут действовать те же правила, что и у линейных, но с некоторыми оговорками. Здесь у матриц умножение окажется одним из самых важных принципов.
Правила решения уравнений
Далее, когда транспонирование и иные важные аспекты тематики изучены, будут даны возможные примеры матричных уравнений с решениями. Пусть дано условие A cdot X = B, где A и B – известны, а X- нет.
Принцип решения зависит от ситуации:
- A cdot X = B. Здесь обе части перемножаются на обратную А-1 слева. На выходе будет E cdot X = A-1 cdot B. Итог – X = A-1 * B.
- X cdot A = B. Здесь действует тот же принцип, что и в предыдущем примере. Но перемножение на обратную A осуществляется справа. Результат – X = B cdot A-1.
- A * X * B = C.
 Известная матрица в левой части перемножается на обратную той, что расположена слева в уравнении. Далее – с правой стороны на матрицу, обратную той, что находилась справа. Результат: X = A-1 * C * B-1.
Известная матрица в левой части перемножается на обратную той, что расположена слева в уравнении. Далее – с правой стороны на матрицу, обратную той, что находилась справа. Результат: X = A-1 * C * B-1.
Когда в заданном примере X – это обычное число, правило умножения заданных матриц не работает. Здесь будет применяться простой принцип – решение линейных уравнений.
Быстрое решение
Чтобы не приходилось думать, каким размером матрицу на матрицу можно перемножить, а также как строить векторные графики при необходимости, стоит посмотреть школьную программу по алгебре и геометрии (старшее звено), а также заглянуть в пособия для учеников ВУЗов.
Если же нужно быстро получить решение по матрицам, в интернете удастся отыскать немало калькуляторов на любой случай. А это видео объяснит, как у матриц проводить умножение на наглядных примерах.
Чтобы применять cdot, а также матричные компоненты в программировании, стоит пройти дистанционные специализированные курсы. Предложения есть как для новичков, так и для продвинутых программистов и математиков.
Предложения есть как для новичков, так и для продвинутых программистов и математиков.
Хотите освоить современную IT-специальность? Огромный выбор курсов по востребованным IT-направлениям есть в Otus!
Также, возможно, вам будет интересен следующий курс:
Калькулятор произведения матриц — Умножение матриц онлайн
Поиск инструмента
Найдите инструмент в dCode по ключевым словам:Просмотрите полный список инструментов dCode
Матричный продукт
Инструмент для расчета матричных продуктов. Алгебра матричных произведений состоит из умножения матриц (квадратных или прямоугольных).
Результаты
Продукт Matrix — dCode
Тег(и) : Matrix
Поделиться
dCode и многое другое
dCode бесплатен, а его инструменты являются ценным помощником в играх, математике, геокэшинге, головоломках и задачах для решения любых задач. день!
Предложение ? обратная связь? Жук ? идея ? Запись в dCode !
Матричный продукт
Произведение двух матриц
Matrix M1 Загрузка. ..
..
(если это сообщение не исчезнет, попробуйте обновить эту страницу)
Загрузка…
(если это сообщение не исчезнет, попробуйте обновить эту страницу)
Произведение матрицы на скаляр (число)
Matrix M Загрузка…
(если это сообщение не исчезнет, попробуйте обновить эту страницу)
См. также: Калькулятор матриц
Алфавит
Строка матрицы Загрузка…
(если это сообщение не исчезнет, попробуйте обновить эту страницу)
Загрузка…
(если это сообщение не исчезнет, попробуйте обновить эту страницу)
Ответы на вопросы (FAQ)
Что такое матричный продукт? (Определение)
Матричный продукт — это название, данное наиболее распространенному матричному умножению 9n a_{ik}b_{kj} $$
Умножение двух матриц $M_1$ и $M_2$ отмечается точкой $\cdot$ или . поэтому $M_1\cdot M_2$
поэтому $M_1\cdot M_2$
Произведение матриц определяется только тогда, когда количество столбцов $M_1$ равно количеству строк $M_2$ (матрицы называются совместимыми)
Как умножить 2 матрицы? (Произведение матриц)
Умножение 2-х матриц $M_1$ и $M_2$ образует результирующую матрицу $M_3$. Матричный продукт заключается в выполнении сложений и умножений по позициям элементов в матрицах $M_1$ и $M_2$.
$$ M_1 = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \ vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} \\ M_2 = \begin{bmatrix} b_{11} & b_{ 12} & \cdots & b_{1p} \\ b_{21} & b_{22} & \cdots & b_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ b_{n1} & b_ {n2} & \cdots & b_{np} \end{bmatrix} \\ M_1 \cdot M_2 = \begin{bmatrix} a_{11}b_{11} +\cdots + a_{1n}b_{n1} & a_ {11}b_{12} +\cdots + a_{1n}b_{n2} & \cdots & a_{11}b_{1p} +\cdots + a_{1n}b_{np} \\ a_{21}b_ {11} +\cdots + a_{2n}b_{n1} и a_{21}b_{12} +\cdots + a_{2n}b_{n2} & \cdots & a_{21}b_{1p} +\ cdots + a_{2n}b_{np} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1}b_{11} +\cdots + a_{mn}b_{n1} & a_{m1} b_{12} +\cdots + a_{mn}b_{n2} & \cdots & a_{m1}b_{1p} +\cdots + a_{mn}b_{np} \end{bmatrix} $$
Для вычисления значения элемента матрицы $M_3$ в позиции $i$ и столбце $j$ извлеките строку $i$ из матрицы $M_1$ и строку $j$ из матрицы $M_2$ и вычислить их скалярное произведение. То есть умножить первый элемент строки $i$ массива $M_1$ на первый элемент столбца $j$ массива $M_2$, затем второй элемент строки $i$ массива $M_1$ на второй элемент столбца $j$ из $M_2$ и так далее, обратите внимание на сумму полученных умножений, это значение скалярного произведения, следовательно, элемента в позиции $i$ и столбца $j$ в $M_3$.
То есть умножить первый элемент строки $i$ массива $M_1$ на первый элемент столбца $j$ массива $M_2$, затем второй элемент строки $i$ массива $M_1$ на второй элемент столбца $j$ из $M_2$ и так далее, обратите внимание на сумму полученных умножений, это значение скалярного произведения, следовательно, элемента в позиции $i$ и столбца $j$ в $M_3$.
Пример: $$ \begin{bmatrix} 1 & 0 \\ -2 & 3 \end{bmatrix} \cdot \begin{bmatrix} 2 & -1 \\ 4 & -3 \end{bmatrix} = \begin{bmatrix} 1 \times 2 + 0 \times 4 & 1 \times -1 + 0 \times -3 \\ -2 \times 2 + 4 \times 3 & -2 \times -1 + 3 \times — 3 \end{bmatrix} = \begin{bmatrix} 2 & -1 \\ 8 & -7 \end{bmatrix} $$
Как умножить матрицу на скаляр?
Произведением матрицы $M=[a_{ij}]$ на скаляр (число) $\lambda$ является матрица того же размера, что и исходная матрица $M$, при этом каждый элемент матрицы умножается на $\лямбда$.
$$ \lambda M = [ \lambda a_{ij} ] $$
Что такое свойства умножения матриц?
Ассоциативность: $$ A \times (B \times C) = (A \times B) \times C $$
Дистрибутивность: $$ A \times (B + C) = A \times B + A \times C $$
$$ (A + B) \times C = A \times C + B \times C $$
$$ \lambda (A \times B) = (\lambda A) \times B = A \times (\lambda B) $$
Порядок операндов имеет значение при умножении матриц на , поэтому $$ M_1. M_2 \neq M_2.M_1 $$
M_2 \neq M_2.M_1 $$
Как перемножить две матрицы несовместимых форм?
Существует матричный продукт , совместимый с матрицами любых размеров: продукт Кронекера.
Исходный код
dCode сохраняет за собой право собственности на исходный код «Matrix Product». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Matrix Product», апплета или фрагмента (конвертер, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Matrix Product» функции (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, скрипт, или доступ к API для «Матричного продукта» не является общедоступным, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложении для Android!
Напоминание: dCode можно использовать бесплатно.
Cite dCode
Копирование и вставка страницы «Matrix Product» или любых ее результатов разрешено, если вы цитируете dCode!
Ссылка на источник (библиография):
Продукт Matrix на dCode.fr [онлайн-сайт], получено 23 сентября 2022 г., https://www.dcode.fr/matrix-multiplication
Сводка
- Матричный продукт
- Алфавит
- Что такое матричный продукт? (Определение)
- Как перемножить 2 матрицы? (Матричное произведение)
- Как умножить матрицу на скаляр?
- Что такое свойства умножения матриц?
- Как перемножить две матрицы несовместимых форм?
Similar pages
- Matrix Calculator
- Matrix Power
- Tensor Product
- Eigenvalues of a Matrix
- Permanent of a Matrix
- Trace of a Matrix
- Minors of a Matrix
- DCODE’S TOOLS LIST
Поддержка
- PayPal
- Patreon
- Подробнее
Форум/Справка
Ключевые слова
, Multiclication, MATRIX, SLACKAR, номел, 2X2, 2X2, 2X2, 2X2, 2X2, номел, 2X2. ,5×5
,5×5
Звенья
▲
Калькулятор умножения матриц — примеры, факты
Калькулятор умножения матриц вычисляет произведение двух заданных матриц. Матрица представляет собой прямоугольный массив или сетку, в которой числа расположены в строках и столбцах.
Что такое калькулятор умножения матриц?
Калькулятор умножения матриц — это онлайн-инструмент, который помогает выполнять умножение матриц. Матрицы широко используются для представления данных при работе с линейными уравнениями, геометрией и статистикой. Чтобы использовать этот калькулятор умножения матриц , введите значения в поля ввода
Калькулятор умножения матриц
ПРИМЕЧАНИЕ: Введите только до 3 цифр.
Как пользоваться калькулятором умножения матриц?
Чтобы найти произведение матриц с помощью онлайн-калькулятора умножения матриц, выполните следующие шаги:
- Шаг 1: Перейдите к онлайн-калькулятору умножения матриц Cuemath.

- Шаг 2: Выберите размеры матриц (2 x 2 или 3 x 3) из раскрывающегося списка и введите значения в калькулятор умножения матриц.
- Шаг 3: Нажмите кнопку «Рассчитать», чтобы найти результирующую матрицу.
- Шаг 4: Нажмите кнопку «Сброс», чтобы очистить поля и ввести новые значения.
Как работает калькулятор умножения матриц?
Матрица, состоящая из m строк и n столбцов, представлена в виде \(A_{m \times n}\). Такая матрица называется прямоугольной. Кроме того, если матрица имеет одинаковое количество строк и столбцов, она называется квадратной матрицей. Например, матрица 2 x 2 будет квадратной матрицей, поскольку она имеет 2 строки и 2 столбца. Чтобы перемножить две матрицы, количество столбцов первой матрицы должно быть таким же, как количество строк второй матрицы. Если это условие не выполняется, умножение матриц невозможно. Таким образом, если у нас есть две матрицы размерами 5 х 3 и 3 х 2 соответственно, то их можно перемножить. Однако матрицу 6 x 1 нельзя умножить на матрицу 2 x 4. Ниже приведена процедура выполнения матричного умножения на матрицах 2 x 2 и 3 x 3.
Однако матрицу 6 x 1 нельзя умножить на матрицу 2 x 4. Ниже приведена процедура выполнения матричного умножения на матрицах 2 x 2 и 3 x 3.
1. Матрицы 2 × 2
A x B = \(\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \times \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} =\begin{bmatrix} a_{11}b_{11} + a_{12}b_ {21} и a_{11}b_{12} + a_{12}b_{22}\\ a_{21}b_{11} + a_{22}b_{21} и a_{21}b_{12} + a_{22}b_{22} \end{bmatrix}\)
2. Матрицы 3 × 3
A x B = \(\begin{bmatrix} a_{11} & a_{12} & a_{ 13}\\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix} \times \begin{bmatrix} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{bmatrix}\)
= \(\begin{bmatrix} a_{11}b_{11} + a_{12}b_{21} + a_{13}b_{31} & a_{11}b_{12} + a_{12} b_{22} + a_{13}b_{32} и a_{11}b_{13} + a_{12}b_{23} + a_{13}b_{33} \\ a_{21}b_{11} + a_{22}b_{21} + a_{23}b_{31} и a_{21}b_{12} + a_{22}b_{22} + a_{23}b_{32} и a_{21} b_{13} + a_{22}b_{23} + a_{23}b_{33}\\ a_{31}b_{11} + a_{32}b_{21} + a_{33}b_{31} & a_{31}b_{12} + a_{32}b_{22} + a_{33}b_{32} & a_{31}b_{13} + a_{32}b_{23} + a_{33} b_{33} \end{bmatrix}\)
Хотите находить сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
С Cuemath находите решения простыми и легкими шагами.
Запишитесь на бесплатный пробный урок
Решенные примеры на калькуляторе умножения матриц
Пример 1:
Умножьте матрицы \(\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\) & \(\begin{bmatrix} 2 & 1 \\ 4 & 2 \end{bmatrix}\) и проверьте это с помощью калькулятора умножения матриц.
Решение:
Умножение = \(\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \times \begin{bmatrix} b_{ 11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} =\begin{bmatrix} a_{11}b_{11} + a_{12}b_{21} & a_{11 }b_{12} + a_{12}b_{22}\\ a_{21}b_{11} + a_{22}b_{21} и a_{21}b_{12} + a_{22}b_{22 } \end{bmatrix}\)
Умножение = \(\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \times \begin{bmatrix} 2 & 1\\ 4 & 2 \end{ bmatrix} = \begin{bmatrix} 10 и 5 \\ 22 и 11 \end{bmatrix}\)
Пример 2 :
Умножьте матрицы \(\begin{bmatrix} 3 & 2 & 5\\ 5 & 2 & 4 \\ 2 & 5 & 6 \end{bmatrix}\) & \(\begin {bmatrix} 2 & 2 & 7\\ 1 & 4 & 6 \\ 3 & 8 & 7 \end{bmatrix}\) и проверьте это с помощью калькулятора умножения матриц.
Решение:
Умножение = \(\begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \\ a_ {31} & a_{32} & a_{33} \end{bmatrix} \times \begin{bmatrix} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{bmatrix}\)
= \(\begin{bmatrix} a_{11}b_{11} + a_{12}b_{21} + a_{13}b_{31} & a_{11}b_{12} + a_{12} b_{22} + a_{13}b_{32} и a_{11}b_{13} + a_{12}b_{23} + a_{13}b_{33} \\ a_{21}b_{11} + a_{22}b_{21} + a_{23}b_{31} и a_{21}b_{12} + a_{22}b_{22} + a_{23}b_{32} и a_{21} b_{13} + a_{22}b_{23} + a_{23}b_{33}\\ a_{31}b_{11} + a_{32}b_{21} + a_{33}b_{31} & a_{31}b_{12} + a_{32}b_{22} + a_{33}b_{32} & a_{31}b_{13} + a_{32}b_{23} + a_{33} b_{33} \end{bmatrix}\)
Умножение = \(\begin{bmatrix} 3 & 2 & 5\\ 5 & 2 & 4 \\ 2 & 5 & 6 \end{bmatrix} \times \begin {bmatrix} 2 & 2 & 7\\ 1 & 4 & 6 \\ 3 & 8 & 7 \end{bmatrix}\)
= \(\begin{bmatrix} 23 & 54 & 68\\ 24 & 50 & 75 \\ 27 & 72 & 86 \end{bmatrix}\)
Точно так же вы можете попробовать калькулятор умножения матриц и умножить следующие матрицы.
- Матрицы = \(\begin{bmatrix} 5 & 7 & 2\\ 1 & 8 & 10 \\ 11 & 18 & 1 \end{bmatrix}\) , \(\begin{bmatrix} 3 & 7 & 8\\ 1 & 7 & 1 \\ 5 & 19 & 1 \end{bmatrix}\)
- Матрицы = \(\begin{bmatrix} 4 и 8 \\ 12 и 16 \end{bmatrix}\), \(\begin{bmatrix} 5 и 10 \\ 15 и 20 \end{bmatrix}\)
- Матрицы
- Умножение матриц
Калькулятор умножения матриц — умножение двух матриц
Знакомство с калькулятором умножения матриц
Калькулятор умножения матриц — это онлайн-инструмент, с помощью которого можно умножать две матрицы одного порядка. Он применяет формулу умножения к двум матрицам, порядок которых может быть до 4. Он вычисляется поэтапно, чтобы избежать сложности метода умножения матриц.
В матричной алгебре умножение матриц является важной концепцией, которую вам всегда нужно решать для умножения матриц 3×3. Находить умножение матриц инструментом онлайн ярче, чем решать его вручную. Мы представляем онлайн-инструмент, который может легко рассчитать расширение.
Находить умножение матриц инструментом онлайн ярче, чем решать его вручную. Мы представляем онлайн-инструмент, который может легко рассчитать расширение.
Формула, используемая калькулятором умножения матриц
Умножение матриц — это одна из операций, выполняемых в матричной алгебре. Но умножение матриц — это не просто сложение и вычитание матриц. Калькулятор умножения следует правилу умножения матрицы, а именно:
«Две матрицы можно перемножить, только если они совместимы. Это означает, что для умножения матриц количество столбцов в первой матрице должно равняться количеству строк во второй матрице».
Посмотрим, как выполняется умножение двух матриц порядка 2×2
$$ A \;=\; \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \; А ТАКЖЕ \; \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} $$
Как умножать матрицы
Существует несколько шагов для умножения двух матриц с помощью формулы умножения матриц:
- Пожалуйста, выберите первую строку матрицы A и первый столбец матрицы B.
 Умножьте каждую соответствующую запись выбранной строки и столбец, а затем добавьте их. Это даст первый элемент результирующей матрицы.
Умножьте каждую соответствующую запись выбранной строки и столбец, а затем добавьте их. Это даст первый элемент результирующей матрицы. - Теперь выберите вторую строку матрицы A и первый столбец матрицы B, умножьте каждый соответствующий элемент выбранной строки и столбца, а затем сложите их. Это даст 2-й элемент столбца результирующей матрицы.
- Аналогично повторите процедуру, выбрав строки матрицы A и второй столбец матрицы B.
Результирующая матрица будет:
$$ С \;=\; А \раз В \;=\; \begin{bmatrix} a_{11}.b_{11}+a_{12}.b_{12} & a_{11}.b_{12}+a_{12}.b_{22} \\ a_{21} .b_{11}+a_{22}.b_{21} и a_{21}.b_{12}+a_{22}.b_{22} \end{bmatrix} $$Или можно записать как:
$$ С \;=\; \begin{bmatrix} c_{11} & c_{12} \\ c_{21} & c_{22} \end{bmatrix} $$
Как использовать калькулятор умножения матриц с шагами?
Есть несколько простых шагов для использования этого инструмента. Вот эти шаги:
- Введите количество строк и столбцов для матрицы A, а затем введите значения всех ее элементов.

- Теперь снова выберите количество строк и столбцов для матрицы B, а затем запишите значения всех элементов B.
- Вы можете использовать случайную кнопку для выбора случайных значений A и B вместо того, чтобы писать вручную.
- Теперь нажмите кнопку расчета.
- Вы получите результат через несколько секунд после нажатия на кнопку расчета.
Зачем использовать калькулятор умножения матриц?
В математике умножение матриц является важным понятием. Но процедура эта какая-то хитрая и длительная. Многие студенты сталкиваются со многими трудностями при решении задачи умножения матриц. Они игнорируют правила умножения. Поэтому им всегда нужна помощь извне, что облегчает им этот метод. Вот почему учащиеся могут использовать этот инструмент умножения матриц для оценки умножения с помощью пошагового решения.
Преимущества использования Калькулятора формул умножения матриц
Этот инструмент имеет множество полезных применений для улучшения ваших навыков решения задач по математике. Эти преимущества:
Эти преимущества:
- Это бесплатный онлайн-инструмент, поэтому вам не нужно платить за умножение матрицы 2×2.
- Матричный калькулятор умножения полезен для учащихся тем, что он решает задачу шаг за шагом, в которой участвует каждое умножение.
- Калькулятор умножения матриц экономит ваше время на ручных вычислениях.
- Может работать с матрицами до 4-го порядка.
- Калькулятор умножения матриц может быть полезен для решения многих реальных задач.
- У него есть случайный вариант, который позволяет вам практиковаться со многими вопросами о том, как умножать матрицы.
Хамза Харун
Последнее обновление 05 апреля 2022 г. Я автор и создатель контента. Мне нравится писать контент на разные темы. Помимо писательства, я SEO-ASO-SMM специалист и любитель футбола.
Помимо писательства, я SEO-ASO-SMM специалист и любитель футбола.
404 — СТРАНИЦА НЕ НАЙДЕНА
Почему я вижу эту страницу?
404 означает, что файл не найден. Если вы уже загрузили файл, имя может быть написано с ошибкой или файл находится в другой папке.
Другие возможные причиныВы можете получить ошибку 404 для изображений, поскольку у вас включена защита от горячих ссылок, а домен отсутствует в списке авторизованных доменов.
Если вы перейдете по временному URL-адресу (http://ip/~username/) и получите эту ошибку, возможно, проблема связана с набором правил, хранящимся в файле .htaccess. Вы можете попробовать переименовать этот файл в .htaccess-backup и обновить сайт, чтобы посмотреть, решит ли это проблему.
Также возможно, что вы непреднамеренно удалили корневую папку документа или вам может потребоваться повторное создание вашей учетной записи. В любом случае, пожалуйста, немедленно свяжитесь с вашим веб-хостингом.
Вы используете WordPress? См. Раздел об ошибках 404 после перехода по ссылке в WordPress.
Как найти правильное написание и папку
Отсутствующие или поврежденные файлыКогда вы получаете ошибку 404, обязательно проверьте URL-адрес, который вы пытаетесь использовать в своем браузере. Это сообщает серверу, какой ресурс он должен использовать попытка запроса.
http://example.com/example/Example/help.html
В этом примере файл должен находиться в папке public_html/example/Example/
Обратите внимание, что CaSe важен в этом примере. На платформах, которые обеспечивают чувствительность к регистру 9Пример 0206 e и пример E не совпадают.
Для дополнительных доменов файл должен находиться в папке public_html/addondomain.com/example/Example/, а имена чувствительны к регистру.
Неработающее изображение Если на вашем сайте отсутствует изображение, вы можете увидеть на своей странице поле с красным размером X , где отсутствует изображение. Щелкните правой кнопкой мыши X и выберите «Свойства». Свойства сообщат вам путь и имя файла, который не может быть найден.
Щелкните правой кнопкой мыши X и выберите «Свойства». Свойства сообщат вам путь и имя файла, который не может быть найден.
Это зависит от браузера. Если вы не видите на своей странице поле с красным X , попробуйте щелкнуть правой кнопкой мыши на странице, затем выберите «Просмотр информации о странице» и перейдите на вкладку «Мультимедиа».
http://example.com/cgi-sys/images/banner.PNG
В этом примере файл изображения должен находиться в папке public_html/cgi-sys/images/ пример. На платформах с учетом регистра символов PNG и png не совпадают.
Ошибки 404 после перехода по ссылкам WordPress
При работе с WordPress ошибки 404 Page Not Found часто могут возникать при активации новой темы или изменении правил перезаписи в файле .htaccess.
Когда вы сталкиваетесь с ошибкой 404 в WordPress, у вас есть два варианта ее исправления.
Вариант 1. Исправьте постоянные ссылки
Исправьте постоянные ссылки - Войдите в WordPress.
- В меню навигации слева в WordPress нажмите Настройки > Постоянные ссылки (Обратите внимание на текущую настройку. Если вы используете пользовательскую структуру, скопируйте или сохраните ее где-нибудь.)
- Выберите По умолчанию .
- Нажмите Сохранить настройки .
- Верните настройки к предыдущей конфигурации (до того, как вы выбрали «По умолчанию»). Верните пользовательскую структуру, если она у вас была.
- Нажмите Сохранить настройки . 9index.php$ — [L]
- Отредактируйте файл на своем компьютере и загрузите его на сервер через FTP
- Использовать режим редактирования программы FTP
- Используйте SSH и текстовый редактор
- Используйте файловый менеджер в cPanel
- Войдите в cPanel.
- В разделе «Файлы» щелкните значок File Manager .
- Установите флажок для Корень документа для и выберите доменное имя, к которому вы хотите получить доступ, из раскрывающегося меню.
- Убедитесь, что установлен флажок Показать скрытые файлы (dotfiles) «.
- Нажмите Перейти . Файловый менеджер откроется в новой вкладке или окне.
- Найдите файл .htaccess в списке файлов. Возможно, вам придется прокрутить, чтобы найти его.
- Щелкните правой кнопкой мыши файл .
 htaccess и выберите Редактировать код в меню. Кроме того, вы можете щелкнуть значок файла .htaccess, а затем Редактор кода Значок вверху страницы.
htaccess и выберите Редактировать код в меню. Кроме того, вы можете щелкнуть значок файла .htaccess, а затем Редактор кода Значок вверху страницы. - Может появиться диалоговое окно с вопросом о кодировании. Просто нажмите Изменить , чтобы продолжить. Редактор откроется в новом окне.
- При необходимости отредактируйте файл.
- Нажмите Сохранить изменения в правом верхнем углу, когда закончите. Изменения будут сохранены.
- Протестируйте свой веб-сайт, чтобы убедиться, что ваши изменения были успешно сохранены. Если нет, исправьте ошибку или вернитесь к предыдущей версии, пока ваш сайт снова не заработает.
- После завершения нажмите Закрыть , чтобы закрыть окно диспетчера файлов.
RewriteCond %{REQUEST_FILENAME} !-f
RewriteCond %{REQUEST_FILENAME} !-d
RewriteRule . /index.php [L]
# Конец WordPress
Если ваш блог показывает неправильное доменное имя в ссылках, перенаправляет на другой сайт или отсутствуют изображения и стиль, все это обычно связано с одной и той же проблемой: в вашем блоге WordPress настроено неправильное доменное имя.
Как изменить файл .htaccess
Файл .htaccess содержит директивы (инструкции), которые сообщают серверу, как вести себя в определенных сценариях, и напрямую влияют на работу вашего веб-сайта.
Перенаправление и перезапись URL-адресов — это две очень распространенные директивы, которые можно найти в файле .htaccess, и многие скрипты, такие как WordPress, Drupal, Joomla и Magento, добавляют директивы в .htaccess, чтобы эти скрипты могли работать.
Возможно, вам потребуется отредактировать файл .htaccess в какой-то момент по разным причинам. В этом разделе рассказывается, как редактировать файл в cPanel, но не о том, что нужно изменить. статьи и ресурсы для этой информации.)
Существует множество способов редактирования файла .htaccess Самый простой способ отредактировать файл . htaccess для большинства людей — через диспетчер файлов в cPanel.
htaccess для большинства людей — через диспетчер файлов в cPanel.
Прежде чем что-либо делать, рекомендуется сделать резервную копию вашего веб-сайта, чтобы вы могли вернуться к предыдущей версии, если что-то пойдет не так.
Откройте файловый менеджерКалькулятор умножения матриц
| 0 | ||||
| АС | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Этот калькулятор предоставляет подробное решение, объясняющее, как умножать две матрицы.
 Перемножить две матрицы можно только в том случае, если количество столбцов первой матрицы равно количеству строк второй
Перемножить две матрицы можно только в том случае, если количество столбцов первой матрицы равно количеству строк второй Матрица размера m × n представляет собой таблицу чисел, состоящую из m строк и n столбцов.
Элементы матрицы обозначаются как ij , где i — номер строки, j — номер столбца.
| You may also find the following calculators helpful |
| Linear Algebra and Analytical Geometers Calculators |
| Matrix Addition and Subtraction Calculator |
| Matrix Multiplication Calculator |
| Matrix Transpose Calculator |
| Matrix Калькулятор определителя |
| Калькулятор обратной матрицы |
| Длина сегмента линии. Онлайн-калькулятор расстояния между точками. |
| Калькулятор векторных координат по двум точкам |
| Калькулятор векторного модуля (длины) |
| Калькулятор векторного сложения и вычитания |
3 Калькулятор векторного произведения точек. Используя длину векторов и косинус угла между векторами. Используя длину векторов и косинус угла между векторами. |
| Калькулятор векторного скалярного произведения. Используя векторные координаты. |
| Калькулятор векторного произведения. Используя векторные координаты. |
| Vector Triple Product Calculator |
| Vector Multiplication by Number Calculator |
| Angle Between Vectors Calculator |
| Vector Collinearity Check Calculator |
| Vector Coplanarity Calculator |
| Combinatorics Calculators |
| Калькулятор перестановок N элементов |
| Комбинации N элементов с помощью M калькулятора |
| Permutations of N Elements by M Calculator |
| Numeral Systems Calculators |
| Roman Numeral Calculator |
| Roman Numerals From 1 to 3999 |
| Numeral Systems Calculator |
Binary Calculator.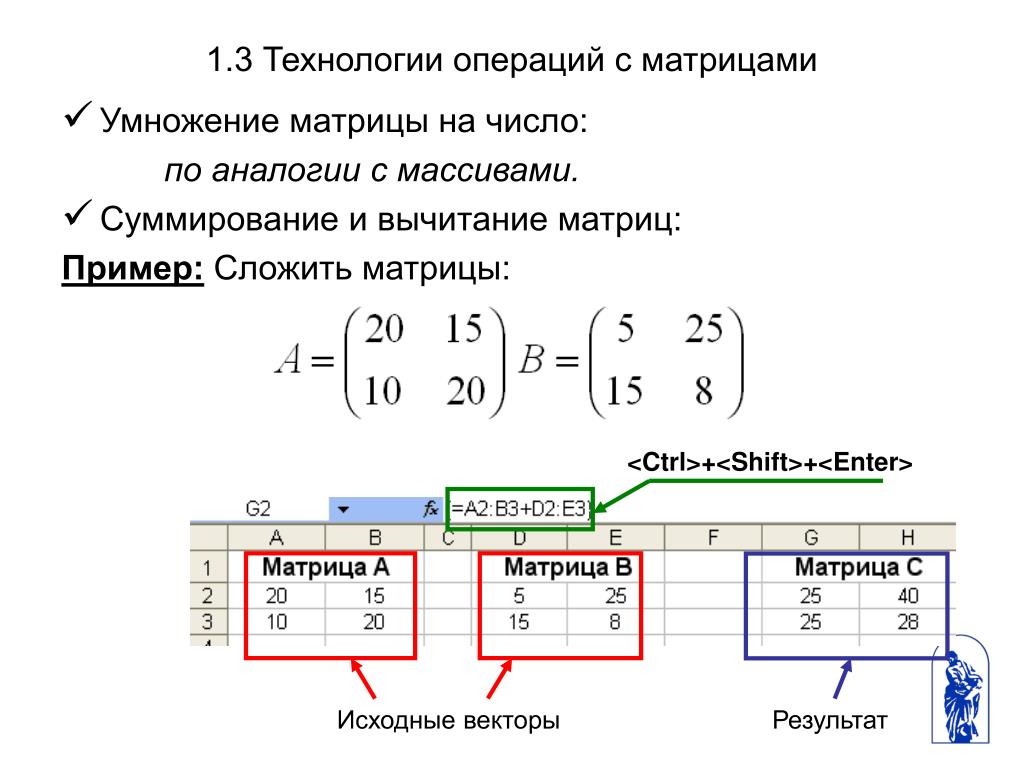 Сложение, вычитание, умножение и деление двоичных чисел. Сложение, вычитание, умножение и деление двоичных чисел. |
| Калькулятор дробей |
| Калькулятор упрощения дробей |
| Калькулятор неправильных дробей |
| Калькулятор смешанных дробей до неправильных |
| Калькулятор дробей с пошаговым решением |
| Калькулятор десятичных дробей |
| Калькулятор дробей |
| Калькулятор сравнения дробей |
| Калькулятор общего знаменателя0628 |
| Trigonometers Calculators |
| Sine Calculator |
| Cosine Calculator |
| Tangent Calculator |
| Cotangent Calculator |
| Secant Calculator |
| Cosecant Calculator |
| Arcsine Калькулятор |
| Калькулятор арккосинуса |
| Калькулятор арктангенса |
| Arccotangent Calculator |
| Arcsecant Calculator |
| Arccosecant Calculator |
| Calculators (Number theory) |
| Mathematical Expressions Calculator |
| Calculator Parentheses |
| Prime Factorization Calculator |
| Калькулятор Gcd и Lcm с шагами |
| Калькулятор Gcd и Lcm с использованием алгоритма Евклида |
| Калькулятор Gcd и Lcm для любого количества чисел |
| Разбить число на его разрядное значение |
Разделить число на отношение. Онлайн -калькулятор с шагами Онлайн -калькулятор с шагами |
| Процентный калькулятор с шагами |
| Научная нотация к калькулятору десятичной конверсии |
| Учительную конвертеру | Учительная нотация | 9Учительная нотация | 933333333333333333 | 3333333339 годы | 3333333333 | 3333333339 гг.0626 | Logarithm Calculator |
| Quadratic Equations Calculator With Steps |
| Remainder Calculator |
| Root Calculator |
| Decimal Period Calculator |
| Big Number Calculator |
| Rounding Numbers Calculator |
| Калькулятор свойств корней и показателей |
| Калькулятор комплексных чисел |
| Area Calculators |
| Area of a Square Calculator |
| Area of a Rectangle Calculator |
| Math Trainers |
| Addition Math Trainer |
| Subtraction Math Trainer |
| Multiplication Math Trainer |
| Дивизионный тренажер по математике |
| Математический тренажер по таблице умножения |
| Онлайн-тренажер по счету для дошкольников |
| Онлайн-тренажер внимательности для дошкольников |
Онлайн-тренажер по математике сложения, вычитания, умножения. Найдите правильный ответ. Найдите правильный ответ. |
| Online Numeric Expression Trainer |
| Converters |
| Length Converter |
| Speed Converter |
| Acceleration Converter |
| Physics Calculators |
Mechanics |
| Speed Time Distance Calculator |
| Acceleration Speed Distance Calculator |
| Displacement Time Calculator |
| Time Calculator |
| Newton’s Second Law Calculator |
| Gravitational Force Calculator |
| Momentum Калькулятор |
| Калькулятор импульсов |
| Калькулятор веса объекта |
Optics |
| Light Reflection and Refraction Calculator |
Electricity and Magnetism |
| Ohm’s Law Calculator |
| Coulomb’s Law Calculator |
| Electric Field Strength Calculator |
| Point Калькулятор электрического заряда Q |
| Калькулятор силы, действующей на заряд |
| Distance From Charge Calculator |
| Potential Charge Energy Calculator |
| Electric Field Potential Calculator |
| Conductor and Sphere Capacitance Calculator |
Capacitors |
| Калькулятор емкости плоскопараллельных, цилиндрических и сферических конденсаторов |
| Калькулятор напряженности электрического поля в плоскопараллельных, цилиндрических и сферических конденсаторах |
| Калькулятор энергии, запасенной в параллельных пластинчатых, цилиндрических и сферических заряженных конденсаторах |
| Калькулятор объемной плотности энергии параллельных пластинчатых, цилиндрических и сферических конденсаторов |
| Астрономические калькуляторы |
| Вес объекта на других планетах |
| Гравитационное ускорение на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор случайных чисел |
| Генератор паролей |
Примеры умножения матриц
Умножьте две матрицы размеров 3 × 2 и 2 × 3
| С = А × В = |
| × |
| = |
|
Раствор
Даны две матрицы
| А = |
| где, | а 11 = 4 | ||||||
| Б = |
| где, | б 11 = 0,45 |
Перемножать две матрицы можно только в том случае, если количество столбцов матрицы A равно количеству строк матрицы B
При умножении матрицы A размера l × m на матрицу B размера m × n мы получаем матрицу размера C
| C = |
| × |
| = |
|
Элемент матрицы с индексом C ij находится по формуле0683 12 ⋅ B 21 = 4 ⋅ 0,45 + 1 ⋅ 3 = 4,8
C 12 = A 11 ⋅ B 12 + A 12 ⋅ B 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 + A . ⋅ 1,4 = 49,4
⋅ 1,4 = 49,4
C 13 = A 11 ⋅ B 13 + A 12 ⋅ B 23 = 4 ⋅ (-9) + 1 ⋅ 0 = -36
= 4 ⋅ (-9) + 1 ⋅ 0 = -36 218444444444444444444444444444444444444444444444444 2184 2184 2184 2184 2184 2184 2184. = a 21 ⋅ b 11 + a 22 ⋅ b 21 = 0 ⋅ 0,45 + 5 ⋅ 3 = 15c 22 0683 21 ⋅ B 12 + A 22 ⋅ B 22 = 0 ⋅ 12 + 5 ⋅ 1,4 = 7
C 23 = A 21 ⋅ B 13 13 + A 21 ⋅ B 13 13 13 + A 22 21 Ϫ B 13 13 + A 21 ⋅ B 13 1 + + + + + . B 23 = 0 ⋅ (-9) + 5 ⋅ 0 = 0
C 31 = A 31 ⋅ B 11 + A 32 ⋅ B 21 = 2 ° 0,45 + 45 + + (——B 21 = 2 °. 3) ⋅ 3 = -8,1
c 32 = a 31 ⋅ b 12 + a 32 ⋅ b 22 = 2 ⋅-1 12. 8
8
C 33 = A 31 ⋅ B 13 + A 32 ⋅ B 23 = 2 ⋅ (-9) + (-3) ⋅ 0 = -18
|
Перейти к калькулятору
Умножьте две матрицы 2 × 2 и 2 × 4.
| С = А × В = |
| × |
| = |
|
Решение
Даны две матрицы
| А = |
| где, | а 11 = 7 | ||||||||
| Б = |
| где, | б 11 = -5 |
Перемножать две матрицы можно только в том случае, если количество столбцов матрицы A равно количеству строк матрицы B
При умножении матрицы A размера l × m на матрицу B размера m × n мы получаем матрицу размера C
| C = |
| × |
| = |
|
Matrix element with index C ij is found by the formula
c 11 = a 11 ⋅ b 11 + a 12 ⋅ b 21 = 7 ⋅ (-5 ) + 1 ⋅ 12 = -23
с 12 = A 11 ⋅ B 12 + A 12 ⋅ B 22 = 7 ⋅ 6 + 1 ⋅ 37 = 79
C 13 = A 4. 12 ⋅ B 23 = 7 ⋅ 2 + 1 ⋅ 1 = 15
12 ⋅ B 23 = 7 ⋅ 2 + 1 ⋅ 1 = 15
C 14 = A 11 ⋅ B 14 + A 12 кор 0 = 63
в 21 = а 21 ⋅ б 11 + а 22 ⋅ б 21 = 0 ⋅ (-5) + 13 ⋅ 6 .0003
C 22 = A 21 ⋅ B 12 + A 22 ⋅ B 22 = 0 ⋅ 6 + 3 ⋅ 37 = 111
C 23 = A 210683 210688. 13 + A 22 ⋅ B 23 = 0 ⋅ 2 + 3 ⋅ 1 = 3
C 24 = A 21 ⋅ B 14 + A 22 4 вно B 14 + A 22 44. B 14 + A 22 44 40683 14 + A 22 4. ⋅ 9 + 3 ⋅ 0 = 0
| С = |
|
Перейти к калькулятору
Умножьте две матрицы размеров 1 × 3 и 3 × 2
| С = А × В = |
| × |
| = |
Раствор
Даны две матрицы
| А = |
| где, | а 11 = 2 | ||||||
| Б = |
| где, | б 11 = 3 |
Перемножать две матрицы можно только в том случае, если количество столбцов матрицы A равно количеству строк матрицы B
матрица l × n C
| C = |
| × |
| = |
|
Matrix element with index C ij is found by the formula
c 11 = a 11 ⋅ b 11 + a 12 ⋅ b 21 + a 13 ⋅ б 31 = 2 ⋅ 3 + (-7) ⋅ 4 + 0 ⋅ 0 = -22
в 12 = а 11 ⋅ б 12 + а 12 ⋅ B 22 + A 13 ⋅ B 32 = 2 ⋅ 6 + (-7) ⋅ 1 + 0 ⋅ 8 = 5
Go Calculator
Матрикс Кальтриса
4.

Калькулятор матриц вычисляет сложение, вычитание, умножение и деление двух матриц одним щелчком мыши. Этот инструмент берет количество строк и столбцов от пользователя для формирования двух матриц. Вы можете указать режим работы, выбрав оператора.
Давайте рассмотрим определение матрицы в следующем разделе. Мы также объясним, как решать матрицы без использования матричного множителя.
Что такое матрица?
В математике матрица представляет собой прямоугольный массив или таблицу чисел, выражений или символов, расположенных в строках и столбцах.
Матрица 2 x 3 имеет две строки и три столбца. Приведенная ниже матрица имеет порядок 3 × 3 .
A =
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
Как добавить матрицы?
Сложение матрицы очень просто. Чтобы добавить две матрицы одного порядка, добавьте соответствующий элемент первой матрицы к соответствующему элементу второй матрицы.
Чтобы добавить две матрицы одного порядка, добавьте соответствующий элемент первой матрицы к соответствующему элементу второй матрицы.
Let,
A =
| 2 | 1 | 3 |
| 0 | 2 | 3 |
| 5 | 1 | 2 |
and B =
| 1 | 3 | 2 |
| 2 | 4 | 8 |
| 1 | 6 | 3 |
Step 1: Write both matrices A и B и поместите знак + между ними.
А + В =
| 2 | 1 | 3 |
| 0 | 2 39330628 | |
| 5 | 1 | 2 |
+
| 1 | 3 | 2 |
| 2 | 4 | 8 |
| 1 | 6 | 3 |
Шаг 2: Добавьте каждый соответствующий элемент обеих матриц.
А + В =
| 2 + 1 | 1 + 3 | 3 + 2 |
| 0 + 2 | 2 + 4 | 3 + 8 |
| 5 + 1 | 1 + 6 | 2 + 3 |
A + B =
| 3 | 4 | 5 |
| 2 | 6 | 11 |
| 6 | 7 | 5 |
How to subtract matrices?
Вычитание матриц аналогично сложению двух матриц. Единственная разница в том, что мы должны вычитать соответствующие элементы, а не добавлять их.
Let,
A =
| 0 | 1 | 4 |
| 2 | 2 | 3 |
| 8 | 1 | 1 |
and B =
| 10 | 3 | 1 |
| 12 | 2 | 8 |
| 1 | 6 | 3 |
Step 1: Запишите обе матрицы A и B и поставьте между ними знак минус (-) .
A — B =
| 0 | 1 | 4 |
| 2 | 2 | 3 |
| 8 | 1 | 1 |
—
| 10 | 3 | 1 |
| 12 | 2 | 8 |
| 1 | 6 | 3 |
Шаг 2: Вычтите каждый соответствующий элемент обеих матриц.
A — B =
| 0 — 10 | 1 — 3 | 4 — 1 |
| 2 — 12 | 2 — 2 | 3 — 8 |
| 8 — 1 | 1 — 6 | 1 — 3 |
А — В =
| -10 | -2 | 3 |
| -10 | 0 | -5 |
| 7 | -5 | -2 |
How to multiply matrices?
Калькулятор умножения матриц может умножать две матрицы за доли секунды. Однако вот метод умножения двух матриц.
Однако вот метод умножения двух матриц.
Пусть,
А =
| 2 | 1 |
| 0 | 2 |
And B =
| 1 | 3 |
| 1 | 6 |
Step 1: Write both matrices A and B and place negative (x ) знаков между ними.
A x B =
| 2 | 1 |
| 0 | 2 |
X
| 1 | 3 |
| 1 | 6 |
Шаг 2: Умножьте каждую строку числа A на все столбцы числа B
A x B =
| 2 x 1 + 1 x 1 | 2 x 3 + 1 x 6 |
| 0 x 1 + 2 x 1 | 0 x 3 + 2 x | 88899 0. |


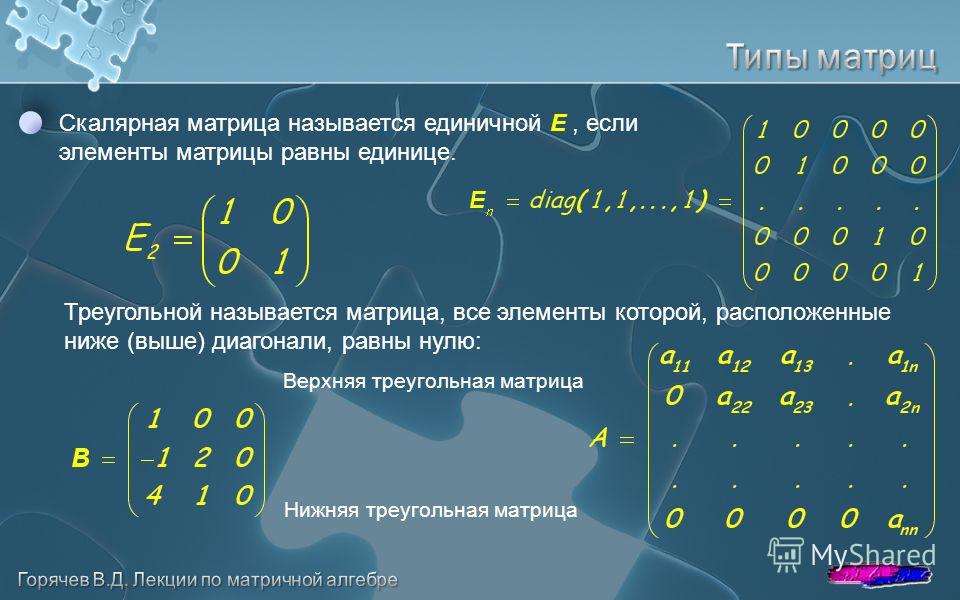
 Сложение и вычитание
Сложение и вычитание


 Известная матрица в левой части перемножается на обратную той, что расположена слева в уравнении. Далее – с правой стороны на матрицу, обратную той, что находилась справа. Результат: X = A-1 * C * B-1.
Известная матрица в левой части перемножается на обратную той, что расположена слева в уравнении. Далее – с правой стороны на матрицу, обратную той, что находилась справа. Результат: X = A-1 * C * B-1.
 Умножьте каждую соответствующую запись выбранной строки и столбец, а затем добавьте их. Это даст первый элемент результирующей матрицы.
Умножьте каждую соответствующую запись выбранной строки и столбец, а затем добавьте их. Это даст первый элемент результирующей матрицы.
 htaccess и выберите Редактировать код в меню. Кроме того, вы можете щелкнуть значок файла .htaccess, а затем Редактор кода Значок вверху страницы.
htaccess и выберите Редактировать код в меню. Кроме того, вы можете щелкнуть значок файла .htaccess, а затем Редактор кода Значок вверху страницы. Калькулятор
Калькулятор