Транспортная задача: метод аппроксимации Фогеля
Среди четырех, чаще всего применяющихся на практике, методов формирования опорного плана в транспортной задаче самый необычный — метод аппроксимации Фогеля. Последовательность действий при его использовании совершенно иная, чем при заполнении транспортной таблицы методом «Северо-Западного угла» или методом «Минимального элемента».
На первый взгляд аппроксимация Фогеля сложнее, но это ложное впечатление. Метод простой и позволяет получить опорный план более приближенный к оптимальному решению, чем в случае применения других методов (за исключением разве что метода «Двойного предпочтения»).
Сущность аппроксимации Фогеля в нахождении разности (по модулю) между парой минимальных тарифов в каждой строке и столбце. Затем строка или столбец с наибольшей разностью заполняются в направлении от клетки с минимальным тарифом к клетке с максимальным. Подробнее далее.
Первым делом находим для каждой строки транспортной таблицы абсолютные разности (по модулю, т.
е. без знака) между двумя минимальными тарифами в этой строке. То же самое делаем и для каждого столбца: ищем в нем два минимальных тарифа и находим их разность по модулю.
Если в строке/столбце две клетки с одинаковыми и минимальными значениями тарифов, то берем именно их. Тогда разность будет равна 0.
Найденные разности выписываем в добавочный столбец (Δi) и добавочную строку (Δj).
Среди вычисленных разностей (и по строкам, и по столбцам!) выбираем наибольшую.
Затем в строке или столбце, которому соответствует максимальная разность, ищем клетку с минимальным тарифом. Заполняем ее максимально возможным объемом грузоперевозки.
Если клеток с минимальным тарифом несколько, то заполняем ту из них, которой соответствует наибольшая разность (Δj — если выбираем по строке, или Δi — если выбираем по столбцу).
Затем повторяем все вышеописанные действия снова, только уже не учитывая заполненные клетки и выбранные ранее разности (Δi и Δj).
И так до тех пор, пока не будет полностью найден опорный план.
Оставшиеся ячейки транспортной матрицы уже и так очевидно каким образом следует заполнить:
В результате мы получаем опорный план:
Зачастую опорный план, полученный аппроксимацией Фогеля, оказывается либо сразу оптимальным (как в этом примере), либо очень близким к нему. Но именно часто, а не всегда!
Галяутдинов Р.Р.
Источники
- Аппроксимация Фогеля // Викиучебник. URL: http://ru.wikibooks.org/wiki/Аппроксимация_Фогеля (дата обращения: 5.03.2014)
© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.
Если понравилась статья, поделитесь с друзьями и подпишитесь на обновления:
Нашли опечатку? Помогите сделать статью лучше! Выделите орфографическую ошибку мышью и нажмите Ctrl + Enter.
Библиографическая запись для цитирования статьи по ГОСТ Р 7.0.5-2008:
Галяутдинов Р.
Р. Транспортная задача: метод аппроксимации Фогеля // Сайт преподавателя экономики. [2014]. URL: http://galyautdinov.ru/post/approksimaciya-fogelya (дата обращения: 17.11.2022).
3. Метод аппроксимации Фогеля
Основным недостатком метода минимального элемента является неучет будущих тарифов: в первых шагах алгоритма тарифы минимальны, на заключительных шагах возможно использование перевозок с высокими тарифами, тем самым, опорный план будетотличаться от оптимального, хотя и не так сильно, какв методе северо-западного угла.
Метод аппроксимации Фогеля лишен выше указанных недостатков, однако довольно сложен для исполнения по сравнению двумя предыдущими методами.
Алгоритм метода Фогеля состоит в следующем:
На каждой итерации вычисляют по всем столбцам и строкам разность между двумя записанными в них минимальными тарифами,
Среди указанных разностей выбирают максимальную.
В строке (или столбце) с выбранной разностью определяют минимальный тариф и заполняют ее, полностью удовлетворяя потребности или полностью исчерпав запасы.
Если минимальный тариф одинаков для нескольких клеток данной строки (столбца), то для заполнения выбирают ту клетку, которая расположена в столбце (строке), соответствующим (ей) наибольшей разности между двумя минимальными тарифами, находящимися в данном (ей) столбце (строке).
Строка с израсходованным запасом или столбец с удовлетворенной потребностью исключаются из рассмотрения, и в соответствующей разности ставится прочерк.
Рассмотрим процесс
составления опорного плана по методу
Фогеля. На первом шаге разности между
двумя соседними минимальными тарифами
равны для строк (2-1=1. 5-4=1, 3-2=1), для столбцов
(7-4=3, 5-2=3, 3-1=2, 6-2=4). Максимальная разность
имеет место для четвертого столбца (4).
На втором шаге итерации вычислим разности между соседними минимальными тарифами оставшихся клеток для строк (7-1=6, 5-4=1, 3-2=1) и для столбцов (7-4=3, 5-2=3, 3-1=2). Максимальная разность будет для первой строки (6). Заполняем клетку А1B3, исчерпав оставшееся сырье первого поставщика, при этом третьему потребителю нужно еще 190-50=140 единиц сырья. В итоге из рассмотрения исключаем первую строку.
На следующем этапе
разности равны для строк (5-4=1, 3-2=1) и для
столбцов (9-4=5, 5-2=3, 9-3=6). Максимальная
разность у третьего столбца (6). Заполняем
клетку А3B3,
полностью удовлетворив потребности
третьего предприятия, в результате чего
у третьего производителя останется
170-140=30 единиц сырья.
Далее разности равны для строк (5-4=1, 9-2=7) и для столбцов (9-4=5, 5-2=3). Разность максимальной будет для третьей строки. Следовательно, заполняем клетку А3B2, исключив из последующих шагов третью строку.
На последнем шаге остается только одна разность для второй строки (5-4=1). Поэтому заполняем оставшиеся клетки данной строки в порядке возрастания тарифов, сначала клетку А2B1, затем А2B2.
В результате опорный план будет задаваться следующей матрицей: , при этом общая стоимость перевозок составит: Q=1*50+2*110+4*120+5*20+2*30+3*140=1330 условных единиц.
Сравнение трех методов нахождения опорного плана позволяет сделать вывод, что план, самый близкий к оптимальному, дает метод аппроксимации Фогеля.
Транспортная проблема | Набор 4 (метод аппроксимации Фогеля)
Улучшить статью
Сохранить статью
- Уровень сложности: Hard
- Последнее обновление: 25 ноя, 2019
Улучшить статью
Сохранить статью
Метод Северо-западный угол и метод Ячейка наименьшей стоимости обсуждались в предыдущих статьях.
В этой статье приближение Фогеля 9Метод 0024 будет обсуждаться.
Решение:
- Для каждой строки найдите наименьшее значение, а затем второе наименьшее значение, возьмите абсолютную разницу этих двух наименьших значений и запишите ее в соответствующей разнице строк, как показано на рисунке ниже. В строке O1 , 1
- Для каждого столбца найдите наименьшее значение, а затем второе наименьшее значение и возьмите абсолютную разницу этих двух наименьших значений, затем запишите ее в соответствующей разнице столбца, как показано на рисунке. В столбце D1 , 2 — наименьшее значение, а 3 — второе наименьшее значение, и их абсолютная разница равна 1 . Аналогично для столбца D2 , D3 и D3 , абсолютные разности равны 2 , 2 и 2 соответственно.
- Эти значения разницы между строками и столбцами также называются штрафом. Теперь выберите максимальное наказание. Максимальный штраф 3 т.е. строка O2 . Теперь найдите ячейку с наименьшей стоимостью в строке O2 и распределите минимум между предложением соответствующей строки и спросом соответствующего столбца. Спрос меньше предложения, поэтому распределите спрос столбца, т.е. 250 на сотовый. Затем отмените столбец D1 .
- В оставшихся ячейках найдите разницу между строками и столбцами.
- Снова выберите максимальный штраф, равный 3 и соответствующий строке O1 . Ячейка с наименьшей стоимостью в строке O1 — это (O1, D2) со стоимостью 1 . Распределите минимум между спросом и предложением из соответствующей строки и столбца в ячейку. Отмените строку или столбец с нулевым значением.
- Теперь найдите отличие строк и столбцов от остальных ячеек.
- Теперь выберите максимальное наказание, которое равно 7 и соответствует столбцу D4 .Ячейка с наименьшей стоимостью в столбце D4 равна (O3, D4) со стоимостью 2 . Спрос меньше, чем предложение для ячейки (O3, D4) . Выделите 200 ячейке и отмените столбец.
- Найдите отличие строк и столбцов от остальных ячеек.
- Теперь максимальный штраф 3 соответствует столбцу D2 . Ячейка с наименьшим значением в D2 равна (O3, D2) . Выделите минимум спроса и предложения и отмените столбец.
- Теперь есть только один столбец, поэтому выберите ячейку с наименьшей стоимостью и распределите значение.
- Теперь есть только одна ячейка, поэтому распределите оставшийся спрос или предложение на ячейку
- Баланса не осталось. Поэтому умножьте выделенное значение ячеек на соответствующую стоимость ячеек и добавьте все, чтобы получить окончательную стоимость, т.е. 9.0023 (300 * 1) + (250 * 2) + (50 * 3) + (250 * 3) + (200 * 2) + (150 * 5) = 2850
| ДОБРО ПОЖАЛОВАТЬ В IJSTR (ISSN 2277-8616) —
|
по май 2020 г. 
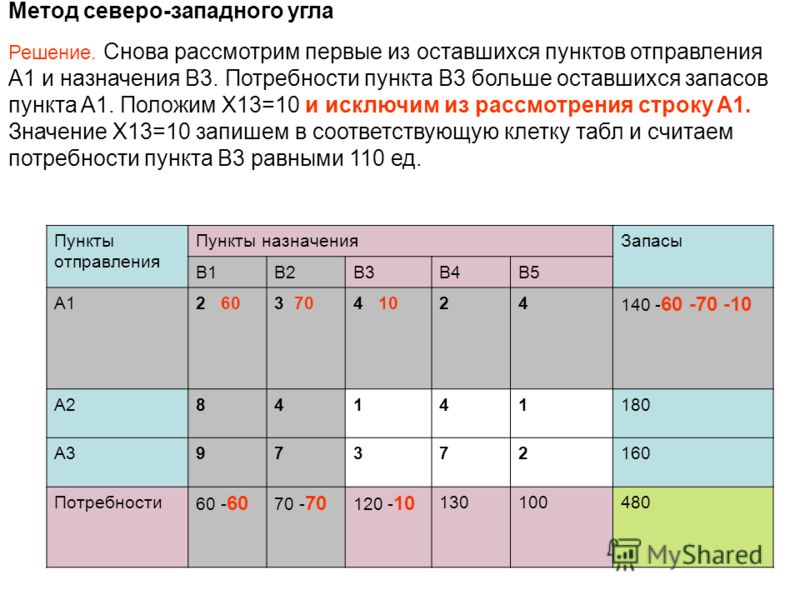
Рецензенты должны проявить интерес, отправив нам свои полные биографические данные. Рецензенты определяют качество материалов. Поскольку ожидается, что они будут экспертами в своих областях, они должны прокомментировать значимость рецензируемой рукописи и то, способствует ли исследование знаниям и продвижению как теории, так и практики в этой области. Заинтересованным рецензентам предлагается отправить свое резюме и краткое изложение конкретных знаний и интересов по адресу 