Онлайн калькулятор метод ньютона: Онлайн калькулятор: Метод Ньютона – Решение уравнений методом Ньютона | Онлайн калькулятор

Онлайн калькулятор: Метод Ньютона

Этот онлайн калькулятор применяет метод Ньютона (также известный как метод касательных) используя калькулятор производных для получения аналитической формулы производной заданной функции (метод Ньютона требует вычисления производной). Под калькулятором можно прочитать краткое описание метода.

Метод Ньютона

Критерий останова (тип)Отличие функции от нуля Точность вычисления

Знаков после запятой: 4

save Сохранить extension Виджет

Метод Ньютона

Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации.

Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к графику исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка берётся в качестве следующего приближения. Далее процесс повторяется, пока не будет достигнута необходимая точность.

Уравнение касательной к графику функции выглядит следующим образом:
,
где — тангенс угла пересечения касательной с осью абсцисс.

Тангенс угла пересечения касательной с осью абсцисс, — не что иное, как значение производной в точке .
С учетом того факта, что в точке пересечения с осью абсцисс значение y равно нулю, можно записать следующее выражение для нахождения точки пересечения (следующей точки приближения):

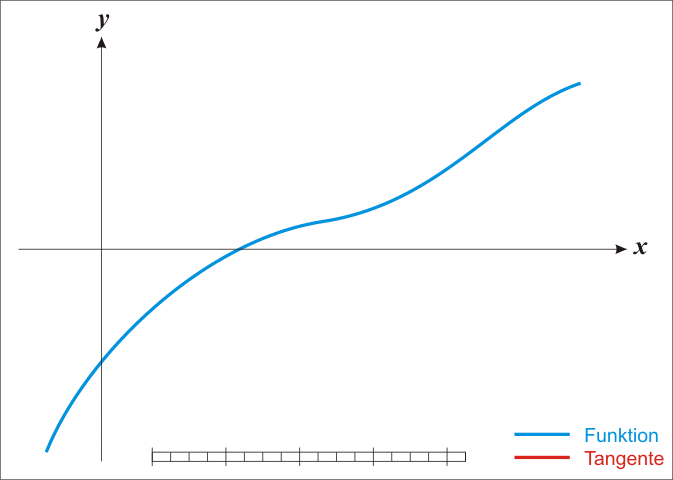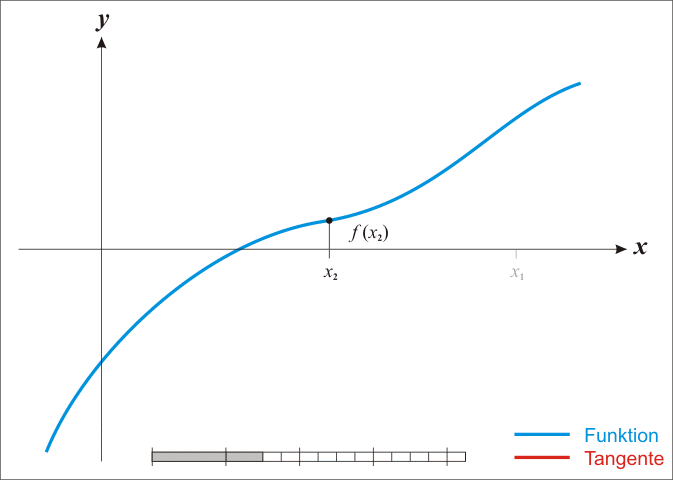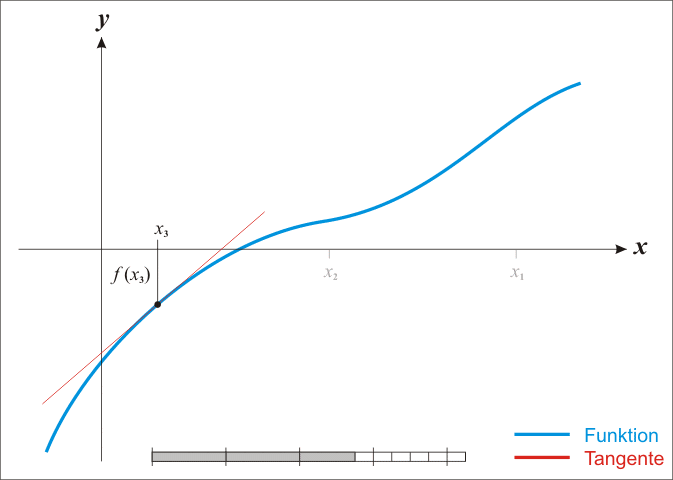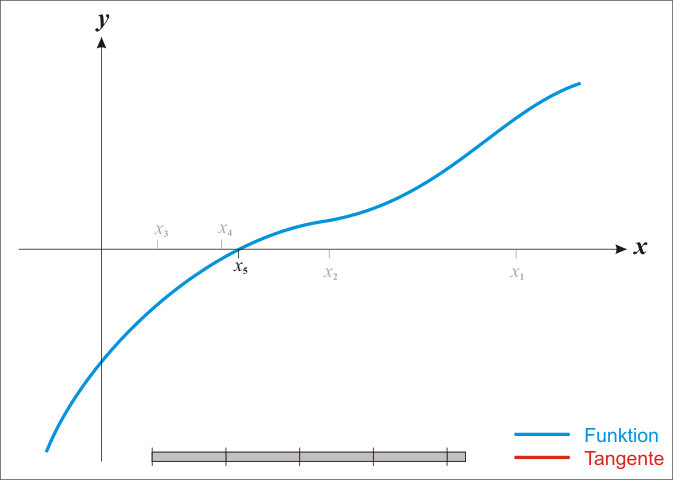Анимация метода Ньютона (Ralf Pfeifer, https://commons.wikimedia.org/wiki/File:NewtonIteration_Ani.gif)

Метод Ньютона является очень мощным методом поиска корней функции, так как имеет квадратичную скорость сходимости — количество значащих цифр примерно удваивается с каждым шагом итерации, однако существуют и ограничения, затрудняющие его применение. Так, например, если начальное приближение недостаточно близко к решению, то метод может не сойтись, если производная не непрерывна в точке корня, то метод может расходиться в любой окрестности корня, если не существует вторая производная в точке корня, то скорость сходимости метода может быть заметно снижена, если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.

Теорема Канторовича дает следующие условия применимости метода для поиска корней функции:

1. функция должна быть ограничена;
2. функция должна быть гладкой, дважды дифференцируемой;
3. её первая производная f'(x) равномерно отделена от нуля;
4. её вторая производная f»(x) должна быть равномерно ограничена.

Решение нелинейных уравнений методом Ньютона онлайн

Для нахождения приближенного значения корней часто применяется метод Ньютона или метод касательных.

Уравнение f (х) = 0 имеет единственное решение на отрезке |аb|, если:

• функция у = f (х) определена и непрерывна при ;
• значения функции на концах отрезка |аb| разнознаковые, т.е. f (а)•f (b)< 0;
• в промежутке |аb| производные f'(x) и f»(x) сохраняют постоянный знак, т.е. функция монотонна и выпукла вверх или вниз;
• производная
  .

Суть метода в том, что на отрезке |аb| берется число х0 при котором f (х0) и производная f ‘(х) имеют один и тот же знак, т.е. f (x0) • f» (x) > 0.

В этой точке касательная к кривой у = f (x) выражена уравнением:

Пусть у = 0, тогда х1 — точка пересечения касательной с осью Ох будет равна:
Таким же образом находим точку х2, х3 и т.д.

Уравнение касательной к функции f (х), проведенной в точке хn, будет иметь вид:
Вычисления заканчиваются, если достигнуто условие: | f (хn) / f’ (xn) | < е,
где е — заданная точность. Это называется сходимостью метода.

Метод Ньютона имеет квадратичную сходимость.

Решение нелинейных уравнений методом Ньютона

Онлайн калькулятор: Метод секущих

Немного теории о методе секущих под калькулятором.

Метод секущих

Критерий останова (тип)Отличие функции от нуля Точность вычисления

Знаков после запятой: 4

save Сохранить extension Виджет

Метод секущих

Метод секущих — модификация метода Ньютона, в котором производная (вычислять ее не всегда удобно) заменена на секущую.
Секущая — прямая, проходящая через две точки на графике функции. В данном методе процесс итераций состоит в том, что в качестве приближений корню уравнения принимаются последовательные значения точек пересечения секущей с осью абсцисс.

Положим, что у нас есть две точки, x0 и x1, в которых значения функции равны соответственно f(x0) и f(x1). Тогда уравнение прямой, проходящей через эти точки, будет

Для точки пересечения с осью абсцисс (у=0) получим уравнение

Это и есть наша итерационная формула. Графическое отображение метода — на рисунке ниже.

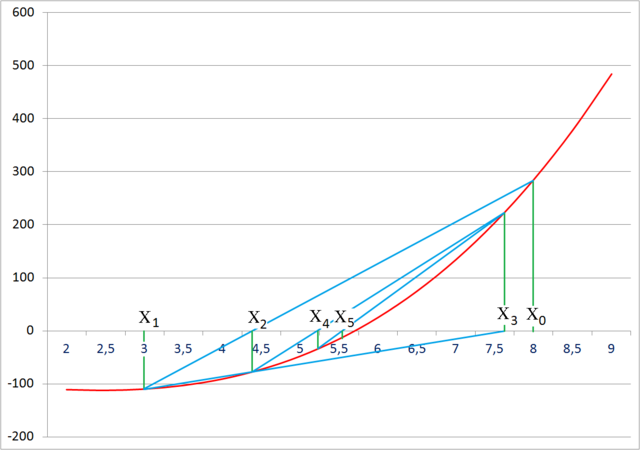
Источник: Метод секущих. Первый случай

Метод работает и в случае, если начальные точки выбраны по одну и ту же сторону от корня (то есть, корня нет на отрезке между начальными приближениями), но при этом возможны случаи, когда метод не сходится.

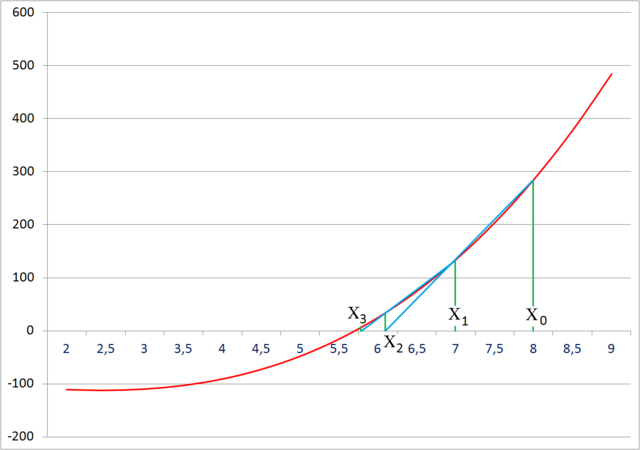
Источник: Метод секущих. Второй случай

Метод секущих является двухшаговым, то есть, новое приближение определяется двумя предыдущими итерациями. Поэтому необходимо задавать два начальных приближения корня.

В качестве критерия останова берут один из следующих:

— значение функции на данной итерации стало меньше заданого ε.

— изменение хk в результате итерации стало меньше заданого ε.

Подробнее: Метод хорд

Решение уравнений методом Ньютона онлайн

Вы ввели следующие уравнение

Решение заданного уравнения имеет следующее значение

Решение произвольных уравнений

Теперь сервис позволяет считать численные вещественные корни уравнений, которые возникают при решении подобных задач

Этот сервис  позволяет ученикам/студентам сосредоточится на понимании задачи, а не умножении, делении, сокращении и упрощении полученной формулы, что конечно же важно, но не настолько что бы в угоду математическим формулам, ученики/студенты теряли смысл решения задачи.

Синтаксис

Jabber:  root <выражение>

WEB:  <выражение>

Выражением может быть любая формула выраженная языком PHP

Система решает уравнения только с одной переменной  и эта переменная обозначается как x (в английской раскладке)

Примеры

Длина детской площадки прямоугольной формы на 5 м больше её ширины. Длину площадки увеличили на 2 м, а ширину — на 5 м, при этом её площадь увеличилась на 280 м2. Найдите площадь новой детской площадки.

Решение выражается уравнением   

Пишем root (x+5)*(x+5+2)-x*(x+5)-280

Получаем ответ 35 — это ширина, а соответственно 40 это длина

---

Решение уравнения x*x-11=0

пишите root x*x-11 и получите 3.3166247903554

Функции PHP

• acos — Арккосинус
• acosh — Гиперболический арккосинус
• asin — Арксинус
• asinh — Гиперболический арксинус
• atan — Арктангенс
• atanh — Гиперболический арктангенс

• cos — Косинус

• cosh — Гиперболический косинус
• exp — Вычисляет число e в степени
• log10 — Десятичный логарифм
• log — Натуральный логарифм
• pi — Возвращает число Пи
• pow — Возведение в степень
• sin — Синус
• sinh — Гиперболический синус
• sqrt — Квадратный корень
• tan — Тангенс
• tanh — Гиперболический тангенс

 

 

• Свойства определителя матрицы (Property determinant) >>

Решить систему нелинейных уравнений онлайн

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Нелинейное уравнение представляет собой алгебраическое и трансцендентное уравнение, содержащее одно неизвестное.

Система нелинейных уравнений имеет следующий вид:

\[\left\{\begin{matrix} f (x,y) = 0\\ g(x,y)=0 \end{matrix}\right.\]

Для решения линейных уравнений используют следующие методы:

* разложение на множители;

* исключение переменных;

* алгебраическое сложение;

* замена переменных;

* системы однородных уравнений;

* метод введения новых переменных;

* графический метод.

Выбор метода напрямую зависит от задания.

Так же читайте нашу статью «Решить систему рациональных уравнений онлайн»

Допустим, нам дано уравнение следующего вида:

\[\left\{\begin{matrix} x + y — 8 =0\\ x^2 + y^2 -82 = 0 \end{matrix}\right.\]

Решение нелинейной системы уравнений стоит начать с выражения у через х в первом уравнении. После необходимо подставить полученное выражение во 2 уравнение:

\[\left\{\begin{matrix} y =8-x\\ x^2-y^2-82 =0 \end{matrix}\right.\]

\[\left\{\begin{matrix} y=8-x\\ x^2+(8-x)^2-82=0 \end{matrix}\right.\]

\[\left\{\begin{matrix} y = 8 -x\\ x^2 -8x — 9=0 \end{matrix}\right.\]

Далее необходимо решить следующее уравнение из системы:

\[x_2 — 8x — 9 = 0 \]

Для этого необходимо найти его корни:

\[x_1 = — 1 , x_2 = 9\]

Основываясь на этих данных, получаем:

\[y+1 = 8 — x_1 = 9 , y_2 = 8 — x_2 = — 1\]

В конечном результате решение системы выглядит следующим образом:

\[\left\{\begin{matrix} x_1 = -1\\ y_1 = 9 \end{matrix}\right.\]

\[\left\{\begin{matrix} x_2 =9\\ y_2 = — 1 \end{matrix}\right.\]

Запишем ответ в таком формате: \[(- 1; 9) , (9; — 1)\]

Где можно решить систему нелинейных уравнений онлайн?

Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто вdести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Онлайн-калькулятор — метод секущих

Калькулятор ниже с помощью метода секущих находит корень уравнения.

Методом секущих называется численный итерационный метод, который максимально приближённо находит корень уравнения.

Метод секущих — это модификация того самого метода Ньютона, в котором производная изменена на секущую.

Подробно о методе секущих можно прочитать здесь:

The field is not filled.

‘%1’ is not a valid e-mail address.

Please fill in this field.

The field must contain at least% 1 characters.

The value must not be longer than% 1 characters.

Field value does not coincide with the field ‘%1’

An invalid character. Valid characters:’%1′.

Expected number.

It is expected a positive number.

Expected integer.

It is expected a positive integer.

The value should be in the range of [%1 .. %2]

The ‘% 1’ is already present in the set of valid characters.

The field must be less than 1%.

The first character must be a letter of the Latin alphabet.

Su

Mo

Tu

We

Th

Fr

Sa

January

February

March

April

May

June

July

August

September

October

November

December

century

B.C.

%1 century

An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3

Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).

%3.%2.%1%4

%3.%2.%1%4 %6:%7

s.sh.

u.sh.

v.d.

z.d.

yes

no

Wrong file format. Only the following formats: %1

Please leave your phone number and / or email.

калькулятор онлайн метод ньютона

Вы искали калькулятор онлайн метод ньютона? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и метод ньютона онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «калькулятор онлайн метод ньютона».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как калькулятор онлайн метод ньютона,метод ньютона онлайн,онлайн полином ньютона,онлайн решение нелинейных уравнений,полином ньютона онлайн,решение нелинейных уравнений онлайн. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и калькулятор онлайн метод ньютона. Просто введите задачу в окошко и нажмите «решить» здесь (например, онлайн полином ньютона).

Где можно решить любую задачу по математике, а так же калькулятор онлайн метод ньютона Онлайн?

Решить задачу калькулятор онлайн метод ньютона вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.