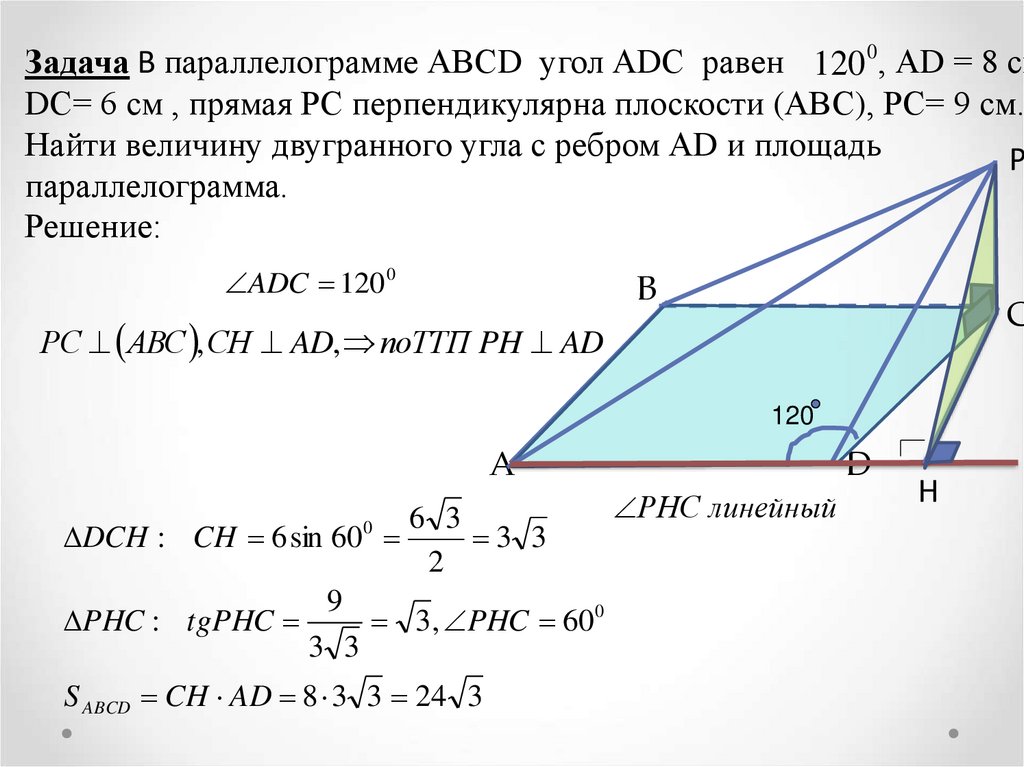
Угол между прямой и плоскостью — что это такое? Как найти?
Правильный ответ такой: все эти случаи можно озаглавить геометрическим понятием «пересечение плоскости прямой под некоторым углом». Об этом мы сегодня и поговорим, а именно:
рассмотрим главные определения и примеры;
изучим свойства и теоремы по теме;
научимся находить угол между прямой и плоскостью.
Определение угла между прямой и плоскостью
Угол между прямой и плоскостью — это угол между прямой и её проекцией на эту плоскость.
Мы уже знакомы с понятиями «угол», «прямая» и «плоскость» (если подзабыли, то можете повторить по нашим материалам). А сейчас давайте вспомним, что такое проекция.
Проекция — это геометрическое изображение на плоскости, полученное проведением перпендикуляров из всех точек данного тела на плоскость.
То есть под углом между прямой и плоскостью в пространстве мы подразумеваем угол между прямой и её отображением на плоскость.
Важное уточнение
Если прямая перпендикулярна плоскости, то можно считать, что угол между ними равен 90°, что следует из определения перпендикулярности прямой и плоскости. Этот случай — самый простой, его мы рассматривать не будем.
Также стоит заметить, что если прямая параллельна плоскости, то у них нет ни одной общей прямой, а значит, угол между ними не определяется.
Как вы думаете, какой тип имеет угол между прямой и плоскостью? Верно, он может быть только острым. Попробуйте доказать это самостоятельно 😊
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Свойства и теоремы
Свойство угла между прямой и плоскостью
Углом между прямой и плоскостью называется наименьший из углов между прямой и произвольной прямой в плоскости.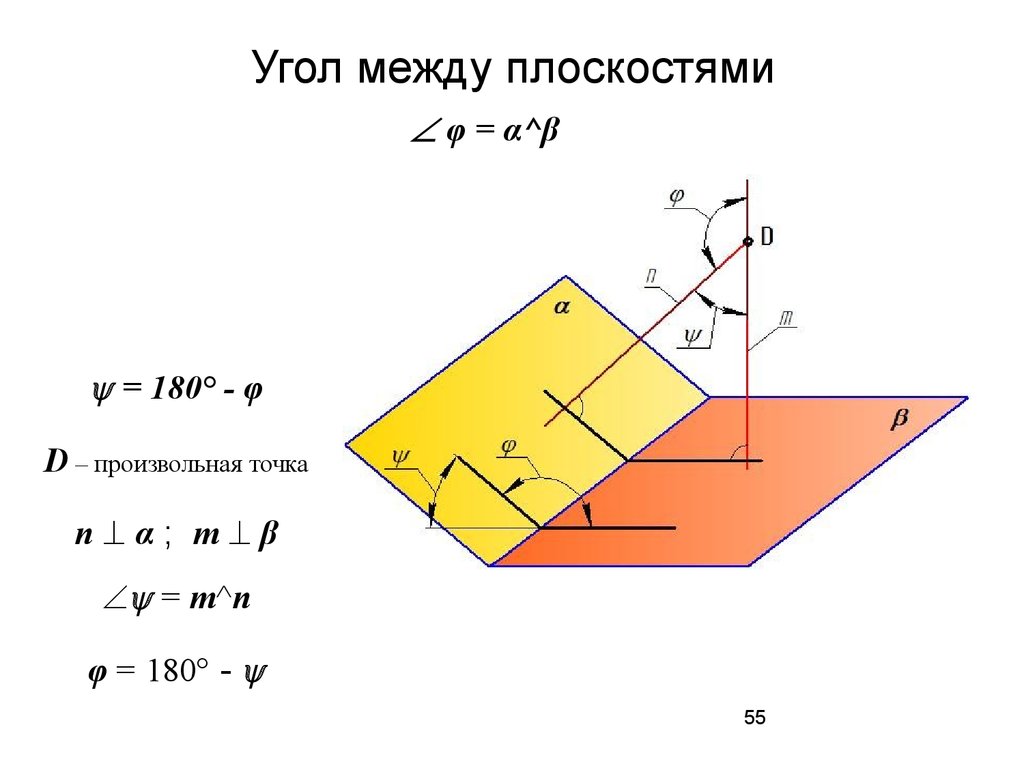
Попробуем привести доказательство. Для этого нарисуем плоскость и проведём к ней прямую АВ, являющуюся наклонной. Тогда АВ1 — проекция прямой на плоскость, АН — произвольная прямая, принадлежащая плоскости, а ВН и ВВ1 — перпендикуляры к плоскости (ВН ⟂ АН, ВВ1 ⟂ АВ). Чтобы лучше представить себе этот объёмный чертеж, можно сделать небольшой макет из сложенного листа бумаги, прислонив его к поверхности стола или тетради.
Чтобы проверить истинность свойства, нам необходимо доказать, что угол ∠ВАВ1 намного меньше, чем угол ∠ВАН.
Обозначим проблему: значения этих углов, как и других исходных, нам неизвестны.
А значит, на помощь может прийти тригонометрия, ведь сравнить углы можно и через их синусы.
Синус — это отношение противолежащего угла к гипотенузе. В таком случае, .
Оба перпендикуляра ВВ1 и ВН проведены из точки В, но только один из них является кратчайшим расстоянием от точки по плоскости, и это перпендикуляр ВВ1. Так как значения синусов представляют собой дроби с одинаковыми знаменателями, большей будет та, у которой больше знаменатель.
Следовательно, sin ∠BAB1 < sin ∠BAH, ∠BAB1 < ∠BAH.
Теорема
Из двух наклонных, проведённых из одной точки к плоскости, меньшая образует с плоскостью больший угол, и наоборот: угол, образованный большей наклонной, будет меньшим из двух.
Существует множество разных доказательств этой теоремы, но мы сосредоточимся на одном из них.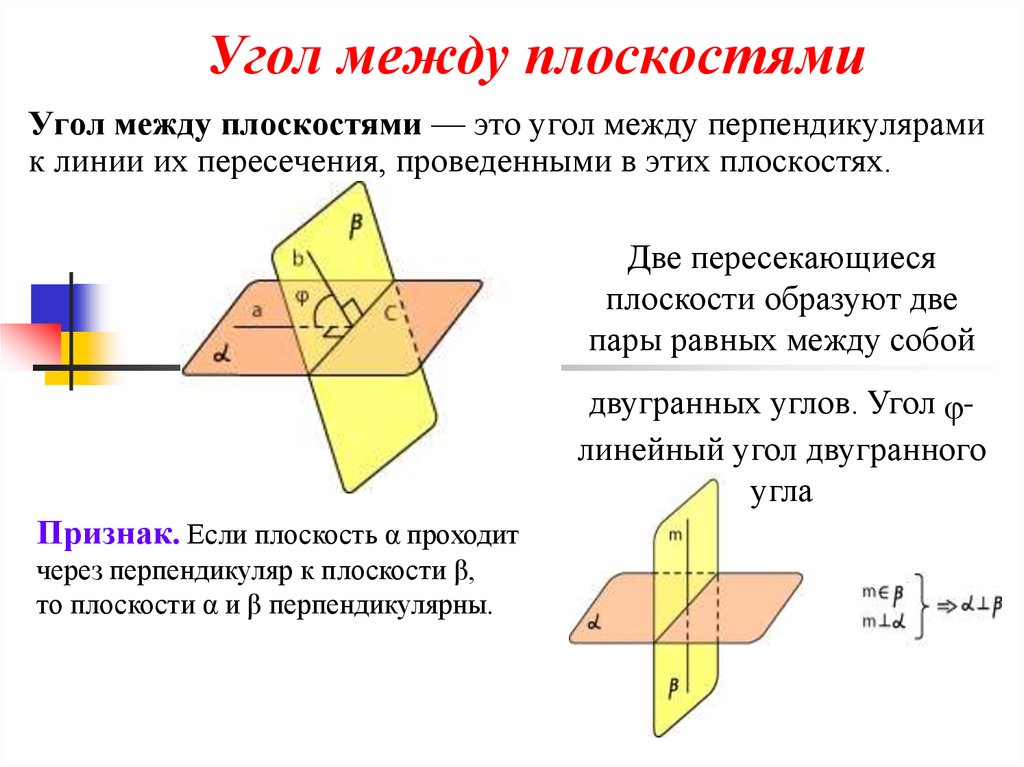
Для этого изобразим плоскость и точку . Из точки А проведём две наклонные прямые, причем АВ < АС, а также перпендикуляр к плоскости АО. Докажем, что ∠АВО > ∠АСО.
Стороны
Отложим на стороне ОС отрезок ОЕ, равный ОВ. Можно ли доказать равенство треугольников АОВ и АОЕ?
В данных треугольниках:
Следовательно, треугольники АОВ и АОЕ равны по двум катетам (или по первому признаку: две стороны и угол между ними).
В таком случае равны и соответственные углы: ∠АВО = ∠АЕО
Угол АЕО является внешним для треугольника АЕС, и по свойству внешнего угла ∠АЕО = ∠АСЕ + ∠САЕ. Не трудно догадаться: раз угол АЕО равен сумме двух других углов треугольника, не смежных с ним, то он больше любого из этих двух углов.
∠АЕО > ∠АСЕ, и так как ∠АЕО = ∠АВО, то ∠АВО > ∠АСЕ.
Что и требовалось доказать. 😎
Как найти угол между прямой и плоскостью
От теории переходим к практике: а как же можно вычислить угол между прямой и плоскостью? Вопрос лёгкий и сложный одновременно. Дело в том, что задач на нахождение угла очень много, и в каждой из них применяется свой алгоритм решения. Большую роль играет предмет и раздел, в котором эта задача приведена: это может быть стереометрия, векторная алгебра и даже физика.
Геометрический метод
Чтобы применить геометрический метод, необходимо опустить перпендикуляр на плоскость из точки, принадлежащей исходной прямой. Выясним, чем в этом задании является перпендикуляр, наклонная и проекция, и решим планиметрическую задачку (чаще всего в таких задачах нам будет необходимо найти один из углов прямоугольного треугольника).
Задача 1
Из точки А на плоскость проведены две наклонные АВ и АС и перпендикуляр АО, причём О, В и С — точки пересечения с плоскостью .
Определите, чему равен АО, если СО = 10, ВО = 26, а угол АСО в два раза больше угла АВО.
Решение:
Отметим на стороне ОВ отрезок, равный ОС. Тогда ОС = ОЕ = 10, а ЕВ = 26 – 10 = 16.
Рассмотрим треугольники АСО и АЕО:
Следовательно, треугольники равны по двум катетам. А значит, угол АСО равен углу АЕО.
Угол АЕО
Тогда найдём АО через прямоугольный треугольник АОЕ по теореме Пифагора:
.
Ответ: .
Алгебраический метод
Алгебраический метод или метод координат для нахождения угла между прямой и плоскостью основывается на особой формуле. Чтобы использовать его, необходимо определить координаты двух точек, принадлежащих прямой, описать уравнение плоскости и применить формулу. По сути в этом методе мы находим угол между вектором и плоскостью.
,
где (x1, y1, z1) — это координаты первой точки,(x2, y2, z2) — координаты второй точки,
А, В и С — это координаты в уравнении плоскости Ax + By + Cz + D = 0.
Иначе эти числа называют координатами вектора нормали плоскости.
Тут может возникнуть вопрос: а что, если в задаче даны не координаты точек, а координаты вектора?
В этом случае вспомним, что координаты вектора находятся через разность координат начала и конца.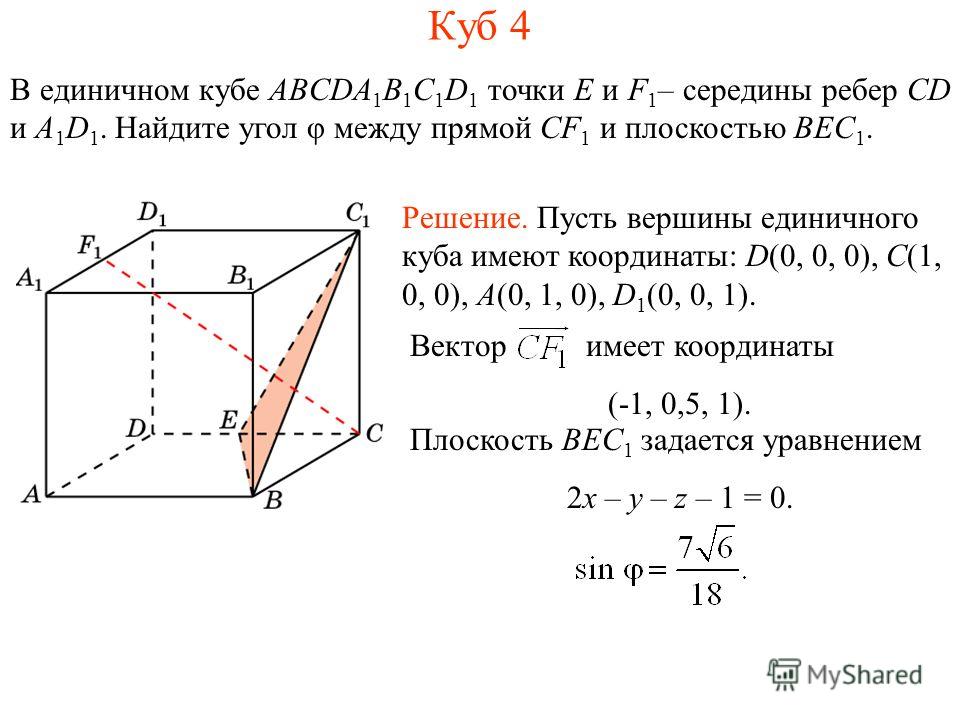
А значит, мы со спокойно душой подставляем эти координаты в формулу вместо (х2 – х1), (y2 – y1) и (z2 – z1).
В некоторых задачах для нахождения угла между прямой и плоскостью вводят понятие направляющего вектора прямой.
Координаты этого вектора можно получить из канонического уравнения прямой:
, где направляющий вектор а имеет координаты (ax, ay).
Тогда угол между прямой и плоскостью можно вычислить по формуле:
.
Задача 2
Найдите угол между прямой и плоскостью 3x – y – z + 1 = 0.
Решение:
Определим координаты направляющего вектора для прямой: (2; –1; 3).
Определим координаты вектора нормали плоскости: (3; –1; –1).
Подставим координаты в формулу для расчёта синуса угла между плоскостью и прямой:
.
Задача 3
Найдите угол между плоскостью, заданной уравнением x + 2y + 2z – 4 = 0, и прямой, которой принадлежат точки А (0, 2, –1) и В (–2, 4, –1).
Решение:
Определим координаты вектора нормали плоскости: (1; 2; 2).
Подставим координаты вектора нормали и координаты точек прямой в формулу:
.
За короткий промежуток времени мы изучили понятие угла между прямой и плоскостью, доказали теоремы, разобрали способы нахождения угла и решили практические задания. Мы — молодцы! 💪
Думаем, вы понимаете, что эта тема очень важна — с её помощью решаются сложные стереометрические задачи, которые встречаются на ОГЭ и ЕГЭ.
Подготовиться к таким серьёзным заданиям помогут курсы профильной математики в онлайн-школе Skysmart. На уроках мы сможем более подробно разобрать задачи с пирамидами и параллелепипедами, а ещё научимся составлять уравнения для любой плоскости. Узнать свои сильные и слабые стороны, составить план обучения и познакомиться с онлайн-платформой можно на вводном уроке — это бесплатно.
2 угол между плоскостями
Вы искали 2 угол между плоскостями? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и двугранный угол между плоскостями как найти, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «2 угол между плоскостями».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни.
Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 2 угол между плоскостями,двугранный угол между плоскостями как найти,как найти двугранный угол между плоскостями,как найти угол между двумя плоскостями,как найти угол между плоскостями,как найти угол между плоскостями методом координат,калькулятор онлайн найти угол между плоскостями,координатный метод угол между плоскостями,косинус угла между плоскостями,метод координат угол между плоскостями,найти косинус острого угла между плоскостями,найти косинус угла между плоскостями,найти угол между плоскостями,найти угол между плоскостями калькулятор онлайн,найти угол между плоскостями онлайн калькулятор,онлайн калькулятор найти угол между плоскостями,онлайн угол между плоскостями,определение угол между плоскостями,определить двугранные углы образованные пересечением двух плоскостей,определить двугранные углы образованные пересечением пар плоскостей,угол между двумя плоскостями,угол между двумя плоскостями как найти,угол между двумя плоскостями координатный метод,угол между плоскостями,угол между плоскостями как найти,угол между плоскостями координатный метод,угол между плоскостями онлайн,угол между плоскостями определение,угол между плоскостями формула,угол между плоскостями это.
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 2 угол между плоскостями. Просто введите задачу в окошко и нажмите
«решить» здесь (например, как найти двугранный угол между плоскостями).
Решить задачу 2 угол между плоскостями вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Угол между падающим лучом и плоскостями рассеяния в рентгеновской дифракции Калькулятор
✖Порядок отражения, говорят, что волны, отраженные под углом, соответствующим n=1, относятся к первому порядку отражения; угол, соответствующий n = 2, является вторым порядком, и так далее. | AngstromCentimeterDecameterDecimeterElectron Compton WavelengthHectometerMeterMicrometerMillimeterNanometerNeutron Compton WavelengthProton Compton Wavelength | +10% -10% | |
✖Interplanar Spacing is the distance between adjacent and parallel planes of the crystal .ⓘ Межплоскостное расстояние [d] | Ангстрем Сантиметр Декаметр Дециметр Длина волны электрона Комптона Гектометр Метр Микрометр Миллиметр Нанометр Длина волны комптона нейтрона Длина волны протона Комптона | +10% -10% |
Рентгеновское излучение можно определить как расстояние между двумя последовательными гребнями или впадинами рентгеновского излучения.ⓘ Длина волны рентгеновского излучения [λ X-ray ] ✖Угол ч/б падающего и отраженного рентгеновского излучения — это угол между волновым вектором падающей плоской волны. | КругЦиклГрадусГрадМилмиллирадианМинутаМинуты дугиТочкаКвадрантЧетвертькругРадианОборотПрямой УголСекундаПолукругСекстантаЗнакПоворот | ⎘ Копировать |
ⓘ Угол между падающим лучом и плоскостью рассеяния в рентгеновской дифракции [θ]👎
Формула
Сброс настроек
👍
Угол между падающим лучом и плоскостями рассеяния в рентгеновской дифракции Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовые единицы
Порядок отражения: 2 —> Преобразование не требуется
Длина волны рентгеновского излучения: 0,45 нм —> 4,5E- 10 метров (проверьте преобразование здесь)
Межплоскостное расстояние: 0,7 нанометра —> 7E-10 метров (проверьте преобразование здесь)
ШАГ 2: Вычисление формулы
ШАГ 3: Преобразование результата в единицу измерения
0,69822247336256 Радиан —> 40,0052008848678 Градус (проверьте преобразование здесь)
< 10+ атомных калькуляторовУгол между падающим лучом и плоскостями рассеяния в рентгеновской дифракции Формула
Угол ч/б падающего и отраженного рентгеновского излучения = asin((Порядок отражения*длина волны рентгеновского излучения)/(2*межплоскостное расстояние))
θ = asin((n порядок *λ рентген )/(2*d))
В чем заключается закон Брэгга для рентгеновской дифракции?
Закон Брэгга был введен сэром У.
Х. Брэгг и его сын сэр В.Л. Брэгг. Закон гласит, что когда рентгеновские лучи падают на поверхность кристалла, их угол падения θ будет отражаться обратно с тем же углом рассеяния.
Как рассчитать угол между падающим лучом и плоскостями рассеяния в рентгеновской дифракции?
Угол между падающим лучом и плоскостями рассеяния в калькуляторе рентгеновской дифракции использует Угол ч/б падающего и отраженного рентгеновского излучения = asin((Порядок отражения*длина волны рентгеновского излучения)/(2*межплоскостное расстояние)) для расчета Угол ч/б падающего и отраженного рентгеновских лучей, Угол между падающим лучом и плоскостями рассеяния в формуле рентгеновской дифракции определяется как угол между падающим рентгеновским излучением и отраженным рентгеновским излучением. Угол черно-белого падающего и отраженного рентгеновского излучения обозначается цифрой 9.0120 θ символ.
Как рассчитать угол между падающим лучом и плоскостями рассеяния при дифракции рентгеновских лучей с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для угла между падающим лучом и плоскостями рассеяния в рентгеновской дифракции, введите Порядок отражения (n порядок ) , Длина волны рентгеновского излучения (λ Рентгеновское излучение ) и Межплоскостное расстояние (d) и нажмите кнопку расчета.
Вот как можно объяснить угол между падающим лучом и плоскостями рассеяния при расчете дифракции рентгеновских лучей с заданными входными значениями -> 40.0052 = asin((2*4.5E-10)/(2*7E-10)) .
часто задаваемые вопросы
Что такое угол между падающим лучом и плоскостями рассеяния в рентгеновской дифракции?
Угол между падающим лучом и плоскостями рассеяния в формуле дифракции рентгеновских лучей определяется как угол между падающим и отраженным рентгеновскими лучами и представляется как θ = asin((n порядок *λ Рентгеновский снимок )/(2*d)) или Угол ч/б падающего и отраженного рентгеновского излучения = asin((Порядок отражения*длина волны рентгеновского излучения)/(2*межплоскостное расстояние)) . Порядок отражения, волны, отраженные под углом, соответствующим n=1, относятся к первому порядку отражения; угол, соответствующий n = 2, является вторым порядком и т. д. Длина волны рентгеновского излучения может быть определена как расстояние между двумя последовательными гребнями или впадинами рентгеновского излучения, а межплоскостное расстояние — это расстояние между соседними и параллельными плоскостями рентгеновского излучения.
кристалл.
Как рассчитать угол между падающим лучом и плоскостями рассеяния в рентгеновской дифракции?
Угол между падающим лучом и плоскостями рассеяния в формуле дифракции рентгеновских лучей определяется как угол между падающим и отраженным рентгеновскими лучами, который рассчитывается с использованием Угол ч/б падающего и отраженного рентгеновских лучей = asin(( Порядок отражения*длина волны рентгеновского излучения)/(2*межплоскостное расстояние)) . Чтобы рассчитать угол между падающим лучом и плоскостями рассеяния в рентгеновской дифракции, вам нужен порядок отражения (n порядок ) , длина волны рентгеновского излучения (λ рентгеновского ) и межплоскостное расстояние (d) . С помощью нашего инструмента вам необходимо ввести соответствующие значения для порядка отражения, длины волны рентгеновского излучения и межплоскостного расстояния и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Доля
Скопировано!
Угол между двумя плоскостями
В геометрии важно знать о различных видах поверхностей. Линия — это одномерная поверхность, а пространство — трехмерная поверхность. Однако плоскость — это двумерная поверхность с нулевой толщиной. Плоскость образована некоторым набором линий, отстоящих друг от друга. Плоскости играют важную роль в трехмерной геометрии. В трехмерном пространстве и в координатной геометрии может существовать бесконечное количество плоскостей. Самолеты имеют определенные особые свойства, в том числе:
Любые две различные плоскости либо параллельны, либо пересекаются по прямой.
Прямая может либо лежать в плоскости, либо пересекать плоскость в одной точке, либо быть параллельной плоскости.
Две прямые параллельны друг другу, если они перпендикулярны одной плоскости.
Две плоскости также параллельны друг другу, если они перпендикулярны одной прямой.
Угол между двумя плоскостями Formula
Угол между двумя плоскостями определяется как угол между нормалью к двум плоскостям. Две плоскости называются перпендикулярными, если их стандартные векторы прямоугольны. Угол разделения двух пересекающихся плоскостей вычисляется как угол разделения нормалей к обеим плоскостям. Угол, который существует между двумя векторами, можно определить с помощью векторного умножения.
Рассмотрим две плоскости, пересекающиеся под углом θ, как показано на рисунке выше. Пусть п 1 и n 2 — векторы нормалей, проведенные к плоскостям. Таким образом, уравнение для обеих плоскостей задается как
\[\bar{r}\].\[\bar{n_{1}}\] = \[d_{1}\]
\[\bar{ r}\].\[\bar{n_{2}}\] = \[d_{2}\]
Косинус угла между двумя пересекающимися плоскостями задается как косинус угла между их нормалями:
{2}}}\] 9{2}}}\].