Раскрытие скобок многочленов. Калькулятор онлайн.Упрощение многочлена.Умножение многочленов
С многочленами, как и с любыми другими алгебраическими выражениями, можно производить различные действия. Разберемся, как складывать и вычитать многочлены.
Пусть даны два многочлена. Чтобы их сложить, их записывают в скобках и ставят знак «плюс» между ними. Потом раскрываем скобки и приводим подобные слагаемые. При вычитании мы ставим между скобками знак «минус».
Раскрываем скобками и приводим подобные слагаемые. Если перед скобкой стоит знак «плюс» то, раскрывая скобки, мы сохраняем знак каждого из одночлена входящего в многочлен, заключенный в скобки. Если перед скобками стоит знак «минус», то, раскрывая скобки, следует заменить знаки у каждого из одночленов входящих в многочлен, заключенный в скобки.
Чтобы привести подобные слагаемые, нужно сложить коэффициенты у подобных одночленов, а потом, полученное число умножить на буквенное выражение.
Примеры
Рассмотрим пример. 3 \)
3 \)
Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.
Этот результат обычно формулируют в виде правила.
Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.
Мы уже неоднократно использовали это правило для умножения на сумму.
Произведение многочленов. Преобразование (упрощение) произведения двух многочленов
Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.
Обычно пользуются следующим правилом.
Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные произведения.
Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов
С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Пожалуй, наиболее часто
встречаются выражения \((a + b)^2, \; (a — b)^2 \) и \(a^2 — b^2 \), т.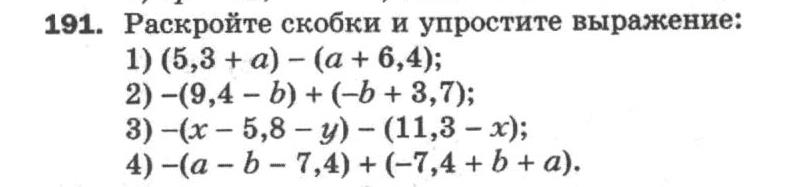 2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.
2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.
Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно — правые части левыми. Самое трудное при этом — увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько примеров использования формул сокращенного умножения.
Урок на тему:
«Сложение и вычитание многочленов. Правила и примеры»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Развивающие и обучающие пособия в интернет-магазине «Интеграл»
Электронное учебное пособие по учебнику Ю.Н. Макарычева
Электронное учебное пособие к учебнику А.Г. Мордковича
Сложение многочленов
Ранее мы познакомились с понятием многочлена. Теперь научимся с многочленами работать. Это умение пригодится при решении сложных уравнений и других математических задач.
Вспомним определение: многочлен — это сумма одночленов!
Значит, чтобы сложить многочлены надо записать их как один многочлен, сохраняя знаки исходные членов.
Но, пока не наработан навык, будем складывать по определенному правилу:
1. Записываем многочлены в скобках и ставим между ними знаки «+».
2. Переписываем без скобок. Если в скобках у первого члена многочлена стоит знак минус, мы его пишем вместо плюса, который стоял перед скобкой. Остальные члены многочлена переписываем, сохраняя знаки.
3. Приводим получившийся многочлен к стандартному виду.
Примеры.
1) Сложить многочлены: a 3 + 2b + с и а 2 + 2b — 1.
Решение.
(а 3 + 2b + с) + (а 2 + 2b — 1).
2. Раскроим скобки: a 3 + 2b + с + а 2 + 2b — 1.
a 3 + 2b + с + а 2 + 2b — 1 = а 3 + 4b + с + а 2 — 1.
2) Сложить многочлены: a 3 + 2b + с и -а 2 + 2b — 1.
Решение.
1. Запишем многочлены в скобках и поставим между скобками знак плюс:
(а 3 + 2b + с) + (-а 2 + 2b — 1).
2. Раскроим скобки: a 3 + 2b + с — а 2 + 2b — 1.
3. Сложим все, что складывается (привести подобные):
a 3 + 2b + с — а 2 + 2b — 1 = а 3 + 4b + с — а 2 — 1.
4. И запишем в красивом (стандартном) виде: a 3 — а 2 + 4b + с — 1.
Вычитание многочленов
Как при сложении, сначала записываем многочлены в скобках, но между скобками ставим знак «-«. Просто убрать скобки, не получится. Нужно поменять знаки членов многочлена на противоположные. Это очень важно помнить, поскольку поможет избежать многих ошибок.
Попробуем решить пример 2 — (1 + 1). Сначала выполняем действия в скобках, потом — вычитание, получим ответ 0. Если просто убрать скобки, ответ будет 2. Если поменять знаки, ответ будет правильный 0.
Примеры.
1) Из многочлена а 3 b + 2ac — 5 вычесть многочлен 2a 3 b + ас + 5.
Решение.
(а 3 b + 2ac — 5) — (2a 3 b + ac + 5).
2. Раскроим скобки: а 3 b + 2ac — 5 — 2а 3 b — ac — 5.
3. Сложим все, что складывается (привести подобные):
а 3 b + 2ac — 5 — 2а 3 b — ac — 5 = -а 3 b + ac — 10.
4. И запишем в красивом (стандартном) виде: -а 3 b + ac — 10.
2) Из многочлена a 3 b + 2ac — 5 вычесть многочлен -2a 3 b + ас + 5.
Решение.
1. Запишем многочлены в скобках и поставим между скобками знак минус:
(а 3 b + 2ac — 5) — (-2a 3 b + ac + 5).
2. Раскроим скобки: а 3 b + 2ac — 5 + 2а 3 b — ac — 5.
Обратите внимание, первый минус в вычитаемом поменялся на плюс! (Всегда внимательно смотрим: где ставить плюс, где — минус? Знак перед скобкой накладывается на знак в скобке: плюс на плюс дает плюс, плюс на минус дает минус, минус на минус дает плюс.)
а 3 b + 2ac — 5 + 2a 3 b — ac — 5 = 3a 3 b + ac — 10.
4. И запишем в красивом (стандартном) виде: 3a 3 b + ac — 10.
Методы сложения и вычитания многочленов очень похожи, только при вычитании меняются знаки. Поэтому эти действия объединили в одно правило.
Чтобы найти алгебраическую сумму многочленов надо записать их в скобках и расставить знаки. Потом раскрыть скобки следующим образом: если перед скобкой стоит знак плюс, то знаки членов многочлена не меняются, если перед скобкой стоит знак минус, то знаки членов многочлена меняются на противоположные.
Потом раскрыть скобки следующим образом: если перед скобкой стоит знак плюс, то знаки членов многочлена не меняются, если перед скобкой стоит знак минус, то знаки членов многочлена меняются на противоположные.
Пример.
Найдите алгебраическую сумму многочленов: А + В – С, где:
А = а 2 b + аb + 4;
В = -5a 2 b + 6ab — 5;
С = -4a 2 b + 3ab + 8.
Решение.
1. Запишем многочлены в скобках: (а 2 b + аb + 4) + (-5a 2 b + 6ab — 5) — (-4a 2 b + 3ab + 8).
2. Раскроим скобки: а 2 b + аb + 4 — 5a 2 b + 6ab — 5 + 4a 2 b — 3ab — 8.
3. Приведем подобные:
а 2 b + аb + 4 — 5a 2 b + 6ab — 5 + 4a 2 b — 3ab — 8 = 4ab – 9.
4. И запишем в стандартном виде: 4ab – 9.
Обратите внимание, что исчезли некоторые члены многочленов.
Действительно а 2 b — 5a 2 b + 4a 2 b = 0.
В таких случаях принято говорить, что a 2 b, 5a 2 b, 4a 2 b взаимно уничтожились.
Примеры для самостоятельного решения
Найти алгебраическую сумму многочленов А – В + С, где:
1) А = х 2 у + 2ху 2 — 3;
В = — 5х 2 у + 3ху + 6;
С = 2х 2 у — 3ху + 6.
2) А = – 4х 2 у + ху – 8;
В = 6х 2 у + 8ху + у;
С = – 3ху + х.
3) А = ху 2 – 7ху – х;
В = 9ху 2 + ху + 6;
С = 5ху 2 + 8ху + х.
исследовательская работа по математике на тему «Нужен ли калькулятор в школе?»
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа села Олекан
Забайкальского края Нерчинского района
Нужен ли калькулятор в школе?
Выполнила: Ван-ку-чин Наталья
ученица 9 класса
Руководитель: Кадашникова
Татьяна Владимировна
Олекан,
2015
Оглавление
Введение……………………………………………………………………3
1. Эволюция калькуляторов………………………………………………4
Эволюция калькуляторов………………………………………………4
2.Виды калькуляторов ……………………………………………………8
3.Микроисследование…………………………………………………….10
Заключение…………………………………………………………………12
Литература …………………………………………………………………13
Введение.
С момента появления калькуляторов жизнь школьников сильно облегчилась. Но так ли уж полезны калькуляторы в школе? Ведь пока их не было, все вычисления изначально проводились на бумаге, а со временем и в уме. А что творится сейчас? Большинство школьников не может умножить 11 на 12 без калькулятора или сложить 253 и 748.Современные дети не могут посчитать правильно ли дали сдачу в магазине.
Кто-то скажет: ну и ладно, а зачем забивать
себе мозги цифрами, если всю эту работу можно скинуть на технику.
Мы решили выбрать эту тему потому, что увидели неоднозначное отношение ребят и учителей нашей школы к применению калькулятора на уроках в школе.
Гипотеза:
Многие говорят: «Без калькулятора – как без рук». Калькулятор незаменимый помощник. Но так ли уж он полезен в школе?
Цель:
Ø Узнать отношение школьников и взрослых к калькулятору,
Ø Выяснить плюсы и минусы калькулятора в школе.
Исходя из этой цели, мною были поставлены следующие задачи:
Ø Выяснить отношение окружающих к калькулятору;
Ø Проанализировать все результаты и сделать выводы.
Предмет исследования:
Ø
Отношение окружающих к
использованию калькулятора на уроках в школе.
Методы исследования:
Ø Изучение теоретического материала.
Ø Практическое выполнение исследования.
Ø Коммуникативный (метод анкетирование).
1.Эволюция калькуляторов
Современным миром
правят цифры. Все, создается с помощью многозначных расчетов. Педагоги до сих пор
стараются научить детей быстрому счету в уме и в «столбик», пугая их тем, что
жители благополучных западных стран якобы уже не способны сосчитать сдачу в
супермаркете. Математика — гимнастика ума, но жизнь часто подсовывает нам
расчеты, для решения которых вручную не хватит и двух жизней. Лень — двигатель
прогресса, поэтому сразу после того, как древним людям перестало хватать
пальцев на руках для подсчета отвоеванных у природы благ, они изобрели
устройства, облегчающие вычислительные муки мозга. Мы знаем о таких
приспособлениях кое-что интересное, и сейчас расскажем это вам.
Строго говоря, калькуляторы были изобретены сразу после того, как человек научился считать. Древнейший артефакт такого рода — «кость Ишанго», найденная в Конго (возраст — около двадцати тысяч лет). Это берцовая кость бабуина, покрытая засечками. Предполагается, что первые математические вычисления в истории человечества делали женщины, рассчитывавшие менструальный цикл по лунному календарю.
Простейший счет велся
на пальцах, а когда их не хватало, использовались любые природные объекты,
заменявшие цифру 10. Примерно пять тысяч лет назад в Вавилоне появилась счетная
доска, известная ныне как абак (абакус). По полю с углублениями передвигались
камушки (десятки). Вероятно, это был инструмент купцов. Изобретение оказалось
очень живучим и продержалось до средневековья. Интересно, что вавилоняне
использовали не десятеричную, а шестидесятеричную (она же двенадцатеричная — по
числу фаланг на пальцах руки, не считая большого) систему исчисления. Отсюда
пошло привычное для нас деление времени на отрезки по 60 секунд и минут, а
также 360 градусов, на которые поделена окружность.
Антикитерский механизм — самое передовое ручное механическое устройство древнего мира (создан в сотом году до нашей эры, на фото оригинал и его реконструкция). Сложность изготовления сопоставима с механизмами шестнадцатого века. Использовался в основном для расчета движения небесных тел, однако в 2008 году было доказано, что антикитерский механизм может выполнять четыре арифметические операции (сложение, вычитание, умножение и деление).
Плавающая точка,
дифференциальные уравнения, число «пи» — все это было известно несколько тысяч
лет назад. Но великие математики древности рассчитывали свои открытия в уме.
Калькуляторы были инструментами инженеров, торговцев и сборщиков налогов. Для
их нужд в Риме был создан первый в мире ручной абак — табличка с подвижными
фишками.
Следующий шаг сделали китайцы, создавшие в шестом-двенадцатом веках нашей эры суаньпань, известный сегодня как счеты. Большая секция костяшек называлась «земля», а малая наверху — «небо». Техника работы с суаньпаном позволяла быстро производить все четыре арифметические операции, а также извлекать корни. Эти счеты использовались в Азии еще десять лет назад, однако сейчас их вытеснили калькуляторы.
Юпана, калькулятор майя. Ученые долго не могли понять предназначение этой маленькой «модели крепости» до тех пор, пока итальянский инженер Николино де Паскуале не установил, что так называемые «дикари» создали матрицу этого калькулятора с использованием последовательности Фибоначчи и системы исчисления с основанием 40 (а не 10, как в Старом Свете).
На Руси счеты
появились в шестнадцатом веке и использовались до конца двадцатого (собственно,
как и во всем мире). Линия с 4 костяшками некогда использовалась для расчетов в
полушках — четвертях копейки. В новое время она отделяет поле целых чисел от
дробных и в расчетах не применяется. Счеты не потеряли ценности до сих пор —
они очень удобны для слепых.
Линия с 4 костяшками некогда использовалась для расчетов в
полушках — четвертях копейки. В новое время она отделяет поле целых чисел от
дробных и в расчетах не применяется. Счеты не потеряли ценности до сих пор —
они очень удобны для слепых.
Логарифмическая линейка — главный инструмент инженера до восьмидесятых годов прошлого века — была изобретена в 1622 году. Ее действие основано на том, что умножение и деление чисел можно выполнить сложением и вычитанием их логарифмов. С помощью такой линейки можно выполнить очень сложные вычисления с точностью до 3-4 десятичных знаков. Первый полет человека в космос рассчитывался именно на таких линейках. В наше время логарифмическими линейками иногда оснащаются дорогие модели механических часов (на фото — Breitling Navitimer).
«Паскалина» Блеза
Паскаля хорошо известна. Она была построена в 1642 году. Однако это гениальное
устройство десятеричного исчисления не получило признания, поскольку во Франции
ходили ливры, равные 20 су, а су равнялся 12 денье.
Не менее известна и «разностная машина» Чарльза Бэббиджа, фигурировавшая в одноименном романе Стерлинга и Гибсона. Она была спроектирована в 1822 году и, будучи построенной, могла бы вычислять многочлены с точностью до восемнадцати знаков после запятой.
К концу 19 века стали популярны арифмометры — компактные механические вычислители. По легенде в 1924 году их производство было налажено в СССР по приказу Дзержинского. Такие «калькуляторы» выпускались у нас до 1970-х под маркой «Феликс».
Самым компактным в истории механическим калькулятором был «Курта» (1938). Он выпускался до 1970-х.
А вот и «убийца» счетов — первый в мире полностью электронный компактный калькулятор Anita (компания Bell, 1961 год). С него началась эра всеобщей калькуляторизации. Калькуляторы вставлялись в столы, портмоне, наручные часы, а с недавних пор всех их вытеснил калькулятор Windows.
2.Виды калькуляторов
Калькуляторы можно разделить на следующие виды:
· Карманные – калькуляторы небольшого размера, которые можно брать с собой;
· Настольные – калькуляторы чуть большего размера, которые удобнее использовать, например, на рабочем столе, людям, производящим большое количество расчетов;
· Калькуляторы с печатью – настольные калькуляторы со встроенным печатным устройством, которое выводит производимые вычисления, промежуточные итоги, графики на бумажную ленту;
·
Онлайн – калькуляторы.
Ну, а если говорить о функциях, то все выпускаемые модели можно условно отнести к одному из типов калькуляторов, о которых мы расскажем ниже.
ПРОСТЕЙШИЕ калькуляторы имеют небольшие размеры и вес, один регистр памяти и небольшое число функций. Предназначены для широкого круга потребителей.
БУХГАЛТЕРСКИЕ калькуляторы имеют дополнительные средства для работы с денежными суммами (кнопки «00» и «000», фиксированное количество разрядов дробной части, автоматическое округление). Как правило, имеют настольные габариты. Предназначены для всех, кто по долгу работы вынужден считать деньги: бухгалтеров, кассиров и т. д.
ИНЖЕНЕРНЫЕ предназначены для сложных научных и инженерных расчётов. Имеют большое количество функций, включая вычисление всех элементарных функций, статистические расчёты, задание углов в градусах, минутах и секундах.
ПРОГРАММИРУЕМЫЕ КАЛЬКУЛЯТОРЫ имеют возможность вводить и исполнять
программы пользователя. Имеют большое количество регистров памяти. По
функциональности приближаются к простейшим компьютерам. В зависимости от модели программируемые
калькуляторы имеют несколько типов встроенных языков программирования.
Имеют большое количество регистров памяти. По
функциональности приближаются к простейшим компьютерам. В зависимости от модели программируемые
калькуляторы имеют несколько типов встроенных языков программирования.
ГРАФИЧЕСКИЕ КАЛЬКУЛЯТОРЫ имеют графический экран, что позволяет чертить графики функций или даже выводить на экран произвольные рисунки.
МЕДИЦИНСКИЕ КАЛЬКУЛЯТОРЫ.
Данный вид калькуляторов используется врачами, фармацевтами, медсёстрами, студентами медицинских факультетов и т.д. Могут быть сделаны как в виде отдельного устройства, планшета для обхода больных, так и в виде программы универсального компьютера. Такой калькулятор реализует функции медицинского справочника, обеспечивает медицинские расчеты со справочным материалом, расчет дозировки лекарств, доступ к базам данных лечебного учреждения и т.д.
Появление компьютера с разнообразным
программным обеспечением не уничтожило калькулятор, а наоборот, сделало его еще
более мощным. В настоящее время мы знаем, что в любом компьютере есть программа
«Калькулятор», у всех есть мобильные телефоны со встроенным калькулятором.
В настоящее время мы знаем, что в любом компьютере есть программа
«Калькулятор», у всех есть мобильные телефоны со встроенным калькулятором.
3. Микроисследование.
Мы решили провести микроисследования о вреде и пользе калькулятора, опросив различные группы людей. Это учащиеся, учителя нашей школы, взрослые (родители, знакомые). Всего 100 человек.
Ø Есть ли у вас калькулятор?
У большинства опрашиваемых калькулятор имеется.
Ø Нужен ли в школе калькулятор?
Большинство школьников считает, что в школе калькулятор нужен, в отличие от взрослых и учителей которые считают, что можно обойтись и без него.
Ø Пользуешься ли ты калькулятором?
Большинство опрашиваемых людей не использует калькулятор.
Ø С какого класса вы начали пользоваться калькулятором?
Большинство школьников считают, что нужно
пользоваться с 4-5 классов. А у взрослых этот вопрос вызвал затруднение (54
человека).
А у взрослых этот вопрос вызвал затруднение (54
человека).
Ø На каких предметах калькулятором можно пользоваться?
Большее количество опрошенных считает, что калькулятором можно пользоваться на уроках алгебры и физики, а на остальных предметах можно обойтись и без него.
Ø Справедлива ли будет оценка за контрольную работу, если на ней пользоваться калькулятором?
Мы выяснили, что большая часть не согласна.
Заключение.
Тщательно изучив мнения учащихся, различные литературные источники и результаты опроса, мы пришли к выводу.
Калькулятор сейчас стал обычным явлением, а с появлением высокотехнологичных телефонов — неотъемлемой частью каждого школьника. Но, оказывается, он не так нужен, как может показаться на первый взгляд. Учебная программа составлена таким образом, что в школьном курсе математики калькулятор не нужен.
И, если ребенок часто к нему
обращается, то это говорит, что нужно и важно подтянуть умение считать в уме. Единственная тема, где без него не обойтись — это решение треугольников с
использованием тригонометрических функций. В некоторых школах в 9 классе используется
учебник по геометрии, где есть задачи на эту тему.
Единственная тема, где без него не обойтись — это решение треугольников с
использованием тригонометрических функций. В некоторых школах в 9 классе используется
учебник по геометрии, где есть задачи на эту тему.
А вот где действительно он нужен — так это на уроках химии и физики.
Задания по математике построены таким образом, что все расчеты выполняются или устно или в столбик на черновике. Поэтому привыкать к калькулятору не надо, даже если в школе пользоваться разрешают. На тестировании использование телефонов, калькуляторов и прочих технических средств может закончиться аннулированием работы.
Калькуляторы нам, конечно, необходимы – ни один профессиональный расчет не выполнить без них, но все-таки в школьные годы необходимо научиться считать «вручную».
Литература.
1. И.Я. Депман, Н.Я. Виленкин «За страницами учебника математики», Просвещение, 1989 г.
2. Энциклопедический словарь юных математиков. А.П.Савин М: Педагогика, 1989.
Интернет-ресурсы.
www.wikipedia.ru
http://matema.ucoz.ru
http://portfolio.1september.ru
Руководство по TI BA II Plus: как лучше пользоваться калькулятором
Софи Мейкон ∙
Хочешь сдать экзамены? Начните готовиться правильно.
Моя электронная почта и я готовлюсь к CFA Level 1CFA Level 2CFA Level 3Passed CFAFRM Part 1FRM Part 2CAIA Level 1CAIA Level 2Не определился
Скорость и точность имеют значение для экзаменов CFA, FRM и CAIA. Стоит потратить некоторое время, чтобы научиться более эффективно использовать калькулятор.
Это руководство Texas Instruments BA II Plus представляет собой окончательный список некоторых малоизвестных, экономящих время функций калькулятора, которые вам необходимо знать для подготовки к экзамену CFA.
Эти советы и рекомендации относятся к моделям калькуляторов BA II Plus и BA II Plus Professional. Также предполагается, что вы уже знакомы с основами, такими как расчет IRR, NPV и временной стоимости денег.
Я начну с обсуждения того, какую версию калькулятора я предпочитаю (и почему), перейду к рекомендуемым настройкам калькулятора для экзаменов CFA, затем перейду к подробностям каждой функции, которую считаю полезной, прежде чем закончить обычными часто задаваемыми вопросами. раздел.
Погружаемся!
Содержание
- Сравнение BA II Plus с BA II Plus Professional
- Калькулятор BA II Plus – 3 рекомендуемые настройки для экзаменов CFA
- 1) Увеличение до 9 знаков после запятой
- 2) Установите период в году на 1 3) Используйте алгебраическую операционную систему (AOS) вместо цепного метода (CHN)
- Как использовать BA II Plus: дополнительные советы и функции, которые вы должны знать
- Круглые скобки (или квадратные скобки) 9Кнопка x
- Функция памяти: Сохранение и вызов значений и очистка памяти
- Функция Stat: Сумасшедший быстрый доступ к стандартному отклонению, дисперсии и среднему значению
- Помощь калькулятора BA II Plus и часто задаваемые вопросы
- Почему мой BA II Plus выполняет округление?
- Могу ли я решить вопросы нормального распределения с помощью BA II Plus?
- Мой BA II Plus не выполняет расчет правильно.
 Нужна помощь в устранении неполадок!
Нужна помощь в устранении неполадок! - Как сбросить калькулятор BA II Plus?
- Каков типичный срок службы батареи BA II Plus?
- Какой аккумулятор нужен для BA II Plus?
- Как заменить батарею калькулятора BA II Plus?
BA II Plus и BA II Plus Professional
Калькулятор BA II Plus используется большинством кандидатов на экзамен CFA, но какой из них выбрать? Версия BA II Plus или BA II Plus Professional?
Тщательно опробовав обе версии, я бы рекомендовал использовать базовую модель BA II Plus вместо версии Professional 9.0080 .
Вот почему.
Я предпочитаю простую модель BA II Plus, потому что:
- она хорошо справляется со своей задачей,
- легче, а
- кнопки нажимаются лучше, без особых усилий – это важнее, чем вы думаете (см. ниже).
В то время как BA II Plus Professional, безусловно, выглядит лучше и ощущается более премиальным, я чувствовал, что усилия, направленные на то, чтобы сделать его премиальным (вес и нажатие кнопки), оказали калькулятору медвежью услугу без дополнительных преимуществ по сравнению с «базовой» моделью:
- Дороже
- Почти на 50% тяжелее, чем BA II Plus (включая крышку) — да, мы измерили.
 Профессиональная версия, кстати, не поставляется с чехлом.
Профессиональная версия, кстати, не поставляется с чехлом. - Дизайн кнопки действительно моя любимая мозоль здесь:
- Конечно, кнопки профессиональной версии кажутся более удобными, однако их сложнее нажимать и они не так чувствительны при вводе данных. Если вы используете это часами, вы не можете позволить себе постоянно проверять правильность ввода данных. Это может представлять совершенно ненужный источник ошибок в расчетах.
- Кроме того, все кнопки профессиональной версии имеют одинаковый цвет, чтобы они выглядели гладкими. Кнопка 2ND чуть светлее остальных. Но это все. Цветовая дифференциация цифр, кнопка 2ND и функции TVM на самом деле очень удобны, по крайней мере, для меня.
- Как насчет дополнительных функций в версии Professional? Я не считаю их необходимыми и не стоящими того, рекламируемая дополнительная функция NFV применима только к очень избранным случаям NPV, и ее в любом случае можно выполнить с помощью NPV самостоятельно.
 Лучше придерживаться стандартной функции NPV и изучить один из способов сделать это, чтобы избежать путаницы и тратить время на ненужные сложности, которые в целом не экономят много времени и часто не проверяются.
Лучше придерживаться стандартной функции NPV и изучить один из способов сделать это, чтобы избежать путаницы и тратить время на ненужные сложности, которые в целом не экономят много времени и часто не проверяются.
Вы на самом деле не nee d BA II Plus Professional. И вам, конечно же, не нужен финансовый калькулятор, чтобы сказать вам, что вы продвинутый бизнес-аналитик, а не просто бизнес-аналитик 🙂
Если у вас нет калькулятора BA II Plus и вы уже определились со своей моделью, вы можно легко получить последнюю модель на Amazon:
BA II Plus
Мой личный предпочтительный выбор BA II Plus:простой, легкий, доступный и выполняет свою работу.
Получить BA II Plus сейчас
BA II Plus Professional
Премиум-версия BA II Plus. Я обнаружил, что нажатие кнопки не так отзывчиво, что увеличивает вероятность совершения ошибок.
Получить BA II Plus Professional сейчас
Убедитесь, что вы не выполняете функцию СБРОСА (например, 2ND +|− ), если только вы не хотите сбросить все настройки до заводских. Дополнительную информацию о том, как сбросить настройки калькулятора, см. в разделе Справка и часто задаваемые вопросы.
Если вы случайно сделали это (или если один из прокторов сделал это с вашим калькулятором перед экзаменами — такое случается), убедитесь, что вы знаете, как изменить настройки вашего калькулятора, как показано ниже.
1) Увеличить до 9 знаков после запятой
| На экране появится «DEC = 9». Если знака «=» нет, нажмите ENTER еще раз, чтобы зарегистрировать настройки. | Ваш калькулятор по умолчанию использует 2 десятичных знака. Для экзаменов CFA мы рекомендуем 9десятичная установка для плавающих десятичных знаков. Плавающие десятичные знаки, по сути, означают, что калькулятор будет отображать столько десятичных знаков (в данном случае до 9) для каждого числа, сколько необходимо. Например, при десятичном числе 9 калькулятор покажет 2 как 2 (без десятичных знаков), но 2,39756732 покажет как 2,39756732. |
2) Установите период в году равным 1
| Это нужно для проверки правильности настройки для большинства расчетов, необходимых для программы экзамена CFA. Установите «P/Y», т.е. период в году = 1. Последние калькуляторы BA II Plus по умолчанию имеют 1, однако гораздо более старые модели имеют по умолчанию 12. Так что стоит проверить на всякий случай. |
3) Использовать алгебраическую операционную систему (AOS) вместо цепного метода (CHN)
| На экране должно отображаться «AOS». Если не просто повторять нажатия клавиш. | В качестве метода расчета выберите алгебраическую операционную систему (AOS). Это означает, что при вычислении 3 + 4 x 5 будет показано 23. Однако цепной метод (Chn) покажет 35. Мы рекомендуем использовать метод AOS, чтобы избежать путаницы. |
Как использовать BA II Plus: Дополнительные советы и функции, которые вы должны знать
Приведенные здесь советы применимы ко всем уровням. Попробуйте их и выберите то, что лучше всего подходит для вас.
Этот раздел не является исчерпывающим разделом обо всех функциях IRR, NPV, TVM и CF, которые вам необходимо знать для ваших экзаменов, а скорее содержит несколько советов, которые, как мы надеемся, ускорят процесс расчета при сохранении точности.
Круглые скобки (или квадратные скобки)
| Я нахожу эти кнопки со скобками весьма полезными для проверки правильности вычислений, поскольку размещение скобок (точно так же, как их запись на бумаге) гарантирует, что вычисления выполняются в предпочтительном порядке. и логический путь. |
Очистка записей и памяти: кнопки Backspace, CE|C и Clear TVM длинное уравнение, вам не нужно перезапускать.

Например, нажатие 2 x 3 → 2 = даст вам 4, так как вы исправили ошибку нажатия 3 без необходимости перезапуска всей операции.
У вас есть лучший контроль и вы можете удалять по символам/цифрам, а не очищать всю предыдущую запись, как функция ниже.
Кнопка CE|C: 2x удаляет все0079 CE|C один раз полностью удаляет предыдущую запись, а двойное нажатие удаляет все.
Таким образом, 2 x 3 CE|C 2 = даст вам 4. 2 x 3 CE|C CE|C просто даст вам 0, так как нажатие CE|C эффективно очищает все вычисления.
Совет профессионала : дважды нажмите кнопку CE|C, чтобы очистить калькулятор, прежде чем перейти к новому расчету.

Это может показаться очевидным, но вы должны сделать это привычкой, так как это основной источник ошибок в вычислениях.
. Однако, если вы хотите очистить все 10 ячеек памяти, нажмите 2ND 0 2ND CE|C . 9х 0,25 = 9,486832981 .
Функция памяти: хранение и напоминание значений и воспоминания о очистке
| Хранив и отзывные номера , чтобы сохранить номер: по номеру. более сложные расчеты. Хранение (STO) и вызов (RCL) чисел в памяти калькулятора значительно ускоряет работу. Чтобы сохранить номер на экране калькулятора, нажмите STO , затем, например, 1 , чтобы назначить его слоту 1. Чтобы вызвать тот же номер, нажмите RCL 1 . Спасатель! | |
| Вспомнить свой последний ответ | Также есть еще одна менее известная полезная функция , которая напоминает последний ответ вашего вычисления. Постоянно обновляет значение и отражает ваш последний ответ. Удобно, если вы забыли сохранить его или он нужен для ввода следующего уравнения. |
| Очистка всей памяти / сохраненных значений | Наконец, вам нужно помнить и знать, как очистить сохраненные значения: 1) Чтобы очистить отдельную память, просто сохраните в ней нулевое значение, т.е. нажмите 0 STO 3 (например, при очистке только слота памяти 3). 2) Чтобы очистить все 10 сохраненных ячеек памяти (номера 0-9) с помощью функции CLR WORK, нажмите 2ND 0 2ND CE|C . |
Статистическая функция: безумные сокращения стандартного отклонения, дисперсии и среднего
Хотя я не буду вдаваться в подробности того, как использовать функции TVM, NPV, IRR или CF (вы все равно должны это знать), функция статистики является одной из относительно неизвестных функций, которая на самом деле экономит массу времени, особенно для тем Quants или Portfolio Management. По сути, для этого идеально подходит любой вопрос, требующий расчета стандартного отклонения или среднего значения из набора данных.
По сути, для этого идеально подходит любой вопрос, требующий расчета стандартного отклонения или среднего значения из набора данных.
Лучше всего проиллюстрировать это с помощью примера с набором данных: 20, 15, 5, -3, 8
| 1) Чтобы настроить калькулятор для расчета статистики по одной переменной, нажмите 2ND 8 . | |
| (Повторяйте, пока не дойдете до настройки «1-V») | 2) Переключайтесь с помощью 2ND ENTER , пока не увидите 1-V. Остальные 4 параметра: LIN, PWR, EXP, Ln предназначены для регрессионного анализа, который нам не понадобится для экзаменов CFA. |
| 3) Очистить экран и ввести данные выше. | |
| 4) Войдите в настройки данных (нажмите 2ND 7 ). 5) Всегда очищайте память от предыдущих записей перед вводом новых данных, нажимая 2ND CE|C (CLR WORK).  | |
| 6) Затем введите данные в X01, X02, X03…. и т. д., и оставьте Y01, Y02, Y03… по умолчанию равным 1. X представляет данные, а Y представляет частоту этой точки данных. | |
| (повторяйте ↓ при необходимости) 92 на соответствующем стандартном отклонении. Быстрый способ получить среднее значение генеральной совокупности и стандартное отклонение! |
Ладно, это может показаться вам пустяком.
Настоящая экономия времени функции Stat проявляется, когда вас просят найти стандартное отклонение или дисперсию в немного более сложном вопросе, подобном этому:0156
 10
10| 1) Предполагая, что ваш калькулятор уже настроен для статистики одной переменной (1-V), очистите свои данные, как обычно, прежде чем начинать новый вопрос, нажав 2ND 7 2ND CE|C. | |
| 2) В этом случае переменные X являются возвратом, переменные Y (частота) — взвешиванием. Важно отметить, что данные частоты (переменные Y) должны быть введены целыми числами для этого калькулятора. Это означает, что для взвешивания мы просто вводим 55 для 55% (, а не 0,55) и так далее. 3) Перейдите к вводу данных в X01, X02, X03 для возврата и Y01, Y02, Y03 для взвешивания. | |
| 4) Наконец, вы входите в функцию Stat, которая должна сказать 1-V, и прокручиваете вниз ваши ответы: a) n=100 (хорошая проверка, что ваши веса в сумме составляют 100 %, а также то, что вы не перепутали переменные) b) среднее x̄=2,195 % c) стандартное отклонение генеральной совокупности (σx ) = 5,23 — это ответ. Вуаля! Теперь – это – сумасшедшая экономия времени. |
Справка по калькулятору BA II Plus и FAQ
Почему мой BA II Plus округляется?
Калькулятор BA II Plus поставляется с настройкой по умолчанию с двумя десятичными разрядами. Чтобы остановить округление, все, что вам нужно сделать, это увеличить количество знаков после запятой, как описано в разделе Рекомендуемые настройки калькулятора .
Обратите внимание, что изменение количества знаков после запятой влияет только на отображение, так как калькулятор фактически не округляет внутренние значения (кроме результатов амортизации и амортизации), которые он использует для расчетов.
Если вы хотите округлить внутренние значения, используйте функцию ОКРУГЛ ( кнопки 2ND STO ).
Могу ли я решить вопросы нормального распределения с помощью BA II Plus?
К сожалению, BA II Plus и BA II Plus Professional не предоставляют вероятности z-значения.
Вам нужно знать, как использовать предоставленные z-таблицы и читать их. и, что более важно, запомните 6 критических z-значений для экзаменов CFA.
Более подробная информация об этих ключевых значениях представлена в нашей статье Бесплатные таблицы распределения вероятностей.
Мой BA II Plus не выполняет расчет правильно. Нужна помощь в устранении неполадок!
В большинстве случаев это скорее человеческий фактор, чем ошибка калькулятора.
Вот несколько вещей, которые нужно проверить для устранения неполадок, при условии, что вы ввели правильные данные:
1) Расчеты TVM:
a) Вы очистили рабочий лист TVM? Перед началом каждого расчета TVM просто очистите предыдущую работу (это хорошая практика) – просто нажмите 2ND FV кнопок.
б) КОНЕЦ и режим BGN : Убедитесь, что ваш калькулятор находится в режиме END, а не в режиме BGN. Если он находится в режиме BGN, вы можете увидеть его в верхней части экрана и просто нажмите 2ND PMT 2ND ENTER 2ND CPT , чтобы переключить его обратно в режим END.
— Полезно знать, что в заводских настройках по умолчанию также стоит режим END.
c) Знаки + и − : Убедитесь, что знаки PMT и FV одинаковы и противоположны PV. Не вводите (+) для FV и PV, например, так как это вызовет ошибку 5 (т. е. решения не существует).
. Еще один совет — дважды проверить, что приток денежных средств положительный, а отток отрицательный.
d) Формат I/Y : Помните, что I/Y задается целыми числами, а не десятичными дробями.
2) Очистите все перед началом: нажмите кнопку CE|C дважды и 2ND 0 2ND CE|C , чтобы очистить все 10 слотов памяти.
3) Проверьте настройки калькулятора: нажмите 2ND . ↓ ↓ ↓ ↓ (кнопка ↓ 4 раза), чтобы пройти основные настройки калькулятора, просто чтобы убедиться, что все правильно.
↓ ↓ ↓ ↓ (кнопка ↓ 4 раза), чтобы пройти основные настройки калькулятора, просто чтобы убедиться, что все правильно.
Как сбросить калькулятор BA II Plus?
1) Нажмите кнопки 2ND , затем +|− .
2) Вы увидите RST? и индикаторы Enter на экране.
— Если вы передумали, просто нажмите 2ND CPT , чтобы отменить сброс. Затем на экране отобразится 0.
. Если вы все еще хотите выполнить сброс, нажмите ENTER , и на экране отобразится RST и 0 , чтобы подтвердить, что ваш калькулятор был сброшен.
Опция полной перезагрузки : Вы также можете сбросить настройки калькулятора, осторожно вставив заостренный предмет в отверстие с надписью RESET на задней панели калькулятора.
Каков типичный срок службы батареи BA II Plus?
В официальном руководстве к калькулятору Texas Instruments BA II Plus не указано, как долго будет работать батарея.
Насколько нам известно, они вечны. Ни в одном из наших калькуляторов не разряжались батарейки, а некоторые из них постоянно используются уже более 10 лет!
Какой аккумулятор нужен для BA II Plus?
Калькулятор BA II Plus питается от одной литиевой батареи CR2032. Он не на солнечной энергии.
Убедитесь, что вы выбрали правильный, так как есть другие батареи аналогичного размера, такие как CR2025 и CR2016.
Как заменить батарею калькулятора BA II Plus?
Вы можете посмотреть наше видео о том, как заменить батарею вашего калькулятора , или следуйте инструкциям ниже.
Приведенная ниже инструкция предназначена только для «базового» калькулятора BA II Plus. Для BA II Plus Professional задняя крышка легко выдвигается без использования отверток.
1) Вещи, которые вам понадобятся : Одна батарейка CR2032, маленькая отвертка Phillips (размер 00) и, желательно, что-нибудь, чтобы открыть корпус калькулятора.
2) Отвинтите все 4 винта на задней стороне калькулятора.
3) Это сложный момент. Даже без винтов корпус калькулятора закрывается пластиковыми защелками. Очень неприятно пытаться преодолеть это вручную, поэтому используйте перочинный нож или маленькую шлицевую отвертку. Посмотрите видео, чтобы узнать, как лучше всего быстро открыть оболочку.
4) Замените батарею. В более старых BA II Plus аккумулятор скрепляется еще двумя винтами Philips. В новой модели его можно просто сдвинуть.
5) Совет профессионала : после замены батареи быстро проверьте, работает ли калькулятор, прежде чем собирать его!
6) Установите крышку на место и снова закрутите винты. Готово!
7) Знайте, что здесь шумно . Замена батареи производит чертову тонну шума. Громовой звук открывания и закрывания корпуса калькулятора, ваше ворчание и разные стуки будут звучать довольно громко в экзаменационном зале. Если ваша батарея нуждается в замене, замените ее примерно за неделю до экзамена.
8) Еще один профессиональный совет : данные вашего калькулятора не сохраняются при удалении батареи. Таким образом, замена батареи имеет тот же эффект, что и сброс настроек калькулятора, поэтому перед повторным использованием сразу же измените настройки на нужные.
Какая функция BA II Plus показалась вам особенно полезной? У вас есть дополнительные советы, которыми вы можете поделиться? Дайте нам знать ваши комментарии ниже!
П.С. – Между тем, вот несколько статей по теме, которые могут оказаться полезными:
- Все еще не знаете, какой калькулятор выбрать? Ознакомьтесь с нашим руководством по калькулятору BA II Plus и HP12C →
- Остановились на калькуляторе HP12C? Не забудьте обратиться к нашему Руководству по калькулятору HP12C для экзамена CFA → .
texas — Googlesuche
AlleBilderShoppingVideosMapsNewsBücher
suchoptionen
Texas Paycheck Calculator — SmartAsset. com
com
smartasset.com › налоги › texas-paycheck-calccator0007
21.12.2022 · Калькулятор зарплаты SmartAsset в Техасе показывает ваш почасовой доход и зарплату после вычета федеральных, государственных и местных налогов. Введите свои данные, чтобы увидеть свой …
Ähnliche Fragen
Как вы рассчитываете годовой доход?
Сколько стоит 70 тысяч в год в Техасе?
Что такое 80 тысяч в год в Техасе?
Сколько стоит 75 тысяч в год в Техасе?
Техасский калькулятор подоходного налога — SmartAsset
smartasset.com › налоги › техасский налоговый калькулятор
22.12.2022 · Узнайте, сколько вы будете платить подоходного налога штата Техас с учетом вашего годового дохода. Настройте свой статус подачи документов, отчисления, …
Калькулятор зарплаты в Техасе — PaycheckCity
www.paycheckcity.com › … › Калькулятор зарплаты
Рассчитайте чистую зарплату в Техасе или получите домашнюю зарплату, введя свой доход -периодическая или годовая зарплата вместе с соответствующей информацией W4 на федеральном уровне, уровне штата и местном уровне . ..
..
Калькулятор подоходного налога 2023 – Техас – зарплата после уплаты налогов – Talent.com
www.talent.com › налоговый калькулятор › Техас
Калькулятор подоходного налога Техас. Узнайте, какая у вас зарплата после уплаты налогов. Введите свой валовой доход.
Калькулятор зарплаты Техаса — ADP
www.adp.com › ресурсы › инструменты › калькуляторы › состояния
Используйте калькулятор зарплаты Техаса ADP для расчета чистой или «берущей домой» оплаты для почасовых или штатных сотрудников. Просто введите заработную плату, налоговые вычеты и …
Texas Зарплата и калькулятор заработной платы — Gusto
gusto.com › ресурсы › калькуляторы › зарплата-оплата…
Информация, предоставляемая калькулятором зарплаты, содержит общую информацию о расчете налогов на заработную плату только для жителей Техаса.
Texas Почасовой расчет заработной платы и расчет заработной платы — Gusto
gusto. com › ресурсы › калькуляторы › почасовая оплата…
com › ресурсы › калькуляторы › почасовая оплата…
Используйте этот калькулятор почасовой оплаты для расчета почасовой оплаты … Текущая налоговая ставка составляет 6 % на первые 7 000 долл. США заработной платы каждого работника каждый …
Калькулятор подоходного налога в Техасе за 2021 год — Forbes
www.forbes.com › Advisor › texas
Если вы зарабатываете 70 000 долларов в год, живя в Техасе, США, вы будете платить налоги в размере 8 387 долларов. Ваша средняя ставка налога составляет 11,98%, а предельная ставка налога составляет 22%.
Texas Paycheck Calculator — Suburban Computer Services
www.suburbancomputer.com › Tips_calculator › stat…
Paycheck Calculator. Этот бесплатный, простой в использовании калькулятор расчета заработной платы рассчитает вашу заработную плату. Поддерживает почасовой доход и зарплату, а также множественную оплату …
Тип оплаты: Зарплата Почасовая
Частота оплаты: Еженедельно Раз в две недели Полумесяц Ежемесячно Ежеквартально Ежегодно Ежедневно
Оплата: Ежегодно?
Удерживаемые суммы: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 .

 Нужна помощь в устранении неполадок!
Нужна помощь в устранении неполадок! Профессиональная версия, кстати, не поставляется с чехлом.
Профессиональная версия, кстати, не поставляется с чехлом. Лучше придерживаться стандартной функции NPV и изучить один из способов сделать это, чтобы избежать путаницы и тратить время на ненужные сложности, которые в целом не экономят много времени и часто не проверяются.
Лучше придерживаться стандартной функции NPV и изучить один из способов сделать это, чтобы избежать путаницы и тратить время на ненужные сложности, которые в целом не экономят много времени и часто не проверяются.


 Мы используем это вместо выборочного стандартного отклонения (несмотря на то, что оно похоже, поскольку n велико), потому что n является произвольным из-за взвешенного характера вопроса.
Мы используем это вместо выборочного стандартного отклонения (несмотря на то, что оно похоже, поскольку n велико), потому что n является произвольным из-за взвешенного характера вопроса.