Матричный онлайн калькулятор (на Java)
Матричный онлайн калькулятор (на Java)
Если Вы видете это строки, то на Вашем компьютере не установлен Java интерпретатор.
Установить
С помощью матричного онлайн калькулятора вы можете сложить, умножить, вычитать матрицы, умножить и делить матрицы на число, вычислить степень матрицы, обратную матрицу, псевдообратную матрицу, определитель матрицы, ранг матрицы, а также удалить линейно зависимые строки из матрицы. Для вычислений набирается формула в специальном окне. Формула может включать сложение, умножение, возведение в степень и т.д. одновременно. В формуле вы можете использовать круглые скобки.
Для быстрого ознакомления с работой калькулятора смотрите видео-инструкцию онлайн калькулятора.
Вы также можете пользоваться текстовой инструкцией онлайн калькулятора.
Краткая инструкция:
- Выберите матрицу из выпадающего списка и задайте количество строк и столбцов. Нажмите на кнопку
- Введите элементы матрицы.
- В нижней части маленького окна с названием «Вычисления» введите формулу и нажмите «Enter» на клавиатуре .
| Формула для вычисления | Набирать формулу | Действие | Результат |
|---|---|---|---|
| A+B | C=A+B | сложение матриц A и B | в матрице C |
| A−C | D=A-C | вычитание матриц A и С | в матрице D |
| A*2 | D=A*2 | умножение матрицы A на скаляр 2 | в матрице D |
| A*C | B=A*C | умножение матриц A и С | в матрице B |
| AT | B=A^T# | транспонирование A | в матрице B |
| A-1 | D=A^-1# | вычисление обратной к A матрицы | в матрице D |
| B+ | A=B^+# | вычисление псевдообратной к B матрицы | в матрице A |
| ранг A | C=rankA | вычисление ранга A | в матрице С |
| полный ранг A | C=fullrankA | удаление линейно зависимых строк A | в матрице С |
| det A | D=detA | вычисление определителя A | в матрице D |
| B2 | A=B^2# | возведение в квадрат B | в матрице A |
| A3−B*(A+C) | D=A^3#-B*(A+C) | вычисление формулы со скобками | в матрице D |
33+3.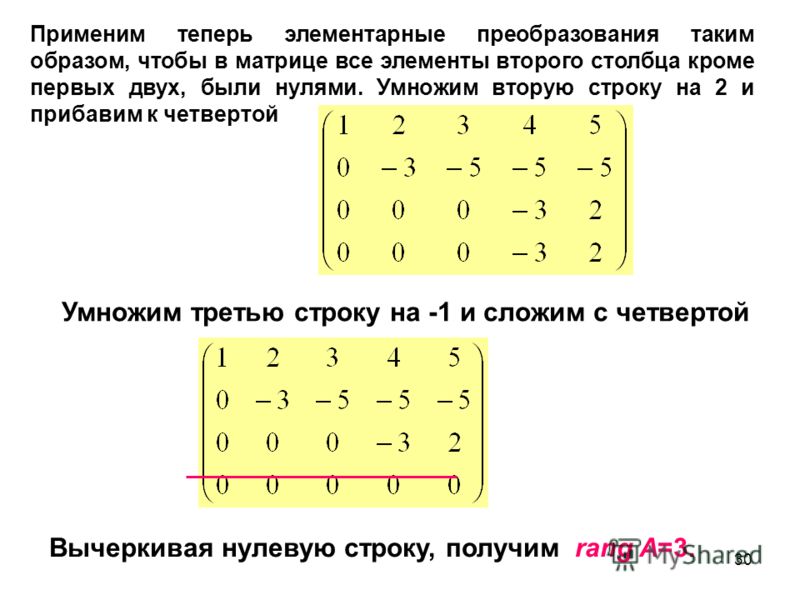 2#+41.6)/4 | вычисление численной формулы со скобками | в матрице B |
Внимание! Данная программа работает на интерпретаторе Java. Интерпретатор Java можно бесплатно скачать и установить на ваш компьютер из официального сайта программы .
- Если ниже вместо калькулятора вы видете серый фон и сообщение о плагине, это значит, что у вас не установлена программа Java. Сначала скачайте и установите программу.
- Если появляется всплывающее окно с вопросом: Do you want to run this application? (хотите ли вы запускать данную программу), то
- вставте галочку перед сообшением I accept the risk and want to run this app( я понимаю риск и хочу запускать программу).
- вставте галочку перед сообщением Do not show this again for this app (не показывать это сообщение снова).
- нажмите на кнопку «Run».
- Если высшеизложенные действия не дают результат, то нужно удалять Java программу из компьютера и устанавливать новую версию.
Отметим, что наша программа совершенно безопасна.
Вы можете использовать другой матричный онлайн калькулятор который работает без Java.
Ни рис. 1 отображен внешний вид матричного онлайн калькулятора. С его помощью вы можете сложить, умножить, вычитать матрицы, умножить и делить матрицы на число, вычислить стерень матрицы, обратную матрицу, псевдообратную матрицу, определитель матрицы, ранг матрицы, а также удалить линейно зависимые строки из матрицы.
Вы можете использовать в формуле круглые скобки.
Для создания матрицы нужного порядка:
- Выберите матрицу (1).
- Задайте нужное количество строк и столбцов матрицы ( 2 и 3).
- Нажмите на кнопку .
Для создания единичной матрицы выберите нужную матрицу и нажмите на кнопку .
Для создания нулевой матрицы выберите нужную матрицу и нажмите на кнопку .
Матрицы можно использовать как числа, задав размерность 1×1.
Точность вычислений задается в элементе 7.
3#.
Перейти к матричному онлайн калькулятору.
Построение матрицы нужного порядка
Для построения матрицы нужного порядка:
- Выбирать матрицу (1).
- Ввести количество строк и столбцов (2 и 3).
- Построить матрицу (нажимать на 4).
Перейти к матричному онлайн калькулятору.
Сложение двух матриц онлайн
Для сложения двух матриц:
- Построить матрицы нужного порядка (Рис. 2).
- Набирать формулу в окне «Вычисления» ( 1 (Рис. 3)) и нажимать на клавишу «Enter» на клавиатуре.
Перейти к матричному онлайн калькулятору.
Умножение двух матриц онлайн
Для умножения двух матриц:
- Построить матрицы нужного порядка(Рис. 2).
- Ввести элементы матриц.
- Набирать формулу в окне «Вычисления» ( 1 (Рис. 4)) и нажимать на клавишу «Enter» на клавиатуре.
Перейти к матричному онлайн калькулятору.
Вычисление обратной матрицы онлайн
Для вычисления обратной матрицы:
- Построить матрицу нужного порядка(Рис. 2).
- Ввести элементы матрицы.
- Набирать формулу в окне «Вычисления» (Рис. 5) и нажимать на клавишу «Enter» на клавиатуре.
Перейти к матричному онлайн калькулятору.
Вычисление сложной формулы онлайн
Для вычисление сложной формулы:
- Построить матрицы нужного порядка(Рис. 2).
- Ввести элементы матриц.
- Набирать формулу в окне «Вычисления» (Рис. 6) и нажимать на клавишу «Enter» на клавиатуре.
Перейти к матричному онлайн калькулятору.
Внимание! Программа работает на интерпретаторе Java.
Если у вас не установлен Java, то программу можно бесплатно загрузить и установить из официального сайта программы ().
Установка займет всего 3-4 минуты.
назад вперед
- Онлайн калькуляторы
- Матричный онлайн калькулятор
- Матричный онлайн калькулятор (на Java)
- Онлайн калькулятор дробей
Калькулятор суммы матриц — MathCracker.
comРешатели Алгебра
Инструкции: Воспользуйтесь нашим пошаговым калькулятором суммы двух матриц, предоставив две ваши матрицы одинакового размера.
При необходимости измените размер матриц, указав количество строк и количество столбцов. Когда у вас есть правильные размеры, которые вы хотите, вы вводите матрицы (вводя числа и перемещаясь по матрице с помощью «TAB»)
Количество строк = Количество столбцов =The number of rows and columns provided needs to be integers that are greater than 1.
The maximum number of rows is 8, and the maximum number of columns is 8 \(A\) = \begin{bmatrix} & \\ & \end{bmatrix}
\(B\) = \begin{bmatrix} & \\ & \end{bmatrix}
Матрицы являются чрезвычайно полезными математическими объектами, которые служат многим различным целям. Действительно, с матрицами можно решать системы линейных уравнений , и вообще, вы можете представлять линейные функции.
Матрицы, как и числа, могут оперировать друг с другом. То есть вы можете их складывать, вычитать и умножать при условии соблюдения определенных основных условий размерности.
И даже при условии, что вы
оценить, что матрица обратима
, вы можете делить на матрицу, как обычное число.
Как суммировать матрицы?
Матрицы могут быть добавлены при условии, что матрицы имеют одинаковый размер. Итак, если вы хотите добавить две матрицы, вы должны выполнить следующие шаги:
Шаг 1: Убедитесь, что матрицы, которые вы хотите добавить, имеют одинаковый размер. Для этого вам нужно оценить количество столбцов и строк для обеих матриц и убедиться, что эти числа совпадают.
Это первая и вторая матрицы имеют одинаковое количество строк, а первая и вторая матрицы имеют одинаковое количество столбцов.
Обратите внимание, что вы можете добавлять матрицы, которые не возведены в квадрат, если две матрицы имеют одинаковые размеры.
Шаг 2: Как только вы узнаете, что две добавляемые вами матрицы имеют одинаковый размер, вам нужно добавить каждый соответствующий компонент из каждой из матриц.
То есть, чтобы получить запись в первой строке, первом столбце матрицы суммы, вы возьмете запись в первой строке, первом столбце первой матрицы и добавите к ней запись в первой строке, сначала столбец второй матрицы.
И вы делаете то же самое для всех компонентов.
Можете ли вы добавить матрицу 3×3 и 3×4?
Строго говоря, нельзя, потому что матрицы 3х3 и 3х4 не имеют одинаковых размеров. Теперь некоторые умные математики утверждают, что вы можете «расширить» «меньшую» матрицу 3×3, чтобы «превратить» ее в матрицу 3×4. Ну, там много слов.
Таким образом, определенно имеет смысл попытаться добавить матрицу 3×3 и 3×4, но для большинства целей мы скажем, что нет, вы не можете их добавить.
И то же самое будет применяться, когда вы пытаетесь добавить матрицы разных размеров. Ответ НЕТ, вы не можете их добавить, но вы определенно можете попытаться придать смысл такой операции.
Вы умеете вычитать матрицы?
Да! Если у вас есть матрицы одинакового размера, вы можете их вычесть. Так же, как вы делаете с дополнением, чтобы вычесть две матрицы вы вычитаете компонент за компонентом.
Вы можете не только складывать или вычитать матрицы, но и
умножить матрицы
A и B при условии, что количество столбцов A совпадает с количеством строк B.
Калькулятор суммы матриц Матричные операции Калькулятор матриц Добавлен калькулятор двух матриц
Онлайн Калькулятор: Детерминант матрицы
Размерность матрицы:
——
2 x 23 x 34 x 45 x 56 x 6
Метод:
——
Разложение по первой строкеСаррюсаПриведением к треугольному виду
Введите значения:
Разложение по первой строке
Чтобы вычислить определитель матрицы разложением по первой строке, необходимо каждый элемент данной строки умножить на соответствующий ему минор;
Миноры соответствущие определенному элементу находим путем исключения i-й строки,j-го столбца из матрицы A, после чего находим определитель полученной матрицы;
i,j — это номер строки и столбца, в которых находиться определенный элемент;
После вычисления произведений каждого элемента первой строки, на соответсвующий ему минор, необходимо их сложить и вычесть;
Знак сложения и вычитания изменяется по порядку, начиная со знака сложения;
Возле первого произведения стоит знак плюс, возле второго знак минус и т.
д.
det(A) =
| 000 | 71 | 8 | 8 | 2 | 000 |
| 7 | 8 | 5 | 2 | ||
| 2 | 5 | 8 | 7 | ||
| 4 | 5 | 5 | 2 |
= a11 * A11 — a12 * A12 + a13 * A13 — a14 * A14;
Итак, найдем миноры каждого элемента первой строки.
Найдем минор элемента под индексом 11
Для этого из матрицы А необходимо исключить 1 строку и 1 столбец, после чего получаем следующую матрицу:
| 000 | 8 | 5 | 2 | 000 |
| 5 | 8 | 7 | ||
| 5 | 5 | 2 |
Далее вычисляем определитель данной матрицы.
Он равен -57, это и есть минор элемента 11.
A11 =
| 000 | 71 | 8 | 8 | 2 | 000 |
| 7 | 8 | 5 | 2 | ||
| 2 | 5 | 8 | 7 | ||
| 4 | 5 | 5 | 2 |
| 000 | 8 | 5 | 2 | 000 |
| 5 | 8 | 7 | ||
| 5 | 5 | 2 |
Найдем минор элемента под индексом 12
Для этого из матрицы А необходимо исключить 1 строку и 2 столбец, после чего получаем следующую матрицу:
| 000 | 7 | 5 | 2 | 000 |
| 2 | 8 | 7 | ||
| 4 | 5 | 2 |
Далее вычисляем определитель данной матрицы.
Он равен -57, это и есть минор элемента 12.
A12 =
| 000 | 71 | 8 | 8 | 2 | 000 |
| 7 | 8 | 5 | 2 | ||
| 2 | 5 | 8 | 7 | ||
| 4 | 5 | 5 | 2 |
| 000 | 7 | 5 | 2 | 000 |
| 2 | 8 | 7 | ||
| 4 | 5 | 2 |
Найдем минор элемента под индексом 13
Для этого из матрицы А необходимо исключить 1 строку и 3 столбец, после чего получаем следующую матрицу:
| 000 | 7 | 8 | 2 | 000 |
| 2 | 5 | 7 | ||
| 4 | 5 | 2 |
Далее вычисляем определитель данной матрицы.
Он равен -3, это и есть минор элемента 13.
A13 =
| 000 | 71 | 8 | 8 | 2 | 000 |
| 7 | 8 | 5 | 2 | ||
| 2 | 5 | 8 | 7 | ||
| 4 | 5 | 5 | 2 |
| 000 | 7 | 8 | 2 | 000 |
| 2 | 5 | 7 | ||
| 4 | 5 | 2 |
Найдем минор элемента под индексом 14
Для этого из матрицы А необходимо исключить 1 строку и 4 столбец, после чего получаем следующую матрицу:
| 000 | 7 | 8 | 5 | 000 |
| 2 | 5 | 8 | ||
| 4 | 5 | 5 |
Далее вычисляем определитель данной матрицы.
Он равен 21, это и есть минор элемента 14.
A14 =
| 000 | 71 | 8 | 8 | 2 | 000 |
| 7 | 8 | 5 | 2 | ||
| 2 | 5 | 8 | 7 | ||
| 4 | 5 | 5 | 2 |
| 000 | 7 | 8 | 5 | 000 |
| 2 | 5 | 8 | ||
| 4 | 5 | 5 |
Теперь необходимо вычислить произведение первого элемента на соответствующий ему минор.
71 * (-57) = -4047;
Далее от данного произведения необходимо вычесть произведение второго элемента на соответствующий ему минор.
-4047 — (8 * (-57)) = -4047 — (-456) = -3591;
Теперь к полученному результату необходимо добавить произведение третьего элемента на соответствующий ему минор.
-3591 (8 * (-3)) = -3591 (-24) = -3615;
И, наконец, от полученного результата необходимо вычесть произведение четвертого элемента на соответствующий ему минор
-3615 — (2 * 21) = -3615 — 42 = -3657;
Результат этого вычитания и есть определитель матрицы A
det(A) = (71 * (-57)) — (8 * (-57)) + (8 * (-3)) — (2 * 21) = -3657;
Ответ:det(A) = -3657
Саррюса
Пусть имеется следующая матрица А:
| 000 | 2 | 5 | 6 | 000 |
| 5 | 8 | 2 | ||
| 3 | 5 | 7 |
Справа от матрицы А, допишем первых два столбца;
| 000 | 2 | 5 | 6 | 000 | 2 | 5 |
| 5 | 8 | 2 | 5 | 8 | ||
| 3 | 5 | 7 | 3 | 5 |
Произведения элементов на главной диагонали и на диагоналях, ей параллельных, берем со знаком плюс;
= (a11a22a33) + (a12a23a31) + (a13a21a32) —
Произведения элементов побочной диагонали и диагоналей, ей параллельных, берем со знаком минус;
= (a13a22a31) — (a11a23a32) — (a12a21a33) =
= (2 * 8 * 7) + (5 * 2 * 3) + (6 * 5 * 5) — (6 * 8 * 3) + (2 * 2 * 5) + (5 * 5 * 7) = -47;
Ответ:det(A) = -47
Приведением к треугольному виду
Приведем матрицу к треугольному виду, тогда произведение элементов главной диагонали даст нам детерминант;
det(A) =
| 000 | 71 | 8 | 8 | 2 | 000 |
| 7 | 8 | 5 | 2 | ||
| 2 | 5 | 8 | 7 | ||
| 4 | 5 | 5 | 2 |
от 2 строки отнимаем 1 строку, умноженую на 0.
09859;
от 3 строки отнимаем 1 строку, умноженую на 0.02817;
от 4 строки отнимаем 1 строку, умноженую на 0.05634;
=
| 000 | 71 | 8 | 8 | 2 | 000 |
| 0 | 7.21128 | 4.21128 | 1.80282 | ||
| 0 | 4.77464 | 7.77464 | 6.94366 | ||
| 0 | 4.54928 | 4.54928 | 1.88732 |
от 3 строки отнимаем 2 строку, умноженую на 0.
66211;
от 4 строки отнимаем 2 строку, умноженую на 0.63086;
=
| 000 | 71 | 8 | 8 | 2 | 000 |
| 0 | 7.21128 | 4.21128 | 1.80282 | ||
| 0 | 0 | 4.98631 | 5.74999 | ||
| 0 | 0 | 1.89255 | 0.74999 |
от 4 строки отнимаем 3 строку, умноженую на 0.37955;
=
| 000 | 71 | 8 | 8 | 2 | 000 |
| 0 | 7. 21128 | 4.21128 | 1.80282 | ||
| 0 | 0 | 4.98631 | 5.74999 | ||
| 0 | 0 | 0 | -1.43242 |
det(A) = 71 * 7.21128 * 4.98631 * -1.43242 = -3657;
Ответ:det(A) = -3657
2×2 Matrix Добавление и вычитание калькулятор
- Login
- Регистр
- Home
- Math
- Finance
- Engineering
Рассчитайте
Отчет. Калькулятор вычитания использует две матрицы $2\times 2$ $A$ и $B$ и вычисляет как их сумму $A+B$, так и их разность $A-B$. Это математический онлайн-инструмент, специально запрограммированный для выполнения матричного сложения и вычитания между двумя матрицами $2\times 2$.
Необходимо выполнить следующие шаги:
- Ввести в поле две матрицы $2\times2$. Элементы матриц должны быть действительными числами.
- Нажмите кнопку » GENERATE WORK «, чтобы произвести вычисления;
- Калькулятор сложения и вычитания матриц 2×2 даст сумму двух матриц $2\times2$ и разницу между первой матрицей и второй матрицей.
Ввод: Две матрицы $2\times2$;
Выход: Две матрицы $2\times2$.
$2\times 2$ Формула сложения матриц:
Сумма двух матриц $A=[a_{ij}]_{2\times2}$ и $B=[a_{ij}]_{2 \times2}$ определяется по следующей формуле $$\begin{align}&\left( \begin{массив}{cc} а_{11} и а_{12} \\ а_{21} и а_{22} \\ \конец{массив} \справа)+ \оставил( \begin{массив}{cc} б_{11} и б_{12} \\ б_{21} и б_{22} \\ \конец{массив} \right)= \left(\begin{массив}{ccc} а_{11}+b_{11}и а_{12}+b_{12} \\ а_{21}+b_{21} &a_{22}+b_{22}\\ \end{массив}\right)\end{align}$$
$2\times 2$ Формула вычитания матрицы:
Разница между $A=[a_{ij}]_{2\times2}$ и $B=[a_{ij}]_{2\times2} $ определяется по следующей формуле $$\begin{align} &\left( \begin{массив}{cc} а_{11} и а_{12} \\ а_{21} и а_{22} \\ \конец{массив} \Правильно)- \оставил( \begin{массив}{cc} б_{11} и б_{12} \\ б_{21} и б_{22} \\ \конец{массив} \right)= \left(\begin{массив}{ccc} а_{11}-b_{11}и а_{12}-b_{12} \\ а_{21}-b_{21} &a_{22}-b_{22}\\ \end{массив}\right)\end{align}$$
Матрицы — мощный инструмент в математике, науке и жизни.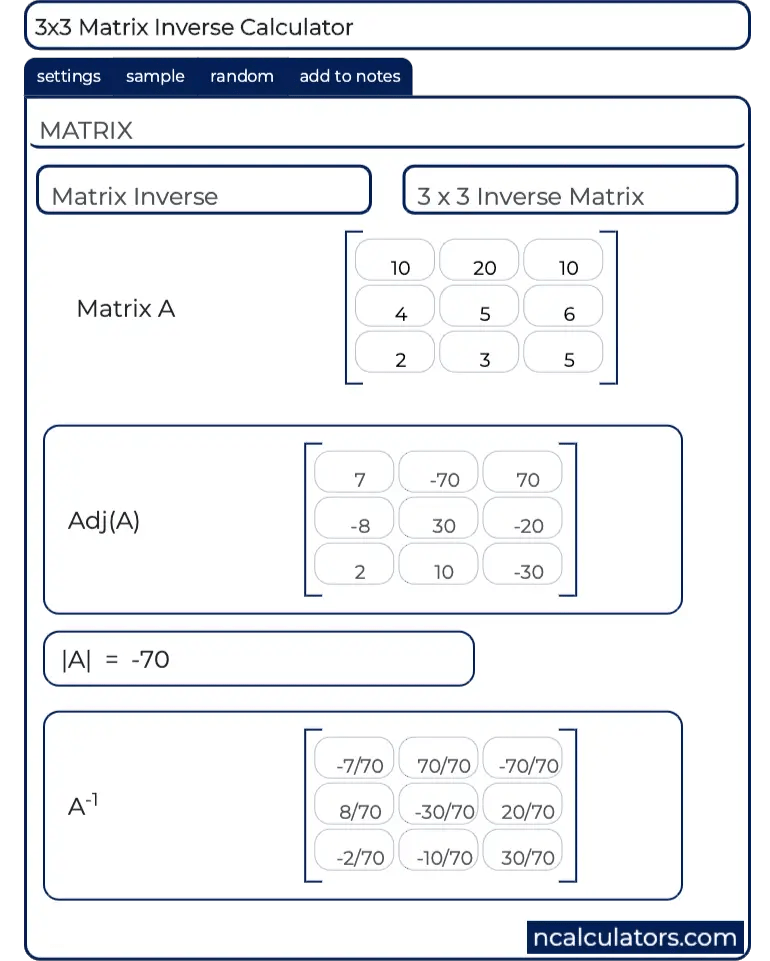
Матрицы повсюду, и у них есть важные приложения. Например, электронная таблица, такая как Excel, или письменная таблица представляет собой матрицу. Слово «матрица» является латинским словом и означает «матка». Этот термин был введен Дж. Дж. Сильвестром (английский математик) в 1850 г.
Первая потребность в матрицах возникла при изучении систем одновременных линейных уравнений.
Матрица представляет собой прямоугольный массив чисел, расположенных следующим образом
$$А=\влево(
\begin{массив}{cccc}
а_{11} и а_{12} и \ldots&a_{1n} \\
a_{21} & a_{22} & \ldots& a_{2n} \\
\ldots &\ldots &\ldots&\ldots\\
a_{m1} & a_{m2} & \ldots&a_{mn} \\
\конец{массив}
\справа)=\слева[
\begin{массив}{cccc}
а_{11} и а_{12} и \ldots&a_{1n} \\
a_{21} & a_{22} & \ldots& a_{2n} \\
\ldots &\ldots &\ldots&\ldots\\
a_{m1} & a_{m2} & \ldots&a_{mn} \\
\конец{массив}
\право]$$
Существует два обозначения матрицы: в круглых скобках или квадратных скобках. Члены матрицы называются ее элементами или ее элементами.
Матрицы чаще всего обозначаются прописными буквами, а соответствующие им строчные буквы с двумя нижними индексами являются элементами матриц.
Например, матрицы обозначаются $A,B,\ldots Z$, а ее элементы — $a_{11}$ или $a_{1,1}$ и т. д. Горизонтальные и вертикальные строки элементов матрицы называются строк и столбцов соответственно.
Размер матрицы — это произведение Декарта на количество содержащихся в ней строк и столбцов. Матрица, состоящая из $m$ строк и $n$ столбцов, называется $m\times n$ матрицей. В этом случае $m$ и $n$ — его размерности. Если матрица состоит только из одной строки, она называется матрицей-строкой}. Если матрица состоит только из одного столбца, она называется матрицей-столбцом. Матрица, содержащая в качестве элементов только нули, называется нулевой матрицей.
Как найти сумму двух матриц 2×2?
Матрицы $A$ и $B$ можно складывать тогда и только тогда, когда их размеры равны. Такие матрицы называются соразмерный для добавления или
вычитание. Их сумма представляет собой матрицу $C=A+B$ с элементами
$$c_{ij}=a_{ij}+b_{ij}$$
Матрица суммы имеет тот же размер, что и матрицы $A$ и $B$.
Это означает, что каждый элемент в $C$ равен сумме элементов в $A$ и $B$, стоящих на соответствующих местах. Например,
$c_{12}=a_{12}+b_{12}$. Если две матрицы имеют разные размеры, их сумма не определена.
Легко доказать, что $A+B=B+A$, другими словами, сложение матриц является коммутативной операцией.
Матрица $2\times 2$ имеет $2$ столбцов и $2$ строк. Например, сумма двух $2\times 2$-матриц $A$ и $B$ есть такая матрица $C$, что $$\begin{align} &C=\left( \begin{массив}{cc} а_{11} и а_{12} \\ а_{21} и а_{22} \\ \конец{массив} \справа)+ \оставил( \begin{массив}{cc} б_{11} и б_{12} \\ б_{21} и б_{22} \\ \конец{массив} \right)= \left(\begin{массив}{ccc} а_{11}+b_{11}и а_{12}+b_{12} \\ а_{21}+b_{21} &a_{22}+b_{22}\\ \end{массив}\right)\end{align}$$ Например, найдем сумму для $$А=\влево( \begin{массив}{cc} 5 и 8 \\ 3 и 8 \\ \конец{массив} \право)\четырехъядерный\mbox{и}\четырехъядерный B=\левый( \begin{массив}{cc} 3 и 8 \\ 8 и 9\\ \конец{массив} \справа)$$ По формуле сложения матриц сумма матриц $A$ и $B$ есть матрица $$A+B=\влево( \begin{массив}{cc} 5+3 и 8+8 \\ 3+8 и 8+9 \\ \конец{массив} \справа)=\слева( \begin{массив}{cc} 8 и 16 \\ 11 и 17 \\ \конец{массив} \right)$$
Как найти вычитание матрицы $2\times2$?
Матрицы $A$ и $B$ можно вычитать тогда и только тогда, когда их размеры равны.
Разность $A-B$ двух $m\times n$ матриц равна сумме $A + (-B)$,
где $-B$ представляет собой аддитивную обратную матрицу $B$. Итак, разностная матрица $C=A-B$ с элементами
$$c_{ij}=a_{ij}+(-b_{ij})=a_{ij}-b_{ij}$$
Матрица $C$ имеет тот же размер, что и матрицы $A$ и $B$. Это означает, что каждый элемент в $C$ равен разности между элементами $A$ и $B$, расположенными в соответствующих места. Например, $c_{12}=a_{12}-b_{12}$. Если две матрицы имеют разные размеры, их различие не определяется.
Вычитание матриц является некоммутативной операцией, т.е. $A-B\ne B-A$. Вычитание двух матриц очень похоже на сложение матриц, с той лишь разницей, что вычитаются соответствующие элементы.
Матрица $2\times 2$ имеет $2$ столбцов и $2$ строк. Например, разность между двумя $2\times 2$-матрицами $A$ и $B$ есть такая матрица $C$, что
$$\begin{align} C=&\left(
\begin{массив}{cc}
а_{11} и а_{12} \\
а_{21} и а_{22} \\
\конец{массив}
\Правильно)-
\оставил(
\begin{массив}{ccc}
б_{11} и б_{12} \\
б_{21} и б_{22} \\
\конец{массив}
\right)= \left(\begin{массив}{ccc}
а_{11}-b_{11}и а_{12}-b_{12} \\
а_{21}-b_{21} &a_{22}-b_{22}\\
\end{массив}\right)\end{align}$$
Применим формулу вычитания матрицы $2\times 2$ для нахождения разности $A-B$ для
$$А=\влево(
\begin{массив}{cc}
5 и 8 \\
3 и 8 \\
\конец{массив}
\право)\четырехъядерный\mbox{и}\четырехъядерный B=\левый(
\begin{массив}{cc}
3 и 8 \\
8 и 9\\
\конец{массив}
\справа)$$
Следовательно, разность между матрицами $A$ и $B$ есть матрица
$$A-B=\влево(
\begin{массив}{cc}
5-3 и 8-8\
3-8 и 8-9\
\конец{массив}
\справа)=\слева(
\begin{массив}{cc}
2 и 0 \\
-5 и -1 \\
\конец{массив}
\справа)$$
Работа по сложению и вычитанию матриц $2\times 2$ с шагами показывает полный пошаговый расчет для нахождения суммы и разности двух матриц $2\times2$ $A$ и $B$ с использованием формул сложения и вычитания матриц.
Для любых других матриц просто введите элементы матриц $2$, элементы которых являются действительными числами, и нажмите кнопку СОЗДАТЬ РАБОТУ. Учащиеся начальной школы могут использовать это сложение и вычитание матриц $2\times 2$ для создания работы, проверки результатов сложения и вычитания матриц, полученных вручную, или для эффективного решения домашних задач. Этот калькулятор может быть интересен для решения линейных уравнений и некоторых других математических и жизненных задач. 9o$ против часовой стрелки вокруг начала координат и т. д., используйте матричные операции $2\times 2$.
Практическая задача 1 :
Найдите сумму $A+B$ и разность $B-A$ матриц $$A=\left(
\begin{массив}{cc}
2 и 10 \\
15 и -6\
\конец{массив}
\право)\четырехъядерный\mbox{и}\четырехъядерный B=\левый(
\begin{массив}{cc}
-13 и -4\
13 и 0 \\
\конец{массив}
\справа)$$ Практическая задача 2 :
Переместите матрицу вершин $\left(
\begin{массив}{cc}
1 и 3 \\
5 и -6 \\
\конец{массив}
\right)$ по матрице $\left(
\begin{массив}{cc}
-1 и 2 \\
-1 и 2 \\
\конец{массив}
\справа)$.
Калькулятор сложения и вычитания матриц 2×2, формула, пример расчета (работа с шагами), реальные задачи и практические задачи были бы очень полезны для учащихся начальной школы (образование K-12), чтобы понять сложение и вычитание двух или более матриц. Используя эту концепцию, они могут смотреть на реальные жизненные ситуации и преобразовывать их в математические модели.
- Калькулятор определителя матрицы 4×4, 3×3 и 2×2
- Калькулятор матрицы транспонирования
- NXN Обратный матричный калькулятор
- 4×4 Кальциральный калькулятор с добавлением матрицы 4×4 3×3 Матрикс Умнозируемый матричный калькулятор. Калькулятор
- Калькулятор исключения Гаусса
Калькулятор сложения матриц 3×3
- Вход в систему
- Регистр
- Главная
- Математика
- Финансы
- Инженерная разработка
Рассчитайте
Отчет об этом объявлении
3X3.
MATRICLEAL. матрицы и вычисляет их сумму. Это математический онлайн-инструмент, специально
запрограммирован для выполнения сложения матриц между двумя матрицами $3\times 3$.
Необходимо выполнить следующие шаги:
- Введите в поле две матрицы $3\times3$. Элементы матриц должны быть действительными числами.
- Нажмите кнопку » GENERATE WORK «, чтобы произвести вычисления;
- Калькулятор сложения матриц 3×3 выдаст сумму двух матриц $3\times3$, представленных в виде матрицы.
Ввод: Две матрицы $3\times3$;
Вывод: Матрица $3\times3$.
$3\times 3$ Формула сложения матриц:
Сумма двух матриц $A=[a_{ij}]_{3\times3}$ и $B=[a_{ij}]_{3\ times3}$ определяется по следующей формуле $$\begin{align}&\left( \begin{массив}{ccc} а_{11} и а_{12} и а_{13} \\ а_{21} и а_{22} и а_{23} \\ а_{31} и а_{32} и а_{33} \\ \конец{массив} \справа)+ \оставил( \begin{массив}{ccc} б_{11} и б_{12} и б_{13} \\ б_{21} и б_{22} и б_{23} \\ б_{31} &б_{32} & б_{33} \\ \конец{массив} \right)= \left(\begin{массив}{ccc} a_{11}+b_{11}& a_{12}+b_{12}& a_{13}+b_{13} \\ a_{21}+b_{21} &a_{22}+b_{22}& a_{23}+b_{23}\\ a_{31}+b_{31} &a_{32}+b_{32} & a_{33}+b_{33}\\ \end{массив}\right)\end{align}$$
Матрицы — мощный инструмент в математике, науке и жизни.
Матрицы повсюду, и у них есть важные приложения. Например, электронная таблица, такая как Excel, или письменная таблица представляет собой матрицу. Слово «матрица» является латинским словом и означает «матка». Этот термин был введен Дж. Дж. Сильвестром (английский математик) в 1850 г.
Первая потребность в матрицах возникла при изучении систем одновременных линейных уравнений.
Матрица представляет собой прямоугольный массив чисел, расположенных следующим образом
$$А=\влево(
\begin{массив}{cccc}
а_{11} и а_{12} и \ldots&a_{1n} \\
a_{21} & a_{22} & \ldots& a_{2n} \\
\ldots &\ldots &\ldots&\ldots\\
a_{m1} & a_{m2} & \ldots&a_{mn} \\
\конец{массив}
\справа)=\слева[
\begin{массив}{cccc}
а_{11} и а_{12} и \ldots&a_{1n} \\
a_{21} & a_{22} & \ldots& a_{2n} \\
\ldots &\ldots &\ldots&\ldots\\
a_{m1} & a_{m2} & \ldots&a_{mn} \\
\конец{массив}
\право]$$
Существует два обозначения матрицы: в круглых скобках или квадратных скобках. Члены матрицы называются ее элементами или ее элементами.
Матрицы чаще всего обозначаются прописными буквами, а соответствующие им строчные буквы с двумя нижними индексами являются элементами матриц.
Например, матрицы обозначаются $A,B,\ldots Z$, а ее элементы — $a_{11}$ или $a_{1,1}$ и т. д. Горизонтальные и вертикальные строки элементов матрицы называются строк и столбцов соответственно.
Размер матрицы — это произведение Декарта на количество содержащихся в ней строк и столбцов. Матрица, состоящая из $m$ строк и $n$ столбцов, называется $m\times n$ матрицей. В этом случае $m$ и $n$ — его размерности. Если матрица состоит только из одной строки, она называется матрицей-строкой. Если матрица состоит только из одного столбца, она называется матрицей-столбцом. Матрица, содержащая в качестве элементов только нули, называется нулевой матрицей.
Как найти сумму двух матриц 3×3?
Матрицы $A$ и $B$ можно складывать тогда и только тогда, когда их размеры равны. Их сумма представляет собой матрицу $C=A+B$ с элементами
$$c_{ij}=a_{ij}+b_{ij}$$
Матрица суммы имеет тот же размер, что и матрицы $A$ и $B$.
Это означает, что каждый элемент в $C$ равен сумме элементов в $A$ и $B$, стоящих на соответствующих местах.
Например,
$c_{13}=a_{13}+b_{13}$. Если две матрицы имеют разные размеры, их сумма не определена.
Легко доказать, что $A+B=B+A$, другими словами, сложение матриц является коммутативной операцией.
Матрица $3\times 3$ имеет $3$ столбцов и $3$ строк. Например, сумма двух $3\times 3$ матриц $A$ и $B$ есть такая матрица $C$, что
$$\begin{align} C=&\left(
\begin{массив}{ccc}
а_{11} и а_{12} и а_{13} \\
а_{21} и а_{22} и а_{23} \\
а_{31} и а_{32} и а_{33} \\
\конец{массив}
\справа)+
\оставил(
\begin{массив}{ccc}
б_{11} и б_{12} и б_{13} \\
б_{21} и б_{22} и б_{23} \\
б_{31} &б_{32} & б_{33} \\
\конец{массив}
\right)= \left(\begin{массив}{ccc}
a_{11}+b_{11}& a_{12}+b_{12}& a_{13}+b_{13} \\
a_{21}+b_{21} &a_{22}+b_{22}& a_{23}+b_{23} \\
a_{31}+b_{31} &a_{32}+b_{32} & a_{33}+b_{33} \\
\end{массив}\right)\end{align}$$
Например, найдем сумму для
$$А=\влево(
\begin{массив}{ccc}
10 и 20 и 10\
4 и 5 и 6 \\
2 и 3 и 5 \\
\конец{массив}
\право)\четырехъядерный\mbox{и}\четырехъядерный B=\левый(
\begin{массив}{ccc}
3 и 2 и 4 \\
3 и 3 и 9\\
4 и 4 и 2 \\
\конец{массив}
\справа)$$
По формуле сложения матриц сумма матриц $A$ и $B$ есть матрица
$$A+B=\влево(
\begin{массив}{ccc}
10+3 и 20+2 и 10+4 \\
4+3 и 5+3 и 6+9 \\
2+4 и 3+4 и 5+2 \\
\конец{массив}
\справа)=\слева(
\begin{массив}{ccc}
13 и 22 и 14\
7 и 8 и 15\
6 и 7 и 7 \\
\конец{массив}
\справа)$$
Работа по сложению матриц $3\times 3$ с шагами показывает полный пошаговый расчет для нахождения суммы двух матриц $3\times3$ $A$ и $B$ по формуле сложения матриц.
Для любых других матриц просто укажите элементы матриц $2$ в виде действительных чисел и нажмите кнопку GENERATE WORK. Учащиеся начальной школы могут использовать это сложение матриц $3\x3$ для создания работы, проверки результатов сложения матриц, полученных вручную, или для эффективного решения домашних заданий.
Реальные задачи с использованием сложения матриц 3×3
Чтобы представить данные с помощью матрицы, мы выберем, какая категория будет представлена столбцами, а какая — строками. Например, было проведено исследование, чтобы выяснить, какие виды спорта наиболее популярны и как они могут привлечь больше людей. Приведенная ниже матрица представляет их выводы (в процентах людей)
Матрицы широко используются в геометрии, физике и компьютерной графике. Под матричными вычислениями можно понимать набор инструментов, предполагающий изучение методов и процедур, используемых для сбора, классификации и анализа данных. Во многих приложениях необходимо вычислить сложение матриц, где этот онлайн-калькулятор сложения матриц 3×3 может помочь нам легко упростить вычисления для соответствующих входных данных.
3×3 Практические задачи на сложение матриц
Практическая задача 1 :
Найдите сумму матриц $$X=\left(
\begin{массив}{ccc}
-4&2&10\
-7 и 15 и -6\
12 и 0 и 5 \\
\конец{массив}
\right)\quad\mbox{and}\quad Y=\left(
\begin{массив}{ccc}
-13 и 0 и -4 \
13 & 0 & 0 \\
45 и 8 и 2\
\конец{массив}
\справа)$$ Практическая задача 2 :
Дан треугольник $\Delta ABC$ в трехмерной координатной плоскости с $A(0,0,1),$ $B(3,6,2)$ и $C(-4,6, 7)$. Перенесите этот треугольник на вектор $\vec a=(1,2,4)$.
Калькулятор сложения матриц 3×3, формула, пример расчета (работа с шагами), реальные задачи и практические задачи были бы очень полезны для учащихся начальной школы (образование K-12), чтобы понять сложение двух или более матриц. Используя эту концепцию, они могут смотреть на реальные жизненные ситуации и преобразовывать их в математические модели.
- Калькулятор определителя матрицы 4×4, 3×3 и 2×2
- Калькулятор транспонированной матрицы
- nxn Калькулятор обратной матрицы
- 4×4 Matrix Addition & Subtraction Calculator
- 3×3 Matrix Subtraction Calculator
- 2×2 Matrix Addition & Subtraction Calculator
- 4×4 Matrix Multiplication Calculator
- 3×3 Matrix Multiplication Calculator
- 2×2 Matrix Multiplication Calculator
- Squared Matrix Calculator
- Gauss Калькулятор исключения
404 — СТРАНИЦА НЕ НАЙДЕНА
Почему я вижу эту страницу?
404 означает, что файл не найден.
Если вы уже загрузили файл, имя может быть написано с ошибкой или файл находится в другой папке.
Вы можете получить ошибку 404 для изображений, поскольку у вас включена защита от горячих ссылок, а домен отсутствует в списке авторизованных доменов.
Если вы перейдете по временному URL-адресу (http://ip/~username/) и получите эту ошибку, возможно, проблема связана с набором правил, хранящимся в файле .htaccess. Вы можете попробовать переименовать этот файл в .htaccess-backup и обновить сайт, чтобы посмотреть, решит ли это проблему.
Также возможно, что вы непреднамеренно удалили корневую папку документа или вам может потребоваться повторное создание вашей учетной записи. В любом случае, пожалуйста, немедленно свяжитесь с вашим веб-хостингом.
Вы используете WordPress? См. Раздел об ошибках 404 после перехода по ссылке в WordPress.
Как найти правильное написание и папку
Отсутствующие или поврежденные файлы Когда вы получаете ошибку 404, обязательно проверьте URL-адрес, который вы пытаетесь использовать в своем браузере.
Это сообщает серверу, какой ресурс он должен использовать попытка запроса.
http://example.com/example/Example/help.html
В этом примере файл должен находиться в папке public_html/example/Example/
Обратите внимание, что в этом примере важен CaSe . На платформах, которые обеспечивают чувствительность к регистру, e xample и E xample не являются одними и теми же местами.
Для дополнительных доменов файл должен находиться в папке public_html/addondomain.com/example/Example/, а имена чувствительны к регистру.
Разбитое изображениеЕсли на вашем сайте отсутствует изображение, вы можете увидеть на своей странице поле с красным размером X , где отсутствует изображение. Щелкните правой кнопкой мыши X и выберите «Свойства». Свойства сообщат вам путь и имя файла, который не может быть найден.
Это зависит от браузера. Если вы не видите на своей странице поле с красным X , попробуйте щелкнуть правой кнопкой мыши на странице, затем выберите «Просмотреть информацию о странице» и перейдите на вкладку «Мультимедиа».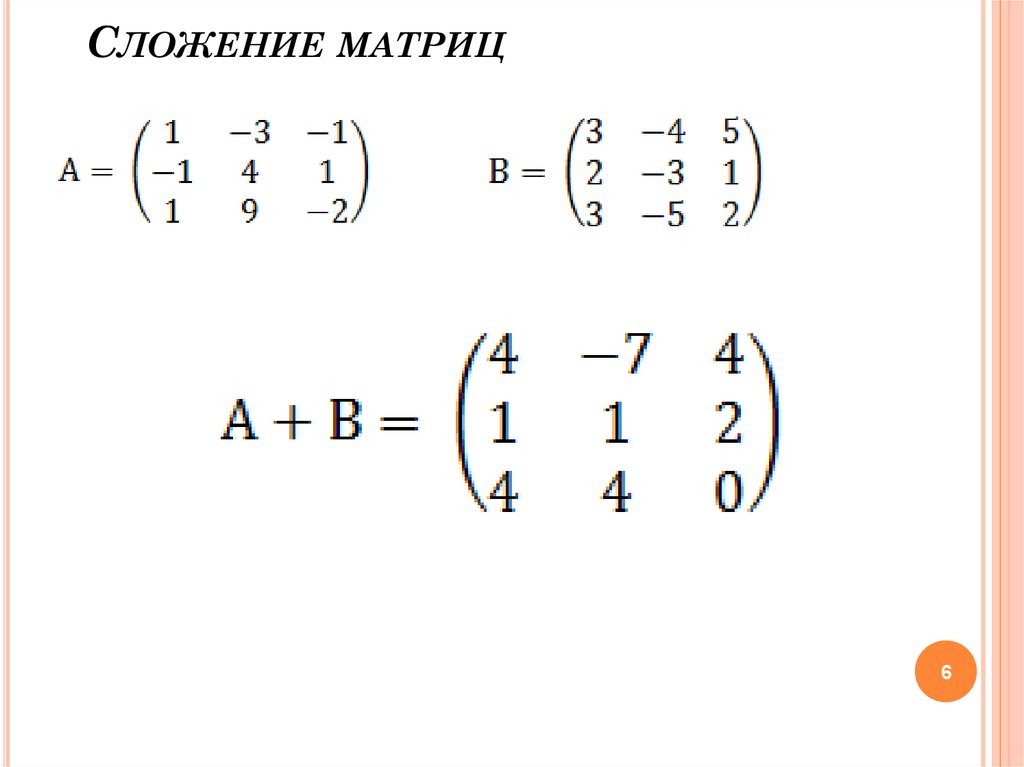
http://example.com/cgi-sys/images/banner.PNG
В этом примере файл изображения должен находиться в папке public_html/cgi-sys/images/
Обратите внимание, что в этом примере важен CaSe . На платформах с учетом регистра символов PNG и png не совпадают.
Ошибки 404 после перехода по ссылкам WordPress
При работе с WordPress ошибки 404 Page Not Found часто могут возникать при активации новой темы или изменении правил перезаписи в файле .htaccess.
Когда вы сталкиваетесь с ошибкой 404 в WordPress, у вас есть два варианта ее исправления.
Вариант 1. Исправьте постоянные ссылки- Войдите в WordPress.
- В меню навигации слева в WordPress нажмите Настройки > Постоянные ссылки (Обратите внимание на текущую настройку. Если вы используете пользовательскую структуру, скопируйте или сохраните ее где-нибудь. )
- Выберите По умолчанию .
- Нажмите Сохранить настройки .
- Верните настройки к предыдущей конфигурации (до того, как вы выбрали «По умолчанию»). Верните пользовательскую структуру, если она у вас была.
- Нажмите Сохранить настройки .
)Во многих случаях это сбросит постоянные ссылки и устранит проблему. Если это не сработает, вам может потребоваться отредактировать файл .htaccess напрямую.
Вариант 2. Измените файл .htaccess Добавьте следующий фрагмент кода 9index.php$ — [L]
RewriteCond %{REQUEST_FILENAME} !-f
RewriteCond %{REQUEST_FILENAME} !-d
RewriteRule . /index.php [L]
# Конец WordPress
Если ваш блог показывает неправильное доменное имя в ссылках, перенаправляет на другой сайт или отсутствуют изображения и стиль, все это обычно связано с одной и той же проблемой: в вашем блоге WordPress настроено неправильное доменное имя.
Как изменить файл .htaccess
Файл .htaccess содержит директивы (инструкции), которые сообщают серверу, как вести себя в определенных сценариях, и напрямую влияют на работу вашего веб-сайта.
Перенаправление и перезапись URL-адресов — это две очень распространенные директивы, которые можно найти в файле .htaccess, и многие скрипты, такие как WordPress, Drupal, Joomla и Magento, добавляют директивы в .htaccess, чтобы эти скрипты могли работать.
Возможно, вам потребуется отредактировать файл .htaccess в какой-то момент по разным причинам. В этом разделе рассматривается, как редактировать файл в cPanel, но не то, что может потребоваться изменить. статьи и ресурсы для этой информации.)
Существует множество способов редактирования файла .htaccess- Отредактируйте файл на своем компьютере и загрузите его на сервер через FTP
- Использовать режим редактирования программы FTP
- Использовать SSH и текстовый редактор
- Используйте файловый менеджер в cPanel
Самый простой способ отредактировать файл .
htaccess для большинства людей — через диспетчер файлов в cPanel.
Прежде чем что-либо делать, рекомендуется сделать резервную копию вашего веб-сайта, чтобы вы могли вернуться к предыдущей версии, если что-то пойдет не так.
Откройте файловый менеджер- Войдите в cPanel.
- В разделе «Файлы» щелкните значок File Manager .
- Установите флажок для Корень документа для и выберите доменное имя, к которому вы хотите получить доступ, из раскрывающегося меню.
- Убедитесь, что установлен флажок Показать скрытые файлы (dotfiles) «.
- Нажмите Перейти . Файловый менеджер откроется в новой вкладке или окне.
- Найдите файл .htaccess в списке файлов. Возможно, вам придется прокрутить, чтобы найти его.
- Щелкните правой кнопкой мыши файл .
