Онлайн калькулятор умножения вектора на число
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Укажите размерность пространства 23
Укажите форму представления вектора Координаты точек начала и конца вектораКоординаты вектора
Задайте координаты вектора
Задайте значение числа q на которое нужно умножить вектор
q =
Как умножить вектор на число
Пример 1. Умножим вектор плоскости на число q. Координаты вектора заданны точками.
Умножим вектор плоскости на число q. Координаты вектора заданны точками.
Координаты точки А вектора AB: (5 ; 9)
Координаты точки B вектора AB: (-2 ; 11)
Числа q на которое нужно умножить вектор AB = 12
Для того, чтобы вектор умножить на число, необходимо каждую координату вектора умножить на данное число.
Вычислим координаты первого вектора по двум точкам A и B:
AB = {Bx — Ax; By — Ay} = {-2 — 5 ; 11 — 9} = {-7 ; 2}
AB ⋅ q = {ABx ⋅ q ; ABy ⋅ q} = {-7 ⋅ 12 ; 2 ⋅ 12} = {-84 ; 24}
Пример 2. Умножим вектор пространства на число q.
Координаты вектора a: (5 ; 9 ; -2)
Числа q на которое нужно умножить вектор a = 2.6
Для того, чтобы вектор умножить на число, необходимо каждую координату вектора умножить на данное число.
a ⋅ q = {ax ⋅ q ; ay ⋅ q ; az ⋅ q} = {5 ⋅ 2. 6 ; 9 ⋅ 2.6 ; -2 ⋅ 2.6} = {13 ; 117/5 ; -26/5} = {13 ; 23.4 ; -5.2}
6 ; 9 ⋅ 2.6 ; -2 ⋅ 2.6} = {13 ; 117/5 ; -26/5} = {13 ; 23.4 ; -5.2}
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона.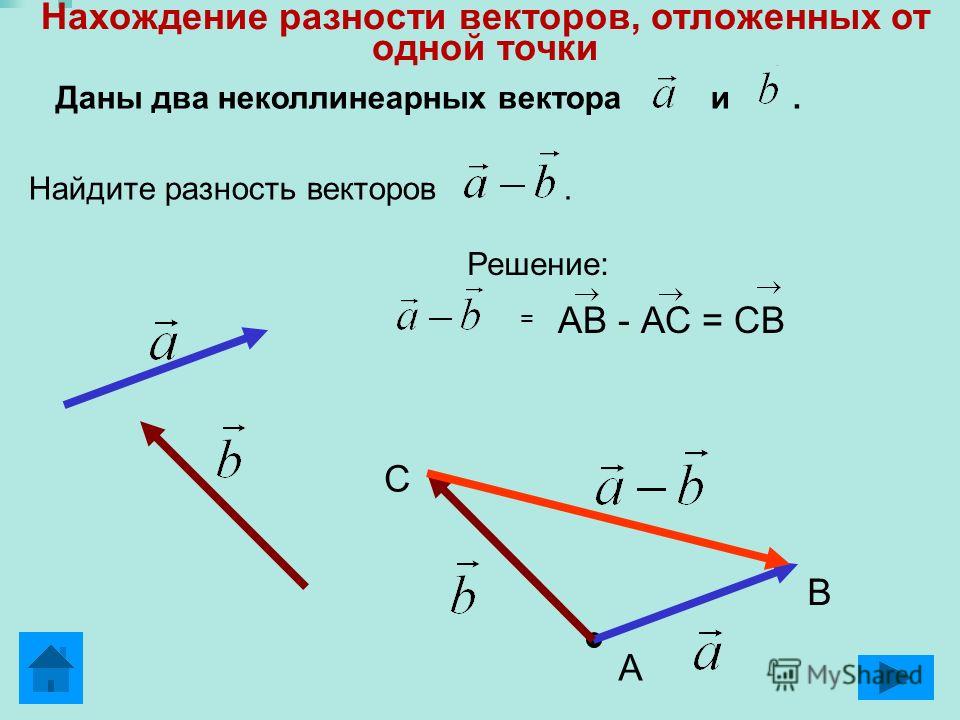 Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Калькулятор Векторного Произведения | Примеры И Формулы
Математические Калькуляторы
Калькулятор векторного произведения векторов находит произведение двух векторов в трехмерном пространстве.
Vector A
Vector B
Vector C = A × B
Оглавление
| ◦Что такое перекрестный продукт? |
| ◦Формула расчета перекрестных произведений |
| ◦Определение перекрестного продукта |
| ◦Как рассчитать векторное произведение двух векторов |
| ◦Что такое кросс-продукт? |
Чтобы определить перекрестное произведение нового вектора, вам необходимо ввести в калькулятор значения x, y и z двух векторов.
Что такое перекрестный продукт?
Перекрестное произведение — это математическая операция, которая берет два вектора и создает новый вектор. Он используется во многих областях, включая инженерию, физику и математику. В этом сообщении блога мы собираемся изучить, что такое перекрестный продукт и что он может сделать для нас. Мы также приведем пример того, как это используется в физике. Так что читайте дальше, чтобы узнать больше!
Формула расчета перекрестных произведений
Формула для вычисления нового вектора векторного произведения двух векторов следующая:
Где θ — угол между a и b в плоскости, содержащей их. (Всегда от 0 до 180 градусов)
‖A‖ и ‖b‖ — модули векторов a и b
и n — единичный вектор, перпендикулярный a и b.
В терминах векторных координат мы можем упростить приведенное выше уравнение до следующего:
a x b = (a2*b3-a3*b2, a3*b1-a1*b3, a1*b2-a2*b1)
Где a и b — векторы с координатами (a1, a2, a3) и (b1, b2, b3).
Направление результирующего вектора можно определить с помощью правила правой руки.
Определение перекрестного продукта
Перекрестное произведение, также известное как векторное произведение, представляет собой математическую операцию. В операции перекрестного произведения результатом произведения двух векторов является новый вектор, перпендикулярный обоим векторам. Величина этого нового вектора равна площади параллелограмма со сторонами двух исходных векторов.
Перекрестное произведение не следует путать с скалярным произведением. Скалярное произведение — это более простая алгебраическая операция, которая возвращает одно число, а не новый вектор.
Как рассчитать векторное произведение двух векторов
Вот пример вычисления перекрестного произведения для двух векторов.
Во-первых, нужно собрать два вектора: вектор A и вектор B. В этом примере мы предположим, что вектор A имеет координаты (2, 3, 4), а вектор B имеет координаты (3, 7, 8).
После этого мы используем упрощенное уравнение, приведенное выше, для расчета результирующих векторных координат продукта.
Наш новый вектор будет обозначен как C, поэтому сначала нам нужно найти координату X. Используя приведенную выше формулу, мы находим X равным -4.
Используя тот же метод, мы затем находим y и z равными 0,4 и 5 соответственно.
Наконец, у нас есть наш новый вектор из перекрестного произведения X b из (-4, -4,5)
Важно помнить, что перекрестное произведение является антикоммутативным, что означает, что результат a X b не совпадает с результатом b X a. По факту:
a X b = -b X a.
Что такое кросс-продукт?
Перекрестное произведение — это векторное произведение, перпендикулярное обоим исходным векторам и имеющее одинаковую величину.
Автор статьи
John Cruz
Джон — аспирант, увлеченный математикой и образованием. В свободное время Джон любит ходить в походы и кататься на велосипеде.
Калькулятор Векторного Произведения русский
Опубликовано: Sun Jul 04 2021
В категории Математические калькуляторы
Добавьте Калькулятор Векторного Произведения на свой сайт
Калькулятор Векторного Произведения на других языках
متجه عبر آلة حاسبة المنتجCalculatrice De Produits Croisés VectorielsVektor Kreuzprodukt Rechnerベクトル外積計算機वेक्टर क्रॉस उत्पाद कैलकुलेटरVektör Çapraz Ürün Hesap MakinesiPerkalian Vektor KalkulatorCalculator Vector De Produse ÎncrucișateВектарны Крыжаваны КалькулятарVektorová Krížová Produktová Kalkulačka
Как добавить Калькулятор Векторного Произведения на мой сайт?
Вы можете легко добавить Калькулятор Векторного Произведения на свой веб-сайт с помощью нашего кода. Вставьте код на свой веб-сайт, и калькулятор автоматически появится на этом месте!
Вставьте код на свой веб-сайт, и калькулятор автоматически появится на этом месте!
Как добавить виджет Калькулятор Векторного Произведения на сайт WordPress?
Добавить Калькулятор Векторного Произведения на ваш сайт Wordpres быстро и легко! Найдите страницу, на которую вы хотите добавить калькулятор, перейдите в режим редактирования, нажмите «Текст» и вставьте туда код.
Как добавить HTML-виджет на страницу WordPress с помощью нового редактора кодаКак добавить HTML-виджет на страницу WordPress с помощью старого редактора кода
Другие математические калькуляторы
Калькулятор Треугольников 30 60 90
Калькулятор Ожидаемой Стоимости
Математический Онлайн Калькулятор
Калькулятор Стандартного Отклонения
Калькулятор Процентов
Калькулятор Дробей
Конвертер Фунтов В Чашки: Мука, Сахар, Молоко..
Калькулятор Окружности
Калькулятор Формулы Двойного Угла
Вычисление Корня
Калькулятор Площади Треугольника
Калькулятор Котерминального Угла
Калькулятор Скалярного Произведения
Калькулятор Средней Точки
Конвертер Значащих Цифр (калькулятор Sig Figs)
Калькулятор Длины Дуги Для Круга
Калькулятор Балльной Оценки
Калькулятор Процентного Увеличения
Калькулятор Процентной Разницы
Калькулятор Линейной Интерполяции
Калькулятор QR-разложения
Калькулятор Транспонирования Матрицы
Калькулятор Гипотенузы Треугольника
Калькулятор Тригонометрии
Калькулятор Стороны И Угла Прямоугольного Треугольника (калькулятор Треугольника)
45 45 90 Калькулятор Треугольника (калькулятор Прямоугольного Треугольника)
Калькулятор Умножения Матриц
Калькулятор Среднего
Генератор Случайных Чисел
Калькулятор Погрешности
Калькулятор Угла Между Двумя Векторами
LCM Calculator — Калькулятор Наименьшего Общего Кратного
Калькулятор Площади В Квадратных Футах
Калькулятор Экспоненты (калькулятор Мощности)
Калькулятор Математического Остатка
Правило Трех Калькуляторов — Прямая Пропорция
Калькулятор Квадратичных Формул
Калькулятор Суммы
Калькулятор Периметра
Калькулятор Z-счета (значение Z)
Калькулятор Фибоначчи
Калькулятор Объема Капсулы
Калькулятор Объема Пирамиды
Калькулятор Объема Треугольной Призмы
Калькулятор Объема Прямоугольника
Калькулятор Объема Конуса
Калькулятор Объема Куба
Калькулятор Объема Цилиндра
Калькулятор Масштабного Коэффициента Расширения
Калькулятор Индекса Разнообразия Шеннона
Калькулятор Теоремы Байеса
Калькулятор Антилогарифмов
Eˣ Калькулятор
Калькулятор Простых Чисел
Калькулятор Экспоненциального Роста
Калькулятор Размера Выборки
Калькулятор Обратного Логарифма (логарифма)
Калькулятор Распределения Пуассона
Мультипликативный Обратный Калькулятор
Калькулятор Процента Оценок
Калькулятор Отношения
Калькулятор Эмпирических Правил
Калькулятор P-значения
Калькулятор Объема Шара
Калькулятор Чистой Приведенной Стоимости
Расстояние между прямыми в пространстве онлайн
С помощю этого онлайн калькулятора можно найти расстояние между прямыми в пространстве. Дается подробное решение с пояснениями. Для вычисления расстояния между прямыми в пространстве, задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».
Дается подробное решение с пояснениями. Для вычисления расстояния между прямыми в пространстве, задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2:
где M1(x1, y1, z1) и M2(x2, y2, z2) − точки, лежащие на прямых L1 и L2, а q1={m1, p1, l1} и q2={m2, p2, l2} − направляющие векторы прямых L1 и L2, соответственно.
Прямые (1) и (2) в пространстве могут совпадать, быть паралленьными, пересекаться, или быть скрещивающимся. Если прямые в пространстве пересекаются или совпадают, то расстояние между ними равно нулю. Мы рассмотрим два случая. Первый − прямые параллельны, и второй − прямые скрещиваются. Остальные являются частыми случаями. Если при вычислении расстояния между параллельными прямыми мы получим расстояние равным нулю, то это значит, что эти прямые совпадают. Если же расстояние между скрещивающимися прямыми равно нулю, то эти прямые пересекаются.
1. Расстояние между параллельными прямыми в пространстве
Рассмотрим два метода вычисления расстояния между прямыми.
Метод 1. От точки M1 прямой L1 проводим плоскость α, перпендикулярно прямой L2. Находим точку M3(x3, y3, y3) пересечения плоскости α и прямой L3. По сути мы находим проекцию точки M1 на прямую L2. Как найти проекцию точки на прямую посмотрите здесь. Далее вычисляем расстояние между точками M1(x1, y1, z1) и M3(x3, y3, z3):
Как найти проекцию точки на прямую посмотрите здесь. Далее вычисляем расстояние между точками M1(x1, y1, z1) и M3(x3, y3, z3):
которое и является расстоянием между прямыми L1 и L2 (Рис.1).
Пример 1. Найти расстояние между прямыми L1 и L2:
Решение. Прямая L1 проходит через точку M1(x1, y1, z1)=M1(1, 2, 1) и имеет направляющий вектор
| q1={m1, p1, l1}={1, −2, 4} |
Прямая L2 проходит через точку M2(x2, y2, z2)=M2(8, 4, 1) и имеет направляющий вектор
| q2={m2, p2, l2}={2, −4, 8} |
Найдем проекцию точки M1 на прямую L2. Для этого построим плоскость α, проходящей через точку M1 и перпендикулярной прямойL2.
Для этого построим плоскость α, проходящей через точку M1 и перпендикулярной прямойL2.
Для того, чтобы плоскость α было перепендикулярна прямой L2, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L2, т.е. в качестве нормального вектора плоскости α можно взять направляющий вектор прямой L2. Тогда уравнение искомой плоскости, проходящей через точку M1(x1, y1, z1) имеет следующий вид:
| m2{x−x1)+p2(y−y1)+ l2(z−z1)=0 | (5) |
Подставляя значения m2, p2, l2, x1, y1, z1 в (5) получим :
| 2(x−1)−4(y−2)+ 8(z−1)=0 |
После упрощения получим уравнение плоскости, проходящей через точку M1 и перпендикулярной прямой L2:
| 2x−4y+ 8z−2=0 | (6) |
Найдем точку пересечения прямой L2 и плоскости α, для этого построим параметрическое уравнение прямой L2.
Выразив переменные x, y, z через параметр t, получим параметрическое уравнение прямой L2:
Чтобы найти точку пересечения прямой L2 и плоскости α, подставим значения переменных x, y, z из (7) в (6):
Решив уравнение получим:
Подставляя полученное значение t в (7), получим точку пересеченияпрямой L2 и плоскости α:
Остается найти расстояние между точками M1 и M3:
Ответ: Расстояние между прямыми L1 и L2 равно d=7.2506.
Метод 2. Найдем расстояние между прямыми L1 и L2 (уравнения (1) и (2)). Во первых, проверяем параллельность прямых L1 и L2. Если направляющие векторы прямых L1 и L2 коллинеарны, т.е. если существует такое число λ, что выполнено равенство q1=λq2, то прямые L1 и L2 параллельны.
Данный метод вычисления расстояния между параллельными векторами основана на понятии векторного произведения векторов. Известно, что норма векторного произведения векторов и q1 дает площадь параллелограмма, образованного этими векторами (Рис.2). Узнав площадь параллелограмма, можно найти вершину параллелограмма d, разделив площадь на основание q1 параллелограмма.
Вычислим координаты вектора :
Вычислим векторное произведение векторов и q1:
Вычисляя определители второго порядка находим координаты вектора c:
| c=(c1, c2, c3). |
Далее находим площадь параллелограмма:
Расстояние между прямыми L1 и L2 равно:
где
Пример 2. Решим пример 1 методом 2. Найти расстояние между прямыми
и
Решение. Прямая L1 проходит через точку M1(x1, y1, z1)=M1(1, 2, 1) и имеет направляющий вектор
| q1={m1, p1, l1}={1, −2, 4} |
Прямая L2 проходит через точку M2(x2, y2, z2)=M2(8, 4, 1) и имеет направляющий вектор
| q2={m2, p2, l2}={2, −4, 8} |
Векторы q1 и q2 коллинеарны. Следовательно прямые L1 и L2 параллельны. Для вычисления расстояния между параллельными прямыми воспользуемся векторным произведением векторов.
Следовательно прямые L1 и L2 параллельны. Для вычисления расстояния между параллельными прямыми воспользуемся векторным произведением векторов.
Построим вектор ={x2−x1, y2−y1, z2−z1}={7, 2, 0}.
Вычислим векторное произведение векторов и q1. Для этого составим 3×3 матрицу, первая строка которой базисные векторы i, j, k, а остальные строки заполнены элементами векторов и q1:
Вычислим определитель этой матрицы, разложив ее по первой строке. Результатом этих вычислений получим векторное произведение векторов и q1:
Таким образом, результатом векторного произведения векторов и q1 будет вектор:
Поскольку векторное произведение векторов и q1 дает плошадь параллелограмма образованным этими векторами, то расстояние между прямыми L1 и L2 равно :
Ответ: Расстояние между прямыми L1 и L2 равно d=7. 25061.
25061.
2. Расстояние между скрещивающимися прямыми в пространстве
Пусть задана декартова прямоугольная симтема координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2 (уравнения (1) и (2)).
Пусть прямые L1 и L2 не параллельны (паралельные прямые мы расстотрели в предыдущем параграфе). Чтобы найти расстояние между прямыми L1 и L2 нужно построить параллельные плоскости α1 и α2 так, чтобы прямая L1 лежал на плоскости α1 а прямая L2 − на плоскости α2. Тогда расстояние между прямыми L1 и L2 равно расстоянию между плоскостями L1 и L2 (Рис. 3).
Поскольку плоскость α1, проходит через прямую L1, то он проходит также через M1(x1, y1, z1). Следовательно справедливо следующее равенство:
Следовательно справедливо следующее равенство:
| A1x1+B1y1+C1z1+D1=0. | (27) |
где n1={A1, B1, C1} − нормальный вектор плоскости α1. Для того, чтобы плоскость α1 проходила через прямую L1, нормальный вектор n1 должен быть ортогональным направляющему вектору q1 прямой L1, т.е. скалярное произведение этих векторов должен быть равным нулю:
| A1m1+B1p1+C1l1=0. | (28) |
Так как плоскость α1 должна быть параллельной прямой L2, то должна выполнятся условие:
A1m2+B1p2+C1l2=0. | (29) |
Решая систему линейных уравнений (27)−(29), с тремя уравнениями и четыремя неизвестными A1, B1, C1, D1, и подставляя в уравнение
| A1x+B1y+C1z+D1=0. | (30) |
получим уравнение плоскости α1. (Как построить уравнение плоскости, проходящей через прямую, параллельно другой прямой подробно изложено здесь).
Аналогичным образом находим уравнение плоскости α2:
| A2x+B2y+C2z+D2=0. | (31) |
Плоскости α1 и α2 параллельны, следовательно полученные нормальные векторыn1={A1, B1, C1} и n2={A2, B2, C2} этих плоскостей коллинеарны. Если эти векторы не равны, то можно умножить (31) на некторое число так, чтобы полученный нормальный вектор n2 совпадал с нормальным вектором уравнения (30).
Если эти векторы не равны, то можно умножить (31) на некторое число так, чтобы полученный нормальный вектор n2 совпадал с нормальным вектором уравнения (30).
Тогда расстояние между параллельными плоскостями вычисляется формулой:
Полученное расстояние между плоскостями α1 и α2 является также расстоянием между прямыми L1 и L2.
Пример 3. Найти расстояние между прямыми
и
Решение. Прямая L1 проходит через точку M1(x1, y1, z1)=M1(2, 1, 4) и имеет направляющий вектор q1={m1, p1, l1}={1, 3, −2}.
Прямая L2 проходит через точку M2(x2, y2, z2)=M2(6, −1, 2) и имеет направляющий вектор q2={m2, p2, l2}={2, −3, 7}.
Шаг 1.
Построим плоскость α1, проходящую через прямую L1, параллельно прямой L2.
Поскольку плоскость α1 проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(2, 1, 4) и нормальный вектор n1={m1, p1, l1} плоскости α1 перпендикулярна направляющему вектору q1 прямой L1. Тогда уравнение плоскости должна удовлетворять условию:
| A1x1+B1y1+C1z1+D1=0. | (34) |
а условие параллельности прямой L1 и искомой плоскости α1 представляется следующим условием:
A1m1+B1p1+C1l1=0.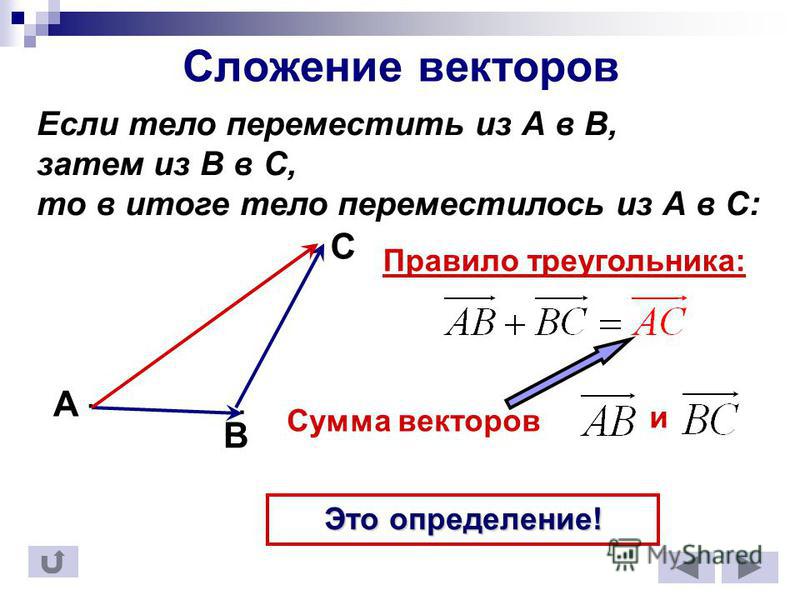 | (35) |
Так как плоскость α1 должна быть параллельной прямой L2, то должна выполнятся условие:
| A1m2+B1p2+C1l2=0. | (36) |
Таким образом мы должны решить систему трех уравнений с четырьмя неизвестными (34)−(36). Подставим значения x1, y1, z1, m1, p1, l1, m2, p2, l2 в (27)−(29):
| A1·2+B1·1+C1·4+D1=0. | (37) |
| A1·1+B1·3+C1·(−2)=0. | (38) |
A1·2+B1·(−3)+C1·7=0.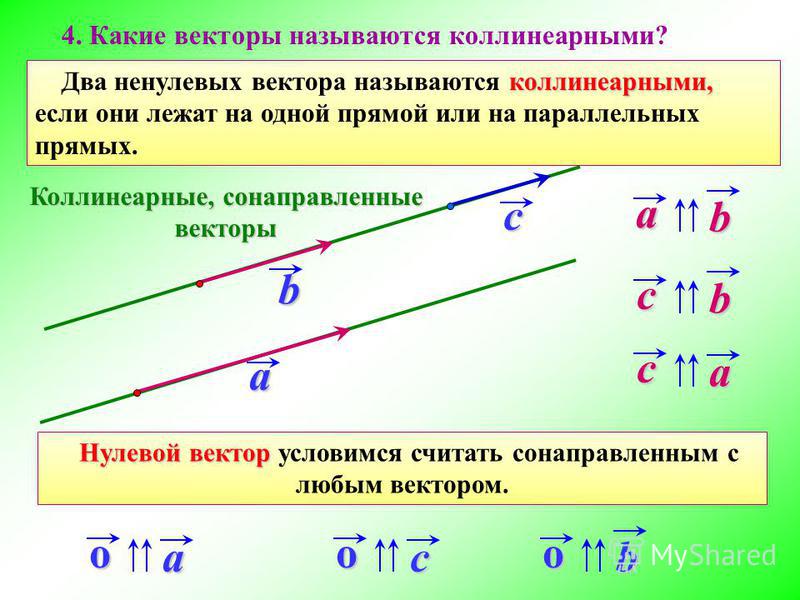 | (39) |
Представим эти уравнения в матричном виде:
Решим систему линейных уравнений (40) отностительно A1, B1, C1, D1:
Искомая плоскость может быть представлена формулой:
| A1x+B1y+C1z+D1=0. | (42) |
Подставляя значения A1, B1, C1, D1 в (42), получим:
Упростим уравнение, умножив на число 17.
Шаг 2.
Построим плоскость α2, проходящую через прямую L2, параллельно прямой L1.
Поскольку плоскость α2 проходит через прямую L2 , то она проходит также через точку M2(x2, y2, z2)=M2(6, −1, 2) и нормальный вектор n2={m2, p2, l2} плоскости α2 перпендикулярна направляющему вектору q2 прямой L2. Тогда уравнение плоскости должна удовлетворять условию:
Тогда уравнение плоскости должна удовлетворять условию:
| A2x2+B2y2+C2z2+D2=0. | (44) |
а условие параллельности прямой L2 и искомой плоскости α2 представляется следующим условием:
| A2m2+B2p2+C2l2=0. | (45) |
Так как плоскость α2 должна быть параллельной прямой L1, то должна выполнятся условие:
| A2m1+B2p1+C2l1=0. | (46) |
Таким образом мы должны решить систему трех уравнений с четырьмя неизвестными (37)−(39). Подставим значения x2, y2, z2, m2, p2, l2, m1, p1, l1 в (37)−(39):
Подставим значения x2, y2, z2, m2, p2, l2, m1, p1, l1 в (37)−(39):
| A1·6+B1·(−1)+C1·2+D1=0. | (47) |
| A1·2+B1·(−3)+C1·7=0. | (48) |
| A1·1+B1·3+C1·(−2)=0. | (49) |
Представим эти уравнения в матричном виде:
Решим систему линейных уравнений (50) отностительно A2, B2, C2, D2:
Искомая плоскость может быть представлена формулой:
A2x+B2y+C2z+D2=0. | (52) |
Подставляя значения A2, B2, C2, D2 в (52), получим:
Упростим уравнение, умножив на число −83.
Шаг 3.
Расстояние между построенными плоскостями (43) и (53) будет расстоянием между прямыми (1) и (2).
Запишем формулы уравнений плоскостей α1 и α2 :
| A1x+B1y+C1z+D1=0. |
| A2x+B2y+C2z+D2=0. |
где n1={A1, B1, C1}={15, −11, −9} и n2={A2, B2, C2}={15, −11, −9} − нормальные векторы плоскостей α1 и α2, соответственно, а свободные члены равны D1=17, D2=−83, соответственно.
Поскольку нормальные векторы плоскостей α1 и α2 совпадают, то можно найти расстояние между плоскостями α1 и α2, используя следующую формулу:
Подставим значения A1, B1, C1, D1, D2 в (54):
Упростим и решим:
Расстояние между прямыми равно: d=4.839339
Тензорное исчисление для чайников
Сергей Гаврилов
Тензорное исчисление для «чайников»
1-1. Инварианты……………………………………………………………………………………………………………………….. | 3 |
Введение в тему…………………………………………………………………………………………………………………. | 3 |
Начнем с вектора . | 4 |
Компоненты вектора…………………………………………………………………………………………………………… | 4 |
Матричное представление…………………………………………………………………………………………………… | 5 |
Переходим к другим координатам ……………………………………………………………………………………….. | 5 |
Длина вектора в прямоугольных координатах……………………………………………………………………….. | 5 |
Скаляр………………………………………………………………………………………………. | 6 |
Скалярное произведение……………………………………………………………………………………………………… | 6 |
Два сюрприза…………………………………………………………………………………………………………………….. | 6 |
И для чего они нужны…………………………………………………………………………………………………………. | 7 |
1-2. Базовые понятия тензорного исчисления……………………………………………………………………………. | 8 |
Ковариантность и контравариантность…………………………………………………………………………………. | 8 |
Правило Эйнштейна . | 8 |
О ковариантных векторах……………………………………………………………………………………………………. | 9 |
Тензоры…………………………………………………………………………………………………………………………….. | 9 |
Запись тензорных выражений ……………………………………………………………………………………………. | 10 |
Тензорные операции. Произведение…………………………………………………………………………………… | 10 |
Свертка…………………………………………………………………………………… | 11 |
Инварианты тензора …………………………………………………………………………………………………………. | 11 |
Метрический тензор …………………………………………………………………………………………………………. | 12 |
Упрощение тензора…………………………………………………………………………………………………………… | 13 |
Свойства метрического тензора …………………………………………………………………………………………. | 13 |
Единичный тензор ……………………………………………………………………………………………………………. | 13 |
2. | 14 |
Физические векторы и тензоры………………………………………………………………………………………….. | 14 |
Пространство СТО……………………………………………………………………………………………………………. | 15 |
Метрика 4-пространства……………………………………………………………………………………………………. | 15 |
Дифференциал интервала………………………………………………………………………………………………….. | 16 |
Четырехвекторы……………………………………………………………………….. | 16 |
Собственное время……………………………………………………………………………………………………………. | 17 |
Преобразования координат………………………………………………………………………………………………… | 17 |
Четырехскорость………………………………………………………………………………………………………………. | 18 |
Преобразования скорости………………………………………………………………………………………………….. | 19 |
4-вектор энергии-импульса………………………………………………………………………………………………… | 19 |
Энергия покоя и кинетическая энергия. | 21 |
4-сила ……………………………………………………………………………………………………………………………… | 22 |
3. Антисимметричные тензоры……………………………………………………………………………………………….. | 23 |
Альтернация…………………………………………………………………………………………………………………….. | 23 |
Векторное произведение. Псевдовекторы……………………………………………………………………………. | 24 |
Псевдотензоры………………………………………………………………………………………………. | 24 |
Псевдотензор Леви-Чивиты……………………………………………………………………………………………….. | 25 |
Для чего нужны псевдовекторы …………………………………………………………………………………………. | 26 |
Антисимметричный 4-тензор …………………………………………………………………………………………….. | 26 |
Векторные компоненты 4-тензора………………………………………………………………………………………. | 27 |
4. Тензоры в электродинамике………………………………………………………………………………………………… | 29 |
Сила Лоренца…………………… | 29 |
Тензор поля……………………………………………………………………………………………………………………… | 30 |
4-сила Лоренца…………………………………………………………………………………………………………………. | 30 |
Преобразование Лоренца для тензора…………………………………………………………………………………. | 31 |
Преобразование компонент поля………………………………………………………………………………………… | 32 |
Инварианты тензора поля…………………………………….. | 32 |
5. Тензорные поля…………………………………………………………………………………………………………………… | 34 |
Дифференцирование по координатам…………………………………………………………………………………. | 34 |
Вектор набла……………………………………………………………………………………………………………………. | 34 |
4-градиент скалярного поля……………………………………………………………………………………………….. | 35 |
Потенциальное поле …………………………………………………………………………………………………………. | 35 |
4-дивергенция векторного поля. | 36 |
4-ротор векторного поля……………………………………………………………………………………………………. | 36 |
Четырехмерный потенциал………………………………………………………………………………………………… | 37 |
Получаем уравнения Максвелла…………………………………………………………………………………………. | 38 |
«Магнитный заряд» ………………………………………………………………………………………………………….. | 39 |
6. Энергия-импульс…………………………………………………………………………………………….. | 41 |
Уравнение непрерывности…………………………………………………………………………………………………. | 41 |
4-ток……………………………………………………………………………………………………………………………….. | 42 |
Еще уравнения Максвелла…………………………………………………………………………………………………. | 42 |
Волновое уравнение………………………………………………………………………………………………………….. | 43 |
4-плотность потока массы …………………………………………………………………………………………………. | 45 |
Тензор энергии-импульса. | 45 |
7. Волны материи……………………………………………………………………………………………………………………. | 48 |
Волновой 4-вектор……………………………………………………………………………………………………………. | 48 |
Плоская волна………………………………………………………………………………………………………………….. | 48 |
Скорость света …………………………………………………………………………………………………………………. | 49 |
Решения волнового уравнения ……………………………………………. | 50 |
Уравнение Клейна-Гордона……………………………………………………………………………………………….. | 50 |
Инвариант волнового вектора ……………………………………………………………………………………………. | 51 |
Дуализм волн и частиц ……………………………………………………………………………………………………… | 51 |
Фотон ……………………………………………………………………………………………………………………………… | 53 |
Эффект Доплера……………………………………………………………………………………………………………….. | 53 |
Формула Эйнштейна. | 54 |
Волны де Бройля………………………………………………………………………………………………………………. | 54 |
Дисперсия волн………………………………………………………………………………………………………………… | 55 |
Уравнение Шредингера…………………………………………………………………………………………………….. | 55 |
Тахион…………………………………………………………………………………………………………………………….. | 56 |
2
1-1. Инварианты
Изучение общей теории относительности (да и специальной – на адекватном уровне) затрудняется особым математическим аппаратом: тензорами. Полагаю, что с тензорами у вас плохо? Мутная какая-то тема…
Полагаю, что с тензорами у вас плохо? Мутная какая-то тема…
Здесь я попытался дать базовые сведения, которые должны помочь понимать физические тексты. Предполагается, что читатель имеет образование в рамках втуза, что-то из институтской математики помнит (и из физики тоже). А вот школьного курса, к сожалению, никак недостаточно.
Ожидается готовность воспринимать новые взгляды, новый непривычный подход. Да и просто желание разобраться. Потому что потребуется изрядная перенастройка мозгов!
Читатель не найдет здесь строгости и полноты изложения, оставим их математикам. Хотелось представить тему как можно доступнее – как ныне говорится, для «чайников». Увы, сам предмет сложен, и ошибется тот, кто решит, что можно освоить материал, не утруждаясь собственной работой мысли.
Также даны обширные иллюстрации применения тензоров в некоторых разделах теоретической физики. Их никоим образом не следует рассматривать как исчерпывающее изложение этих физических тем – на то существуют учебники!
Введение в тему
Запишем в качестве примера известную школьную формулу закона Ньютона с векторами силы и ускорения:
F ma.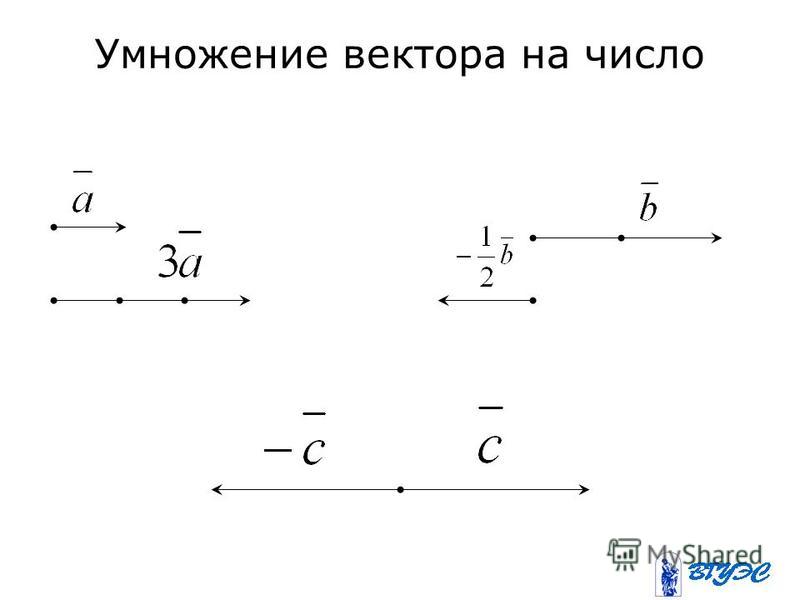
Мы, конечно, можем считать ее сокращенной записью трех уравнений:
Fx max ,
Fy may ,
Fz maz .
На самом деле здесь нечто большее. Первое уравнение – это инвариантная запись, в отличие от формы неинвариантной, через компоненты векторов. Что это означает?
Инвариантная форма никак не изменится при переходе к другим координатам. В то время как Fx , Fy , Fz , ax , ay , az зависят от принятых координат.
Запись физических уравнений в инвариантном виде является более «правильной»! Поскольку законы природы не могут же зависеть от произвольного, случайного выбора системы координат. Между прочим, инвариантная форма не содержит в явном виде информации о размерности (числе измерений) пространства – эта размерность должна подразумеваться особо.
Пока что нам удалось инвариантно записать умножение вектора на коэффициент m. Негусто, кажется… С другими операциями (как скалярное произведение) уже возникнут трудности. Тем более, когда от векторов мы перейдем к более сложным объектам. Потребуются особые приемы. Им и предстоит научиться.
Потребуются особые приемы. Им и предстоит научиться.
Тензор – то, что отвечает трем пунктам:
1)это математическое представление некоторого объекта (геометрического или физического), существующего в пространстве, в виде таблицы величин – компонент тензора;
2)значения компонент зависят от принятой системы координат, и изменяются (преобразуются) при переходе к другим координатам;
3
3) преобразование компонент таково, что оставляет, тем не менее, неизменными некоторые особые величины – инварианты.
Итак, тензор это таблица или матрица чисел (компонент, зависящих от выбранных ко-
ординат). В то же время задача тензорного исчисления – развить такую форму записи тензоров, чтобы обойтись без таблиц компонент. То есть, инвариантную форму. Которая,
тем не менее, позволит записывать любые (инвариантные) операции над тензорами.
Начнем с вектора
Частным примером тензора и является вектор, который привычно видится чем-то вроде палки, заостренной на конце. При всей комичности такого представления, оно отчасти даже полезно. Ясно, что вектор это цельный, самостоятельный объект, независимый от того, как мы его представим математически.
При всей комичности такого представления, оно отчасти даже полезно. Ясно, что вектор это цельный, самостоятельный объект, независимый от того, как мы его представим математически.
Принцип целостности вообще любого тензора может показаться тривиальным… Но мы убедимся, что из него вытекают особые следствия.
Во всяком случае, пока отметим, что вектор объективно имеет длину.
Вектор рассматривается в пространстве. Пространство характеризуется числом измерений, фиксированным для данного класса задач.
Мы не сомневаемся в том, что в пространстве введены векторные операции: сложение векторов и умножение вектора на число.
В трехмерном пространстве рассмотрим перемещение из точки А в точку В. Его принято изображать вектором, то есть направленным отрезком из А в В. Это так называемый вектор перемещения x (обычный геометрический вектор). Впрочем, считают, что вектор не меняется при параллельном переносе.
Очевидно, что при сложении перемещений – результирующее перемещение (векторная сумма) определяется по известному правилу параллелограмма.
Компоненты вектора
Нужно уметь производить с нашим объектом (вектором) операции – пользоваться
векторной алгеброй. Для этого вводят систему координат, или базис.
В пространстве (до поры будем считать его трехмерным) выберем три вектора e1,e2,e3 . Это будут единичные векторы, или орты. Непременное условие: орты линейно не-
зависимы. Это значит, что ни один из них нельзя представить в виде линейной комбинации остальных (такое было бы, если бы тройка векторов лежала в одной плоскости).
Несложно доказать, что любой вектор x можно представить однозначным образом в виде: x x1e1 x2e2 x3e3 , то есть в качестве линейной комбинации ортов. Коэффициенты
(x1, x2 , x3 ) и есть компоненты вектора x в принятом базисе. Если больше нравится, можете называть их координатами вектора.
Примечание: верхние индексы – это не показатели степени, а попросту индексы! Степени тут всюду первые, ведь мы занимаемся чисто линейными преобразованиями.
Имея в виду представление через компоненты, вектор далее нередко будем обозначать по типу: (x1, x2, x3), или, короче, xi .
Все помнят, конечно, что операции с векторами представляются в координатах так: x y (x1 y1, x2 y2, x3 y3) – сложение векторов,
ax (ax1, ax2, ax3) – умножение вектора на число.
4
Матричное представление
Тензор это таблица величин, и вектор, в частности – тоже. Значит, для них естественно матричное представление, иногда привлекать его бывает удобно. Разумеется, вектор это матрица-столбец или матрица-строка. Так, вектор xi (x1, x2, x3) можно изобразить матрицей:
x1x2 .x3
Полезно вспомнить хотя бы базовые понятия, относящиеся к матрицам – они далее пригодятся.
Упоминание матриц не вызывает энтузиазма у читателей. Но они потребуются только на этапе обоснований, а вообще-то суть дела в том, чтобы обходиться без них.
Переходим к другим координатам
Если мы выберем другой базис (например, повернем оси координат), то компоненты вектора изменятся. Разумеется, новые компоненты (x’1, x’2 , x’3 ) можно выразить через преж-
ние (x1, x2 , x3 ), если знать углы поворота осей. Задача кажется весьма громоздкой, с синусами и косинусами… В общем же виде она проста:
Задача кажется весьма громоздкой, с синусами и косинусами… В общем же виде она проста:
x’1 a x1 | a x2 | a x3 , |
|
11 | 12 | 13 |
|
x’2 a21x1 | a22x2 | a23x3 , | (1.1) |
x’1 a x1 | a x2 | a x3 . |
|
31 | 32 | 33 |
|
Можно записать коэффициенты aik в виде матрицы преобразования:
a11 | a12 | a13 |
|
| a22 | a23 |
|
a21 | . | ||
| a32 | a33 |
|
a31 |
|
Правда, пока неясно, чему равны эти коэффициенты… Но есть хорошая новость: мы и не будем здесь интересоваться их конкретными выражениями. Достаточно иметь в виду, что они существуют и известны (могут быть выведены, или взяты из справочной литературы).
Достаточно иметь в виду, что они существуют и известны (могут быть выведены, или взяты из справочной литературы).
Важно одно: любой объект, компоненты которого преобразуются согласно (1.1), является вектором. А если нет – то не является. Хотя бы он изображался тройкой чисел!
Внимание: если в некоторой системе координат все компоненты вектора равны нулю, то они нулевые и в любой другой системе! Это же относится к тензорам вообще.
Длина вектора в прямоугольных координатах
Если мы имеем декартову, то есть ортогональную (а еще точнее – ортонормальную) систему координат, то длина геометрического вектора х (ее квадрат) выражается через компоненты общеизвестным образом по теореме Пифагора:
x2 (x1)2 (x2)2 (x3)2 . | (1.2) |
Двойка за скобками здесь изображает уже показатель степени, разумеется.
При переходе к другому базису, когда значения компонент изменятся, длина должна остаться той же самой. Ведь она является атрибутом собственно вектора! По нашему уговору, она не может зависеть от выбора координат. Говорят, что длина инвариантна относительно перехода к другим координатам; является инвариантом вектора.
Ведь она является атрибутом собственно вектора! По нашему уговору, она не может зависеть от выбора координат. Говорят, что длина инвариантна относительно перехода к другим координатам; является инвариантом вектора.
5
По существу это определяет требования к формулам преобразования координат, то есть к той самой матрице коэффициентов aik : их значения не могут быть произвольными!
Скаляр
Вероятно, еще из школы вам запало в память правило: величины делятся на векторные и скалярные; все, что не вектор, то скаляр.
В тензорном исчислении скаляр это тоже тензор (самый простой – нулевого ранга).
Это число-инвариант, не меняющееся при переходе к другим координатам. Примени-
тельно к вектору, его длина – классический скаляр. Далее мы узнаем, что скаляры получаются как окончательный результат свертки тензоров.
Любая из компонент вектора – число. И не вектор… Но скаляром его тоже не считают: ведь эта величина не инвариантна.
Скалярное произведение
Напомню о понятии скалярного произведения двух векторов. Оно выражается через координаты так:
Оно выражается через координаты так:
xy x1y1 x2 y2 x3y3 .
Собственно говоря, квадрат длины вектора – это просто его скалярное произведе-
ние на себя (так называемый скалярный квадрат).
Внимание: мы принимаем, что скалярное произведение существует, и обладает некоторыми известными свойствами! Такое пространство называют евклидовым.
Скалярное произведение тоже инвариантно (как любой скаляр). Ведь оно несет геометрический смысл, независимый от координатного представления: произведение длин векторов и косинуса угла.
Теперь вы подготовлены к тому, чтобы понять, в каком смысле говорят об инвари-
антности вектора, да и вообще любого тензора. Идея, что тензор является чем-то целост-
ным, выливается в утверждение об его инвариантности при преобразованиях координат, имея в виду все то, что вы уже успели узнать.
Наверняка затронутые до сих пор вопросы кажутся тривиальными, общеизвестными. Но теперь – важное предупреждение. Следующий параграф, хотя и рябит формулами (элементарными по сути), требует внимательного прочтения: он ключевой для понимания всего.
Два сюрприза
Прямоугольные координаты это случай все-таки специальный. Система координат может быть, скажем, косоугольной (единичные векторы не ортогональны). Ясно, что формула для скалярного квадрата окажется сложнее, чем (1.2). Однако (и тут снова хорошая новость!) мы выводить ее не собираемся. Достаточно записать в общем виде:
x2 g11(x1)2 g22(x2)2 g33(x3)2 g12x1x2 g13x1x3 g23x2x3 g21x2x1 g31x3x1 g32x3x2 .
Откуда такое? Да просто из соображений размерности – это квадратичная форма! Некие коэффициенты gik зависят от конкретной системы координат.
Конечно, можно привести подобные члены, и тогда слагаемых выйдет 6, а не 9… Но мы, наоборот, специально вводим из соображений симметрии gik gki : так будет удобнее.
Теперь запишем то же самое немного иначе:
x2 (g11x1)x1 (g22x2)x2 (g33x3)x3 (g12x1)x2 (g13x1)x3 (g23x2)x3
6
(g21x2)x1 (g31x3)x1 (g32x3)x2 .
И окончательно:
x2 x x1 | x | x2 x x3 . | (1.3) |
1 | 2 | 3 |
|
Здесь мы просто ввели обозначения:
x1 g11x1 g12x2 g13x3 ,
x2 | g21x1 | g22x2 | g23x3 , | (1.4) | ||||||
x g | 31 | x1 | g | 32 | x2 | g | 33 | x3 . |
| |
3 |
|
|
|
|
|
|
| |||
Сюрприз: формула (1.3) нам знакома – снова скалярное произведение! В случае декартовых координат квадрат длины это скалярное произведение вектора на себя же. А здесь, для общего случая, – это скалярное произведение вектора xi на… что? На некоторый другой вектор xi(x1, x2, x3).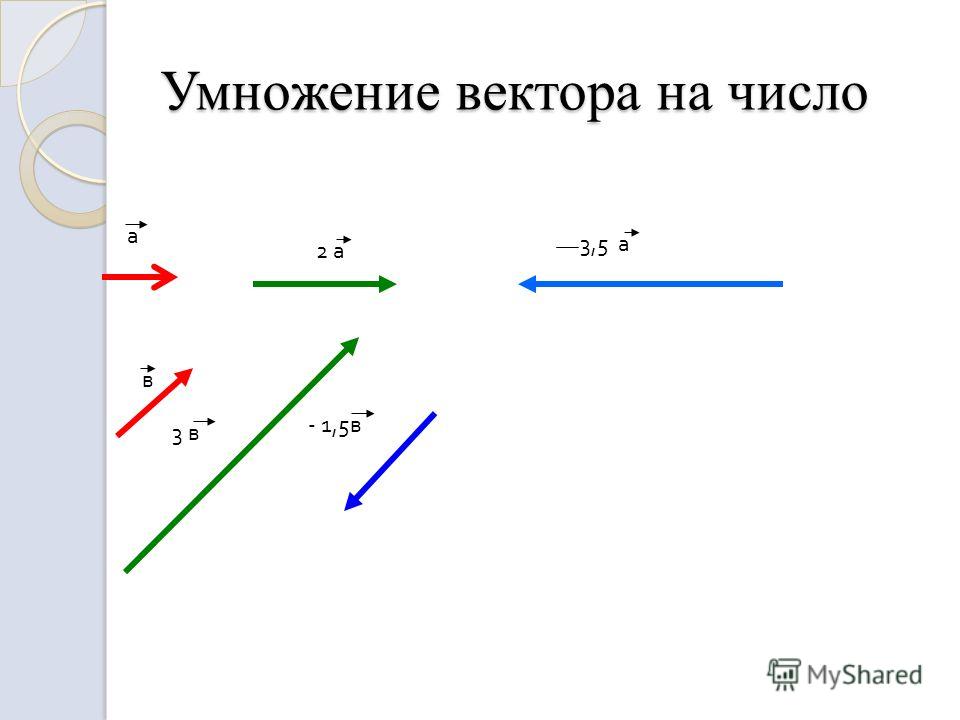 Его называют ковектором, то есть сопряженным вектором.
Его называют ковектором, то есть сопряженным вектором.
Ковектор является тоже вектором – факт вообще-то неочевидный… Тем не менее, это так. Потому что его произведение с вектором – скаляр (скалярный квадрат). Вообще линейные операции с тензорами приводят к тензорам же!
Но, позвольте: формулы (1.4) нам тоже известны, это формулы преобразования координат, сравним их с (1.1). Получается (опять сюрприз), ковектор – это никакой не другой, а тот же самый вектор х! Но только представленный в некоторой другой системе координат (ее называют иногда дуальной).
Вот вы и познакомились с главной уловкой тензорного исчисления.
И для чего они нужны
Ясно, что в ортогональном базисе оба представления вектора xi и xi совпадают (то
есть имеют идентичные компоненты). Дуальная система координат здесь попросту совпадает с главной. И только в общем случае компоненты будут различаться.
Но тогда, казалось бы, приведенные выше построения, хотя и любопытны, но излишни. Просто условимся использовать декартовы координаты!
Увы, такое возможно не всегда.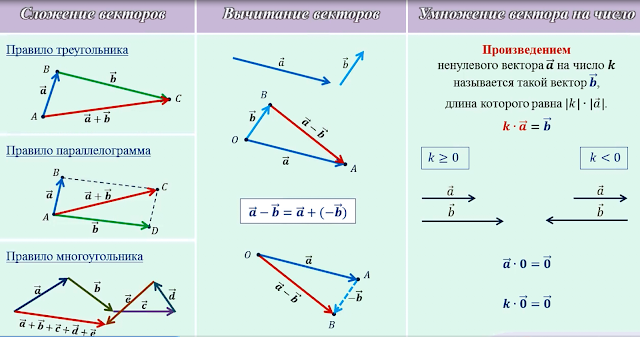 Например, в искривленных пространствах пересечение сетки параллельных прямых не может быть всюду под прямым углом. В них вообще может не существовать параллельных прямых! (рассмотрите в качестве двумерного примера поверхность сферы, где «прямыми» являются окружности больших кругов). А такие хитрые пространства встречаются в физике.
Например, в искривленных пространствах пересечение сетки параллельных прямых не может быть всюду под прямым углом. В них вообще может не существовать параллельных прямых! (рассмотрите в качестве двумерного примера поверхность сферы, где «прямыми» являются окружности больших кругов). А такие хитрые пространства встречаются в физике.
Разделы, еще ожидающие вас впереди, как раз и посвящены применению тензорного аппарата в некоторых разделах физики.
7
1-2. Базовые понятия тензорного исчисления
В конце предыдущего раздела мы нашли способ записывать инвариант (скалярный квадрат) в инвариантной форме. В самом деле, наша формула x2 x1x1 x2x2 x3x3 – в лю-
бой системе координат выглядит одинаково – помните наши два сюрприза? Преобразования координат в ней есть… но как бы скрыты. Далее нам предстоит убедиться, что и в более сложных случаях также легко обеспечивается простая форма записи. В этой простоте и состоит главная идея.
Правда, такое видимое упрощение достигается ценой введения разного типа представления одного и того же вектора. Это как раз и обозначается различным размещением индекса: вверху или внизу (а вы, наверно, гадали – почему?) Они называются: контравариант-
Это как раз и обозначается различным размещением индекса: вверху или внизу (а вы, наверно, гадали – почему?) Они называются: контравариант-
ное и ковариантное представление.
Ковариантность и контравариантность
Один и тот же вектор можно записать как в ковариантных, так и в контравари-
антных компонентах. Обычно какие-то из них являются для рассматриваемого вектора естественными. То есть действующими именно в тех координатах, которые присущи задаче.
Координаты геометрического вектора (вектора перемещения) являются есте-
ственно контравариантными. Контравариантный вектор обозначается в форме xi , то есть с индексом наверху.
Компоненты контравариантного вектора изменяются как бы противоположно изменению векторов базиса (отсюда название). Вот примитивный поясняющий пример. Пусть мы перешли от одной системы координат к другой – такой, что:
x’1 kx1 , x’2 x2 , x’3 x3 (k 1).
Говоря попросту, мы изменили масштаб первой оси, сделав его более мелким. Новая
Новая
единица длины на этой оси уменьшилась, и составляет 1 от старой. А соответствующая но- k
вая компонента вектора, напротив того, увеличилась в k раз – как бы противоположно масштабу оси. Это и есть контравариантность.
Для ковариантного вектора все наоборот… Но это мы разберем чуть ниже.
Хотя тот же самый вектор перемещения можно представить и в ковариантной форме: xi . Его ковариантные компоненты x1, x2, x3 – это составляющие не в базисе нашей задачи. А
в некоторой другой (дуальной) системе координат. Просто мы знаем, как к ней переходить: через коэффициенты gik . И потому такой переход держим в уме, оставляем его за кадром.
Правило Эйнштейна
Тензорное исчисление зародилось в середине XIX века, но было не слишком в ходу. Свое настоящее признание оно получило в связи с общей теорией относительности Эйнштейна, которая не может быть изложена иначе, как в тензорной форме.
Правило Эйнштейна позволяет еще более упростить запись многих тензорных выражений.
В соответствии с этим правилом, выражение для скалярного квадрата запишется компактнее:
x2 x1x1 x2x2 x3x3 xi xi .
8
Правило состоит в том, что по индексу, встречающемуся дважды (один раз наверху, другой раз внизу) подразумевается суммирование. То есть, aibi – это просто сокращенная
запись выражения: aibi . Здесь индекс i (пробегающий значения 1, 2, 3) называется немым:
i
в результирующее выражение он не вошел – как бы «сократился». В подобных случаях говорят, что произведена свертка. Подробно о ней будет ниже.
О ковариантных векторах
В пространстве задано скалярное поле . Построим частные производные:
| , |
| , |
| . |
1 | 2 | 3 | |||
x | x | x | |||
Их смысл – изменение величины поля вдоль данного направления на единицу протяженности.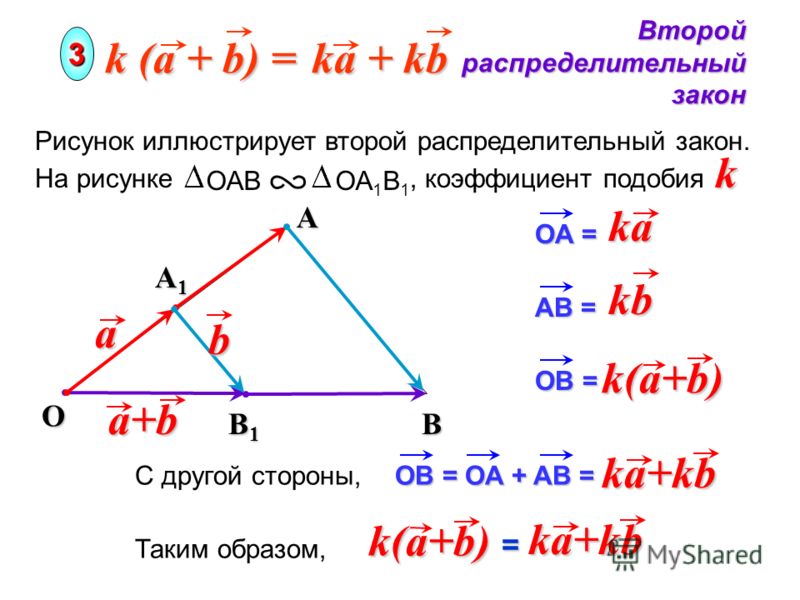
Если эти величины рассматривать как компоненты, то можно убедиться, что мы имеем дело с вектором у: при повороте осей пересчет координат будет по стандартным формулам. Такой вектор, как известно, называют градиентом поля.
Пусть масштаб первой оси снова сжали в k раз. Единица протяженности сократилась, но само поле-то не изменилось. Ясно, что изменение поля в пересчете на новую, уменьшенную единицу будет соответственно меньше:
|
|
|
| 1 | |||
|
|
|
|
| . | ||
1 | 1 | k | 1 | ||||
x’ |
| (kx ) |
|
| x | ||
Компонента вектора изменилась в те же сторону, что и масштаб оси!
Такое свойство векторов называется ковариантностью. Вектор градиента естественно ковариантен в том базисе, в котором задано поле. Таким образом:
Вектор градиента естественно ковариантен в том базисе, в котором задано поле. Таким образом:
grad xi yi .
Отметим себе простое правило: если контравариантные компоненты стоят в знаменателе, то мы получим ковариантность. И наоборот, разумеется.
Тензоры
Перепишем еще раз формулы (1.4) получения ковариантных компонент из исходных контравариантных:
x1 g11x1 g12x2 g13x3 ,
x2 | g21x1 | g22x2 | g23x3 , | (1.4) | ||||||
x g | 31 | x1 | g | 32 | x2 | g | 33 | x3 . |
| |
3 |
|
|
|
|
|
|
| |||
И присмотримся к выражениям. Мы увидим в них результат умножения двух матриц:
Мы увидим в них результат умножения двух матриц:
|
| g | g | g |
|
| x1 |
| |
x x | x | g11 | g12 | g13 |
|
| x | 2 . | |
1 2 | 3 | 21 | 22 | 23 |
|
|
|
|
|
|
|
| g32 |
|
|
|
| 3 |
|
|
| g31 | g33 |
| x |
|
| ||
Помните, мы упомянули, что вектор это частный случай тензора? Пора уточнить, что вектор это тензор первого ранга (иногда вместо «ранг» говорят «валентность»). Контравариантный вектор принято изображать матрицей-столбцом. Ковариантный – матрицейстрокой.
Контравариантный вектор принято изображать матрицей-столбцом. Ковариантный – матрицейстрокой.
9
А в лице матрицы 3х3 ( gik ) мы знакомимся здесь с тензором второго ранга. Тензор
третьего ранга придется уже представить себе в виде трехмерной, кубической таблицы. И так далее.
Количество индексов в символическом обозначении соответствует рангу тензора. А длины строк и столбцов всегда соответствуют числу измерений пространства (в нашем примере оно трехмерно).
Тензор второго ранга это вектор, компоненты которого, в свою очередь, являются векторами.
Запись тензорных выражений
Запишем (1.4) сокращенной записью:
x g | ik | xk . | (1.5) |
i |
|
|
Что мы можем усмотреть из (1.5)? Многое.
1) Это запись, укороченная по правилу Эйнштейна. В полном виде она выглядит так:
xi gik xk . | (1.5а) |
k |
|
Здесь k это немой индекс (не попадающий в результат).
2) gik это условное обозначение ковариантного тензора второго ранга. Второго –
потому что два индекса. Ковариантного – потому что индексы внизу. А внизу потому, что есть правило: повторяющиеся индексы должны чередоваться (верх – низ). При комбинировании ковариантных и контравариантных компонент законы их преобразования взаимно «сокращаются».
3)Результат является ковариантным вектором (i внизу), потому что и справа индекс i ковариантный.
4)Количество измерений пространства (количество значений, которые пробегает индекс суммирования) здесь явно не видно, и должно подразумеваться из контекста задачи.
5)Соответственно, под (1.5а) следует понимать три формулы для i 1, 2,3:
x1 g1k xk ,
k
x2 g2k xk ,
k
x3 g3k xk .
k
Но это все тоже остается за кадром, как неинвариантная форма, от которой мы ухо-
дим.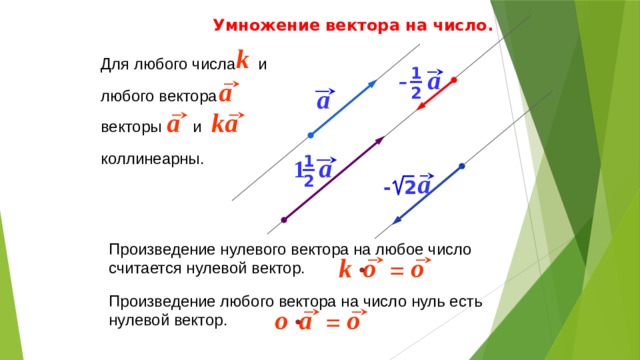
Тензорные операции. Произведение
Возможно покомпонентное сложение тензоров одинаковой структуры, умножение их на число – на этом особо задерживаться не будем. Пространство тензоров, как и в случае векторов, полагаем линейным, то есть результат таких операций будет снова тензором.
По большому счету придется иметь в виду две основные операции с тензорами: пере-
множение и свертка. Эти операции над тензорами приводят к тензорам же.
Вот иллюстрация тензорного произведения:
10
Калькулятор 2D-векторного скалярного произведения
«Калькулятор 2D-векторного скалярного произведения» пригодится, когда вы пытаетесь решить задачи, связанные со скалярным произведением векторов. Вместо того, чтобы вычислять скалярное произведение (также известное как скалярное произведение) вручную, вы можете использовать этот онлайн-калькулятор, который сделает за вас математику, просто введя в калькулятор компоненты двух векторов.
| Vector V1: | ||
| Vector V2: |
| Scalar Product: |
★ ★ ★ ★ ★ [ 33 Votes ]
Калькулятор двумерного векторного скалярного произведения — все основы, которые вам нужно знать
Если вы хотите узнать больше об этом калькуляторе, его использовании и различных терминах, связанных с ним, эта статья для вас.
Типы векторного умножения
Существует два типа векторного умножения:
- перекрестное произведение (обозначается символом «x»)
- скалярное произведение, также известное как скалярное произведение (обозначается символом «.» )
Основное различие между этими двумя типами умножения состоит в том, что результатом произведения перекрестной операции является вектор, а произведение точечной операции дает единственное число, т. е. только величину.
Что представляет собой скалярное произведение двух векторов?
Скалярное произведение двух векторов дает нам представление о том, насколько один вектор идет в направлении другого вектора.
Давайте разберемся с этим на примере:
Например, если вы потянули объект на двадцать метров под наклонным углом, в вашем векторе силы будет как вертикальная, так и горизонтальная составляющая. Если вы вычислите скалярное произведение в этом случае, оно даст вам количество силы, действующей в направлении перемещения объекта, то есть в направлении смещения.
Что такое формула скалярного произведения?
Все наши вычисления будут выполняться в двумерном пространстве, что означает, что каждый вектор может быть представлен двумя компонентами:
a = [a1, a2]
b = [b1, b2]
определяется как произведение величины двух векторов на косинус угла между ними. Если вы хотите рассчитать угол между двумя векторами, вы можете использовать 2D Vector Angle Calculator.
Формула для нахождения скалярного произведения двух векторов:
а.б = |а| × |б| × cosθ
Где:
- a.b — скалярное произведение двух векторов, а именно «a» и «b»
- |a| и |б| — величина векторов соответственно
- θ — угол между двумя векторами
Из приведенной выше формулы мы можем сделать вывод, что если угол между двумя векторами, т.е. θ, равен 90 градусам, то скалярное произведение двух векторов будет равно нулю (поскольку cos90 = 0 градусов). Точно так же, если угол между двумя векторами равен 0 градусов, скалярное произведение даст максимальное значение, то есть умножение только величин (поскольку cos0 = 1).
В некоторых случаях вы можете использовать скалярное произведение как инструмент для нахождения угла между двумя векторами. В это время косинус будет равен отношению скалярного произведения к модулю векторов, т. е.
cosθ = a × b / (|a| × |b|)
Вы можете получить значение угла θ, найдя обратное значение, которое вы получили в правой части уравнения.
Алгебраическое представление скалярного произведения
Алгебраически скалярное произведение двух векторов в 2D может быть представлено как-
a.b = a1 × b1 + a2 × b2
Где
- a.b — скалярное произведение двух векторов, а именно «a» и «b»,
- a1 и a2 — величины векторов в «x» и Направление «y» соответственно
- b1 и b2 — величины векторов в направлениях «x» и «y» соответственно
Как использовать калькулятор двумерного векторного скалярного произведения?
Первым шагом является ввод компонентов двух векторов соответственно в обязательные поля, а именно Vector V1 и Vector V2.
Первое поле содержит значение x-компоненты вектора, а второе поле содержит y-компоненту вектора (только в случае двумерных векторов).
Следующим шагом будет нажатие Enter, и калькулятор сделает свою работу. Он будет представлять результат как скалярное произведение двух векторов.
Векторы могут содержать десятичные и целые числа, но не функции, дроби или переменные.
Применение скалярного произведения
- Если вы хотите узнать, перпендикулярны ли два вектора друг другу или нет, скалярное произведение — это самый простой и простой способ узнать то же самое.
- Закон косинусов можно доказать с помощью скалярного произведения.
- Многие физические величины определяются как скалярное произведение. Работа определяется как скалярное произведение перемещения и силы. Мощность определяется как скалярное произведение скорости и силы.
Резюме
В эту современную эпоху технологий вместо того, чтобы тратить время на ручные математические вычисления, используется больше формул и их быстрое применение. Этот простой пользовательский интерфейс в виде «Калькулятора 2D-векторного скалярного произведения» может предоставить вам желаемые результаты, зачем вам зависеть от ручного расчета математических формул и тратить много времени?
Этот простой пользовательский интерфейс в виде «Калькулятора 2D-векторного скалярного произведения» может предоставить вам желаемые результаты, зачем вам зависеть от ручного расчета математических формул и тратить много времени?
404 — СТРАНИЦА НЕ НАЙДЕНА
Почему я вижу эту страницу?
404 означает, что файл не найден. Если вы уже загрузили файл, имя может быть написано с ошибкой или файл находится в другой папке.
Другие возможные причиныВы можете получить ошибку 404 для изображений, поскольку у вас включена защита от горячих ссылок, а домен отсутствует в списке авторизованных доменов.
Если вы перейдете по временному URL-адресу (http://ip/~username/) и получите эту ошибку, возможно, проблема связана с набором правил, хранящимся в файле .htaccess. Вы можете попробовать переименовать этот файл в .htaccess-backup и обновить сайт, чтобы посмотреть, решит ли это проблему.
Также возможно, что вы непреднамеренно удалили корневую папку документа или ваша учетная запись должна быть создана заново. В любом случае, пожалуйста, немедленно свяжитесь с вашим веб-хостингом.
В любом случае, пожалуйста, немедленно свяжитесь с вашим веб-хостингом.
Вы используете WordPress? См. Раздел об ошибках 404 после перехода по ссылке в WordPress.
Как найти правильное написание и папку
Отсутствующие или поврежденные файлыКогда вы получаете ошибку 404, обязательно проверьте URL-адрес, который вы пытаетесь использовать в своем браузере. Это сообщает серверу, какой ресурс он должен использовать попытка запроса.
http://example.com/example/Example/help.html
В этом примере файл должен находиться в папке public_html/example/Example/
Обратите внимание, что CaSe важен в этом примере. На платформах с учетом регистра e xample и E xample не совпадают.
Для дополнительных доменов файл должен находиться в папке public_html/addondomain.com/example/Example/, а имена чувствительны к регистру.
Разбитое изображение Если на вашем сайте отсутствует изображение, вы можете увидеть на своей странице поле с красным цветом X , где отсутствует изображение. Щелкните правой кнопкой мыши на X и выберите «Свойства». Свойства сообщат вам путь и имя файла, который не может быть найден.
Щелкните правой кнопкой мыши на X и выберите «Свойства». Свойства сообщат вам путь и имя файла, который не может быть найден.
Это зависит от браузера. Если вы не видите на своей странице поле с красным X , попробуйте щелкнуть правой кнопкой мыши страницу, затем выберите «Просмотр информации о странице» и перейдите на вкладку «Мультимедиа».
http://example.com/cgi-sys/images/banner.PNG
В этом примере файл изображения должен находиться в папке public_html/cgi-sys/images/
Обратите внимание, что в этом примере важен CaSe . На платформах с учетом регистра символов PNG и png не совпадают.
Ошибки 404 после перехода по ссылкам WordPress
При работе с WordPress ошибки 404 Page Not Found часто могут возникать при активации новой темы или изменении правил перезаписи в файле .htaccess.
Когда вы сталкиваетесь с ошибкой 404 в WordPress, у вас есть два варианта ее исправления.
- Войдите в WordPress.
- В меню навигации слева в WordPress нажмите Настройки > Постоянные ссылки (Обратите внимание на текущую настройку. Если вы используете настраиваемую структуру, скопируйте или сохраните ее где-нибудь.)
- Выберите По умолчанию .
- Нажмите Сохранить настройки .
- Верните настройки к предыдущей конфигурации (до того, как вы выбрали «По умолчанию»). Верните пользовательскую структуру, если она у вас была.
- Нажмите Сохранить настройки .
Во многих случаях это сбросит постоянные ссылки и устранит проблему. Если это не сработает, вам может потребоваться отредактировать файл .htaccess напрямую.
Вариант 2. Измените файл .htaccess Добавьте следующий фрагмент кода 9index.php$ — [L]
RewriteCond %{REQUEST_FILENAME} !-f
RewriteCond %{REQUEST_FILENAME} !-d
RewriteRule . /index.php [L]
/index.php [L]
# Конец WordPress
Если ваш блог показывает неправильное доменное имя в ссылках, перенаправляет на другой сайт или отсутствуют изображения и стиль, все это обычно связано с одной и той же проблемой: в вашем блоге WordPress настроено неправильное доменное имя.
Как изменить файл .htaccess
Файл .htaccess содержит директивы (инструкции), которые сообщают серверу, как вести себя в определенных сценариях, и напрямую влияют на работу вашего веб-сайта.
Перенаправление и перезапись URL-адресов — это две очень распространенные директивы, которые можно найти в файле .htaccess, и многие скрипты, такие как WordPress, Drupal, Joomla и Magento, добавляют директивы в .htaccess, чтобы эти скрипты могли работать.
Возможно, вам потребуется отредактировать файл .htaccess в какой-то момент по разным причинам. В этом разделе рассказывается, как редактировать файл в cPanel, но не о том, что нужно изменить. статьи и ресурсы для этой информации. )
)
- Отредактируйте файл на своем компьютере и загрузите его на сервер через FTP
- Использовать режим редактирования программы FTP
- Использовать SSH и текстовый редактор
- Использовать файловый менеджер в cPanel
Самый простой способ отредактировать файл .htaccess для большинства людей — через диспетчер файлов в cPanel.
Как редактировать файлы .htaccess в файловом менеджере cPanelПрежде чем что-либо делать, рекомендуется сделать резервную копию вашего веб-сайта, чтобы вы могли вернуться к предыдущей версии, если что-то пойдет не так.
Откройте файловый менеджер- Войдите в cPanel.
- В разделе «Файлы» щелкните значок File Manager .
- Установите флажок для Корень документа для и выберите доменное имя, к которому вы хотите получить доступ, из раскрывающегося меню.

- Убедитесь, что установлен флажок Показать скрытые файлы (dotfiles) «.
- Нажмите Перейти . Файловый менеджер откроется в новой вкладке или окне.
- Найдите файл .htaccess в списке файлов. Возможно, вам придется прокрутить, чтобы найти его.
- Щелкните правой кнопкой мыши файл .htaccess и выберите Редактировать код в меню. Кроме того, вы можете щелкнуть значок файла .htaccess, а затем Редактор кода значок в верхней части страницы.
- Может появиться диалоговое окно с вопросом о кодировании. Просто нажмите Изменить , чтобы продолжить. Редактор откроется в новом окне.
- При необходимости отредактируйте файл.
- Нажмите Сохранить изменения в правом верхнем углу, когда закончите. Изменения будут сохранены.
- Протестируйте свой веб-сайт, чтобы убедиться, что ваши изменения были успешно сохранены.
 Если нет, исправьте ошибку или вернитесь к предыдущей версии, пока ваш сайт снова не заработает.
Если нет, исправьте ошибку или вернитесь к предыдущей версии, пока ваш сайт снова не заработает. - После завершения нажмите Закрыть , чтобы закрыть окно диспетчера файлов.
| Калькулятор векторных точек и умножения
Введите матрицу размера m x n ниже в форму
a11,a12,a13,...a1n
a21,a22,a23,...a2n
am1,am2,am3,...amn
Калькулятор скалярного произведения — это бесплатный онлайн-метод измерения скалярное произведение двух векторов. Инструмент онлайн-калькулятора ускоряет измерение и показывает произведение векторов в секунды.
Скалярная величина, полученная в результате определенных операций над
Компоненты вектора определяются как скалярное произведение, также известное как
скалярная величина. Жирная точка представляет произведение двух
векторов, который используется для оценки того, являются ли два вектора
ортогональный. Формула расчета произведения, если a и b равны
два вектора могут быть заданы как:
Формула расчета произведения, если a и b равны
два вектора могут быть заданы как:
a * b = |a| × |б| × cos(θ)
Калькулятор также можно использовать для расчета угла между два вектора, когда косинус есть отношение скалярного произведения к величины векторов:
cos(θ) = a * b / (|a| * |b|)
Калькулятор векторного скалярного произведения
При решении задач на умножение векторов вектор калькулятор работает как удовольствие. Вместо ручного расчета скалярного произведения, просто введите компоненты двух векторов в этот инструмент и пусть он сделает всю работу за вас.
Продолжайте читать, чтобы узнать, как использовать формулу, определить произведение двух векторов и упрощение матричной формулы.
Калькулятор векторного умножения
Скалярное произведение (также известное как скалярное произведение), обозначаемое
символ «,» и перекрестное произведение, обозначенное символом «×»,
являются двумя основными формами векторного умножения.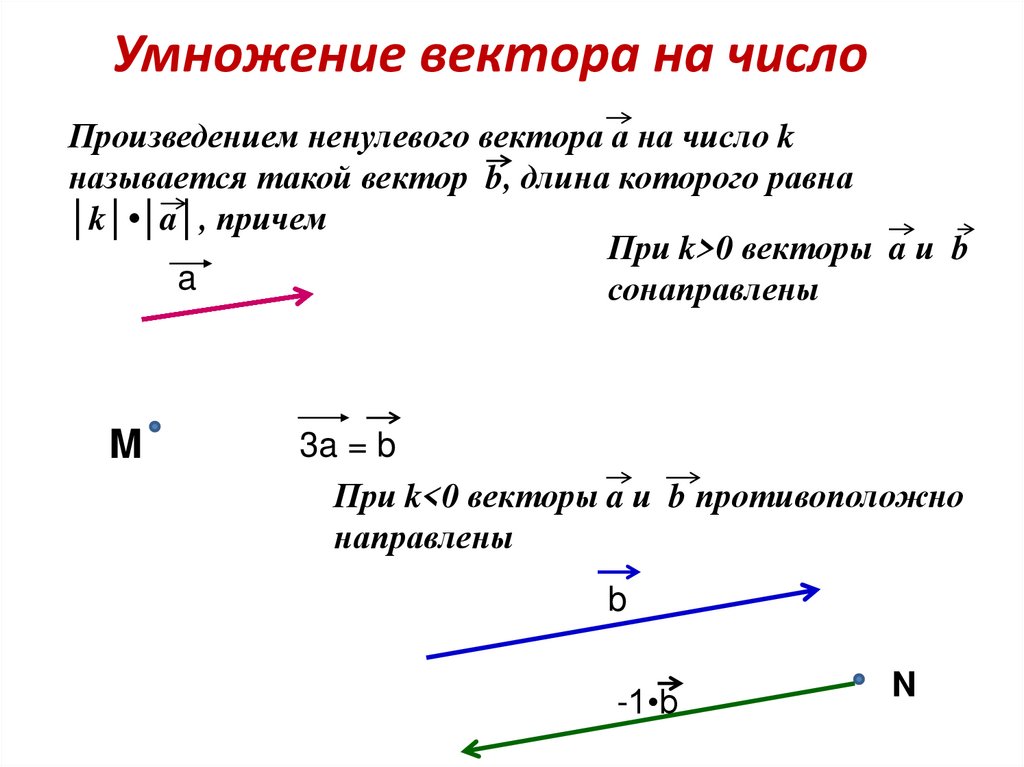 критический
разница в том, что произведение точечной операции является одним числом,
в то время как выход перекрестной операции является вектором.
критический
разница в том, что произведение точечной операции является одним числом,
в то время как выход перекрестной операции является вектором.
Как определить скалярное произведение вектора:
- Выберите вектор a.
- Выберите вектор b.
- Определите произведение первой переменной каждого вектора.
- Вычислить произведение секунд каждого вектора (средних) переменная.
- Вычислите произведение третьей переменной каждого вектора.
- Чтобы найти произведение векторов a и b, сложите все эти результаты вместе.
Матричный точечный продукт
Работа продукта может быть применима к более похожим настройки, такие как матрицы, а также векторы. В результате получаем другая матрица C, которая выглядит так: cij = ai1b1j + ai2b2j + … + ainbnj = Σk aikbkj
Аналогично скалярному произведению простых векторов, за исключением процесс должен быть повторен для каждой переменной несколько раз.
Однако не все матрицы можно перемножать. Если рассматривать А как
матрица m * n и B как матрица k * l, то n должно равняться k в
результирующая матрица C = A * B, и l должно равняться m в результирующей
матрица D = B * A. Другими словами, количество элементов левой матрицы
столбцы должны совпадать с количеством строк во втором.
Если рассматривать А как
матрица m * n и B как матрица k * l, то n должно равняться k в
результирующая матрица C = A * B, и l должно равняться m в результирующей
матрица D = B * A. Другими словами, количество элементов левой матрицы
столбцы должны совпадать с количеством строк во втором.
Скалярное произведение
Когда два вектора записаны в сферических координатах, также можно вычислить скалярное произведение. Чтобы решить задачу, мы должны использовать радиус r и два угла θ, φ, чтобы выразить наши новые координаты. Аналогично
x₁ = r₁ × sin(φ)₁ × cos(θ)₁,
y₁ = r₁ × sin(φ)₁ × sin(θ)₁,
z₁ = r₁ × cos(φ)₁
, для x2, y2 и z2 результат будет следующим:
a * b = x₁ * x₂ + y₁ * y₂ + z₁ * z₂ = r₁ * r₂ * sin(φ)₁ * cos(θ)₁ * sin(φ)₂ * cos(θ)₂ + r₁ * r₂ * sin( φ)₁ * sin(θ)₁ * sin(φ)₂ * sin(θ)₂ + r₁ × r₂ * cos(φ)₁ * cos(φ)₂
Когда мы используем косинус уравнения разности углов, формула принимает вид:
a * b = r₁ * r₂ * (sinφ₁ * sinφ₂ * cos(θ ₁ — θ ₂) + cosφ₁ * cosφ₂)
Калькулятор скалярного произведения u и v
Рассмотрим формулу подробнее. Мы можем найти образ
скалярное произведение путем рисования обоих векторов, разделенных углом
а затем попытаемся найти образ скалярного произведения, и мы
см., что это составлено из двух элементов, умноженных вместе:
проекция одного вектора на курс второго вектора, и
то же самое для второго вектора.
Мы можем найти образ
скалярное произведение путем рисования обоих векторов, разделенных углом
а затем попытаемся найти образ скалярного произведения, и мы
см., что это составлено из двух элементов, умноженных вместе:
проекция одного вектора на курс второго вектора, и
то же самое для второго вектора.
Результат — это просто произведение их длин, поскольку они оба параллельны. Процедуру можно провести двумя способами, но эффект все тот же. Подводя итог этой части, u и v Произведение калькулятора — это произведение длин двух векторов, проецируемых в сторону одного из них.
Произведение вектора на себя, a2 = aa, является одним из примеров. Произведение представляет собой квадрат длины вектора. поскольку проекция и вектор — это одно и то же. В других словами, мы можем использовать квадратный корень из следующего произведения, чтобы найти длину любого вектора: |a| = √(аа).
Калькулятор скалярного произведения
Калькулятор скалярного произведения вычисляет скалярное произведение (скалярное произведение), величины и
угол между двумя векторами. Калькулятор можно использовать для скалярного произведения
расчет 2D или 3D векторов.
Калькулятор можно использовать для скалярного произведения
расчет 2D или 3D векторов.
Расчет скалярного произведения может выполняться для двух различных векторных форм: компонентов вектора или величины и угол между векторами.
Калькулятор скалярного произведения:
| ВХОДНЫЕ ПАРАМЕТРЫ | |||
| Векторная форма: | Компоненты вектора Величины и углы | ||
| КОМПОНЕНТЫ ВЕКТОРА | |||
| Вектор | |||
| ВЕЛИЧИНА И УГОЛ | ||
| |А| | |Б| | θ (градусы) |
Примечание. Используйте точку «.» как десятичный разделитель.
Используйте точку «.» как десятичный разделитель.
| РЕЗУЛЬТАТЫ | |||
| Параметр | Символ | Значение | Блок |
| Скалярное произведение векторов A и B | — | — | |
| Величина вектора A | |А| | — | |
| Величина вектора B | |Б| | — | |
| Угол между векторами | θ | — | 9 градусов0009 |
Скалярный продукт — это тип векторного умножения, результат которого является скалярным и больше не имеет направления.
$$\overrightarrow{a} \cdot \overrightarrow{b} = \overrightarrow{b} \cdot \overrightarrow{a}$$
$$\overrightarrow{a} \cdot (\overrightarrow{b} + \overrightarrow{ c}) = \overrightarrow{a} \cdot \overrightarrow{b} + \overrightarrow{a} \cdot \overrightarrow{c}$$
$$(\lambda \overrightarrow{a}) \cdot \overrightarrow{b} =\lambda \cdot (\overrightarrow{a} + \overrightarrow{b})= \overrightarrow{a} \cdot (\lambda \ стрелка вверх{b})$$
Калькулятор векторного векторного произведения — [100% бесплатно]
В математике вы можете выполнять вычисления, чтобы получить векторное произведение двух произвольных векторов. Чтобы упростить вам задачу, этот калькулятор перекрестного произведения может сделать расчеты за вас. Вместо того, чтобы выполнять расчеты самостоятельно, что может быть очень утомительным процессом, этому калькулятору требуются только некоторые значения для получения окончательных результатов. Читайте дальше, чтобы узнать больше об этом калькуляторе векторного перекрестного произведения и о некоторых распространенных вопросах по той же теме.
Загрузка калькулятора…
Содержание
Как использовать калькулятор перекрестного произведения?
Как и большинство онлайн-калькуляторов, этот прост и удобен в использовании. Вместо ручных вычислений этот калькулятор векторного умножения предоставит вам перекрестные произведения за считанные секунды. Вот шаги для его использования:
- Сначала введите 3 значения для вектора a (x, y, z).
- Затем введите 3 значения для вектора b (x, y, z).
- После ввода всех значений автоматически будут получены перекрестные произведения вектора c (x, y, z)
Что такое метод перекрестного произведения?
Как ручное вычисление, так и калькулятор перекрестного произведения используют другой процесс, чем метод перекрестного произведения. Этот метод предполагает сравнение двух фракций. В этом методе вы умножаете числитель первой дроби на знаменатель второй и наоборот. Затем вы сравниваете свои ответы, чтобы увидеть, равны ли дроби или нет.
Затем вы сравниваете свои ответы, чтобы увидеть, равны ли дроби или нет.
Метод перекрестного произведения — это тип сокращения, который позволяет найти общий знаменатель без изменения значения дробей. Конечно, использование этого метода означает, что вы можете сравнивать только две дроби за раз. Если вам нужно сравнить больше, вы должны продолжать повторять процесс.
Что такое векторное произведение двух векторов?
Перекрестное произведение двух неколлинеарных и произвольных векторов, вектора a и вектора b представляет собой вектор c, который имеет перпендикулярную связь с обоими векторами. Следовательно, если у вас есть плоскость, на которой лежат вектора a и вектор b, вектор c будет перпендикулярен указанной плоскости.
Вы можете определить направление вектора c с помощью руки и правила правой руки. Если средний и указательный пальцы вашей правой руки указывают направление вектора a и вектора b, ваш большой палец покажет направление вектора c. Помимо использования этого калькулятора векторного векторного произведения, вы можете вручную вычислить по следующей формуле:
Помимо использования этого калькулятора векторного векторного произведения, вы можете вручную вычислить по следующей формуле:
c = a × b = |a| * |б| * sinθ * n,
где:
a и b относятся к произвольным векторам
|a| и |б| относится к величине произвольных векторов
c относится к результирующему вектору векторного произведения
θ относится к углу между векторами по вектору a и вектору b
При ручных вычислениях можно также использовать эту формулу:
a × b = (a₂b₃ – a₃b₂) * i + (a₃b₁ – a₁b₃) * j + (a₁b₂ – a₂b₁) * к
Как определить направление векторного произведения?
Скалярное произведение обозначает сходство вектора с одним числом. Рассчитайте точечный продукт со следующей формулой:
DOT Product = (A x , A Y , A Z ) * (B x , B Y , B , B , B , B , B , B , B , B , B , B , B , B .
) = a x b x + a y b y + a z b z = ||vec{a}|| ||век{б}|| cos(ϴ)
Чтобы вычислить кандидата на перекрестное произведение, используйте следующую формулу:
кандидат на перекрестное произведение = сумма разности = ||vec{a}|| ||век{б}|| sin(ϴ)
Но, взглянув на эти формулы, вы поймете, что в них отсутствуют некоторые детали. Следовательно, вам нужно выразить эти различия в виде вектора, помня при этом о следующих моментах:
- Размер векторного произведения относится к числовому значению «количества различий», а sin(θ) — это процент.
- Основой направления векторного произведения являются оба входа, что означает, что ни один из них не благоприятствует.
- Результирующий вектор отдельно представляет x * y и x * z, хотя они оба отличаются от x.
- Вы можете определить плоскость, используя 2 вектора, и результирующее векторное произведение будет указывать в направлении, отличном от этих векторов.

Теперь, чтобы определить направление результирующего вектора, вы можете использовать правило правой руки. Для этого вытяните большой палец и первые два пальца. Ваши два пальца указывают направление векторов, а большой палец указывает направление полученной точки пересечения.
Что такое векторное произведение в физике?
Прежде чем мы обсудим, что такое векторное произведение в физике, давайте кратко изложим все, что мы обсуждали до сих пор. Перекрестное произведение, также известное в физике как вектор вектора a и вектора be, может быть символически записано как:
𝑎 × 𝑏 или 𝑎 ∧ 𝑏.
По определению векторное произведение представляет собой вектор с величиной:
| 𝑎 × 𝑏 | = | 𝑎 | |𝑏 | грех𝜃
где:
𝜃 относится к углу между вектором 𝑎 и вектором 𝑏
Направление 𝑎 × 𝑏 является вектором, который перпендикулярен как вектору a, так и вектору b. Лучший способ определить это направление — использовать правило правой руки. Вы также можете увидеть эту концепцию в физике, например, в том, как движется винт. Если вы покрутите винт, то он начнет двигаться вперед.
Лучший способ определить это направление — использовать правило правой руки. Вы также можете увидеть эту концепцию в физике, например, в том, как движется винт. Если вы покрутите винт, то он начнет двигаться вперед.
В качестве альтернативы, если вы вытяните большой палец и первые два пальца и расположите их под прямым углом друг к другу, формула изменится. На этот раз ваш большой и указательный пальцы будут указывать в одном направлении, а ваш второй палец будет указывать в другом направлении или в направлении 𝑎 × 𝑏. Перекрестные произведения или векторные произведения часто встречаются в физике.
Вы даже можете использовать физику, чтобы помочь вам определить направление векторного произведения, как мы проиллюстрировали в наших двух примерах:
- Если вы повернете винт от 𝑎 к 𝑏, он будет двигаться вверх
- Если вы расположите первые три пальца вашей руки под прямым углом, направление от 𝑎 к 𝑏 будет направлением вашего второго пальца
Калькулятор перекрестного произведения — онлайн калькулятор перекрестного произведения
Калькулятор перекрестного произведения вычисляет векторное произведение заданных двух векторов.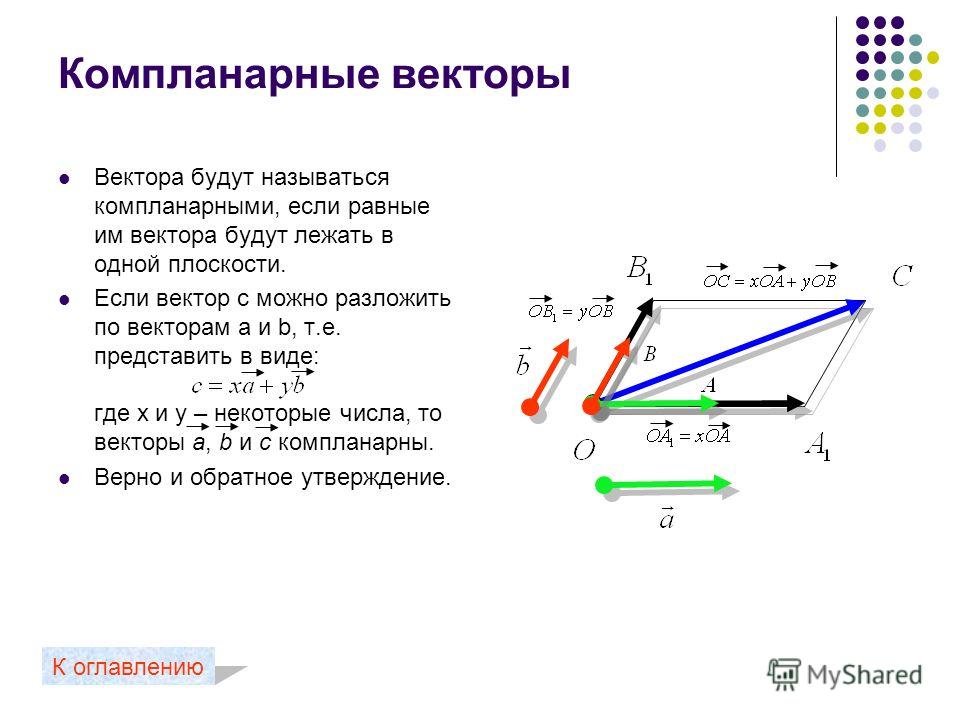 В результате перекрестного произведения двух векторов получается третий вектор, перпендикулярный двум исходным векторам. Далее, направление вектора, полученного в результате перекрестного произведения двух векторов, можно определить по правилу правой руки.
В результате перекрестного произведения двух векторов получается третий вектор, перпендикулярный двум исходным векторам. Далее, направление вектора, полученного в результате перекрестного произведения двух векторов, можно определить по правилу правой руки.
Что такое Калькулятор перекрестного произведения?
Калькулятор векторного произведения — это онлайн-инструмент, который вычисляет векторное произведение двух векторов. Если два вектора имеют одинаковое или противоположное направление, то их векторное произведение равно нулю. Более того, если какой-либо вектор имеет нулевую длину, то векторное произведение снова будет равно нулю. Чтобы использовать калькулятор векторного произведения , введите значения в соответствующие поля.
Калькулятор перекрестного произведения
*Используйте только 2 цифры.
Как использовать Калькулятор перекрестного произведения?
Чтобы найти перекрестное произведение с помощью онлайн-калькулятора перекрестного произведения, выполните следующие действия:
- Шаг 1: Перейдите к онлайн-калькулятору перекрестного произведения Cuemath.

- Шаг 2: Введите коэффициенты двух векторов в соответствующие поля ввода калькулятора векторного произведения.
- Шаг 3: Нажмите кнопку «Вычислить» , чтобы вычислить векторное произведение.
- Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести другие значения.
Как работает калькулятор перекрестного произведения?
Векторы — это величины, имеющие как величину, так и направление. Векторы помогают одновременно представлять разные величины в одном выражении. Над векторами можно выполнять ряд арифметических операций, таких как сложение, вычитание и умножение. Существует два типа умножения векторов. Это точечный продукт и векторный продукт.
Стандартная форма представления вектора:
a = \(a_{1}i\hat{}+a_{2}j\hat{}+a_{3}k\hat{}\)
b = \(b_{1}i\шляпа{}+b_{2}j\шляпа{}+b_{3}k\шляпа{}\)
Где \(a_{1}\), \( a_{2}\), \(a_{3}\) и \(b_{1}\), \(b_{2}\), \(b_{3}\) являются числовыми значениями. \(i\hat{}\), \(j\hat{}\) и \(k\hat{}\) — единичные векторы вдоль оси x, оси y и оси z соответственно.
\(i\hat{}\), \(j\hat{}\) и \(k\hat{}\) — единичные векторы вдоль оси x, оси y и оси z соответственно.
Когда два вектора перемножаются друг с другом и произведение также является векторной величиной, то результирующий вектор называется перекрестное произведение или векторное произведение. Перекрестное произведение представлено a × b. Перекрестное произведение двух векторов определяется как:
a × b = \({\begin{bmatrix} i\hat{} &j\hat{} &k\hat{} \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \end{bmatrix}}\)
Если мы используем расширение кофактора для решения этой матрицы, векторное произведение будет дано следующим образом:
(a × b) = (\(a_{2}\)\(b_{3}\) — \(a_{3}\)\(b_{2}\))\(i\шляпа{} \) — (\(а_{1}\)\(б_{3}\) — \(a_{3}\)\(b_{1}\))\(j\hat{}\) + (\(a_{1}\)\(b_{2}\) — \( а_{2}\)\(б_{1}\))\(к\шляпа{}\).
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
С Cuemath находите решения простыми и легкими шагами.
Запись на бесплатный пробный урок
Решенные примеры векторного произведения
Пример 1: Найдите векторное произведение двух векторов a = 4\(i\hat{}\) + 2\(j\hat{}\ ) – 5\(k\hat{}\) и b = 3\(i\hat{}\) – 2\(j\hat{}\) + \(k\hat{}\) и проверить это с помощью Калькулятор перекрестного произведения.
Решение:
Даны a = 4\(i\hat{}\) + 2\(j\hat{}\) – 5\(k\hat{}\) и b = 3\(i \шляпа{}\) – 2\(j\шляпа{}\) + \(k\шляпа{}\)
(a × b) = (\(a_{2}\)\(b_{3} \) — \(a_{3}\)\(b_{2}\))\(i\hat{}\) — (\(a_{1}\)\(b_{3}\) — \(a_{3}\)\(b_{1}\))\(j\шляпа{}\) + (\(a_{1}\)\(b_{2}\) — \(a_{ 2}\)\(b_{1}\))\(k\шляпа{}\).
= ((2 × 1) — (-5) × (-2))\(i\шляпа{}\) — (4 × 1 — (5) × (3))\(j\шляпа{} \) + ((4) × (-2) — (2 × 3))\(k\шляпа{}\)
= (2 — 10)\(i\шляпа{}\) — (4 + 15 )\(j\шляпа{}\) + (-8 — 6)\(k\шляпа{}\)
= -8\(i\hat{}\) — 19\(j\hat{}\) — 14\(k\hat{}\)
Следовательно, векторное произведение двух векторов равно -8\ (i\hat{}\) — 19\(j\hat{}\) — 14\(k\hat{}\)
Пример 2: Найдите векторное произведение двух векторов a = 3\(i \шляпа{}\) + 6\(j\шляпа{}\) – 5\(k\шляпа{}\) и b = 5\(i\шляпа{}\) – 8\(j\шляпа{} \) + \(k\hat{}\) и проверьте это с помощью калькулятора перекрестных произведений.

 ……………………………………………………………………………………………………………….
………………………………………………………………………………………………………………. ………………………………
……………………………… …………………………………………………………………………………………………………..
………………………………………………………………………………………………………….. ……………………………………….
………………………………………. Тензоры в релятивистской механике……………………………………………………………………………………
Тензоры в релятивистской механике…………………………………………………………………………………… ………………………………………
……………………………………… ……………………………………………………………………………….
………………………………………………………………………………. …………………
………………… ………………………………………………………………………………………………
……………………………………………………………………………………………… ……………………………………………………………
…………………………………………………………… ………………………………………………………………………………………….
…………………………………………………………………………………………. …………………..
………………….. ………………………………………………………………………………………………….
…………………………………………………………………………………………………. ……………………………………………..
…………………………………………….. …………………………………………………………………………………………………………
…………………………………………………………………………………………………………
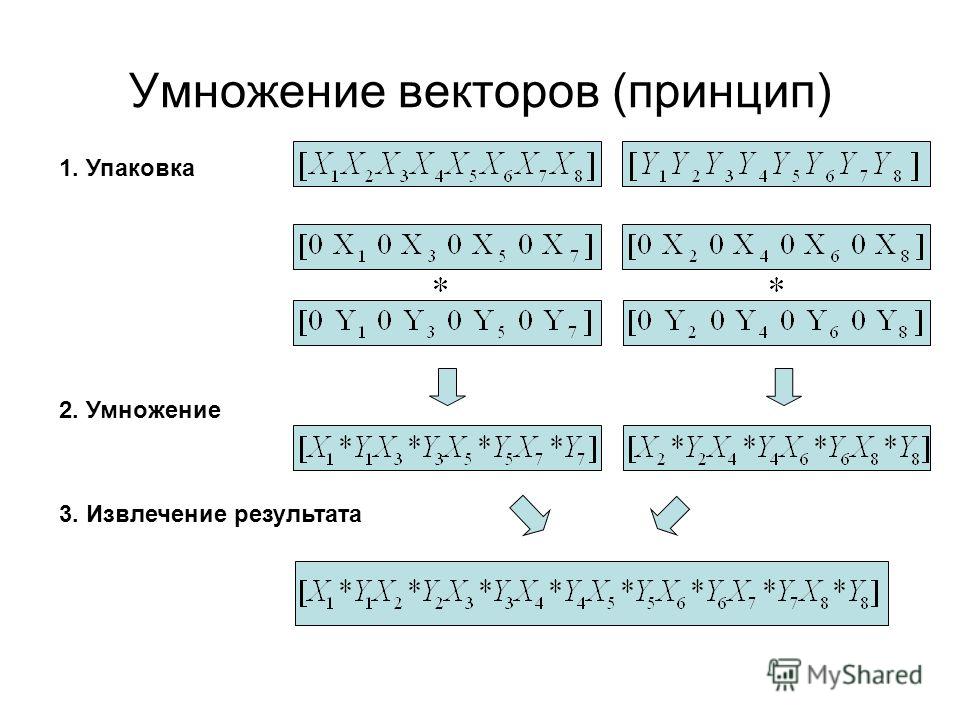

 Если нет, исправьте ошибку или вернитесь к предыдущей версии, пока ваш сайт снова не заработает.
Если нет, исправьте ошибку или вернитесь к предыдущей версии, пока ваш сайт снова не заработает. ) = a x b x + a y b y + a z b z = ||vec{a}|| ||век{б}|| cos(ϴ)
) = a x b x + a y b y + a z b z = ||vec{a}|| ||век{б}|| cos(ϴ) 
