исследование на четность функции онлайн
Вы искали исследование на четность функции онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и исследование функции на четность и нечетность онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «исследование на четность функции онлайн».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как исследование на четность функции онлайн,исследование функции на четность и нечетность онлайн,исследование функции на четность и нечетность онлайн с решением,исследование функции на четность онлайн,исследовать на четность и нечетность функции онлайн,исследовать на четность функцию,исследовать на четность функцию онлайн,исследовать функции на четность и нечетность онлайн,исследовать функцию на четность,исследовать функцию на четность и нечетность,исследовать функцию на четность и нечетность онлайн,исследовать функцию на четность онлайн,как проверить четность функции,калькулятор четности и нечетности функции,калькулятор четности нечетности функции,онлайн исследование функции на четность,онлайн исследовать функцию на четность,онлайн калькулятор четность и нечетность функции,онлайн калькулятор четность функции,онлайн определение четности и нечетности функции,онлайн определение четности функции,онлайн проверка функции на четность,онлайн проверка функции на четность и нечетность,онлайн четность нечетность,определение четности и нечетности функции онлайн,определение четности функции онлайн,определить функция четная или нечетная онлайн,определить четная или нечетная функция онлайн,определить четность и нечетность функции онлайн,определить четность или нечетность функции онлайн,определить четность функции онлайн,проверить на четность и нечетность онлайн,проверить на четность функцию,проверить функцию на четность,проверить функцию на четность и нечетность онлайн,проверить четность функции онлайн,проверка на четность и нечетность функции онлайн,проверка на четность функции,проверка на четность функции онлайн,проверка функции на четность и нечетность онлайн,проверка функции на четность онлайн,функция четная и нечетная онлайн,функция четная или нечетная онлайн,функция четная нечетная онлайн,четная и нечетная функция онлайн,четная или нечетная функция онлайн,четная нечетная функция онлайн,четность и нечетность функции онлайн,четность и нечетность функции онлайн калькулятор,четность и нечетность функции онлайн решение,четность нечетность онлайн,четность нечетность функции онлайн,четность функции как проверить,четность функции онлайн,четность функции онлайн калькулятор.
Где можно решить любую задачу по математике, а так же исследование на четность функции онлайн Онлайн?
Решить задачу исследование на четность функции онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Определить четность функции онлайн калькулятор.
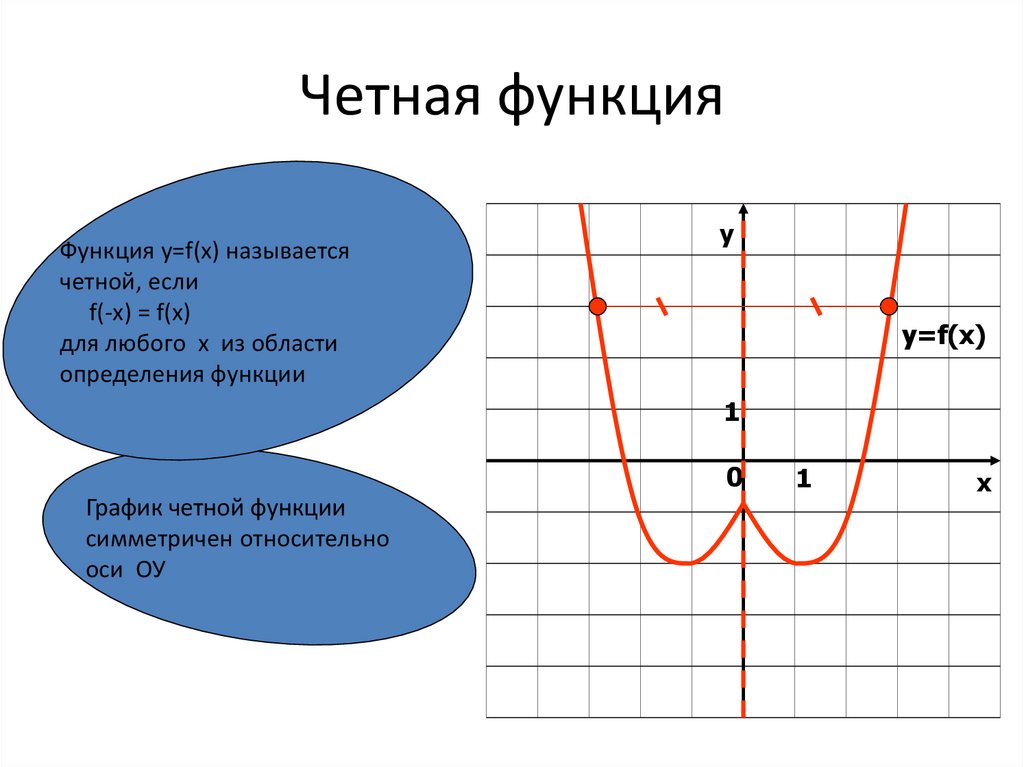
 3 симметрична относительно начала координат.
3 симметрична относительно начала координат.Четность и нечетность функции являются одним из основных ее свойств, и на четность занимает внушительную часть школьного курса по математике. Она во много определяет характер поведения функции и значительно облегчает построение соответствующего графика.
Определим четность функции. Вообще говоря, исследуемую функцию считают четной, если для противоположных значений независимой переменной (x), находящихся в ее области определения, соответствующие значения y (функции) окажутся равными.
Дадим более строгое определение. Рассмотрим некоторую функцию f (x), которая задана в области D. Она будет четной, если для любой точки x, находящейся в области определения:
- -x (противоположная точка) также лежит в данной области определения,
- f (-x) = f (x).
Из приведенного определения следует условие, необходимое для области определения подобной функции, а именно, симметричность относительно точки О, являющейся началом координат, поскольку если некоторая точка b содержится в области определения четной функции, то соответствующая точка — b тоже лежит в этой области. (-x))=- h(x). Следовательно, h(x) — нечетная.
(-x))=- h(x). Следовательно, h(x) — нечетная.
Кстати, следует напомнить, что есть функции, которые невозможно классифицировать по этим признакам, их называют ни четными, ни нечетными.
Четные функции обладают рядом интересных свойств:
- в результате сложения подобных функций получают четную;
- в результате вычитания таких функций получают четную;
- четной, также четная;
- в результате умножения двух таких функций получают четную;
- в результате умножения нечетной и четной функций получают нечетную;
- в результате деления нечетной и четной функций получают нечетную;
- производная такой функции — нечетная;
- если возвести нечетную функцию в квадрат, получим четную.
Четность функции можно использовать при решении уравнений.
Чтобы решить уравнение типа g(x) = 0, где левая часть уравнения представляет из себя четную функцию, будет вполне достаточно найти ее решения для неотрицательных значений переменной. Полученные корни уравнения необходимо объединить с противоположными числами.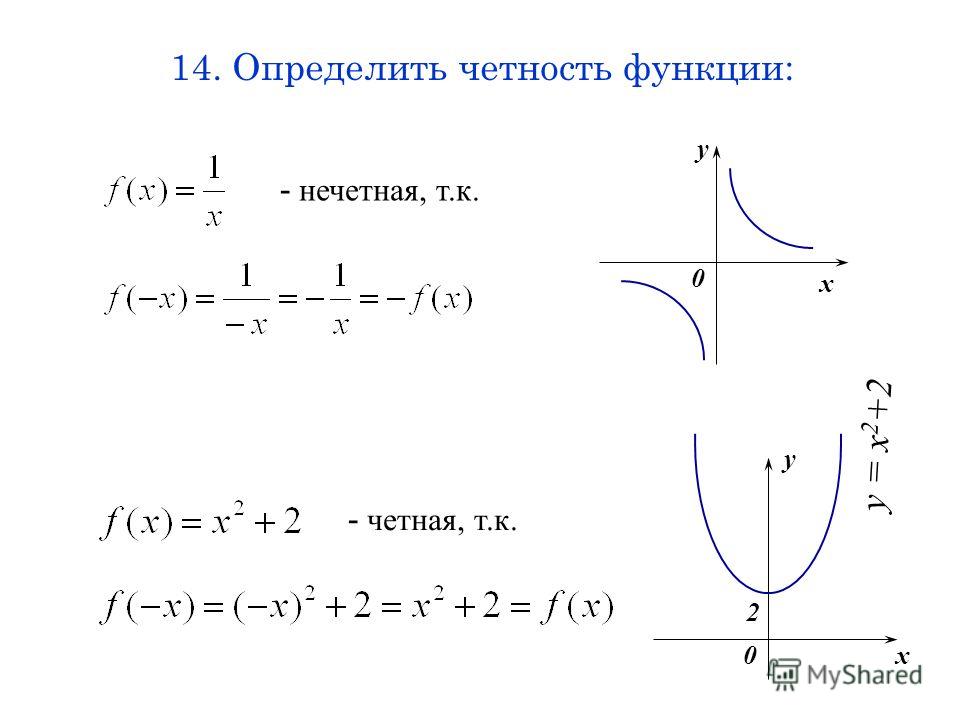 2+2 может быть нечетным, причем для любого значения параметра. Действительно, легко проверить, что множество корней данного уравнения содержит решения «парами». Проверим, является ли 0 корнем. При подстановке его в уравнение, получаем 2=2 . Таким образом, кроме «парных» 0 также является корнем, что и доказывает их нечетное количество.
2+2 может быть нечетным, причем для любого значения параметра. Действительно, легко проверить, что множество корней данного уравнения содержит решения «парами». Проверим, является ли 0 корнем. При подстановке его в уравнение, получаем 2=2 . Таким образом, кроме «парных» 0 также является корнем, что и доказывает их нечетное количество.
Функция
называется четной (нечетной), если для
любогои выполняется равенство
.
График четной
функции симметричен относительно оси
.
График нечетной функции симметричен относительно начала координат.
Пример 6.2. Исследовать на четность или нечетность функции
1)
;
2)
;
3)
.
Решение .
1) Функция определена
при
.
Найдем
.
Т.е.
.
Значит, данная функция является четной.
2) Функция определена
при
Т.е.
.
Таким образом, данная функция нечетная.
3) функция определена для , т.е. для
,
.
Поэтому функция не является ни четной,
ни нечетной.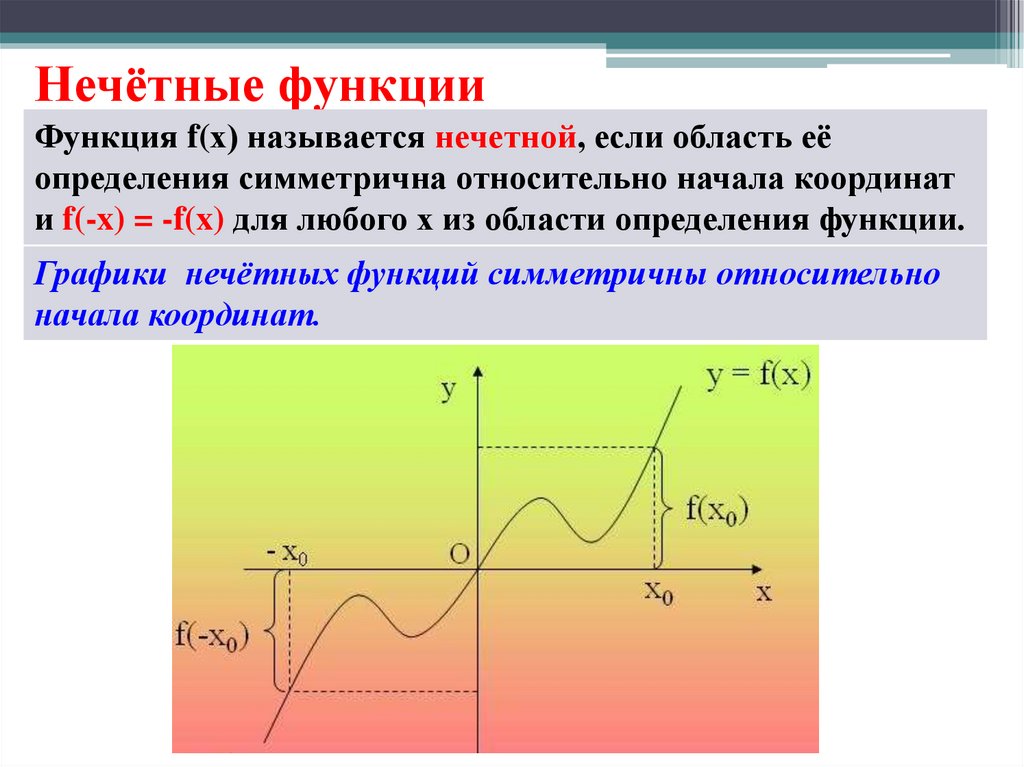 Назовем ее функцией общего
вида.
Назовем ее функцией общего
вида.
3. Исследование функции на монотонность.
Функция
называется возрастающей (убывающей) на
некотором интервале, если в этом интервале
каждому большему значению аргумента
соответствует большее (меньшее) значение
функции.
Функции возрастающие (убывающие) на некотором интервале называются монотонными.
Если функция
дифференцируема на интервале
и имеет положительную (отрицательную)
производную
,
то функция
возрастает (убывает) на этом интервале.
Пример 6.3 . Найти интервалы монотонности функций
1)
;
3)
.
Решение .
1) Данная функция определена на всей числовой оси. Найдем производную .
Производная равна
нулю, если
и
.
Область определения – числовая ось,
разбивается точками
,
на интервалы. Определим знак производной
в каждом интервале.
В интервале
производная отрицательна, функция на
этом интервале убывает.
В интервале
производная положительна, следовательно,
функция на этом интервале возрастает.
2) Данная функция
определена, если
или
.
Определяем знак квадратного трехчлена в каждом интервале.
Таким образом, область определения функции
Найдем производную
,
,
если
,
т.е.
,
но
.
Определим знак производной в интервалах
.
В интервале
производная отрицательна, следовательно,
функция убывает на интервале
.
В интервале
производная положительна, функция
возрастает на интервале
.
4. Исследование функции на экстремум.
Точка
называется точкой максимума (минимума)
функции
,
если существует такая окрестность точки,
что для всех
из этой окрестности выполняется
неравенство
.
Точки максимума и минимума функции называются точками экстремума.
Если функция
в точкеимеет экстремум, то производная функции
в этой точке равна нулю или не существует
(необходимое условие существования
экстремума).
Точки, в которых
производная равна нулю или не существует
называются критическими.
5. Достаточные условия существования экстремума.
Правило 1 .
Если при переходе (слева направо) через
критическую точку
производная
меняет знак с «+» на «–», то в точкефункция
имеет максимум; если с «–» на «+», то
минимум; если
не меняет знак, то экстремума нет.
Правило 2 .
Пусть в точке
первая производная функции
равна нулю
,
а вторая производная существует и
отлична от нуля. Если
,
то– точка максимума, если
,
то– точка минимума функции.
Пример 6.4 . Исследовать на максимум и минимум функции:
1)
;
2)
;
3)
;
4)
.
Решение.
1) Функция определена
и непрерывна на интервале
.
Найдем производную
и решим уравнение
,
т.е.
.Отсюда
– критические точки.
Определим знак
производной в интервалах
,
.
При переходе через
точки
и
производная меняет знак с «–» на «+»,
поэтому по правилу 1
– точки минимума.
При переходе через
точку
производная меняет знак с «+» на «–»,
поэтому
– точка максимума.
,
.
2) Функция определена
и непрерывна в интервале
.
Найдем производную
.
Решив уравнение
,
найдем
и
– критические точки. Если знаменатель
,
т.е.
,
то производная не существует. Итак,
– третья критическая точка. Определим
знак производной в интервалах.
Следовательно,
функция имеет минимум в точке
,
максимум в точках
и
.
3) Функция определена
и непрерывна, если
,
т.е. при
.
Найдем производную
.
Найдем критические
точки:
Окрестности точек
не принадлежат области определения,
поэтому они не являются т. экстремума.
Итак, исследуем критические точки
и
.
4) Функция определена
и непрерывна на интервале
.
Используем правило 2. Найдем производную
.
Найдем критические точки:
Найдем вторую
производную
и определим ее знак в точках
В точках
функция имеет минимум.
В точках
функция имеет максимум.
Нули функции
Нулём функции называется то значение х , при котором функция обращается в 0, то есть f(x)=0.
Нули – это точки пересечения графика функции с осью Ох.
Четность функции
Функция называется чётной, если для любого х из области определения выполняется равенство f(-x) = f(x)
Четная функция симметрична относительно оси Оу
Нечетность функции
Функция называется нечётной, если для любого х из области определения выполняется равенство f(-x) = -f(x).
Нечетная функция симметрична относительно начала координат.
Функция которая не является ни чётной,ни нечётной называется функцией общего вида.
Возрастание функции
Функция f(x) называется возрастающей, если большему значению аргумента соответствует большее значение функции, т.е.
Убывание функции
Функция f(x) называется убывающей, если большему значению аргумента соответствует меньшее значение функции, т. е.
е.
Промежутки, на которых функция либо только убывает, либо только возрастает, называются промежутками монотонности . Функция f(x) имеет 3 промежутка монотонности:
Находят промежутки монотонности с помощью сервиса Интервалы возрастания и убывания функции
Локальный максимум
Точка х 0 называется точкой локального максимума, если для любого х из окрестности точки х 0 выполняется неравенство: f(x 0) > f(x)
Локальный минимум
Точка х 0 называется точкой локального минимума, если для любого х из окрестности точки х 0 выполняется неравенство: f(x 0)
Точки локального максимума и точки локального минимума называются точками локального экстремума.
точки локального экстремума.
Периодичность функции
Функция f(x) называется периодичной, с периодом Т , если для любого х выполняется равенство f(x+T) = f(x) .
Промежутки знакопостоянства
Промежутки, на которых функция либо только положительна, либо только отрицательна, называются промежутками знакопостоянства.
Непрерывность функции
Функция f(x) называется непрерывной в точке x 0 , если предел функции при x → x 0 равен значению функции в этой точке, т.е. .
Точки разрыва
Точки, в которых нарушено условие непрерывности называются точками разрыва функции.
x 0 — точка разрыва.
Общая схема для построения графиков функций
1. Найти область определения функции D(y).
2. Найти точки пересечения графика функций с осями координат.
3. Исследовать функцию на четность или нечетность.
4. Исследовать функцию на периодичность.
5. Найти промежутки монотонности и точки экстремума функции.
6. Найти промежутки выпуклости и точки перегиба функции.
7. Найти асимптоты функции.
8. По результатам исследования построить график.
Пример: Исследовать функцию и построить ее график: y = x 3 – 3x
1) Функция определена на всей числовой оси, т. е. ее область определения D(y) = (-∞; +∞).
2) Найдем точки пересечения с осями координат:
с осью ОХ: решим уравнение x 3 – 3x = 0
с осью ОY: y(0) = 0 3 – 3*0 = 0
3) Выясним, не является ли функция четной или нечетной:
y(-x) = (-x) 3 – 3(-x) = -x 3 + 3x = — (x 3 – 3x) = -y(x)
Отсюда следует, что функция является нечетной.
4) Функция непериодична.
5) Найдем промежутки монотонности и точки экстремума функции: y’ = 3x 2 — 3.
Критические точки: 3x 2 – 3 = 0, x 2 =1, x= ±1.
y(-1) = (-1) 3 – 3(-1) = 2
y(1) = 1 3 – 3*1 = -2
6) Найдем промежутки выпуклости и точки перегиба функции: y’’ = 6x
Критические точки: 6x = 0, x = 0.
y(0) = 0 3 – 3*0 = 0
7) Функция непрерывна, асимптот у нее нет.
8) По результатам исследования построим график функции.
Калькулятор четных, нечетных или ни одной функции
Поиск инструмента
Найдите инструмент в dCode по ключевым словам:Просмотрите полный список инструментов dCode
Четная или нечетная функция
Инструмент для проверки четности функции (четные или нечетные функции): он определяет способность функции (ее кривую ) для проверки симметричных отношений.
Результаты
Четная или нечетная функция — dCode
Теги: Функции
Поделиться
dCode и другие
dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Калькулятор четных и нечетных функций
Выражение функции f(x)= или y=Переменная
| Я хочу | Проверить, является ли функция четной или нечетной Проверить, является ли функция четной Проверить, является ли функция нечетной Вычислить f(-x ) Вычислить -f(-x) |
См. также: Решатель уравнений
также: Решатель уравнений
Ответы на вопросы (FAQ)
Что такое четность функции? (Определение)
Четность функции – это свойство, придающее кривой характеристики функции симметрию (осевую или центральную).
— Функция чётная, если равенство $$ f(x) = f(-x) $$ верно для всех $ x $ из области определения. Четная функция предоставит идентичное изображение для противоположных значений. Графически это подразумевает, что противоположные абсциссы имеют одинаковые ординаты, это означает, что ось ординат y является осью симметрии кривой, представляющей $f$.
— Функция называется нечетной, если равенство $$ f(x) = -f(-x) $$ верно для всех $ x $ из области определения. Нечетная функция предоставит противоположное изображение для противоположных значений. Графически это означает, что противоположные абсциссы имеют противоположные ординаты, это означает, что начало координат (центральная точка) (0,0) является центром симметрии кривой, представляющей $ f $. 3 = f(x)$, поэтому функция куба $f(x)$ нечетна.
3 = f(x)$, поэтому функция куба $f(x)$ нечетна.
Доказав равенство для единственного значения типа $f(2) = -f(-2) $, мы не можем сделать вывод о наличии нечетности, а лишь можем сказать, что 2 и -2 имеют противоположные образы функцией $f $.
Как проверить, является ли функция ни четной, ни нечетной?
Функция не является ни нечетной, ни четной, если не выполняется ни одно из двух вышеприведенных равенств, то есть: $$ f(x) \neq f(-x) $$ и $$ f(x) \neq -f (-x) $$
Пример: Определить четность $ f(x) = x/(x+1) $, первое вычисление: $ f(-x) = -x/(-x+1) = x/(x-1) \neq f(x) $ и второе вычисление: $ -f(-x) = -(-x/(-x+1)) = -x/(x-1) = x /(-x+1) \neq f(x) $, поэтому функция $f $ не является ни четной, ни нечетной.
Какова четность тригонометрических функций (cos, sin, tan)?
В тригонометрии функции часто бывают симметричными:
Функция косинуса $ \cos(x) $ четна.
Функция синуса $ \sin(x) $ нечетная.
Касательная функция $ \tan(x) $ нечетна.
Почему функции называются четными или нечетными?
Развертки в сходящихся степенных рядах или многочленах четных (соответственно нечетных) функций имеют четные степени (соответственно нечетные).
Есть ли функция одновременно четная и нечетная?
Да, функция $ f(x) = 0 $ (функция с постоянным нулем) является одновременно четной и нечетной, поскольку она соблюдает 2 равенства $ f(x) = f(-x) = 0 $ и $ f(x) = -f(-x) = 0 $
Исходный код
dCode сохраняет право собственности на исходный код «Четная или нечетная функция». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Четная или нечетная функция», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Четного или Odd Function» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т.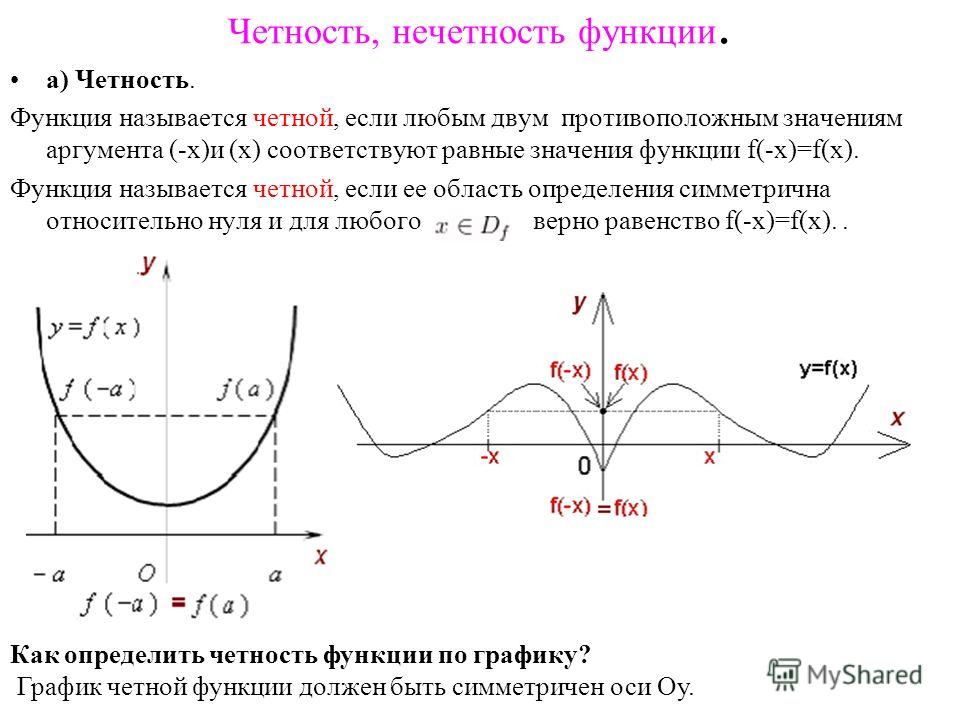 д.) и все данные загрузка, сценарий или доступ к API для «Четной или нечетной функции» не являются общедоступными, то же самое для автономного использования на ПК, мобильном телефоне, планшете, iPhone или в приложении для Android!
д.) и все данные загрузка, сценарий или доступ к API для «Четной или нечетной функции» не являются общедоступными, то же самое для автономного использования на ПК, мобильном телефоне, планшете, iPhone или в приложении для Android!
Напоминание: dCode можно использовать бесплатно.
Cite dCode
Копирование и вставка страницы «Четная или нечетная функция» или любых ее результатов разрешена, если вы цитируете dCode!
Цитировать как источник (библиографию):
Четная или нечетная функция на dCode.fr [онлайн-сайт], получено 29 октября 2022 г., https://www.dcode.fr/even-odd-function
Сводка
- Калькулятор четных и нечетных функций
- Что такое четность функции? (Определение)
- Как проверить четность функции?
- Как проверить, является ли функция нечетной?
- Как проверить, является ли функция ни четной, ни нечетной?
- Какова четность тригонометрических функций (cos, sin, tan)?
- Почему функции называются четными или нечетными?
- Существует ли функция, которая одновременно является четной и нечетной?
Похожие страницы
- Решатель уравнений
- Период функции
- Расширение ряда
- N-я производная
- Fourier Transform
- Stationary Point of a Function
- Minimum of a Function
- DCODE’S TOOLS LIST
Support
- Paypal
- Patreon
- More
Forum/Help
Keywords
even ,нечетная,функция,четность,симметрия,тригонометрический,косинус,синус
Ссылки
▲
Калькулятор четных, нечетных или ни одной функции
Поиск инструмента
Найдите инструмент в dCode по ключевым словам:Просмотрите полный список инструментов dCode
Четная или нечетная функция
Инструмент для проверки четности функции (четные или нечетные функции): он определяет способность функции (ее кривую ) для проверки симметричных отношений.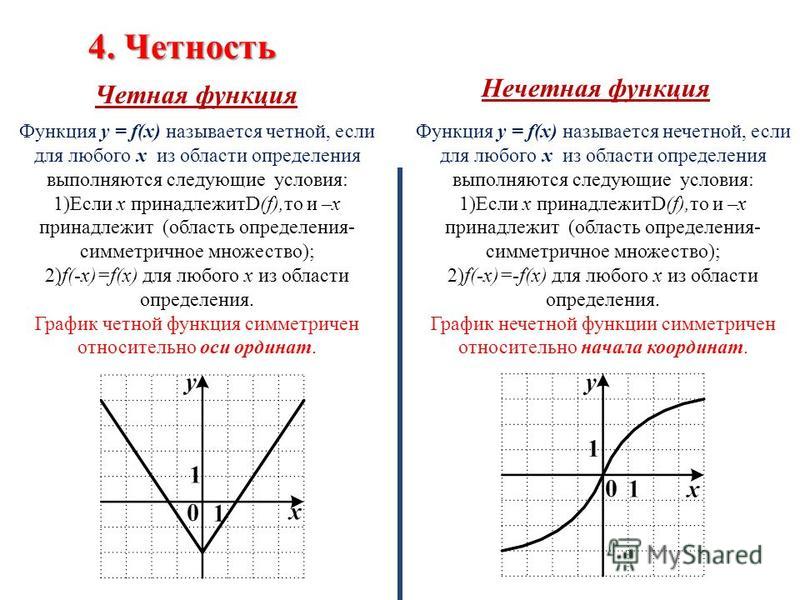
Результаты
Четная или нечетная функция — dCode
Теги: Функции
Поделиться
dCode и многое другое решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Калькулятор четных и нечетных функций
Выражение функции f(x)= или y=Переменная
| Я хочу | Проверить, является ли функция четной или нечетной Проверить, является ли функция четной Проверить, является ли функция нечетной Вычислить f(-x ) Вычислить -f(-x) |
См. также: Решатель уравнений
Ответы на вопросы (FAQ)
Что такое четность функции? (Определение)
Четность функции – это свойство, придающее кривой характеристики функции симметрию (осевую или центральную).
— Функция чётная, если равенство $$ f(x) = f(-x) $$ верно для всех $ x $ из области определения. Четная функция предоставит идентичное изображение для противоположных значений.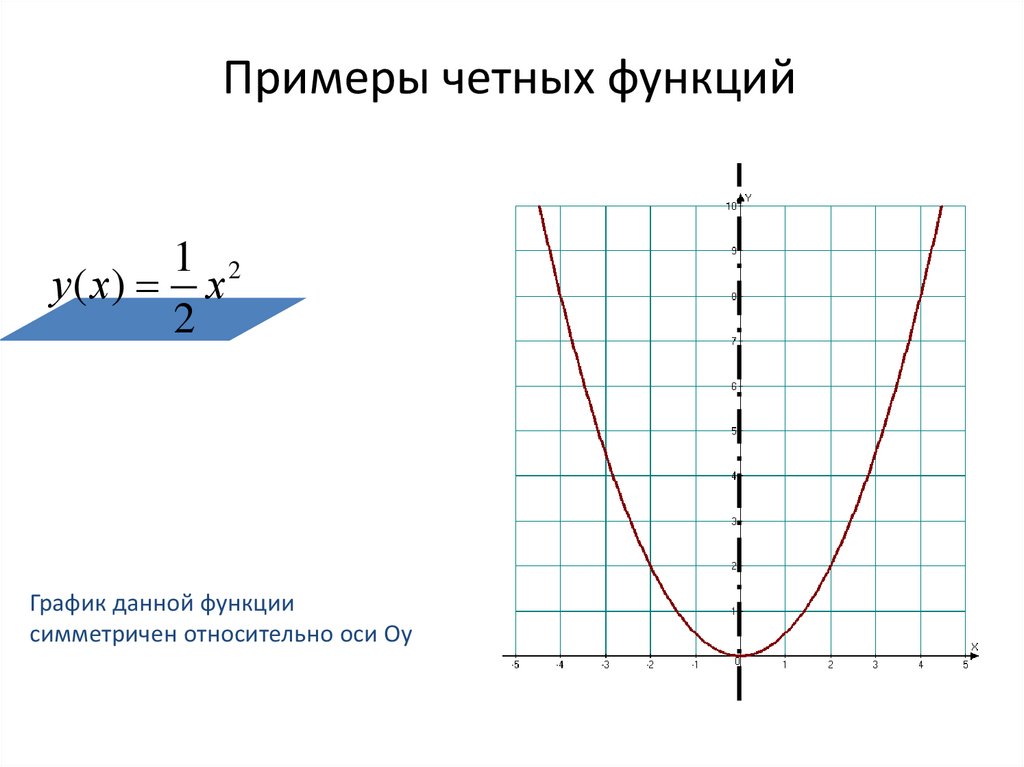 Графически это предполагает, что противоположные абсциссы имеют одинаковые ординаты, это означает, что ось ординат y является осью симметрии кривой, представляющей $f$.
Графически это предполагает, что противоположные абсциссы имеют одинаковые ординаты, это означает, что ось ординат y является осью симметрии кривой, представляющей $f$.
— Функция называется нечетной, если равенство $$ f(x) = -f(-x) $$ верно для всех $ x $ из области определения. Нечетная функция предоставит противоположное изображение для противоположных значений. Графически это означает, что противоположные абсциссы имеют противоположные ординаты, это означает, что начало координат (центральная точка) (0,0) является центром симметрии кривой, представляющей $ f $.
Примечание: если нечетная функция определена в 0, то кривая проходит в начале координат: $ f(0) = 0 $ 92 = f(x)$, поэтому функция квадрата $f(x)$ четна.
Изучение/доказательство этого равенства для одного значения вида $ f(1) = f(-1) $ не позволяет сделать вывод о наличии четности, а лишь сказать, что 1 и -1 имеют одинаковый образ функцией $ ф $.
Как проверить, является ли функция нечетной?
Чтобы определить/сказать, что функция нечетная, проверьте равенство $ f(x) = -f(-x) $, если формула верна, то функция четная. 3 = f(x)$, поэтому функция куба $f(x)$ нечетна.
3 = f(x)$, поэтому функция куба $f(x)$ нечетна.
Доказав равенство для единственного значения типа $f(2) = -f(-2) $, мы не можем сделать вывод о наличии нечетности, а лишь можем сказать, что 2 и -2 имеют противоположные образы функцией $f $.
Как проверить, является ли функция ни четной, ни нечетной?
Функция не является ни нечетной, ни четной, если не выполняется ни одно из двух вышеприведенных равенств, то есть: $$ f(x) \neq f(-x) $$ и $$ f(x) \neq -f (-x) $$
Пример: Определить четность $ f(x) = x/(x+1) $, первое вычисление: $ f(-x) = -x/(-x+1) = x/(x-1) \neq f(x) $ и второе вычисление: $ -f(-x) = -(-x/(-x+1)) = -x/(x-1) = x /(-x+1) \neq f(x) $, поэтому функция $f $ не является ни четной, ни нечетной.
Какова четность тригонометрических функций (cos, sin, tan)?
В тригонометрии функции часто бывают симметричными:
Функция косинуса $ \cos(x) $ четна.
Функция синуса $ \sin(x) $ нечетная.
Касательная функция $ \tan(x) $ нечетна.
Почему функции называются четными или нечетными?
Развертки в сходящихся степенных рядах или многочленах четных (соответственно нечетных) функций имеют четные степени (соответственно нечетные).
Есть ли функция одновременно четная и нечетная?
Да, функция $ f(x) = 0 $ (функция с постоянным нулем) является одновременно четной и нечетной, поскольку она соблюдает 2 равенства $ f(x) = f(-x) = 0 $ и $ f(x) = -f(-x) = 0 $
Исходный код
dCode сохраняет право собственности на исходный код «Четная или нечетная функция». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Четная или нечетная функция», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Четного или Odd Function» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т.