Матрицы. Определение, виды и основные понятия | Математика
Определение матрицы
Матрицей называется прямоугольная таблица, составленная из чисел. Для обозначения матрицы применяются круглые скобки и прописные буквы А, В, С и так далее.
Например,
| (1.1) |
есть общий вид записи матрицы из чисел.
Числа составляющие матрицу, называются ее элементами.
Помощь с решением задач
Горизонтальные ряды матрицы называются строками матрицы, вертикальные — столбцами.
Индексы у элемента , где
означают, что этот элемент расположен в i-й строке и j-м столбце.
Например, элемент расположен во второй строке и в третьем столбце.
Числа и , указывающие количество строк и столбцов матрицы, называются размерами матрицы.
Наряду с обозначением (1.1) матрица обозначается также в форме:
(1. 2) 2) |
,где
Виды матриц
Матрица, у которой число строк равно числу ее столбцов называется квадратной матрицей. При этом число ее строк (столбцов) называется порядком матрицы.
Например, матрица есть квадратная матрица третьего порядка.
Квадратная матрица n-го порядка записывается в виде
| (1.3) |
В квадратной матрице (1.3) числа образуют главную диагональ матрицы, а числа побочную диагональ.
Квадратная матрица, у которой все числа, не стоящие на главной диагонали, равны нулю, называется диагональной матрицей.
Например, матрица есть диагональная матрица второго порядка.
Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной матрицей. Единичную матрицу обозначают прописной буквой Е.
Например, матрица есть единичная матрица второго порядка.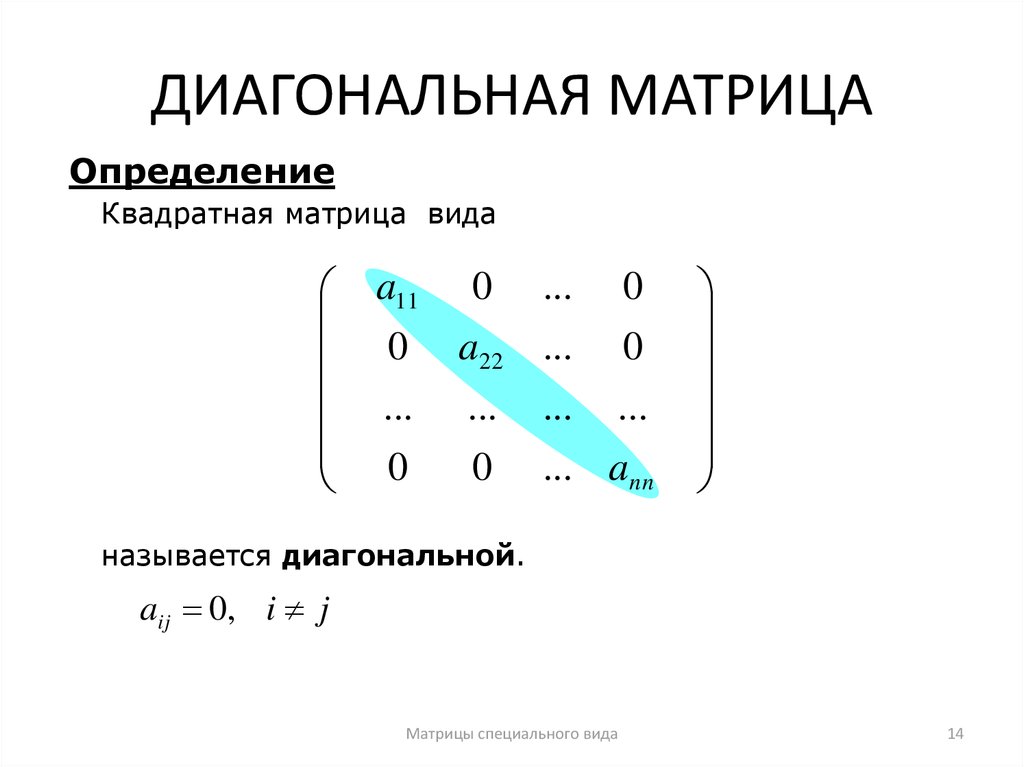
Матрица, состоящая только из одной строки, называется матрицей-строкой, состоящая только из одного столбца матрицей — столбцом.
Например, матрица А=(2 О 5 4) есть матрица — строка.
Матрица называется транспонированной по отношению к матрице А, если столбцы (строки) матрицы являются соответствующими строчками (столбцами) матрицы .
Например, если матрица равна
, то
- Действия над матрицами
- Курс математики
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
Скачать рамки A4
Скачать миллиметровки
Скачать шрифты ГОСТ
Сохранить или поделиться с друзьями
Помощь с решением
Поиск математических формул
Построить матрицу пространственных весов для сети (Пространственная статистика)—ArcGIS Pro
| Подпись | Описание | Тип данных |
Входной класс пространственных объектов | Класс точечных объектов, представляющий местоположения в сети. | Feature Class |
Поле уникального ID | Целое поле, содержащее уникальное значение для каждого объекта во входном классе объектов. Если у вас нет поля с уникальными значениями ID, вы можете создать его путем добавления нового целого поля в вашу таблицу классов объектов и вычислив значения полей, которые были бы равны полю FID или OBJECTID. | Field |
Выходной файл матрицы пространственных весов | Выходной файл сетевой матрицы пространственных весов (. | File |
Входной источник сетевых данных | Набор сетевых данных, используемый для поиска соседей каждого входного объекта. Наборы сетевых данных обычно представляют уличные сети, но могут также представлять и другие виды транспортных сетей, такие как железные дороги или пешеходные дорожки. Набор сетевых данных должен содержать по крайней мере один атрибут, связанный с расстоянием, временем в пути или стоимостью. | Network Data Source |
Режим передвижения | Режим передвижения для анализа. Режим передвижения определяет, как пешеход, легковой автомобиль, грузовик или другое транспортное средство перемещается по сети и представляет собой набор сетевых параметров, таких как ограничения на передвижение и правила разворота. | String |
Пороговое расстояние импеданса | Максимальное расстояние импеданса, допустимое для соседей объекта. Любой объект, расстояние до которого больше этого значения, не будет использоваться в качестве соседа. По умолчанию пороговое расстояние не используется. | Linear Unit |
Пороговое время импеданса (Дополнительный) | Time Unit | |
Пороговая стоимость импеданса (Дополнительный) | Максимальная стоимость импеданса, допустимая для соседей объекта. | Double |
Максимальное число соседей (Дополнительный) | Целое число, отражающее максимальное количество соседних объектов для каждого объекта. Фактическое число соседей, используемых для каждого объекта, может быть меньше из-за предельных значений импеданса. | Long |
Время дня (Дополнительный) | При анализе будут учитываться дорожные условия в соответствии с временем суток. Дорожные условия могут влиять на расстояние, которое может быть пройдено за заданное время. Вместо конкретной даты можно задать день недели, при помощи следующих условных дат:
Например, чтобы указать, что маршрут должен начинаться в 5:00 во вторник, следует указать значение параметра, равное 02.01.1900 17:00. | Date |
Часовой пояс (Дополнительный) | Указывает часовой пояс для параметра Время суток.
| String |
Барьеры (Дополнительный) | Объекты, которые представляют собой заблокированные перекрестки, места перекрытия дорог, места дорожных аварий или другие местоположения, в которых заблокирован проход по дорожной сети. | Feature Layer |
Допуск поиска (Дополнительный) | Максимальное расстояние, используемое для присвоения каждого входного объекта местоположению в сети. Если какие-либо из входных точек не попадают точно на линию сети, они будут присвоены ближайшему местоположению в сети для анализа. | Linear Unit |
Определение пространственных взаимоотношений (Дополнительный) | Указывает, как будут определены веса для каждого соседа.
| String |
Порядок (Дополнительный) | Показатель степени, используемый, когда для параметра Определение пространственных взаимоотношений задано значение Обратный. | Double |
Стандартизация строк (Дополнительный) | Указывает, будет ли применяться ли стандартизация строк. Нормализация ряда рекомендуется, когда расположение входных точек является потенциально предвзятым в зависимости от дизайна примера или от установленной схемы агрегации. Также рекомендуется нормализовать строки при взвешивании соседей на основе обратного расстояния, времени или стоимости.
| Boolean |
arcpy.stats.GenerateNetworkSWM(Input_Feature_Class, Unique_ID_Field, Output_Spatial_Weights_Matrix_File, Input_Network_Data_Source, Travel_Mode, Impedance_Distance_Cutoff, {Impedance_Temporal_Cutoff}, {Impedance_Cost_Cutoff}, {Maximum_Number_of_Neighbors}, {Time_of_Day}, {Time_Zone}, {Barriers}, {Search_Tolerance}, {Conceptualization_of_Spatial_Relationships}, {Exponent}, {Row_Standardization})| Имя | Описание | Тип данных |
Input_Feature_Class | Класс точечных объектов, представляющий местоположения в сети. Для каждого объекта вычисляются соседи и веса, которые хранятся в выходном файле матрицы пространственных весов. | Feature Class |
Unique_ID_Field | Целое поле, содержащее уникальное значение для каждого объекта во входном классе объектов. Если у вас нет поля с уникальными значениями ID, вы можете создать его путем добавления нового целого поля в вашу таблицу классов объектов и вычислив значения полей, которые были бы равны полю FID или OBJECTID. | Field |
Output_Spatial_Weights_Matrix_File | Выходной файл сетевой матрицы пространственных весов (.swm), в котором будут храниться соседи и веса для каждого входного объекта. | File |
Input_Network_Data_Source | Набор сетевых данных, используемый для поиска соседей каждого входного объекта. | Network Data Source |
Travel_Mode | Режим передвижения для анализа. Режим передвижения определяет, как пешеход, легковой автомобиль, грузовик или другое транспортное средство перемещается по сети и представляет собой набор сетевых параметров, таких как ограничения на передвижение и правила разворота. Объект arcpy.na.TravelMode и строка, содержащая действительное представление JSON режима перемещения, также могут использоваться как ввод для параметра. | String |
Impedance_Distance_Cutoff | Максимальное расстояние импеданса, допустимое для соседей объекта. | Linear Unit |
Impedance_Temporal_Cutoff (Дополнительный) | Максимальное время в пути для импеданса, допустимое для соседей объекта. Любой объект, время в пути до которого больше этого значения, не будет использоваться в качестве соседа. По умолчанию пороговое время не используется. | Time Unit |
Impedance_Cost_Cutoff (Дополнительный) | Максимальная стоимость импеданса, допустимая для соседей объекта. Любой объект, стоимость перемещения до которого больше этого значения, не будет использоваться в качестве соседа. | Double |
Maximum_Number_of_Neighbors (Дополнительный) | Целое число, отражающее максимальное количество соседних объектов для каждого объекта. Фактическое число соседей, используемых для каждого объекта, может быть меньше из-за предельных значений импеданса. | Long |
Time_of_Day (Дополнительный) | При анализе будут учитываться дорожные условия в соответствии с временем суток. Дорожные условия могут влиять на расстояние, которое может быть пройдено за заданное время. Если дата или время не указаны, то анализ не будет учитывать влияние дорожных условий. Вместо конкретной даты можно задать день недели, при помощи следующих условных дат:
Например, чтобы указать, что маршрут должен начинаться в 5:00 во вторник, следует указать значение параметра, равное 02.01.1900 17:00. | Date |
Time_Zone (Дополнительный) | Указывает часовой пояс параметра Time_of_Day.
| String |
Barriers (Дополнительный) | Объекты, которые представляют собой заблокированные перекрестки, места перекрытия дорог, места дорожных аварий или другие местоположения, в которых заблокирован проход по дорожной сети. | Feature Layer |
Search_Tolerance (Дополнительный) | Максимальное расстояние, используемое для присвоения каждого входного объекта местоположению в сети. Если какие-либо из входных точек не попадают точно на линию сети, они будут присвоены ближайшему местоположению в сети для анализа. Однако если объект находится дальше значения допуска поиска от любого места в сети, он не будет присвоен сети и не будет включен в анализ. | Linear Unit |
Conceptualization_of_Spatial_Relationships (Дополнительный) | Указывает, как будут определены веса для каждого соседа.
| String |
Exponent (Дополнительный) | Показатель степени, используемый, когда INVERSE указано для параметра Conceptualization_of_Spatial_Relationships. | Double |
Row_Standardization (Дополнительный) | Указывает, будет ли применяться ли стандартизация строк. Нормализация ряда рекомендуется, когда расположение входных точек является потенциально предвзятым в зависимости от дизайна примера или от установленной схемы агрегации. Также рекомендуется нормализовать строки при взвешивании соседей на основе обратного расстояния, времени или стоимости.
| Boolean |
Пример кода
GenerateNetworkSWM, пример 1 (окно Python)В следующем скрипте окна Python показано, как использовать инструмент GenerateNetworkSWM.
import arcpy
arcpy.env.workspace = "c:\Data"
# Use a network data source hosted on ArcGIS Online.
arcpy.stats.GenerateNetworkSWM(r"Data.gdb\Hospital", "MyID",
"Hospital.swm", "https://www.arcgis.com/",
"Driving Time", None, None, None, None, None,
"LOCAL_TIME_AT_LOCATIONS", None, "5000 Meters",
"FIXED", 1, "ROW_STANDARDIZATION")
# Use a network data source stored on a local drive.
arcpy.stats.GenerateNetworkSWM(r"Data.gdb\Hospital", "MyID", "Hospital.swm",
r"Data. gdb\transportation\streets_ND",
"Driving Time", None, None, None, None, None,
"LOCAL_TIME_AT_LOCATIONS", None, "5000 Meters",
"FIXED", 1, "ROW_STANDARDIZATION")
gdb\transportation\streets_ND",
"Driving Time", None, None, None, None, None,
"LOCAL_TIME_AT_LOCATIONS", None, "5000 Meters",
"FIXED", 1, "ROW_STANDARDIZATION")GenerateNetworkSWM, пример 2 (автономный скрипт)В следующем скрипте окна Python показано, как использовать инструмент GenerateNetworkSWM.
# Create a Spatial Weights Matrix based on Network Data
# Import system modules
import arcpy
# Set the environment property to overwrite existing output
arcpy.env.overwriteOutput = True
# Check out the ArcGIS Network Analyst extension
arcpy.CheckOutExtension("Network")
# Local variables...
workspace = r"c:\Data"
try:
# Set the current workspace (to avoid having to specify the full path to
# the feature classes each time)
arcpy.env.workspace = workspace
# Create Spatial Weights Matrix based on Network Data
# Process: Generate Network Spatial Weights...
arcpy.stats. GenerateNetworkSWM(r"Data.gdb\Hospital","MyID",
"Hospital.swm", r"Data.gdb\Transportation\Streets_ND",
"Driving Time", None, None, None, None, None,
"LOCAL_TIME_AT_LOCATIONS", None, "5000 Meters", "FIXED",
1,"ROW_STANDARDIZATION")
# Create Spatial Weights Matrix based on Euclidean Distance
# Process: Generate Spatial Weights Matrix...
arcpy.stats.GenerateSpatialWeightsMatrix(
r"Data.gdb\Hospital", "MyID", r"Euclidean6Neighs.swm",
"K_NEAREST_NEIGHBORS", "EUCLIDEAN", 1, None, 6,
"ROW_STANDARDIZATION", None, None, '', None, None)
# Calculate Moran's Index of Spatial Autocorrelation for
# average hospital visit times using Network Spatial Weights
# Process: Spatial Autocorrelation (Morans I)...
moransINet = arcpy.stats.SpatialAutocorrelation("Data.gdb\Hospital",
"VisitTime", "NO_REPORT", "GET_SPATIAL_WEIGHTS_FROM_FILE",
"EUCLIDEAN_DISTANCE", "ROW", None, "Hospital.
GenerateNetworkSWM(r"Data.gdb\Hospital","MyID",
"Hospital.swm", r"Data.gdb\Transportation\Streets_ND",
"Driving Time", None, None, None, None, None,
"LOCAL_TIME_AT_LOCATIONS", None, "5000 Meters", "FIXED",
1,"ROW_STANDARDIZATION")
# Create Spatial Weights Matrix based on Euclidean Distance
# Process: Generate Spatial Weights Matrix...
arcpy.stats.GenerateSpatialWeightsMatrix(
r"Data.gdb\Hospital", "MyID", r"Euclidean6Neighs.swm",
"K_NEAREST_NEIGHBORS", "EUCLIDEAN", 1, None, 6,
"ROW_STANDARDIZATION", None, None, '', None, None)
# Calculate Moran's Index of Spatial Autocorrelation for
# average hospital visit times using Network Spatial Weights
# Process: Spatial Autocorrelation (Morans I)...
moransINet = arcpy.stats.SpatialAutocorrelation("Data.gdb\Hospital",
"VisitTime", "NO_REPORT", "GET_SPATIAL_WEIGHTS_FROM_FILE",
"EUCLIDEAN_DISTANCE", "ROW", None, "Hospital. swm", None)
# Calculate Moran's Index of Spatial Autocorrelation for
# average hospital visit times using Euclidean Spatial Weights
# Process: Spatial Autocorrelation (Morans I)...
moransIEuc = arcpy.stats.SpatialAutocorrelation("Data.gdb\Hospital",
"VisitTime", "NO_REPORT", "GET_SPATIAL_WEIGHTS_FROM_FILE",
"EUCLIDEAN_DISTANCE", "ROW", None, r"Euclidean6Neighs.swm",
None)
except arcpy.ExecuteError:
# If an error occurred when running the tool, print out the error message.
print(arcpy.GetMessages())
swm", None)
# Calculate Moran's Index of Spatial Autocorrelation for
# average hospital visit times using Euclidean Spatial Weights
# Process: Spatial Autocorrelation (Morans I)...
moransIEuc = arcpy.stats.SpatialAutocorrelation("Data.gdb\Hospital",
"VisitTime", "NO_REPORT", "GET_SPATIAL_WEIGHTS_FROM_FILE",
"EUCLIDEAN_DISTANCE", "ROW", None, r"Euclidean6Neighs.swm",
None)
except arcpy.ExecuteError:
# If an error occurred when running the tool, print out the error message.
print(arcpy.GetMessages())Этимология, происхождение и значение слова matrix по этимонлайну
Реклама
конец 14 века, matris, matrice, «матка, матка», от старофранцузского matrice «матка, матка» и непосредственно от латинского mātrix (родительный падеж mātricis) «беременное животное». ,» в позднелатинском «матка», также «источник, начало», от māter (родительный падеж mātris) «мать» (см. мать (n.1)).
мать (n.1)).
Многие переносные и технические значения происходят от понятия «то, что окружает или дает начало» чему-то. Общее значение «места или среды, где что-то развивается» зафиксировано к 1550-м годам; что означает «форма, в которой что-то отливается или формуется» к 1620-м годам; смысл «вмещающей или вмещающей массы» относится к 1640-м гг.
Математический смысл «прямоугольного массива величин (обычно квадратного)» состоит в том, что он рассматривается как набор компонентов, в которые могут быть помещены величины. Логический смысл «массива возможных комбинаций истинностных значений» засвидетельствован 1914 г. Как глагол в телевещании с 1951 г.
обновлено 04 декабря 2018 г. матричный
матричный
matrilineal
matrilocal
matrimonial
matrimony
matrix
matroclinous
matron
matronize
matronly
matronymic
- A
- B
- C
- D
- E
- F
- G
- H
- I
- J
- K
- L
- M
- N
- O
- R
- S
- T
- U
- V
- W
- X
- Y
- Z
4
Матрица в математике | Значение матрицы в математике
Содержание
Знание матрицы (множественного числа матриц) необходимо для различных разделов математики. Матрицы — один из самых мощных инструментов в математике. Этот математический аппарат значительно упрощает нашу работу по сравнению с другими простыми методами. Матрицы обеспечивают компактный способ решения системы линейных уравнений. Помимо решения уравнений, матрицы используются в программах электронных таблиц для персональных компьютеров, а также в физических операциях, таких как увеличение, вращение и отражение через плоскость.
Матрицы — один из самых мощных инструментов в математике. Этот математический аппарат значительно упрощает нашу работу по сравнению с другими простыми методами. Матрицы обеспечивают компактный способ решения системы линейных уравнений. Помимо решения уравнений, матрицы используются в программах электронных таблиц для персональных компьютеров, а также в физических операциях, таких как увеличение, вращение и отражение через плоскость.
Давайте разберемся, что такое матрица в математике, ее свойства и использование на примерах.
Что такое матрица в математике?
Матрица, форма единственного числа матриц, представляет собой расположение чисел, переменных, символов или выражений в прямоугольной таблице, содержащей различное количество строк и столбцов. Это массивы прямоугольной формы, для которых определены различные операции, такие как сложение, умножение и транспонирование. Числа или записи в матрице известны как ее элементы. Горизонтальные элементы матрицы называются строками, а вертикальные — столбцами.
Предположим, вы хотите представить информацию о количестве тетрадей и ручек для трех друзей Рави, Ракеша и Саураба, у которых в сумках есть следующие предметы.
У Рави 12 тетрадей и 3 ручки
У Ракеша 8 тетрадей и 2 ручки
У Саураба 15 тетрадей и 4 ручки
Теперь это можно представить в табличной форме как
| Блокноты | Ручки | |
| Ravi | 12 | 3 |
| Rakesh | 8 | 2 |
| Saurabh | 15 | 4 |
In a matrix form, it can быть выражено как
В приведенной выше матрице строки обозначают трех учеников – Рави, Ракеша и Саураба, а столбцы обозначают количество двух предметов – блокнотов и ручек.
Также может быть представлен как
В приведенной выше матрице строки обозначают количество двух предметов — блокнотов и ручек, а столбцы — трех учеников — Рави, Ракеша и Саурабха.
Определение матрицы
Матрица — это упорядоченный прямоугольный массив чисел, состоящий из $m$ горизонтальных строк и $n$ вертикальных столбцов. Числа или функции называются элементами или элементами матрицы. Матрицы обозначаются заглавными буквами.
Приведенная выше матрица называется матрицей $m \times n$ или матрицей размера $m \times n$. Для записи $a_{ij}$ $i$ — это индекс строки, а $j$ — индекс столбца.
Общая матрица иногда обозначается как $[ a_{ij}]_{m \times n}$.
Примеры матриц
Пример 1: Рассмотрим следующую матрицу.
Размер матрицы $2 \times 3$, элементы (или элементы) матрицы $b_{11} = 1$, $b_{12} = -4$, $b_{13} = 3$ , $b_{21} = 5$, $b_{22} = 0$ и $b_{23} = 7$.
Пример 2: Рассмотрим следующую матрицу.
Размер матрицы $1 \times 3$, элементы (или элементы) матрицы $p_{11} = 1$, $p_{12} = 2$ и $p_{13} = 9$.
Заказ Матрицы
Матрица, состоящая из $m$ строк и $n$ столбцов, называется матрицей порядка $m \times n$ или просто матрицей $m \times n$ (читается как матрица $m$ на $n$).
Таким образом, ссылаясь на приведенные выше примеры матриц, мы имеем $\text{B}$ как матрицу $3 \times 2$ и $\text{P}$ как матрицу $3 \times 3$.
Вы видите, что количество элементов в матрице $\text{B}$ равно $6$, а количество элементов в матрице $\text{P}$ равно $3$.
В общем случае количество элементов в матрице порядка $m \times n$ равно $m \times n = mn$.
Свойства матриц
Свойства матриц полезны при выполнении многочисленных операций с двумя или более матрицами. Алгебраические операции сложения, вычитания, умножения, обратного умножения матриц и с участием различных типов матриц могут быть легко выполнены с использованием свойств матриц. Аддитивное, мультипликативное тождество и инверсия матриц также включены в это исследование свойств матриц.
Свойства матриц можно в общих чертах разделить на следующие пять свойств.
- Свойства дополнения матрицы
- Свойства скалярного умножения матрицы
- Свойства умножения матриц
- Свойства матрицы транспонирования
- Свойства обратной матрицы и другие свойства.

Свойства дополнения матрицы
Добавление матриц удовлетворяет следующим свойствам матриц.
- Коммутативный закон: Для данных двух матриц, матрицы $\text{A}$ и матрицы $\text{B}$ одного порядка, скажем, $m \times n$, тогда $\text{A} + \text{B} = \text{B} + \text{A}$.
- Ассоциативный закон: Для любых трех матриц $\text{A}$, $\text{B}$, $\text{C}$ одного и того же порядка $m \times n$ имеем $(\ текст{A} + \text{B}) + \text{C} = \text{A} + (\text{B} + \text{C})$
- Существование аддитивной идентичности: Пусть $\text{A}$ — матрица порядка $m \times n$, а $\text{O}$ — нулевая матрица или нулевая матрица того же порядка $m \times n$, тогда $\text{A} + \text{O} = \text{O} + \text{A} = \text{A}$. Другими словами, $\text{O}$ является аддитивным тождеством для сложения матриц.
- Существование аддитивной обратной: Пусть $\text{A}$ — матрица порядка $m \times n$.
 и пусть -$\text{A}$ — другая матрица порядка $m \times n$ такая, что $\text{A} + (– \text{A}) = (– \text{A}) + \text {А}= \текст{О}$. Таким образом, матрица $– \text{A}$ является аддитивной обратной к $\text{A}$ или отрицательной к матрице $\text{A}$.
и пусть -$\text{A}$ — другая матрица порядка $m \times n$ такая, что $\text{A} + (– \text{A}) = (– \text{A}) + \text {А}= \текст{О}$. Таким образом, матрица $– \text{A}$ является аддитивной обратной к $\text{A}$ или отрицательной к матрице $\text{A}$.
Свойства скалярного умножения матрицы
Свойства скалярного умножения матрицы включают скалярную константу и матрицу. Для матриц $\text{A}$ и $\text{B}$ порядка $m \times n$ и $k$ и $l$ как скалярных величин свойство скалярного умножения матриц состоит в следующем.
- Произведение константы на сумму матриц равно сумме отдельного произведения константы и матрицы. $k(\text{A} + \text{B}) = k \text{A} + k \text{B}$
- Произведение суммы констант на матрицу равно сумме произведения каждой из констант на матрицу. $(k + l) \text{A} = k \text{A} + l \text{A}$
Примечание: Обе матрицы $\text{A}$ и $\text{B}$ имеют один и тот же порядок, а константы $k$ и $l$ являются любыми действительными числами.
Свойства умножения матриц
Следующие свойства умножения матриц помогают выполнять многочисленные операции, связанные с умножением матриц. Условие умножения матриц: количество столбцов в первой матрице должно быть равно количеству строк во второй матрице.
- Ассоциативное свойство: Для любых трех матриц $\text{A}$, $\text{B}$ и $\text{C}$, следующих условиям умножения матриц, имеем $(\text{AB} ) \text{C} = \text{A}( \text{BC})$. Здесь определены обе части матричного умножения.
- Распределяющее свойство: Для любых трех матриц $\text{A}$, $\text{B}$ и $\text{C}$, следующих условиям умножения матриц, имеем $\text{A}( \ текст{B} + \text{C}) = \text{AB} + \text{AC}$.
- Существование мультипликативной идентичности: Для квадратной матрицы $\text{A}$ порядка $m \times n$ и единичной матрицы $\text{I}$ того же порядка имеем $\text {AI} = \text{IA} = \text{A}$. Здесь произведение единичной матрицы на данную матрицу дает ту же матрицу.
 9{-1}$.
9{-1}$.
Практические задачи
- Что означает матрица в математике?
- Что понимается под порядком матрицы?
- Каковы различные свойства матриц?
- Сформируйте следующие матрицы
- $\text{A}$ порядка $2 \times 2$, где $a_{11} = -1$, $a_{12} = 5$, $a_{21} = 7$ и $a_{ 22} = 0$
- $\text{B}$ порядка $2 \times 3$, где $b_{11} = 8$, $b_{12} = 7$, $b_{13} = \frac{2}{3}$ , $b_{21} = 9$, $b_{22} = 1$ и $b_{23} = 8$
- $\text{C}$ порядка $3 \times 2$, где $c_{11} = 7$, $c_{12} = 8$, $c_{21} = 0$, $c_{22} = -5$, $c_{31} = 11$ и $c_{32} = 1$
Часто задаваемые вопросы
Что такое матрицы?
Матрицы, множественная форма матрицы, представляют собой расположение чисел, переменных, символов или выражений в прямоугольной таблице, содержащей различное количество строк и столбцов.
В чем разница между матрицей и матрицами?
Матрицы — форма множественного числа матрицы, которая представляет собой прямоугольный массив или таблицу, в которой числа или элементы расположены в строках и столбцах. Они могут иметь любое количество столбцов и строк.
Они могут иметь любое количество столбцов и строк.
Почему мы изучаем матрицу в математике?
Матрицы помогают решать линейные уравнения. Матрицы — чрезвычайно ценные объекты, которые можно найти в самых разных приложениях. Применение матриц в математике используется в широком спектре научных областей, а также в математических областях. Инженерная математика используется почти во всех аспектах нашей жизни.
Какова размерность матрицы?
Размерность матрицы или порядок матрицы — это количество строк на количество столбцов. Если в матрице $m$ строк и $n$ столбцов, то это $m \times n$ матрица.
Что такое элементы матрицы?
Числа $a_{ij}$ называются элементами матрицы. Эти числа могут быть числами любого типа — действительными или мнимыми.
Заключение
Матрица — это упорядоченный прямоугольный массив чисел, состоящий из $m$ горизонтальных строк и $n$ вертикальных столбцов. Числа или функции называются элементами или элементами матрицы.

 Для каждого объекта вычисляются соседи и веса, которые хранятся в выходном файле матрицы пространственных весов.
Для каждого объекта вычисляются соседи и веса, которые хранятся в выходном файле матрицы пространственных весов. swm), в котором будут храниться соседи и веса для каждого входного объекта.
swm), в котором будут храниться соседи и веса для каждого входного объекта.
 Любой объект, стоимость перемещения до которого больше этого значения, не будет использоваться в качестве соседа. По умолчанию пороговая стоимость не используется.
Любой объект, стоимость перемещения до которого больше этого значения, не будет использоваться в качестве соседа. По умолчанию пороговая стоимость не используется. Если дата или время не указаны, то анализ не будет учитывать влияние дорожных условий.
Если дата или время не указаны, то анализ не будет учитывать влияние дорожных условий. Это значение по умолчанию.
Это значение по умолчанию.
 Веса, назначенные каждому соседу, вычисляются путем взятия обратного расстояния, времени или стоимости к степени экспоненты. Значение по умолчанию – 1, и оно должно быть в диапазоне от 0,01 до 4. Веса падают быстрее по мере увеличения экспоненты.
Веса, назначенные каждому соседу, вычисляются путем взятия обратного расстояния, времени или стоимости к степени экспоненты. Значение по умолчанию – 1, и оно должно быть в диапазоне от 0,01 до 4. Веса падают быстрее по мере увеличения экспоненты. Это значение по умолчанию.
Это значение по умолчанию.
 Наборы сетевых данных обычно представляют уличные сети, но могут также представлять и другие виды транспортных сетей, такие как железные дороги или пешеходные дорожки. Набор сетевых данных должен содержать по крайней мере один атрибут, связанный с расстоянием, временем в пути или стоимостью.
Наборы сетевых данных обычно представляют уличные сети, но могут также представлять и другие виды транспортных сетей, такие как железные дороги или пешеходные дорожки. Набор сетевых данных должен содержать по крайней мере один атрибут, связанный с расстоянием, временем в пути или стоимостью. Любой объект, расстояние до которого больше этого значения, не будет использоваться в качестве соседа. По умолчанию пороговое расстояние не используется.
Любой объект, расстояние до которого больше этого значения, не будет использоваться в качестве соседа. По умолчанию пороговое расстояние не используется. По умолчанию пороговая стоимость не используется.
По умолчанию пороговая стоимость не используется.


 Веса, назначенные каждому соседу, вычисляются путем взятия обратного расстояния, времени или стоимости к степени экспоненты. Значение по умолчанию – 1, и оно должно быть в диапазоне от 0,01 до 4. Веса падают быстрее по мере увеличения экспоненты.
Веса, назначенные каждому соседу, вычисляются путем взятия обратного расстояния, времени или стоимости к степени экспоненты. Значение по умолчанию – 1, и оно должно быть в диапазоне от 0,01 до 4. Веса падают быстрее по мере увеличения экспоненты. Это значение по умолчанию.
Это значение по умолчанию. gdb\transportation\streets_ND",
"Driving Time", None, None, None, None, None,
"LOCAL_TIME_AT_LOCATIONS", None, "5000 Meters",
"FIXED", 1, "ROW_STANDARDIZATION")
gdb\transportation\streets_ND",
"Driving Time", None, None, None, None, None,
"LOCAL_TIME_AT_LOCATIONS", None, "5000 Meters",
"FIXED", 1, "ROW_STANDARDIZATION") GenerateNetworkSWM(r"Data.gdb\Hospital","MyID",
"Hospital.swm", r"Data.gdb\Transportation\Streets_ND",
"Driving Time", None, None, None, None, None,
"LOCAL_TIME_AT_LOCATIONS", None, "5000 Meters", "FIXED",
1,"ROW_STANDARDIZATION")
# Create Spatial Weights Matrix based on Euclidean Distance
# Process: Generate Spatial Weights Matrix...
arcpy.stats.GenerateSpatialWeightsMatrix(
r"Data.gdb\Hospital", "MyID", r"Euclidean6Neighs.swm",
"K_NEAREST_NEIGHBORS", "EUCLIDEAN", 1, None, 6,
"ROW_STANDARDIZATION", None, None, '', None, None)
# Calculate Moran's Index of Spatial Autocorrelation for
# average hospital visit times using Network Spatial Weights
# Process: Spatial Autocorrelation (Morans I)...
moransINet = arcpy.stats.SpatialAutocorrelation("Data.gdb\Hospital",
"VisitTime", "NO_REPORT", "GET_SPATIAL_WEIGHTS_FROM_FILE",
"EUCLIDEAN_DISTANCE", "ROW", None, "Hospital.
GenerateNetworkSWM(r"Data.gdb\Hospital","MyID",
"Hospital.swm", r"Data.gdb\Transportation\Streets_ND",
"Driving Time", None, None, None, None, None,
"LOCAL_TIME_AT_LOCATIONS", None, "5000 Meters", "FIXED",
1,"ROW_STANDARDIZATION")
# Create Spatial Weights Matrix based on Euclidean Distance
# Process: Generate Spatial Weights Matrix...
arcpy.stats.GenerateSpatialWeightsMatrix(
r"Data.gdb\Hospital", "MyID", r"Euclidean6Neighs.swm",
"K_NEAREST_NEIGHBORS", "EUCLIDEAN", 1, None, 6,
"ROW_STANDARDIZATION", None, None, '', None, None)
# Calculate Moran's Index of Spatial Autocorrelation for
# average hospital visit times using Network Spatial Weights
# Process: Spatial Autocorrelation (Morans I)...
moransINet = arcpy.stats.SpatialAutocorrelation("Data.gdb\Hospital",
"VisitTime", "NO_REPORT", "GET_SPATIAL_WEIGHTS_FROM_FILE",
"EUCLIDEAN_DISTANCE", "ROW", None, "Hospital. swm", None)
# Calculate Moran's Index of Spatial Autocorrelation for
# average hospital visit times using Euclidean Spatial Weights
# Process: Spatial Autocorrelation (Morans I)...
moransIEuc = arcpy.stats.SpatialAutocorrelation("Data.gdb\Hospital",
"VisitTime", "NO_REPORT", "GET_SPATIAL_WEIGHTS_FROM_FILE",
"EUCLIDEAN_DISTANCE", "ROW", None, r"Euclidean6Neighs.swm",
None)
except arcpy.ExecuteError:
# If an error occurred when running the tool, print out the error message.
print(arcpy.GetMessages())
swm", None)
# Calculate Moran's Index of Spatial Autocorrelation for
# average hospital visit times using Euclidean Spatial Weights
# Process: Spatial Autocorrelation (Morans I)...
moransIEuc = arcpy.stats.SpatialAutocorrelation("Data.gdb\Hospital",
"VisitTime", "NO_REPORT", "GET_SPATIAL_WEIGHTS_FROM_FILE",
"EUCLIDEAN_DISTANCE", "ROW", None, r"Euclidean6Neighs.swm",
None)
except arcpy.ExecuteError:
# If an error occurred when running the tool, print out the error message.
print(arcpy.GetMessages())
 и пусть -$\text{A}$ — другая матрица порядка $m \times n$ такая, что $\text{A} + (– \text{A}) = (– \text{A}) + \text {А}= \текст{О}$. Таким образом, матрица $– \text{A}$ является аддитивной обратной к $\text{A}$ или отрицательной к матрице $\text{A}$.
и пусть -$\text{A}$ — другая матрица порядка $m \times n$ такая, что $\text{A} + (– \text{A}) = (– \text{A}) + \text {А}= \текст{О}$. Таким образом, матрица $– \text{A}$ является аддитивной обратной к $\text{A}$ или отрицательной к матрице $\text{A}$.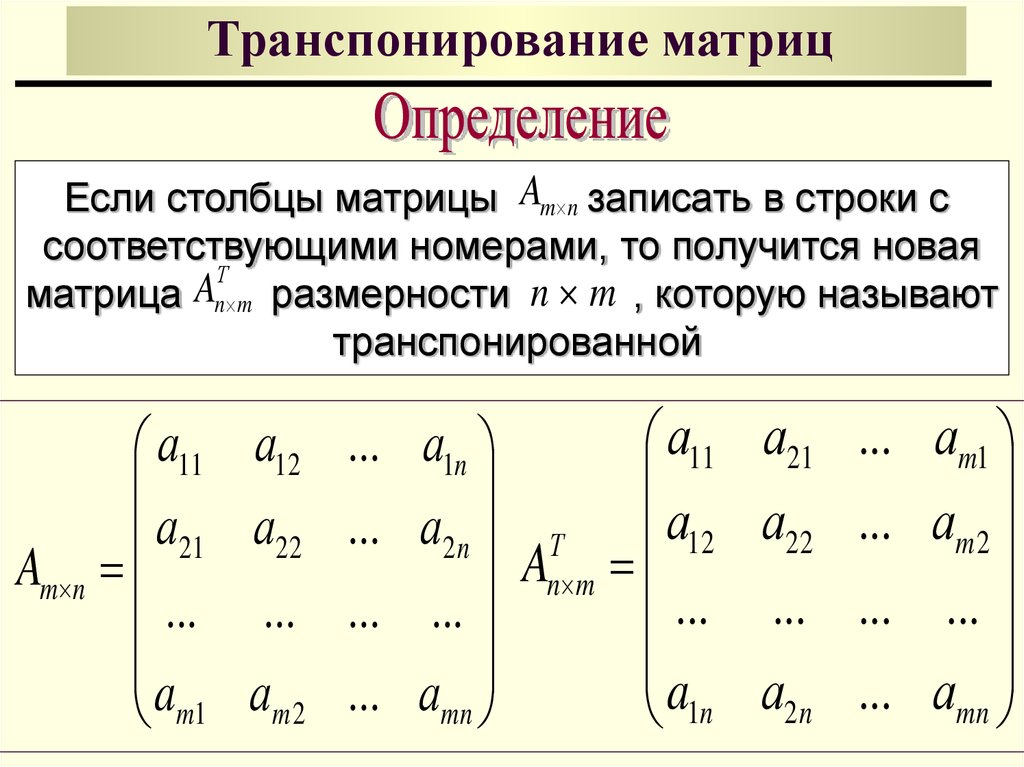 9{-1}$.
9{-1}$.