Онлайн преобразование логических выражений: Математическая логика · oнлайн с подробным объяснением

alexxlab / / Разное

Преобразование логических выражений — презентация онлайн

Тема:
Преобразование
логических
выражений
Учитель информатики и ИКТ Бородина И.В.
МБОУ СОШ №13 ст. Новоджерелиевская
2011-2012 уч.год

2. Что нужно знать:

ЧТО НУЖНО ЗНАТЬ:
1). Условные обозначения логических операций:
¬ A,
не A (отрицание, инверсия)
A
A B,
A B
A и B (логическое умножение, конъюнкция)
A B, A B
A или B (логическое сложение, дизъюнкция)
A→B
импликация (следование)
A ↔ B,
A B
А В
исключающее или (только одно из А или В)
А
А В
эквиваленция (эквивалентность, равносильность)
В
А
В
А+В

3. Что нужно знать:

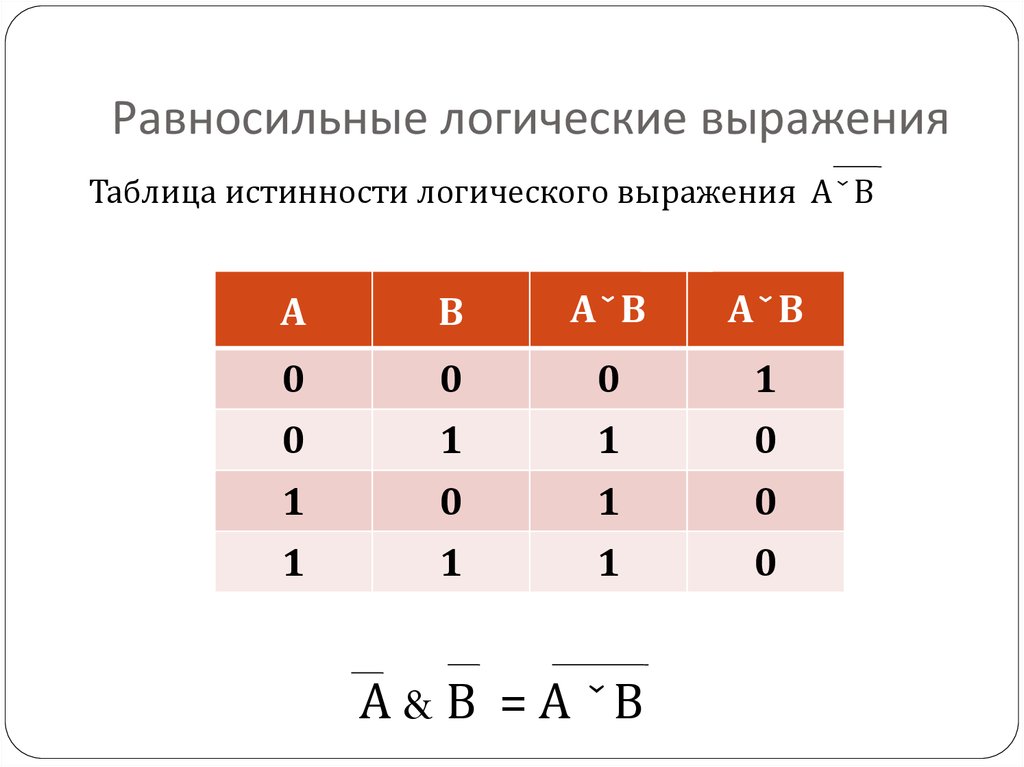
ЧТО НУЖНО ЗНАТЬ:
2). Таблицы истинности логических операций «И», «ИЛИ», «НЕ»,
«импликация», «эквиваленция», «исключающее ИЛИ»
А
В
А·В
А
В
А+В
А
A
0
0
0
0
0
0
0
1
0
1
0
0
1
1
1
0
1
0
0
1
0
1
1
1
1
1
1
1
А
В
А В
А
В
А В
А
В
А В
0
0
1
0
0
1
0
0
0
0
1
1
0
1
0
0
1
1
1
0
0
1
0
0
1
0
1
1
1
1
1
1
1
1
1
0

4.

Что нужно знать:ЧТО НУЖНО ЗНАТЬ:
3). Операцию «импликация» можно выразить через «ИЛИ» и «НЕ»:
A → B = ¬ A B или в других обозначениях A → B = A B
4). Операцию «эквиваленция» также можно выразить через «ИЛИ» и
«НЕ»:
A ↔ B = (¬ A ¬ B) (A B) или в других обозначениях A B = А B А В
5). Законы исключающее «ИЛИ»
А В = А В , А В = АВ АВ
6). Если в выражении нет скобок, сначала выполняются все операции «НЕ»,
затем – «И», затем – «ИЛИ», и самая последняя – «импликация».
7). Логическое произведение A∙B∙C∙… равно 1 (выражение истинно) только
тогда, когда все сомножители равны 1 (а в остальных случаях равно 0).
8). Логическая сумма A+B+C+… равна 0 (выражение ложно) только тогда,
когда все слагаемые равны 0 (а в остальных случаях равна 1)

5. Правила преобразования логических выражений (законы алгебры логики):

ПРАВИЛА ПРЕОБРАЗОВАНИЯ ЛОГИЧЕСКИХ
ВЫРАЖЕНИЙ (ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ):
Закон
Для И
двойного отрицания
исключения третьего
исключения
констант
Для ИЛИ
A A
A ·A 0
A A 1
A · 1 = A; A · 0 = 0
A + 0 = A; A + 1 = 1
повторения
A·A=A
A+A=A
поглощения
A · (A + B) = A
A+A· B =A
переместительный
A· B = B ·A
A+B=B+A
сочетательный
A · (B · C) = (A · B) · C
A + (B + C) = (A + B) + C
распределительный
A + B · C = (A + B) · (A + C)
A · (B + C) = A · B + A · C
де Моргана
A ·B A B
A B A ·B
Сколько различных решений имеет система уравнений
(X2 X1) (X2 X3) (¬X2 ¬ X3)= 1
(X3 X1) (X3 X4) (¬X3 ¬ X4)= 1
. ..
(X9 X1) (X9 X10) (¬X9 ¬ X10)= 1
X10 X1 = 0
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все
различные наборы значений x1, x2, …, x10, при которых выполнена данная система
равенств. В качестве ответа нужно указать количество таких наборов.
Решение (табличный метод):
1). Перепишем уравнения,
используя более простые
обозначения операций
( X 2 X1 ) X 2 X 3 X 2 X 3 1
( X 3 X1 ) X 3 X 4 X 3 X 4 1
…
( X 9 X1 ) X 9 X10 X 9 X10 1
X10 X1 0
2). Заметим, что по свойству
операции эквивалентности
X 2 X3 X 2 X3 ( X2 X3)
поэтому уравнения можно
переписать в виде
( X 2 X1 ) ( X 2 X 3 ) 1
( X 3 X1 ) ( X 3 X 4 ) 1
…
( X 9 X1 ) ( X 9 X 10 ) 1
X10 X1 0
3). По таблице истинности находим варианты
( X 3 X1 ) ( X 3 X 4 ) 1
( X 2 X1 ) ( X 2 X 3 ) 1
1
0
1
0
0
1
0
1
1
1
1
1
Х1
Х2
Х3
Х1
Х2
Х3
Х4
0
0
1
0
0
1
1
1
1
0
1
1
0
0
0
1
1
0
1
1
1
1
0
0
1
0
0
0
0
0
0
0
0
0
1
1
1
0
1
1
1
1
0
1
. ..
4). Подключили Х4 – получили 8 решений, подключим X5 – получим
10 решений, X6 – получим 12 решений, X7 – получим 14 решений,
X8 – получим 16 решений, X9 – получим 18 решений, X10 – получим
20 решений.
5). Остается одно последнее уравнение X10 X1 = 0, из которого
следует, что X10 не равен X1, то есть из полученных 20 решений
нужно отбросить 2 решения, таким образом, получается 20 – 2 = 18
решений
Ответ: 18 решений
Сколько различных решений имеет система уравнений
(X1 X2) (¬X1 ¬X2) (X1 X3) = 1
(X2 X3) (¬X2 ¬X3) (X2 X4) = 1
…
(X8 X9) (¬X8 ¬X9) (X8 X10) = 1
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все
различные наборы значений x1, x2, …, x10, при которых выполнена данная система
равенств. В качестве ответа нужно указать количество таких наборов.
Решение (табличный метод):
1). Перепишем уравнения,
используя более простые
обозначения операций
X1 X 2 X1 X 2 ( X1 X 3 ) 1
X 2 X3 X 2 X3 ( X 2 X 4 ) 1
. ..
X 8 X 9 X 8 X 9 ( X 8 X10 ) 1
2). Заметим, что по свойству
операции эквивалентности
X1 X 2 X1 X 2 ( X1 X 2 )
поэтому уравнения можно
переписать в виде
( X1 X 2 ) ( X1 X 3 ) 1
(X2 X3) (X2 X4) 1
…
( X 8 X 9 ) ( X 8 X10 ) 1
3). Будем решать уравнения последовательно табличным методом
(X2 X3) (X2 X4) 1
( X1 X 2 ) ( X1 X 3 ) 1
1
0
1
0
0
1
0
1
1
1
1
1
Х1
Х2
Х3
Х1
Х2
Х3
Х4
0
0
1
0
0
1
0
1
1
0
1
1
0
1
0
1
0
1
1
0
1
0
0
0
0
0
1
1
1
1
0
1
0
1
0
1
0
1
0
0
0
1
1
1
…
4). Подключили Х4 – получили 8 решений, подключим X5 – получим 10 решений,
X6 – получим 12 решений, X7 – получим 14 решений, X8 – получим 16 решений,
X9 – получим 18 решений, X10 – получим 20 решений.
Ответ: 20 решений
Сколько различных решений имеет система уравнений
(X1 X2) (X2 X10) (¬X2 ¬ X10)= 1
(X2 X3) (X3 X10) (¬X3 ¬ X10)= 1
. ..
(X8 X9) (X9 X10) (¬X9 ¬ X10)= 1
X10 X1 = 0
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все
различные наборы значений x1, x2, …, x10, при которых выполнена данная система
равенств. В качестве ответа вам нужно указать количество таких наборов.
Решение (табличный метод):
1). Перепишем уравнения,
используя более простые
обозначения операций
2). Заметим, что по свойству
операции эквивалентности
X 2 X10 X 2 X10 ( X 2 X10 )
поэтому уравнения можно
переписать в виде
( X1 X 2 ) X 2 X10 X 2 X10 1
( X 1 X 2 ) ( X 2 X 10 ) 1
( X 2 X 3 ) X 3 X10 X 3 X10 1
( X 2 X 3 ) ( X 3 X 10 ) 1
…
( X 8 X 9 ) X 9 X10 X 9 X10 1
X 10 X 1 0
…
( X 8 X 9 ) ( X 9 X 10 ) 1
X10 X1 0
3). По таблице истинности находим варианты
( X 2 X 3 ) ( X 3 X 10 ) 1
( X 1 X 2 ) ( X 2 X 10 ) 1
1
0
1
0
0
1
0
1
1
1
1
1
Х1
Х2
Х10
Х1
Х2
Х10
Х3
0
0
1
0
0
1
1
1
0
0
1
0
1
1
1
1
0
0
1
1
0
0
0
1
1
1
0
0
0
1
0
0
0
1
1
1
0
0
0
0
1
1
1
1
. ..
4). Подключили Х3 – получили 8 решений, подключим X4 – получим 10
решений, X5 – получим 12 решений, X6 – получим 14 решений, X7 –
получим 16 решений, X8 – получим 18 решений, X9 – получим 20
решений.
5). Остается одно последнее уравнение X10 X1 = 0, из которого
следует, что X10 не равен X1, то есть из полученных 20 решений нужно
отбросить 2 решения, таким образом, получается 20 – 2 = 18 решений
Ответ: 18 решений
Сколько различных решений имеет система уравнений
¬(X1 X2) (X1 X3) (¬X1 ¬X3)= 0
¬(X2 X3) (X2 X4) (¬X2 ¬X4)= 0
…
¬(X8 X9) (X8 X10) (¬X8 ¬X10)= 0
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все
различные наборы значений x1, x2, …, x10, при которых выполнена данная система
равенств. В качестве ответа вам нужно указать количество таких наборов.
Решение (табличный метод):
1). Перепишем уравнения,
используя более простые
обозначения операций
2). Заметим, что
( X1 X 3 ) ( X1 X 3 ) ( X1 X 3 ) ( Х 1 Х 3 ) ( Х1 Х 3 )
поэтому уравнения можно переписать в виде
( X1 X 2 ) ( X1 X 3 ) ( X1 X 3 ) 0
( X1 X 2 ) ( X1 X 3 ) 0
(X2 X3) (X2 X4 ) (X2 X4 ) 0
(X2 X3) (X2 X4 ) 0
. ..
( X 8 X 9 ) ( X 8 X10 ) ( X 8 X10 ) 0
…
( X 8 X 9 ) ( Х 8 Х10 ) 0
3). По таблице истинности находим варианты
( X1 X 2 ) ( X1 X 3 ) 0
(X2 X3) (X2 X4 ) 0
0
0
0
0
0
1
0
1
1
0
1
0
Х1
Х2
Х3
Х1
Х2
Х3
Х4
0
0
0
0
0
0
1
1
1
0
1
1
1
1
0
0
1
0
1
1
1
0
0
0
1
0
0
1
0
1
1
0
1
1
0
1
0
1
0
1
1
0
1
0
…
4). Подключили Х4 – получили 8 решений, подключим X5 – получим 10 решений,
X6 – получим 12 решений, X7 – получим 14 решений, X8 – получим 16 решений,
X9 – получим 18 решений, X10 – получим 20 решений.
Ответ: 20 решений
Сколько различных решений имеет система уравнений
((X1 X2) (X3 X4)) (¬(X1 X2) ¬(X3 X4)) = 1
((X3 X4) (X5 X6)) (¬(X3 X4) ¬(X5 X6)) = 1
…
((X7 X8) (X9 X10)) (¬(X7 X8) ¬(X9 X10)) = 1
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все
различные наборы значений x1, x2, …, x10, при которых выполнена данная система
равенств. В качестве ответа вам нужно указать количество таких наборов.
Решение (табличный метод):
1). Перепишем уравнения,
используя более простые
обозначения операций
(( Х1 Х 2 ) ( X 3 X 4 )) (( X1 Х 2 ) ( Х 3 Х 4 )) 1
(( Х 3 Х 4 ) ( X 5 X 6 )) (( X 3 Х 4 ) ( X 5 Х 6 )) 1
…
(( Х 7 Х 8 ) ( X 9 X10 )) (( X 7 Х 8 ) ( X 9 Х10 )) 1
2). Раскроем скобки и перепишем
систему уравнений в виде
( Х1 Х 2 ) ( X 3 X 4 ) ( X1 Х 2 ) ( Х 3 Х 4 ) 1
(Х3 Х4 ) (X5 X6 ) (X3 Х4 ) (Х5 Х6 ) 1
…
( Х 7 Х 8 ) ( X 9 X10 ) ( X 7 Х 8 ) ( Х 9 Х10 ) 1
3). Используя закон исключающее
«ИЛИ», перепишем систему уравнений
в виде
( Х1 Х 2 ) ( X 3 X 4 ) 1
(Х3 Х4) (X5 X6) 1
…
( Х 7 Х 8 ) ( X 9 X 10 ) 1
4). По таблице истинности находим варианты
( Х1 Х 2 ) ( X 3 X 4 ) 1
(Х3 Х4) (X5 X6) 1
0
1
0
1
1
0
1
0
Х1
Х2
Х3
Х4
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
1
0
0
0
1
0
0
1
0
1
1
0
1
1
1
1
0
4). Количество переменных:
X4 – получили 8 решений, X6 – получили
16 решений, X8 – получим 32 решения,
X10 – получим 64 решения.
Ответ: 64 решения
…
Х1
Х2
Х3
Х4
Х5
Х6
0
1
0
0
0
1
1
0
0
1
1
1
0
1
1
0
1
0
0
0
0
1
1
0
1
0
1
1
0
1
1
0
0
0
0
1
0
1
0
1
0
0
1
0
0
1
0
1
1
1
0
1
0
1
0
1
1
1
1
0
0
1
0
1
Используемые
источники
Ссылка на используемый источник при
подготовке презентации:
http://kpolyakov.narod.ru/download/B15.doc

Page not found — Сайт skobelevserg!

  • Главная
  • Информатика
  • Практикумы
  • Подготовка к ОГЭ
  • Рабочие программы
  • Используемая литература
  • Об авторах

Unfortunately the page you’re looking doesn’t exist (anymore) or there was an error in the link you followed or typed. This way to the home page.

  • Главная
  • Информатика
    • 5 класс (ФГОС)
      • Информация вокруг нас
      • Компьютер — универсальная машина для работы с информацией
      • Ввод информации в память компьютера
      • Управление компьютером
      • Хранение информации
      • Передача информации
      • Кодирование информации
      • Текстовая информация
      • Представление информации в виде таблиц
      • Наглядные формы представления информации
      • Компьютерная графика
      • Обработка информации
    • 6 класс (ФГОС)
      • Объекты окружающего мира
      • Компьютерные объекты
      • Отношения объектов и их множеств
      • Разновидности объектов и их классификация
      • Системы объектов
      • Персональный компьютер как система
      • Как мы познаем окружающий мир
      • Понятие как форма мышления
      • Информационное моделирование
      • Знаковые информационные модели
      • Табличные информационные объекты
      • Графики и диаграммы
      • Схемы
      • Что такое алгоритм
      • Исполнители вокруг нас
      • Формы записи алгоритмов
      • Типы алгоритмов
      • Управление исполнителем Чертежник
      • Компьютерный практикум
    • 7 класс (ФГОС)
      • Информация и информационные процессы
      • Компьютер универсальное устройство для работы с информацией
      • Обработка графической информации
      • Обработка текстовой информации
      • Технология мультимедиа
    • 8 класс (ФГОС)
      • Математические основы информатики
      • Основы алгоритмизации
      • Начала программирования
    • 9 класс (ФГОС)
      • Моделирование и формализация
      • Алгоритмизация и программирование
      • Обработка числовой информации в электронных таблицах
      • Коммуникационные технологии
    • 10 класс (ФГОС)
      • Информация и информационные процессы
      • Компьютер и его программное обеспечение
      • Представление информации в компьютере
      • Элементы теории множеств и алгебры логики
      • Современные технологии создания и обработки информационных объектов
    • 11 класс (ФГОС)
      • Обработка информации в электронных таблицах
      • Алгоритмы и элементы программирования
      • Информационное моделирование
      • Сетевые информационные технологии
      • Основы социальной информатики
  • Практикумы
    • Google формы
    • Основы работы в Microsoft PowerPoint
    • Создание анимации в презентациях
    • Основы работы в Microsoft Word
    • Основы работы в Microsoft Excel
    • Создание простейшей базы данных
    • Практикум по MS Excel
  • Подготовка к ОГЭ
  • Рабочие программы
  • Используемая литература
  • Об авторах
    • Блоги
    • Сайты

логика — преобразование булевой алгебры

Задавать вопрос

спросил

Изменено 2 года, 1 месяц назад

Просмотрено 194 раза

$\begingroup$

Я читал в Интернете, что $ $ {\ Displaystyle (А \ cdot {\ overline {B}}) + ({\ overline {A}} \ cdot B) \ эквив (A + B) \ cdot ({\ overline {A}} + {\ overline {B}})}$$

, и я могу это проверить, но я не совсем уверен, как взять левую часть и преобразовать ее в правую. Любая помощь будет оценена по достоинству, спасибо.

  • логика
  • булевская алгебра

$\endgroup$

1

$\begingroup$

  1. Поскольку правая рука может трансформироваться следующим образом: $$(A+B)\cdot ({\overline {A}}+{\overline {B}}) \equiv \\ A \cdot \overline {A}+A \cdot\overline {B} + B \cdot \overline {A} + B \cdot \overline {B} \equiv \\ А \ cdot {\ overline {B}} + {\ overline {A}} \ cdot B $ $ и зная, что эквивалентность работает в обоих направлениях, теперь вы можете записать эту эквивалентность в противоположном направлении, чтобы достичь желаемого.

  2. Для второго способа используем $\overline{A\cdot B}=\overline{A} + \overline {B}$ и $\overline{A+ B}=\overline{A} \cdot \overline {B} $: $$A\cdot {\overline {B}}+{\overline {A}}\cdot B \equiv \overline {\overline{A}+B}+\overline {A+\overline {B}} \equiv \ \ \overline {(\overline{A}+B) \cdot (A+\overline {B})} \equiv \overline {A\cdot B + \overline{A} \cdot \overline {B}} \equiv \overline {A\cdot B} \cdot \overline{\overline{A} \cdot \overline {B}} \equiv \\ (A + B) \ cdot ({\ overline {A}} + {\ overline {B}}) $$

$\endgroup$

3

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

. 9Логика 0000 — Как преобразовать следующее логическое выражение в английский язык

спросил

Изменено 8 лет, 1 месяц назад

Просмотрено 245 раз

$\begingroup$

Я не совсем понимаю семантику замены логических выражений на английский язык

Преобразуйте следующие операторы исчисления предикатов на английский язык. Позволять $A(x)$ представляют утверждение, что $x$ является бухгалтером, $B(x)$ представляют собой утверждение о том, что $x$ является бизнесменом, $E(x)$ представляет утверждение о том, что $x$ — инженер, а $M(x, y)$ представляет утверждение, что $x$ управляет $y$.

  1. $\forall x\существует y, A(x) \vee E(x) \подразумевает B(y) \клин M(y, x)$
  2. $\существует x\для всех y\существует z, E(x) \клин (A(y) \клин M(y, x) \ подразумевает M(y, z))$

Например, я думал, что первое утверждение: Для всех людей, которые являются либо бухгалтерами, либо инженерами, есть бизнесмен, который ими управляет.

Должна ли эта фраза включать другую грамматическую структуру, например такую: Для всех людей, которые являются либо бухгалтерами, либо инженерами, есть бизнесмен, который ими управляет.

А потом я подумал, что второе утверждение будет Все люди, которые бухгалтеры и управляют инженером, также управляют другим человеком. Но я не уверен, имеет ли это смысл, учитывая, что $E(x)$ не входит в выражение $(A(y) \wedge M(y, x) \implis M(y, z))$, где $M (y,x)$ означает, что $y$ управляет $x$.

$\endgroup$

1

$\begingroup$

Мне кажется, что два перевода 1. вполне эквивалентны: «их» может быть «он или она» (но я не англоговорящий…).

Но учтите, что $\forall$ означает «все», но не обязательно, что «все» должно быть «более одного».

Так что формулу лучше читать так: «каждый бухгалтер или инженер управляется бизнесменом».

Для 2. :

$∃x∀y∃z,E(x)∧(A(y)∧M(y,x) \Rightarrow M(y,z))$

у нас есть первый Инженер : $∃x,E(x)$.

Тогда у нас есть условие для бухгалтеров , которые управляют им: $∀y∃z,(A(y)∧M(y,x) \Rightarrow M(y,z))$, то есть:

для всех $y$, если $y$ является бухгалтером и Управляет $x$, затем $y$ Управляет $z$ для некоторого $z$.

Собираем все вместе:

Есть

Инженер и все Бухгалтер который Управляет им, Управляет кем-то.

Два квантора существования $\exists x$ и $\exists z$ не заставляют нас выбирать другого человека: см. вашего «другого человека».

$\endgroup$

$\begingroup$

Ваш первый пример прекрасен и интуитивно понятен. Однако я не понимаю, какой объем квалификаторов вы имеете в виду (не пропущена ли открывающая скобка?).

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *