Онлайн решение интегралов методом замены переменной: Таблица интегралов

Интегрирование функций методом замены переменных

Примеры на интегрирование функций методом замены переменных взято из материалов контрольной работы, которую задавали студентам 1, 2 курсов математических факультетов. Для экономии Вашего времени сами условия задач пропущенные, везде нужно или «Найти неопределенный интеграл» или «Вычислить интеграл». Текста в комментариях к каждому заданию ровно столько, сколько нужно Вам для усвоения материала и изучение методики и схем интегрирования.

Пример 1. При интегрировании дробной функции необходимо в знаменателе корень квадратный превратить в показатель, далее разделить числитель на знаменатель и полученные слагаемые проинтегрировать. Если не вдаваться в детали то в конечном варианте интеграл примет значение

Для большинства студентов ход вычислений должен быть понятным, если переход между последними двумя строками Вы не можете осуществить то начните с того, что откройте или распечатайте основные формулы интегрирования.

Пример 2. Имеем под интегралом дробь от синус функции, которую упрощаем делением числителя на знаменатель. Далее знаменатель дроби во втором интеграле расписываем по теореме косинуса, а синус вносим под дифференциал. Таким образом перейдем к новой переменной t=cos(x) в интегрировании.

Второй интеграл по табличным формулам равный разнице логарифмов от простых множителей знаменателя

Возвращаемся к замене которую выполняли. На этом интегрирования можно было и завершить, а можно записать в компактном виде. Но для этого необходимо знать или иметь под рукой тригонометрические формулы и свойства логарифма.

Пример 3. Для вычисления интеграла запишем знаменатель дроби в виде разности квадратов, а дальше умножим на минус единицу и сведем к разности логарифмов от простых множителей

Минус перед логарифмом преобразовали в показатель функции, поэтому дробь под логарифмом в конечном варианте перевернута.

Пример 4. Очень поучительное задание на интегрирование, побольше бы таких на контрольных и тестах. Если бы в степени имели 3 или 4, то поднимать еще хоть как-то было бы можно. Здесь же стоит 10, поэтому возводить к 10 степени мало кто захочет. Выражение в скобках в подобных заданиях на интегрирование обозначьте за новую переменную t=2x+5. Далее применяем табличную формулу и после того как проинтегрировали не забываем подставить замену.

Хорошо запомните схему вычисления этого интеграла.

Пример 5. На первый взгляд сложный интеграл, однако схема вычислений достаточно проста. Обозначим арккосинус за новую переменную t=arccos(x) и запишем ее дифференциал. Как видите дифференциал равен dx разделить на знаменатель. И такая схема присущая большинству сложных примеров на неопределенные интегралы. Поэтому Ваша основная задача — научиться видеть замены переменных, схемы возведения под табличную формулу, удачно выбирать функцию под правило интегрирования по частям. А для этого нужно решить много интегралов, поэтому лучше учиться на готовых ответах + самостоятельная работа.

Пример 6. Под интегралом имеем дробную иррациональную функцию от экспоненты. Для вычисления интеграла обозначим функцию под корнем за новую переменную. Также преобразуем экспоненту в числителе и найдем дифференциал от новой переменной.

После таких действий полученный интеграл по сложности ничем не будет уступать первому из рассмотренных примеров. После интегрирования не забываем вернуться к выполненной в начале замене переменных.

Пример 7. Для вычисления этого и подобных примеров Вы должны знать что производная от логарифма равна единице разделенной на переменную. Таким образом большинство интегралов где содержится показательная функция от логарифма и «икс» в знаменателе за новую переменную выбирайте логарифм t=ln(x). В результате интеграл существенно упростится и получим компактный ответ

Остальные ответы в следующих материалах. Помните что такого рода интегралы задают на контрольной и тестах, поэтому внимательно разбирайте ответы к заданиям.

Готовые решения контрольной по интегрированию

• > Следующие ответы
• Контрольная работа по интегрированию № 1
• Контрольная работа по интегрированию № 2

• Назад
• Вперёд

Задачи и упражнения

1. Применяя метод непосредственного интегрирования, найти следующие интегралы:

a) ; б) ;

в) ; г) ;

д) ; е) ;

ж) ; з) .

2. Применяя метод замены переменной, найти следующие интегралы:

а) ; б) ; в) ;

г) ; д) ; е) ;

ж) ; з) ; и) ;

к) ; л) ; м) .

3. Применяя метод интегрирования по частям, найти следующие интегралы:

а) ; б) ; в) ;

г) ; д) ; е) ;

ж) ; з) ; и) .

Лекция 2. НеоПРЕДЕЛЕННЫЙ иНТЕГРАЛ

(продолжение)

План

1. Интегрирование выражений, содержащих квадратный трехчлен.

5. Интегрирование простейших рациональных дробей.

6. Интегрирование простейших иррациональных функций.

7. Интегрирование тригонометрических функций.

Ключевые понятия

Многочлен. Рациональная дробь. Иррациональная функция. Тригонометрическая функция.

1. Интегрирование выражений, содержащих квадратный трехчлен

Пусть подынтегральная функция содержит квадратный трехчлен .

1. Интегралы вида вычисляются следующим образом. Из квадратного трехчлена в знаменателе выделим полный квадрат:

где , если и , если .

Далее сделаем подстановку , откуда , . Получим

.

Последний интеграл является табличным и вычисляется по формулам 15, 16 таблицы основных неопределенных интегралов.

Пример 1. Вычислить интеграл .

Решение. Выделим в знаменателе полный квадрат:

.

Сделаем подстановку . Тогда и

.

Возвращаясь к переменной х, получим

.

2. Интегралы вида вычисляются аналогично интегралам пункта 1 путем выделения полного квадрата из квадратного трехчлена и последующей замены переменной. В результате исходный интеграл сводится к одному из табличных интегралов вида 12, 13.

Пример 2. Вычислить интеграл .

Решение. Преобразуем квадратный трехчлен следующим образом: . Получим . Положим , тогда , . В результате получаем

=. Переходя к переменной х, получим

.

3. Интегралы вида и вычисляются путем выделения полного квадрата из квадратного трехчлена и последующей замены переменной. Затем полученный интеграл разбивается на два: первый из этих интегралов можно вычислить, воспользовавшись формулами (2), (3), а второй интеграл является табличным.

Пример 3. Вычислить интеграл .

Решение. Так как , то по-ложим . Тогда и = [полученный интеграл разобьем на два] = . Второй из этих ин-тегралов – табличный: . Для нахождения первого воспользуемся следующим преобразованием дифференциала: . В результате получим = [воспользуемся формулой (3)] = . Окончательно имеем , где . Возвращаясь к переменной х, получим

.

2. Интегрирование простейших рациональных дробей

Определение. Рациональной дробью называется дробь вида , где и – многочлены степени и соответственно.

Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя, т. е. , и неправильной – в противном случае ().

Простейшей рациональной дробью называется правильная дробь одного из следующих видов:

1) ; 2) ; 3) ; 4) .

Интегралы от рациональных дробей 1), 2) находятся методом замены переменной:

[положим тогда ] =

[возвращаемся к переменной x] =;

[] = [возвращаемся к переменной x] =.

Пример 4. Вычислить интеграл .

Решение. [ сделаем замену ] = .

Интегралы от рациональных дробей 3), 4) вычисляются аналогично интегралам , рассмотренным в п. 1.

Обзор методов интегрирования в пространстве и времени

Интегрирование является одним из наиболее важных математических инструментов, особенно для численного моделирования. Уравнения в частных производных (УЧП) обычно выводятся, например, из интегральных уравнений баланса.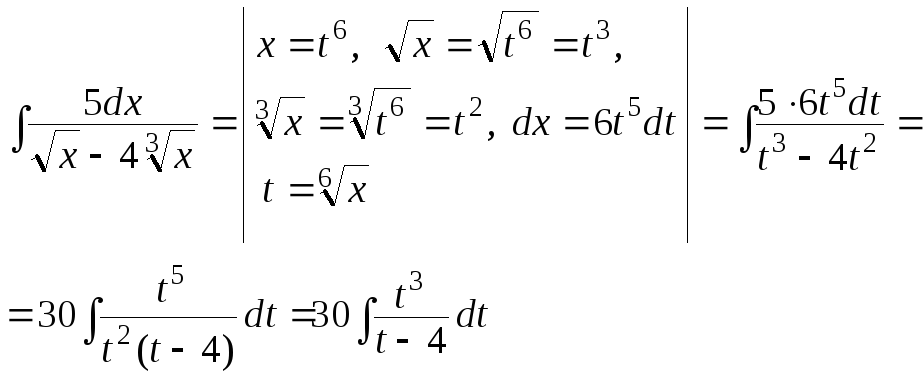 Когда УЧП необходимо решить численно, интегрирование также часто играет важную роль. В этом сообщении блога представлен обзор методов интеграции, доступных в программном обеспечении COMSOL, и показано, как их можно использовать.

Важность интегралов

COMSOL использует метод конечных элементов, который преобразует определяющее УЧП в интегральное уравнение — другими словами, в слабой форме. Присмотревшись к программе моделирования COMSOL, вы поймете, что многие граничные условия формулируются в виде интегралов. Пара примеров из них: Полный тепловой поток или Плавающий потенциал . Интеграция также играет ключевую роль в постобработке, поскольку COMSOL предоставляет множество производных значений, основанных на интеграции, например 9.{t_1}\int_{\Omega}F(u)\ \mathrm{d A} \mathrm{d} t

, где [t_0,t_1] — временной интервал, \Omega — пространственная область, а F(u ) — произвольное выражение в зависимой переменной u. Выражение может включать производные по пространству и времени или любое другое производное значение.

Наиболее удобный способ получения интегралов — использовать «Производные значения» в разделе «Результаты» новой ленты (или построитель моделей, если вы не используете Windows®).

Как добавить объемные, поверхностные или линейные интегралы в качестве производных значений.

Вы можете обратиться к любому доступному решению, выбрав соответствующий набор данных. Поле Expression представляет собой интегральное выражение и позволяет использовать зависимые или производные переменные. Для переходных симуляций пространственный интеграл оценивается на каждом временном шаге. В качестве альтернативы окно настроек предлагает операции с рядом данных, где Интеграция может быть выбрана для временной области. Это приводит к пространственно-временной интеграции.

Пример настроек интеграции поверхности с дополнительной интеграцией времени посредством операции Data Series.

Среднее значение — еще одно производное значение, связанное с интеграцией. Он равен интегралу, который делится на объем, площадь или длину рассматриваемой области. Операция Average Data Series дополнительно делит по временному горизонту. Производные значения очень полезны, но поскольку они доступны только для постобработки, они не могут обрабатывать все типы интеграции. Вот почему COMSOL предлагает более мощные и гибкие инструменты интеграции. Мы демонстрируем эти методы на примере модели ниже. 92 прописывается. Стационарное решение и решение, зависящее от времени, через 100 секунд показаны на следующих рисунках.

Стационарное решение, нажмите на картинку, чтобы увеличить.

Переходное решение через 100 с, щелкните изображение, чтобы увеличить его.

Пространственное интегрирование с помощью операторов связи компонентов

Операторы связи компонентов необходимы, например, когда несколько интегралов объединяются в одно выражение, когда интегралы запрашиваются во время вычисления или в случаях, когда требуется набор интегралов по путям. Операторы связывания компонентов определяются в разделе «Определения» соответствующего компонента. На этом этапе оператор еще не оценивается. Фиксируются только его имя и выбор домена.

Как добавить операторы связывания компонентов для последующего использования.

В нашем примере мы сначала хотим вычислить пространственный интеграл по стационарной температуре, который определяется выражением

\int_{\Omega}T(x,y)\\mathrm{d}x\mathrm{d} y = 301,65

В программном обеспечении COMSOL мы используем оператор интегрирования, который по умолчанию называется intop1 .

Окно настроек оператора интеграции.

Как оценить оператор интегрирования.

На следующем шаге мы покажем, как в модели можно использовать оператор интегрирования. Мы могли бы, например, спросить, какую мощность нагрева нам нужно применить, чтобы получить среднюю температуру 303,15 К, что соответствует повышению средней температуры на 10 К по сравнению с комнатной температурой. Во-первых, нам нужно вычислить разницу между желаемой и фактической средней температурой. Среднее значение вычисляется путем деления интеграла по T на интеграл по постоянной функции 1, которая дает площадь области. К счастью, этот тип вычислений можно легко выполнить с помощью Средний оператор в COMSOL. По умолчанию такой оператор называется aveop1 . (Обратите внимание, что среднее значение по домену такое же, как и интеграл для нашего примера. Это связано с тем, что домен имеет единичную площадь.) Соответствующая разница определяется выражением

303,15-\int_{\Omega}T(x,y) \mathrm{d} x\mathrm{d} y = 1.50

Далее нужно найти общий тепловой поток на левой и нижней границе, чтобы удовлетворялась искомая средняя температура. Для этого введем дополнительную степень свободы с именем 92. Это значение должно быть задано как общее граничное условие внутреннего теплового потока для достижения средней температуры 303,15 К во всей области.

Вычисление первообразной с помощью интегральной связи

Часто задаваемый вопрос, который мы получаем в службу поддержки: Как можно получить пространственную первообразную? Следующее применение интеграционной связи отвечает на этот вопрос. Первообразная является аналогом производной и геометрически позволяет вычислять произвольные области, ограниченные графиками функций. Одним из важных приложений является расчет вероятностей в статистическом анализе. Чтобы продемонстрировать это, мы фиксируем y=0 в нашем примере и обозначаем первообразную T(x,0) через u(x). Это означает, что \frac{\partial u}{\partial x}=T(x,0). Представлением первообразной является следующий интеграл 9{\bar x}T(x,0)\mathrm{d} x

, где мы используем \bar x, чтобы различать интегрирование и выходную переменную. В отличие от приведенных выше интегралов здесь в результате мы имеем функцию, а не скалярную величину. Нам нужно включить информацию о том, что для каждого \bar x\in[0,1] соответствующее значение u(\bar x) требует решения интеграла. К счастью, это легко настроить в среде COMSOL и требует, так сказать, всего три компонента. Во-первых, можно использовать логическое выражение, чтобы переформулировать интеграл как 91T(x,0)\cdot(x\leq\bar x)\ \mathrm{d} x

Во-вторых, нам нужен оператор интегрирования, который действует на нижней границе области нашего примера. Обозначим его intop2 . В-третьих, нам нужно включить различие интегрирования и выходной переменной. Обозначение для этой ситуации: источник и назначение для x и \bar x соответственно. При использовании оператора связи интегрирования доступен встроенный оператор dest , который указывает, что соответствующее выражение не принадлежит переменной интегрирования. Точнее, это означает \bar x=dest(x) в COMSOL. Объединение логического выражения и оператора назначения приводит к выражению T*(x<=dest(x)) , что является именно тем входным выражением, которое нам нужно для intop2 . В целом, мы можем вычислить первообразную с помощью intop2(T*(x<=dest(x))) , что приведет к следующему графику в нашем примере:

, и логическое выражение.

COMSOL предоставляет два других оператора связи интегрирования, а именно общая проекция и линейная проекция . Их можно использовать для получения набора интегралов по путям в любом направлении области. Другими словами, интегрирование выполняется только по одному измерению. В результате получается функция на одну размерность меньше области определения. Для 2D-примера результатом является 1D-функция, которую можно вычислить на любой границе. Некоторые дополнительные сведения о том, как использовать эти операторы, будут опубликованы в следующем блоге о связях компонентов.

Пространственная интеграция с помощью дополнительного физического интерфейса

Наиболее гибким способом пространственной интеграции является добавление дополнительного интерфейса PDE. Вспомним пример с первообразной и предположим, что мы хотим вычислить первообразную не только для y=0. Задача может быть сформулирована в терминах УЧП

\frac{\partial u}{\partial x}=T(x,y)

с краевым условием Дирихле u=0 на левой границе. Самым простым интерфейсом для реализации этого уравнения является интерфейс Coefficient Form PDE , который требует только следующих нескольких настроек:

Как использовать дополнительный физический интерфейс для пространственной интеграции.

Зависимая переменная u представляет собой первообразную по x и доступна во время расчета и постобработки. Помимо гибкости, еще одним преимуществом этого метода является точность, поскольку интеграл не получается как производное значение, а является частью расчета и оценки внутренней погрешности.

Временная интеграция с помощью встроенных операторов

Мы уже упоминали операции с рядом данных, которые можно использовать для интегрирования времени. Еще один очень полезный метод интегрирования по времени предоставляется встроенными операторами timeint и timeavg для интегрирования по времени или среднего по времени соответственно. Они легко доступны при постобработке и используются для интегрирования любого выражения, зависящего от времени, в течение заданного интервала времени. В нашем примере нас может интересовать среднее значение температуры между 90 и 100 секундами, то есть: 9{100}T(x,y,t)\ \mathrm{d} t

На следующем поверхностном графике показан результирующий интеграл, который является пространственной функцией в (x,y) :

Как использовать встроенный оператор интегрирования времени timeavg .

Аналогичные операторы доступны для интегрирования на сферических объектах, а именно ballint , circint , diskint и sphint .

Временное интегрирование посредством дополнительных физических интерфейсов

Если в модели должны быть доступны временные интегралы, их необходимо определить как дополнительные зависимые переменные. Подобно приведенному выше примеру формы коэффициента PDE , это можно сделать, добавив интерфейс ODE ветви Mathematics. Предположим, например, что на каждом временном шаге модель запрашивает интеграл времени от начала до настоящего времени по величине полного теплового потока, который измеряет накопленную энергию. Переменная для полного теплового потока автоматически рассчитывается COMSOL и называется ht.tfluxMag . Интеграл можно рассчитать как дополнительную зависимую переменную с Распределенным ODE , который является подузлом интерфейса ODE домена и DAE . Исходным термином этого ODE домена является подынтегральная функция , как показано на следующем рисунке.

Как использовать дополнительный физический интерфейс для временной интеграции.

Какая польза от такого расчета? Интеграл можно повторно использовать в другом физическом интерфейсе, на который может повлиять накопленная в системе энергия. Более того, он теперь доступен для всех видов постобработки, что удобнее и быстрее, чем встроенные операторы. Например, ознакомьтесь с моделью «Отложение углерода в гетерогенном катализе», где ОДУ домена используется для расчета пористости катализатора как зависящей от времени переменной поля в присутствии химических реакций.

Интеграция аналитических функций и выражений

До сих пор мы показали, как интегрировать переменные решения во время расчета или постобработки. Мы еще не рассмотрели интегралы аналитических функций или выражений. Для этого в COMSOL предусмотрен встроенный оператор интегрирования ( выражение , переменная интегрирования

, нижняя граница , верхняя граница ).