Онлайн решение системы нелинейных уравнений: Решение систем уравнений · Калькулятор Онлайн

Метод Ньютона онлайн

Метод Ньютона используется для нахождения корней функции f(x) = 0. Если необходимо найти минимум функции f(x) → min методом Ньютона, то необходимо использовать данный калькулятор.

Назначение сервиса. Сервис предназначен для отыскания корней уравнений f(x) в онлайн режиме следующими методами:

• Метод хорд, Метод итераций, Комбинированный метод, Метод половинного деления (метод дихотомии)
• Метод золотого сечения, Модифицированный метод Ньютона, Метод секущих, Метод Ньютона (метод касательных)

Инструкция. Введите выражение F(x), нажмите Далее. Полученное решение сохраняется в файле Word. Также создается шаблон решения в Excel.

• Решение онлайн
• Видеоинструкция
• Оформление Word

F(x) =

Искать в интервале от до . 2+3x-12.

см. также Решение нелинейных уравнений. Примеры решений.

Пусть дано уравнение f(x)=0, где f(x) определено и непрерывно в некотором конечном или бесконечном интервале a ≤ x ≤ b. Всякое значение ξ, обращающее функцию f(x) в нуль, то есть такое, что f(ξ)=0 называется корнем уравнения или нулем функции f(x). Число ξ называется корнем k-ой кратности, если при x = ξ вместе с функцией f(x) обращаются в нуль ее производные до (k-1) порядка включительно: f(ξ)=f’(ξ)= … =fk-1(ξ) = 0. Однократный корень называется простым.
Приближенное нахождение корней уравнения складывается из двух этапов:

1. Отделение корней, то есть установление интервалов [αi,βi], в которых содержится один корень уравнения.
   1. f(a)•f(b)<0, т. е. значения функции на его концах имеют противоположные знаки.
   2. f’(x) сохраняет постоянный знак, т.е. функция монотонна (эти два условия достаточны, но НЕ необходимы) для единственности корня на искомом отрезке).
   3. f”(x) сохраняет постоянный знак, т.е. функция выпукла вверх, либо – вниз.
2. Уточнение приближенных корней, то есть доведение их до заданной точности.

Геометрическая интерпретация метода Ньютона (метод касательных)

Пусть корень ξ уравнения f(x)=0 отделен на отрезке [a,b]. Предположим мы нашли (n-1)-ое приближение корня x_n-1. Тогда n-ое приближение x_n мы можем получить следующим образом. Положим
x_n = x_n-1 + h_n-1 . (3.15)
Раскладывая в ряд f(x=ξ) в точке x _n-1, получим
f(x_n) = f(x_n-1+h_n-1) = f(x_n-1) + f’(x_n-1)h_n-1=0
Отсюда следует
. (3.16)
Подставим (3.16) в формулу (3.15), получим
(3.17)

Рис.1. Геометрическая интерпретация метода Ньютона

Геометрически метод Ньютона эквивалентен замене дуги кривой y=f(x) касательной, проведенной в некоторой точке кривой (см. рис.1).
В точке B имеем f(x₀)f’’(x₀)>0. Здесь x₀=b. Проведем касательную в точке B, получим на пересечении касательной осью OX точку x₁. Далее проводим касательную в точке B₁, получим точку x₂ и т.д.
Если положить x₀=a, то в точке x₀ будем иметь f(x

0)f’’(x₀)<0. Тогда  касательная в точке A пересекла бы ось OX в точке x’₁, лежащей вне отрезка [a,b], то есть при таком выборе начальной точки, метод Ньютона оказывается расходящимся. Достаточные условия сходимости метода Ньютона определяются следующей теоремой.

Теорема 5. Если f(a)f(b)<0, причем f′(x) и f″(x) отличны от нуля и сохраняют определенные знаки при a≤x≤b, то исходя из начального приближения x₀∈[a,b], удовлетворяющего неравенству
f(x₀)f’’(x₀)>0 (3. 18)
можно вычислить методом Ньютона (3.17) единственный корень ξ уравнения f(x)=0 с любой степенью точности.
Доказательство: Пусть f(a)<0, f(b)>0, f′(x)>0, f″(x)>0, a≤x≤b. Согласно неравенству (3.18) в качестве точки x₀ мы должны взять ту границу отрезка, для которой f(x

0)>0, т.е. в данном случае т. b.
Итак, имеем x₀>ξ. Докажем, что все приближения x_n> ξ и следовательно все f(x_n)>0. Пусть теперь x_n-1> ξ. Положим ξ = x_n-1 + (ξ-x_n-1).
Применяя формулу Тейлора, получим

где ξ <c_n-1<x_n-1.
Так как f″(x)>0, то имеем
f(x_n-1)+f′(x_n-1)(ε-x_n-1)<0 и, следовательно
ч.т.д. (3.19)
Из (3.19) учитывая знаки f(x_n-1) и f′(x_n-1) имеем x_n<x_n-1, то есть получаем ограниченную монотонную убывающую последовательность x₀>x₁> . 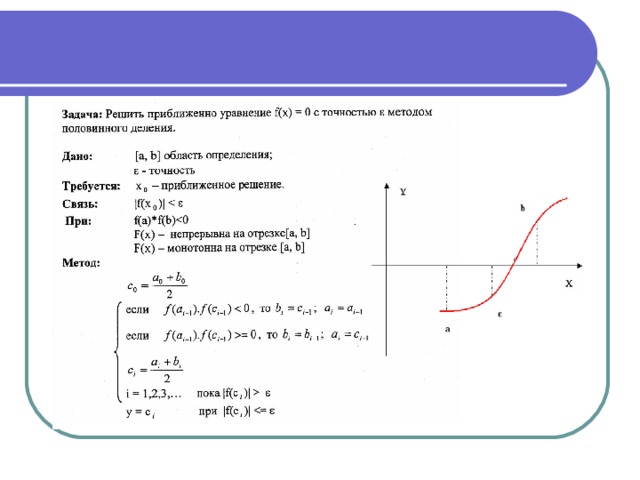.. >x_n>x_n+1>ε. Следовательно, существует .
Переходя к пределу в формуле (3.17) получим
, то есть f(ξ)=0, и следовательно,  ξ- корень ,ч.т.д.
Оценим скорость сходимости метода Ньютона. Из (3.17) следует
. (3.20)
Представим f(ξ) в виде

, откуда
. (3.21)
Подставим (3.21) в (3.20), получим

Отсюда
. (3.22)
Здесь ,

Таким образом, скорость сходимости метода Ньютона квадратичная.
Рис.2

Критерий завершения итерационного процесса имеет вид

|x_n – x_n-1|<ε.

Замечание. В общем случае совпадение с точностью до ε двух последовательных приближений x_n-1 и x_n не гарантирует, что с той же точностью совпадет x_n и ξ (см. рис. 2). Поэтому целесообразно проверять кроме разности |x_n – x_n-1|<ε также значение функции f(x_n): |f(x_n)|< ε₁

.

Пример. f(x) = x⁴-3x³+75x-10000=0.
Найти отрицательный корень с пятью верными знаками.
Решение: Полагая x=0, -10, -100, получим f(0)=-10⁴, f(-10) = -150, f(-100) ≈ 10⁸. Таким образом -100<ξ<-10. Сузим интервал, так как f(-11)=3433, то -11< ξ <-10.
В интервале [-11, -10] f(x)<0, f’’(x)>0. Так как f(-11)f’’(-11)>0, то x₀=-11.
Последовательные приближения даны в таблице.

n	xn	f(xn)	f’(xn)	hn=- f(xn)/ f’(xn)
0	-11	3453	-5183	0.7
1	-10.3	134.3	-4234	0.03
2	-10.27	37.8	-4196	0. 009
3	-10.261	0.2
4	-10.260	<0

Получим -10.261<ξ<-10.260.

Метод золотого сечения

Точки деления интервала выбираются таким образом, чтобы отношение длин подынтервалов удовлетворяло соотношению (см. рис.)

. (3.32)

Так как Δ_k = Δ_k+1 + Δ_k+2, то имеем
. (3.33)
С учетом (3.32) из (3.33) получим уравнение

,

корнем которого является золотое сечение.
.
Скорость сходимости МЗС имеет порядок с коэффициентом 1/γ = γ -1 = 0.618.

Вычисления и решения онлайн

Вычисления и решения онлайн

En

> решение уравнений онлайн калькулятор
разложение на множители решение уравнений онлайн с двумя неизвестными
5 класс
дроби
> решение уравнений онлайн с графиком
с корнями
факторизация
factorization
разложение на множители
factorization
алгебра
Алгебраические уравнения онлайн
Решение систем нелинейных уравнений с ограничениями онлайн
Решение систем линейных уравнений с ограничениями онлайн
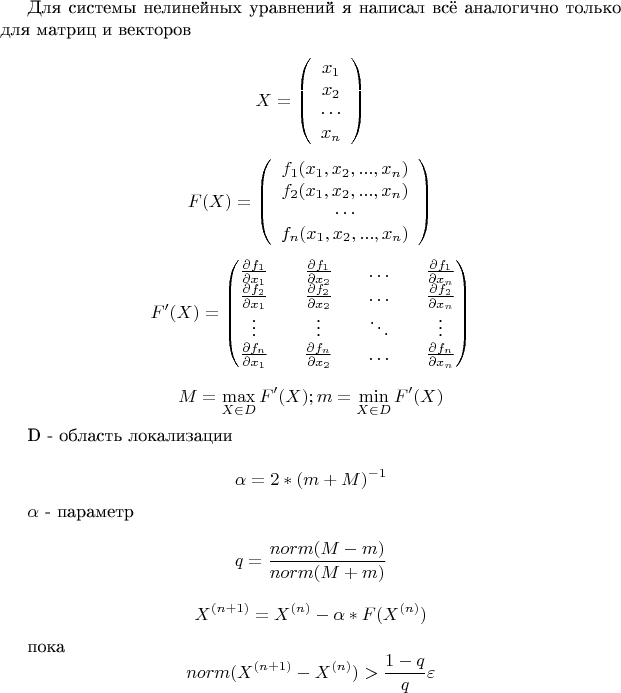
Система нелинейных уравнений
уравнения с неравенствами
уравнения неравенств с модулем

уравнение неравенства с одной переменной
уравнения неравенства с параметрами
Условие сходимости метода
уравнения неравенства системы с параметром
Solution of the equations with one unknown online FREE
Solve a Simultaneous Set of any Equations online FREE
System of Equations Solver online FREE
Solve the following system online and free
> To find the exact solution to a system of equations
> Then the solutions to the original system
[«Найти»,»Find»], [«Условие»,»Input»], [«Ошибка»,»Error»], [«Ответ»,»Result»], [«Нет решения»,»No solution»], [«Точность»,»Accuracy»], [«Пожалуйста,подождите . ..»,»Please Wait …»], [«Отказ»,»Cancel»], [«Решение уравнений»,»Equation Solver»], [«Решение уравнений с одним неизвестным»,»Solution of the equations with one unknown»], [«Вычисления и решения онлайн»,»Online calculator and solver»], [«Главная», «Home»], [«Калькулятор», «Calculator»], [«Простой калькулятор», «Simple calculator»], [«Калькулятор с переменными», «Calculator with variables»], [«Уравнения», «Equations»], [«Уравнение с одним неизвестным», «Equation with one unknown»], [«Уравнение с одним неизвестным и переменными», «Equation with one unknown for given variables»], [«Не задана переменная», «Variable is not specified»], [«Введите условие», «Enter a formula»], [«Еще попытка», «Try again»], [«Не нашла», «Did not find»], [«Не знаю как это решать», «I do not know how to solve it»], [«Лишний символ `=`», «Excess symbol `=`»], [«Неверно задана переменная», «Invalid variable»], [«Не задана», «Not specified»], [«Переменная», «Variable»], [«Найти еще», «Find more»], [«Система уравнений», «System of Equations»], [«Уравнение с неравенствами», «Equation with inequalities»], [«Наименьшее общее кратное», «The least common multiple»], [«Наибольший общий делитель», «The greatest common divisor»], [«Простое число», «Prime number»], [«Большее простое число», «Large prime number»], [«Разложение на множители», «Factorization»], [«Еще нужно время», «Still needs time»], [«Max функции», «Max of a function»], [«Min функции», «Min of a function»], [«Max с ограничениями», «Max on the domain»], [«Min с ограничениями», «Min on the domain»], [«Сумма бесконечного ряда», «The sum of the infinite series»], [«Сумма ряда», «The sum of the series»], [«Ряды», «Series»], [«Сумма ряда с шагом», «A particular series»],

Онлайн-калькулятор системы нелинейных уравнений с решением (пошагово)

Вот удобный онлайн-калькулятор, который решает нелинейные уравнения за считанные секунды и отображает значения переменных в поле вывода. Все, что вам нужно сделать, это ввести уравнение в поле ввода и нажать кнопку расчета в Калькуляторе нелинейных уравнений и получить решения без особых усилий.

Калькулятор нелинейных уравнений: Изучение систем нелинейных уравнений очень важно в алгебре. Наш бесплатный и удобный онлайн-калькулятор нелинейных уравнений помогает учащимся получить правильные знания о концепции и улучшить свои знания по предмету.

Поскольку он охватывает определение нелинейных уравнений и шаги для их всестороннего решения вместе с пошаговым решением. Воспользуйтесь возможностью использовать Калькулятор решения нелинейных уравнений и сэкономьте свое время при решении сложных задач.

Нелинейное уравнение – это уравнение, в котором степень члена равна 2 и более 2. Кривые формируются при нанесении на график значений нелинейного уравнения. Стандартная форма нелинейного уравнения: ax² + by² = c, где a, b, c — константы, а a0, x и y — переменные. Некоторые примеры систем нелинейных уравнений: 2x²+ 3y² = 7, x² + 12xy + y² = 0,9.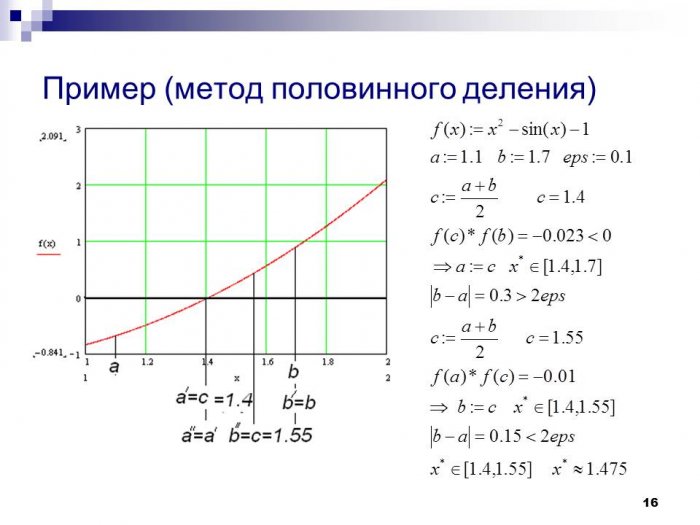 0003

Как решать системы нелинейных уравнений?

Существует три метода решения нелинейных уравнений, которые поясняются на примерах:

1. Метод подстановки:

Одним из лучших методов решения линейных и нелинейных уравнений является подстановка. Процедура использования метода подстановки в линейных уравнениях аналогична нелинейным уравнениям. Прежде всего, рассмотрите решение одного уравнения, а затем подставьте результат во второе уравнение, чтобы найти другую переменную, и так далее. Тем не менее, вы получите различные варианты возможных результатов.

Дальнейшие действия:

1. Сначала разберитесь с уравнениями и начните решать уравнения для одной из переменных.
2. Затем подставьте полученное на первом шаге выражение в заданное нелинейное уравнение.
3. Найдите остальные переменные данных уравнений.
4. Наконец, проверьте свои ответы в обоих уравнениях.

Пример:

Решите систему уравнений: x − y = −1 и 2y = x² + 1

Решение:
Даны системы уравнений:
x − y = −1  ——(1)
2y = x² + 1 ——(2)
Возьмем уравнение (1 ) и решим переменную x, получим
x — y = -1
x = y — 1
Теперь подставим полученное выражение во второе уравнение
y = x² + 1 ——(2)
y = (y-1)² + 1
y = (y²-2y+1) +1
y = y² — 2y + 2
0 = y² — 3y + 2
0 = (y−2)(y−1)
y — 2 = 0
y = 2
И
y — 1 = 0
y = 1
Подставьте значения y в уравнение (1) и решите значение x.
Если y = 2, то x = y-1 = 2-1 = 1
Если y = 1, то x = y-1 = 1-1 = 0
Решения: (1,2) и (0,1), что можно проверить, подставив эти значения (x, y) в оба исходных уравнения.

2. Метод исключения:

Метод исключения является вторым лучшим подходом к решению нелинейных уравнений с двумя переменными. Следующие шаги помогут вам четко понять процесс и с легкостью решить значения переменных.

Шаги для подражания:

1. Во-первых, проверьте, есть ли в данных уравнениях одинаковые переменные второй степени.
2. Если в системе есть одинаковые переменные, продолжите метод исключения, добавляя или вычитая.
3. В общем, метод исключения гораздо проще, когда он включает только два уравнения с двумя переменными (система два на два), а не систему три на три, поскольку шагов меньше.

Найдите приведенные ниже простые примеры уравнений и изучите возможные типы решений.

Пример:

Решите систему нелинейных уравнений методом исключения:
x² + y² = 1
2x² + 3y²  = 7

Решение:
Даны нелинейные уравнения …(
x² 1 +
x²… 1)
2x² + 3y²  = 7 …. .(2)
Теперь рассмотрим уравнение (1) и умножим на 2
2(x²) + 2(y²) = 2(1)
2x² + 2y² = 2 ……. .(3)
Вычесть (3) из (2)
2x² + 3y² = 7
-2x² -2y² = -2
⇒y² = 5
⇒ y = √5 , y = -√5
Подставить значения y в уравнения (1)
Если y = √5, то
x² + y² = 1
x² + 5 = 1
x² = 1-5
x² = -4
x = 2i, x = −2i
Если y = -√5, то x = 2i , x = −2i
Решениями нелинейных уравнений x² + y² = 1, 2x² + 3y²  = 7 являются (x=2i, y=√5), (x=−2i, y=√5), (x= 2i, y=−√5), (x=−2i, y=−√5).

1. Как формируются нелинейные уравнения?

Обычно нелинейное уравнение задается формулой ax²+by² = c, где a,b,c — постоянные значения, а x, y — переменные.

2. Как выглядит график нелинейного уравнения?

График нелинейного уравнения представляет кривые и отображает изменение наклона в разных точках.

3. Какие методы используются для решения нелинейных уравнений?

Существует три метода решения нелинейных уравнений: замена, исключение и построение графика.

4. Могу ли я найти калькулятор нелинейных уравнений онлайн?

Да, вы можете найти онлайн-калькулятор нелинейных уравнений на сайте Linearequationscalculator.com. Это надежный и заслуживающий доверия образовательный онлайн-портал, который предлагает различные бесплатные и удобные онлайн-калькуляторы для математических концепций.

11.6: Решение систем нелинейных уравнений

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

5192

• OpenStax
• OpenStax

Цели обучения

К концу этого раздела вы сможете:

• Решать систему нелинейных уравнений с помощью построения графиков
• Решить систему нелинейных уравнений с помощью замены
• Решить систему нелинейных уравнений методом исключения
• Используйте систему нелинейных уравнений для решения приложений

Прежде чем начать, пройдите этот тест на готовность.

1. Решите систему, построив график: \(\left\{\begin{array}{l}{x-3 y=-3} \\ {x+y=5}\end{array}\right.\) .
   Если вы пропустили эту проблему, просмотрите пример 4.2.
2. Решите систему подстановкой: \(\left\{\begin{array}{l}{x-4 y=-4} \\ {-3 x+4 y=0}\end{array}\right. \)
   Если вы пропустили эту проблему, просмотрите пример 4.7.
3. Решите систему методом исключения: \(\left\{\begin{array}{l}{3 x-4 y=-9} \\ {5 x+3 y=14}\end{array}\right. \)
   Если вы пропустили эту проблему, просмотрите пример 4.9.

Решение системы нелинейных уравнений с помощью графика

Мы научились решать системы линейных уравнений с двумя переменными с помощью графика, замены и исключения. Мы будем использовать эти же методы при рассмотрении нелинейных систем уравнений с двумя уравнениями и двумя переменными. А 9{2}+2}\end{array}\right.\)

Определение \(\PageIndex{1}\)

Система нелинейных уравнений — это система, в которой хотя бы одно из уравнений не является линейным .

Как и в случае систем линейных уравнений, решение нелинейной системы представляет собой упорядоченную пару, которая делает оба уравнения верными. В нелинейной системе может быть более одного решения. Мы увидим это, решая систему нелинейных уравнений с помощью графика.

Когда мы решали системы линейных уравнений, решением системы была точка пересечения двух прямых. В системах нелинейных уравнений графики могут быть кругами, параболами или гиперболами, может быть несколько точек пересечения и, следовательно, несколько решений. Как только вы определите графики, визуализируйте различные способы пересечения графиков и, таким образом, сколько решений может быть.

Для решения систем нелинейных уравнений с помощью графика мы используем в основном те же шаги, что и для систем линейных уравнений, слегка модифицированных для нелинейных уравнений. Шаги перечислены ниже для справки.

Решение системы нелинейных уравнений с помощью графика.

1. Определите график каждого уравнения. Зарисуйте возможные варианты пересечения.
2. Постройте график первого уравнения.
3. Постройте график второго уравнения в той же прямоугольной системе координат. 9{2}=4\)

   Центр: \((2,-3)\) радиус: \(2\)

   Нарисуйте линию, \(y=-1\).

   Это горизонтальная линия.

   Определите точки пересечения. Точка пересечения выглядит как \((2,-1)\).

   Убедитесь, что решение соответствует обоим уравнениям.

   9{2}=4}\end{массив}\right.\)

   Ответ

   Рисунок 11.5.8

   Решение системы нелинейных уравнений с помощью подстановки

   Графический метод хорошо работает, когда точки пересечения представляют собой целые числа и поэтому легко считываются с графика. Но чаще сложно прочитать координаты точек пересечения. Метод подстановки — это алгебраический метод, который хорошо работает во многих ситуациях. Особенно хорошо это работает, когда легко решить одно из уравнений для одной из переменных.

   Метод подстановки очень похож на метод подстановки, который мы использовали для систем линейных уравнений. Шаги перечислены ниже для справки.

   Решение системы нелинейных уравнений путем замены

   1. Определите график каждого уравнения. Зарисуйте возможные варианты пересечения.
   2. Решите одно из уравнений для любой переменной.
   3. Подставьте выражение из шага 2 в другое уравнение.
   4. Решите полученное уравнение. 9{2} = 9} & {\ text {эллипс}} \\ {y = 3 x-3} & {\ text {строка}} \ конец {массив} \ справа. \) Зарисовать возможные варианты пересечения эллипса и прямой. Уравнение \(y=3x-3\) решается относительно \(y\).   Подставьте \(3x-3\) вместо \(y\) в первом уравнении. Решите уравнение для \(х\).   Подставьте \(x=0\) и \(x=1\) в \(y=3x-3\), чтобы найти \(y\)-.     Упорядоченные пары: \((0,-3), (1,0)\). 9{2} -y = 0} & {\ text {parabola}} \\ {y = x-2} & {\ text {line}} \ end {массив} \ right. \) Нарисуйте возможные варианты пересечения параболы и прямой. Уравнение \(y=x-2\) решается относительно \(y\).   Подставьте \(x-2\) вместо \(y\) в первом уравнении. 9{2}-x=0} \\ {y=3 x-2}\end{массив}\right.\)

      Ответ

      \(\left(\frac{4}{9},-\frac{2}{3}\right),(1,1)\)

      Решение системы нелинейных уравнений с помощью исключения

      Когда мы изучали системы линейных уравнений, мы использовали метод исключения для решения системы. Мы также можем использовать исключение для решения систем нелинейных уравнений. Это хорошо работает, когда в уравнениях квадраты обеих переменных. При использовании исключения мы пытаемся сделать коэффициенты одной переменной противоположными, поэтому, когда мы складываем уравнения вместе, эта переменная исключается.

      Метод исключения очень похож на метод исключения, который мы использовали для систем линейных уравнений. Шаги перечислены для справки.

      Решение системы уравнений методом исключения

      1. Определите график каждого уравнения. Зарисуйте возможные варианты пересечения.
      2. Запишите оба уравнения в стандартной форме.
      3. Сделайте коэффициенты одной переменной противоположными.
         Решите, какую переменную вы удалите.
         Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположны.
      4. Добавьте уравнения, полученные на шаге 3, чтобы исключить одну переменную.
      5. Найдите оставшуюся переменную. {2}-y=4}\end{массив}\right.\) 9{2}\)/ Найдите \(y\).   Подставьте \(y=0\) и \(y=-1\) в одно из исходных уравнений. Затем найдите \(x\).   Запишите каждое решение в виде упорядоченной пары. Упорядоченные пары: \((-2,0)(2,0)\). \((\sqrt{3},-1)(-\sqrt{3},-1)\) Убедитесь, что каждая упорядоченная пара является решением обоих исходных уравнений.   Мы оставим вам чеки по каждому из четырех решений. Решения: \((-2,0),(2,0),(\sqrt{3},-1)\) и \((-\sqrt{3},-1)\). Таблица 11.5.5

         Упражнение \(\PageIndex{9}\)

         Решите систему методом исключения: \(\left\{\begin{array}{l}{x^{2}+y ^{2}=9{2}=3} \\ {y=\pm \sqrt{3}} &\quad {y=\pm \sqrt{3}}\end{массив}\) Запишите каждое решение в виде упорядоченной пары. Упорядоченные пары: \((-2, \sqrt{3}),(-2,-\sqrt{3})\), \((2, \sqrt{3}),\) и \(( 2,-\sqrt{3})\). Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.   Мы оставим вам чеки по каждому из четырех решений. 9{2}=4}\end{массив}\right.\)

         Ответ

         \((-2,0),(2,0)\)

         Использование системы нелинейных уравнений для решения приложений

         Системы нелинейных уравнений можно использовать для моделирования и решения многих приложений. В качестве примера мы рассмотрим повседневную геометрическую ситуацию.

         Пример \(\PageIndex{7}\)

         Разница квадратов двух чисел равна \(15\). Сумма чисел равна \(5\). Найдите числа.

         Решение :

         Таблица 11.5.7

         Определите, что мы ищем.	Два разных номера.
         Определите переменные.	\(х\)=первое число \(у\)=второе число
         Преобразуйте информацию в систему уравнений.
         Первое предложение.	Разность квадратов двух чисел равна \(15\).
         Второе предложение.	Сумма чисел равна \(5\).
         Решите систему подстановкой.
         Решите второе уравнение относительно \(x\).
         Подставьте \(x\) в первое уравнение.
         Расширение и упрощение.
         Найдите \(y\).
         Подставьте обратно во второе уравнение.
         	Цифры \(1\) и \(4\).

         Упражнение \(\PageIndex{13}\)

         Разность квадратов двух чисел равна \(−20\). Сумма чисел равна \(10\). Найдите числа.

         Ответить

         \(4\) и \(6\)

         Упражнение \(\PageIndex{14}\)

         Разница квадратов двух чисел равна \(35\). Сумма чисел равна \(−1\). Найдите числа.

         Ответить

         \(-18\) и \(17\)

         Пример \(\PageIndex{8}\)

         Майра купила небольшой \(25\)” телевизор для своей кухни. Размер телевизора измеряется по диагонали экрана. Экран также имеет площадь \(300\) квадратных дюймов. Какова длина и ширина экрана телевизора?

         Решение :

         9{2}\), чтобы очистить дроби.

         Таблица 11.5.8

         Определите, что мы ищем.	Длина и ширина прямоугольника.
         Определите переменные.	Пусть \(x\)= ширина прямоугольника \(y\)=длина прямоугольника
         Нарисуйте схему, чтобы визуализировать ситуацию.
         	Площадь равна \(300\) квадратных дюймов.
         Преобразуйте информацию в систему уравнений.	Диагональ прямоугольного треугольника равна \(25\) дюймов.
         	Площадь прямоугольника равна \(300\) квадратных дюймов.
         Поставить в стандартную форму.
         Решить факторингом.
         Поскольку \(y\) является стороной прямоугольника, мы отбрасываем отрицательные значения.
         Подставьте обратно во второе уравнение.
         	Если длина составляет \(15\) дюймов, ширина равна \(20\) дюймов.
         	Если длина составляет \(20\) дюймов, ширина — \(15\) дюймов.

         Упражнение \(\PageIndex{15}\)

         Эдгар купил маленький \(20\)” телевизор для своего гаража. Размер телевизора измеряется по диагонали экрана. Экран также имеет площадь \(192\) квадратных дюймов. Какова длина и ширина экрана телевизора?

         Ответить

         Если длина составляет \(12\) дюймов, ширина равна \(16\) дюймов. Если длина составляет \(16\) дюймов, ширина — \(12\) дюймов.

         Упражнение \(\PageIndex{16}\)

         Семья Харпер купила небольшую микроволновую печь для своей гостиной. Диагональ двери составляет \(15\) дюймов. Дверь также имеет площадь \(108\) квадратных дюймов. Какова длина и ширина дверцы микроволновки?

         Ответить

         Если длина составляет \(12\) дюймов, ширина — \(9\) дюймов. Если длина составляет \(9\) дюймов, ширина — \(12\) дюймов.

         Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики решения нелинейных уравнений.

         • Нелинейные системы уравнений
         • Решение системы нелинейных уравнений
         • Решение системы нелинейных уравнений методом исключения
         • Система нелинейных уравнений – применение площади и периметра

         Основные понятия

         • Как решить систему нелинейных уравнений с помощью графика.
           1. Определите график каждого уравнения. Зарисуйте возможные варианты пересечения.
           2. Постройте график первого уравнения.
           3. Постройте график второго уравнения в той же прямоугольной системе координат.
           4. Определить, пересекаются ли графики.
           5. Определите точки пересечения.
           6. Убедитесь, что каждая упорядоченная пара является решением обоих исходных уравнений.
         • Как решить систему нелинейных уравнений подстановкой.
           1. Определите график каждого уравнения. Зарисуйте возможные варианты пересечения.
           2. Решите одно из уравнений для любой переменной.
           3. Подставьте выражение из шага 2 в другое уравнение.
           4. Решите полученное уравнение.
           5. Подставьте каждое решение на шаге 4 в одно из исходных уравнений, чтобы найти другую переменную.
           6. Запишите каждое решение в виде упорядоченной пары.
           7. Проверить, что каждая упорядоченная пара является решением обоих исходных уравнений.
         • Как решить систему уравнений методом исключения.
           1. Определите график каждого уравнения. Зарисуйте возможные варианты пересечения.
           2. Запишите оба уравнения в стандартной форме.
           3. Сделайте коэффициенты одной переменной противоположными.
              Решите, какую переменную вы удалите.
              Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположны.
           4. Добавьте уравнения, полученные на шаге 3, чтобы исключить одну переменную.
           5. Найдите оставшуюся переменную.
           6. Подставьте каждое решение из шага 5 в одно из исходных уравнений. Затем найдите другую переменную.
           7. Запишите каждое решение в виде упорядоченной пары.
           8. Проверить, что каждая упорядоченная пара является решением обоих исходных уравнений.

              No related posts.