Калькулятор систем неравенств
Система неравенств записывается следующим образом:

Решить данную систему неравенств, означает найти совокупность всех значений переменной x удовлетворяющих каждому неравенству системы.
Рассмотрим конкретный пример. Пусть нам дана система неравенств:

Для её решения воспользуемся числовой прямой и изобразим интервалы значений переменной x соответствующие каждому неравенству системы:

Синим цветом обозначена совокупность всех значений переменной
х,
удовлетворяющих неравенству
 ,
оранжевым цветом — неравенству
,
оранжевым цветом — неравенству
 и зелёным цветом — неравенству
и зелёным цветом — неравенству

Чтобы найти решение системы неравенств нужно объединить интервалы значений переменной х удовлетворяющие каждому неравенству системы. Из рисунка (смотрим слева направо) следует, что:

Полученный результат также можно изобразить графически на числовой оси:

Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha может решать и более сложные системы неравенств, чем только что рассмотренная. Обращаем Ваше внимание, что символ ≥ необходимо вводить в калькулятор как >= (в виде двух символов больше и равно), а символ ≤ — как <=.
Неравенства онлайн
Неравенства онлайн для решения математики. Быстро найти решение неравенства в режиме онлайн. Сайт www.matcabi.net позволяет найти решение почти любого заданного неравенства онлайн. Математические неравенства онлайн для решения математики. Быстро найти решение неравенства в режиме онлайн. Сайт www.matcabi.net позволяет найти решение почти любого заданного алгебраического, тригонометрического или трансцендентного неравенства онлайн. При изучении практически любого раздела математики на разных этапах приходится решать неравенства онлайн. Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.matcabi.net решение неравенства онлайн займет несколько минут. Основное преимущество www.matcabi.net при решении математических неравенства онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические неравенства онлайн, тригонометрические неравенства онлайн, трансцендентные неравенства онлайн, а также неравенства с неизвестными параметрами в режиме онлайн. Неравенства служат мощным математическим аппаратом решения практических задач. C помощью математических неравенств можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины неравенств можно найти, сформулировав задачу на математическом языке в виде неравенств и решить полученную задачу в режиме онлайн на сайте www.matcabi.net. Любое алгебраическое неравенство, тригонометрическое неравенство или неравенства содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения неравенств. При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн. Поэтому для решения математических неравенств онлайн мы рекомендуем сайт www.matcabi.net, который станет вашим незаменимым калькулятором для решения алгебраических неравенств онлайн, тригонометрических неравенств онлайн, а также трансцендентных неравенств онлайн или неравенств с неизвестными параметрами. Для практических задач по нахождению инетравол решений различных математических неравенств ресурса www.matcabi.net вполне достаточно. Решая неравенства онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение неравенств на сайте www.matcabi.net. Необходимо правильно записать неравенство и моментально получите онлайн решение, после чего останется только сравнить ответ с Вашим решением неравенства. Проверка ответа займет не более минуты, достаточно решить неравенство онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении неравенств онлайн будь то алгебраическое, тригонометрическое, трансцендентное или неравенство с неизвестными параметрами.
Рассмотрим пример решения тригонометрического неравенства онлайн на сайте Контрольная Работа РУ.
Этот сайт даёт полное решение тригонометрического неравенства.

Плюс для некоторых неравенств есть решение, изображённое на графике.
Итак, рассмотрим пример:
Требуется решить тригонометрическое неравенство cos(x/4-pi/3) > 1/2 и найти x, при которых выполняется это неравенство.
Для этого переходим на страницу
>>неравенства онлайн<<и нажимаем Решить неравенство!
.
Получаем ответ 8*pi*n<x<1/3*(24*pi*n+8*pi), где n принадлежит N.
А также следующее подробное решение:
Дано неравенство: $$\cos{\left (\frac{x}{4} — \frac{\pi}{3} \right )} > \frac{1}{2}$$ Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние: $$\cos{\left (\frac{x}{4} — \frac{\pi}{3} \right )} = \frac{1}{2}$$ Решаем:
Дано уравнение $$\cos{\left (\frac{x}{4} — \frac{\pi}{3} \right )} = \frac{1}{2}$$ — это простейшее тригонометрическое ур-ние.
Это ур-ние преобразуется в $$\frac{x}{4} + \frac{\pi}{6} = 2 \pi n + \operatorname{asin}{\left (\frac{1}{2} \right )}$$ $$\frac{x}{4} + \frac{\pi}{6} = 2 \pi n — \operatorname{asin}{\left (\frac{1}{2} \right )} + \pi$$ Или $$\frac{x}{4} + \frac{\pi}{6} = 2 \pi n + \frac{\pi}{6}$$ $$\frac{x}{4} + \frac{\pi}{6} = 2 \pi n + \frac{5 \pi}{6}$$ , где n — любое целое число.
Перенесём $$\frac{\pi}{6}$$ в правую часть ур-ния с противоположным знаком, итого: $$\frac{x}{4} = 2 \pi n$$ $$\frac{x}{4} = 2 \pi n + \frac{2 \pi}{3}$$ Разделим обе части полученного ур-ния на $$\frac{1}{4}$$ $$x_{1} = 8 \pi n$$ $$x_{2} = 8 \pi n + \frac{8 \pi}{3}$$ $$x_{1} = 8 \pi n$$ $$x_{2} = 8 \pi n + \frac{8 \pi}{3}$$ Данные корни $$x_{1} = 8 \pi n$$ $$x_{2} = 8 \pi n + \frac{8 \pi}{3}$$ являются точками смены знака неравенства в решениях.
/8*pi*n - 1/10 pi\ cos|------------- - --| > 1/2 | 1 1| \ 4 3 / /1 pi \ cos|-- + -- - 2*pi*n| > 1/2 \40 3 /
Тогда $$x < 8 \pi n$$ не выполняется, значит одно из решений нашего неравенства будет при: $$x > 8 \pi n \wedge x < 8 \pi n + \frac{8 \pi}{3}$$
_____
/ \
-------ο-------ο-------
x1 x2
Иррациональные неравенства бывают как простые но так и сложные — и всех их можно решить онлайн и с подробным решением с помощью калькулятора неравенств.
Итак:
Простые иррациональные неравенства
Будем считать, что простые неравенства будут содержат только одну часть иррациональности. Тогда рассмотрим пример:
2*x >= sqrt(2/3 + x) + 3
Введём это неравенство в форму калькулятора

Тогда, вы получите подробное решение:
Дано неравенство:
_________
2*x >= 3 + \/ 2/3 + x Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние:
_________
2*x = 3 + \/ 2/3 + x Решаем:
Дано уравнение
_________
2*x = 3 + \/ 2/3 + x Перенесём правую часть уравнения левую часть уравнения со знаком минус
_________ -\/ 2/3 + x = 3 - 2*x
Возведём обе части ур-ния в(о) 2-ую степень
2
2/3 + x = 9 - 12*x + 4*x Перенесём правую часть уравнения левую часть уравнения со знаком минус
25 2 - -- - 4*x + 13*x = 0 3
Это уравнение вида
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
___
\/ D - b
x1 = ---------
2*a
___
-b - \/ D
x2 = ----------
2*a где D = b^2 — 4*a*c — это дискриминант.
Т.к.
, то
(13)^2 - 4 * (-4) * (-25/3) = 107/3
Т.к. D > 0, то уравнение имеет два корня.
x1 = (-b + sqrt(D)) / (2*a)
x2 = (-b - sqrt(D)) / (2*a)
или
_____
13 \/ 321
x1 = -- - -------
8 24
_____
13 \/ 321
x2 = -- + -------
8 24
Т.к.
_________ \/ 2/3 + x = -3 + 2*x
и
_________ \/ 2/3 + x >= 0
то
или
_____
13 \/ 321
x2 = -- + -------
8 24
_____
13 \/ 321
x1 = -- + -------
8 24
_____
13 \/ 321
x1 = -- + -------
8 24 Данные корни
_____
13 \/ 321
x1 = -- + -------
8 24 являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки:
Возьмём например точку
=
_____
13 \/ 321
-- + ------- - 1
8 24 =
_____
5 \/ 321
- + -------
8 24 подставляем в выражение
_________
2*x >= 3 + \/ 2/3 + x
______________________
/ _____ \ / _____
|13 \/ 321 | / 2 13 \/ 321
2*|-- + ------- - 1| >= 3 + / - + -- + ------- - 1
\8 24 / \/ 3 8 24
_____ ______________
5 \/ 321 / _____
- + ------- >= / 31 \/ 321
4 12 3 + / -- + -------
\/ 24 24 но
_____ ______________
5 \/ 321 / _____
- + ------- < / 31 \/ 321
4 12 3 + / -- + -------
\/ 24 24 Тогда
_____
13 \/ 321
x <= -- + -------
8 24 не выполняется
значит решение неравенства будет при:
_____
13 \/ 321
x >= -- + -------
8 24
_____
/
-------•-------
x1Средние иррациональные неравенства
Средними же будем считать уравнения, которые содержат две иррациональные части в неравенстве.
Например,
sqrt(x — 13) > sqrt(x + 8) — 3
надо ввести в форму в калькуляторе

Результат будет таким:
Дано неравенство:
_________ _______ \/ -13 + x > -3 + \/ 8 + x
Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние:
_________ _______ \/ -13 + x = -3 + \/ 8 + x
Решаем:
Дано уравнение
_________ _______ \/ -13 + x = -3 + \/ 8 + x
преобразуем:
_________ _______ \/ -13 + x - \/ 8 + x = -3
Возведём обе части ур-ния в(о) 2-ую степень
2
/ _________ _______\
\\/ -13 + x - \/ 8 + x / = 9или
2 __________________ 2 1 *(x - 13) - 2*\/ (x - 13)*(x + 8) + (-1) *(x + 8) = 9
или
_________________
/ 2
-5 - 2*\/ -104 + x - 5*x + 2*x = 9преобразуем:
_________________
/ 2
-2*\/ -104 + x - 5*x = 14 - 2*xВозведём обе части ур-ния в(о) 2-ую степень
2 2
-416 - 20*x + 4*x = (14 - 2*x)
2 2
-416 - 20*x + 4*x = 196 - 56*x + 4*x Перенесём правую часть уравнения левую часть уравнения со знаком минус
Переносим свободные слагаемые (без x)
из левой части в правую, получим:
Разделим обе части ур-ния на 36
Т.к.
_________________ / 2 \/ -104 + x - 5*x = -7 + x
и
_________________ / 2 \/ -104 + x - 5*x >= 0
то
или
проверяем:
__________ ________
3 + \/ -13 + x1 - \/ 8 + x1 = 0=
__________ ________ \/ -13 + 17 + 3 - \/ 8 + 17 = 0
=
— тождество
Тогда, окончательный ответ:
Данные корни
являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки:
Возьмём например точку
=
=
подставляем в выражение
_________ _______ \/ -13 + x > -3 + \/ 8 + x
__________ ________ \/ -13 + 16 > -3 + \/ 8 + 16
___ ___ \/ 3 > -3 + 2*\/ 6
Тогда
не выполняется
значит решение неравенства будет при:
_____
/
-------ο-------
x1Сложные иррациональные неравенства
Самыми сложными же будут неравенства с тремя частями иррациональностями, значит будет такой пример:
sqrt(x + 5) — sqrt(x — 1) <= sqrt(2*x + 4)
В форме калькулятора это будет выглядеть так:

Сначала мы должны рассмотреть символы неравенства:
- Символ <означает меньше чем.
- Символ> означает больше чем.
- Символ \ (\ leq \) означает меньше или равно. Обычно это пишется как <= на компьютерах, потому что его легче набирать.
- Символ \ (\ geq \) означает больше или равно.Иногда это пишется как> = на компьютерах, потому что его легче набирать.
Существуют бесконечные решения для неравенства. В свете этого факта может быть проще всего найти решение для неравенства путем графического решения системы.
Как графически решить системы неравенств
1) Запишите неравенство в форме пересечения наклона или в форме \ (y = mx + b \).
Например, если попросить решить \ (x + y \ leq 10 \), мы сначала переписываем как \ (y \ leq -x + 10 \).
2) Временно замените данный символ неравенства (в данном случае \ (\ leq \)) на равный символ. При этом вы можете рассматривать неравенство как уравнение. НО НЕ забывайте заменять символ равенства на исходный символ неравенства в конце проблемы!
Итак, \ (y \ leq -x + 10 \) становится \ (y = -x + 10 \) на данный момент.
3) Постройте график линии, найденной на шаге 2. Это сформирует «границу» неравенства — на одной стороне линии условие будет истинным, а на другой — нет.Посмотрите, как построить график здесь.
4) Вернемся к ранее найденному неравенству как \ (y \ leq -x + 10 \). Обратите внимание, что это правда, когда у меньше или равно. На шаге 3 мы построили линию (равный случаю), поэтому теперь нам нужно учесть меньший случай. Поскольку у меньше, чем определенное значение на нижней стороне оси, мы заштрихуем область ниже линии, чтобы указать, что неравенство верно для всех точек ниже линии:
5) Проверить. Подключите точку не на линии, как (0,0).Убедитесь, что выполняется неравенство. В данном случае это означает \ (0 \ leq -0 + 10 \), что, безусловно, верно. Мы заштриховали правильную сторону линии.
Пример:
Найдите все значения x и y, которые удовлетворяют: \ (y \ geq \ frac {-3} {2} x + 6 \).
Обратите внимание, что это неравенство уже находится в форме перехвата наклона. Я заменим данный символ неравенства на символ равенства, чтобы построить линию.
\ (y \ geq \ frac {-3} {2} x + 6 \) становится \ (y = \ frac {-3} {2} x + 6 \). Теперь нарисуйте эту линию, как показано:
Так как это тот случай, когда неравенство истинно для значений y, больших или равных чему-либо, мы заштриховали область над линией.Все точки на или над этой линией графа будут удовлетворять нашему неравенству. Опять же, выберите любую точку над линией графика, чтобы убедиться, что она удовлетворяет или раскрывает ИСТИННОЕ утверждение в терминах исходного неравенства. Например, (5,3). Подключите это, и у нас есть \ (3 \ geq \ frac {-3} {2} * 5 + 6 \). Упростим его до \ (3 \ geq -1.5 \), и мы увидим, что неравенство верно в точке (5,3). Так как эта точка была выше нашей линии, она должна быть затенена, что подтверждает наше решение.
Множественные неравенства — система неравенств
Система неравенств имеет более одного утверждения неравенства, которое должно быть выполнено.Графически это означает, что нам нужно сделать то, что мы только что сделали — построить линию, представленную каждым неравенством, а затем найти область графика, которая верна для ОБА неравенств. Для двух приведенных выше примеров мы можем объединить оба графика и построить площадь, разделяемую двумя неравенствами.
Какое решение установлено? Решение, установленное для ОБА неравенств, будет ЛЮБОЙ ТОЧКОЙ, где ОБА районы заштрихованы вместе или где ОБА заштрихованные регионы встречаются.
Первоначально мистер Фелиз, © 2005
,Неравенство
Раздел неравенств QuickMath позволяет решить практически любое неравенство или систему неравенств в одной переменной. В большинстве случаев вы можете найти точные решения. Даже когда это невозможно, QuickMath может дать вам приблизительные решения практически любого уровня точности, который вам требуется. Кроме того, вы можете построить области, удовлетворяемые одним или несколькими неравенствами, по двум переменным, четко видя, где происходят пересечения этих областей.
Что такое неравенства?
Неравенства состоят из двух или более алгебраических выражений, соединенных символами неравенства. Символы неравенства:| < | менее |
| > | больше |
| <= | меньше или равно |
| > = | больше или равно |
| ! = Или <> | не равно |
Вот несколько примеров неравенства:
|
Решить
Команда Solve может использоваться для решения одного неравенства для одного
неизвестно со страницы основного решения
или одновременно решить систему многих неравенств в одном неизвестном из расширенной страницы решения.2 — 5 <0
Другими словами, QuickMath попытается найти решения, удовлетворяющие обоим неравенствам одновременно.
Перейти на страницу решения
Участок
Команда Plot из раздела Графики построит график любого неравенства две переменные. Для того чтобы построить область, удовлетворяющую одному неравенству с участием х и у, перейдите к основному Страница построения неравенства, где вы можете ввести неравенство и указать верхний и нижний пределы по x и y, которые вы хотите построить график для.Продвинутый Страница построения графика неравенства позволяет построить объединение или пересечение до 8 регионов на одном графике. Вы можете контролировать такие вещи, как или не показывать оси, где должны располагаться оси и какой аспект Соотношение участка должно быть. Кроме того, у вас есть возможность показать каждый отдельный регион сам по себе.
Уравнение говорит, что два выражения равны, а неравенство говорит что одно выражение больше, больше или равно, меньше или меньше или равно другому.Как и в случае с уравнениями, значение переменной для что неравенство истинно, является решением неравенства, и множество всех такими решениями является множество решений неравенства. Два неравенства с В одном и том же наборе решений находятся эквивалентные неравенства. Неравенства решаются с Следующие свойства неравенства.
СВОЙСТВА НЕРАВЕНСТВА
Для действительных чисел a, b и c:
(a) 
(одинаковое число может быть добавлено к обеим сторонам неравенства без изменения решение установлено.)
(б) 
(Обе стороны неравенства могут быть умножены на одно и то же положительное число без изменения набора решений.)
(с) 
(Обе стороны неравенства могут быть умножены на одно и то же отрицательное число
без изменения набора решений, пока направление неравенства
символ перевернут.)
Замена <на> приводит к эквивалентным свойствам.
ПРИМЕЧАНИЕ Поскольку деление определяется в терминах умножения, слово «умноженный» может быть заменен «разделенным» на части (b) и (с) свойств неравенства.
Обратите особое внимание на часть (с): если обе стороны неравенства умноженное на отрицательное число, направление символа неравенства должно быть наоборот. Например, начиная с истинного утверждения — 3 <5 и умножая обе стороны положительным числом 2 дают
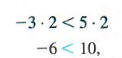
по-прежнему верное утверждение. С другой стороны, начиная с — 3 <5 и умножение обеих сторон на отрицательное число -2 дает истинный результат, только если направление символа неравенства меняется на противоположное.
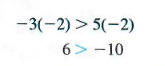
Аналогичная ситуация существует при делении обеих сторон на отрицательное число. В
Таким образом, можно сделать следующее заявление.
При умножении или делении обеих сторон неравенства на отрицательное
число, мы должны изменить направление символа неравенства, чтобы получить
эквивалентное неравенство.
ЛИНЕЙНЫЕ НЕРАВЕНСТВА Линейное неравенство определяется аналогично линейное уравнение.
Линейное неравенство в одной переменной — это неравенство, которое можно записать в форма

, где <> 0.
Пример 1
Решить неравенство -3x + 5> -7.
Используйте свойства неравенства. Добавление — 5 с обеих сторон дает
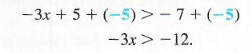
Теперь умножьте обе стороны на -1/3. (Мы также можем разделить на -3.) Поскольку -1/3 < 0, изменить направление символа неравенства.
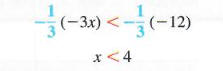
Исходное неравенство удовлетворяется любым вещественным числом меньше 4. множество решений можно записать {x | x <4}. График набора решений показан в Фигура 2.6, где скобка используется, чтобы показать, что само 4 не принадлежит к набору решений.
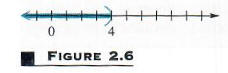
Набор {x | x <4}, решение для неравенства в Примере 1, является примером
интервала. Упрощенная нотация, называемая интервальной нотацией, используется для
интервалы записи. С этим обозначением интервал в Примере 1 может быть записан
как (-оо, 4). Символ -oo не является действительным числом; он используется, чтобы показать, что
интервал включает в себя все действительные числа меньше 4.Интервал (-oo, 4) является примером
открытый интервал, поскольку конечная точка 4 не является частью интервала. Примеры
другие наборы, написанные в интервальной записи, показаны ниже. Квадратная скобка
используется, чтобы показать, что число является частью графика, а скобка используется для
указать, что число не является частью графика. Всякий раз, когда два действительных числа а и
b используются для записи интервала в следующей таблице, предполагается, что
<б.
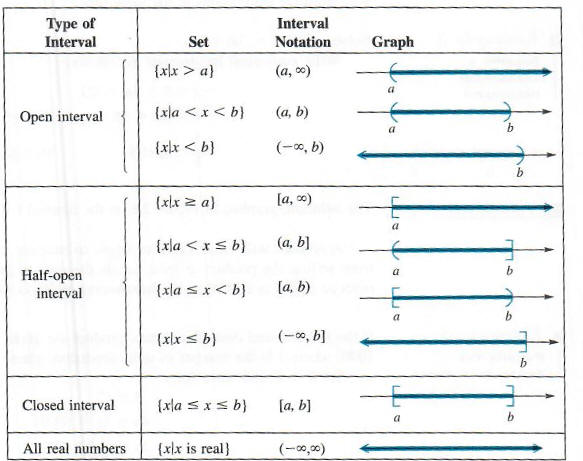
Пример 2
Решить 4 — 3y <7 + 2y.Запишите решение в интервальной записи и графике
решение в строке номера. Напишите следующую серию эквивалентов
неравенства.
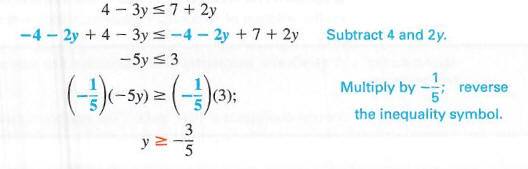
В нотации построителя множеств набор решений {y | y> = 3/5}, находясь в интервале
Обозначение набора решений (-3/5, оо). На рисунке 2.7 приведен график набора решений.
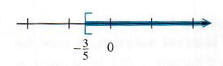
Отныне решения всех неравенств будут записываться с интервалом нотации.
ТРЕХЧАСТНОЕ НЕРАВЕНСТВО Неравенство -2 <5 + 3 м <20 в следующем
пример говорит, что 5 + 3 м между -2 и 20.Это неравенство можно решить
используя расширение свойств неравенства, приведенных выше, работая со всеми
три выражения одновременно.
Решить -2 <5 + 3m <20.
Запишите эквивалентные неравенства следующим образом.
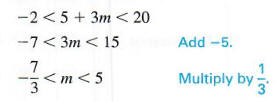
Решение представлено на рисунке 2.8

КВАДРАТИЧЕСКИЕ НЕРАВЕНСТВА Решение квадратичных неравенств зависит от
решение квадратных уравнений.
Квадратичное неравенство — это неравенство, которое можно записать в виде

Мы обсудим квадратные неравенства в следующем разделе.
Перейти на страницу построения графиков неравенства
,Системы линейных неравенств (стр. 1 из 2)  Как только вы узнали, как график линейный неравенства, вы можно перейти к решению систем линейных неравенств. «Система» из линейные неравенства — это набор линейных неравенств, с которыми вы имеете дело все сразу. Обычно вы начинаете с двух или трех линейных неравенств. Техника решения этих систем довольно проста. Вот пример.
Так же, как с решением одиночные линейные неравенства, как правило, лучше всего решить как можно больше неравенства как можно больше для « y » с одной стороны.Решив первые два неравенства, я переставил система: «Решающие» системы линейных неравенств означает «отображение каждого отдельного неравенства, а затем найти совпадения различных решений «. Так что я график каждое неравенство, а затем найти перекрывающиеся части решения регионы.
Топ | 1 | 2 | Возвращение Индексировать Далее >>
|
Системы неравенств Практические проблемы

Теперь, когда вы изучили все шаги, необходимые для решения систем проблем с неравенством слов, я знаю, что вы хотите практиковать некоторые самостоятельно. Да, конечно. Это истинный тест того, насколько хорошо Вы изучили этот блок на неравенства.
Несколько вещей, которые нужно запомнить, прежде чем углубляться в эти проблемы:
Решение проблем со словами
- Прочитайте каждую проблему дважды.Второй раз — используйте подсветку, чтобы выделить ключевые слова.
- Сосредоточьтесь на символе неравенства и убедитесь, что он имеет смысл с учетом контекста проблемы.
- При создании графика помните, что только часть, которая затенена и неравенствами, является областью решения.
- Не забудьте ответить на вопрос, заданный в задаче. Это цель решения проблемы. (Подсказка: всегда лучше ответить вопросы к словесным задачам в полных предложениях.)
- Всегда хорошая идея проверить ваши ответы. Если проблема требует от вас обосновать ваш ответ , то это означает, что вы должны показать работу для проверки своего ответа.
Хорошо … давайте приступим к делу. Нажмите здесь, чтобы распечатать таблицу для ваших практических задач. Вот твои две проблемы.
Практическая задача 1
Джейсон покупает крылья и хот-доги для вечеринки. Одна упаковка крыльев стоит 7 долларов. Хот-доги стоят 4 доллара за фунт.Он должен потратить менее 40 долларов.
- Напишите неравенство, чтобы представить стоимость еды Джейсона для вечеринки.
- Джейсон знает, что он будет покупать не менее 5 фунтов хот-догов. Напишите неравенство, чтобы представить эту ситуацию.
- График неравенства и тени пересечения.
- Определите два решения и обоснуйте ваши ответы.
Практическая задача 2
Футбольные клубы мальчиков и девочек пытаются собрать деньги на новую форму.Футбольный клуб мальчиков продает конфеты по 2 доллара за штуку, а футбольный клуб девочек — свечи по 4 доллара. Они должны собрать более 800 долларов.
- Напишите неравенство, чтобы выразить доход от двух сборщиков средств.
- Девушки рассчитывают продать как минимум 100 свечей. Напишите неравенство, чтобы представить эту ситуацию.
- График неравенства на сетке и затенение пересечения.
- Дайте два возможных решения этой системе. Обосновать ответ.
Решения
1.Джейсон покупает крылья и хот-доги для вечеринки. Одна упаковка крыльев стоит 7 долларов. Хот-доги стоят 4 доллара за фунт. Он должен потратить менее 40 долларов.


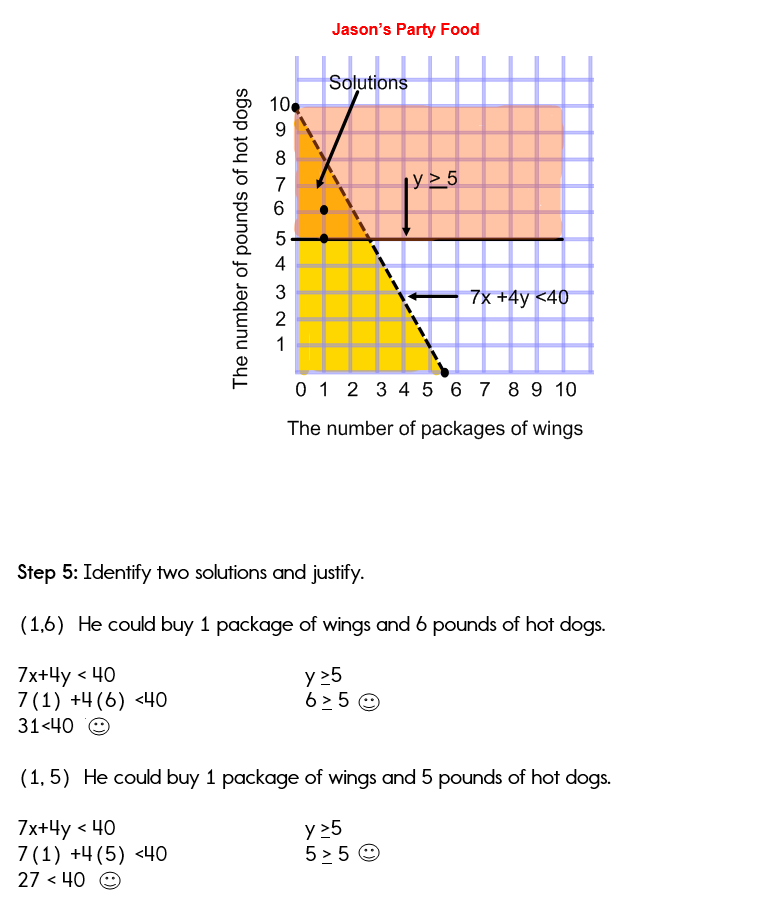
Ваш окончательный ответ может отличаться в зависимости от того, какие заказанные пары вы выбрали из набора решений. Просто убедитесь, что ваш ответ имеет смысл в отношение к проблеме.
2. Футбольные клубы юношей и девушек пытаются собрать деньги на новые униформа. Футбольный клуб мальчиков продает конфеты по 2 доллара за штуку и женский футбольный клуб продает свечи за 4 доллара.Они должны поднять больше чем 800 долларов.

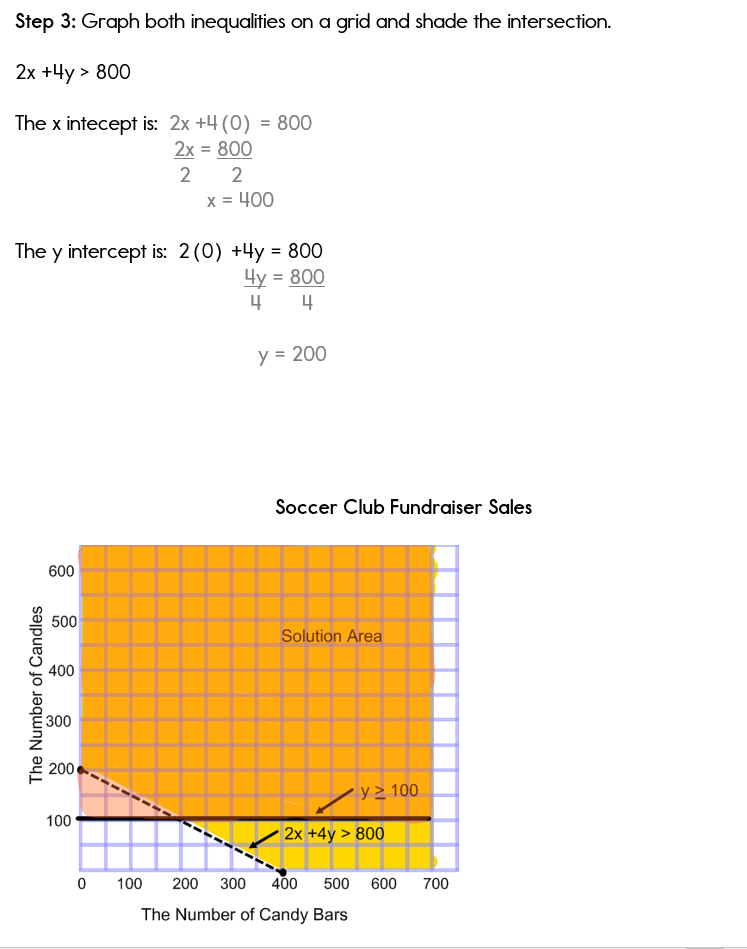

Как ты? Чувствуете себя довольно хорошо о неравенстве? Надеюсь, что если Не возвращайтесь и просмотрите все примеры и попробуйте снова.
- Домой >
- Неравенства >
- Системы Слово Проблемы Практика
