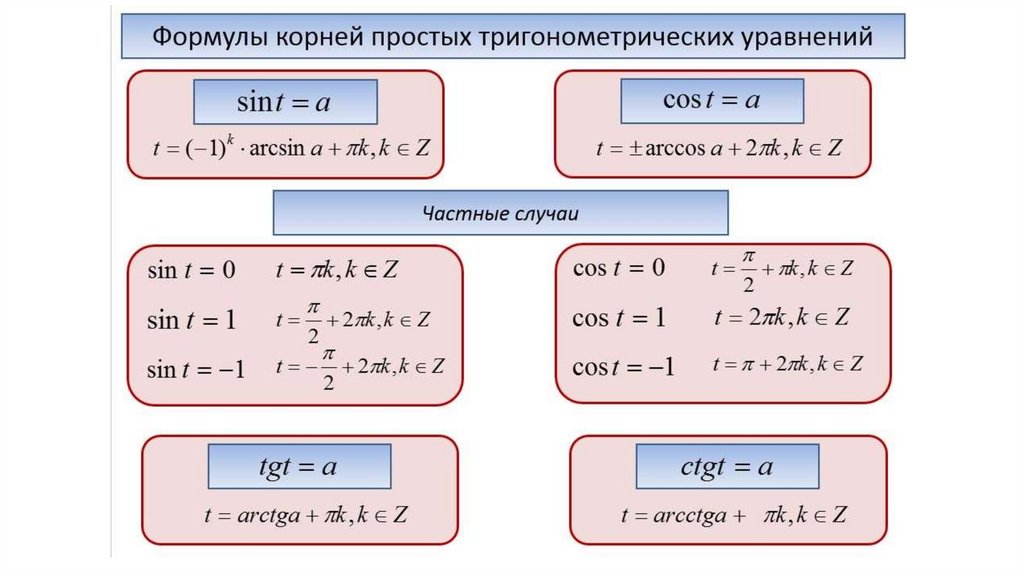
Онлайн решение тригонометрических уравнений на промежутке: Решение тригонометрических уравнений онлайн · Как пользоваться Контрольная Работа РУ

Содержание

Решение тригонометрических уравнений на промежутке

Бахвалова Ольга Михайловна

Разделы: Математика

Цель урока:

а) закрепить умения решать простейшие тригонометрические уравнения;

б) научить выбирать корни тригонометрических уравнений из заданного промежутка

Ход урока.

1. Актуализация знаний.

а)Проверка домашнего задания: классу дано опережающее домашнее задание – решить уравнение и найти способ выбора корней из данного промежутка.

1)cos x = -0,5, где хI [- ]. Ответ: .

2) sin x = , где хI [0;2?]. Ответ: ; .

3)cos 2x = -, где хI [0;]. Ответ:

Ученики записывают решение на доске кто-то с помощью графика, кто-то методом подбора.

В это время класс работает устно.

Найдите значение выражения:

а) tg – sin + cos + sin . Ответ: 1.

б) 2arccos 0 + 3 arccos 1. Ответ: ?

в) arcsin + arcsin . Ответ: .

г) 5 arctg (-) – arccos (-). Ответ:– .

– Проверим домашнее задание, откройте свои тетради с домашними работами.

Некоторые из вас нашли решение методом подбора, а некоторые с помощью графика.

См. приложение 1

Приложение 2

Приложение 3

2.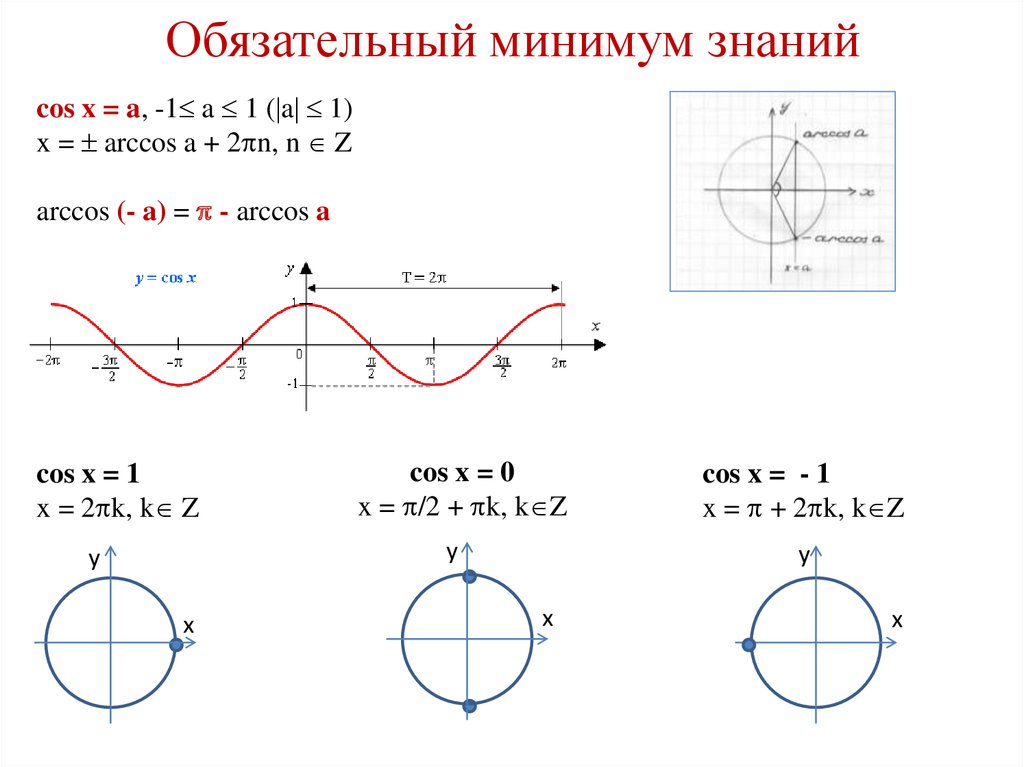 Вывод о способах решения данных заданий и постановка проблемы, т. е. сообщение темы и цели урока.

– а) С помощью подбора решать сложно, если задан большой промежуток.

– б) Графический способ не даёт точных результатов, требует проверку, и занимает много времени.

– Поэтому должен быть ещё как минимум один способ, наиболее универсальный -попробуем его найти. Итак, чем мы будем заниматься сегодня на уроке? (Учиться выбирать корни тригонометрического уравнения на заданном промежутке.)

– Пример 1. (Ученик выходит к доске)

cos x = -0,5, где хI [- ].

Вопрос: Отчего зависит ответ на данное задание? (От общего решения уравнения. Запишем решение в общем виде). Решение записывается на доске

х = + 2?k, где k R.

– Запишем это решение в виде совокупности:

– Как вы считаете, при какой записи решения удобно выбирать корни на промежутке? (из второй записи). Но это ведь опять способ подбора. Что нам необходимо знать, чтобы получить верный ответ? (Надо знать значения k).

(Составим математическую модель для нахождения k).

— < k< ,	— < -k < ,
<k<,	< k< ,
так как kI Z, то k = 0, отсюда х = =	из данного неравенства видно, что целочисленныхзначений k нет.

Ответ: .

Вывод: Чтобы выбрать корни из заданного промежутка при решении тригонометрического уравнения надо:

для решения уравнения вида sin x = a, cos x = a удобнее записать корни уравнения, как две серии корней.
для решения уравнений вида tg x = a, ctg x = a записать общую формулу корней.
составить математическую модель для каждого решения в виде двойного неравенства и найти целое значение параметра k или n.

подставить эти значения в формулу корней и вычислить их.

3. Закрепление.

Пример №2 и №3 из домашнего задания решить, используя полученный алгоритм. Одновременно у доски работают два ученика, с последующей проверкой работ.

4. Самостоятельная работа.

Самопроверка с выбором ответа. Выбрать № правильного ответа, получив закодированное число (312).

1) sin x = -, x

2) 3 tg x = -, x I [0; 2]

3) 2 cos , х [ ]

Приложение. Ответы к примерам

5. Домашнее задание:

1 уровень: № 295 (а,б), № 317 (а,б)

2 уровень: № 307 (в), № 308 (б), № 326(б), № 327(б).

6. Итог урока.

4.04.2007

Отбор корней в тригонометрическом уравнении из ЕГЭ по математике

Одно из заданий второй части ЕГЭ по математике — решение тригонометрических уравнений с корнем. Основная его сложность в том, что нужно уметь не только упрощать выражения и находить ответ, но и проводить отбор корней. Как это сделать, мы разберем в статье.

Что такое тригонометрическое уравнение

Тригонометрическое уравнение содержит в себе функцию синуса, косинуса, тангенса или котангенса. Решение без отбора корней происходит по следующим формулам:

sinx = a при |a| ≤ 1 → x = (-1)narcsina + πn;
cosx = a при |a| ≤ 1 → x = ± arccosa + 2πn;
tgx = b при b — любое число → x = arctgb + πn;
сtgx = b при b — любое число → x = arcсtgb + πn.

Многие корни тригонометрических уравнений имеют конечные значения. Например, при sinx = -1 ответ следующий: x = π/2 + 2πn. Полная таблица достаточно большая, поэтому ее мы приводить тут не будем.

Отбор

Прежде чем изучить методы отбора корней, решим один несложный пример.

Задание.

а) Решите cos2x — 3cosx + 2 = 0

б) Найдите все ответы, принадлежащие отрезку -4; -52

Решение.

Первое слагаемое распишем по формуле косинуса двойного угла:

2cos2x — 1 — 3cosx + 2 = 0

Приведем однородные слагаемые:

2cos2x — 3cosx + 1 = 0

Произведем замену:

Пусть cosx = t, где |t| ≤ 1

Получаем:

2t2 — 3t + 1 = 0

Находим дискриминант:

D = (-3)2 — 4 • 2 • 1 = 9 — 8 = 1

Решаем:

x1=3+122=44=1

x2=3-122=24=12

Возвращаемся к исходной переменной и получаем:

cosx = 1 → x = 2πn, n ∈ Z

cosx = ½ → x = ± π/3 + 2πk, k ∈ Z

Области допустимых значений нет, поэтому оба значения используем при решении пункта «б».

Теперь проведем отбор корней разными способами.

Арифметический

Для решения нужно перебирать все значения целочисленного параметра и считать корни. Разберем на примере cosx = 1.

Решение. x = 2πn

При n = -1 получаем x = 2 • (-1)π = -2π = -4π/2. Это больше, чем -5π/2, следовательно, ответ: не принадлежит отрезку.

При n = -2 получаем x = 2 • (-2)π = -4π. Число принадлежит отрезку.

При n = -3 получаем x = 2 • (-3)π = -6π. Это меньше, чем -4π, следовательно, значение не принадлежит отрезку.

Далее то же самое нужно сделать с остальными корнями. Тогда вы получите ответ.

Алгебраический

Чтобы отобрать корни, нужно решить неравенства относительно известного целочисленного параметра. Рассмотрим на примере первого значения.

Решение. -4π ≤ 2πn ≤ -5π/2

Делим все части неравенства на «2π»:

-2 ≤ n ≤ -5/4

Согласно условию, n ∈ Z. Рассматриваем только ответ n = -2. Получаем x = -4π.

Геометрический

Рисуем единичную окружность, наносим на нее числа из области и корни. После определяем, попадают ли они в промежуток. Отсчет промежутка происходит против часовой стрелки!

По рисунку видно, что в указанный промежуток попадает два корня. Первый: -4π. Второй нужно посчитать. Для этого к «-4π» мы прибавляем «π/3». Получаем: -11π/3.

Функционально-графический

Для решения нарисуем функцию косинуса на области от y = -1 до y = 0,5. Зная значения промежутка, найдем абсциссы точек пересечения на заданном отрезке.

Как видно по рисунку, у нас получаются те же корни, что и в предыдущем методе.

Теперь вы знаете основные способы отбора корней в тригонометрических уравнениях. Это поможет вам правильно решать задания из второй части. Дома вам сложно практиковаться, не хватает помощи учителя? Тогда записывайтесь на курсы подготовки к ЕГЭ в центре «Уникум» при Российском университете дружбы народов. Центр предлагает не только полезные уроки с экспертами ЕГЭ, но и доступ к учебному порталу. На нем вы сможете делать домашние задания, решать пробные варианты экзамена и изучать полезные материалы. Форматы курсов разные — очный и дистанционный.

Содержание данной статьи носит ознакомительный характер. Для подготовки к сдаче ЕГЭ пользуйтесь дополнительными источниками информации!

3.8 Решение тригонометрических уравнений | Предварительное исчисление

Цели обучения

В этом разделе вы:

Решите линейные тригонометрические уравнения с помощью синуса и косинуса.
Решите уравнения с одной тригонометрической функцией.
Решите тригонометрические уравнения с помощью калькулятора.
Решение тригонометрических уравнений квадратной формы.
Решите тригонометрические уравнения, используя фундаментальные тождества.
Решите тригонометрические уравнения с несколькими углами.

Египетские пирамиды возле современного города. (кредит: Oisin Mulvihill)

Фалес Милетский (около 625–547 гг. до н. э.) известен как основатель геометрии. Легенда гласит, что он рассчитал высоту Великой пирамиды в Гизе в Египте, используя теорию

подобных треугольников , которую он разработал, измерив тень своего посоха. Основанная на пропорциях, эта теория находит применение в ряде областей, включая фрактальную геометрию, инженерию и архитектуру. Часто угол возвышения и угол наклона находят с помощью подобных треугольников.
В предыдущих разделах этой главы мы рассмотрели тригонометрические тождества. Тождества верны для всех значений в домене переменной. В этом разделе мы начинаем изучение тригонометрических уравнений для изучения реальных сценариев, таких как определение размеров пирамид.
Решение линейных тригонометрических уравнений с помощью синуса и косинуса
Тригонометрические уравнения, как следует из названия, включают в себя тригонометрические функции. Во многом подобно решению полиномиальных уравнений или рациональных уравнений, только определенные значения переменной будут решениями, если решения вообще есть. Кроме того, как и в случае с рациональными уравнениями, область определения функции должна быть рассмотрена, прежде чем мы предположим, что какое-либо решение является допустимым.
Часто мы решаем тригонометрическое уравнение на заданном интервале. Однако столь же часто нас будут просить найти все возможные решения, а поскольку тригонометрические функции являются периодическими, решения повторяются в каждом периоде. Другими словами, тригонометрические уравнения могут иметь бесконечное число решений. Период как функции синуса, так и функции косинуса равен [латекс]2\пи[/латекс]. Другими словами, через каждые [латекс]2\пи[/латекс] значения y- повторяются, поэтому [ латекс]\mathrm{sin}\left(\theta\right)=\mathrm{sin}\left(\theta\pm2k\pi\right)[/latex]. Если нам нужно найти все возможные решения, то мы должны добавить [латекс]2\pi k,[/латекс], где [латекс]к[/латекс] — целое число, к исходному решению.
Аналогичные правила указывают все возможные решения для других тригонометрических функций. Решение тригонометрических уравнений требует тех же методов, что и решение алгебраических уравнений. Читаем уравнение слева направо, по горизонтали, как предложение. Мы ищем известные шаблоны, факторизуем, находим общие знаменатели и заменяем определенные выражения переменной, чтобы упростить процесс решения. Однако с тригонометрическими уравнениями у нас также есть преимущество использования тождеств, которые мы разработали в предыдущих разделах.
Пример 1. Решение линейного тригонометрического уравнения с функцией косинуса
Найдите все возможные точные решения уравнения [латекс]\mathrm{cos}\left(\theta\right) =\frac{1}{2}. [/latex]
Показать решение
Пример 2. Решение линейного уравнения с функцией синуса
Найдите все возможные точные решения уравнения [латекс]\mathrm{sin}\left(t\right)=\frac{1}{2}.[/ латекс]
Показать решение
Пример 3. Решение тригонометрического уравнения в линейной форме
Точно решить уравнение: [латекс]2\текст{ }\mathrm{cos}\left(\theta\right) -3=-5,\text{ }\text{ }0\le \theta <2\ pi .[/latex]
Показать решение
Попробуйте #1
Решите в точности следующее линейное уравнение на отрезке [латекс]\влево[0,2\пи \вправо):\текст{ }2\текст{ }\mathrm{sin}\left(x \right)+1=0.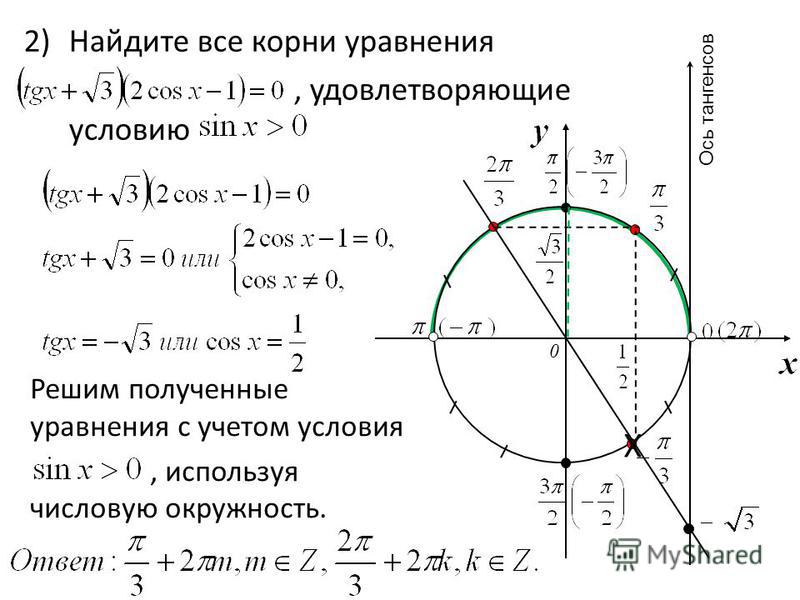 [/latex]
Показать решение
Решение уравнений, включающих одну тригонометрическую функцию
Когда нам дают уравнения, включающие только одну из шести тригонометрических функций, их решения включают использование алгебраических методов и информации, которую мы знаем из единичного круга. Нам нужно сделать несколько соображений, когда уравнение включает тригонометрические функции, отличные от синуса и косинуса. Проблемы, связанные с обратными величинами основных тригонометрических функций, необходимо рассматривать с алгебраической точки зрения. Другими словами, мы напишем уравнение в терминах обратной функции и решим углы, используя наиболее знакомые нам функции. Кроме того, уравнение, включающее функцию тангенса, немного отличается от уравнения, содержащего функцию синуса или косинуса. Во-первых, как мы знаем, период касательной равен [латекс]\пи,[/латекс], а не [латекс]2\пи.[/латекс] Кроме того, областью определения касательной являются все действительные числа, за исключением нечетных целых кратных of [latex]\frac{\pi }{2},[/latex], если, конечно, проблема не накладывает свои собственные ограничения на домен.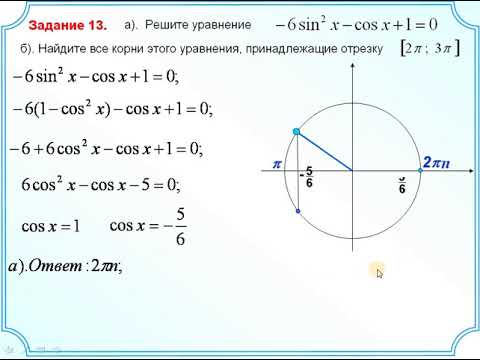
Пример 4. Решение тригонометрического уравнения с косекансом
Точно решить следующее уравнение: [latex]\mathrm{csc}\left(\theta\right) =-2,\text{ }0\le \theta <4 \pi .[/latex]
Показать решение
Пример 5. Решение уравнения с касательной
Точно решить уравнение: [латекс]\mathrm{tan}\left(\theta -\frac{\pi }{2}\right)=1,\text{ } 0\le \theta <2\pi .[/latex]
Показать решение
Попробуйте #2
Найдите все решения для [латекс]\mathrm{tan}\left(x\right)=\sqrt[\leftroot{1}\uproot{2} ]{3}.[/latex]

Показать решение
Пример 6. Найдите все решения уравнения с касательной
Найдите все точные решения уравнения [латекс]2\left(\mathrm{tan}\left(x\right)+3\right)=5+\ mathrm{tan}\left(x\right),\text{ }0\le x<2\pi .[/latex]
Показать решение
Решение тригонометрических уравнений с помощью калькулятора
Не все функции можно решить точно, используя только единичную окружность. Когда мы должны решить уравнение, включающее угол, отличный от одного из специальных углов, нам нужно будет использовать калькулятор. Убедитесь, что он установлен в правильном режиме, либо в градусах, либо в радианах, в зависимости от критериев данной задачи.
Пример 7. Использование калькулятора для решения тригонометрического уравнения, содержащего синус ]\theta[/latex] в радианах.
Показать решение
Пример 8. Использование калькулятора для решения тригонометрического уравнения с секущей
Используйте калькулятор для решения уравнения ответ в радианах.
Показать решение
Попробуйте #3
Решить [латекс]\mathrm{csc}\left(\theta\right) =3.[/latex]
Показать решение
Решение тригонометрических уравнений в квадратной форме
Решение квадратного уравнения может быть более сложным, но опять же, мы можем использовать алгебру, как и для любого квадратного уравнения. Посмотрите на схему уравнения. Есть ли в уравнении более одной тригонометрической функции или только одна? Какая тригонометрическая функция является квадратом? Если представлена только одна функция и один из ее членов возведен в квадрат, подумайте о стандартной форме квадратного числа. Замените тригонометрическую функцию переменной, такой как [latex]x[/latex] или [latex]u.[/latex] Если подстановка делает уравнение похожим на квадратное уравнение, то мы можем использовать те же методы решения квадратного уравнения для решения тригонометрические уравнения.
How To
Дано тригонометрическое уравнение, решить с помощью алгебры .
Ищите шаблон, который предполагает алгебраическое свойство, такое как разность квадратов или факторинговая возможность.
Замените тригонометрическое выражение одной переменной, например [latex]x[/latex] или [latex]u.[/latex]

Решите уравнение так же, как решаются алгебраические уравнения.
Замените тригонометрическое выражение на переменную в результирующих выражениях. 9{2}\left(\theta\right) +\mathrm{cos}\left(\theta\right) =0.[/latex]
Показать решение
Решение тригонометрических уравнений с использованием фундаментальных тождеств
Хотя алгебру можно использовать для решения ряда тригонометрических уравнений, мы также можем использовать фундаментальные тождества, поскольку они упрощают решение уравнений. Помните, что методы, которые мы используем для решения, отличаются от методов проверки личности. Здесь применяются основные правила алгебры, в отличие от переписывания одной стороны тождества, чтобы она соответствовала другой стороне. В следующем примере мы используем два тождества для упрощения уравнения.
В этом разделе нам нужно будет использовать несколько новых идентификаторов. Их называют двухугольными тождествами. Мы не будем тратить время на то, чтобы показать, откуда берутся следующие тождества. Имейте в виду, что есть и другие тригонометрические тождества, которые мы не рассмотрели в этом материале. Если вам интересно, вы можете найти формулы суммы и разности для синуса и косинуса и использовать их для создания некоторых других тождеств, в том числе показанных ниже.
Определение 9{2}\left(\theta\right)-1\end{align*}[/latex]
Пример 13. Решение уравнения с помощью формулы двойного угла
Точно решить уравнение с помощью формулы двойного угла: [латекс]\mathrm{cos}\left(2\theta\right)=\mathrm{cos}\left(\theta\right).[/latex]
Показать решение
Решение тригонометрических уравнений с кратными углами
Иногда невозможно решить тригонометрическое уравнение с тождествами, имеющими кратные углы, например [латекс]\mathrm{sin}\left(2x\right)[/latex] или [латекс]\mathrm{cos}\left(3x\right).[/latex] Столкнувшись с этими уравнениями, вспомните, что [latex]y=\mathrm{sin}\left(2x\right)[/latex] равно горизонтальное сжатие в 2 раза функции [latex]y=\mathrm{sin}\left(x\right). [/latex] На интервале [latex]2\pi,[/latex] мы можем график двух периодов [latex]y=\mathrm{sin}\left(2x\right),[/latex] вместо одного цикла [latex]y=\mathrm{sin}\left(x\right). [/latex] Такое сжатие графика наводит нас на мысль, что 9 может быть в два раза больше.0023 x — перехваты или решения для [латекс]\mathrm{sin}\left(2x\right)=0[/latex] по сравнению с [латекс]\mathrm{sin}\left(x\right)=0.[ /latex] Эта информация поможет нам решить уравнение аналогичного типа, показанное в примере.
Пример 14. Решение тригонометрического уравнения с несколькими углами [0,2\pi \right).[/latex]
Показать решение
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики решения тригонометрических уравнений.
Решение тригонометрических уравнений I
Решение тригонометрических уравнений II
Решение тригонометрических уравнений III
Решение тригонометрических уравнений IV
Решение тригонометрических уравнений V
Решение тригонометрических уравнений VI
Ключевые понятия
При решении линейных тригонометрических уравнений мы можем использовать алгебраические методы точно так же, как при решении алгебраических уравнений. Ищите шаблоны, такие как разность квадратов, квадратичная форма или выражение, которое хорошо поддается замене.
Уравнения, содержащие одну тригонометрическую функцию, можно решить или проверить с помощью единичной окружности.
Мы также можем решать тригонометрические уравнения с помощью графического калькулятора.
Многие уравнения имеют квадратную форму. Мы можем использовать подстановку, чтобы сделать уравнение более простым, а затем использовать те же методы, которые мы используем для решения алгебраического квадратного уравнения: разложение на множители, формулу квадратного уравнения и т. д.
Мы также можем использовать тождества для решения тригонометрического уравнения.
Мы можем использовать подстановку для решения тригонометрического уравнения с несколькими углами, которое представляет собой сжатие стандартной тригонометрической функции. Нам нужно будет принять во внимание сжатие и убедиться, что мы нашли все решения на заданном интервале.
Решение тригонометрических уравнений с использованием тригонометрических тождеств
Горячая математика
Уравнение, которое содержит тригонометрические функции называется тригонометрическое уравнение .
Пример:
грех 2 Икс + потому что 2 Икс «=» 1 2 грех Икс − 1 «=» 0 загар 2 2 Икс − 1 «=» 0
Тригонометрические тождества являются уравнениями, включающими тригонометрические функции, которые верны для любого значения вовлеченных переменных. Вы можете использовать тригонометрические тождества вместе с алгебраическими методами для решения тригонометрических уравнений.
Посторонние решения
Ан постороннее решение является корнем преобразованного уравнения, которое не является корнем исходного уравнения, поскольку оно было исключено из области определения исходного уравнения.
При решении тригонометрических уравнений иногда можно получить уравнение в одной тригонометрической функции, возведя в квадрат каждую сторону, но этот метод может привести к посторонним решениям.
Пример :
Найдите все решения уравнения на интервале [ 0 , 2 π ) .
2 грех 2 Икс «=» 2 + потому что Икс
Уравнение содержит функции синуса и косинуса.
Мы перепишем уравнение так, чтобы оно содержало только функции косинуса, используя тождество Пифагора грех 2 Икс «=» 1 − потому что 2 Икс .
2 ( 1 − потому что 2 Икс ) «=» 2 + потому что Икс 2 − 2 потому что 2 Икс «=» 2 + потому что Икс − 2 потому что 2 Икс − потому что Икс «=» 0 2 потому что 2 Икс + потому что Икс «=» 0
Факторинг потому что Икс мы получаем, потому что Икс ( 2 потому что Икс + 1 ) «=» 0 .
Используя свойство нулевого продукта , мы получим потому что Икс «=» 0 , и 2 потому что Икс + 1 «=» 0 который дает потому что Икс «=» − 1 2 .
В интервале [ 0 , 2 π ) , мы знаем это потому что Икс «=» 0 когда Икс «=» π 2 и Икс «=» 3 π 2 . С другой стороны, мы также знаем, что потому что Икс «=» − 1 2 когда Икс «=» 2 π 3 и Икс «=» 4 π 3 .
No related posts.