Задачи, приводящие к понятию определенного интеграла 11 класс онлайн-подготовка на Ростелеком Лицей
Идея и методы решения задач, приводящих к понятию определенных интегралов
Первая задача. Задача о площади криволинейной трапеции.
Вторая задача. Задача о массе неоднородного стержня.
Третья задача. Задача о перемещении точки.
Мы рассмотрим идею и метод для решения этих задач.
Задача 1
Первая задача. (О площади криволинейной трапеции)
Формулируется следующим образом:
Найти площадь фигуры, ограниченную линиями: на отрезке ,
– ось . Найти площадь . Особенность заключается в том, что верхняя линия в криволинейной трапеции задается функцией. Идея метода – разбить отрезок на определенные маленькие отрезки и считать площади каждого прямоугольника (рис.
1).
Рис. 1. Иллюстрация к первой задаче
Рассмотрим подробно первое действие. А именно разбиение отрезка на равных частей. Отрезок разбивается на равных частей точками .
Величина .
Важно отметить особенности построения. Если , независимо от того, разобьем мы отрезок на 100, 200 или больше частей.
Второе действие. Зафиксируем и приближенно найдем площадь в
Как мы это сделаем? Площадь искомой криволинейной трапеции заменим поступенчастой линией. Значение функции на отрезке [] мы заменим значением функции в левом конце . Таким образом, мы имеем прямоугольники. У них одинаковые основания. А высота – значения функции в левом конце.
Площадь первого прямоугольника .
Площадь второго прямоугольника .
И так далее.
Таким образом, мы разбили площадь на отдельные прямоугольники, сосчитали площадь каждого прямоугольника и суммируем эти площади, получаем:
Итак, при фиксированном примерное значение функции мы имеем.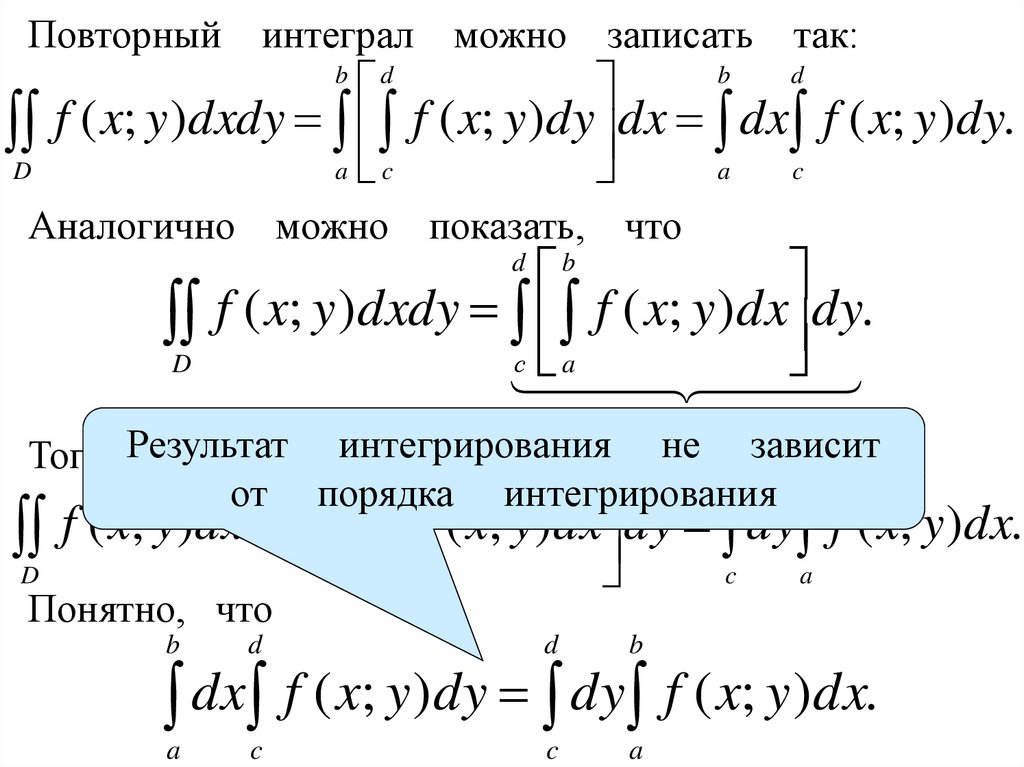
Но это примерное. Как получить точное?
Устремим . Тогда ступенчатая ломаная будет стремиться занять положение функции . И сумма будет стремиться к искомой площади. Более точно: .
Задача 2
Вторая задача. (О вычислении массы неоднородного стержня ).
Стержень неоднородный. Разместим его в координатной плоскости, как показано на рисунке.
Рис. 2. Иллюстрация ко второй задаче
Нам дано: Плотность , .
Найти: Массу стержня.
Рассмотрим частный случай, когда стержень однородный (). Тогда масса стержня легко считается. . Но у нас стержень неоднородный, величина – непостоянная, надо найти массу такого стержня. Метод решения этой задачи аналогичен методу решения, который мы использовали в первой задаче. А именно: разбиение стержня на равных частей с почти одинаковой плотностью на отрезке . Но массу стержня здесь мы умеем считать . Таким образом, разбили стержень и умеем считать массу каждого маленького отрезка этого стержня.
Далее, как и в первой задаче, проведем необходимые вычисления на каждом отрезке.
;
;
………………
.
Складываем, получаем:
Ясно, что мы получили примерное значение искомой величины. Точность увеличивается, если увеличивается , . . Более точно:
Задача 3
Третья задача (о перемещении точки)
Дано: скорость точки .
Найти: длину пути .
Суть задачи заключается в том, что по скорости надо найти длину пути.
Например, мы едем на машине, скорость в каждый момент времени мы знаем. Нужно вычислить путь.
Решение.
Рис. 3. Иллюстрация к третьей задаче
Разбиваем отрезок на равных отрезков ;
Далее вычисляем путь на каждом из отрезков
;
;
………………
.
Если отрезок маленький, то значение скорости – почти постоянная величина.
Суммируем все пути:
. Более точно: .
Одна математическая модель для трех задач
Итак, мы рассмотрели три задачи, которые описываются с помощью одной и той же математической модели (рис. 4).
Рис. 4. Математическая модель
О площади под кривой . Была дана функция Нужно было найти площадь криволинейной трапеции.
О массе стержня . Здесь – плотность. Требовалось найти массу . Масса равнялась площади под этой кривой.
О перемещении точки. Была дана . Скорость известна в каждый момент времени. Нужно было найти перемещение. Перемещение равнялось площади : .
Общий метод решения
То есть решение трех задач – это нахождение данной площади. Напомним метод, с помощью которого мы решали и пытались решить каждую из трех задач.
Общий метод решения задач (рис. 5):
Рис. 5. Общий метод решения задач
Разбиение отрезка на равных отрезков. Каждое Δx одинаковой длины.
Вычисление . То есть вычисление площади каждого из прямоугольников, площади под ступенчатой линией.
.
Если мы сумеем найти предел, то мы получим искомую площадь криволинейной трапеции: .
Обсудим все же идею суммирования:
Вот мы находим и устремляем . Но что это означает?
Каждый прямоугольник фиксирован, если – величина постоянная. Фиксирована высота и основание. Если , то сторона прямоугольника почти что равна нулю. И получается, что мы складываем почти отрезки. Во что же превращается прямоугольник, если почти равна нулю? Он превращается почти в отрезок. Получается, мы складываем бесконечно много площадей бесконечно малых.
Можно задать вопрос: существует ли такой предел таких сумм, которые называются интегральными? На школьном уровне нам понятно, что предел существует из геометрических соображений. И это площадь под криволинейной трапецией. Особую значимость представляет сам принцип бесконечного разбиения и суммирования бесконечного числа бесконечно малых площадей.
И в результате, рано или поздно, мы получим искомую площадь.
В частном случае мы уже сейчас можем находить площади криволинейных трапеций.
Частный случай
Дано: Криволинейная трапеция
Найти:.
Решение.
Трапеция задана следующим образом (рис. 6):
Рис. 6. Трапеция ABCD
Полуокружность с центром в точке с радиусом ,
Чтобы найти площадь, нужно из площади прямоугольника вычесть площадь половины круга. .
Ответ:
Итак, мы рассмотрели три задачи, приводящие к понятию определенного интеграла, которому и посвятим следующий урок.
Список литературы
- Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
- Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Pm298.ru (Источник).
- Pm298.ru (Источник).
- Ib.mazurok.com (Источник).
Домашнее задание
- Найти площадь фигуры, ограниченной графиками функций .
- Найти площадь фигуры, которую задает полуокружность с центром в точке с радиусом ,
Справка онлайн — Справка Origin
Все книгиКниги, не связанные с программированием Руководство пользователя Учебники Быстрая справка Справка OriginКниги по программированию X-Function Origin C LabTalk Programming Python Python (внешний) Automation Server LabVIEW VI Приложения Разработка приложений Code Builder Лицензия Orlab 9 gMOCA0012 | |||
Содержимое
ОписаниеИнтеграция Инструмент выполняет численное интегрирование на активном графике данных с использованием правила трапеций. Вы можете рассчитать математическую область (алгебраическая сумма трапеций) или Абсолютная площадь (сумма абсолютных значений трапеций). Пропущенные значения игнорируются. Использование средства интеграции
X-функция Integ1 вызывается для выполнения вычисления. Пользователь может указать, что площадь, положение пика, ширина пика и высота пика (максимальное отклонение от оси X) записываются в журнал результатов. Кроме того, вы можете выбрать интегрирование с использованием простой базовой линии, определяемой прямой линией, соединяющей конечные точки кривой, и построить график интегральной кривой.
Параметры диалогаАлгоритмЧисленное интегрирование включает вычисление определенного интеграла по приближенной функции:Поскольку исходные данные дискретны, мы используем пару соседних значений, чтобы сформировать трапецию для аппроксимации площади под сегментом кривой, определяемой двумя точками: Как показано выше, кривая делится на части, и мы вычисляем сумму каждой трапеции, чтобы оценить интеграл по формуле:
При заданной базовой линии математическая площадь может быть рассчитана по формуле Если вычислить сумму абсолютного значения площади каждой трапеции, мы можем получить абсолютную площадь: Как показано выше, базовая линия и кривая разделены на пять трапеций (или треугольников). Из выражения определяем, что , и , находящиеся выше базовой линии, положительны, а и , находящиеся ниже базовой линии, отрицательны. Таким образом, математическая площадь этой кривой должна быть и абсолютная площадь этой кривой должна быть . | |||
1 Использование средства интеграции
Английский | немецкий |日本語
7.7: Приблизительное интегрирование — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4489
Цели обучения
- Аппроксимировать значение определенного интеграла, используя правила средней точки и правила трапеций.
- Определите абсолютную и относительную погрешность при использовании метода численного интегрирования.
- Оцените абсолютную и относительную погрешность, используя формулу ограничения погрешности.
- Распознайте, когда правила средней точки и трапеции завышают или занижают истинное значение интеграла.
- Используйте правило Симпсона для аппроксимации значения определенного интеграла с заданной точностью.
Первопроизводные многих функций либо не могут быть выражены, либо не могут быть легко выражены в замкнутой форме (то есть через известные функции). Следовательно, вместо непосредственного вычисления определенных интегралов этих функций мы прибегаем к различным приемам численное интегрирование для аппроксимации их значений. В этом разделе мы рассмотрим некоторые из этих методов. Кроме того, мы исследуем процесс оценки ошибки при использовании этих методов.
Правило средней точки
Ранее в этом тексте мы определили определенный интеграл функции по интервалу как предел сумм Римана .
b_af(x)\,dx\ ). Напомним, что сумма Римана функции \(f(x)\) по интервалу \([a,b]\) получается выбором разбиения 9n_{i=1}f(m_i)Δx\) соответствует сумме площадей прямоугольников, аппроксимирующих площадь между графиком \(f(x)\) и осью \(x\) над \([ а, б]\). На графике показаны прямоугольники, соответствующие \(M_4\) для неотрицательной функции на замкнутом интервале \([a,b].\)
Пример \(\PageIndex{1}\): использование правила средней точки с \(M_4\) 92\,dx\) с использованием четырех подынтервалов. Сравните результат с действительным значением этого интеграла.
Решение: Каждый подинтервал имеет длину \( Δx=\dfrac{1−0}{4}=\dfrac{1}{4}.\) Следовательно, подынтервалы состоят из
\[\left[0,\ tfrac{1}{4}\right],\,\left[\tfrac{1}{4},\tfrac{1}{2}\right],\,\left[\tfrac{1}{2} ,\tfrac{3}{4}\right],\, \text{and}\, \left[\tfrac{3}{4},1\right].
2_1\frac{1}{x }\,дх.\)
- Подсказка
\( Δx=\frac{1}{2}, \quad m_1=\frac{5}{4},\quad \text{and} \quad m_2=\frac{7}{4}.\)
- Ответить
\(\dfrac{24}{35}\приблизительно 0,685714\)
Правило трапеций
Мы также можем аппроксимировать значение определенного интеграла, используя трапеции, а не прямоугольники. На рисунке \(\PageIndex{2}\) область под кривой аппроксимирована трапециями, а не прямоугольниками.
Рисунок \(\PageIndex{2}\): Трапеции можно использовать для аппроксимации площади под кривой, таким образом аппроксимируя определенный интеграл. Правило трапеций для оценки определенных интегралов использует трапеции, а не прямоугольники для аппроксимации площади под кривой. Чтобы получить представление об окончательной форме правила, рассмотрите трапеции, показанные на рисунке \(\PageIndex{2}\). Мы предполагаем, что длина каждого подынтервала равна \(Δx\).
Во-первых, напомним, что площадь трапеции с высотой \(h\) и длинами оснований \(b_1\) и \(b_2\) определяется выражением \(\text{Area}=\frac{1}{ 2}h(b_1+b_2)\). Мы видим, что первая трапеция имеет высоту \(Δx\) и параллельные основания длины \(f(x_0)\) и \(f(x_1)\). Таким образом, площадь первой трапеции на рисунке \(\PageIndex{2}\) равна 9b_af(x)\,dx≈\frac{Δx}{2}\Big[f(x_0)+2\,f(x_1)+2\,f(x_2)+2\,f(x_3)+f( x_4)\Big].\nonumber \]
Обобщая, сформулируем формально следующее правило.
Правило трапеций
Предположим, что \(f(x)\) непрерывно над \([a,b]\). Пусть \(n\) — натуральное число и \(Δx=\dfrac{b−a}{n}\). Пусть \([a,b]\) разбит на \(n\) подынтервалов, каждый длиной \(Δx\), с концами в \( P=\{x_0,x_1,x_2…,x_n\}.\ )
Набор
\[T_n=\frac{Δx}{2}\Big[f(x_0)+2\, f(x_1)+2\, f(x_2)+⋯+2\, f(x_ {n−1})+f(x_n)\Big]. \номер\] 9nf(x_i)Δx.\)
То есть \(L_n\) и \(R_n\) аппроксимируют интеграл, используя левую и правую конечные точки каждого подынтервала соответственно.
Кроме того, внимательное изучение рисунка \(\PageIndex{3}\) позволяет нам сделать следующие замечания об использовании правил трапеций и правил середины для оценки определенного интеграла неотрицательной функции. Правило трапеций имеет тенденцию систематически завышать значение определенного интеграла на интервалах, где функция вогнута вверх, и систематически занижать значение определенного интеграла на интервалах, где функция вогнута вниз. С другой стороны, правило средней точки имеет тенденцию несколько усреднять эти ошибки, частично переоценивая и частично занижая значение определенного интеграла на тех же самых типах интервалов. Это приводит нас к гипотезе о том, что в целом правило средней точки имеет тенденцию быть более точным, чем правило трапеций. 92_1\frac{1}{x}\,dx.\)
- Подсказка
Множество \(Δx=\dfrac{1}{2}.\) Концы подинтервалов являются элементами множества \(P=\left\{1,\frac{3}{2},2\right \}.\)
- Ответить
\(\dfrac{17}{24} \приблизительно 0,708333\)
Абсолютная и относительная погрешность
Важным аспектом использования этих правил численной аппроксимации является вычисление погрешности их использования для оценки значения определенного интеграла.
Сначала нам нужно определить абсолютную ошибку и относительную ошибку.
Определение: абсолютная и относительная ошибка
Если \(B\) является нашей оценкой некоторой величины, имеющей фактическое значение \(A\), то абсолютная ошибка определяется выражением \(|A−B|\ ).
Относительная ошибка представляет собой ошибку в процентах от фактического значения и определяется как \[\left\lvert\frac{A−B}{A}\right\rvert⋅100\%. \nonumber \]
Пример \(\PageIndex{4}\): вычисление погрешности правила средней точки правило средней точки, приведенное в примере \(\PageIndex{1}\). 92_1\frac{1}{x}\,dx\) в \(\frac{24}{35}\) с использованием \(M_2\). Фактическое значение этого интеграла равно \(\ln 2\). Используя \(\frac{24}{35}≈0,6857\) и \(\ln 2≈0,6931,\), вычислите абсолютную ошибку и относительную ошибку.
- Подсказка
Используйте предыдущие примеры в качестве руководства.
- Ответить
абсолютная ошибка \(\приблизительно 0,0074,\) и относительная ошибка \(\приблизительно 1,1\%\)
Границы ошибки для средней точки и правил трапеций
В двух предыдущих примерах мы смогли сравнить нашу оценку интеграла с фактическим значением интеграла; однако у нас обычно нет такой роскоши.
В общем, если мы аппроксимируем интеграл, мы делаем это потому, что не можем легко вычислить точное значение самого интеграла. Поэтому часто полезно иметь возможность определить верхнюю границу ошибки приближения интеграла. Следующая теорема дает оценки ошибок для правил средней точки и правил трапеций. Теорема сформулирована без доказательства. 92}\,dx−M_n \right\rvert <0,01.\nonumber \]
Анализ
У нас может возникнуть соблазн округлить \(8,24\) в меньшую сторону и выбрать \(n=8\), но это будет неправильным, потому что у нас должно быть целое число больше или равно \(8,24\). Мы должны иметь в виду, что оценки ошибки обеспечивают верхнюю границу только ошибки. На самом деле фактическая оценка может быть гораздо лучшим приближением, чем указано в границе погрешности.
Упражнение \(\PageIndex{4}\)
92\,дх.\)- Подсказка
\(f»(x)=2,\) поэтому \(M=2.\)
- Ответить
\(\dfrac{1}{192}\)
Правило Симпсона
С помощью правила средней точки мы оценили площади областей под кривыми, используя прямоугольники.
В некотором смысле мы аппроксимировали кривую кусочно-постоянными функциями. С помощью правила трапеций мы аппроксимировали кривую, используя кусочно-линейные функции. Что, если бы мы вместо этого аппроксимировали кривую с помощью кусочно-квадратичных функций? С 9{x_4}_{x_2}f(x)\,dx\) с интегралом от другой квадратичной функции, проходящей через \( (x_2,f(x_2)), \,(x_3,f(x_3)),\) и \((x_4,f(x_4)).\) Этот процесс продолжается с каждой последующей парой подынтервалов.
Чтобы понять формулу, которую мы получаем для правила Симпсона, мы начнем с вывода формулы для этого приближения для первых двух подынтервалов. Проходя через вывод, мы должны помнить о следующих соотношениях: 9{x_4}_{x_0}f(x)\,dx≈\frac{Δx}{3}(f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f( x_3)+f(x_4)).\nonumber \]
Шаблон продолжается, когда мы добавляем пары подынтервалов к нашему приближению.
Общее правило можно сформулировать следующим образом.
Правило Симпсона
Предположим, что \(f(x)\) непрерывно над \([a,b]\). Пусть \(n\) — четное положительное число и \(Δx=\dfrac{b−a}{n}\). Пусть \([a,b]\) разбит на \(n\) подынтервалов, каждый длиной \(Δx\), с концами в \(P=\{x_0,x_1,x_2,…,x_n\}. \) Набор 9b_af(x)\,dx.\nonumber \]
Точно так же, как правило трапеций является средним значением правил левой и правой руки для оценки определенных интегралов, правило Симпсона может быть получено из правил средней точки и правил трапеций с помощью взвешенное среднее. Можно показать, что \(S_{2n}=\left(\frac{2}{3}\right)M_n+\left(\frac{1}{3}\right)T_n\).
Также можно ограничить ошибку при использовании правила Симпсона для аппроксимации определенного интеграла. Граница ошибки задается следующим правилом: 92_1\frac{1}{x}\,dx.\)
- Подсказка
\[S_2=\frac{1}{3}Δx\left(f(x_0)+4f(x_1)+f(x_2)\right) \nonnumber \]
- Ответить
\(\frac{25}{36} \примерно 0,694444\)
Ключевые понятия
- Мы можем использовать численное интегрирование для оценки значений определенных интегралов, когда трудно найти замкнутую форму интеграла или когда требуется приблизительное значение только определенного интеграла.
- Наиболее часто используемыми методами численного интегрирования являются правило средней точки, правило трапеций и правило Симпсона.
- Правило средней точки аппроксимирует определенный интеграл, используя прямоугольные области, тогда как правило трапеций аппроксимирует определенный интеграл, используя трапециевидные приближения.
- Правило Симпсона аппроксимирует определенный интеграл, сначала аппроксимируя исходную функцию с помощью кусочно-квадратичных функций.
b_af(x)\,dx\)
- числовое интегрирование
- различные численные методы, используемые для оценки значения определенного интеграла, включая правило средней точки, правило трапеций и правило Симпсона
- относительная ошибка Ошибка
- в процентах от фактического значения, заданного как \[\text{относительная ошибка}=\left|\frac{A−B}{A}\right|⋅100\%\nonumber \]
- Правило Симпсона 9b_af(x)\,dx\) задается как \[T_n=\frac{Δx}{2}\big(f(x_0)+2\, f(x_1)+2\, f(x_2)+⋯+ 2\, f(x_{n−1})+f(x_n)\big).
