Операционное исчисление: ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ • Большая российская энциклопедия

ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ • Большая российская энциклопедия

ОПЕРАЦИО́ННОЕ ИСЧИСЛЕ́НИЕ, один из ме­то­дов ма­те­ма­тич. ана­ли­за, по­зво­ляю­щий в ря­де слу­ча­ев с по­мо­щью про­стых пра­вил ре­шать слож­ные за­да­чи. О. и. при­ме­ня­ет­ся в ав­то­ма­ти­ке, ме­ха­ни­ке, элек­тро­тех­ни­ке. В ос­но­ве О. и. ле­жит идея за­ме­ны изу­чае­мых функ­ций (ори­ги­на­лов) др. функ­ция­ми (изо­бра­же­ния­ми), по­лу­чае­мы­ми из пер­вых по оп­ре­де­лён­ным пра­ви­лам (обыч­но изо­бра­же­ние – функ­ция, по­лу­чае­мая из дан­ной с по­мо­щью Ла­п­ла­са пре­об­ра­зо­ва­ния). При та­кой за­ме­не опе­ра­тор $p=\frac{d}{dt}$ ин­тер­пре­ти­ру­ет­ся как ал­геб­ра­ич. ве­ли­чи­на, вслед­ст­вие че­го ин­тег­ри­ро­ва­ние не­ко­то­рых клас­сов ли­ней­ных диф­фе­рен­ци­аль­ных урав­не­ний и ре­ше­ние ря­да др. за­дач ма­те­ма­тич. ана­ли­за сво­дит­ся к ре­ше­нию бо­лее про­стых ал­геб­ра­ич. за­дач. Так, ре­ше­ние ли­ней­но­го диф­фе­рен­ци­аль­но­го урав­не­ния сво­дит­ся к бо­лее про­стой за­да­че ре­ше­ния ал­геб­ра­ич. урав­не­ния: из ал­геб­ра­ич. урав­не­ния на­хо­дят изо­бра­же­ние ре­ше­ния дан­но­го диф­фе­рен­ци­аль­но­го урав­не­ния, по­сле че­го по изо­бра­же­нию вос­ста­нав­ли­ва­ют са­мо ре­ше­ние. Опе­ра­ции на­хо­ж­де­ния изо­бра­же­ния по ори­ги­на­лу (и на­обо­рот) об­лег­ча­ют­ся на­ли­чи­ем об­шир­ных таб­лиц «ори­ги­нал – изо­бра­же­ние».

Для раз­ви­тия О. и. боль­шое зна­че­ние име­ли ра­бо­ты О. Хе­ви­сай­да. Он пред­ло­жил (1892) фор­маль­ные пра­ви­ла об­ра­ще­ния с опе­ра­то­ром $p=\frac{d}{dt}$ и не­ко­то­ры­ми функ­ция­ми от это­го опе­ра­то­ра. Поль­зу­ясь О. и., Хе­ви­сайд ре­шил ряд важ­ных за­дач элек­тро­ди­на­ми­ки, од­на­ко О. и. в его ра­бо­тах не по­лу­чи­ло ма­те­ма­тич. обос­но­ва­ния, мно­гие его ре­зуль­та­ты ос­та­ва­лись не­до­ка­зан­ны­ми.

Стро­гое обос­но­ва­ние О. и. бы­ло да­но с по­мо­щью ин­те­граль­но­го пре­об­ра­зо­ва­ния Ла­п­ла­са. Ес­ли при этом пре­об­ра­зо­ва­нии функ­ция $f(t)$, $0 \leq t \lt \infty$, пе­ре­хо­дит в функ­цию $F(z)$ ком­плекс­но­го пе­ре­мен­но­го $z=x+iy$, то про­из­вод­ная $f'(t)$ пе­ре­хо­дит в функ­цию $zF(z)-f(0)$, а ин­теграл $\int_0^t f(u)du$ пе­ре­хо­дит в функ­цию $\frac{F(z)}{z}$, т. {4t}.$$

Име­ют­ся разл. обоб­ще­ния О. и. Су­ще­ст­ву­ет мно­го­мер­ное О. и., ос­но­ван­ное на тео­рии крат­ных ин­те­гра­лов. Соз­да­ны О. и. для диф­фе­рен­ци­аль­ных опера­то­ров, от­лич­ных от опе­ра­то­ра $p=\frac{d}{dt}$, напр. для опе­ра­то­ра $B=\frac{d}{dt}t\frac{d}{dt}$.

3.Операционное исчисление

Операционное исчисление представляет собой своеобразный и эффективный метод решения различных математических задач, прежде всего, дифференциальных уравнений. В основе операционного исчисления лежит понятие преобразования Лапласа.

3.1. Преобразование Лапласа

 Преобразованием Лапласа .  называется преобразование, которое  ставит в соответствие функции f(t) действительной переменной t  функцию F(p) комплексной переменной p по формуле 

(3.1)

Несобственный интеграл в правой части формулы (3 1), зависящий от комплексного параметра p, называется интегралом Лапласа.

Интеграл сходится и действительно определяет собой некоторую функцию F(p), если подынтегральная функция f(t) удовлетворяет следующим условиям:

1) f(t) кусочно — непрерывная функция;

2) f(t) = 0 при t < 0;

3) f(t) по абсолютной величине возрастает не быстрее заранее выбранной показательной функции, то есть можно найти такие постоянные M и  , что

.

Число называется показателем роста функции f(t).

 Функция f(t) действительного аргумента t, удовлетворяющая перечисленным выше трем условиям, называется  оригиналом , а функция F(p) комплексного аргумента p, определяемая согласно ( 3.1),  называется  изображением по Лапласу  функции f(t) или просто  изображением .

Символически соответствие между оригиналом и изображением записывается обычно так:

или .

Совокупность всех оригиналов f(t) называется пространством оригиналов, а совокупность всех изображений F(p) – пространством изображений.

Изображения простейших функций

1. Пусть оригинал имеет вид

 

Эта функция широко применяется в приложениях и называется единичной функцией или функцией Хевисайда.

Изображение этой функции найдем по формуле (3. 1):

 

.

Следовательно,

. (3.2)

2. Изображение  показательной функции.  Пусть  , тогда

 

Следовательно,

. (3.3)

 

Нахождение изображений непосредственно по формуле (3.1) обычно затруднительно. Во многих случаях изображения по Лапласу могут быть найдены значительно проще, если воспользоваться свойствами преобразования Лапласа.

Свойства преобразования Лапласа

Для практического применения преобразования Лапласа необходимо знать не только изображения отдельных функций, но и правила отображения выполняемых над ними операций. Эти правила формулируются в виде многочисленных теорем, объединяемых общим названием «свойства преобразования Лапласа». Рассмотрим некоторые основные из них.

1. Теорема линейности  . Если ,то для любых постоянныхилинейной комбинации оригиналов соответствует такая же линейная комбинация изображений, то есть

  . (3.4)

 Пример.  Найти изображения функций cos t и sin t.

Согласно формулам Эйлера

 

  .

 

Учитывая формулу (3.3) и применяя теорему линейности, получим 

(3.5)

Аналогично

(3.6)

2. Теорема подобия.  Если f(t) = F(p) , то

 

(3.7)

то есть умножение аргумента оригинала на некоторое число a приводит к делению аргумента изображения и самого изображения на то же число ( к подобному изменению изображения ).

 Пример.  Найти изображения функций и.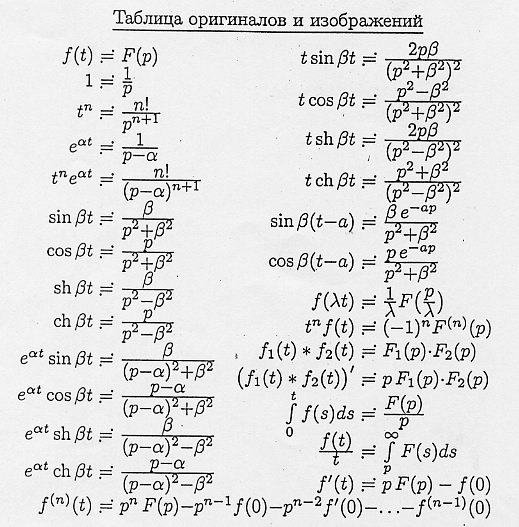 Учитывая изображения (3.5) и (3.6)  и применяя теорему подобия, получим

. (3.8)

Аналогично

. (3.9)

3. Теорема смещения изображения

.  Если f(t) = F(p), то для любого числа a (действительного или комплексного)

 

(3.10)

 

то есть умножение оригинала на приводит к смещению аргумента изображения на a.

 Пример. Найти изображения функций и  .

 Учитывая формулы (3.8) и (3.9) и применяя теорему смещения изображения, находим

. (3.11)

Аналогично

  . (3.12)

 

4.Теорема запаздывания. Если f(t) = F(p), то для любого положительного 

. (3.13)

 то есть «включение» оригинала с запаздыванием на время  равносильно

умножению изображения на .

   Пример. Найти изображение функции f(at — b), если f(t) =F(p). Применяя теоремы подобия и запаздывания, получим

 

 В частности,

  (3.14)

. (3.15)

 5. Теорема дифференцирования оригинала.  Если f(t) = F(p), то

, (3.16)

то есть  дифференцирование оригинала сводится к умножению его  изображения на p и вычитанию начального значения функции . В (2.16) — правосторонний предел функции f(t).

(3. 17)

…………………………………….

(3.18)

В частности, если все начальные значения функции и ее производных равны нулю, то

(3.19)

Для практических приложений эта теорема является самой важной. Из нее следует, что дифференцирование в пространстве оригиналов заменяется существенно более простой операцией — умножением изображения на степень аргумента. Эта теорема лежит в основе операционного метода решения дифференциальных уравнений.

6.Теорема дифференцирования изображения. Если f(t) = F(p), то

……………………..

.

Учитывая, что и применяя последовательно теорему дифференцирования изображения, найдем изображения степенных функций:

(3.

20)

7. Теорема интегрирования оригинала  . Если f(t) = F(p), то

 

. (3.21)

 

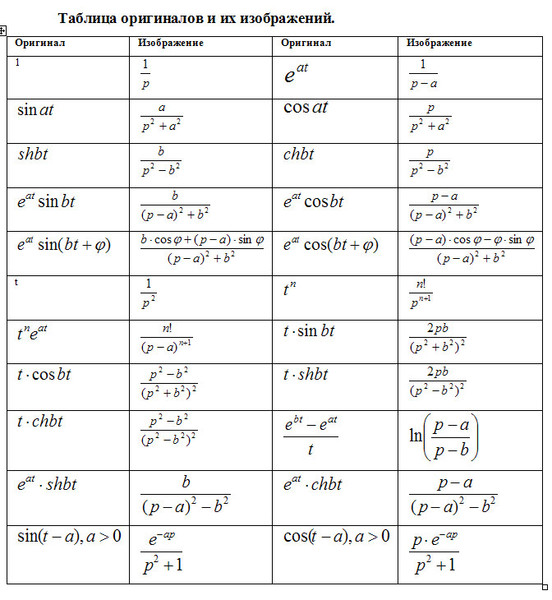
Соответствие между некоторыми основными оригиналами и изображениями указано в таблице 4.

Таблица 4

Таблица соответствия

Операционное исчисление — Математическая энциклопедия

Один из методов математического анализа, позволяющий во многих случаях свести к изучению дифференциальных операторов, псевдодифференциальных операторов и некоторых видов интегральных операторов (ср. Дифференциальный оператор; Интегральный оператор ; псевдодифференциальный оператор) и решения содержащих их уравнений, к рассмотрению более простых алгебраических задач. Развитие и систематическое использование операционного исчисления началось с работ О.

Хевисайда (1892), который предложил формальные правила работы с оператором дифференцирования $ d/dt $ и решил ряд прикладных задач. Однако он не дал операционному исчислению математической основы; это было сделано с помощью преобразования Лапласа; Я. Микусинский (1953) облек операционное исчисление в алгебраическую форму, используя понятие функционального кольца. Наиболее общее понятие операционного исчисления получают с помощью обобщенных функций (см. Обобщенная функция).

Простейший вариант операционного исчисления выглядит следующим образом. Пусть $К$ — множество функций (с действительными или комплексными значениями), заданных в области $ 0 \leq t < \infty $ и абсолютно интегрируема на любом конечном интервале. Интеграл 9{ t } f( t - \tau ) g( \tau ) d \tau $$

называется сверткой функций $f,g\inK$. При обычной операции сложения и операции свертки $K$ становится кольцом без делителей нуля (теорема Титчмарша, 1924 г.). Элементы частного поля $P$ этого кольца называются операторами и записываются как $a/b$; тот факт, что деление на $K$ не всегда возможно именно источником нового понятия, оператора, обобщающего понятие функции.

{ t } f( \tau ) d \tau \правильно \} . $$ 9{n-} 1 }{(n- 1) ! } f( \tau ) d \tau $$

Это формула Коши, обобщение которой на случай произвольного (нецелого) индекса служит для определения дробного интегрирования.

2) $ [ \alpha ] = \{ \alpha \} / \{ 1 \} $( где $\альфа$ — постоянная функция) — числовой оператор; поскольку $[\alpha][\beta] = [\alpha\beta]$, $ [\альфа + \бета] = [\альфа] + [\бета] $, $[\alpha]\{f\} = \{\alphaf\}$, в то время как $ \{ \alpha \} \{ \beta \} = \{ \alpha \beta t \} $, числовые операторы ведут себя как обычные числа. Таким образом, оператор есть обобщение не только функции, но и числа; $ [ 1] $ является единицей кольца $K$. 9{\ альфа т} \} = \frac{1}{s- a } . $$

Конечно, недифференцируемую функцию можно умножить на оператор дифференцирования $s$; однако результатом будет, вообще говоря, оператор.

4) $ D \{ f \} = \{ — tf( t) \} $ является алгебраической производной. Оно распространяется на произвольные операторы обычным образом. Оказывается, действие этого оператора на функцию оператора дифференцирования $ s $ совпадает с дифференцированием по $s$.

9{n} + \dots + \alpha _ {0} } , $$

$$ \beta _ {v} = \alpha _ {v+} 1 \gamma _ {0} + \dots + \alpha _ {n} \gamma _ {n-} v- 1 . $$

Решение в обычном виде получается разложением на элементарные дроби по переменной $s$, с последующим обратным преобразованием по соответствующим таблицам функций.

При использовании операционного исчисления для уравнений в частных производных (а также для более общих псевдодифференциальных уравнений) применяется дифференциальное и интегральное исчисление операторных функций, т. е. функций с операторными значениями. Для этих функций должны быть развиты понятия непрерывности, производной, сходимости рядов, интегралов и т. д.

Пусть $f(\lambda,t)$ — функция, определенная для $ t \geq 0 $ и $\lambda\in[a,b]$. Параметрическая оператор-функция $ f( \lambda ) $ определяется по формуле $f(\lambda) = \{f(\lambda,t)\}$; он помещает операторы определенного типа — функции в $t$— в соответствии со значениями $\lambda$ рассматривается. Оператор-функция называется непрерывной при $ \lambda \in [ a, b] $ если его можно представить в виде произведения оператора $q$ и параметрическая функция $ f _ {1} ( \lambda ) = \{ f _ {1} ( \lambda , t) \} $ такой, что $ f _ {1} ( \lambda , t) $ непрерывна в обычном смысле.

Примеры.

1) Используя параметрическую функцию $ h( \lambda ) = \{ h( \lambda , t) \} $:

$$ h( \lambda , t) = \left \{ \begin{массив}{cll} 0 &\textrm{ для } &0 \leq t < \lambda , \\ t - \lambda &\textrm{ for } &0 \leq \lambda \leq t, \\ \конец{массив} \правильно .$$

Функция Хевисайда определяется:

$$ H( \lambda ) = s \{h(\lambda , t) \} . $$

Значения гиперболической показательной функции 9{-} ст f( t) dt, $$

его преобразование Лапласа. В результате достаточно широкий класс операторов описывается функциями одного параметра $s$; кроме того, это формальное подобие уточняется в математических терминах путем установления определенного изоморфизма. {- \lambda s } f $ отождествляется с распределением Шварца с носителем, ограниченным снизу.

Понятие распределения Шварца и оператора Микусинского не включают друг друга, но оба обобщают понятие функции и ее производных.

Термин «операционное исчисление» также используется в смысле функционального исчисления; т. е. гомоморфизм некоторой алгебры функций в алгебру операторов. Наконец, фраза «операционное исчисление» или «операторное исчисление, операторное исчисление» встречается в контексте упорядоченного по времени операторного исчисления (операторного исчисления с упорядоченным по времени Фейнмана-Дайсона), разработанного в 1919 г.50-х годов для изучения квантовой электродинамики [a4], [a5] и интегралов произведений (см. Интеграл произведений), [a6].

Список литературы

9134

01010101010101010101010110101101101010111011010. Т.К. Беме, «Операционное исчисление», II , PWN & Pergamon (1987)

[A1]	J. Mikusiński, «Оперативное расчет», 1 , PWN & Pergamon (1987) (переводится с лака)
[a3]	Б. ван дер Пол, Х. Бреммер, «Операционное исчисление на основе двустороннего интеграла Лапласа», Cambridge Univ. Press (1959)
[a4]	Р. П. Фейнман, «Операторное исчисление, имеющее приложения в квантовой электродинамике» Phys. , 84 (1951) стр. 108–128
[a5]	Т.Л. Гилл, В.В. Закари, «Упорядоченные по времени операторы и алгебры Фейнмана – Дайсона» J. Math. физ. , 28 (1987) стр. 1459–1470
[a6]	Дж. Д. Доллард, Ч.Н. Фридман, «Интеграция продуктов» , Addison-Wesley (1979)

Как процитировать эту запись:
Операционное исчисление. Математическая энциклопедия. URL: http://encyclopediaofmath. org/index.php?title=Operational_calculus&oldid=49500

Эта статья адаптирована из оригинальной статьи М.И. Войцеховский (создатель), появившийся в Математической энциклопедии — ISBN 140200609.8. См. оригинальную статью

Операционное исчисление — Математическая энциклопедия

Один из методов математического анализа, позволяющий во многих случаях свести изучение дифференциальных операторов, псевдодифференциальных операторов и некоторых типов интегральных операторов (ср. , Дифференциальный оператор, Интегральный оператор, Псевдодифференциальный оператор) и решение уравнений, содержащих их, к рассмотрению более простых алгебраических задач. Развитие и систематическое использование операционного исчисления началось с работ О. Хевисайда (1892), который предложил формальные правила работы с оператором дифференцирования $ d/dt $ и решил ряд прикладных задач. Однако он не дал операционному исчислению математической основы; это было сделано с помощью преобразования Лапласа; Я. Микусинский (1953) облек операционное исчисление в алгебраическую форму, используя понятие функционального кольца. Наиболее общее понятие операционного исчисления получают с помощью обобщенных функций (см. Обобщенная функция).

Простейший вариант операционного исчисления выглядит следующим образом. Пусть $К$ — множество функций (с действительными или комплексными значениями), заданных в области $ 0 \leq t < \infty $ и абсолютно интегрируема на любом конечном интервале. Интеграл 9{ t } f( t - \tau ) g( \tau ) d \tau $$

называется сверткой функций $f,g\inK$. При обычной операции сложения и операции свертки $K$ становится кольцом без делителей нуля (теорема Титчмарша, 1924 г.). Элементы частного поля $P$ этого кольца называются операторами и записываются как $a/b$; тот факт, что деление на $K$ не всегда возможно именно источником нового понятия, оператора, обобщающего понятие функции. Для обозначения необходимого в операционном исчислении различия между понятиями функции и ее значения в точке используются следующие обозначения:

$$ \{ f( t) \} \textrm{ для функции } f \textrm{ переменная } т; $$

$$ f( t) \textrm{ для значения } \{ f( t) \} \textrm{ в точке } t. { t } f( \tau ) d \tau \правильно \} . $$ 9{n-} 1 }{(n- 1) ! } f( \tau ) d \tau $$

Это формула Коши, обобщение которой на случай произвольного (нецелого) индекса служит для определения дробного интегрирования.

2) $ [ \alpha ] = \{ \alpha \} / \{ 1 \} $( где $\альфа$ — постоянная функция) — числовой оператор; поскольку $[\alpha][\beta] = [\alpha\beta]$, $ [\альфа + \бета] = [\альфа] + [\бета] $, $[\alpha]\{f\} = \{\alphaf\}$, в то время как $ \{ \alpha \} \{ \beta \} = \{ \alpha \beta t \} $, числовые операторы ведут себя как обычные числа. Таким образом, оператор есть обобщение не только функции, но и числа; $ [ 1] $ является единицей кольца $K$. 9{\ альфа т} \} = \frac{1}{s- a } . $$

Конечно, недифференцируемую функцию можно умножить на оператор дифференцирования $s$; однако результатом будет, вообще говоря, оператор.

4) $ D \{ f \} = \{ — tf( t) \} $ является алгебраической производной. Оно распространяется на произвольные операторы обычным образом. Оказывается, действие этого оператора на функцию оператора дифференцирования $ s $ совпадает с дифференцированием по $s$.

9{n} + \dots + \alpha _ {0} } , $$

$$ \beta _ {v} = \alpha _ {v+} 1 \gamma _ {0} + \dots + \alpha _ {n} \gamma _ {n-} v- 1 . $$

Решение в обычном виде получается разложением на элементарные дроби по переменной $s$, с последующим обратным преобразованием по соответствующим таблицам функций.

При использовании операционного исчисления для уравнений в частных производных (а также для более общих псевдодифференциальных уравнений) применяется дифференциальное и интегральное исчисление операторных функций, т. е. функций с операторными значениями. Для этих функций должны быть развиты понятия непрерывности, производной, сходимости рядов, интегралов и т. д.

Пусть $f(\lambda,t)$ — функция, определенная для $ t \geq 0 $ и $\lambda\in[a,b]$. Параметрическая оператор-функция $ f( \lambda ) $ определяется по формуле $f(\lambda) = \{f(\lambda,t)\}$; он помещает операторы определенного типа — функции в $t$— в соответствии со значениями $\lambda$ рассматривается. Оператор-функция называется непрерывной при $ \lambda \in [ a, b] $ если его можно представить в виде произведения оператора $q$ и параметрическая функция $ f _ {1} ( \lambda ) = \{ f _ {1} ( \lambda , t) \} $ такой, что $ f _ {1} ( \lambda , t) $ непрерывна в обычном смысле.

Примеры.

1) Используя параметрическую функцию $ h( \lambda ) = \{ h( \lambda , t) \} $:

$$ h( \lambda , t) = \left \{ \begin{массив}{cll} 0 &\textrm{ для } &0 \leq t < \lambda , \\ t - \lambda &\textrm{ for } &0 \leq \lambda \leq t, \\ \конец{массив} \правильно .$$

Функция Хевисайда определяется:

$$ H( \lambda ) = s \{h(\lambda , t) \} . $$

Значения гиперболической показательной функции 9{-} ст f( t) dt, $$

его преобразование Лапласа. В результате достаточно широкий класс операторов описывается функциями одного параметра $s$; кроме того, это формальное подобие уточняется в математических терминах путем установления определенного изоморфизма. {- \lambda s } f $ отождествляется с распределением Шварца с носителем, ограниченным снизу.

Понятие распределения Шварца и оператора Микусинского не включают друг друга, но оба обобщают понятие функции и ее производных.

Термин «операционное исчисление» также используется в смысле функционального исчисления; т. е. гомоморфизм некоторой алгебры функций в алгебру операторов. Наконец, фраза «операционное исчисление» или «операторное исчисление, операторное исчисление» встречается в контексте упорядоченного по времени операторного исчисления (операторного исчисления с упорядоченным по времени Фейнмана-Дайсона), разработанного в 1919 г.50-х годов для изучения квантовой электродинамики [a4], [a5] и интегралов произведений (см. Интеграл произведений), [a6].

Список литературы

9134

01010101010101010101010110101101101010111011010. Т.К. Беме, «Операционное исчисление», II , PWN & Pergamon (1987)

[A1]	J. Mikusiński, «Оперативное расчет», 1 , PWN & Pergamon (1987) (переводится с лака)
[a3]	Б. ван дер Пол, Х. Бреммер, «Операционное исчисление на основе двустороннего интеграла Лапласа», Cambridge Univ. Press (1959)
[a4]	Р. П. Фейнман, «Операторное исчисление, имеющее приложения в квантовой электродинамике» Phys. , 84 (1951) стр. 108–128
[a5]	Т.Л. Гилл, В.В. Закари, «Упорядоченные по времени операторы и алгебры Фейнмана – Дайсона» J. Math. физ. , 28 (1987) стр. 1459–1470
[a6]	Дж. Д. Доллард, Ч.Н. Фридман, «Интеграция продуктов» , Addison-Wesley (1979)

Как процитировать эту запись:
Операционное исчисление. Математическая энциклопедия. URL: http://encyclopediaofmath.