Определение геометрической прогрессии: Геометрическая прогрессия — урок. Алгебра, 9 класс.

Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. УРОК – ПРЕЗЕНТАЦИЯ. ТЕМА : Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии

900igr.net

2. ЦЕЛЬ УРОКА :

Формирование понятия геометрической
прогрессии, используя сопоставление и
противопоставления понятию
арифметической прогрессии.
Познакомить со свойствами
геометрической прогрессии и формулой nго члена.
Закрепить на примерах решения задач.

3. Изучение понятия геометрической прогрессии и вывод формулы n-го члена геометрической прогрессии.

4. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущ

Геометрической прогрессией
называется
последовательность отличных от
нуля чисел, каждый член которой,
начиная со второго, равен
предыдущему члену, умноженному
на одно и тоже число.

5. Определение

Числовая
последовательность, в
которой каждый
следующий член
получается из
предыдущего
прибавлением одного и
того же числом
d,называется
арифметической
прогрессией.
Числовая
последовательность
отличных от нуля
чисел, в которой
каждый следующий
член получается из
предыдущего
умножением на одно
и тоже число q,
называется
геометрической
прогрессией.
Число d –
называется
разностью
Число q –
называется
знаменателем
арифметической геометрической
прогрессии.
прогрессии.

7. Обозначение

Арифметическая
прогрессия
a
n
Геометрическая
прогрессия
b
n

8. Допустимые значения

Арифметическая
прогрессия
a1 , d
любые числа
Геометрическая
прогрессия
,
b1 q
числа неравные
нулю

9. Рекуррентная формула

Арифметическая
прогрессия
Геометрическая
прогрессия
an 1 an d
bn 1 bn q
n N
n N

10. Нахождение

разность
арифметической
прогрессии
d a n 1 a
n
знаменатель
геометрической
прогрессии
q
b
b
n 1
n
n N
n N

11. Используя рекуррентную формулу, получим формулу общего члена геометрической прогрессии.

b b q
b b q b q q b q
b b q b q q b q
b b q b q q b q
2
3
1
2
1
1
2
4
3
1
4
1
3
1
3
5
2
1
4
b
n
n 1
b1 b

13.

Формула n-го членаарифметическая
прогрессия
геометрическая
прогрессия
an a1 d n 1 bn b1 b
n 1
n N
n N

14. Характеристическое свойство

арифметическая
прогрессия
a
n
a
n 1
a n 1
геометрическая
прогрессия
b
b
n
n 1 bn 1
2
или
2
n N
b
n
b b
n 1
n N
n 1

15. Геометрическая прогрессия в геометрии:

16. Решение задач

17. Задача 1

Найдите первые 5 членов
геометрической прогрессии , если
первый член -2, а знаменатель -0.5.
Ответ: -2; 1; -0,5; 0,25; — 0,125

18. Задача 2.

В правильный треугольник, сторона
которого равна 16 см, вписан второй
треугольник так, что его вершинами
являются середины сторон первого. Во
второй треугольник таким же способом
вписан третий и т.д. Найдите периметр
пятого треугольника.
Ответ: 3 см.

20. Задача 3 (решить двумя способами)

Найдите знаменатель геометрической
прогрессии, если ее четвертый член
25, а шестой член 16.
4
4
Ответ:
;
5
5

21. Задача 4.

1
Между числами
и 27 вставьте
9
четыре числа, чтобы получилась
геометрическая прогрессия.
Найдите эти числа.
1
Ответ:
; 1; 3; 9
3

22. Задача 5.

Дана геометрическая прогрессия (bn),
1
b
4
b5 216
в которой
и
b
2
b6 4
Найти первый член геометрической
прогрессии.
Ответ: 12 или
15
3
7

English     Русский Правила

Геометрическая прогрессия | План-конспект урока по алгебре (9 класс):

Тема: Геометрическая прогрессии

I. Цель урока: формирование  умений решать задачи с применением геометрической прогрессии

II. Задачи урока:

Образовательные: сформировать навыки решения типовых задач (нахождение n – го члена, знаменателя геометрической прогрессии, задавать геометрическую прогрессию)

Развивающие:

• Развивать навыки сравнения, анализа.
• Развивать коммуникативные способности детей, развивать математическую речь.
• Формировать у учащихся навыки первичного самоконтроля.
• Использование метапредметных связей через исторический экскурс

Воспитательные:

• Воспитывать культуру математического мышления
• Развитие ключевых компетенций (коммуникативной, информационной, самоорганизации, самообразования)

Организация продуктивной деятельности школьников, направленной на достижение ими следующих результатов:

1. личностных:

• уверенно и грамотно выражать свои мысли на математическом языке и языке формул;
• не боятся ошибок, развивать умение отстаивать свое мнение.

2. метапредметных:

освоение способов деятельности:

• познавательной

• структурирование объекта познания;
• сравнение, сопоставление, классификация  объектов по одному или нескольким признакам;

• коммуникативной

• умение вступать в речевое общение, участвовать в диалоге;
• проведение информационно-смыслового анализа текста;

• рефлексивной

• самостоятельная организация учебной деятельности;
• оценивание своих учебных достижений.

III. Урок систематизации и закреплении знаний.

Ход урока

1. Организационный момент

2. Мотивация учебной деятельности; сообщение темы, цели и задач урока

Эпиграфом нашего урока будут слова известного математика А.Н. Колмогорова

 « Математические знания могут применяться умело с пользой лишь в том случае, если они усвоены творчески».

Дорогой друг!

    Сегодня у тебя необычный урок математики. Сегодня ты еще раз убедишься в том, что математика не только интересна сама по себе, но она необычайно полезна. В ходе сегодняшнего урока тебя ожидает большая радость творчества и огромное поле приложения математических знаний и умений.     Желаю тебе успехов и творческих  радостей на уроке!

Мы изучаем тему «Последовательности». Изучили арифметическую прогрессию, ещё какая тема ОГЭ осталась? Да, это тема « Геометрическая прогрессия»

Запишите, пожалуйста, тему урока…

Какая же будет цель нашего сегодняшнего урока?

Цель: изучить геометрическую прогрессию

Какие задачи надо поставить перед собой, чтобы эту цель достичь?

Задачи: научиться решать задачи по данной теме  (может быть вариант: мы должны разобраться, какими свойствами обладают её члены; может быть почему её так назвали и др. )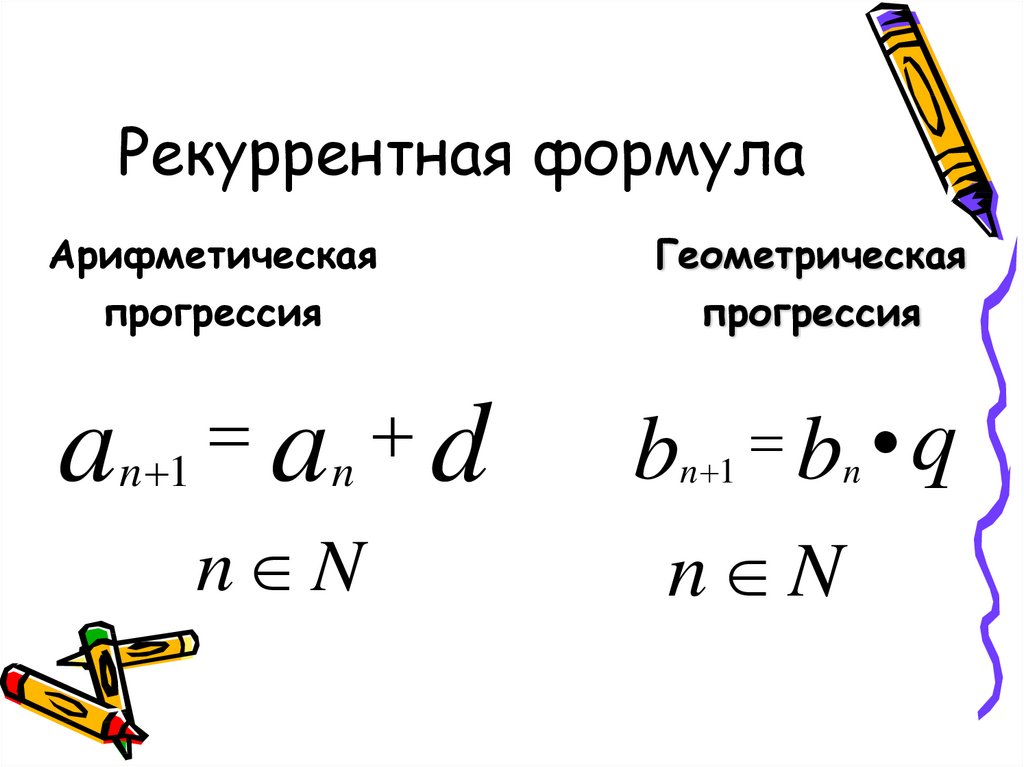

3. Актуализация знаний: проверка творческого домашнего задания

4. Открытие новых знаний (закрепление материала + изучение через проблемную ситуацию)

Но в начале  познакомься с легендой о шахматной доске. Чтобы понять ее, вовсе не нужно уметь играть в шахматы: достаточно знать, что игра происходит на доске, разграфленной на 64 клетки (попеременно черные и белые).

Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений.  Узнав, что она изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку. Изобретатель, его звали Сета, явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.

-Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал, -сказал царь.

   Мудрец поклонился.

   -Я достаточно богат, чтобы исполнить самое смелое твое пожелание, — продолжал царь. — Назови награду, которая тебя удовлетворит, и ты получишь ее.

   Сета молчал.

   -Не робей, — ободрил его царь. – Выскажи свое желание. Я не пожалею ничего, чтобы исполнить его.

   -Велика доброта твоя, повелитель. Но дай срок обдумать ответ. Завтра я сообщу тебе мою просьбу.

Когда на другой день Сета снова явился к ступеням трона, он удивил царя беспримерной скромностью своей просьбы.

  -Повелитель, — сказал Сета, — прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.

  -Простое пшеничное зерно? – изумился царь.

  -Да, повелитель. За вторую клетку прикажи выдать 2 зерна,  за третью — 4, за четвертую — 8, за пятую — 16, за шестую -32…

   -Довольно, — с раздражением прервал его царь. – Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию: за каждую вдвое больше против предыдущей. Но знай, что просьба твоя недостойна моей щедрости. Прося такую ничтожную награду, ты непочтительно пренебрегаешь моей милостью.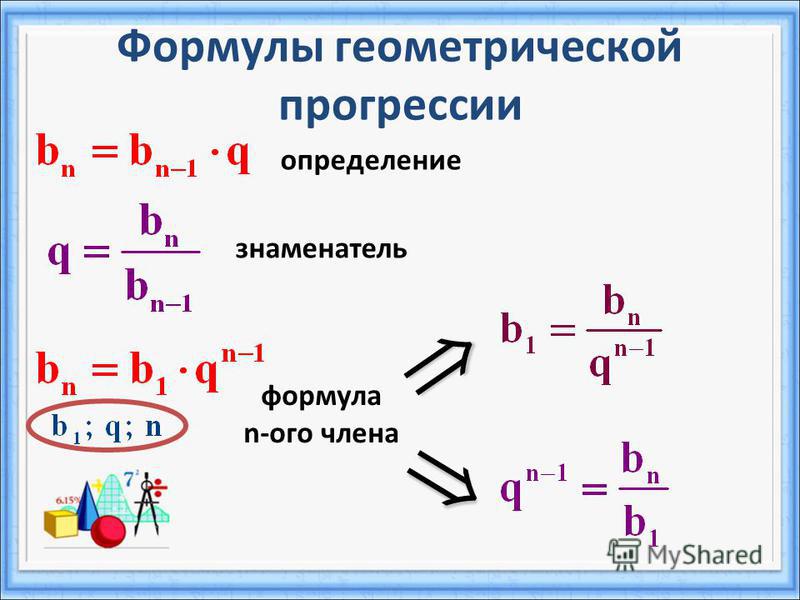 Ступай. Слуги мои вынесут тебе твой мешок с пшеницей.

Сета улыбнулся хитро, покинул дворец и стал дожидаться  у ворот дворца.

Почему так хитро улыбнулся Сета?

   Прав ли был индусский царь, считая просьбу Сеты ничтожной, полагая, что все зерна пшеницы уместятся в один мешок?

   Об этом ты узнаешь чуточку позже.

   А сейчас поподробнее рассмотрим последовательность чисел, соответствующих количеству зерен пшеницы, если, как попросил Сета, за каждую следующую клетку нужно дать вдвое больше, чем было в предыдущей.

 Получается последовательность: 1, 2, 4, 8, 16, 32, 64,…. (запиши ее в тетрадь)

      Запиши еще одну последовательность: 2, 6, 18, 54, 162, ….

   Члены этой последовательности, начиная со второго, получаются путем умножения предыдущего на 3.

Приведенные примеры последовательностей являются геометрическими прогрессиями.

   А теперь попробуй сформулировать определение геометрической прогрессии. Замечание: члены прогрессии должны быть отличны от нуля!

Определение: Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

   Обозначим, например, через (bn) — геометрическую прогрессию, тогда по определению

bn+1= bn⋅q, где  bn ≠0, n  — натуральное число, q  — некоторое число.

   Из определения геометрической прогрессии следует, что отношение любого ее члена, начиная со второго, к предыдущему члену равно q, т.е.

bn+1/ bn = q

   Число q  называют знаменателем геометрической прогрессии. Очевидно, что q ≠ 0.

Выполни самостоятельно:

Найти знаменатель геометрической прогрессии:

 а) 3; 6; 12; 24;…

 б) 3; 3; 3; 3; …..

 в)1; 0,1; 0,01; 0,001;…

Проверь себя!

      а) q = 2          б) q = 1          в) q = 0,1

    Ошибок нет?  Молодец!     Если есть неправильные ответы, обратись к учителю.

    По аналогии с арифметической прогрессией, выводится формула n-го члена геометрической  прогрессии.  Пусть b1 – первый член геометрической прогрессии, q – знаменатель, тогда:

                    b2 = b1 ·q

                    b3 = b2 · q = (b1 · q) · q = d1 · q2

                    b4 = b3 · q = (b1 · q2) · q = b1 · q3

                    b5 = ………………. .= b1 · q4

  Продолжи эту цепочку рассуждений в тетради и вырази bn через b1 и q.

Проверь себя!

  bn=b1• qn-1 –формула  n-го члена геометрической прогрессии. ( правильно, то 1 балл)

Эта формула используется для решения многих задач. Рассмотри примеры решения некоторых задач.

5. Закрепление

 1. В геометрической прогрессии (bn) известны

b1 =-2 и q = 3, найти: b3, b4

Решение:

        b3 = b1 • q2 = -2· 32 = -18

             b4 = b1 • q3 = -2· 33 = -54  (1 балл)

 2.Найти пятый член геометрической прогрессии (bn):-20; 40; ….

Решение: Найдем знаменатель, для этого нужно 40 разделить на -20, получится q = -2.

b5 = b1• q4 = -20 • (-2)4 = -20 • 16 = -320 (1 балл)

6. Самостоятельная работа обучающего характера

     Выполни самостоятельно:

  В геометрической прогрессии (xn) найти:

 а) x5, если x1 = 16; q = ½

 б) x3, если x1 = 3/4; q = 2/3.

 в) x10, если x1 = 48; q = -1.

Проверь себя!

   а) x5 = 1  (1 балл)

   б) x3 = 1/3 (1 балл)

   в) x10 = -48 (1 балл)

  Если ты испытывал затруднения, обратись к учителю.

Итак, просьба мудрого Сеты помогла тебе понять определение геометрической прогрессии, и теперь настало время узнать что-же было дальше….

За обедом царь вспомнил об изобретателе шахмат и послал узнать, унес ли Сета свою жалкую награду.

   -Повелитель, — ответили ему, — математики твои трудятся без устали и надеются еще до рассвета закончить подсчет.

Утром царю доложили, что старшина придворных математиков просит выслушать важное донесение.

  Царь приказал ввести его.

– Мы добросовестно исчислили все количество зерен, которое желает получить Сета. Число это так велико…..

-Как бы велико оно ни было, — надменно перебил царь, — житницы мои не оскудеют. Награда обещана и должна быть выдана..

   — Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зерен, которое потребовал Сета. Нет его и в житницах целого царства. Не найдется такого числа зерен и на всем пространстве Земли. И если желаешь непременно выдать обещанную награду, то прикажи превратить земные  царства в пахотные поля, прикажи осушить моря и океаны, прикажи растопить льды и снега, покрывающие далекие северные пустыни.

С изумлением внимал царь словам старца.

     — Назови мне это чудовищное число, сказал он в раздумьи.  

18 446 744 073 709 551 615

-Восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот сорок четыре триллиона семьдесят три биллиона семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать, о повелитель!

Масса такого числа зерен больше триллиона тонн.    Индусский царь не в состоянии был выдать подобной награды.    Но будь он силен в математике, он бы не попал впросак…

Подведение итогов (самопроверка) Слайд

Самооценка

6б      – «5»

5б      – «4»

3 – 4б – «3»

7. Итог урока.

Домашнее задание.

Д.З.: п.8.1 учебника повторить,

№480, №481(г,д,з)

Творческое задание: №12 из «Распечатай и реши» 5 задач на нахождение членов геометрической прогрессии

Итак, урок приближается к концу: – Дополните фразы:

Сегодня на уроке я….

– узнал…

– учился…

–…

Урок сегодня завершён,
Но каждый должен знать:
Познание, упорство, труд
К прогрессу в жизни приведут!

Я желаю, чтобы агеометрические прогрессии и вообще математика вели по жизни вас только вперёд! Я благодарю всех за работу! Мне было приятно с вами общаться! Досвидания! 

Геометрическая прогрессия Определение и значение

• Основные определения
• Тест
• Примеры
• Британский
• Научный
• Культурный

Показывает уровень сложности слова на основе уровня сложности.

Сохрани это слово!

Показывает уровень оценки в зависимости от сложности слова.

---

сущ. Математика.

последовательность терминов, в которой соотношение между любыми двумя последовательными терминами такое же, как в последовательности 1, 3, 9, 27, 81 или 144, 12, 1, 1/12, 1/144.

ВИКТОРИНА

ВЫ ПРОЙДЕТЕ ЭТИ ГРАММАТИЧЕСКИЕ ВОПРОСЫ ИЛИ НАТЯНУТСЯ?

Плавно переходите к этим распространенным грамматическим ошибкам, которые ставят многих людей в тупик. Удачи!

Вопрос 1 из 7

Заполните пропуск: Я не могу понять, что _____ подарил мне этот подарок.

Также называется геометрическим рядом.

Происхождение геометрической прогрессии

Впервые записано в 1550–1560 гг.

Слова рядом с геометрической прогрессией

геометр, геометрический изомер, геометризировать, среднее геометрическое, геометрический темп, геометрическая прогрессия, геометрическое соотношение, геометрия, геометрический ряд, геометрид, геометризировать

Dictionary. com Unabridged На основе Random House Unabridged Dictionary, © Random House, Inc. 2023

Как использовать геометрическую прогрессию в предложении

• Однако на своем собственном пути «всезнайка в отношениях» идет своим путем, различное естественное развитие.

  Признания сценариста романтической комедии: Лиз Туччилло рассказывает о «Сексе в большом городе», «Береги себя» и многом другом|Кевин Фэллон|5 декабря 2014 г.|DAILY BEAST

• [Я] должен был создать развитие своего эмоционального состояния.

  The Daily Beast: Von Trier рассказывает о девушке по имени Джо, которая проходит путь от подросткового возраста до взрослой жизни.

  Эксперт по сексуальной зависимости диагностирует «нимфоманку» Ларса фон Триера|Лиззи Крокер|23 марта 2014 г.|DAILY BEAST

• Изделия создавали легкий камуфляж, используя кружево, геометрические узоры и цветы для создания ультралегкой ткани.

  Валентино, Шанель и Александр МакКуин на Неделе моды в Париже|Лиза Форман|4 марта 2014 г. |DAILY BEAST

• Я всегда любила одежду и моду, и это был естественный прогресс с открытием магазина и теперь это.

  Модные секреты «настоящей домохозяйки»|Эрин Каннингем|24 февраля 2014 г.|DAILY BEAST

• Гибнущая формация теряет моральную силу в более быстром прогрессе, чем простая потеря членов, казалось бы, оправдана.

  Дневник Галлиполи, том I|Иан Гамильтон

• Если бы у нее не было трех любовных романов, находящихся на разных, но обнадеживающих стадиях развития, под ее крышей и под ее покровительством!

  At Last|Marion Harland

• Ряд, рассматриваемый в тексте, согласуется с этой линейной прогрессией ни в чем, кроме того, что является прогрессией.

  Система логики: рациональная и индуктивная|Джон Стюарт Милль

• Результат оказался для турок довольно плохим; они упали, как множество кеглей, перед железнодорожной прогрессией Крота.

  Мальчик-мастер Джека Харкавея среди турок|Брейсбридж Хеминг

• От древнего форта на мысе до Каса-Бланки и города за его пределами это был череда восхитительных зрелищ и звуков.

  Gardens of the Caribbees, v. 1/2|Ida May Hill Starr

Определения геометрической прогрессии из Британского словаря

геометрическая прогрессия

---

существительное

последовательность чисел, каждое из которых отличается от последующего постоянным отношением, как 1, 2, 4, 8, … Сравните арифметическую прогрессию

Английский словарь Коллинза — полное и полное цифровое издание 2012 г. © William Collins Sons & Co. Ltd., 1979, 1986 © HarperCollins Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012

Научные определения геометрической прогрессии

геометрическая прогрессия

---

Последовательность чисел, в которой каждое число умножается на тот же коэффициент для получения следующего числа в последовательность. В геометрической прогрессии отношение любых двух соседних чисел одинаково. Например, 5, 25, 125, 625, … , где каждое число умножается на 5, чтобы получить следующее число, а отношение любого числа к следующему числу всегда равно 1 к 5.

Сравните арифметическую прогрессию.

Научный словарь American Heritage® Авторские права © 2011. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.

Культурные определения геометрической прогрессии

геометрическая прогрессия

---

В математике — последовательность чисел, в которой каждое число получается из предыдущего путем умножения на константу. Например, последовательность 1, 2, 4, 8, 16, 32… (в которой каждое число умножается на 2, чтобы получить следующее) является геометрической прогрессией.

примечания для геометрической прогрессии

Многие процессы, связанные с ростом и распространением, такие как увеличение населения, можно описать как геометрическую прогрессию.

Новый словарь культурной грамотности, третье издание Авторское право © 2005 г., издательство Houghton Mifflin Harcourt Publishing Company. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.

Что такое геометрическая прогрессия?

10 декабря 2020 г. от Prasanna

Геометрическая прогрессия (ГП)

Определение:
Прогрессия называется ГП. если отношение каждого его члена к предыдущему члену всегда постоянно. Это постоянное отношение называется обыкновенным отношением и обычно обозначается буквой r.

Пример:

Общий термин G.P.

(1) Мы знаем, что a, ar, ar ² , ar ³ , ……. ar ^{n − 1} — последовательность G.P.
Здесь первый член равен ‘ a ’, а обыкновенное отношение равно ‘ r ’.
Общий термин или n ^th термин G. P. это T _n = ar ^{n − 1} .

(2) р ^й член с конца конечной Г.П. : Если Г.П. состоит из ‘ n ’ терминов, p ^й термин с конца = (n – p + 1) ^й термин с начала = ar ^n–p .
Кроме того, термин p ^th с конца G.P. с последним членом l и обыкновенным отношением r равно

Подбор терминов в Г.П.

(1) Когда продукт дан, используется следующий способ выбора определенного количества терминов:

(2) Когда продукт не дается, тогда используется следующий способ выбора терминов

Количество терминов	Термины, которые необходимо принять
3	a, ar, ar 2
4	a, ar, ar 2 , ar 3
5	a, ar, ar 2 , ar 3 , ar 4

Сумма первых ‘n’ членов G.

P.

Если a — первый член, r — знаменатель, то сумма первых n членов G.P. определяется как

Сумма бесконечных членов Г.П.

Среднее геометрическое

Свойства Г.П.

1. Если все условия G.P. если его умножить или разделить на ту же ненулевую константу, то он останется GP с тем же обыкновенным отношением.
2. Обратная величина терминов данного G.P. сформировать Г.П. с обыкновенным отношением, обратным общему отношению исходного G.P.
3. Если каждый член G.P. при возведении знаменателя r в ту же степень k результирующая последовательность также образует G.P. с обыкновенным отношением r ^к .
4. В конечном ТП произведение членов, равноудаленных от начала и конца, всегда одно и то же и равно произведению первого и последнего членов. т. е. если a ₁ , a ₂ , a ₃ , …… a _n находятся в G.P.
   Затем A ₁ A _N = A ₂ A _N-1 = A ₃ A _N-2 = A ₄ A _N-2 = A ₄ A _N-2 = A ₄ A _N-2 = ₄ A _N-2 =
   4 A _N-2 = ₄ . _n-r+1
5. Если условия данного G.P. выбираются через равные промежутки времени, то сформированная таким образом новая последовательность также образует Г.П.
6. Если a ₁ , a ₂ , a ₃ , …… a _n  является G.P. ненулевых, неотрицательных терминов, затем log a ₁ , log a ₂ , log a ₃ , …… log a _n  является AP и наоборот.
7. Три ненулевых числа a, b, c находятся в GP, тогда и только тогда, когда b ² = ac.
8. Если первый срок G.P. из n членов есть a, а последний член равен l, то произведение всех членов G.P. (ал) ^н/2 .
9. Если в G.P. знаменатель которого равен r и S _m  обозначает сумму первых m слагаемых, тогда сумма их произведения, взятая два на два, равна \(\frac { r }{ r+1 } { S }_{ n }{ S }_{ n-1 }\).
10. If a ^x1 , a ^x2 , a ^x3 , ……, a ^xn  are in G.

    No related posts.