Курс математического анализа
Курс математического анализа
ОглавлениеПРЕДИСЛОВИЕГлава 1. ВВЕДЕНИЕ § 1.2. Множество. Интервал, отрезок § 1.3. Функция § 1.4. Понятие непрерывности функции § 1.5. Производная § 1.6. Первообразная. Неопределенный интеграл § 1.7. Понятие определенного интеграла. Площадь криволинейной фигуры Глава 2. ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО § 2.1. Рациональные и иррациональные числа § 2.2. Определение неравенства § 2.3. Основная лемма. Определение арифметических действий § 2.4. Основные свойства действительных чисел § 2.5. Изоморфизм различных представлений действительных чисел. Физические величины § 2.6. Неравенства для абсолютных величин § 2.7. Точные верхняя и нижняя грани множества § 2.8. Символика математической логики Глава 3. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ § 3.1. Понятие предела последовательности § 3.2. Арифметические действия с пределами § 3.3. Бесконечно малая и бесконечно большая величины § 3.  b b§ 4.8. Еще о числе е § 4.9. lim sin oo/oo § 4.10. Порядок переменной, эквивалентность (асимптотика) Глава 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ДЛЯ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ § 5.1. Производная § 5.2. Дифференциал функции § 5.3. Производная функции от функции § 5.4. Производная обратной функции § 5.6. Производные и дифференциалы высшего порядка § 5.7. Возрастание и убывание функции на интервале и в точке. Локальный экстремум § 5.8. Теоремы о среднем значении. Критерии возрастания и убывания функции на интервале. Достаточные критерии локальных экстремумов § 5.9. Формула Тейлора § 5.10. Формулы Тейлора для важнейших элементарных функций § 5.11. Ряд Тейлора § 5.12. Выпуклость кривой в точке. Точка перегиба § 5.13. Выпуклость кривой на отрезке § 5.14. Раскрытие неопределенностей § 5.16. Схема построения графика функции § 5.17. Кусочно непрерывные и кусочно гладкие функции Глава 6. n-МЕРНОЕ ПРОСТРАНСТВО.  ГЕОМЕТРИЯ КРИВОЙ ГЕОМЕТРИЯ КРИВОЙ§ 6.1. n-мерное пространство. Линейное множество § 6.2. Евклидово n-мерное пространство. Пространство со скалярным произведением § 6.3. Линейное нормированное пространство § 6.4. Вектор-функция в n-мерном евклидовом пространстве § 6.5. Непрерывная кривая. Гладкая кривая § 6.6. Геометрический смысл производной вектор-функции § 6.7. Длина дуги кривой § 6.8. Касательная § 6.9. Основной триэдр кривой § 6.10. Соприкасающаяся плоскость § 6.11. Кривизна и радиус кривизны кривой § 6.12. Эволюта § 6.13. Формулы Френе. Свойства эволюты Глава 7. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ § 7.1. Открытое множество § 7.2. Предел функции § 7.3. Непрерывная функция § 7.4. Частные производные и производная по направлению § 7.5. Дифференцируемая функция. Касательная плоскость § 7.6. Производная сложной функции. Производная по направлению. Градиент § 7.7. Независимость от порядка дифференцирования § 7.  8. Дифференциал функции. Дифференциал высшего порядка 8. Дифференциал функции. Дифференциал высшего порядка§ 7.9. Теорема Больцано-Вейерштрасса § 7.10. Замкнутые и открытые множества § 7.11. Функции на множестве. Свойства непрерывных функций на замкнутом ограниченном множестве § 7.12. Лемма о вложенных прямоугольниках и лемма Бореля § 7.13. Формула Тейлора § 7.14. локальный (абсолютный) экстремум функции § 7.15. Теоремы существования неявной функции § 7.16. Теорема существования решения системы уравнений § 7.17. Отображения § 7.18. Гладкая поверхность § 7.19. Дифференциалы неявных функций. Линеаризация § 7.20. Локальный относительный экстремум § 7.22. Система зависимых функций Глава 8. НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ. АЛГЕБРА МНОГОЧЛЕНОВ § 8.1. Введение. Методы замены переменной и интегрирования по частям § 8.2. Комплексные числа § 8.3. Комплексные функции § 8.4. Многочлены § 8.5. Разложение рациональной функции на простейшие дроби § 8.  6. Интегрирование рациональных дробей 6. Интегрирование рациональных дробей§ 8.7. Интегрирование алгебраических иррациональностей § 8.8. Подстановки Эйлера § 8.9. Биномиальные дифференциалы. Теорема Чебышева § 8.10. Интегрирование тригонометрических выражений § 8.11. Тригонометрические подстановки § 8.12. Несколько важных интегралов, не выражаемых в элементарных функциях Глава 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ РИМАНА § 9.2. Ограниченность интегрируемой функции § 9.3. Суммы Дарбу § 9.4. Основная теорема § 9.5. Теоремы о существовании интеграла от непрерывной и монотонной функции на [a, b] § 9.6. Аддитивные и однородные свойства интеграла § 9.7. Неравенства и теорема о среднем § 9.8. Интеграл как функция верхнего предела. Теорема Ньютона-Лейбница § 9.9. Вторая теорема о среднем § 9.10. Видоизменение функции § 9.11. Несобственные интегралы § 9.12. Несобственные интегралы от неотрицательных функций § 9.13. Интегрирование по частям § 9.14. Несобственный интеграл и ряд § 9.  15. Несобственные интегралы с особенностями в нескольких точках 15. Несобственные интегралы с особенностями в нескольких точках§ 9.16. Формула Тейлора с остатком в интегральной форме § 9.17. Формулы Валлиса и Стирлинга Глава 10. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛОВ. ПРИБЛИЖЕННЫЕ МЕТОДЫ § 10.1. Площадь в полярных координатах § 10.2. Объем тела вращения § 10.3. Длина дуги гладкой кривой § 10.5. Интерполяционный многочлен Лагранжа § 10.6. Квадратурные формулы прямоугольников § 10.7. Формула Симпсона Глава 11. РЯДЫ § 11.1. Понятие ряда § 11.2. Действия с рядами § 11.3. Ряды с неотрицательными членами § 11.4. Ряд Лейбница § 11.5. Абсолютно сходящиеся ряды § 11.6. Условно и безусловно сходящиеся ряды с действительными членами § 11.7. Последовательности и ряды функций. Равномерная сходимость § 11.8. Интегрирование и дифференцирование равномерно сходящихся рядов на отрезке § 11.9. Кратные ряды. Перемножение абсолютно сходящихся рядов § 11.  z, cos z, sinz комплексной переменной z, cos z, sinz комплексной переменнойГлава 12. КРАТНЫЕ ИНТЕГРАЛЫ § 12.2. Мера Жордана § 12.3. Важные примеры квадрируемых по Жордану множеств § 12.4. Еще один критерий измеримости множества. Полярные координаты § 12.5. Другие случаи измеримости § 12.6. Понятие кратного интеграла § 12.7. Верхняя и нижняя интегральные суммы. Основная теорема § 12.8. Интегрируемость непрерывной функции на замкнутом измеримом множестве. Другие критерии § 12.9. Свойства кратных интегралов § 12.10. Сведение кратного интеграла к интегрированию по отдельным переменным § 12.11. Непрерывность интеграла по параметру § 12.12. Геометрическая интерпретация знака определителя § 12.13. Замена переменных в кратном интеграле. Простейший случай § 12.14. Замена переменных в кратном интеграле § 12.15. Доказательство леммы 1 § 12.14 § 12.16. Полярные координаты в плоскости § 12.17. Полярные и цилиндрические координаты в пространстве § 12.18. Гладкая поверхность § 12.  19. Площадь поверхности 19. Площадь поверхностиГлава 13. ТЕОРИЯ ПОЛЯ. ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ ПО ПАРАМЕТРУ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ § 13.2. Криволинейный интеграл второго рода § 13.3. Поле потенциала § 13.4. Ориентация плоской области § 13.5. Формула Грина. Выражение площади через криволинейный интеграл § 13.6. Интеграл по поверхности первого рода § 13.7. Ориентация поверхностей § 13.8. Интеграл по ориентированной плоской области § 13.9. Поток вектора через ориентированную поверхность § 13.10. Дивергенция. Теорема Гаусса-Остроградского § 13.11. Ротор вектора. Формула Стокса § 13.12. Дифференцирование интеграла по параметру § 13.13. Несобственный интеграл § 13.14. Равномерная сходимость несобственного интеграла § 13.15. Равномерно сходящийся интеграл для неограниченной области Глава 14. ЛИНЕЙНЫЕ НОРМИРОВАННЫЕ ПРОСТРАНСТВА. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ § 14.2. Пространство L'(L) § 14.3. Пространство L2 (L2) § 14.  4. Пространство … 4. Пространство …§ 14.5. Полнота системы элементов в банаховом пространстве § 14.6. Ортогональная система в пространстве со скалярным произведением § 14.7. Ортогонализация системы § 14.8. Полнота системы функций в … Глава 15. РЯДЫ ФУРЬЕ. ПРИБЛИЖЕНИЕ ФУНКЦИЙ ПОЛИНОМАМИ § 15.2. Сумма Дирихле § 15.3. Формулы для остатка ряда Фурье § 15.4. Теоремы об осцилляции § 15.5. Критерий сходимости рядов Фурье. Полнота тригонометрической системы функций § 15.6. Комплексная форма записи ряда Фурье § 15.7. Дифференцирование и интегрирование рядов Фурье § 15.8. Оценка остатка ряда Фурье § 15.9. Алгебраические многочлены. Многочлены Чебышева § 15.10. Теорема Вейерштрасса § 15.11. Многочлены Лежандра Глава 16. ИНТЕГРАЛ ФУРЬЕ. ОБОБЩЕННЫЕ ФУНКЦИИ § 16.1. Понятие интеграла Фурье § 16.2. Сходимость простого интеграла Фурье к порождающей его функции § 16.3. Преобразование Фурье. Повторный интеграл Фурье. Косинус- и синус-преобразования Фурье  {2} + 2x > 4x + 5\). {2} + 2x > 4x + 5\).В таком случае говорят о множестве решений неравенства, то есть о всех значениях переменной, для которой данное неравенство выполняется (в некоторых случаях это множество может состоять из одной точки или вообще быть пустым). ОБОЗНАЧЕНИЕ НЕРАВЕНСТВ: Неравенства можно обозначать четырьмя способами:
Если неравенство строгое, то граничная точка в решение не входит (поэтому ее «выкалывают» на координатной оси). ДВОЙНЫЕ НЕРАВЕНСТВА: Виды двойных неравенств не отличаются от видов обыкновенных, разница лишь в том, что промежуток обозначается уже двумя числами, а не одним. Например: \(1 < x \leq 4\) Эта запись обозначает, что x больше 1 и при этом меньше либо равно 4. 1. Числовой промежуток будет записываться в соответствии со строгостью знаков к определенным числам. Скобка возле числа 1 будет круглой, а возле числа 4 – квадратной: \(x \in (1;4\rbrack\) 2. Аналогично строгости знаков и виду скобок на числовой прямой будут закрашены или не закрашены точки. Число 1 будет отмечаться выколотой точкой, а число 4 закрашенной. Тогда на координатной прямой это двойное неравенство будет выглядеть так: ПРАВИЛА ПРЕОБРАЗОВАНИЯ НЕРАВЕНСТВ: 1. Любое слагаемое в неравенстве можно перенести из одной части уравнения в другую, изменив его знак на противоположный: \({x + 5 > 0 }{x > \ –5}\) 2. Можно умножать и делить левую и правую части уравнения на одно и то же положительное число: \({2y > \left. \ 16 \right| : 2 }{y > 8}\) 3. Можно умножать и делить левую и правую части уравнения на одно и то же отрицательное число, заменяя при этом знак неравенства на противоположный: \({–\frac{t}{2} \leq \left. 4. Для двойных неравенств соблюдаются те же правила, с разницей в том, что алгебраические преобразования производятся сразу над всеми его частями: \({2 \leq x + 5 \leq 8 }{–3 \leq x \leq 3}\) 5. Как и в уравнениях можно раскрывать скобки и упрощать выражения во всех частях неравенства или, наоборот, раскладывать на множители. Пример 1: Решить неравенство: \(5(1\ –\ x) < 12\) 1. Преобразуем неравенства так, чтобы с одной стороны было только выражение, содержащее переменную, а с другой только число: \(5(1\ –\ x) < 12\) \(5\ –\ 5x < 12\) \(–5x < 7\) 2. Делим на коэффициент перед переменной, при необходимости меняя знак на противоположный: \(–5x < \left. \ 7 \right| : (–5)\) \(x > \ –1,4\) Ответ: \(x \in (–1,4; + \infty)\). определение неравенства | Open Education Sociology DictionaryHome > I Words > неравенство Table of Contents Определение неравенства ( существительное ) Неравномерное и несправедливое распределение возможностей, престижа и вознаграждения для отдельных лиц или групп; социальное неравенство. Виды неравенства
Неравенство произношениеРуководство по использованию произношения СИЛЛИФИКАЦИЯ: в · E · Qual · I · TY 9000 9000 9000 9000. Audio— Американец 9000.9000 9000..Фонетическое правописание
Международный фонетический алфавит
Использование
Связанные видеоyoutube.com/embed/zBodqwAlW3A?start=351&feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»> youtube.com/embed/c8PEv5SV4sU?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>6.RINGINGIMIRIMIRIMON
 Связанные терминыПримечание: читайте бесплатно в открытой библиотеке. Дэвис, Кингсли и Уилберт Э. Мур. 1945. «Некоторые принципы стратификации». American Sociological Review 10(2):242–49. Хаухарт, Роберт С. 2003. «Теория стратификации Дэвиса-Мура: жизненный путь социально сконструированного классика». Американский социолог 34(4):5–24. doi:10.1007/s12108-003-1013-y. Хьюз, Майкл и Кэролин Дж. Кролер. 2008. Социология: ядро . 8-е изд. Бостон: Макгроу-Хилл. Кендалл, Диана. 2011. Социология в наше время . 8-е изд. Белмонт, Калифорния: Уодсворт. Макионис, Джон. 2012. Социология . 14-е изд. Река Аппер-Сэдл, Нью-Джерси: Пирсон/Прентис Холл. Маргер, Мартин. 1985. Расовые и этнические отношения: американские и глобальные перспективы . Белмонт, Калифорния: Уодсворт. Макнами, Стивен Дж. и Роберт К. Миллер-младший. 2013. Миф о меритократии . 3-е изд. Лэнхэм, Мэриленд: Роуман и Литтлфилд. Works ConsultedАберкромби, Николас, Стивен Хилл и Брайан Тернер. 2006. Социологический словарь Penguin . 5-е изд. Лондон: Пингвин. Брюс, Стив и Стивен Йерли. Диллон, Мишель. 2014. Введение в социологическую теорию: теоретики, концепции и их применимость в двадцать первом веке . 2-е изд. Молден, Массачусетс: Уайли-Блэквелл. Британская энциклопедия. (N.d.) Цифровое обучение Britannica . (https://britannicalearn.com/). Джари, Дэвид и Джулия Джари. 2000. Социологический словарь Коллинза . 3-е изд. Глазго, Шотландия: HarperCollins. Корнблюм, Уильям. 2008. Социология в меняющемся мире . 8-е изд. Белмонт, Калифорния: Уодсворт. Макмиллан. (Nd) Словарь Macmillan . (https://www.macmillandictionary.com/). Марш, Ян и Майк Китинг, ред. 2006. Социология: осмысление общества . 3-е изд. Харлоу, Англия: Pearson Education. Издательство Оксфордского университета. (Nd) Оксфордские словари . (https://www.oxforddictionaries.com/). Издательство Оксфордского университета. Ритцер, Джордж, изд. 2007. Социологическая энциклопедия Блэквелла . Молден, Массачусетс: Блэквелл. Скотт, Джон и Гордон Маршаллы. 2005. Социологический словарь . Нью-Йорк: Издательство Оксфордского университета. Столли, Кэти С. 2005. Основы социологии . Вестпорт, Коннектикут: Greenwood Press. Тейлор и Фрэнсис. (N.d.) Справочники Routledge Online . (https://www.routledgehandbooks.com/). Тернер, Брайан С., изд. 2006. Кембриджский социологический словарь . Кембридж: Издательство Кембриджского университета. участников Википедии. (Nd) Википедия, Бесплатная энциклопедия . Фонд Викимедиа. (https://en.wikipedia.org/). Уайли. (N.d.) Интернет-библиотека Wiley . (http://onlinelibrary.wiley.com/). Приведите определение неравенстваASA – Американская социологическая ассоциация (5-е издание) Bell, Kenton, ed. АПА – Американская психологическая ассоциация (6-е издание) неравенство. (2018). В К. Белл (ред.), Открытый социологический словарь образования . Получено с https://sociologydictionary.org/inequality/ Чикаго / Turabian: Дата автора — Чикагское руководство по стилю (16-е издание) Bell, Kenton, ed. 2018. «неравенство». В Открытом образовательном социологическом словаре . По состоянию на 8 февраля 2023 г. https://sociologydictionary.org/inequality/. MLA – Ассоциация современного языка (7-е издание) «неравенство». Открытый образовательный социологический словарь . Эд. Кентон Белл. 2018. Интернет. 8 февраля 2023 г. Определение и значение неравенства | Dictionary.com.[ ин-и-квол-и-ти ] / ˌɪn ɪˈkwɒl ɪ ti / Сохранить это слово! См. Показывает уровень оценки в зависимости от сложности слова. существительное во множественном числе в·равенствах. условие неравенства; отсутствие равенства; несоответствие: неравенство размеров. Несоответствие или относительная недостаточность природных данных: поразительное неравенство интеллекта, талантов и физической выносливости. несправедливость; фаворитизм; пристрастность. неровности поверхности. экземпляр неровности. изменчивость климата. Астрономия. Математика. утверждение, что две величины не равны, обозначается символом ≠; в качестве альтернативы, символом <, означающим, что количество, предшествующее символу, меньше, чем последующее, или символом >, означающим, что количество, предшествующее символу, больше, чем следующее. ВИДЕО ДЛЯ НЕРАВЕНСТВАМы попросили этих людей объяснить самые грустные английские фразыНекоторые слова по своей сути грустные, а некоторые другие, в зависимости от контекста, могут быть еще более удручающими. Согласны ли вы со словами, которые эти люди считают самыми печальными? БОЛЬШЕ ВИДЕО НА DICTIONARY.COM ВИКТОРИНА ТЫ ПРОШЕШЬ ИЛИ НАТЯНУСЬ НА ЭТИ ВОПРОСЫ ПО ГРАММАТИКЕ? Плавно переходите к этим распространенным грамматическим ошибкам, которые ставят многих людей в тупик. Удачи! Вопрос 1 из 7 Заполните пропуск: Я не могу понять, что _____ подарил мне этот подарок. Происхождение неравенстваВпервые зафиксировано в 1375–1425 гг.; позднесреднеанглийское inequalite «неравномерность, несоответствие», от старофранцузского inequalite, от латинского inaequālitāt-основа inaequālitās «неравномерность, неравенство, непоследовательность»; см. происхождение в не- 3 , равенство Слова рядом с неравенствомнеописуемый, неумелый, неумелый, неумелый, неравный, неравенство, неравносторонний, несправедливый, неравенство, неэквивалентный, неистребимый Dictionary.com Полный текст На основе Random House Unabridged Dictionary, © Random House, Inc. 2023 Слова, относящиеся к неравенствупредвзятость, различие, дискриминация, неравенство, разнообразие, несправедливость, несправедливость, шероховатость, контраст, диспропорция, непохожесть, непохожесть, неравномерность, партийность , грубость, неравномерность, несправедливость, вариация, неравномерность, несоизмеримость Как использовать неравенство в предложении |



 \ 10 \right| \bullet \left( –2 \right) }{t \geq \ –20}\)
\ 10 \right| \bullet \left( –2 \right) }{t \geq \ –20}\)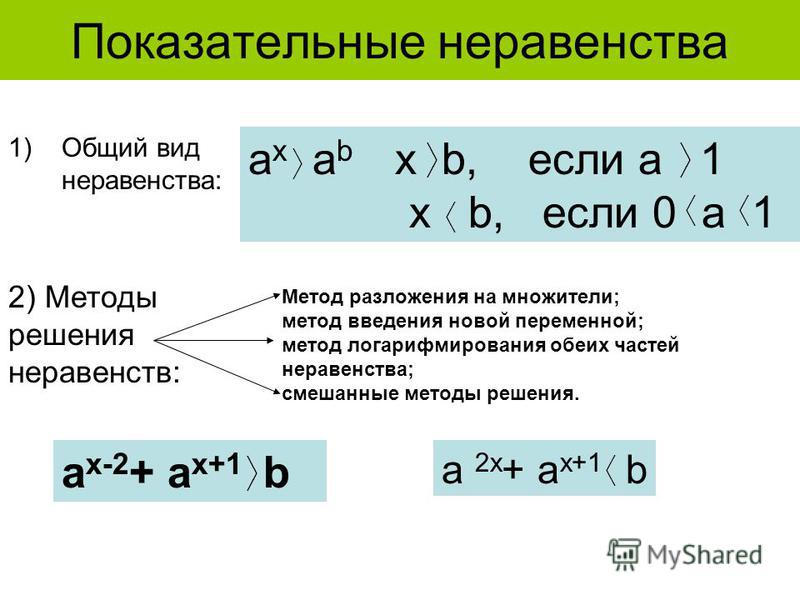

 Начиная со статьи [Мелвина] Тумина в 1953 году, теория Дэвиса-Мура вызывала регулярный анализ, комментарии, критику и дебаты на протяжении 1970-х годов. Хотя профессиональная работа над этой теорией практически прекратилась с конца 1980-х гг., теория Дэвиса-Мура остается, пожалуй, единственной наиболее широко цитируемой статьей в американских учебниках по вводной социологии и стратификации и является «обязательным к прочтению» сотнями, если не тысячами, студентов и студентов. курсы для выпускников по всей территории Соединенных Штатов» (Hauhart 2003:5).
Начиная со статьи [Мелвина] Тумина в 1953 году, теория Дэвиса-Мура вызывала регулярный анализ, комментарии, критику и дебаты на протяжении 1970-х годов. Хотя профессиональная работа над этой теорией практически прекратилась с конца 1980-х гг., теория Дэвиса-Мура остается, пожалуй, единственной наиболее широко цитируемой статьей в американских учебниках по вводной социологии и стратификации и является «обязательным к прочтению» сотнями, если не тысячами, студентов и студентов. курсы для выпускников по всей территории Соединенных Штатов» (Hauhart 2003:5). Эта структура обычно создавалась для белых мужчин из среднего и высшего среднего класса, которые в течение многих лет были преобладающими организационными участниками» (Kendall 2011:19).4).
Эта структура обычно создавалась для белых мужчин из среднего и высшего среднего класса, которые в течение многих лет были преобладающими организационными участниками» (Kendall 2011:19).4). Но поскольку давление и требования доминирующих групп в значительной степени опосредованы внутренней историей учебных заведений и потребностями и идеологиями людей, которые на самом деле в них работают, цели и результаты также часто будут противоречивыми» (Apple 19).90:x–xi).
Но поскольку давление и требования доминирующих групп в значительной степени опосредованы внутренней историей учебных заведений и потребностями и идеологиями людей, которые на самом деле в них работают, цели и результаты также часто будут противоречивыми» (Apple 19).90:x–xi). дои: 10.2307/2085643.
дои: 10.2307/2085643. 2006. Социологический словарь SAGE . Тысяча дубов, Калифорния: SAGE.
2006. Социологический словарь SAGE . Тысяча дубов, Калифорния: SAGE. (N.d.) Oxford Reference . (http://www.oxfordreference.com/).
(N.d.) Oxford Reference . (http://www.oxfordreference.com/). 2018. «неравенство». В Открытом образовательном социологическом словаре . Проверено 8 февраля 2023 г. (https://sociologydictionary.org/inequality/).
2018. «неравенство». В Открытом образовательном социологическом словаре . Проверено 8 февраля 2023 г. (https://sociologydictionary.org/inequality/). синонимы для: неравенство / неравенства на Thesaurus.com
синонимы для: неравенство / неравенства на Thesaurus.com


 |TechCrunch
|TechCrunch